| Order-5 dodecahedral honeycomb | |
|---|---|
 Perspective projection view from center of Poincaré disk model | |
| Type | Hyperbolic regular honeycomb Uniform hyperbolic honeycomb |
| Schläfli symbol | {5,3,5} t0{5,3,5} |
| Coxeter-Dynkin diagram | |
| Cells | {5,3} (regular dodecahedron) |
| Faces | {5} (pentagon) |
| Edge figure | {5} (pentagon) |
| Vertex figure |  icosahedron |
| Dual | Self-dual |
| Coxeter group | K3, |
| Properties | Regular |
In hyperbolic geometry, the order-5 dodecahedral honeycomb is one of four compact regular space-filling tessellations (or honeycombs) in hyperbolic 3-space. With Schläfli symbol {5,3,5}, it has five dodecahedral cells around each edge, and each vertex is surrounded by twenty dodecahedra. Its vertex figure is an icosahedron.
A geometric honeycomb is a space-filling of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions.
Honeycombs are usually constructed in ordinary Euclidean ("flat") space, like the convex uniform honeycombs. They may also be constructed in non-Euclidean spaces, such as hyperbolic uniform honeycombs. Any finite uniform polytope can be projected to its circumsphere to form a uniform honeycomb in spherical space.
Description
The dihedral angle of a Euclidean regular dodecahedron is ~116.6°, so no more than three of them can fit around an edge in Euclidean 3-space. In hyperbolic space, however, the dihedral angle is smaller than it is in Euclidean space, and depends on the size of the figure; the smallest possible dihedral angle is 60°, for an ideal hyperbolic regular dodecahedron with infinitely long edges. The dodecahedra in this dodecahedral honeycomb are sized so that all of their dihedral angles are exactly 72°.
Images

Related polytopes and honeycombs
There are four regular compact honeycombs in 3D hyperbolic space:
 {5,3,4} |
 {4,3,5} |
 {3,5,3} |
 {5,3,5} |
There is another honeycomb in hyperbolic 3-space called the order-4 dodecahedral honeycomb, {5,3,4}, which has only four dodecahedra per edge. These honeycombs are also related to the 120-cell which can be considered as a honeycomb in positively curved space (the surface of a 4-dimensional sphere), with three dodecahedra on each edge, {5,3,3}. Lastly the dodecahedral ditope, {5,3,2} exists on a 3-sphere, with 2 hemispherical cells.
There are nine uniform honeycombs in the Coxeter group family, including this regular form. Also the bitruncated form, t1,2{5,3,5}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , of this honeycomb has all truncated icosahedron cells.
, of this honeycomb has all truncated icosahedron cells.
| family honeycombs | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| {5,3,5} |
r{5,3,5} |
t{5,3,5} |
rr{5,3,5} |
t0,3{5,3,5} | |||||||

|

|

|

|

| |||||||
| 2t{5,3,5} |
tr{5,3,5} |
t0,1,3{5,3,5} |
t0,1,2,3{5,3,5} | ||||||||

|

|

|

| ||||||||
The Seifert–Weber space is a compact manifold that can be formed as a quotient space of the order-5 dodecahedral honeycomb.
This honeycomb is a part of a sequence of polychora and honeycombs with icosahedron vertex figures:
| {p,3,5} polytopes | |||||||
|---|---|---|---|---|---|---|---|
| Space | S | H | |||||
| Form | Finite | Compact | Paracompact | Noncompact | |||
| Name | {3,3,5} |
{4,3,5} |
{5,3,5} |
{6,3,5} |
{7,3,5} |
{8,3,5} |
... {∞,3,5} |
| Image | 
|

|

|

|

|

|

|
| Cells | {3,3} |
{4,3} |
{5,3} |
{6,3} |
{7,3} |
{8,3} |
{∞,3} |
This honeycomb is a part of a sequence of regular polytopes and honeycombs with dodecahedral cells:
| {5,3,p} polytopes | |||||||
|---|---|---|---|---|---|---|---|
| Space | S | H | |||||
| Form | Finite | Compact | Paracompact | Noncompact | |||
| Name | {5,3,3} | {5,3,4} | {5,3,5} | {5,3,6} | {5,3,7} | {5,3,8} | ... {5,3,∞} |
| Image | 
|

|

|

|

|
|

|
| Vertex figure |
{3,3} |
{3,4} |
{3,5} |
{3,6} |
{3,7} |
{3,8} |
{3,∞} |
| {p,3,p} regular honeycombs | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Space | S | Euclidean E | H | ||||||||
| Form | Finite | Affine | Compact | Paracompact | Noncompact | ||||||
| Name | {3,3,3} | {4,3,4} | {5,3,5} | {6,3,6} | {7,3,7} | {8,3,8} | ...{∞,3,∞} | ||||
| Image | 
|

|

|

|

|

|

| ||||
| Cells |  {3,3} |
 {4,3} |
 {5,3} |
 {6,3} |
 {7,3} |
 {8,3} |
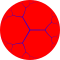 {∞,3} | ||||
| Vertex figure |
 {3,3} |
 {3,4} |
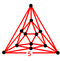 {3,5} |
 {3,6} |
 {3,7} |
 {3,8} |
 {3,∞} | ||||
Rectified order-5 dodecahedral honeycomb
| Rectified order-5 dodecahedral honeycomb | |
|---|---|
| Type | Uniform honeycombs in hyperbolic space |
| Schläfli symbol | r{5,3,5} t1{5,3,5} |
| Coxeter diagram | |
| Cells | r{5,3} {3,5} |
| Faces | triangle {3} pentagon {5} |
| Vertex figure |  pentagonal prism |
| Coxeter group | , |
| Properties | Vertex-transitive, edge-transitive |
The rectified order-5 dodecahedral honeycomb, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , has alternating icosahedron and icosidodecahedron cells, with a pentagonal prism vertex figure.
, has alternating icosahedron and icosidodecahedron cells, with a pentagonal prism vertex figure.
Related tilings and honeycomb

There are four rectified compact regular honeycombs:
| Image | 
|

|

|

|
|---|---|---|---|---|
| Symbols | r{5,3,4} |
r{4,3,5} |
r{3,5,3} |
r{5,3,5} |
| Vertex figure |

|

|
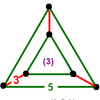
|
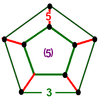
|
| Space | S | H | ||||
|---|---|---|---|---|---|---|
| Form | Finite | Compact | Paracompact | Noncompact | ||
| Name | r{3,3,5} |
r{4,3,5} |
r{5,3,5} |
r{6,3,5} |
r{7,3,5} |
... r{∞,3,5} |
| Image | 
|

|

|

|
||
| Cells {3,5} |
r{3,3} |
r{4,3} |
r{5,3} |
r{6,3} |
r{7,3} |
r{∞,3} |
Truncated order-5 dodecahedral honeycomb
| Truncated order-5 dodecahedral honeycomb | |
|---|---|
| Type | Uniform honeycombs in hyperbolic space |
| Schläfli symbol | t{5,3,5} t0,1{5,3,5} |
| Coxeter diagram | |
| Cells | t{5,3} {3,5} |
| Faces | triangle {3}
decagon {10} |
| Vertex figure |  pentagonal pyramid |
| Coxeter group | , |
| Properties | Vertex-transitive |
The truncated order-5 dodecahedral honeycomb, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , has icosahedron and truncated dodecahedron cells, with a pentagonal pyramid vertex figure.
, has icosahedron and truncated dodecahedron cells, with a pentagonal pyramid vertex figure.
Related honeycombs
| Image | 
|

|

|

|
|---|---|---|---|---|
| Symbols | t{5,3,4} |
t{4,3,5} |
t{3,5,3} |
t{5,3,5} |
| Vertex figure |

|

|
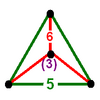
|

|
Bitruncated order-5 dodecahedral honeycomb
| Bitruncated order-5 dodecahedral honeycomb | |
|---|---|
| Type | Uniform honeycombs in hyperbolic space |
| Schläfli symbol | 2t{5,3,5} t1,2{5,3,5} |
| Coxeter diagram | |
| Cells | t{3,5} |
| Faces | pentagon {5} hexagon {6} |
| Vertex figure |  tetragonal disphenoid |
| Coxeter group | , ] |
| Properties | Vertex-transitive, edge-transitive, cell-transitive |
The bitruncated order-5 dodecahedral honeycomb, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , has truncated icosahedron cells, with a tetragonal disphenoid vertex figure.
, has truncated icosahedron cells, with a tetragonal disphenoid vertex figure.
Related honeycombs
| Image | 
|

|

|
|---|---|---|---|
| Symbols | 2t{4,3,5} |
2t{3,5,3} |
2t{5,3,5} |
| Vertex figure |
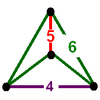
|
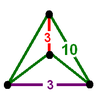
|
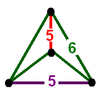
|
Cantellated order-5 dodecahedral honeycomb
| Cantellated order-5 dodecahedral honeycomb | |
|---|---|
| Type | Uniform honeycombs in hyperbolic space |
| Schläfli symbol | rr{5,3,5} t0,2{5,3,5} |
| Coxeter diagram | |
| Cells | rr{5,3} r{3,5} {}x{5} |
| Faces | triangle {3} square {4} pentagon {5} |
| Vertex figure |  wedge |
| Coxeter group | , |
| Properties | Vertex-transitive |
The cantellated order-5 dodecahedral honeycomb, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , has rhombicosidodecahedron, icosidodecahedron, and pentagonal prism cells, with a wedge vertex figure.
, has rhombicosidodecahedron, icosidodecahedron, and pentagonal prism cells, with a wedge vertex figure.
Related honeycombs
| Four cantellated regular compact honeycombs in H | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Cantitruncated order-5 dodecahedral honeycomb
| Cantitruncated order-5 dodecahedral honeycomb | |
|---|---|
| Type | Uniform honeycombs in hyperbolic space |
| Schläfli symbol | tr{5,3,5} t0,1,2{5,3,5} |
| Coxeter diagram | |
| Cells | tr{5,3} t{3,5} {}x{5} |
| Faces | square {4} pentagon {5} hexagon {6} decagon {10} |
| Vertex figure |  mirrored sphenoid |
| Coxeter group | , |
| Properties | Vertex-transitive |
The cantitruncated order-5 dodecahedral honeycomb, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , has truncated icosidodecahedron, truncated icosahedron, and pentagonal prism cells, with a mirrored sphenoid vertex figure.
, has truncated icosidodecahedron, truncated icosahedron, and pentagonal prism cells, with a mirrored sphenoid vertex figure.
Related honeycombs
| Image | 
|

|

|

|
|---|---|---|---|---|
| Symbols | tr{5,3,4} |
tr{4,3,5} |
tr{3,5,3} |
tr{5,3,5} |
| Vertex figure |

|

|

|

|
Runcinated order-5 dodecahedral honeycomb
| Runcinated order-5 dodecahedral honeycomb | |
|---|---|
| Type | Uniform honeycombs in hyperbolic space |
| Schläfli symbol | t0,3{5,3,5} |
| Coxeter diagram | |
| Cells | {5,3} {}x{5} |
| Faces | square {4} pentagon {5} |
| Vertex figure | 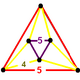 triangular antiprism |
| Coxeter group|, ] | |
| Properties | Vertex-transitive, edge-transitive |
The runcinated order-5 dodecahedral honeycomb, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , has dodecahedron and pentagonal prism cells, with a triangular antiprism vertex figure.
, has dodecahedron and pentagonal prism cells, with a triangular antiprism vertex figure.
Related honeycombs
| Image | 
|

|

|
|---|---|---|---|
| Symbols | t0,3{4,3,5} |
t0,3{3,5,3} |
t0,3{5,3,5} |
| Vertex figure |
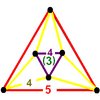
|
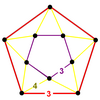
|
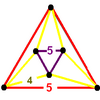
|
Runcitruncated order-5 dodecahedral honeycomb
| Runcitruncated order-5 dodecahedral honeycomb | |
|---|---|
| Type | Uniform honeycombs in hyperbolic space |
| Schläfli symbol | t0,1,3{5,3,5} |
| Coxeter diagram | |
| Cells | t{5,3} rr{5,3} {}x{5} {}x{10} |
| Faces | triangle {3} square {4} pentagon {5} decagon {10} |
| Vertex figure |  isosceles-trapezoidal pyramid |
| Coxeter group | , |
| Properties | Vertex-transitive |
The runcitruncated order-5 dodecahedral honeycomb, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , has truncated dodecahedron, rhombicosidodecahedron, pentagonal prism, and decagonal prism cells, with an isosceles-trapezoidal pyramid vertex figure.
, has truncated dodecahedron, rhombicosidodecahedron, pentagonal prism, and decagonal prism cells, with an isosceles-trapezoidal pyramid vertex figure.
The runcicantellated order-5 dodecahedral honeycomb is equivalent to the runcitruncated order-5 dodecahedral honeycomb.
Related honeycombs
| Four runcitruncated regular compact honeycombs in H | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Omnitruncated order-5 dodecahedral honeycomb
| Omnitruncated order-5 dodecahedral honeycomb | |
|---|---|
| Type | Uniform honeycombs in hyperbolic space |
| Schläfli symbol | t0,1,2,3{5,3,5} |
| Coxeter diagram | |
| Cells | tr{5,3} {}x{10} |
| Faces | square {4} hexagon {6} decagon {10} |
| Vertex figure |  phyllic disphenoid |
| Coxeter group|, ] | |
| Properties | Vertex-transitive |
The omnitruncated order-5 dodecahedral honeycomb, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , has truncated icosidodecahedron and decagonal prism cells, with a phyllic disphenoid vertex figure.
, has truncated icosidodecahedron and decagonal prism cells, with a phyllic disphenoid vertex figure.
Related honeycombs
| Three omnitruncated regular compact honeycombs in H | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
See also
- Convex uniform honeycombs in hyperbolic space
- Regular tessellations of hyperbolic 3-space
- 57-cell - An abstract regular polychoron which shared the {5,3,5} symbol.
References
- Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. (Tables I and II: Regular polytopes and honeycombs, pp. 294–296)
- Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999 ISBN 0-486-40919-8 (Chapter 10: Regular honeycombs in hyperbolic space, Summary tables II, III, IV, V, p212-213)
- Norman Johnson Uniform Polytopes, Manuscript
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- N.W. Johnson: Geometries and Transformations, (2018) Chapter 13: Hyperbolic Coxeter groups

 ,
,


 , ]
, ]