| Hyperrectangle Orthotope | |
|---|---|
 A rectangular cuboid is a 3-orthotope A rectangular cuboid is a 3-orthotope | |
| Type | Prism |
| Faces | 2n |
| Edges | n × 2 |
| Vertices | 2 |
| Schläfli symbol | {}×{}×···×{} = {} |
| Coxeter diagram | |
| Symmetry group | , order 2 |
| Dual polyhedron | Rectangular n-fusil |
| Properties | convex, zonohedron, isogonal |
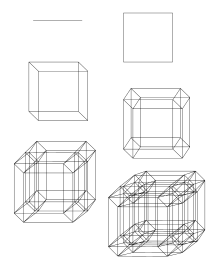
In geometry, a hyperrectangle (also called a box, hyperbox, -cell or orthotope), is the generalization of a rectangle (a plane figure) and the rectangular cuboid (a solid figure) to higher dimensions. A necessary and sufficient condition is that it is congruent to the Cartesian product of finite intervals. This means that a -dimensional rectangular solid has each of its edges equal to one of the closed intervals used in the definition. Every -cell is compact.
If all of the edges are equal length, it is a hypercube. A hyperrectangle is a special case of a parallelotope.
Formal definition
For every integer from to , let and be real numbers such that . The set of all points in whose coordinates satisfy the inequalities is a -cell.
Intuition
A -cell of dimension is especially simple. For example, a 1-cell is simply the interval with . A 2-cell is the rectangle formed by the Cartesian product of two closed intervals, and a 3-cell is a rectangular solid.
The sides and edges of a -cell need not be equal in (Euclidean) length; although the unit cube (which has boundaries of equal Euclidean length) is a 3-cell, the set of all 3-cells with equal-length edges is a strict subset of the set of all 3-cells.
Types
A four-dimensional orthotope is likely a hypercuboid.
The special case of an n-dimensional orthotope where all edges have equal length is the n-cube or hypercube.
By analogy, the term "hyperrectangle" can refer to Cartesian products of orthogonal intervals of other kinds, such as ranges of keys in database theory or ranges of integers, rather than real numbers.
Dual polytope
| n-fusil | |
|---|---|
 Example: 3-fusil Example: 3-fusil | |
| Type | Prism |
| Faces | 2n |
| Vertices | 2 |
| Schläfli symbol | {}+{}+···+{} = n{} |
| Coxeter diagram | |
| Symmetry group | , order 2 |
| Dual polyhedron | n-orthotope |
| Properties | convex, isotopal |
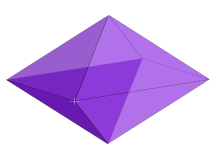
The dual polytope of an n-orthotope has been variously called a rectangular n-orthoplex, rhombic n-fusil, or n-lozenge. It is constructed by 2n points located in the center of the orthotope rectangular faces.
An n-fusil's Schläfli symbol can be represented by a sum of n orthogonal line segments: { } + { } + ... + { } or n{ }.
A 1-fusil is a line segment. A 2-fusil is a rhombus. Its plane cross selections in all pairs of axes are rhombi.
| n | Example image |
|---|---|
| 1 | Line segment { } |
| 2 | 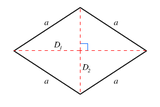 Rhombus { } + { } = 2{ } |
| 3 | 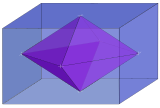 Rhombic 3-orthoplex inside 3-orthotope { } + { } + { } = 3{ } |
See also
Notes
- ^ N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite symmetry groups, 11.5 Spherical Coxeter groups, p.251
- ^ Coxeter, 1973
- Foran (1991)
- Rudin (1976:39)
- Foran (1991:24)
- Rudin (1976:31)
- Hirotsu, Takashi (2022). "Normal-sized hypercuboids in a given hypercube". arXiv:2211.15342.
- See e.g. Zhang, Yi; Munagala, Kamesh; Yang, Jun (2011), "Storing matrices on disk: Theory and practice revisited" (PDF), Proc. VLDB, 4 (11): 1075–1086, doi:10.14778/3402707.3402743.
References
- Coxeter, Harold Scott MacDonald (1973). Regular Polytopes (3rd ed.). New York: Dover. pp. 122–123. ISBN 0-486-61480-8.
External links
- Weisstein, Eric W. "Orthotope". MathWorld.
- Foran, James (1991-01-07). Fundamentals of Real Analysis. CRC Press. ISBN 9780824784539. Retrieved 23 May 2014.
- Rudin, Walter (1976). Principles of Mathematical Analysis. McGraw-Hill.
| Dimension | ||
|---|---|---|
| Dimensional spaces |  | |
| Other dimensions | ||
| Polytopes and shapes | ||
| Number systems | ||
| Dimensions by number | ||
| See also | ||
| Category | ||
 to
to  ). Only the edges of the higher-dimensional cells are shown.
). Only the edges of the higher-dimensional cells are shown. -cell or orthotope), is the generalization of a
-cell or orthotope), is the generalization of a  from
from  to
to  and
and  be
be  . The set of all points
. The set of all points  in
in  whose coordinates satisfy the inequalities
whose coordinates satisfy the inequalities  is a
is a  is especially simple. For example, a 1-cell is simply the interval
is especially simple. For example, a 1-cell is simply the interval  with
with  . A 2-cell is the rectangle formed by the Cartesian product of two closed intervals, and a 3-cell is a rectangular solid.
. A 2-cell is the rectangle formed by the Cartesian product of two closed intervals, and a 3-cell is a rectangular solid.