
The parallel operator (pronounced "parallel", following the parallel lines notation from geometry; also known as reduced sum, parallel sum or parallel addition) is a binary operation which is used as a shorthand in electrical engineering, but is also used in kinetics, fluid mechanics and financial mathematics. The name parallel comes from the use of the operator computing the combined resistance of resistors in parallel.
Overview
The parallel operator represents the reciprocal value of a sum of reciprocal values (sometimes also referred to as the "reciprocal formula" or "harmonic sum") and is defined by:
where a, b, and are elements of the extended complex numbers
The operator gives half of the harmonic mean of two numbers a and b.
As a special case, for any number :
Further, for all distinct numbers :
with representing the absolute value of , and meaning the minimum (least element) among x and y.
If and are distinct positive real numbers then
The concept has been extended from a scalar operation to matrices and further generalized.
Notation
The operator was originally introduced as reduced sum by Sundaram Seshu in 1956, studied as operator ∗ by Kent E. Erickson in 1959, and popularized by Richard James Duffin and William Niles Anderson, Jr. as parallel addition or parallel sum operator : in mathematics and network theory since 1966. While some authors continue to use this symbol up to the present, for example, Sujit Kumar Mitra used ∙ as a symbol in 1970. In applied electronics, a ∥ sign became more common as the operator's symbol around 1974. This was often written as doubled vertical line (||) available in most character sets (sometimes italicized as //), but now can be represented using Unicode character U+2225 ( ∥ ) for "parallel to". In LaTeX and related markup languages, the macros \| and \parallel are often used (and rarely \smallparallel is used) to denote the operator's symbol.
Properties
Let represent the extended complex plane excluding zero, and the bijective function from to such that One has identities
and
This implies immediately that is a field where the parallel operator takes the place of the addition, and that this field is isomorphic to
The following properties may be obtained by translating through the corresponding properties of the complex numbers.
Field properties
As for any field, satisfies a variety of basic identities.
It is commutative under parallel and multiplication:
It is associative under parallel and multiplication:
Both operations have an identity element; for parallel the identity is while for multiplication the identity is 1:
Every element of has an inverse under parallel, equal to the additive inverse under addition. (But 0 has no inverse under parallel.)
The identity element is its own inverse,
Every element of has a multiplicative inverse :
Multiplication is distributive over parallel:
Repeated parallel
Repeated parallel is equivalent to division,
Or, multiplying both sides by n,
Unlike for repeated addition, this does not commute:
Binomial expansion
Using the distributive property twice, the product of two parallel binomials can be expanded as
The square of a binomial is
The cube of a binomial is
In general, the nth power of a binomial can be expanded using binomial coefficients which are the reciprocal of those under addition, resulting in an analog of the binomial formula:
Logarithm and exponential
The following identities hold:
Factoring parallel polynomials
As with a polynomial under addition, a parallel polynomial with coefficients in (with ) can be factored into a product of monomials:
for some roots (possibly repeated) in
Analogous to polynomials under addition, the polynomial equation
implies that for some k.
Quadratic formula
A linear equation can be easily solved via the parallel inverse:
To solve a parallel quadratic equation, complete the square to obtain an analog of the quadratic formula
Including zero
The extended complex numbers including zero, is no longer a field under parallel and multiplication, because 0 has no inverse under parallel. (This is analogous to the way is not a field because has no additive inverse.)
For every non-zero a,
The quantity can either be left undefined (see indeterminate form) or defined to equal 0.
Precedence
In the absence of parentheses, the parallel operator is defined as taking precedence over addition or subtraction, similar to multiplication.
Applications
There are applications of the parallel operator in electronics, optics, and study of periodicity:
Circuit analysis
In electrical engineering, the parallel operator can be used to calculate the total impedance of various serial and parallel electrical circuits. There is a duality between the usual (series) sum and the parallel sum.
For instance, the total resistance of resistors connected in parallel is the reciprocal of the sum of the reciprocals of the individual resistors.
Likewise for the total capacitance of serial capacitors.
Lens equation
In geometric optics the thin lens approximation to the lens maker's equation.
Synodic period
The time between conjunctions of two orbiting bodies is called the synodic period. If the period of the slower body is T2, and the period of the faster is T1, then the synodic period is
Examples
Question:
- Three resistors , and are connected in parallel. What is their resulting resistance?
Answer:
- The effectively resulting resistance is ca. 57 kΩ.
Question:
- A construction worker raises a wall in 5 hours. Another worker would need 7 hours for the same work. How long does it take to build the wall if both workers work in parallel?
Answer:
- They will finish in close to 3 hours.
Implementation

Suggested already by Kent E. Erickson as a subroutine in digital computers in 1959, the parallel operator is implemented as a keyboard operator on the Reverse Polish Notation (RPN) scientific calculators WP 34S since 2008 as well as on the WP 34C and WP 43S since 2015, allowing to solve even cascaded problems with few keystrokes like 270↵ Enter180∥120∥.
Projective view
Given a field F there are two embeddings of F into the projective line P(F): z → and z → . These embeddings overlap except for and . The parallel operator relates the addition operation between the embeddings. In fact, the homographies on the projective line are represented by 2 x 2 matrices M(2,F), and the field operations (+ and ×) are extended to homographies. Each embedding has its addition a + b represented by the following matrix multiplications in M(2,A):
The two matrix products show that there are two subgroups of M(2,F) isomorphic to (F,+), the additive group of F. Depending on which embedding is used, one operation is +, the other is
Notes
- ^ While the use of the symbol ∥ for "parallel" in geometry reaches as far back as 1673 in John Kersey the elder's work, this came into more use only since about 1875. The usage of a mathematical operator for parallel circuits originates from network theory in electrical engineering. Sundaram Seshu introduced a reduced sum operator in 1956, Kent E. Erickson proposed an asterisk (∗) to symbolize the operator in 1959, whilst Richard James Duffin and William Niles Anderson, Jr. used a colon (:) for the parallel addition since 1966. Sujit Kumar Mitra used a middot (∙) for it in 1970. The first usage of the parallel symbol (∥) for this operator in applied electronics is unknown, but might have originated from Stephen D. Senturia [d] and Bruce D. Wedlock's 1974 book "Electronic Circuits and Applications", which evolved from their introductory electronics course at Massachusetts Institute of Technology (MIT) with concepts of teaching network theory and electronics derived from an earlier course taught by Campbell "Cam" Leach Searle. It was further popularized through John W. McWane's 1981 book "Introduction to Electronics and Instrumentation", which grew out of an identically-named MIT course developed as part of the influential Technical Curriculum Development Project between 1974 and 1979. This symbol was probably also introduced because the other used symbols could be easily confused with signs commonly used for multiplication and division in some contexts.
- ^ In electrical circuits the parallel operator can be applied to, respectively, parallel resistances (R in ) or inductances (L in ) as well as to impedances (Z in ) or reactances (X in ). Ignoring the operator symbol's then-misleading glyph it can also be applied to series circuits of, respectively, conductances (G in ) or capacitances (C in ) as well as to admittances (Y in ) or susceptances (B in ).
References
- ^ Duffin, Richard James (1971) . "Network Models". Written at Durham, North Carolina, USA. In Wilf, Herbert Saul; Hararay, Frank (eds.). Mathematical Aspects of Electrical Network Analysis. Proceedings of a Symposium in Applied Mathematics of the American Mathematical Society and the Society for Industrial and Applied Mathematics held in New York City, 1969-04-02/03. Vol. III of SIAM-AMS Proceedings (illustrated ed.). Providence, Rhode Island: American Mathematical Society (AMS) / Society for Industrial and Applied Mathematics (SIAM). pp. 65–92 . ISBN 0-8218-1322-6. ISSN 0080-5084. LCCN 79-167683. ISBN 978-0-8218-1322-5. Report 69-21. Retrieved 2019-08-05. pp. 68–69:
To have a convenient short notation for the joint resistance of resistors connected in parallel let A:B = AB/(A+B) A:B may be regarded as a new operation termed parallel addition Parallel addition is defined for any nonnegative numbers. The network model shows that parallel addition is commutative and associative. Moreover, multiplication is distributive over this operation. Consider now an algebraic expression in the operations (+) and (:) operating on positive numbers A, B, C, etc. To give a network interpretation of such a polynomial read A + B as "A series B" and A : B as "A parallel B" then it is clear that the expression is the joint resistance of the network
(206 pages) - Kersey (the elder), John (1673). "Chapter I: Concerning the Scope of this fourth Book and the Signification of Characters, Abbreviations and Citations used therein". The Elements of that Mathematical Art, commonly called Algebra. Vol. Book IV - The Elements of the Algebraical Arts. London: Thomas Passinger, Three-Bibles, London-Bridge. pp. 177–178. Archived from the original on 2020-08-05. Retrieved 2019-08-09.
- Cajori, Florian (1993) . "§ 184, § 359, § 368". A History of Mathematical Notations – Notations in Elementary Mathematics. Vol. 1 (two volumes in one unaltered reprint ed.). Chicago, US: Open court publishing company. pp. 193, 402–403, 411–412. ISBN 0-486-67766-4. LCCN 93-29211. Retrieved 2019-07-22. pp. 402–403, 411–412:
§359. ∥ for parallel occurs in Oughtred's Opuscula mathematica hactenus inedita (1677) , a posthumous work (§ 184) §368. Signs for parallel lines. when Recorde's sign of equality won its way upon the Continent, vertical lines came to be used for parallelism. We find ∥ for "parallel" in Kersey, Caswell, Jones, Wilson, Emerson, Kambly, and the writers of the last fifty years who have been already quoted in connection with other pictographs. Before about 1875 it does not occur as often Hall and Stevens use "par or ∥" for parallel John Kersey, Algebra (London, 1673), Book IV, p. 177. W. Jones, Synopsis palmarioum matheseos (London, 1706). John Wilson, Trigonometry (Edinburgh, 1714), characters explained. W. Emerson, Elements of Geometry (London, 1763), p. 4. L. Kambly [de], Die Elementar-Mathematik, Part 2: Planimetrie, 43. edition (Breslau, 1876), p. 8. H. S. Hall and F. H. Stevens, Euclid's Elements, Parts I and II (London, 1889), p. 10.
- "INA 326/INA 327 – Precision, Rail-to-Rail I/O Instrumentation Amplifier" (PDF). Burr-Brown / Texas Instruments. 2018 . pp. 3, 9, 13. SBOS222D. Archived (PDF) from the original on 2019-07-13. Retrieved 2019-07-13.
- Bober, William; Stevens, Andrew (2016). "Chapter 7.6. Laplace Transforms Applied to Circuits". Numerical and Analytical Methods with MATLAB for Electrical Engineers. Applied and Computational Mechanics (1 ed.). CRC Press. p. 224. ISBN 978-1-46657607-0. ISBN 1-46657607-3. (388 pages)
- ^ Ranade, Gireeja; Stojanovic, Vladimir, eds. (Fall 2018). "Chapter 15.7.2 Parallel Resistors" (PDF). EECS 16A Designing Information Devices and Systems I (PDF) (lecture notes). University of California, Berkeley. p. 12. Note 15. Archived (PDF) from the original on 2018-12-27. Retrieved 2018-12-28. p. 12:
This mathematical relationship comes up often enough that it actually has a name: the "parallel operator", denoted ∥. When we say x∥y, it means . Note that this is a mathematical operator and does not say anything about the actual configuration. In the case of resistors the parallel operator is used for parallel resistors, but for other components (like capacitors) this is not the case.
(16 pages) - ^ Ellerman, David Patterson (1995-03-21). "Chapter 12: Parallel Addition, Series-Parallel Duality, and Financial Mathematics". Intellectual Trespassing as a Way of Life: Essays in Philosophy, Economics, and Mathematics (PDF). The worldly philosophy: studies in intersection of philosophy and economics (illustrated ed.). Rowman & Littlefield Publishers, Inc. pp. 237–268. ISBN 0-8476-7932-2. Archived (PDF) from the original on 2016-03-05. Retrieved 2019-08-09. p. 237:
When resistors with resistance a and b are placed in series, their compound resistance is the usual sum (hereafter the series sum) of the resistances a + b. If the resistances are placed in parallel, their compound resistance is the parallel sum of the resistances, which is denoted by the full colon
(271 pages) - ^ Ellerman, David Patterson (May 2004) . "Introduction to Series-Parallel Duality" (PDF). University of California at Riverside. CiteSeerX 10.1.1.90.3666. Archived from the original on 2019-08-10. Retrieved 2019-08-09.
The parallel sum of two positive real numbers x:y = arises in electrical circuit theory as the resistance resulting from hooking two resistances x and y in parallel. There is a duality between the usual (series) sum and the parallel sum.
(24 pages) - ^ Basso, Christophe P. (2016). "Chapter 1.1.2 The Current Divider". Linear Circuit Transfer Functions: An Introduction to Fast Analytical Techniques (1 ed.). Chichester, West Sussex, New Jersey, USA: John Wiley & Sons Ltd. p. 12. ISBN 978-1-11923637-5. LCCN 2015047967. Retrieved 2018-12-28. (464 pages)
- ^ Cotter, Neil E., ed. (2015-10-12) . "ECE1250 Cookbook – Nodes, Series, Parallel" (lecture notes). Cookbooks. University of Utah. Archived (PDF) from the original on 2020-08-20. Retrieved 2019-08-11.
One convenient way to indicate two resistors are in parallel is to put a ∥ between them.
- Böcker, Joachim (2019-03-18) . "Grundlagen der Elektrotechnik Teil B" (PDF) (in German). Universität Paderborn. p. 12. Archived (PDF) from the original on 2018-04-17. Retrieved 2019-08-09. p. 12:
Für die Berechnung des Ersatzwiderstands der Parallelschaltung wird gern die Kurzschreibweise ∥ benutzt.
- ^ Georg, Otfried (2013) . "Chapter 2.11.4.3: Aufstellen der Differentialgleichung aus der komplexen Darstellung - MATHCAD Anwendung 2.11-6: Benutzerdefinierte Operatoren". Elektromagnetische Felder und Netzwerke: Anwendungen in Mathcad und PSpice. Springer-Lehrbuch (in German) (1 ed.). Springer-Verlag. pp. 246–248. doi:10.1007/978-3-642-58420-6. ISBN 978-3-642-58420-6. ISBN 3-642-58420-9. Retrieved 2019-08-04. (728 pages)
-
 Associative Composition Algebra/Homographies at Wikibooks
Associative Composition Algebra/Homographies at Wikibooks
- ^ Mitra, Sujit Kumar (February 1970). "A Matrix Operation for Analyzing Series-parallel Multiports". Journal of the Franklin Institute. Brief Communication. 289 (2). Franklin Institute: 167–169. doi:10.1016/0016-0032(70)90302-9. p. 167:
The purpose of this communication is to extend the concept of the scalar operation Reduced Sum introduced by Seshu and later elaborated by Erickson to matrices, to outline some interesting properties of this new matrix operation, and to apply the matrix operation in the analysis of series and parallel n-port networks. Let A and B be two non-singular square matrices having inverses, A and B respectively. We define the operation ∙ as A ∙ B = (A + B) and the operation ⊙ as A ⊙ B = A ∙ (−B). The operation ∙ is commutative and associative and is also distributive with respect to multiplication.
(3 pages) - ^ Duffin, Richard James; Hazony, Dov; Morrison, Norman Alexander (March 1966) . "Network synthesis through hybrid matrices". SIAM Journal on Applied Mathematics. 14 (2). Society for Industrial and Applied Mathematics (SIAM): 390–413. doi:10.1137/0114032. JSTOR 2946272. (24 pages)
- ^ Anderson, Jr., William Niles; Duffin, Richard James (1969) . "Series and parallel addition of matrices". Journal of Mathematical Analysis and Applications. 26 (3). Academic Press, Inc.: 576–594. doi:10.1016/0022-247X(69)90200-5. p. 576:
we define the parallel sum of A and B by the formula A(A + B)B and denote it by A : B. If A and B are nonsingular this reduces to A : B = (A + B) which is the well known electrical formula for addition of resistors in parallel. Then it is shown that the Hermitian semi-definite matrices form a commutative partially ordered semigroup under the parallel sum operation.
- Mitra, Sujit Kumar; Puri, Madan Lal (October 1973). "On Parallel Sum and Difference of Matrices" (PDF). Journal of Mathematical Analysis and Applications. 44 (1). Academic Press, Inc.: 92–97. doi:10.1016/0022-247X(73)90027-9. Archived from the original (PDF) on 2019-04-13.
- Mitra, Sujit Kumar; Bhimasankaram, Pochiraju; Malik, Saroj B. (2010). Matrix Partial Orders, Shorted Operators and Applications. Series in Algebra. Vol. 10 (illustrated 1st ed.). World Scientific Publishing Co. Pte. Ltd. ISBN 978-981-283-844-5. ISBN 981-283-844-9. Retrieved 2019-08-19. (446 pages)
- Eriksson-Bique, Sirkka-Liisa Anneli ; Leutwiler, Heinz (February 1989) . "A generalization of parallel addition" (PDF). Aequationes Mathematicae. 38 (1). Birkhäuser Verlag: 99–110. doi:10.1007/BF01839498. Archived (PDF) from the original on 2020-08-20. Retrieved 2020-08-20.
- Seshu, Sundaram (September 1956). "On Electrical Circuits and Switching Circuits". IRE Transactions on Circuit Theory. CT-3 (3). Institute of Radio Engineers (IRE): 172–178. doi:10.1109/TCT.1956.1086310. (7 pages) (NB. See errata.)
- Seshu, Sundaram; Gould, Roderick (September 1957). "Correction to 'On Electrical Circuits and Switching Circuits'". IRE Transactions on Circuit Theory. Correction. CT-4 (3). Institute of Radio Engineers (IRE): 284. doi:10.1109/TCT.1957.1086390. (1 page) (NB. Refers to previous reference.)
- ^ Erickson, Kent E. (March 1959). "A New Operation for Analyzing Series-Parallel Networks". IRE Transactions on Circuit Theory. CT-6 (1). Institute of Radio Engineers (IRE): 124–126. doi:10.1109/TCT.1959.1086519. p. 124:
The operation ∗ is defined as A ∗ B = AB/A + B. The symbol ∗ has algebraic properties which simplify the formal solution of many series-parallel network problems. If the operation ∗ were included as a subroutine in a digital computer, it could simplify the programming of certain network calculations.
(3 pages) (NB. See comment.) - Kaufman, Howard (June 1963). "Remark on a New Operation for Analyzing Series-Parallel Networks". IEEE Transactions on Circuit Theory. CT-10 (2). Institute of Electrical and Electronics Engineers (IEEE): 283. doi:10.1109/TCT.1963.1082126. p. 283:
Comments on the operation ∗ a∗b = ab/(a+b)
(1 page) (NB. Refers to previous reference.) - Senturia, Stephen D. ; Wedlock, Bruce D. (1975) . "Part A. Learning the Language, Chapter 3. Linear Resistive Networks, 3.2 Basic Network Configurations, 3.2.3. Resistors in Parallel". Written at Massachusetts Institute of Technology, Cambridge, Massachusetts, USA. Electronic Circuits and Applications (1 ed.). New York, London, Sydney, Toronto: John Wiley & Sons, Inc. pp. viii–ix, 44–46 . ISBN 0-471-77630-0. LCCN 74-7404. S2CID 61070327. pp. viii, ix, 45:
This textbook evolved from a one-semester introductory electronics course taught by the authors at the Massachusetts Institute of Technology. The course is used by many freshmen as a precursor to the MIT Electrical Engineering Core Program. The preparation of a book of this size has drawn on the contribution of many people. The concept of teaching network theory and electronics as a single unified subject derives from Professor Campbell Searle, who taught the introductory electronics course when one of us (S.D.S.) was a first-year physics graduate student trying to learn electronics. In addition, Professor Searle has provided invaluable constructive criticism throughout the writing of this text. Several members of the MIT faculty and nearly 40 graduate technical assistants have participated in the teaching of this material over the past five years, many of whom have made important contributions through their suggestions and examples. Among these, we especially wish to thank O. R. Mitchell, Irvin Englander, George Lewis, Ernest Vincent, David James, Kenway Wong, Gim Hom, Tom Davis, James Kirtley, and Robert Donaghey. The chairman of the MIT Department of Electrical Engineering, Professor Louis D. Smullin, has provided support and encouragement during this project, as have many colleagues throughout the department. The first result states that the total voltage across the parallel combination of R1 and R2 is the same as that which occurs across a single resistance of value R1 R2 (R1 + R2). Because this expression for parallel resistance occurs so often, it is given a special notation (R1∥R2). That is, when R1 and R2 are in parallel, the equivalent resistance is
(xii+623+5 pages) (NB. A teacher's manual was available as well. Early print runs contains a considerable number of typographical errors. See also: Wedlock's 1978 book.) - Wolf, Lawrence J. (1977) . "Section 4. Instructional Materials – 4.3. The MIT Technical Curriculum Development Project – Introduction to Electronics and Instrumentation". In Aldridge, Bill G.; Mowery, Donald R.; Wolf, Lawrence J.; Dixon, Peggy (eds.). Science and Engineering Technology – Curriculum Guide: A Guide to a Two-Year Associate Degree Curriculum (PDF). Saint Louis Community College–Florissant Valley, St. Louis, Missouri, USA: National Science Teachers Association, Washington DC, USA. pp. 21, 77. Archived (PDF) from the original on 2017-02-15. Retrieved 2019-08-08. p. 21:
Introduction to Electronics and Instrumentation is a new and contemporary approach to the introductory electronics course. Designed for students with no prior experience with electronics, it develops the skills and knowledge necessary to use and understand modern electronic systems. John W. McWane
(NB. The SET Project was a two-year post-secondary curriculum developed between 1974 and 1977 preparing technicians to use electronic instruments.) - Wiesner, Jerome Bert; Johnson, Howard Wesley; Killian, Jr., James Rhyne, eds. (1978-04-11). "School of Engineering – Center for Advanced Engineering Study (C.A.E.S.) – Research and Development – Technical Curriculum Research and Development Project". Report of the President and the Chancellor 1977–78 – Massachusetts Institute of Technology (PDF). Massachusetts Institute of Technology (MIT). pp. 249, 252–253. Archived (PDF) from the original on 2015-09-10. Retrieved 2019-08-08. pp. 249, 252–253:
The Technical Curriculum Research and Development Program, sponsored by the Imperial Organization of Social Services [fa] of Iran, is entering the fourth year of a five-year contract. Curriculum development in electronics and mechanical engineering continues. Administered jointly by C.A.E.S. and the Department of Materials Science and Engineering, the Project is under the supervision of Professor Merton C. Flemings. It is directed by Dr. John W. McWane. Curriculum Materials Development. This is the principal activity of the project and is concerned with the development of innovative, state-of-the-art course materials in needed areas of engineering technology new introductory course in electronics is entitled Introduction to Electronics and Instrumentation and consists of eight modules dc Current, Voltage, and Resistance; Basic Circuit Networks; Time Varying Signals; Operational Amplifiers; Power Supplies; ac Current, Voltage, and Impedance; Digital Circuits; and Electronic Measurement and Control. This course represents a major change and updating of the way in which electronics is introduced, and should be of great value to STI as well as to many US programs.
- Wedlock, Bruce D. (1978). Basic circuit networks. Introduction to electronics and instrumentation. Massachusetts Institute of Technology (MIT), Technical Curriculum Research and Development Project. (81 pages) (NB. This formed the basis for Part I of McWane's 1981 book. See also: Senturia's and Wedlock's 1975 book.)
- McWane, John W. (1981-05-01). Introduction to Electronics and Instrumentation (illustrated ed.). North Scituate, Massachusetts, USA: Breton Publishers, Wadsworth, Inc. pp. 78, 96–98, 100, 104. ISBN 0-53400938-7. ISBN 978-0-53400938-0. Retrieved 2019-08-04. p. xiii, 96–98, 100:
Bruce D. Wedlock was the principle contributing author to Part I, BASIC CIRCUIT NETWORKS including the design of the companion examples. Most of the development of the IEI program was undertaken as part of the Technical Curriculum Research and Development Project of the MIT Center of Advanced Engineering Study. shorthand notation shorthand symbol ∥
(xiii+545 pages) (NB. In 1981, a 216-pages laboratory manual accompanying this book existed as well. The work grew out of an MIT course program "The MIT Technical Curriculum Development Project - Introduction to Electronics and Instrumentation" developed between 1974 and 1979. In 1986, a second edition of this book was published under the title "Introduction to Electronics Technology".) - "7.5.3 Selection of the External Resistance". TPL5110 Nano-Power System Timer for Power Gating (PDF) (Datasheet). Revision A. Texas Instruments Incorporated. September 2018 . pp. 13–14. SNAS650A. Archived (PDF) from the original on 2022-09-25. Retrieved 2022-09-25. (27 pages)
- "A7987: 61 V, 3 A asynchronous step-down switching regulator with adjustable current limitation for automotive" (PDF) (Datasheet). Revision 3. STMicroelectronics NV. 2020-09-22 . pp. 17, 18, 20. DS12928. Archived (PDF) from the original on 2022-07-18. Retrieved 2022-07-18. (36 pages)
- Paul, Steffen; Paul, Reinhold (2014-10-24). "Chapter 2.3.2: Zusammenschaltungen linearer resistiver Zweipole – Parallelschaltung". Grundlagen der Elektrotechnik und Elektronik 1: Gleichstromnetzwerke und ihre Anwendungen (in German). Vol. 1 (5 ed.). Springer-Verlag. p. 78. ISBN 978-3-64253948-0. ISBN 3-64253948-3. Retrieved 2019-08-04. p. 78:
Bei abgekürzter Schreibweise achte man sorgfältig auf die Anwendung von Klammern. Das Parallelzeichen ∥ der Kurzschreibweise hat die gleiche Bedeutung wie ein Multiplikationszeichen. Deshalb können Klammern entfallen.
(446 pages) - Dale, Paul; Bonin, Walter (2012-11-30) . WP 34S Owner's Manual (PDF) (3.1 ed.). pp. 1, 14, 32, 66, 116. Archived (PDF) from the original on 2019-07-09. Retrieved 2019-07-13. (211 pages)
- Bonin, Walter (2015) . WP 34S Owner's Manual (3.3 ed.). CreateSpace Independent Publishing Platform. ISBN 978-1-5078-9107-0.
- Bonin, Walter (2016-07-11) . WP 34S Owner's Manual (4 ed.). CreateSpace Independent Publishing Platform. ISBN 978-1-53366238-5. ISBN 1-53366238-X. (410 pages)
- Dowrick, Nigel (2015-05-03) . "Complex Lock mode for WP-34s". HP Museum. Archived from the original on 2019-04-03. Retrieved 2019-08-07.
- Bonin, Walter (2020) . WP 43S Owner's Manual (PDF). 0.16 (draft ed.). p. 119. ISBN 978-1-72950098-9. ISBN 1-72950098-6. Archived (PDF) from the original on 2022-07-21. Retrieved 2020-08-20. (328 pages)
- Bonin, Walter (2020) . WP 43S Reference Manual (PDF). 0.16 (draft ed.). p. 127. ISBN 978-1-72950106-1. ISBN 1-72950106-0. Archived (PDF) from the original on 2022-07-21. Retrieved 2020-08-20. (315 pages)
Further reading
- Pekarev, Èdward L.; Šmul'jan, Ju. L. (1976-04-30). "Parallel Addition and Parallel Subtraction of Operators". Mathematics of the USSR-Izvestiya. 10 (2). American Mathematical Society: 351–370. Bibcode:1976IzMat..10..351P. doi:10.1070/IM1976v010n02ABEH001694.
- Duffin, Richard James; Morley, Tom D. (July 1978). "Almost Definite Operators and Electro-mechanical Systems". SIAM Journal on Applied Mathematics. 35 (1). Society for Industrial and Applied Mathematics (SIAM): 21–30. doi:10.1137/0135003. JSTOR 2101028. (10 pages)
- Morley, Tom D. (July 1979). "Parallel Summation, Maxwell's Principle and the Infimum of Projections" (PDF). Journal of Mathematical Analysis and Applications. 70 (1). Department of Mathematics, University of Illinois at Urbana-Champaign, Urbana, Illinois, USA: 33–41. doi:10.1016/0022-247X(79)90073-8. Archived from the original on 2020-08-20. Retrieved 2020-08-20.
- Seeger, Alberto (May 1990) . "Direct and Inverse Addition in Convex Analysis and Applications" (PDF). Journal of Mathematical Analysis and Applications. 148 (2). Department of Mathematics, University of Washington, Seattle, Washington, USA: Academic Press, Inc.: 317–349. doi:10.1016/0022-247X(90)90004-Y. Archived (PDF) from the original on 2020-08-20. Retrieved 2020-08-20. (33 pages)
- Bryant, Randal E.; Tygar, J. Doug; Huang, Lawrence P. (1994). "Geometric characterization of series-parallel variable resistor networks" (PDF). IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications. 41 (11): 686–698. doi:10.1109/81.331520. Archived from the original (PDF) on 2017-08-14.
- Antezana, Jorge; Corach, Gustavo; Stojanoff, Demetrio (April 2006) . "Bilateral Shorted Operators and Parallel Sums" (PDF). Linear Algebra and Its Applications. 414 (2–3). La Plata, Argentina & Buenos Aires, Argentina: 570–588. arXiv:math/0509327. doi:10.1016/j.laa.2005.10.039. Archived (PDF) from the original on 2017-08-09. Retrieved 2020-08-20. (19 pages)
- Chansangiam, Pattrawut (February 2016) . "Mathematical aspects for electrical network connections". KKU Engineering Journal. 43 (1): 47–54. doi:10.14456/kkuenj.2016.8. Archived (PDF) from the original on 2020-08-20. Retrieved 2020-08-20.
- Besenyei, Ádám (2016-09-01). "The irresistible inequality of Milne" (PDF). Budapest: Department of Applied Analysis and Computational Mathematics, Eötvös Loránd University. CIA2016. Archived (PDF) from the original on 2019-08-08. Retrieved 2019-08-11.
- "7.5 Electrical Characteristics: VCC = 5 V / 7.6 Electrical Characteristics: VCC = 2.7 V / 9.1.2.1 Inverting Comparator with Hysteresis". TLV3201, TLV3202: TLV320x 40-ns, microPOWER, Push-Pull Output Comparators (PDF). Revision B. Dallas, Texas, USA: Texas Instruments Incorporated. 2022-06-03 . pp. 5, 6, 13–14 . SBOS561B. Archived (PDF) from the original on 2022-08-17. Retrieved 2022-08-18. p. 5:
PARAMETER TYP UNIT INPUT IMPEDANCE Common mode 10 ∥ 2 Ω ∥ pF Differential 10 ∥ 4 Ω ∥ pF
(37 pages) (NB. Unusual usage of ∥ for both values and units.)
 .
. (pronounced "parallel", following the
(pronounced "parallel", following the 
 are elements of the
are elements of the 
 :
:

 :
:

 representing the
representing the  meaning the
meaning the  and
and  are distinct positive real numbers then
are distinct positive real numbers then 
 represent the
represent the  and
and  the
the  to
to  One has identities
One has identities



 satisfies a variety of basic identities.
satisfies a variety of basic identities.


 while for multiplication the identity is 1:
while for multiplication the identity is 1:

 the additive inverse under addition. (But 0 has no inverse under parallel.)
the additive inverse under addition. (But 0 has no inverse under parallel.)


 of
of  :
:











 in
in  (with
(with  ) can be
) can be 
 (possibly repeated) in
(possibly repeated) in 

 for some k.
for some k.


 is no longer a field under parallel and multiplication, because 0 has no inverse under parallel. (This is analogous to the way
is no longer a field under parallel and multiplication, because 0 has no inverse under parallel. (This is analogous to the way  is not a field because
is not a field because 
 can either be left undefined (see
can either be left undefined (see 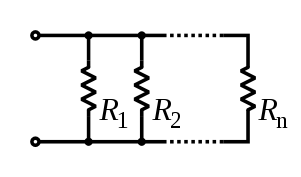



 ,
,  and
and  are connected in
are connected in 



 . Note that this is a mathematical operator and does not say anything about the actual configuration. In the case of resistors the parallel operator is used for parallel resistors, but for other components (like capacitors) this is not the case.
. Note that this is a mathematical operator and does not say anything about the actual configuration. In the case of resistors the parallel operator is used for parallel resistors, but for other components (like capacitors) this is not the case. 