Misplaced Pages

In mathematics, a fundamental pair of periods is an ordered pair of complex numbers that defines a lattice in the complex plane. This type of lattice is the underlying object with which elliptic functions and modular forms are defined.

Definition

A fundamental pair of periods is a pair of complex numbers ${\displaystyle \omega _{1},\omega _{2}\in \mathbb {C} }$ such that their ratio ${\displaystyle \omega _{2}/\omega _{1}}$ is not real. If considered as vectors in ${\displaystyle \mathbb {R} ^{2}}$, the two are linearly independent. The lattice generated by ${\displaystyle \omega _{1}}$ and ${\displaystyle \omega _{2}}$ is

${\displaystyle \Lambda =\left\{m\omega _{1}+n\omega _{2}\mid m,n\in \mathbb {Z} \right\}.}$

This lattice is also sometimes denoted as ${\displaystyle \Lambda (\omega _{1},\omega _{2})}$ to make clear that it depends on ${\displaystyle \omega _{1}}$ and ${\displaystyle \omega _{2}.}$ It is also sometimes denoted by ${\displaystyle \Omega {\vphantom {(}}}$ or ${\displaystyle \Omega (\omega _{1},\omega _{2}),}$ or simply by ${\displaystyle (\omega _{1},\omega _{2}).}$ The two generators ${\displaystyle \omega _{1}}$ and ${\displaystyle \omega _{2}}$ are called the lattice basis. The parallelogram with vertices ${\displaystyle (0,\omega _{1},\omega _{1}+\omega _{2},\omega _{2})}$ is called the fundamental parallelogram.

While a fundamental pair generates a lattice, a lattice does not have any unique fundamental pair; in fact, an infinite number of fundamental pairs correspond to the same lattice.

Algebraic properties

A number of properties, listed below, can be seen.

Equivalence

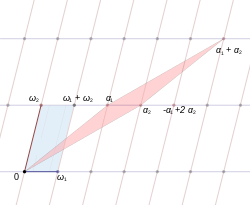
Two pairs of complex numbers ${\displaystyle (\omega _{1},\omega _{2})}$ and ${\displaystyle (\alpha _{1},\alpha _{2})}$ are called equivalent if they generate the same lattice: that is, if ${\displaystyle \Lambda (\omega _{1},\omega _{2})=\Lambda (\alpha _{1},\alpha _{2}).}$

No interior points

The fundamental parallelogram contains no further lattice points in its interior or boundary. Conversely, any pair of lattice points with this property constitute a fundamental pair, and furthermore, they generate the same lattice.

Modular symmetry

Two pairs ${\displaystyle (\omega _{1},\omega _{2})}$ and ${\displaystyle (\alpha _{1},\alpha _{2})}$ are equivalent if and only if there exists a 2 × 2 matrix ${\textstyle {\begin{pmatrix}a&b\\c&d\end{pmatrix}}}$ with integer entries ${\displaystyle a,}$ ${\displaystyle b,}$ ${\displaystyle c,}$ and ${\displaystyle d}$ and determinant ${\displaystyle ad-bc=\pm 1}$ such that

${\displaystyle {\begin{pmatrix}\alpha _{1}\\\alpha _{2}\end{pmatrix}}={\begin{pmatrix}a&b\\c&d\end{pmatrix}}{\begin{pmatrix}\omega _{1}\\\omega _{2}\end{pmatrix}},}$

that is, so that

${\displaystyle {\begin{aligned}\alpha _{1}=a\omega _{1}+b\omega _{2},\\\alpha _{2}=c\omega _{1}+d\omega _{2}.\end{aligned}}}$

This matrix belongs to the modular group ${\displaystyle \mathrm {SL} (2,\mathbb {Z} ).}$ This equivalence of lattices can be thought of as underlying many of the properties of elliptic functions (especially the Weierstrass elliptic function) and modular forms.

Topological properties

The abelian group ${\displaystyle \mathbb {Z} ^{2}}$ maps the complex plane into the fundamental parallelogram. That is, every point ${\displaystyle z\in \mathbb {C} }$ can be written as ${\displaystyle z=p+m\omega _{1}+n\omega _{2}}$ for integers ${\displaystyle m,n}$ with a point ${\displaystyle p}$ in the fundamental parallelogram.

Since this mapping identifies opposite sides of the parallelogram as being the same, the fundamental parallelogram has the topology of a torus. Equivalently, one says that the quotient manifold ${\displaystyle \mathbb {C} /\Lambda }$ is a torus.

Fundamental region

Define ${\displaystyle \tau =\omega _{2}/\omega _{1}}$ to be the half-period ratio. Then the lattice basis can always be chosen so that ${\displaystyle \tau }$ lies in a special region, called the fundamental domain. Alternately, there always exists an element of the projective special linear group ${\displaystyle \operatorname {PSL} (2,\mathbb {Z} )}$ that maps a lattice basis to another basis so that ${\displaystyle \tau }$ lies in the fundamental domain.

The fundamental domain is given by the set ${\displaystyle D,}$ which is composed of a set ${\displaystyle U}$ plus a part of the boundary of ${\displaystyle U}$:

${\displaystyle U=\left\{z\in H:\left|z\right|>1,\,\left|\operatorname {Re} (z)\right|<{\tfrac {1}{2}}\right\}.}$

where ${\displaystyle H}$ is the upper half-plane.

The fundamental domain ${\displaystyle D}$ is then built by adding the boundary on the left plus half the arc on the bottom:

${\displaystyle D=U\cup \left\{z\in H:\left|z\right|\geq 1,\,\operatorname {Re} (z)=-{\tfrac {1}{2}}\right\}\cup \left\{z\in H:\left|z\right|=1,\,\operatorname {Re} (z)\leq 0\right\}.}$

Three cases pertain:

• If ${\displaystyle \tau \neq i}$ and ${\textstyle \tau \neq e^{i\pi /3}}$, then there are exactly two lattice bases with the same ${\displaystyle \tau }$ in the fundamental region: ${\displaystyle (\omega _{1},\omega _{2})}$ and ${\displaystyle (-\omega _{1},-\omega _{2}).}$
• If ${\displaystyle \tau =i}$, then four lattice bases have the same ${\displaystyle \tau }$: the above two ${\displaystyle (\omega _{1},\omega _{2})}$, ${\displaystyle (-\omega _{1},-\omega _{2})}$ and ${\displaystyle (i\omega _{1},i\omega _{2})}$, ${\displaystyle (-i\omega _{1},-i\omega _{2}).}$
• If ${\textstyle \tau =e^{i\pi /3}}$, then there are six lattice bases with the same ${\displaystyle \tau }$: ${\displaystyle (\omega _{1},\omega _{2})}$, ${\displaystyle (\tau \omega _{1},\tau \omega _{2})}$, ${\displaystyle (\tau ^{2}\omega _{1},\tau ^{2}\omega _{2})}$ and their negatives.

In the closure of the fundamental domain: ${\displaystyle \tau =i}$ and ${\textstyle \tau =e^{i\pi /3}.}$

See also

• A number of alternative notations for the lattice and for the fundamental pair exist, and are often used in its place. See, for example, the articles on the nome, elliptic modulus, quarter period and half-period ratio.
• Elliptic curve
• Modular form
• Eisenstein series

References

• Tom M. Apostol, Modular functions and Dirichlet Series in Number Theory (1990), Springer-Verlag, New York. ISBN 0-387-97127-0 (See chapters 1 and 2.)
• Jurgen Jost, Compact Riemann Surfaces (2002), Springer-Verlag, New York. ISBN 3-540-43299-X (See chapter 2.)

• Riemann surfaces
• Modular forms
• Elliptic functions
• Lattice points