 A miniature 16 MHz quartz crystal enclosed in a hermetically sealed HC-49/S package, used as the resonator in a crystal oscillator. A miniature 16 MHz quartz crystal enclosed in a hermetically sealed HC-49/S package, used as the resonator in a crystal oscillator. | |
| Type | Electromechanical |
|---|---|
| Working principle | Piezoelectricity, Resonance |
| Inventor | Alexander M. Nicholson, Walter Guyton Cady |
| First production | 1918 |
| Electronic symbol | |
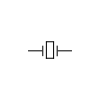 | |
A crystal oscillator is an electronic oscillator circuit that uses a piezoelectric crystal as a frequency-selective element. The oscillator frequency is often used to keep track of time, as in quartz wristwatches, to provide a stable clock signal for digital integrated circuits, and to stabilize frequencies for radio transmitters and receivers. The most common type of piezoelectric resonator used is a quartz crystal, so oscillator circuits incorporating them became known as crystal oscillators. However, other piezoelectric materials including polycrystalline ceramics are used in similar circuits.
A crystal oscillator relies on the slight change in shape of a quartz crystal under an electric field, a property known as inverse piezoelectricity. A voltage applied to the electrodes on the crystal causes it to change shape; when the voltage is removed, the crystal generates a small voltage as it elastically returns to its original shape. The quartz oscillates at a stable resonant frequency (relative to other low-priced oscillators) with frequency accuracy measured in parts per million (ppm). It behaves like an RLC circuit, but with a much higher Q factor (lower energy loss on each cycle of oscillation and higher frequency selectivity) than can be reliably achieved with discrete capacitors (C) and inductors (L), which suffer from parasitic resistance (R). Once a quartz crystal is adjusted to a particular frequency (which is affected by the mass of electrodes attached to the crystal, the orientation of the crystal, temperature and other factors), it maintains that frequency with high stability.
Quartz crystals are manufactured for frequencies from a few tens of kilohertz to hundreds of megahertz. As of 2003, around two billion crystals were manufactured annually. Most are used for consumer devices such as wristwatches, clocks, radios, computers, and cellphones. However, in applications where small size and weight is needed crystals can be replaced by thin-film bulk acoustic resonators, specifically if ultra-high frequency (more than roughly 1.5 GHz) resonance is needed. Quartz crystals are also found inside test and measurement equipment, such as counters, signal generators, and oscilloscopes.
Terminology

A crystal oscillator is an electric oscillator type circuit that uses a piezoelectric resonator, a crystal, as its frequency-determining element. Crystal is the common term used in electronics for the frequency-determining component, a wafer of quartz crystal or ceramic with electrodes connected to it. A more accurate term for "crystal" is piezoelectric resonator. Crystals are also used in other types of electronic circuits, such as crystal filters.
Piezoelectric resonators are sold as separate components for use in crystal oscillator circuits. They are also often incorporated in a single package with the crystal oscillator circuit.
History


Piezoelectricity was discovered by Jacques and Pierre Curie in 1880. Paul Langevin first investigated quartz resonators for use in sonar during World War I. The first crystal-controlled oscillator, using a crystal of Rochelle salt, was built in 1917 and patented in 1918 by Alexander M. Nicholson at Bell Telephone Laboratories, although his priority was disputed by Walter Guyton Cady. Cady built the first quartz crystal oscillator in 1921. Other early innovators in quartz crystal oscillators include G. W. Pierce and Louis Essen.
Quartz crystal oscillators were developed for high-stability frequency references during the 1920s and 1930s. Prior to crystals, radio stations controlled their frequency with tuned circuits, which could easily drift off frequency by 3–4 kHz. Since broadcast stations were assigned frequencies only 10 kHz (Americas) or 9 kHz (elsewhere) apart, interference between adjacent stations due to frequency drift was a common problem. In 1925, Westinghouse installed a crystal oscillator in its flagship station KDKA, and by 1926, quartz crystals were used to control the frequency of many broadcasting stations and were popular with amateur radio operators. In 1928, Warren Marrison of Bell Laboratories developed the first quartz-crystal clock. With accuracies of up to 1 second in 30 years (30 ms/y, or 0.95 ns/s), quartz clocks replaced precision pendulum clocks as the world's most accurate timekeepers until atomic clocks were developed in the 1950s. Using the early work at Bell Laboratories, American Telephone and Telegraph Company (AT&T) eventually established their Frequency Control Products division, later spun off and known today as Vectron International.
A number of firms started producing quartz crystals for electronic use during this time. Using what are now considered primitive methods, about 100,000 crystal units were produced in the United States during 1939. Through World War II crystals were made from natural quartz crystal, virtually all from Brazil. Shortages of crystals during the war caused by the demand for accurate frequency control of military and naval radios and radars spurred postwar research into culturing synthetic quartz, and by 1950 a hydrothermal process for growing quartz crystals on a commercial scale was developed at Bell Laboratories. By the 1970s virtually all crystals used in electronics were synthetic.
In 1968, Juergen Staudte invented a photolithographic process for manufacturing quartz crystal oscillators while working at North American Aviation (now Rockwell) that allowed them to be made small enough for portable products like watches.
Although crystal oscillators still most commonly use quartz crystals, devices using other materials are becoming more common, such as ceramic resonators.

Principle
A crystal is a solid in which the constituent atoms, molecules, or ions are packed in a regularly ordered, repeating pattern extending in all three spatial dimensions.
Almost any object made of an elastic material could be used like a crystal, with appropriate transducers, since all objects have natural resonant frequencies of vibration. For example, steel is very elastic and has a high speed of sound. It was often used in mechanical filters before quartz. The resonant frequency depends on size, shape, elasticity, and the speed of sound in the material. High-frequency crystals are typically cut in the shape of a simple rectangle or circular disk. Low-frequency crystals, such as those used in digital watches, are typically cut in the shape of a tuning fork. For applications not needing very precise timing, a low-cost ceramic resonator is often used in place of a quartz crystal.
When a crystal of quartz is properly cut and mounted, it can be made to distort in an electric field by applying a voltage to an electrode near or on the crystal. This property is known as inverse piezoelectricity. When the field is removed, the quartz generates an electric field as it returns to its previous shape, and this can generate a voltage. The result is that a quartz crystal behaves like an RLC circuit, composed of an inductor, capacitor and resistor, with a precise resonant frequency.
Quartz has the further advantage that its elastic constants and its size change in such a way that the frequency dependence on temperature can be very low. The specific characteristics depend on the mode of vibration and the angle at which the quartz is cut (relative to its crystallographic axes). Therefore, the resonant frequency of the plate, which depends on its size, does not change much. This means that a quartz clock, filter or oscillator remains accurate. For critical applications the quartz oscillator is mounted in a temperature-controlled container, called a crystal oven, and can also be mounted on shock absorbers to prevent perturbation by external mechanical vibrations.
Modeling
Electrical model
A quartz crystal can be modeled as an electrical network with low-impedance (series) and high-impedance (parallel) resonance points spaced closely together. Mathematically, using the Laplace transform, the impedance of this network can be written as:

or
where is the complex frequency (), is the series resonant angular frequency, and is the parallel resonant angular frequency.
Adding capacitance across a crystal causes the (parallel) resonant frequency to decrease. Adding inductance across a crystal causes the (parallel) resonant frequency to increase. These effects can be used to adjust the frequency at which a crystal oscillates. Crystal manufacturers normally cut and trim their crystals to have a specified resonant frequency with a known "load" capacitance added to the crystal. For example, a crystal intended for a 6 pF load has its specified parallel resonant frequency when a 6.0 pF capacitor is placed across it. Without the load capacitance, the resonant frequency is higher.
Resonance modes
A quartz crystal provides both series and parallel resonance. The series resonance is a few kilohertz lower than the parallel one. Crystals below 30 MHz are generally operated between series and parallel resonance, which means that the crystal appears as an inductive reactance in operation, this inductance forming a parallel resonant circuit with externally connected parallel capacitance.

Any small additional capacitance in parallel with the crystal pulls the frequency lower. Moreover, the effective inductive reactance of the crystal can be reduced by adding a capacitor in series with the crystal. This latter technique can provide a useful method of trimming the oscillatory frequency within a narrow range; in this case inserting a capacitor in series with the crystal raises the frequency of oscillation. For a crystal to operate at its specified frequency, the electronic circuit has to be exactly that specified by the crystal manufacturer. Note that these points imply a subtlety concerning crystal oscillators in this frequency range: the crystal does not usually oscillate at precisely either of its resonant frequencies.
Crystals above 30 MHz (up to >200 MHz) are generally operated at series resonance where the impedance appears at its minimum and equal to the series resistance. For these crystals the series resistance is specified (<100 Ω) instead of the parallel capacitance. To reach higher frequencies, a crystal can be made to vibrate at one of its overtone modes, which occur near multiples of the fundamental resonant frequency. Only odd numbered overtones are used. Such a crystal is referred to as a 3rd, 5th, or even 7th overtone crystal. To accomplish this, the oscillator circuit usually includes additional LC circuits to select the desired overtone.
Temperature effects
A crystal's frequency characteristic depends on the shape or "cut" of the crystal. A tuning-fork crystal is usually cut such that its frequency dependence on temperature is quadratic with the maximum around 25 °C. This means that a tuning-fork crystal oscillator resonates close to its target frequency at room temperature, but slows when the temperature either increases or decreases from room temperature. A common parabolic coefficient for a 32 kHz tuning-fork crystal is −0.04 ppm/°C:
In a real application, this means that a clock built using a regular 32 kHz tuning-fork crystal keeps good time at room temperature, but loses 2 minutes per year at 10 °C above or below room temperature and loses 8 minutes per year at 20 °C above or below room temperature due to the quartz crystal.
Crystal oscillator circuits
The crystal oscillator circuit sustains oscillation by taking a voltage signal from the quartz resonator, amplifying it, and feeding it back to the resonator. The rate of expansion and contraction of the quartz is the resonant frequency, and is determined by the cut and size of the crystal. When the energy of the generated output frequencies matches the losses in the circuit, an oscillation can be sustained.
An oscillator crystal has two electrically conductive plates, with a slice or tuning fork of quartz crystal sandwiched between them. During startup, the controlling circuit places the crystal into an unstable equilibrium, and due to the positive feedback in the system, any tiny fraction of noise is amplified, ramping up the oscillation. The crystal resonator can also be seen as a highly frequency-selective filter in this system: it only passes a very narrow subband of frequencies around the resonant one, attenuating everything else. Eventually, only the resonant frequency is active. As the oscillator amplifies the signals coming out of the crystal, the signals in the crystal's frequency band becomes stronger, eventually dominating the output of the oscillator. The narrow resonance band of the quartz crystal filters out the unwanted frequencies.
The output frequency of a quartz oscillator can be either that of the fundamental resonance or of a multiple of that resonance, called a harmonic frequency. Harmonics are an exact integer multiple of the fundamental frequency. But, like many other mechanical resonators, crystals exhibit several modes of oscillation, usually at approximately odd integer multiples of the fundamental frequency. These are termed "overtone modes", and oscillator circuits can be designed to excite them. The overtone modes are at frequencies which are approximate, but not exact odd integer multiples of that of the fundamental mode, and overtone frequencies are therefore not exact harmonics of the fundamental.
High frequency crystals are often designed to operate at third, fifth, or seventh overtones. Manufacturers have difficulty producing crystals thin enough to produce fundamental frequencies over 30 MHz. To produce higher frequencies, manufacturers make overtone crystals tuned to put the 3rd, 5th, or 7th overtone at the desired frequency, because they are thicker and therefore easier to manufacture than a fundamental crystal that would produce the same frequency—although exciting the desired overtone frequency requires a slightly more complicated oscillator circuit. A fundamental crystal oscillator circuit is simpler and more efficient and has more pullability than a third overtone circuit. Depending on the manufacturer, the highest available fundamental frequency may be 25 MHz to 66 MHz.

A major reason for the wide use of crystal oscillators is their high Q factor. A typical Q value for a quartz oscillator ranges from 10 to 10, compared to perhaps 10 for an LC oscillator. The maximum Q for a high stability quartz oscillator can be estimated as Q = 1.6 × 10/f, where f is the resonant frequency in megahertz.
One of the most important traits of quartz crystal oscillators is that they can exhibit very low phase noise. In many oscillators, any spectral energy at the resonant frequency is amplified by the oscillator, resulting in a collection of tones at different phases. In a crystal oscillator, the crystal mostly vibrates in one axis, therefore only one phase is dominant. This property of low phase noise makes them particularly useful in telecommunications where stable signals are needed, and in scientific equipment where very precise time references are needed.
Environmental changes of temperature, humidity, pressure, and vibration can change the resonant frequency of a quartz crystal, but there are several designs that reduce these environmental effects. These include the TCXO, MCXO, and OCXO which are defined below. These designs, particularly the OCXO, often produce devices with excellent short-term stability. The limitations in short-term stability are due mainly to noise from electronic components in the oscillator circuits. Long-term stability is limited by aging of the crystal.
Due to aging and environmental factors (such as temperature and vibration), it is difficult to keep even the best quartz oscillators within one part in 10 of their nominal frequency without constant adjustment. For this reason, atomic oscillators are used for applications requiring better long-term stability and accuracy.
Spurious frequencies

For crystals operated at series resonance or pulled away from the main mode by the inclusion of a series inductor or capacitor, significant (and temperature-dependent) spurious responses may be experienced. Though most spurious modes are typically some tens of kilohertz above the wanted series resonance, their temperature coefficient is different from the main mode, and the spurious response may move through the main mode at certain temperatures. Even if the series resistances at the spurious resonances appear higher than the one at the wanted frequency, a rapid change in the main mode series resistance can occur at specific temperatures when the two frequencies are coincidental. A consequence of these activity dips is that the oscillator may lock at a spurious frequency at specific temperatures. This is generally minimized by ensuring that the maintaining circuit has insufficient gain to activate unwanted modes.
Spurious frequencies are also generated by subjecting the crystal to vibration. This modulates the resonant frequency to a small degree by the frequency of the vibrations. SC-cut (Stress Compensated) crystals are designed to minimize the frequency effect of mounting stress and they are therefore less sensitive to vibration. Acceleration effects including gravity are also reduced with SC-cut crystals, as is frequency change with time due to long term mounting stress variation. There are disadvantages with SC-cut shear mode crystals, such as the need for the maintaining oscillator to discriminate against other closely related unwanted modes and increased frequency change due to temperature when subject to a full ambient range. SC-cut crystals are most advantageous where temperature control at their temperature of zero temperature coefficient (turnover) is possible, under these circumstances an overall stability performance from premium units can approach the stability of rubidium frequency standards.
Commonly used crystal frequencies
Main article: Crystal oscillator frequenciesCrystals can be manufactured for oscillation over a wide range of frequencies, from a few kilohertz up to several hundred megahertz. Many applications call for a crystal oscillator frequency conveniently related to some other desired frequency, so hundreds of standard crystal frequencies are made in large quantities and stocked by electronics distributors. For example 3.579545 MHz crystals, which were made in large quantities for NTSC color television receivers, are now popular for many non-television applications (although most modern television receivers now use other frequency crystals for the color decoder). Using frequency dividers, frequency multipliers and phase-locked loop circuits, it is practical to derive a wide range of frequencies from one reference frequency.
Crystal structures and materials
Quartz








The most common material for oscillator crystals is quartz. At the beginning of the technology, natural quartz crystals were used but now synthetic crystalline quartz grown by hydrothermal synthesis is predominant due to higher purity, lower cost and more convenient handling. One of the few remaining uses of natural crystals is for pressure transducers in deep wells. During World War II and for some time afterwards, natural quartz was considered a strategic material by the USA. Large crystals were imported from Brazil. Raw "lascas", the source material quartz for hydrothermal synthesis, are imported to USA or mined locally by Coleman Quartz. The average value of as-grown synthetic quartz in 1994 was 60 USD/kg.
Types
Two types of quartz crystals exist: left-handed and right-handed. The two differ in their optical rotation but they are identical in other physical properties. Both left and right-handed crystals can be used for oscillators, if the cut angle is correct. In manufacture, right-handed quartz is generally used. The SiO4 tetrahedrons form parallel helices; the direction of twist of the helix determines the left- or right-hand orientation. The helixes are aligned along the c-axis and merged, sharing atoms. The mass of the helixes forms a mesh of small and large channels parallel to the c-axis. The large ones are large enough to allow some mobility of smaller ions and molecules through the crystal.
Quartz exists in several phases. At 573 °C at 1 atmosphere (and at higher temperatures and higher pressures) the α-quartz undergoes quartz inversion, transforms reversibly to β-quartz. The reverse process however is not entirely homogeneous and crystal twinning occurs. Care must be taken during manufacturing and processing to avoid phase transformation. Other phases, e.g. the higher-temperature phases tridymite and cristobalite, are not significant for oscillators. All quartz oscillator crystals are the α-quartz type.
Quality
Infrared spectrophotometry is used as one of the methods for measuring the quality of the grown crystals. The wavenumbers 3585, 3500, and 3410 cm are commonly used. The measured value is based on the absorption bands of the OH radical and the infrared Q value is calculated. The electronic grade crystals, grade C, have Q of 1.8 million or above; the premium grade B crystals have Q of 2.2 million, and special premium grade A crystals have Q of 3.0 million. The Q value is calculated only for the z region; crystals containing other regions can be adversely affected. Another quality indicator is the etch channel density; when the crystal is etched, tubular channels are created along linear defects. For processing involving etching, e.g. the wristwatch tuning fork crystals, low etch channel density is desirable. The etch channel density for swept quartz is about 10–100 and significantly more for unswept quartz. Presence of etch channels and etch pits degrades the resonator's Q and introduces nonlinearities.
Production
See also: Crystal growthQuartz crystals can be grown for specific purposes.
Crystals for AT-cut are the most common in mass production of oscillator materials; the shape and dimensions are optimized for high yield of the required wafers. High-purity quartz crystals are grown with especially low content of aluminium, alkali metal and other impurities and minimal defects; the low amount of alkali metals provides increased resistance to ionizing radiation. Crystals for wrist watches, for cutting the tuning fork 32768 Hz crystals, are grown with very low etch channel density.
Crystals for SAW devices are grown as flat, with large X-size seed with low etch channel density.
Special high-Q crystals, for use in highly stable oscillators, are grown at constant slow speed and have constant low infrared absorption along the entire Z axis. Crystals can be grown as Y-bar, with a seed crystal in bar shape and elongated along the Y axis, or as Z-plate, grown from a plate seed with Y-axis direction length and X-axis width. The region around the seed crystal contains a large number of crystal defects and should not be used for the wafers.
Crystals grow anisotropically; the growth along the Z axis is up to 3 times faster than along the X axis. The growth direction and rate also influences the rate of uptake of impurities. Y-bar crystals, or Z-plate crystals with long Y axis, have four growth regions usually called +X, −X, Z, and S. The distribution of impurities during growth is uneven; different growth areas contain different levels of contaminants. The Z regions are the purest, the small occasionally present S regions are less pure, the +X region is yet less pure, and the -X region has the highest level of impurities. The impurities have a negative impact on radiation hardness, susceptibility to twinning, filter loss, and long and short term stability of the crystals. Different-cut seeds in different orientations may provide other kinds of growth regions. The growth speed of the −X direction is slowest due to the effect of adsorption of water molecules on the crystal surface; aluminium impurities suppress growth in two other directions. The content of aluminium is lowest in Z region, higher in +X, yet higher in −X, and highest in S; the size of S regions also grows with increased amount of aluminium present. The content of hydrogen is lowest in Z region, higher in +X region, yet higher in S region, and highest in −X. Aluminium inclusions transform into color centers with gamma-ray irradiation, causing a darkening of the crystal proportional to the dose and level of impurities; the presence of regions with different darkness reveals the different growth regions.
The dominant type of defect of concern in quartz crystals is the substitution of an Al(III) for a Si(IV) atom in the crystal lattice. The aluminium ion has an associated interstitial charge compensator present nearby, which can be a H ion (attached to the nearby oxygen and forming a hydroxyl group, called Al−OH defect), Li ion, Na ion, K ion (less common), or an electron hole trapped in a nearby oxygen atom orbital. The composition of the growth solution, whether it is based on lithium or sodium alkali compounds, determines the charge compensating ions for the aluminium defects. The ion impurities are of concern as they are not firmly bound and can migrate through the crystal, altering the local lattice elasticity and the resonant frequency of the crystal. Other common impurities of concern are e.g. iron(III) (interstitial), fluorine, boron(III), phosphorus(V) (substitution), titanium(IV) (substitution, universally present in magmatic quartz, less common in hydrothermal quartz), and germanium(IV) (substitution). Sodium and iron ions can cause inclusions of acnite and elemeusite crystals. Inclusions of water may be present in fast-grown crystals; interstitial water molecules are abundant near the crystal seed. Another defect of importance is the hydrogen containing growth defect, when instead of a Si−O−Si structure, a pair of Si−OH HO−Si groups is formed; essentially a hydrolyzed bond. Fast-grown crystals contain more hydrogen defects than slow-grown ones. These growth defects source as supply of hydrogen ions for radiation-induced processes and forming Al-OH defects. Germanium impurities tend to trap electrons created during irradiation; the alkali metal cations then migrate towards the negatively charged center and form a stabilizing complex. Matrix defects can also be present; oxygen vacancies, silicon vacancies (usually compensated by 4 hydrogens or 3 hydrogens and a hole), peroxy groups, etc. Some of the defects produce localized levels in the forbidden band, serving as charge traps; Al(III) and B(III) typically serve as hole traps while electron vacancies, titanium, germanium, and phosphorus atoms serve as electron traps. The trapped charge carriers can be released by heating; their recombination is the cause of thermoluminescence.
The mobility of interstitial ions depends strongly on temperature. Hydrogen ions are mobile down to 10 K, but alkali metal ions become mobile only at temperatures around and above 200 K. The hydroxyl defects can be measured by near-infrared spectroscopy. The trapped holes can be measured by electron spin resonance. The Al−Na defects show as an acoustic loss peak due to their stress-induced motion; the Al−Li defects do not form a potential well so are not detectable this way. Some of the radiation-induced defects during their thermal annealing produce thermoluminescence; defects related to aluminium, titanium, and germanium can be distinguished.
Swept crystals are crystals that have undergone a solid-state electrodiffusion purification process. Sweeping involves heating the crystal above 500 °C in a hydrogen-free atmosphere, with a voltage gradient of at least 1 kV/cm, for several hours (usually over 12). The migration of impurities and the gradual replacement of alkali metal ions with hydrogen (when swept in air) or electron holes (when swept in vacuum) causes a weak electric current through the crystal; decay of this current to a constant value signals the end of the process. The crystal is then left to cool, while the electric field is maintained. The impurities are concentrated at the cathode region of the crystal, which is cut off afterwards and discarded. Swept crystals have increased resistance to radiation, as the dose effects are dependent on the level of alkali metal impurities; they are suitable for use in devices exposed to ionizing radiation, e.g. for nuclear and space technology. Sweeping under vacuum at higher temperatures and higher field strengths yields yet more radiation-hard crystals. The level and character of impurities can be measured by infrared spectroscopy. Quartz can be swept in both α and β phase; sweeping in β phase is faster, but the phase transition may induce twinning. Twinning can be mitigated by subjecting the crystal to compression stress in the X direction, or an AC or DC electric field along the X axis while the crystal cools through the phase transformation temperature region.
Sweeping can also be used to introduce one kind of an impurity into the crystal. Lithium, sodium, and hydrogen swept crystals are used for, e.g., studying quartz behavior.
Very small crystals for high fundamental-mode frequencies can be manufactured by photolithography.
Crystals can be adjusted to exact frequencies by laser trimming. A technique used in the world of amateur radio for slight decrease of the crystal frequency may be achieved by exposing crystals with silver electrodes to vapors of iodine, which causes a slight mass increase on the surface by forming a thin layer of silver iodide; such crystals however had problematic long-term stability. Another method commonly used is electrochemical increase or decrease of silver electrode thickness by submerging a resonator in lapis lazuli dissolved in water, citric acid in water, or water with salt, and using the resonator as one electrode, and a small silver electrode as the other.
By choosing the direction of current one can either increase or decrease the mass of the electrodes. Details were published in "Radio" magazine (3/1978) by UB5LEV.
Raising frequency by scratching off parts of the electrodes is not advised as this may damage the crystal and lower its Q factor. Capacitor trimmers can be also used for frequency adjustment of the oscillator circuit.
Other materials
Some other piezoelectric materials than quartz can be employed. These include single crystals of lithium tantalate, lithium niobate, lithium borate, berlinite, gallium arsenide, lithium tetraborate, aluminium phosphate, bismuth germanium oxide, polycrystalline zirconium titanate ceramics, high-alumina ceramics, silicon-zinc oxide composite, or dipotassium tartrate. Some materials may be more suitable for specific applications. An oscillator crystal can be also manufactured by depositing the resonator material on the silicon chip surface. Crystals of gallium phosphate, langasite, langanite and langatate are about 10 times more pullable than the corresponding quartz crystals, and are used in some VCXO oscillators.
Stability
The frequency stability is determined by the crystal's Q. It is inversely dependent on the frequency, and on the constant that is dependent on the particular cut. Other factors influencing Q are the overtone used, the temperature, the level of driving of the crystal, the quality of the surface finish, the mechanical stresses imposed on the crystal by bonding and mounting, the geometry of the crystal and the attached electrodes, the material purity and defects in the crystal, type and pressure of the gas in the enclosure, interfering modes, and presence and absorbed dose of ionizing and neutron radiation.
The stability of AT cut crystals decreases with increasing frequency. For more accurate higher frequencies it is better to use a crystal with lower fundamental frequency, operating at an overtone.
A badly designed oscillator circuit may suddenly begin oscillating on an overtone. In 1972, a train in Fremont, California crashed due to a faulty oscillator. An inappropriate value of the tank capacitor caused the crystal in a control board to be overdriven, jumping to an overtone, and causing the train to speed up instead of slowing down.
Temperature
Temperature influences the operating frequency; various forms of compensation are used, from analog compensation (TCXO) and microcontroller compensation (MCXO) to stabilization of the temperature with a crystal oven (OCXO). The crystals possess temperature hysteresis; the frequency at a given temperature achieved by increasing the temperature is not equal to the frequency on the same temperature achieved by decreasing the temperature. The temperature sensitivity depends primarily on the cut; the temperature compensated cuts are chosen as to minimize frequency/temperature dependence. Special cuts can be made with linear temperature characteristics; the LC cut is used in quartz thermometers. Other influencing factors are the overtone used, the mounting and electrodes, impurities in the crystal, mechanical strain, crystal geometry, rate of temperature change, thermal history (due to hysteresis), ionizing radiation, and drive level.
Crystals tend to suffer anomalies in their frequency/temperature and resistance/temperature characteristics, known as activity dips. These are small downward frequency or upward resistance excursions localized at certain temperatures, with their temperature position dependent on the value of the load capacitors.
Mechanical stress
Mechanical stresses also influence the frequency. The stresses can be induced by mounting, bonding, and application of the electrodes, by differential thermal expansion of the mounting, electrodes, and the crystal itself, by differential thermal stresses when there is a temperature gradient present, by expansion or shrinkage of the bonding materials during curing, by the air pressure that is transferred to the ambient pressure within the crystal enclosure, by the stresses of the crystal lattice itself (nonuniform growth, impurities, dislocations), by the surface imperfections and damage caused during manufacture, and by the action of gravity on the mass of the crystal; the frequency can therefore be influenced by position of the crystal. Other dynamic stress inducing factors are shocks, vibrations, and acoustic noise. Some cuts are less sensitive to stresses; the SC (stress-compensated) cut is an example. Atmospheric pressure changes can also introduce deformations to the housing, influencing the frequency by changing stray capacitances.
Atmospheric humidity influences the thermal transfer properties of air, and can change electrical properties of plastics by diffusion of water molecules into their structure, altering the dielectric constants and electrical conductivity.
Other factors influencing the frequency are the power supply voltage, load impedance, magnetic fields, electric fields (in case of cuts that are sensitive to them, e.g., SC cuts), the presence and absorbed dose of γ-particles and ionizing radiation, and the age of the crystal.
Aging
Crystals undergo slow gradual change of frequency with time, known as aging. There are many mechanisms involved. The mounting and contacts may undergo relief of the built-in stresses. Molecules of contamination either from the residual atmosphere, outgassed from the crystal, electrodes or packaging materials, or introduced during sealing the housing can be adsorbed on the crystal surface, changing its mass; this effect is exploited in quartz crystal microbalances. The composition of the crystal can be gradually altered by outgassing, diffusion of atoms of impurities or migrating from the electrodes, or the lattice can be damaged by radiation. Slow chemical reactions may occur on or in the crystal, or on the inner surfaces of the enclosure. Electrode material, e.g. chromium or aluminium, can react with the crystal, creating layers of metal oxide and silicon; these interface layers can undergo changes in time. The pressure in the enclosure can change due to varying atmospheric pressure, temperature, leaks, or outgassing of the materials inside. Factors outside of the crystal itself are e.g. aging of the oscillator circuitry (and e.g. change of capacitances), and drift of parameters of the crystal oven. External atmosphere composition can also influence the aging; hydrogen can diffuse through nickel housing. Helium can cause similar issues when it diffuses through glass enclosures of rubidium standards.
Gold is a favored electrode material for low-aging resonators; its adhesion to quartz is strong enough to maintain contact even at strong mechanical shocks, but weak enough to not support significant strain gradients (unlike chromium, aluminium, and nickel). Gold also does not form oxides; it adsorbs organic contaminants from the air, but these are easy to remove. However, gold alone can undergo delamination; a layer of chromium is therefore sometimes used for improved binding strength. Silver and aluminium are often used as electrodes; however both form oxide layers with time that increases the crystal mass and lowers frequency. Silver can be passivated by exposition to iodine vapors, forming a layer of silver iodide. Aluminium oxidizes readily but slowly, until about 5 nm thickness is reached; increased temperature during artificial aging does not significantly increase the oxide forming speed; a thick oxide layer can be formed during manufacture by anodizing. Exposition of silver-plated crystal to iodine vapors can also be used in amateur conditions for lowering the crystal frequency slightly; the frequency can also be increased by scratching off parts of the electrodes, but that carries risk of damage to the crystal and loss of Q.
A DC voltage bias between the electrodes can accelerate the initial aging, probably by induced diffusion of impurities through the crystal. Placing a capacitor in series with the crystal and a several-megaohm resistor in parallel can minimize such voltages.
Aging decreases logarithmically with time, the largest changes occurring shortly after manufacture. Artificially aging a crystal by prolonged storage at 85 to 125 °C can increase its long-term stability.
Mechanical damage
Crystals are sensitive to shock. The mechanical stress causes a short-term change in the oscillator frequency due to the stress-sensitivity of the crystal, and can introduce a permanent change of frequency due to shock-induced changes of mounting and internal stresses (if the elastic limits of the mechanical parts are exceeded), desorption of contamination from the crystal surfaces, or change in parameters of the oscillator circuit. High magnitudes of shocks may tear the crystals off their mountings (especially in the case of large low-frequency crystals suspended on thin wires), or cause cracking of the crystal. Crystals free of surface imperfections are highly shock-resistant; chemical polishing can produce crystals able to survive tens of thousands of g.
Crystals have no inherent failure mechanisms; some have operated in devices for decades. Failures may be, however, introduced by faults in bonding, leaky enclosures, corrosion, frequency shift by aging, breaking the crystal by too high mechanical shock, or radiation-induced damage when non-swept quartz is used. Crystals can be also damaged by overdriving.
Frequency fluctuations
Crystals suffer from minor short-term frequency fluctuations as well. The main causes of such noise are e.g. thermal noise (which limits the noise floor), phonon scattering (influenced by lattice defects), adsorption/desorption of molecules on the surface of the crystal, noise of the oscillator circuits, mechanical shocks and vibrations, acceleration and orientation changes, temperature fluctuations, and relief of mechanical stresses. The short-term stability is measured by four main parameters: Allan variance (the most common one specified in oscillator data sheets), phase noise, spectral density of phase deviations, and spectral density of fractional frequency deviations. The effects of acceleration and vibration tend to dominate the other noise sources; surface acoustic wave devices tend to be more sensitive than bulk acoustic wave (BAW) ones, and the stress-compensated cuts are even less sensitive. The relative orientation of the acceleration vector to the crystal dramatically influences the crystal's vibration sensitivity. Mechanical vibration isolation mountings can be used for high-stability crystals.
Phase noise plays a significant role in frequency synthesis systems using frequency multiplication; a multiplication of a frequency by N increases the phase noise power by N. A frequency multiplication by 10 times multiplies the magnitude of the phase error by 10 times. This can be disastrous for systems employing PLL or FSK technologies.
Magnetic fields have little effect on the crystal itself, as quartz is diamagnetic; eddy currents or AC voltages can however be induced into the circuits, and magnetic parts of the mounting and housing may be influenced.
After the power-up, the crystals take several seconds to minutes to "warm up" and stabilize their frequency. The oven-controlled OCXOs require usually 3–10 minutes for heating up to reach thermal equilibrium; the oven-less oscillators stabilize in several seconds as the few milliwatts dissipated in the crystal cause a small but noticeable level of internal heating.
Drive level
The crystals have to be driven at the appropriate drive level. Low-frequency crystals, especially flexural-mode ones, may fracture at too high drive levels. The drive level is specified as the amount of power dissipated in the crystal. The appropriate drive levels are about 5 μW for flexural modes up to 100 kHz, 1 μW for fundamental modes at 1–4 MHz, 0.5 μW for fundamental modes 4–20 MHz and 0.5 μW for overtone modes at 20–200 MHz. Too low drive level may cause problems with starting the oscillator. Low drive levels are better for higher stability and lower power consumption of the oscillator. Higher drive levels, in turn, reduce the impact of noise by increasing the signal-to-noise ratio.
Crystal cuts
The resonator plate can be cut from the source crystal in many different ways. The orientation of the cut influences the crystal's aging characteristics, frequency stability, thermal characteristics, and other parameters. These cuts operate at bulk acoustic wave (BAW); for higher frequencies, surface acoustic wave (SAW) devices are employed.
| Cut | Frequency range | Mode | Angles | Description |
|---|---|---|---|---|
| AT | 500 kHz – 300 MHz | thickness shear (c mode, slow quasi-shear) | 35°15′, 0° (< 25 MHz) 35°18′, 0° (> 10 MHz) |
The most common cut, developed in 1934. The plate contains the crystal's x axis and is inclined by 35°15′ from the z (optical) axis. The frequency-temperature curve is a sine-shaped curve with inflection point at around 25~35 °C . Has frequency constant 1.661 MHz⋅mm. Most (estimated over 90%) of all crystals are this variant. Used for oscillators operating in wider temperature range, for a frequency range of 500 kHz–200 MHz; also used in oven-controlled oscillators. Sensitive to mechanical stresses, whether caused by external forces or by temperature gradients. Thickness-shear crystals typically operate in fundamental mode at 1–30 MHz, 3rd overtone at 30–90 MHz, and 5th overtone at 90–150 MHz; according to other source they can be made for fundamental mode operation up to 300 MHz, though that mode is usually used only to 100 MHz and according to yet another source the upper limit for fundamental frequency of the AT cut is limited to 40 MHz for small diameter blanks. Can be manufactured either as a conventional round disk, or as a strip resonator; the latter allows much smaller size. The thickness of the quartz blank is about (1.661 mm)/(frequency in MHz), with the frequency somewhat shifted by further processing. The third overtone is about 3 times the fundamental frequency; the overtones are higher than the equivalent multiple of the fundamental frequency by about 25 kHz per overtone. Crystals designed for operating in overtone modes have to be specially processed for plane parallelism and surface finish for the best performance at a given overtone frequency. |
| SC | 500 kHz – 200 MHz | thickness shear | 35°15′, 21°54′ | A special cut (Stress Compensated) developed in 1974, is a double-rotated cut (35°15′ and 21°54′) for oven-stabilized oscillators with low phase noise and good aging characteristics. Less sensitive to mechanical stresses. Has faster warm-up speed, higher Q, better close-in phase noise, less sensitivity to spatial orientation against the vector of gravity, and less sensitivity to vibrations. Its frequency constant is 1.797 MHz⋅mm. Coupled modes are worse than the AT cut, resistance tends to be higher; much more care is required to convert between overtones. Operates at the same frequencies as the AT cut. The frequency-temperature curve is a third order downward parabola with inflection point at 95 °C and much lower temperature sensitivity than the AT cut. Suitable for OCXOs in e.g. space and GPS systems. Less available than AT cut, more difficult to manufacture; the order-of-magnitude improvement of parameters is traded for an order of magnitude tighter crystal orientation tolerances. Aging characteristics are 2~3 times better than of the AT cuts. Less sensitive to drive levels. Far fewer activity dips. Less sensitive to plate geometry. Requires an oven, does not operate well at ambient temperatures as the frequency rapidly falls off at lower temperatures. Has several times lower motional capacitance than the corresponding AT cut, reducing the possibility to adjust the crystal frequency by attached capacitor; this restricts usage in conventional TCXO and VCXO devices, and other applications where the frequency of the crystal has to be adjustable. The temperature coefficients for the fundamental frequency is different than for its third overtone; when the crystal is driven to operate on both frequencies simultaneously, the resulting beat frequency can be used for temperature sensing in e.g. microcomputer-compensated crystal oscillators. Sensitive to electric fields. Sensitive to air damping, to obtain optimum Q it has to be packaged in vacuum. Temperature coefficient for b mode is −25 ppm/°C , for dual mode 80 to over 100 ppm/°C . |
| BT | 500 kHz – 200 MHz | thickness shear (b mode, fast quasi-shear) | −49°8′, 0° | A special cut, similar to AT cut, except the plate is cut at 49° from the z axis. Operates in thickness shear mode, in b mode (fast quasi-shear). It has well known and repeatable characteristics. Has frequency constant 2.536 MHz⋅mm. Has poorer temperature characteristics than the AT cut. Due to the higher frequency constant, can be used for crystals with higher frequencies than the AT cut, up to over 50 MHz . |
| IT | thickness shear | A special cut, a double-rotated cut with improved characteristics for oven-stabilized oscillators. Operates in thickness shear mode. The frequency-temperature curve is a third order downward parabola with inflection point at 78 °C . Rarely used. Has similar performance and properties to the SC cut, more suitable for higher temperatures. | ||
| FC | thickness shear | A special cut, a double-rotated cut with improved characteristics for oven-stabilized oscillators. Operates in thickness shear mode. The frequency-temperature curve is a third order downward parabola with inflection point at 52 °C . Rarely used. Employed in oven-controlled oscillators; the oven can be set to lower temperature than for the AT / IT / SC cuts, to the beginning of the flat part of the temperature-frequency curve (which is also broader than of the other cuts); when the ambient temperature reaches this region, the oven switches off and the crystal operates at the ambient temperature, while maintaining reasonable accuracy. This cut therefore combines the power saving feature of allowing relatively low oven temperature with reasonable stability at higher ambient temperatures. | ||
| AK | thickness shear | a double rotated cut with better temperature-frequency characteristics than AT and BT cuts and with higher tolerance to crystallographic orientation than the AT, BT, and SC cuts (calculated to be a factor 50 against a standard AT cut). It operates in thickness-shear mode. | ||
| CT | 300 – 900 kHz | face shear | 38°, 0° | The frequency-temperature curve is a downward parabola. |
| DT | 75 – 800 kHz | face shear | −52°, 0° | Similar to CT cut. The frequency-temperature curve is a downward parabola. The temperature coefficient is lower than the CT cut; where the frequency range permits, DT is preferred over CT. |
| SL | face-shear | −57°, 0° | ||
| GT | 100 kHz – 3 MHz | width-extensional | 51°7′ | Its temperature coefficient between −25 ... +75 °C is near-zero, due to cancelling effect between two modes. |
| E, 5°X | 50 – 250 kHz | longitudinal | Has reasonably low temperature coefficient, widely used for low-frequency crystal filters. | |
| MT | 40 – 200 kHz | longitudinal | ||
| ET | 66°30′ | |||
| FT | −57° | |||
| NT | 8 – 130 kHz | length-width flexure (bending) | ||
| XY, tuning fork | 3 – 85 kHz | length-width flexure | The dominant low-frequency crystal, as it is smaller than other low-frequency cuts, less expensive, has low impedance and low C0 / C1 ratio. The chief application is the 32.768 kHz RTC crystal. Its second overtone is about six times the fundamental frequency. | |
| H | 8 – 130 kHz | length-width flexure | Used extensively for wideband filters. The temperature coefficient is linear. | |
| J | 1 – 12 kHz | length-thickness flexure | J cut is made of two quartz plates bonded together, selected to produce out of phase motion for a given electrical field. | |
| RT | A double rotated cut. | |||
| SBTC | A double rotated cut. | |||
| TS | A double rotated cut. | |||
| X 30° | A double rotated cut. | |||
| LC | thickness shear | 11.17° / 9.39° | A double rotated cut ("linear coefficient") with a linear temperature-frequency response; can be used as a sensor in crystal thermometers. Temperature coefficient is 35.4 ppm/°C . | |
| AC | 31° | Temperature-sensitive, can be used as a sensor. Single mode with steep frequency-temperature characteristics. Temperature coefficient is 20 ppm/°C . | ||
| BC | −60° | Temperature-sensitive. | ||
| NLSC | Temperature-sensitive. Temperature coefficient is about 14 ppm/°C . | |||
| Y | Temperature-sensitive, can be used as a sensor. Single mode with steep frequency-temperature characteristics. The plane of the plate is perpendicular to the y axis of the crystal. Also called parallel or 30-degree. Temperature coefficient is about 90 ppm/°C . | |||
| X | Used in one of the first crystal oscillators in 1921 by W.G. Cady, and as a 50 kHz oscillator in the first crystal clock by Horton and Marrison in 1927. The plane of the plate is perpendicular to the x axis of the crystal. Also called perpendicular, normal, Curie, zero-angle, or ultrasonic. |
The letter ‘T’ in the cut name marks a temperature-compensated cut – a cut oriented in a way that the temperature coefficients of the lattice are minimal; the FC and SC cuts are also temperature-compensated.
The high frequency cuts are mounted by their edges, usually on springs; the stiffness of the spring has to be optimal, as if it is too stiff, mechanical shocks could be transferred to the crystal and cause it to break, and too little stiffness may allow the crystal to collide with the inside of the package when subjected to a mechanical shock, and break. Strip resonators, usually AT cuts, are smaller and therefore less sensitive to mechanical shocks. At the same frequency and overtone, the strip has less pullability, higher resistance, and higher temperature coefficient.
The low frequency cuts are mounted at the nodes where they are virtually motionless; thin wires are attached at such points on each side between the crystal and the leads. The large mass of the crystal suspended on the thin wires makes the assembly sensitive to mechanical shocks and vibrations.
The crystals are usually mounted in hermetically sealed glass or metal cases, filled with a dry and inert atmosphere, usually vacuum, nitrogen, or helium. Plastic housings can be used as well, but those are not hermetic and another secondary sealing has to be built around the crystal.
Several resonator configurations are possible, in addition to the classical way of directly attaching leads to the crystal. E.g. the BVA resonator (Boîtier à Vieillissement Amélioré, Enclosure with Improved Aging), developed in 1976; the parts that influence the vibrations are machined from a single crystal (which reduces the mounting stress), and the electrodes are deposited not on the resonator itself but on the inner sides of two condenser discs made of adjacent slices of the quartz from the same bar, forming a three-layer sandwich with no stress between the electrodes and the vibrating element. The gap between the electrodes and the resonator act as two small series capacitors, making the crystal less sensitive to circuit influences. The architecture eliminates the effects of the surface contacts between the electrodes, the constraints in the mounting connections, and the issues related to ion migration from the electrodes into the lattice of the vibrating element. The resulting configuration is rugged, resistant to shock and vibration, resistant to acceleration and ionizing radiation, and has improved aging characteristics. AT cut is usually used, though SC cut variants exist as well. BVA resonators are often used in spacecraft applications.
In the 1930s to 1950s, it was fairly common for people to adjust the frequency of the crystals by manual grinding. The crystals were ground using a fine abrasive slurry, or even a toothpaste, to increase their frequency. A slight decrease by 1–2 kHz when the crystal was overground was possible by marking the crystal face with a pencil lead, at the cost of a lowered Q.
The frequency of the crystal is slightly adjustable ("pullable") by modifying the attached capacitances. A varactor, a diode with capacitance depending on applied voltage, is often used in voltage-controlled crystal oscillators, VCXO. The crystal cuts are usually AT or rarely SC, and operate in fundamental mode; the amount of available frequency deviation is inversely proportional to the square of the overtone number, so a third overtone has only one-ninth of the pullability of the fundamental mode. SC cuts, while more stable, are significantly less pullable.
Circuit notations and abbreviations
On electrical schematic diagrams, crystals are designated with the class letter Y (Y1, Y2, etc.). Oscillators, whether they are crystal oscillators or others, are designated with the class letter G (G1, G2, etc.). Crystals may also be designated on a schematic with X or XTAL (a phonetic abbreviation, comparable to using Xmas for Christmas), or a crystal oscillator with XO.
Crystal oscillator types and their abbreviations:
- ATCXO — Analog temperature controlled crystal oscillator
- CDXO — Calibrated dual crystal oscillator
- DTCXO — Digital temperature compensated crystal oscillator
- EMXO — Evacuated miniature crystal oscillator
- GPSDO — Global positioning system disciplined oscillator
- MCXO — Microcomputer-compensated crystal oscillator
- OCVCXO — oven-controlled voltage-controlled crystal oscillator
- OCXO — Oven-controlled crystal oscillator
- RbXO — Rubidium crystal oscillators (RbXO), a crystal oscillator (can be an MCXO) synchronized with a built-in rubidium standard which is run only occasionally to save power
- TCVCXO — Temperature-compensated voltage-controlled crystal oscillator
- TCXO — Temperature-compensated crystal oscillator
- TMXO – Tactical miniature crystal oscillator
- TSXO — Temperature-sensing crystal oscillator, an adaptation of the TCXO
- VCTCXO — Voltage-controlled temperature-compensated crystal oscillator
- VCXO — Voltage-controlled crystal oscillator
See also
- Clock generator
- Clock drift – Clock drift measurements of crystal oscillators can be used to build random number generators.
- Crystal filter
- Erhard Kietz, who worked on electronic tuning forks and with quartz crystals for precise signal frequencies
- Issac Koga – inventor of the temperature-stable R1 Koga cut
- Pierce oscillator
- Thin-film thickness monitor
- Variable-frequency oscillator (VFO)
References
- ^ Graf, Rudolf F. (1999). Modern Dictionary of Electronics, 7th Ed. US: Newnes. pp. 162, 163. ISBN 978-0750698665.
- Amos, S. W.; Roger Amos (2002). Newnes Dictionary of Electronics, 4th Ed. US: Newnes. p. 76. ISBN 978-0750656429.
- Laplante, Phillip A. (1999). Comprehensive Dictionary of Electrical Engineering. US: Springer. ISBN 978-3540648352.
- Paul Horowitz, Winfield Hill, The Art of Electronics Second Edition, Cambridge University Press, 1989, ISBN 0-521-37095-7, pg. 300 ff
- Lombardi, Michael (2003). Encyclopedia of Physical Science and Technology (3rd ed.).
- Nicholson, Alexander M. Generating and transmitting electric currents U.S. patent 2,212,845, filed April 10, 1918, granted August 27, 1940
- Bottom, Virgil E. (1981). "A history of the quartz crystal industry in the USA". Proc. 35th Frequency Control Symp. IEEE. Archived from the original on 2008-09-20.
- ^ Marrison, Warren (1948). "The Evolution of the Quartz Crystal Clock". Bell System Technical Journal. 27 (3). AT&T: 510–588. doi:10.1002/j.1538-7305.1948.tb01343.x. Archived from the original on 2011-07-17.
- ^ Bayard, Thomas L. (April 1926). "The New "Crystal Pilot"" (PDF). Popular Radio. 9 (4). New York: Popular Radio, Inc.: 342–347. Retrieved 2014-08-24.
- Virgil E. Bottom, A History of the Quartz Crystal Industry in the USA, Proceedings of the 35th Annual Frequency Control Symposium 1981. Ieee-uffc.org. Retrieved on 2012-06-21.
- Microwaves and RF Journal. Retrieved July 17, 2011 Archived September 28, 2011, at the Wayback Machine. Mwrf.com. Retrieved on 2012-06-21.
- Inventors Staudte The Quartz Watch Archived 2010-04-01 at the Wayback Machine. Invention.smithsonian.org. Retrieved on 2012-06-21.
- Virgil E Bottom (1982). Introduction to Quartz Crystal Unit Design. Van Nostrand Reinhold. ISBN 978-0-442-26201-3.
- Quartz Crystal Theory of Operation and Design Notes. foxonline.com
- Specifying Quartz Crystals. Maxim-ic.com (2001-11-19). Retrieved on 2012-06-21.
- Crystal selection Archived 2013-04-29 at the Wayback Machine. pletronics.com. Retrieved on 2012-06-21.
- "Crystal Specification" Archived 2013-07-28 at the Wayback Machine. Euroquartz.co.uk. Retrieved on 2012-06-21.
- "Quartz Crystal Application Notes" Archived 2015-06-23 at the Wayback Machine. Beckwithelectronics.com. Retrieved on 2012-06-21.
- "Quartz Crystals Application Notes". (PDF) . Retrieved on 2012-06-21.
- Frequently Asked Questions about Crystals. foxonline.com
- "Radio Frequency Spectrum Management and Time and Frequency Standards". Retrieved 2019-02-24.
- Reference Data for Radio Engineers (Ninth ed.). Elsevier. 2002. p. Chapter 1. ISBN 978-0-7506-7291-7.
- Gordon T. Austin, Quartz Crystal. minerals.usgs.gov
- ^ Synthetic Quartz Crystal Terms and Definitions
- The Quartz Page: Quartz Structure. Quartzpage.de (2010-10-23). Retrieved on 2012-06-21.
- ^ John R. Vig et al. Method of making miniature high frequency SC-cut quartz crystal resonators U.S. patent 4,554,717, Issue date: November 26, 1985.
- Quartz Hydrothermal Growth. Roditi.com. Retrieved on 2010-02-08.
- Iwasaki, Fumiko; Kurashige, Masakazu (1982-05-01). "Defects in synthetic quartz and their effects on the vibrational characteristics". Ferroelectrics. 43 (1): 43. Bibcode:1982Fer....43...43I. doi:10.1080/00150198208202002.
- Quartz Tech. 4timing.com. Retrieved on 2010-02-08.
- Shinohara, A. H.; Suzuki, C. K. (1996). Proceedings of 1996 IEEE International Frequency Control Symposium. pp. 72–77. doi:10.1109/FREQ.1996.559821. ISBN 0-7803-3309-8.
- Fumiko Iwasaki; Armando H. Shinohara; Hideo Iwasaki; Carlos K. Suzuki (1990). "Effect of Impurity Segregation on Crystal Morphology of Y-Bar Synthetic Quartz" (PDF). Jpn. J. Appl. Phys. 29 (6): 1139–1142. Bibcode:1990JaJAP..29.1139I. doi:10.1143/JJAP.29.1139. S2CID 97694219. Archived (PDF) from the original on 2022-10-09.
- Harish Bahadur (2006). "Radiation induced modification of impurity-related point defects in crystalline quartz – a review" (PDF). Crystal Research and Technology. 41 (7): 631–635. Bibcode:2006CryRT..41..631B. doi:10.1002/crat.200510641. S2CID 95333080. Archived (PDF) from the original on 2022-10-09.
- Harish Bahadur Investigations on irradiation and structural characteristics of high quality cultured quartz crystals used in satellite communication Archived 2011-07-16 at the Wayback Machine
- Arthur Ballato et al. Method of sweeping quartz U.S. patent 4,311,938, Issue date: January 19, 1982/
- Frequency Control|Teaching Resources Archived 2010-07-06 at the Wayback Machine. Ieee-uffc.org. Retrieved on 2010-02-08.
- ^ James Claude King Vacuum electrolysis of quartz U.S. patent 3,932,777, Issue date: Jan 13, 1976.
- Infrared study of defects in alpha quartz caused by sweeping effects. authors.aps.org (April 1997). Retrieved on 2012-06-21.
- Arthur Ballato Method of making a crystal oscillator desensitized to accelerationfields U.S. patent 4,871,986, Issue date: October 3, 1989.
- Recent Development of Bulk and Surface Acoustic Wave Technology for Frequency Control Applications, December 23, 2002 Institute of Applied Mechanics National Taiwan University, C. S. Lam, TXC Corporation.
- Fumio Nakajima Quartz crystal oscillator angular velocity detector circuits U.S. patent 5,420,548, Issue date: May 30, 1995.
- Bernd Neubig, VCXOs with wide pull-in range using alternatives to quartz. VHF Communications, 2/2003, pp. 66–70.
- Making oscillator selection crystal clear Archived 2016-06-29 at the Wayback Machine EDN (2008-07-20). Retrieved on 2018-03-30.
- Frequency Control|Teaching Resources Archived 2010-07-05 at the Wayback Machine. Ieee-uffc.org. Retrieved on 2010-02-08.
- Frequency Control|Teaching Resources Archived 2010-07-06 at the Wayback Machine. Ieee-uffc.org. Retrieved on 2010-02-08.
- ^ Jerry C. Whitaker (1996-12-23). The electronics handbook. CRC Press. pp. 198–. ISBN 978-0-8493-8345-8. Retrieved 2011-04-26.
- Frequency Control|Teaching Resources Archived 2010-07-06 at the Wayback Machine. Ieee-uffc.org. Retrieved on 2010-02-08.
- Quartz crystal resonators and oscillators for frequency control and timing applications: a tutorial by John R. Vig, U.S. Army Communications-Electronics Command
- Frequency Control|Teaching Resources Archived 2010-07-05 at the Wayback Machine. Ieee-uffc.org. Retrieved on 2010-02-08.
- ^ Crystal Terminology Archived 2005-01-26 at the Wayback Machine. Actcrystals.com. Retrieved on 2010-02-08.
- Design of crystal oscillator circuits, a course by B. Neubig
- Image of several crystal cuts. Mazepath.com (image). Eotvos and novel equivalence principle tests. 3 July 2007. Archived from the original on 28 December 2015. Retrieved 8 February 2010.
- ^
Lichter, Jerry A. Crystals and oscillators (PDF) (Report). 9113. - Rosen, Carol Zwick; Hiremath, Basavaraj V.; Newnham, Robert E., eds. (1992) . Piezoelectricity. New York, NY: American Institute of Physics. ISBN 0883186470. OCLC 22766216.
- "AT cut". Crystal and frequency control glossary. icmfg.com. Archived from the original on 6 November 2009. Retrieved 8 February 2010.
- "Crystal technology". 4timing.com. Retrieved 8 February 2010.
- "Introduction to quartz frequency standards". Quartz and the quartz crystal unit. oscilent.com. Retrieved 8 February 2010.
- "Quartz blanks". Hoffman Materials (hoffmanmaterials.com). Archived from the original on 2012-07-09. Retrieved 2010-02-08.
- ^ Making it crystal clear: Crystal oscillators in communications. CSD. commsdesign.com (Report). May 1998. Archived from the original on 11 October 2008. Retrieved 8 February 2010.
- ^ US 4499395, Kahan, Alfred, "Cut angles for quartz crystal resonators", issued 12 Feb 1985
- "OCXOs – oven controlled crystal oscillators". OCXO Application Notes. ofc.com. Archived from the original on 1 March 2012. Retrieved 8 February 2010.
- ^
Kruse, P.W. (1997). Uncooled Infrared Imaging Arrays and Systems. Academic Press. pp. 273 ff. ISBN 978-0-12-752155-8. Retrieved 2011-04-26. - "Crystal and frequency control glossary". Icmfg.com. Archived from the original on 5 February 2013. Retrieved 8 February 2010.
- US 4985687, Long, Bruce R., "Low power temperature-controlled frequency-stabilized oscillator", issued 15 Jan 1991
- US 4419600, Sinha, Bikash K., "Stress-compensated quartz resonators", issued 6 Dec 1983
- ^ US 5686779, Vig, John R., "High sensitivity temperature sensor and sensor array", issued 11 Nov 1997
- "Y cut crystal". engineersedge.com. 25 August 2009. 4074. Archived from the original on 30 July 2012. Retrieved 8 February 2010.
- ^ "Frerking". UFFC History. ieee-uffc.org. 23 March 1959. Archived from the original on 12 May 2009. Retrieved 8 February 2010.
- Glossary of terms used in the quartz oscillator-plate industry (PDF). minsocam.org (Report). AM 30 461. Retrieved 21 June 2012.
- "Quartz crystal FAQs". International Crystal (icmfg.com). Archived from the original on 2012-02-17. Retrieved 2010-02-08.
- "Re: [time-nuts] Super stable BVA Quartz resonators... BVA??]". mail-archive.com. 7 December 2007. msg 10485. Retrieved 8 February 2010.
- "Re: [time-nuts] Super stable BVA Quartz resonators... BVA??]". mail-archive.com. 2007-12-08. msg 10505. Retrieved 2010-02-08.
- Oven crystal oscillator (PDF). oscilloquartz.ch (Report). 8600. Archived from the original (PDF) on 7 July 2011. Retrieved 21 June 2012.
- "Norton". UFFC History. ieee-uffc.org. 4 October 1957. Archived from the original on 28 January 2010. Retrieved 8 February 2010.
- "Crystal grinding: When electronics were really hands-on". PowerSource. EDN (blog). 1470000147. Archived from the original on 30 July 2012. Retrieved 8 February 2010 – via edn.com.
- "Crystal oscillators: Looking good in wireless systems". EDN Access. EDN. 20 November 1997. Archived from the original on 23 November 2008. Retrieved 8 February 2010 – via edn.com.
- IEEE Std 315-1975
- ANSI Y32.2-1975
Further reading
- Poddar, A. K.; Rohde, Ulrich L. (2012-10-19). "Crystal Oscillators". Wiley Encyclopedia of Electrical and Electronics Engineering. pp. 1–38. doi:10.1002/047134608X.W8154. ISBN 978-0471346081.
- Rohde, Ulrich L. (August 1997). Microwave and Wireless Synthesizers: Theory and Design. John Wiley & Sons. ISBN 978-0-471-52019-1.
- Poddar, A. K.; Rohde, Ulrich L. (21–24 May 2012). "Techniques minimize the phase noise in crystal oscillator circuits". 2012 IEEE International Frequency Control Symposium Proceedings. Frequency Control Symposium (FCS), 2012 IEEE International. IEEE. pp. 1–7. doi:10.1109/FCS.2012.6243701. ISBN 978-1-4577-1820-5.
- Poddar, A. K.; Rohde, U. L.; Apte, A. M. (2013-08-30). "How Low Can They Go?: Oscillator Phase Noise Model, Theoretical, Experimental Validation, and Phase Noise Measurements". IEEE Microwave Magazine. 14 (6). IEEE: 50–72. doi:10.1109/MMM.2013.2269859. S2CID 22624948.
- Rohde, Ulrich L.; Poddar, A. K.; Apte, A. M. (2013-08-30). "Getting Its Measure: Oscillator Phase Noise Measurement Techniques and Limitations". IEEE Microwave Magazine. 14 (6). IEEE: 73–86. doi:10.1109/MMM.2013.2269860. S2CID 40924332.
- Rohde, Ulrich L. (31 May – 2 June 1978). Mathematical Analysis and Design of an Ultra-Low Noise 100 MHz Oscillator with Differential Limiter and Its Possibilities in Frequency Standards. Proceedings of the 32nd Annual Symposium on Frequency Control. Atlantic City, NJ. pp. 409––. doi:10.1109/FREQ.1978.200269.
- Neubig, Bernd; Briese, Wolfgang (1997). Das große Quarzkochbuch [The Crystal Cookbook] (PDF) (in German) (1 ed.). Feldkirchen, Germany: Franzis Verlag. ISBN 978-3-7723-5853-1. Archived from the original (PDF) on 2019-02-23. Retrieved 2019-02-23. (Alternative downloads: QSL: - 0 1 2 3 4 5 6 7 8 9 10. AXTAL ZIP: - 0 1 2 3 4 5 6 7 8 9 10.)
External links
- Introduction to quartz frequency standards
- "What is a quartz crystal device?". QIAJ. Quartz Crystal Industry Assoc. of Japan. 2007. Retrieved 2008-08-10.
- Marvin E., Frerking (1996). "Fifty years of progress in quartz crystal frequency standards". Proc. 1996 IEEE Frequency Control Symposium. Institute of Electrical and Electronics Engineers. pp. 33–46. Archived from the original on 2009-05-12. Retrieved 2009-03-31.
- Distortions in Crystal Oscillators
- Quartz crystal resonators and oscillators
- Multipage summary of quartz crystals & their oscillators, filters, etc
| Electronic oscillators | |
|---|---|
| Theory | |
| LC oscillators | |
| RC oscillators | |
| Quartz oscillators | |
| Relaxation oscillators | |
| Other | |


 is the complex frequency (
is the complex frequency ( ),
),  is the series resonant
is the series resonant  is the parallel resonant angular frequency.
is the parallel resonant angular frequency.
