In numerical linear algebra, the QR algorithm or QR iteration is an eigenvalue algorithm: that is, a procedure to calculate the eigenvalues and eigenvectors of a matrix. The QR algorithm was developed in the late 1950s by John G. F. Francis and by Vera N. Kublanovskaya, working independently. The basic idea is to perform a QR decomposition, writing the matrix as a product of an orthogonal matrix and an upper triangular matrix, multiply the factors in the reverse order, and iterate.
The practical QR algorithm
Formally, let A be a real matrix of which we want to compute the eigenvalues, and let A0 := A. At the k-th step (starting with k = 0), we compute the QR decomposition Ak = Qk Rk where Qk is an orthogonal matrix (i.e., Q = Q) and Rk is an upper triangular matrix. We then form Ak+1 = Rk Qk. Note that so all the Ak are similar and hence they have the same eigenvalues. The algorithm is numerically stable because it proceeds by orthogonal similarity transforms.
Under certain conditions, the matrices Ak converge to a triangular matrix, the Schur form of A. The eigenvalues of a triangular matrix are listed on the diagonal, and the eigenvalue problem is solved. In testing for convergence it is impractical to require exact zeros, but the Gershgorin circle theorem provides a bound on the error.
Using Hessenberg form
In the above crude form the iterations are relatively expensive. This can be mitigated by first bringing the matrix A to upper Hessenberg form (which costs arithmetic operations using a technique based on Householder reduction), with a finite sequence of orthogonal similarity transforms, somewhat like a two-sided QR decomposition. (For QR decomposition, the Householder reflectors are multiplied only on the left, but for the Hessenberg case they are multiplied on both left and right.) Determining the QR decomposition of an upper Hessenberg matrix costs arithmetic operations. Moreover, because the Hessenberg form is already nearly upper-triangular (it has just one nonzero entry below each diagonal), using it as a starting point reduces the number of steps required for convergence of the QR algorithm.
If the original matrix is symmetric, then the upper Hessenberg matrix is also symmetric and thus tridiagonal, and so are all the Ak. In this case reaching Hessenberg form costs arithmetic operations using a technique based on Householder reduction. Determining the QR decomposition of a symmetric tridiagonal matrix costs operations.
Iteration phase
If a Hessenberg matrix has element for some , i.e., if one of the elements just below the diagonal is in fact zero, then it decomposes into blocks whose eigenproblems may be solved separately; an eigenvalue is either an eigenvalue of the submatrix of the first rows and columns, or an eigenvalue of the submatrix of remaining rows and columns. The purpose of the QR iteration step is to shrink one of these elements so that effectively a small block along the diagonal is split off from the bulk of the matrix. In the case of a real eigenvalue that is usually the block in the lower right corner (in which case element holds that eigenvalue), whereas in the case of a pair of conjugate complex eigenvalues it is the block in the lower right corner.
The rate of convergence depends on the separation between eigenvalues, so a practical algorithm will use shifts, either explicit or implicit, to increase separation and accelerate convergence. A typical symmetric QR algorithm isolates each eigenvalue (then reduces the size of the matrix) with only one or two iterations, making it efficient as well as robust.
A single iteration with explicit shift
The steps of a QR iteration with explicit shift on a real Hessenberg matrix are:
- Pick a shift and subtract it from all diagonal elements, producing the matrix . A basic strategy is to use , but there are more refined strategies that would further accelerate convergence. The idea is that should be close to an eigenvalue, since making this shift will accelerate convergence to that eigenvalue.
- Perform a sequence of Givens rotations on , where acts on rows and , and is chosen to zero out position of . This produces the upper triangular matrix . The orthogonal factor would be , but it is neither necessary nor efficient to produce that explicitly.
- Now multiply by the Givens matrices , , …, on the right, where instead acts on columns and . This produces the matrix , which is again on Hessenberg form.
- Finally undo the shift by adding to all diagonal entries. The result is . Since commutes with , we have that .
The purpose of the shift is to change which Givens rotations are chosen.
In more detail, the structure of one of these matrices are where the in the upper left corner is an identity matrix, and the two scalars and are determined by what rotation angle is appropriate for zeroing out position . It is not necessary to exhibit ; the factors and can be determined directly from elements in the matrix should act on. Nor is it necessary to produce the whole matrix; multiplication (from the left) by only affects rows and , so it is easier to just update those two rows in place. Likewise, for the Step 3 multiplication by from the right, it is sufficient to remember , , and .
If using the simple strategy, then at the beginning of Step 2 we have a matrix where the denotes “could be whatever”. The first Givens rotation zeroes out the position of this, producing Each new rotation zeroes out another subdiagonal element, thus increasing the number of known zeroes until we are at The final rotation has chosen so that . If , as is typically the case when we approach convergence, then and . Making this rotation produces which is our upper triangular matrix. But now we reach Step 3, and need to start rotating data between columns. The first rotation acts on columns and , producing The expected pattern is that each rotation moves some nonzero value from the diagonal out to the subdiagonal, returning the matrix to Hessenberg form. This ends at Algebraically the form is unchanged, but numerically the element in position has gotten a lot closer to zero: there used to be a factor gap between it and the diagonal element above, but now the gap is more like a factor , and another iteration would make it factor ; we have quadratic convergence. Practically that means iterations per eigenvalue suffice for convergence, and thus overall we can complete in QR steps, each of which does a mere arithmetic operations (or as little as operations, in the case that is symmetric).
Visualization
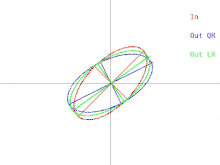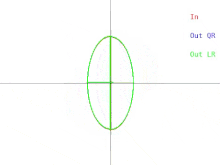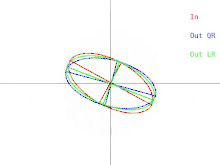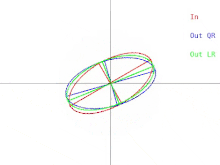
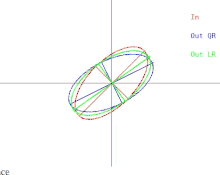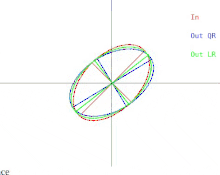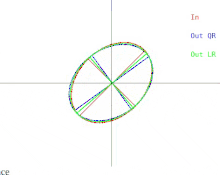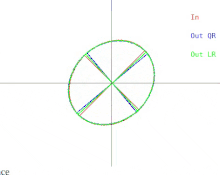
The basic QR algorithm can be visualized in the case where A is a positive-definite symmetric matrix. In that case, A can be depicted as an ellipse in 2 dimensions or an ellipsoid in higher dimensions. The relationship between the input to the algorithm and a single iteration can then be depicted as in Figure 1 (click to see an animation). Note that the LR algorithm is depicted alongside the QR algorithm.
A single iteration causes the ellipse to tilt or "fall" towards the x-axis. In the event where the large semi-axis of the ellipse is parallel to the x-axis, one iteration of QR does nothing. Another situation where the algorithm "does nothing" is when the large semi-axis is parallel to the y-axis instead of the x-axis. In that event, the ellipse can be thought of as balancing precariously without being able to fall in either direction. In both situations, the matrix is diagonal. A situation where an iteration of the algorithm "does nothing" is called a fixed point. The strategy employed by the algorithm is iteration towards a fixed-point. Observe that one fixed point is stable while the other is unstable. If the ellipse were tilted away from the unstable fixed point by a very small amount, one iteration of QR would cause the ellipse to tilt away from the fixed point instead of towards. Eventually though, the algorithm would converge to a different fixed point, but it would take a long time.
Finding eigenvalues versus finding eigenvectors
It's worth pointing out that finding even a single eigenvector of a symmetric matrix is not computable (in exact real arithmetic according to the definitions in computable analysis). This difficulty exists whenever the multiplicities of a matrix's eigenvalues are not knowable. On the other hand, the same problem does not exist for finding eigenvalues. The eigenvalues of a matrix are always computable.
We will now discuss how these difficulties manifest in the basic QR algorithm. This is illustrated in Figure 2. Recall that the ellipses represent positive-definite symmetric matrices. As the two eigenvalues of the input matrix approach each other, the input ellipse changes into a circle. A circle corresponds to a multiple of the identity matrix. A near-circle corresponds to a near-multiple of the identity matrix whose eigenvalues are nearly equal to the diagonal entries of the matrix. Therefore, the problem of approximately finding the eigenvalues is shown to be easy in that case. But notice what happens to the semi-axes of the ellipses. An iteration of QR (or LR) tilts the semi-axes less and less as the input ellipse gets closer to being a circle. The eigenvectors can only be known when the semi-axes are parallel to the x-axis and y-axis. The number of iterations needed to achieve near-parallelism increases without bound as the input ellipse becomes more circular.
While it may be impossible to compute the eigendecomposition of an arbitrary symmetric matrix, it is always possible to perturb the matrix by an arbitrarily small amount and compute the eigendecomposition of the resulting matrix. In the case when the matrix is depicted as a near-circle, the matrix can be replaced with one whose depiction is a perfect circle. In that case, the matrix is a multiple of the identity matrix, and its eigendecomposition is immediate. Be aware though that the resulting eigenbasis can be quite far from the original eigenbasis.
Speeding up: Shifting and deflation
The slowdown when the ellipse gets more circular has a converse: It turns out that when the ellipse gets more stretched - and less circular - then the rotation of the ellipse becomes faster. Such a stretch can be induced when the matrix which the ellipse represents gets replaced with where is approximately the smallest eigenvalue of . In this case, the ratio of the two semi-axes of the ellipse approaches . In higher dimensions, shifting like this makes the length of the smallest semi-axis of an ellipsoid small relative to the other semi-axes, which speeds up convergence to the smallest eigenvalue, but does not speed up convergence to the other eigenvalues. This becomes useless when the smallest eigenvalue is fully determined, so the matrix must then be deflated, which simply means removing its last row and column.
The issue with the unstable fixed point also needs to be addressed. The shifting heuristic is often designed to deal with this problem as well: Practical shifts are often discontinuous and randomised. Wilkinson's shift—which is well-suited for symmetric matrices like the ones we're visualising—is in particular discontinuous.
The implicit QR algorithm
In modern computational practice, the QR algorithm is performed in an implicit version which makes the use of multiple shifts easier to introduce. The matrix is first brought to upper Hessenberg form as in the explicit version; then, at each step, the first column of is transformed via a small-size Householder similarity transformation to the first column of (or ), where , of degree , is the polynomial that defines the shifting strategy (often , where and are the two eigenvalues of the trailing principal submatrix of , the so-called implicit double-shift). Then successive Householder transformations of size are performed in order to return the working matrix to upper Hessenberg form. This operation is known as bulge chasing, due to the peculiar shape of the non-zero entries of the matrix along the steps of the algorithm. As in the first version, deflation is performed as soon as one of the sub-diagonal entries of is sufficiently small.
Renaming proposal
Since in the modern implicit version of the procedure no QR decompositions are explicitly performed, some authors, for instance Watkins, suggested changing its name to Francis algorithm. Golub and Van Loan use the term Francis QR step.
Interpretation and convergence
The QR algorithm can be seen as a more sophisticated variation of the basic "power" eigenvalue algorithm. Recall that the power algorithm repeatedly multiplies A times a single vector, normalizing after each iteration. The vector converges to an eigenvector of the largest eigenvalue. Instead, the QR algorithm works with a complete basis of vectors, using QR decomposition to renormalize (and orthogonalize). For a symmetric matrix A, upon convergence, AQ = QΛ, where Λ is the diagonal matrix of eigenvalues to which A converged, and where Q is a composite of all the orthogonal similarity transforms required to get there. Thus the columns of Q are the eigenvectors.
History
The QR algorithm was preceded by the LR algorithm, which uses the LU decomposition instead of the QR decomposition. The QR algorithm is more stable, so the LR algorithm is rarely used nowadays. However, it represents an important step in the development of the QR algorithm.
The LR algorithm was developed in the early 1950s by Heinz Rutishauser, who worked at that time as a research assistant of Eduard Stiefel at ETH Zurich. Stiefel suggested that Rutishauser use the sequence of moments y0 A x0, k = 0, 1, ... (where x0 and y0 are arbitrary vectors) to find the eigenvalues of A. Rutishauser took an algorithm of Alexander Aitken for this task and developed it into the quotient–difference algorithm or qd algorithm. After arranging the computation in a suitable shape, he discovered that the qd algorithm is in fact the iteration Ak = LkUk (LU decomposition), Ak+1 = UkLk, applied on a tridiagonal matrix, from which the LR algorithm follows.
Other variants
One variant of the QR algorithm, the Golub-Kahan-Reinsch algorithm starts with reducing a general matrix into a bidiagonal one. This variant of the QR algorithm for the computation of singular values was first described by Golub & Kahan (1965). The LAPACK subroutine DBDSQR implements this iterative method, with some modifications to cover the case where the singular values are very small (Demmel & Kahan 1990). Together with a first step using Householder reflections and, if appropriate, QR decomposition, this forms the DGESVD routine for the computation of the singular value decomposition. The QR algorithm can also be implemented in infinite dimensions with corresponding convergence results.
References
- J.G.F. Francis, "The QR Transformation, I", The Computer Journal, 4(3), pages 265–271 (1961, received October 1959). doi:10.1093/comjnl/4.3.265
- Francis, J. G. F. (1962). "The QR Transformation, II". The Computer Journal. 4 (4): 332–345. doi:10.1093/comjnl/4.4.332.
- Vera N. Kublanovskaya, "On some algorithms for the solution of the complete eigenvalue problem," USSR Computational Mathematics and Mathematical Physics, vol. 1, no. 3, pages 637–657 (1963, received Feb 1961). Also published in: Zhurnal Vychislitel'noi Matematiki i Matematicheskoi Fiziki, vol.1, no. 4, pages 555–570 (1961). doi:10.1016/0041-5553(63)90168-X
- ^ Golub, G. H.; Van Loan, C. F. (1996). Matrix Computations (3rd ed.). Baltimore: Johns Hopkins University Press. ISBN 0-8018-5414-8.
- ^ Demmel, James W. (1997). Applied Numerical Linear Algebra. SIAM.
- ^ Trefethen, Lloyd N.; Bau, David (1997). Numerical Linear Algebra. SIAM.
- Ortega, James M.; Kaiser, Henry F. (1963). "The LL and QR methods for symmetric tridiagonal matrices". The Computer Journal. 6 (1): 99–101. doi:10.1093/comjnl/6.1.99.
- "linear algebra - Why is uncomputability of the spectral decomposition not a problem?". MathOverflow. Retrieved 2021-08-09.
- Watkins, David S. (2007). The Matrix Eigenvalue Problem: GR and Krylov Subspace Methods. Philadelphia, PA: SIAM. ISBN 978-0-89871-641-2.
- Parlett, Beresford N.; Gutknecht, Martin H. (2011), "From qd to LR, or, how were the qd and LR algorithms discovered?" (PDF), IMA Journal of Numerical Analysis, 31 (3): 741–754, doi:10.1093/imanum/drq003, hdl:20.500.11850/159536, ISSN 0272-4979
- Bochkanov Sergey Anatolyevich. ALGLIB User Guide - General Matrix operations - Singular value decomposition . ALGLIB Project. 2010-12-11. URL: Accessed: 2010-12-11. (Archived by WebCite at https://www.webcitation.org/5utO4iSnR?url=http://www.alglib.net/matrixops/general/svd.php
- Deift, Percy; Li, Luenchau C.; Tomei, Carlos (1985). "Toda flows with infinitely many variables". Journal of Functional Analysis. 64 (3): 358–402. doi:10.1016/0022-1236(85)90065-5.
- Colbrook, Matthew J.; Hansen, Anders C. (2019). "On the infinite-dimensional QR algorithm". Numerische Mathematik. 143 (1): 17–83. arXiv:2011.08172. doi:10.1007/s00211-019-01047-5.
Sources
- Demmel, James; Kahan, William (1990). "Accurate singular values of bidiagonal matrices". SIAM Journal on Scientific and Statistical Computing. 11 (5): 873–912. CiteSeerX 10.1.1.48.3740. doi:10.1137/0911052.
- Golub, Gene H.; Kahan, William (1965). "Calculating the singular values and pseudo-inverse of a matrix". Journal of the Society for Industrial and Applied Mathematics, Series B: Numerical Analysis. 2 (2): 205–224. Bibcode:1965SJNA....2..205G. doi:10.1137/0702016. JSTOR 2949777.
External links
- Eigenvalue problem at PlanetMath.
- Notes on orthogonal bases and the workings of the QR algorithm by Peter J. Olver
- Module for the QR Method
- C++ Library
| Numerical linear algebra | |
|---|---|
| Key concepts | |
| Problems | |
| Hardware | |
| Software | |
 so all the Ak are
so all the Ak are  arithmetic operations using a technique based on
arithmetic operations using a technique based on  arithmetic operations. Moreover, because the Hessenberg form is already nearly upper-triangular (it has just one nonzero entry below each diagonal), using it as a starting point reduces the number of steps required for convergence of the QR algorithm.
arithmetic operations. Moreover, because the Hessenberg form is already nearly upper-triangular (it has just one nonzero entry below each diagonal), using it as a starting point reduces the number of steps required for convergence of the QR algorithm.
 arithmetic operations using a technique based on Householder reduction. Determining the QR decomposition of a symmetric tridiagonal matrix costs
arithmetic operations using a technique based on Householder reduction. Determining the QR decomposition of a symmetric tridiagonal matrix costs  operations.
operations.
 has element
has element  for some
for some  , i.e., if one of the elements just below the diagonal is in fact zero, then it decomposes into blocks whose eigenproblems may be solved separately; an eigenvalue is either an eigenvalue of the submatrix of the first
, i.e., if one of the elements just below the diagonal is in fact zero, then it decomposes into blocks whose eigenproblems may be solved separately; an eigenvalue is either an eigenvalue of the submatrix of the first  rows and columns, or an eigenvalue of the submatrix of remaining rows and columns. The purpose of the QR iteration step is to shrink one of these
rows and columns, or an eigenvalue of the submatrix of remaining rows and columns. The purpose of the QR iteration step is to shrink one of these  elements so that effectively a small block along the diagonal is split off from the bulk of the matrix. In the case of a real eigenvalue that is usually the
elements so that effectively a small block along the diagonal is split off from the bulk of the matrix. In the case of a real eigenvalue that is usually the  block in the lower right corner (in which case element
block in the lower right corner (in which case element  holds that eigenvalue), whereas in the case of a pair of conjugate complex eigenvalues it is the
holds that eigenvalue), whereas in the case of a pair of conjugate complex eigenvalues it is the  block in the lower right corner.
block in the lower right corner.
 and subtract it from all diagonal elements, producing the matrix
and subtract it from all diagonal elements, producing the matrix  . A basic strategy is to use
. A basic strategy is to use  , but there are more refined strategies that would further accelerate convergence. The idea is that
, but there are more refined strategies that would further accelerate convergence. The idea is that  on
on  acts on rows
acts on rows  and
and  , and
, and  of
of  . This produces the upper triangular matrix
. This produces the upper triangular matrix  . The orthogonal factor
. The orthogonal factor  would be
would be  , but it is neither necessary nor efficient to produce that explicitly.
, but it is neither necessary nor efficient to produce that explicitly. by the Givens matrices
by the Givens matrices  ,
,  , …,
, …,  on the right, where
on the right, where  instead acts on columns
instead acts on columns  , which is again on Hessenberg form.
, which is again on Hessenberg form. . Since
. Since  , we have that
, we have that  .
. where the
where the  identity matrix, and the two scalars
identity matrix, and the two scalars  and
and  are determined by what rotation angle
are determined by what rotation angle  is appropriate for zeroing out position
is appropriate for zeroing out position  and
and  can be determined directly from elements in the matrix
can be determined directly from elements in the matrix  where the
where the  denotes “could be whatever”. The first Givens rotation
denotes “could be whatever”. The first Givens rotation  zeroes out the
zeroes out the  Each new rotation zeroes out another subdiagonal element, thus increasing the number of known zeroes until we are at
Each new rotation zeroes out another subdiagonal element, thus increasing the number of known zeroes until we are at
 The final rotation
The final rotation  has
has  chosen so that
chosen so that  . If
. If  , as is typically the case when we approach convergence, then
, as is typically the case when we approach convergence, then  and
and  . Making this rotation produces
. Making this rotation produces
 which is our upper triangular matrix. But now we reach Step 3, and need to start rotating data between columns. The first rotation acts on columns
which is our upper triangular matrix. But now we reach Step 3, and need to start rotating data between columns. The first rotation acts on columns  and
and  , producing
, producing
 The expected pattern is that each rotation moves some nonzero value from the diagonal out to the subdiagonal, returning the matrix to Hessenberg form. This ends at
The expected pattern is that each rotation moves some nonzero value from the diagonal out to the subdiagonal, returning the matrix to Hessenberg form. This ends at
 Algebraically the form is unchanged, but numerically the element in position
Algebraically the form is unchanged, but numerically the element in position  has gotten a lot closer to zero: there used to be a factor
has gotten a lot closer to zero: there used to be a factor  , and another iteration would make it factor
, and another iteration would make it factor  ; we have quadratic convergence. Practically that means
; we have quadratic convergence. Practically that means  iterations per eigenvalue suffice for convergence, and thus overall we can complete in
iterations per eigenvalue suffice for convergence, and thus overall we can complete in  QR steps, each of which does a mere
QR steps, each of which does a mere  arithmetic operations (or as little as
arithmetic operations (or as little as  which the ellipse represents gets replaced with
which the ellipse represents gets replaced with  where
where  is approximately the smallest eigenvalue of
is approximately the smallest eigenvalue of  . In higher dimensions, shifting like this makes the length of the smallest semi-axis of an ellipsoid small relative to the other semi-axes, which speeds up convergence to the smallest eigenvalue, but does not speed up convergence to the other eigenvalues. This becomes useless when the smallest eigenvalue is fully determined, so the matrix must then be deflated, which simply means removing its last row and column.
. In higher dimensions, shifting like this makes the length of the smallest semi-axis of an ellipsoid small relative to the other semi-axes, which speeds up convergence to the smallest eigenvalue, but does not speed up convergence to the other eigenvalues. This becomes useless when the smallest eigenvalue is fully determined, so the matrix must then be deflated, which simply means removing its last row and column.
 as in the explicit version; then, at each step, the first column of
as in the explicit version; then, at each step, the first column of  is transformed via a small-size Householder similarity transformation to the first column of
is transformed via a small-size Householder similarity transformation to the first column of  (or
(or  ), where
), where  , is the polynomial that defines the shifting strategy (often
, is the polynomial that defines the shifting strategy (often  , where
, where  are the two eigenvalues of the trailing
are the two eigenvalues of the trailing  are performed in order to return the working matrix
are performed in order to return the working matrix