| This article may need to be rewritten to comply with Misplaced Pages's quality standards. You can help. The talk page may contain suggestions. (July 2018) |
 Example of a quick return mechanism.
Example of a quick return mechanism.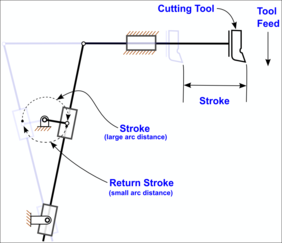 Quick return applied to a shaper.
Quick return applied to a shaper.
A quick return mechanism is an apparatus to produce a reciprocating motion in which the time taken for travel in return stroke is less than in the forward stroke. It is driven by a circular motion source (typically a motor of some sort) and uses a system of links with three turning pairs and a sliding pair. A quick-return mechanism is a subclass of a slider-crank linkage, with an offset crank.
Quick return is a common feature of tools in which the action is performed in only one direction of the stroke, such as shapers and powered saws, because it allows less time to be spent on returning the tool to its initial position.
History

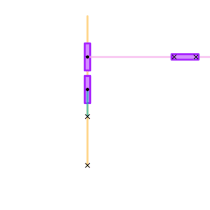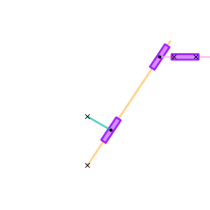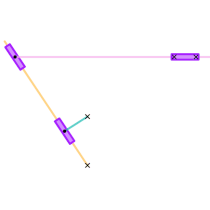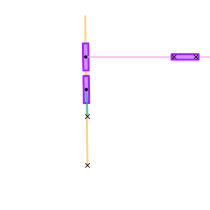 Whitworth's quick return mechanisms.
Whitworth's quick return mechanisms.
During the early-nineteenth century, cutting methods involved hand tools and cranks, which were often lengthy in duration. Joseph Whitworth changed this by creating the quick return mechanism in the mid-1800s. Using kinematics, he determined that the force and geometry of the rotating joint would affect the force and motion of the connected arm. From an engineering standpoint, the quick return mechanism impacted the technology of the Industrial Revolution by minimizing the duration of a full revolution, thus reducing the amount of time needed for a cut or press.
Applications
Quick return mechanisms are found throughout the engineering industry in different machines:
Design
The disc influences the force of the arm, which makes up the frame of reference of the quick return mechanism. The frame continues to an attached rod, which is connected to the circular disc. Powered by a motor, the disc rotates and the arm follows in the same direction (linear and left-to-right, typically) but at a different speed. When the disc nears a full revolution, the arm reaches its furthest position and returns to its initial position at a quicker rate, hence its name. Throughout the cut, the arm has a constant velocity. Upon returning to its initial position after reaching its maximum horizontal displacement, the arm reaches its highest velocity.
The quick return mechanism was modeled after the crank and slider (arm), and this is present in its appearance and function; however, the crank is usually hand powered and the arm has the same rate throughout an entire revolution, whereas the arm of a quick return mechanism returns at a faster rate. The "quick return" allows for the arm to function with less energy during the cut than the initial cycle of the disc.
Specifications
When using a machine that involves this mechanism, it is very important to not force the machine into reaching its maximum stress capacity; otherwise, the machine will break. The durability of the machine is related to the size of the arm and the velocity of the disc, where the arm might not be flexible enough to handle a certain speed. Creating a graphical layout for a quick return mechanism involves all inversions and motions, which is useful in determining the dimensions for a functioning mechanism. A layout would specify the dimensions of the mechanism by highlighting each part and its interaction among the system. These interactions would include torque, force, velocity, and acceleration. By relating these concepts to their respective analyses (kinematics and dynamics), one can comprehend the effect each part has on another.
Mechanics
In order to derive the force vectors of these mechanisms, one must approach a mechanical design consisting of both kinematic and dynamic analyses.
Kinematic Analysis
Breaking the mechanism up into separate vectors and components allows us to create a kinematic analysis that can solve for the maximum velocity, acceleration, and force the mechanism is capable of in three-dimensional space. Most of the equations involved in the quick return mechanism setup originate from Hamilton's principle.
The position of the arm can be found at different times using the substitution of Euler's formula:
into the different components that have been pre-determined, according to the setup.
This substitution can solve for various radii and components of the displacement of the arm at different values. Trigonometry is needed for the complete understanding of the kinematic analyses of the mechanism, where the entire design can be transcribed onto a plane layout, highlighting all of the vector components.
An important concept for the analysis of the velocity of the disc relative to the arm is the angular velocity of the disc:
If one desires to calculate the velocity, one must derive the angles of interaction at a single moment of time, making this equation useful.
Dynamic Analysis
In addition to the kinematic analysis of a quick return mechanism, there is a dynamic analysis present. At certain lengths and attachments, the arm of the mechanism can be evaluated and then adjusted to certain preferences. For example, the differences in the forces acting upon the system at an instant can be represented by D'Alembert's principle. Depending on the structural design of the quick return mechanism, the law of cosines can be used to determine the angles and displacements of the arm. The ratio between the working stroke (engine) and the return stroke can be simplified through the manipulation of these concepts.
Despite similarities between quick return mechanisms, there are many different possibilities for the outline of all forces, speeds, lengths, motions, functions, and vectors in a mechanism.
See also
- Slider-crank linkage – Mechanism for converting rotary motion into linear motion
- Crank (mechanism) – Simple machine transferring motion to or from a rotating shaft at a distance from the centreline
References
- "Sir Joseph Whitworth". The Whitworth Society. Retrieved January 31, 2016.
- Podhorodeski, Ron (March 2005). "Quick-Return Mechanism Design and Analysis Projects". International Journal of Mechanical Engineering Education.
- Stumph III, Herbert Edward (May 2000). "Kinematic Synthesis of Four and Six Link Mechanisms Used in Mechanical Presses" (PDF). University of Dayton, School of Engineering.
- ^ Beale, D. G.; Scott, R. A. (1990-09-08). "The stability and response of a flexible rod in a quick return mechanism" (PDF). Journal of Sound and Vibration. 141 (2): 277–289. Bibcode:1990JSV...141..277B. doi:10.1016/0022-460X(90)90840-V. hdl:2027.42/28391.
- Echempati, Raghu (June 23, 2013). "Quick Return Mechanism Revisited". American Society for Engineering Education.
- Patel, Shrikant R. (May 2013). "Dynamic Analysis of Quick Return Mechanism Using MATLAB" (PDF). International Journal of Engineering Science and Innovative Technology (IJESIT).
- Hsieh, Wen-Hsiang (September 2009). "A Study on a Novel Quick Return Mechanism" (PDF). Transactions of the Canadian Society for Mechanical Engineering. 33 (3).

