
|

|

|
| Type I | Type II | Type III |
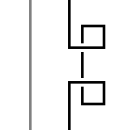
|
| Type I' |
In the mathematical area of knot theory, a Reidemeister move is any of three local moves on a link diagram. Kurt Reidemeister (1927) and, independently, James Waddell Alexander and Garland Baird Briggs (1926), demonstrated that two knot diagrams belonging to the same knot, up to planar isotopy, can be related by a sequence of the three Reidemeister moves.
Each move operates on a small region of the diagram and is one of three types:
- Twist and untwist in either direction.
- Move one loop completely over another.
- Move a string completely over or under a crossing.
No other part of the diagram is involved in the picture of a move, and a planar isotopy may distort the picture. The numbering for the types of moves corresponds to how many strands are involved, e.g. a type II move operates on two strands of the diagram.
One important context in which the Reidemeister moves appear is in defining knot invariants. By demonstrating a property of a knot diagram which is not changed when we apply any of the Reidemeister moves, an invariant is defined. Many important invariants can be defined in this way, including the Jones polynomial.
The type I move is the only move that affects the writhe of the diagram. The type III move is the only one which does not change the crossing number of the diagram.
In applications such as the Kirby calculus, in which the desired equivalence class of knot diagrams is not a knot but a framed link, one must replace the type I move with a "modified type I" (type I') move composed of two type I moves of opposite sense. The type I' move affects neither the framing of the link nor the writhe of the overall knot diagram.
Trace (1983) showed that two knot diagrams for the same knot are related by using only type II and III moves if and only if they have the same writhe and winding number. Furthermore, combined work of Östlund (2001), Manturov (2004), and Hagge (2006) shows that for every knot type there are a pair of knot diagrams so that every sequence of Reidemeister moves taking one to the other must use all three types of moves. Alexander Coward demonstrated that for link diagrams representing equivalent links, there is a sequence of moves ordered by type: first type I moves, then type II moves, type III, and then type II. The moves before the type III moves increase crossing number while those after decrease crossing number.
Coward & Lackenby (2014) proved the existence of an exponential tower upper bound (depending on crossing number) on the number of Reidemeister moves required to pass between two diagrams of the same link. In detail, let be the sum of the crossing numbers of the two diagrams, then the upper bound is where the height of the tower of s (with a single at the top) is .
Lackenby (2015) proved the existence of a polynomial upper bound (depending on crossing number) on the number of Reidemeister moves required to change a diagram of the unknot to the standard unknot. In detail, for any such diagram with crossings, the upper bound is .
Hayashi (2005) proved there is also an upper bound, depending on crossing number, on the number of Reidemeister moves required to split a link.
References
- Reidemeister (1927), pp. 24–25.
- Alexander & Briggs (1926), p. 562.
- Reidemeister (1927), p. 25.
- Östlund (2001), p. 1219.
- Trace (1983), p. 723.
- Alexander & Briggs (1926), p. 564.
- Trace (1983), p. 722.
- Östlund (2001), pp. 1215–1227.
- Coward & Lackenby (2014), p. 1024.
- Lackenby (2015), p. 1.
- Hayashi (2005), p. 1.
 Media related to Reidemeister moves at Wikimedia Commons
Media related to Reidemeister moves at Wikimedia Commons- Alexander, James W.; Briggs, Garland B. (1926), "On types of knotted curves", Annals of Mathematics, 28 (1/4): 562–586, doi:10.2307/1968399, JSTOR 1968399, MR 1502807
- Coward, Alexander; Lackenby, Marc (2014), "An upper bound on Reidemeister moves", American Journal of Mathematics, 136 (4): 1023–1066, arXiv:1104.1882, doi:10.1353/ajm.2014.0027, MR 3245186, S2CID 55882290
- Galatolo, Stefano (1999), "On a problem in effective knot theory", Atti Accad. Naz. Lincei Cl. Sci. Fis. Mat. Natur. Rend. Lincei (9) Mat. Appl., 9 (4): 299–306, MR 1722788
- Hagge, Tobias (2006), "Every Reidemeister move is needed for each knot type", Proc. Amer. Math. Soc., 134 (1): 295–301, doi:10.1090/S0002-9939-05-07935-9, MR 2170571
- Hass, Joel; Lagarias, Jeffrey C. (2001), "The number of Reidemeister moves needed for unknotting", Journal of the American Mathematical Society, 14 (2): 399–428, arXiv:math/9807012, doi:10.1090/S0894-0347-01-00358-7, MR 1815217, S2CID 15654705
- Hayashi, Chuichiro (2005), "The number of Reidemeister moves for splitting a link", Mathematische Annalen, 332 (2): 239–252, doi:10.1007/s00208-004-0599-x, MR 2178061, S2CID 119728321
- Lackenby, Marc (2015), "A polynomial upper bound on Reidemeister moves", Annals of Mathematics, Second Series, 182 (2): 491–564, arXiv:1302.0180, doi:10.4007/annals.2015.182.2.3, MR 3418524, S2CID 119662237
- Manturov, Vassily Olegovich (2004), Knot theory, Boca Raton, FL: Chapman & Hall/CRC, doi:10.1201/9780203402849, ISBN 0-415-31001-6, MR 2068425
- Östlund, Olof-Petter (2001), "Invariants of knot diagrams and relations among Reidemeister moves", J. Knot Theory Ramifications, 10 (8): 1215–1227, arXiv:math/0005108, doi:10.1142/S0218216501001402, MR 1871226, S2CID 119177881
- Reidemeister, Kurt (1927), "Elementare Begründung der Knotentheorie", Abh. Math. Sem. Univ. Hamburg, 5 (1): 24–32, doi:10.1007/BF02952507, MR 3069462, S2CID 120149796
- Trace, Bruce (1983), "On the Reidemeister moves of a classical knot", Proceedings of the American Mathematical Society, 89 (4): 722–724, doi:10.2307/2044613, JSTOR 2044613, MR 0719004
| Knot theory (knots and links) | |
|---|---|
| Hyperbolic |
|
| Satellite | |
| Torus | |
| Invariants | |
| Notation and operations | |
| Other | |
 be the sum of the crossing numbers of the two diagrams, then the upper bound is
be the sum of the crossing numbers of the two diagrams, then the upper bound is  where the height of the tower of
where the height of the tower of  s (with a single
s (with a single  .
.
 crossings, the upper bound is
crossings, the upper bound is  .
.