The relative strength index (RSI) is a technical indicator used in the analysis of financial markets. It is intended to chart the current and historical strength or weakness of a stock or market based on the closing prices of a recent trading period. The indicator should not be confused with relative strength.
The RSI is classified as a momentum oscillator, measuring the velocity and magnitude of price movements. Momentum is the rate of the rise or fall in price. The relative strength RS is given as the ratio of higher closes to lower closes. Concretely, one computes two averages of absolute values of closing price changes, i.e. two sums involving the sizes of candles in a candle chart. The RSI computes momentum as the ratio of higher closes to overall closes: stocks which have had more or stronger positive changes have a higher RSI than stocks which have had more or stronger negative changes.
The RSI is most typically used on a 14-day timeframe, measured on a scale from 0 to 100, with high and low levels marked at 70 and 30, respectively. Short or longer timeframes are used for alternately shorter or longer outlooks. High and low levels—80 and 20, or 90 and 10—occur less frequently but indicate stronger momentum.
The relative strength index was developed by J. Welles Wilder and published in a 1978 book, New Concepts in Technical Trading Systems, and in Commodities magazine (now Modern Trader magazine) in the June 1978 issue. It has become one of the most popular oscillator indices.
The RSI provides signals that tell investors to buy when the security or currency is oversold and to sell when it is overbought.
RSI with recommended parameters and its day-to-day optimization was tested and compared with other strategies in Marek and Šedivá (2017). The testing was randomised in time and companies (e.g., Apple, Exxon Mobil, IBM, Microsoft) and showed that RSI can still produce good results; however, in longer time it is usually overcome by the simple buy-and-hold strategy.
Calculation
For each trading period an upward change U or downward change D is calculated. Up periods are characterized by the close being higher than the previous close:
Conversely, a down period is characterized by the close being lower than the previous period's close,
If the last close is the same as the previous, both U and D are zero. Note that both U and D are nonnegative numbers.
Averages are now calculated from sequences of such U and D, using an n-period smoothed or modified moving average (SMMA or MMA), which is the exponentially smoothed moving average with α = 1 / n. Those are positively weighted averages of those positive terms, and behave additively with respect to the partition.
Wilder originally formulated the calculation of the moving average as: newval = (prevval * (n - 1) + newdata) / n, which is equivalent to the aforementioned exponential smoothing. So new data is simply divided by n, or multiplied by α and previous average values are modified by (n - 1) / n, i.e. 1 - α. Some commercial packages, like AIQ, use a standard exponential moving average (EMA) as the average instead of Wilder's SMMA. The smoothed moving averages should be appropriately initialized with a simple moving average using the first n values in the price series.
The ratio of these averages is the relative strength or relative strength factor:
The relative strength factor is then converted to a relative strength index between 0 and 100:
If the average of U values is zero, both RS and RSI are also zero. If the average of U values equals the average of D values, the RS is 1 and RSI is 50. If the average of U values is maximal, so that the average of D values is zero, then the RS value diverges to infinity, while the RSI is 100.
Interpretation
Basic configuration
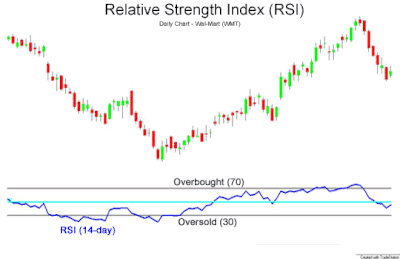

The RSI is presented on a graph above or below the price chart. The indicator has an upper line and a lower line, typically at 70 and 30 respectively, and a dashed mid-line at 50. Wilder recommended a smoothing period of 14 (see exponential smoothing, i.e. α = 1/14 or N = 14).
Principles
Wilder posited that when price moves up very rapidly, at some point it is considered overbought. Likewise, when price falls very rapidly, at some point it is considered oversold. In either case, Wilder deemed a reaction or reversal imminent.
The level of the RSI is a measure of the stock's recent trading strength. The slope of the RSI is directly proportional to the velocity of a change in the trend. The distance traveled by the RSI is proportional to the magnitude of the move.
Wilder believed that tops and bottoms are indicated when RSI goes above 70 or drops below 30. Traditionally, RSI readings greater than the 70 level are considered to be in overbought territory, and RSI readings lower than the 30 level are considered to be in oversold territory. In between the 30 and 70 level is considered neutral, with the 50 level a sign of no trend.
Divergence
Wilder further believed that divergence between RSI and price action is a very strong indication that a market turning point is imminent. Bearish divergence occurs when price makes a new high but the RSI makes a lower high, thus failing to confirm. Bullish divergence occurs when price makes a new low but RSI makes a higher low.
Furthermore, traders often use "hidden" divergences to indicate possible trend reversals. A hidden bullish divergence occurs when the price makes a lower high, while the RSI makes a higher high. Conversely, a hidden bearish divergence occurs when price makes a higher low, but the RSI makes a lower low.
Overbought and oversold conditions
Wilder thought that "failure swings" above 50 and below 50 on the RSI are strong indications of market reversals. For example, assume the RSI hits 76, pulls back to 72, then rises to 77. If it falls below 72, Wilder would consider this a "failure swing" above 70.
Finally, Wilder wrote that chart formations and areas of support and resistance could sometimes be more easily seen on the RSI chart as opposed to the price chart. The center line for the relative strength index is 50, which is often seen as both the support and resistance line for the indicator.
Uptrends and downtrends
| This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (June 2014) (Learn how and when to remove this message) |
In addition to Wilder's original theories of RSI interpretation, Andrew Cardwell has developed several new interpretations of RSI to help determine and confirm trend. First, Cardwell noticed that uptrends generally traded between RSI 40 and 80, while downtrends usually traded between RSI 60 and 20. Cardwell observed when securities change from uptrend to downtrend and vice versa, the RSI will undergo a "range shift."

Next, Cardwell noted that bearish divergence: 1) only occurs in uptrends, and 2) mostly only leads to a brief correction instead of a reversal in trend. Therefore, bearish divergence is a sign confirming an uptrend. Similarly, bullish divergence is a sign confirming a downtrend.
Reversals
| This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (June 2014) (Learn how and when to remove this message) |
Finally, Cardwell discovered the existence of positive and negative reversals in the RSI. Reversals are the opposite of divergence. For example, a positive reversal occurs when an uptrend price correction results in a higher low compared to the last price correction, while RSI results in a lower low compared to the prior correction. A negative reversal happens when a downtrend rally results in a lower high compared to the last downtrend rally, but RSI makes a higher high compared to the prior rally.
In other words, despite stronger momentum as seen by the higher high or lower low in the RSI, price could not make a higher high or lower low. This is evidence the main trend is about to resume. Cardwell noted that positive reversals only happen in uptrends while negative reversals only occur in downtrends, and therefore their existence confirms the trend.
Cutler's RSI
A variation called Cutler's RSI is based on a simple moving average of U and D, instead of the exponential average above. Cutler had found that since Wilder used a smoothed moving average to calculate RSI, the value of Wilder's RSI depended upon where in the data file his calculations started. Cutler termed this Data Length Dependency. Cutler's RSI is not data length dependent, and returns consistent results regardless of the length of, or the starting point within a data file.
Cutler's RSI generally comes out slightly different from the normal Wilder RSI, but the two are similar, since SMA and SMMA are also similar.
General definitions
| This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (February 2023) (Learn how and when to remove this message) |
In analysis,
- If is a real function with positive -norm on a set , then divided by its norm integral, the normalized function , is an associated distribution.
- If is a distribution, one can evaluate measurable subsets of the domain. To this end, the associated indicator function may be mapped to an "index" in the real unit interval, via the pairing .
Now for defined as being equal to if and only if the value of is positive, the index is a quotient of two integrals and is a value that assigns a weight to the part of that is positive. A ratio of two averages over the same domain is also always computed as the ratio of two integrals or sums.
Yet more specifically, for a real function on an ordered set (e.g. a price curve), one may consider that function's gradient , or some weighted variant thereof. In the case where is an ordered finite set (e.g. a sequence of timestamps), the gradient is given as the finite difference.
In the relative strength index, evaluates a sequence derived from closing prices observed in an interval of so called market periods . The positive value equals the absolute price change , i.e. at , multiplied by an exponential factor according to the SMMA weighting for that time. The denominator is the sum of all those numbers. In the numerator one computes the SMMA of only , or in other words multiplied by the indicator function for the positive changes. The resulting index in this way weighs , which includes only the positive changes, over the changes in the whole interval.
See also
- Stochastic Oscillator
- MACD, moving average convergence/divergence
- True strength index, a similar momentum-based indicator
References
- ^ J. Welles Wilder, New Concepts in Technical Trading Systems, ISBN 0-89459-027-8
- John J. Murphy (2009). The Visual Investor: How to Spot Market Trends (2nd ed.). John Wiley and Sons. p. 100. ISBN 9780470382059.
- Deng, S.; Sakurai, A. (2013-03-01). "Foreign Exchange Trading Rules Using a Single Technical Indicator from Multiple Timeframes". 2013 27th International Conference on Advanced Information Networking and Applications Workshops. pp. 207–212. doi:10.1109/WAINA.2013.7. ISBN 978-1-4673-6239-9. S2CID 14825935.
- Marek, Patrice; Šedivá, Blanka (2017). "Optimization and Testing of RSI". 11th International Scientific Conference on Financial Management of Firms and Financial Institutions.
- "Relative Strength Index". Investors Underground. Day Trading Encyclopedia. Retrieved 29 June 2016.
- "RSI". StockCharts. StockCharts.com. Retrieved 29 June 2016.
- Cutler's RSI page at Aspen Graphics Technical Analysis Software
External links
| Technical analysis | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Concepts | |||||||||||||||
| Charts | |||||||||||||||
| Patterns |
| ||||||||||||||
| Indicators |
| ||||||||||||||
| Analysts | |||||||||||||||







 is a
is a  -norm
-norm , then
, then  divided by its norm integral, the normalized function
divided by its norm integral, the normalized function  , is an associated
, is an associated  is a distribution, one can evaluate measurable subsets
is a distribution, one can evaluate measurable subsets  of the domain. To this end, the associated
of the domain. To this end, the associated  may be mapped to an "index"
may be mapped to an "index"  in the real
in the real  .
. defined as being equal to
defined as being equal to 
 is positive, the index
is positive, the index  is a quotient of two integrals and is a value that assigns a weight to the part of
is a quotient of two integrals and is a value that assigns a weight to the part of  is an ordered
is an ordered  evaluates a sequence
evaluates a sequence  so called market periods
so called market periods  . The positive value
. The positive value  equals the absolute price change
equals the absolute price change  , i.e.
, i.e.  at
at  , multiplied by an
, multiplied by an  is the sum of all those numbers. In the numerator one computes the SMMA of only
is the sum of all those numbers. In the numerator one computes the SMMA of only  , or in other words
, or in other words