
Top row: Four-bar cognate linkages.
Middle row: Geared five-bar cognate linkages, derived from top row.
Bottom row: Closely related six-bar cognate linkages, derived from middle row.
In kinematics, cognate linkages are linkages that ensure the same coupler curve geometry or input-output relationship, while being dimensionally dissimilar. In case of four-bar linkage coupler cognates, the Roberts–Chebyshev Theorem, after Samuel Roberts and Pafnuty Chebyshev, states that each coupler curve can be generated by three different four-bar linkages. These four-bar linkages can be constructed using similar triangles and parallelograms, and the Cayley diagram (named after Arthur Cayley).
Overconstrained mechanisms can be obtained by connecting two or more cognate linkages together.
Roberts–Chebyshev theorem
The theorem states, for a given coupler curve produced by a four-bar linkage with four revolute (hinge) joints, there exist three four-bar linkages, three geared five-bar linkages, and more six-bar linkages which will generate the same path.
For a coupler curve produced by a four-bar linkage with four revolute joints and a prismatic (slider) joint, there exist only two four-bar linkages, as the third would be composed of two sliders, making it a four-bar linkage with two degrees of freedom.
Construction of four-bar coupler cognates
Cayley diagram
 Cayley diagram for generating 4-bar coupler cognates.
Cayley diagram for generating 4-bar coupler cognates. Animation showing the construction of two four-bar cognate linkages from an initial four-bar cognate.
Animation showing the construction of two four-bar cognate linkages from an initial four-bar cognate.
From original triangle, ΔA1DB1:
- Sketch Cayley diagram.
- Using parallelograms, find A2 and B3 ▱OAA1DA2 and ▱OBB1DB3.
- Using similar triangles, find C2 and C3 ΔA2C2D and ΔDC3B3.
- Using a parallelogram, find OC ▱OCC2DC3.
- Check similar triangles ΔOAOCOB.
- Separate left and right cognate.
- Put dimensions on Cayley diagram.
Dimensional relationships
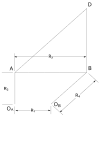
The lengths of the four members can be found by using the law of sines. Both KL and KR are found as follows.
| Linkage | Ground | Crank 1 | Crank 2 | Coupler |
|---|---|---|---|---|
| Original | R1 | R2 | R3 | R4 |
| Left cognate | KLR1 | KLR3 | KLR4 | KLR2 |
| Right cognate | KRR1 | KRR2 | KRR3 | KRR4 |
Conclusions
- If and only if the original is a Class I chain Both 4-bar cognates will be class I chains.
- If the original is a drag-link (double crank), both cognates will be drag links.
- If the original is a crank-rocker, one cognate will be a crank-rocker, and the second will be a double-rocker.
- If the original is a double-rocker, the cognates will be crank-rockers.
Construction of geared five-bar cognates

A five-bar linkage has two degrees of freedom, and thus there does not exist a five-bar linkage which is capable of acting as a cognate. However, it is possible to generate a 5-bar cognate using gears.
- Select four-bar linkage of choice.
- Construct two parallelograms off of the center coupler link and the links connected to the ground.
- On each parallelogram, find the sides opposite of the connecting link. Apply a 1:1 gear train between them.
- Separate cognates.
The utilization of the 1:1 gear train is used because of the behavior of parallelogram linkages. Opposite 'sides' of the parallelogram linkages share the same rotational motion function. Because both parallelograms were constructed off of the center coupler link, the new links connected to the ground share identical rotational motion functions, allowing for a 1:1 gear train to be used to connect them together.
Construction of six-bar coupler cognates
 Animation showing the construction of a six-bar cognate linkages from an initial four-bar cognate.
Animation showing the construction of a six-bar cognate linkages from an initial four-bar cognate. Animation showing the construction of Chebyshev's table linkage using the two cognate linkages Chebyshev linkage and Chebyshev lambda linkage.
Animation showing the construction of Chebyshev's table linkage using the two cognate linkages Chebyshev linkage and Chebyshev lambda linkage.The pink link indicates the former ground link that has become a rectilinear link.
Alternative to geared five-bar cognates
The geared five-bar cognate linkage utilizes a 1:1 gear train to ensure two links have the same rotational motion function. However, an alternative to using a gear train to achieve 1:1 rotation is to connect them together using a parallelogram linkage, adding one additional link.
Pairing previously derived cognates together
An important behavior with four-bar linkages is that once the positions of two links is defined, the other two links in the four-bar linkage can be defined.
One characteristic with cognate linkages is that they often share at least two links in identical configuration. These links are usually oriented 180 degrees of each other, so when pairing, these links can be fused. This creates a 4-bar linkage with two additional links, both of which are defined by the original four-bar linkage. The former ground link of the fusing 4-bar linkage becomes a rectilinear link that travels follows the same coupler curve.
Each of these paired six-bar cognate linkages can also be converted into another cognate linkage by flipping the linkage over, and switching the roles of the rectilinear link and the ground link.
Construction of coupler cognates with more links
Appending onto the method of the six-bar pairings, the links do not necessarily have to overlap, but rather just need to meet the criterion such that:
- There is a pair of two links in identical configuration.
- The former ground link of one of the linkages is directly attached to the point producing the coupler curve.
Rather than overlapping the paired links, they can be attached in a fashion which forms a parallelogram, resulting in eight-bar cognate linkages. Triplet cognate linkage pairings and further extensions are also possible, allowing for the number of links of cognate linkages to increase theoretically indefinitely.
Function cognates

Function cognate linkages are linkages which share the same motion functions for their input and output links. This is performed using a six-bar Watt II linkage arrangement.
- Split the six bar linkage into two quadrilaterals (shown as and ).
- Translate the ground joint to a new location, .
- With the new ground joint , form two similar quadrilaterals (shown as and ).
- Reform the shared link .
- Separate Cognates.
Similar quadrilaterals will have links which share the same motion function. Because one link is shared between the two quadrilaterals, then as long as the new quadrilaterals are similar to the original, both will still share a link with the same motion function.
If the new quadrilaterals do not share the same ground joint (as shown with joint C'), they can still be connected together using a parallelogram linkage, forming an 8-bar function cognate.
See also
- Arthur Cayley - Cayley Diagram
- Four-bar linkage
- Kinematic pair
- Linkage (mechanical)
- Pafnuty Chebyshev - Roberts–Chebyshev Theorem
- Samuel Roberts - Roberts–Chebyshev Theorem
Notes
- There are specific overconstrained configurations that have a DOF of 0, however they are not useful in the construction of cognate linkages.
References
- Roberts and Chebyshev (Springer) Retrieved 2012-10-12
- Uicker, John J.; Pennock, Gordon R.; Shigley, Joseph E. (2003). Theory of Machines and Mechanisms. Oxford University Press. ISBN 0-19-515598-X.
- Samuel Roberts (1875) "On Three-bar Motion in Plane Space", Proceedings of the London Mathematical Society, vol 7.
- Hartenberg, R.S. & J. Denavit (1964) Kinematic synthesis of linkages, p 169, New York: McGraw-Hill, weblink from Cornell University.
Further reading
- Simionescu, P.A.; Smith, M.R. (2001). "Four- and six-bar function cognates and overconstrained mechanisms". Mechanism and Machine Theory. 36 (8): 913–924. doi:10.1016/S0094-114X(01)00031-3.
- Simionescu, P.A.; Smith, M.R. (2000). "Applications of Watt II function generator cognates". Mechanism and Machine Theory. 35 (11): 1535–1549. doi:10.1016/S0094-114X(00)00011-2.
- Soni, A.H. (1970). "Coupler cognate mechanisms of certain parallelogram forms of watt's six-link mechanism". Journal of Mechanisms. 5 (2): 203–215. doi:10.1016/0022-2569(70)90023-6.

 Both 4-bar cognates will be class I chains.
Both 4-bar cognates will be class I chains. and
and  ).
). to a new location,
to a new location,  .
. and
and  ).
). .
.