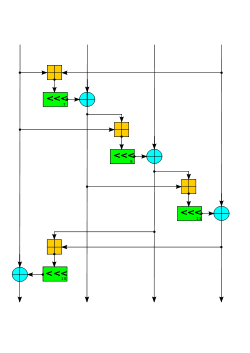
 The Salsa quarter-round function. Four parallel copies make a round. The Salsa quarter-round function. Four parallel copies make a round. | |
| General | |
|---|---|
| Designers | Daniel J. Bernstein |
| First published | 2007 (designed 2005) |
| Successors | ChaCha |
| Related to | Rumba20 |
| Certification | eSTREAM portfolio |
| Cipher detail | |
| Key sizes | 128 or 256 bits |
| State size | 512 bits |
| Structure | ARX |
| Rounds | 20 |
| Speed | 3.91 cpb on an Intel Core 2 Duo |
| Best public cryptanalysis | |
| 2008 cryptanalysis breaks 8 out of 20 rounds to recover the 256-bit secret key in 2 operations, using 2 keystream pairs. | |
Salsa20 and the closely related ChaCha are stream ciphers developed by Daniel J. Bernstein. Salsa20, the original cipher, was designed in 2005, then later submitted to the eSTREAM European Union cryptographic validation process by Bernstein. ChaCha is a modification of Salsa20 published in 2008. It uses a new round function that increases diffusion and increases performance on some architectures.
Both ciphers are built on a pseudorandom function based on add–rotate–XOR (ARX) operations — 32-bit addition, bitwise addition (XOR) and rotation operations. The core function maps a 256-bit key, a 64-bit nonce, and a 64-bit counter to a 512-bit block of the key stream (a Salsa version with a 128-bit key also exists). This gives Salsa20 and ChaCha the unusual advantage that the user can efficiently seek to any position in the key stream in constant time. Salsa20 offers speeds of around 4–14 cycles per byte in software on modern x86 processors, and reasonable hardware performance. It is not patented, and Bernstein has written several public domain implementations optimized for common architectures.
Structure
Internally, the cipher uses bitwise addition ⊕ (exclusive OR), 32-bit addition mod 2 ⊞, and constant-distance rotation operations <<< on an internal state of sixteen 32-bit words. Using only add-rotate-xor operations avoids the possibility of timing attacks in software implementations. The internal state is made of sixteen 32-bit words arranged as a 4×4 matrix.
| 0 | 1 | 2 | 3 |
| 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 |
The initial state is made up of eight words of key ( ), two words of stream position ( ), two words of nonce (essentially additional stream position bits) ( ), and four fixed words ( ):
| "expa" | Key | Key | Key |
| Key | "nd 3" | Nonce | Nonce |
| Pos. | Pos. | "2-by" | Key |
| Key | Key | Key | "te k" |
The constant words spell "expand 32-byte k" in ASCII (i.e. the 4 words are "expa", "nd 3", "2-by", and "te k"). This is an example of a nothing-up-my-sleeve number. The core operation in Salsa20 is the quarter-round QR(a, b, c, d) that takes a four-word input and produces a four-word output:
b ^= (a + d) <<< 7; c ^= (b + a) <<< 9; d ^= (c + b) <<< 13; a ^= (d + c) <<< 18;
Odd-numbered rounds apply QR(a, b, c, d) to each of the four columns in the 4×4 matrix, and even-numbered rounds apply it to each of the four rows. Two consecutive rounds (column-round and row-round) together are called a double-round:
// Odd round QR( 0, 4, 8, 12) // column 1 QR( 5, 9, 13, 1) // column 2 QR(10, 14, 2, 6) // column 3 QR(15, 3, 7, 11) // column 4 // Even round QR( 0, 1, 2, 3) // row 1 QR( 5, 6, 7, 4) // row 2 QR(10, 11, 8, 9) // row 3 QR(15, 12, 13, 14) // row 4
An implementation in C/C++ appears below.
#include <stdint.h>
#define ROTL(a,b) (((a) << (b)) | ((a) >> (32 - (b))))
#define QR(a, b, c, d)( \
b ^= ROTL(a + d, 7), \
c ^= ROTL(b + a, 9), \
d ^= ROTL(c + b,13), \
a ^= ROTL(d + c,18))
#define ROUNDS 20
void salsa20_block(uint32_t out, uint32_t const in)
{
int i;
uint32_t x;
for (i = 0; i < 16; ++i)
x = in;
// 10 loops × 2 rounds/loop = 20 rounds
for (i = 0; i < ROUNDS; i += 2) {
// Odd round
QR(x, x, x, x); // column 1
QR(x, x, x, x); // column 2
QR(x, x, x, x); // column 3
QR(x, x, x, x); // column 4
// Even round
QR(x, x, x, x); // row 1
QR(x, x, x, x); // row 2
QR(x, x, x, x); // row 3
QR(x, x, x, x); // row 4
}
for (i = 0; i < 16; ++i)
out = x + in;
}
In the last line, the mixed array is added, word by word, to the original array to obtain its 64-byte key stream block. This is important because the mixing rounds on their own are invertible. In other words, applying the reverse operations would produce the original 4×4 matrix, including the key. Adding the mixed array to the original makes it impossible to recover the input. (This same technique is widely used in hash functions from MD4 through SHA-2.)
Salsa20 performs 20 rounds of mixing on its input. However, reduced-round variants Salsa20/8 and Salsa20/12 using 8 and 12 rounds respectively have also been introduced. These variants were introduced to complement the original Salsa20, not to replace it, and perform better in the eSTREAM benchmarks than Salsa20, though with a correspondingly lower security margin.
XSalsa20 with 192-bit nonce
In 2008, Bernstein proposed a variant of Salsa20 with 192-bit nonces called XSalsa20. XSalsa20 is provably secure if Salsa20 is secure, but is more suitable for applications where longer nonces are desired. XSalsa20 feeds the key and the first 128 bits of the nonce into one block of Salsa20 (without the final addition, which may either be omitted, or subtracted after a standard Salsa20 block), and uses 256 bits of the output as the key for standard Salsa20 using the last 64 bits of the nonce and the stream position. Specifically, the 256 bits of output used are those corresponding to the non-secret portions of the input: indexes 0, 5, 10, 15, 6, 7, 8 and 9.
eSTREAM selection of Salsa20
Salsa20/12 has been selected as a Phase 3 design for Profile 1 (software) by the eSTREAM project, receiving the highest weighted voting score of any Profile 1 algorithm at the end of Phase 2. Salsa20 had previously been selected as a Phase 2 Focus design for Profile 1 (software) and as a Phase 2 design for Profile 2 (hardware) by the eSTREAM project, but was not advanced to Phase 3 for Profile 2 because eSTREAM felt that it was probably not a good candidate for extremely resource-constrained hardware environments.
The eSTREAM committee recommends the use of Salsa20/12, the 12-round variant, for "combining very good performance with a comfortable margin of security."
Cryptanalysis of Salsa20
As of 2015, there are no published attacks on Salsa20/12 or the full Salsa20/20; the best attack known breaks 8 of the 12 or 20 rounds.
In 2005, Paul Crowley reported an attack on Salsa20/5 with an estimated time complexity of 2 and won Bernstein's US$1000 prize for "most interesting Salsa20 cryptanalysis". This attack and all subsequent attacks are based on truncated differential cryptanalysis. In 2006, Fischer, Meier, Berbain, Biasse, and Robshaw reported an attack on Salsa20/6 with estimated time complexity of 2, and a related-key attack on Salsa20/7 with estimated time complexity of 2.
In 2007, Tsunoo et al. announced a cryptanalysis of Salsa20 which breaks 8 out of 20 rounds to recover the 256-bit secret key in 2 operations, using 2 keystream pairs. However, this attack does not seem to be competitive with the brute force attack.
In 2008, Aumasson, Fischer, Khazaei, Meier, and Rechberger reported a cryptanalytic attack against Salsa20/7 with a time complexity of 2, and they reported an attack against Salsa20/8 with an estimated time complexity of 2. This attack makes use of the new concept of probabilistic neutral key bits for probabilistic detection of a truncated differential. The attack can be adapted to break Salsa20/7 with a 128-bit key.
In 2012, the attack by Aumasson et al. was improved by Shi et al. against Salsa20/7 (128-bit key) to a time complexity of 2 and Salsa20/8 (256-bit key) to 2.
In 2013, Mouha and Preneel published a proof that 15 rounds of Salsa20 was 128-bit secure against differential cryptanalysis. (Specifically, it has no differential characteristic with higher probability than 2, so differential cryptanalysis would be more difficult than 128-bit key exhaustion.)
ChaCha variant
 The ChaCha quarter-round function. Four parallel copies make a round. The ChaCha quarter-round function. Four parallel copies make a round. | |
| General | |
|---|---|
| Designers | Daniel J. Bernstein |
| First published | 2008 |
| Derived from | Salsa20 |
| Related to | Rumba20 |
| Cipher detail | |
| Key sizes | 128 or 256 bits |
| State size | 512 bits |
| Structure | ARX |
| Rounds | 20 |
| Speed | 3.95 cpb on an Intel Core 2 Duo |
In 2008, Bernstein published the closely related ChaCha family of ciphers, which aim to increase the diffusion per round while achieving the same or slightly better performance. The Aumasson et al. paper also attacks ChaCha, achieving one round fewer (for 256-bit ChaCha6 with complexity 2, ChaCha7 with complexity 2, and 128-bit ChaCha6 within 2) but claims that the attack fails to break 128-bit ChaCha7.
Like Salsa20, ChaCha's initial state includes a 128-bit constant, a 256-bit key, a 64-bit counter, and a 64-bit nonce (in the original version; as described later, a version of ChaCha from RFC 7539 is slightly different), arranged as a 4×4 matrix of 32-bit words. But ChaCha re-arranges some of the words in the initial state:
| "expa" | "nd 3" | "2-by" | "te k" |
| Key | Key | Key | Key |
| Key | Key | Key | Key |
| Counter | Counter | Nonce | Nonce |
The constant is the same as Salsa20 ("expand 32-byte k"). ChaCha replaces the Salsa20 quarter-round QR(a, b, c, d) with:
a += b; d ^= a; d <<<= 16; c += d; b ^= c; b <<<= 12; a += b; d ^= a; d <<<= 8; c += d; b ^= c; b <<<= 7;
Notice that this version updates each word twice, while Salsa20's quarter round updates each word only once. In addition, the ChaCha quarter-round diffuses changes more quickly. On average, after changing 1 input bit the Salsa20 quarter-round will change 8 output bits while ChaCha will change 12.5 output bits.
The ChaCha quarter round has the same number of adds, xors, and bit rotates as the Salsa20 quarter-round, but the fact that two of the rotates are multiples of 8 allows for a small optimization on some architectures including x86. Additionally, the input formatting has been rearranged to support an efficient SSE implementation optimization discovered for Salsa20. Rather than alternating rounds down columns and across rows, they are performed down columns and along diagonals. Like Salsa20, ChaCha arranges the sixteen 32-bit words in a 4×4 matrix. If we index the matrix elements from 0 to 15
| 0 | 1 | 2 | 3 |
| 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 |
then a double round in ChaCha is:
// Odd round QR(0, 4, 8, 12) // column 1 QR(1, 5, 9, 13) // column 2 QR(2, 6, 10, 14) // column 3 QR(3, 7, 11, 15) // column 4 // Even round QR(0, 5, 10, 15) // diagonal 1 (main diagonal) QR(1, 6, 11, 12) // diagonal 2 QR(2, 7, 8, 13) // diagonal 3 QR(3, 4, 9, 14) // diagonal 4
ChaCha20 uses 10 iterations of the double round. An implementation in C/C++ appears below.
#include <stdint.h>
#define ROTL(a,b) (((a) << (b)) | ((a) >> (32 - (b))))
#define QR(a, b, c, d) ( \
a += b, d ^= a, d = ROTL(d, 16), \
c += d, b ^= c, b = ROTL(b, 12), \
a += b, d ^= a, d = ROTL(d, 8), \
c += d, b ^= c, b = ROTL(b, 7))
#define ROUNDS 20
void chacha_block(uint32_t out, uint32_t const in)
{
int i;
uint32_t x;
for (i = 0; i < 16; ++i)
x = in;
// 10 loops × 2 rounds/loop = 20 rounds
for (i = 0; i < ROUNDS; i += 2) {
// Odd round
QR(x, x, x, x); // column 1
QR(x, x, x, x); // column 2
QR(x, x, x, x); // column 3
QR(x, x, x, x); // column 4
// Even round
QR(x, x, x, x); // diagonal 1 (main diagonal)
QR(x, x, x, x); // diagonal 2
QR(x, x, x, x); // diagonal 3
QR(x, x, x, x); // diagonal 4
}
for (i = 0; i < 16; ++i)
out = x + in;
}
ChaCha is the basis of the BLAKE hash function, a finalist in the NIST hash function competition, and its faster successors BLAKE2 and BLAKE3. It also defines a variant using sixteen 64-bit words (1024 bits of state), with correspondingly adjusted rotation constants.
XChaCha
Although not announced by Bernstein, the security proof of XSalsa20 extends straightforwardly to an analogous XChaCha cipher. Use the key and the first 128 bits of the nonce (in input words 12 through 15) to form a ChaCha input block, then perform the block operation (omitting the final addition). Output words 0–3 and 12–15 (those words corresponding to non-key words of the input) then form the key used for ordinary ChaCha (with the last 64 bits of nonce and 64 bits of block counter).
Reduced-round ChaCha
Aumasson argues in 2020 that 8 rounds of ChaCha (ChaCha8) probably provides enough resistance to future cryptanalysis for the same security level, yielding a 2.5× speedup. A compromise ChaCha12 (based on the eSTREAM recommendation of a 12-round Salsa) also sees some use. The eSTREAM benchmarking suite includes ChaCha8 and ChaCha12.
ChaCha20 adoption
Google had selected ChaCha20 along with Bernstein's Poly1305 message authentication code in SPDY, which was intended as a replacement for TLS over TCP. In the process, they proposed a new authenticated encryption construction combining both algorithms, which is called ChaCha20-Poly1305. ChaCha20 and Poly1305 are now used in the QUIC protocol, which replaces SPDY and is used by HTTP/3.
Shortly after Google's adoption for TLS, both the ChaCha20 and Poly1305 algorithms were also used for a new chacha20-poly1305@openssh.com cipher in OpenSSH. Subsequently, this made it possible for OpenSSH to avoid any dependency on OpenSSL, via a compile-time option.
ChaCha20 is also used for the arc4random random number generator in FreeBSD, OpenBSD, and NetBSD operating systems, instead of the broken RC4, and in DragonFly BSD for the CSPRNG subroutine of the kernel. Starting from version 4.8, the Linux kernel uses the ChaCha20 algorithm to generate data for the nonblocking /dev/urandom device. ChaCha8 is used for the default PRNG in Golang. Rust's CSPRNG uses ChaCha12.
ChaCha20 usually offers better performance than the more prevalent Advanced Encryption Standard (AES) algorithm on systems where the CPU does not feature AES acceleration (such as the AES instruction set for x86 processors). As a result, ChaCha20 is sometimes preferred over AES in certain use cases involving mobile devices, which mostly use ARM-based CPUs. Specialized hardware accelerators for ChaCha20 are also less complex compared to AES accelerators.
ChaCha20-Poly1305 (IETF version; see below) is the exclusive algorithm used by the WireGuard VPN system, as of protocol version 1.
Internet standards
An implementation reference for ChaCha20 has been published in RFC 7539. The IETF's implementation modified Bernstein's published algorithm by changing the 64-bit nonce and 64-bit block counter to a 96-bit nonce and 32-bit block counter. The name was not changed when the algorithm was modified, as it is cryptographically insignificant (both form what a cryptographer would recognize as a 128-bit nonce), but the interface change could be a source of confusion for developers. Because of the reduced block counter, the maximum message length that can be safely encrypted by the IETF's variant is 2 blocks of 64 bytes (256 GiB). For applications where this is not enough, such as file or disk encryption, RFC 7539 proposes using the original algorithm with 64-bit nonce.
| "expa" | "nd 3" | "2-by" | "te k" |
| Key | Key | Key | Key |
| Key | Key | Key | Key |
| Counter | Nonce | Nonce | Nonce |
Use of ChaCha20 in IKE and IPsec has been standardized in RFC 7634. Standardization of its use in TLS is published in RFC 7905.
In 2018, RFC 7539 was obsoleted by RFC 8439. RFC 8439 merges in some errata and adds additional security considerations.
See also
- Speck – an add-rotate-xor cipher developed by the NSA
- ChaCha20-Poly1305 – an AEAD scheme combining ChaCha20 with the Poly1305 MAC
Notes
- Since the majority of the work consists of performing the repeated rounds, the number of rounds is inversely proportional to the performance. That is, halving the number of rounds roughly doubles the performance. Reduced-round variants are thus appreciably faster.
References
- ^ Daniel J. Bernstein (2007-12-24). "The Salsa20 family of stream ciphers" (PDF). cr.yp.to.
- Daniel J. Bernstein (2013-05-16). "Salsa 20 speed; Salsa20 software".
- ^ Jean-Philippe Aumasson; Simon Fischer; Shahram Khazaei; Willi Meier; Christian Rechberger (2008-03-14). "New Features of Latin Dances" (PDF). International Association for Cryptologic Research.
- ^ Bernstein, Daniel (28 January 2008), ChaCha, a variant of Salsa20 (PDF), retrieved 2018-06-03
- Daniel J. Bernstein (2013-05-16). "Snuffle 2005: the Salsa20 encryption function".
- "Salsa20: Software speed". 2007-05-11.
- Daniel J. Bernstein. "Extending the Salsa20 nonce (updated in 2011)" (PDF). cr.yp.to. Retrieved 2022-08-18.
- Daniel J. Bernstein. "Extending the Salsa20 nonce (original version)" (PDF). cr.yp.to. Retrieved 2022-08-18.
- "Salsa20/12". ECRYPT II. Retrieved 2017-08-22.
- "The eSTREAM Project: End of Phase 2". eSTREAM. 2008-04-29.
- Hongjun Wu (2007-03-30). "eSTREAM PHASE 3: End of Phase 1". eSTREAM.
- "eSTREAM: Short Report on the End of the Second Phase" (PDF). eSTREAM. 2007-03-26.
- "Salsa20/12, The eSTREAM portfolio page". www.ecrypt.eu.org.
- Paul Crowley (2006-02-09). "Truncated differential cryptanalysis of five rounds of Salsa20".
- Simon Fischer; Willi Meier; Côme Berbain; Jean-François Biasse; M. J. B. Robshaw (2006). "Non-randomness in eSTREAM Candidates Salsa20 and TSC-4". Progress in Cryptology - INDOCRYPT 2006: 7th International Conference on Cryptology in India, Kolkata, India, December 11-13, 2006, Proceeding. Lecture Notes in Computer Science. Vol. 4329. pp. 2–16. CiteSeerX 10.1.1.121.7248. doi:10.1007/11941378_2. ISBN 978-3-540-49767-7.
- Yukiyasu Tsunoo; Teruo Saito; Hiroyasu Kubo; Tomoyasu Suzaki; Hiroki Nakashima (2007-01-02). "Differential Cryptanalysis of Salsa20/8" (PDF). ECRYPT.
- Zhenqing Shi; Bin Zhang; Dengguo Feng; Wenling Wu (2012). "Improved Key Recovery Attacks on Reduced-Round Salsa20 and ChaCha". Information Security and Cryptology – ICISC 2012. Lecture Notes in Computer Science. Vol. 7839. pp. 337–351. doi:10.1007/978-3-642-37682-5_24. ISBN 978-3-642-37681-8.
- Nicky Mouha; Bart Preneel (2013). "Towards Finding Optimal Differential Characteristics for ARX: Application to Salsa20" (PDF). International Association for Cryptologic Research.
- ^ Daniel J. Bernstein (2008-04-25). "The ChaCha family of stream ciphers".
- Neves, Samuel (2009-10-07), Faster ChaCha implementations for Intel processors, archived from the original on 2017-03-28, retrieved 2016-09-07,
two of these constants are multiples of 8; this allows for a 1 instruction rotation in Core2 and later Intel CPUs using the pshufb instruction
- Y. Nir; A. Langley (May 2015). "ChaCha20 and Poly1305 for IETF Protocols: RFC 7539".
- Arciszewski, Scott (10 January 2020). "XChaCha: eXtended-nonce ChaCha and AEAD_XChaCha20_Poly1305 (Expired Internet-Draft)". Ietf Datatracker.
- Aumasson, Jean-Philippe (2020). Too Much Crypto (PDF). Real World Crypto Symposium.
- ^ "rand_chacha: consider ChaCha12 (or possibly ChaCha8) over ChaCha20 · Issue #932 · rust-random/rand". GitHub.
- "ChaCha". Cryptography Primer.
- "Do the ChaCha: better mobile performance with cryptography". The Cloudflare Blog. 2015-02-23. Retrieved 2021-07-13.
- Thomson, Martin; Turner, Sean (May 2021). "RFC 9001". datatracker.ietf.org. Retrieved 2021-07-13.
- Bishop, Mike (2 February 2021). "draft: IETF QUIC HTTP". datatracker.ietf.org. Retrieved 2021-07-13.
- Miller, Damien (2016-05-03). "ssh/PROTOCOL.chacha20poly1305". Super User's BSD Cross Reference: PROTOCOL.chacha20poly1305. Retrieved 2016-09-07.
- Murenin, Constantine A. (2013-12-11). Unknown Lamer (ed.). "OpenSSH Has a New Cipher — Chacha20-poly1305 — from D.J. Bernstein". Slashdot. Retrieved 2016-09-07.
- Murenin, Constantine A. (2014-04-30). Soulskill (ed.). "OpenSSH No Longer Has To Depend On OpenSSL". Slashdot. Retrieved 2016-09-07.
- "Revision 317015". 2017-04-16. Retrieved 2018-03-16.
Replace the RC4 algorithm for generating in-kernel secure random numbers with Chacha20
- guenther (Philip Guenther), ed. (2015-09-13). "libc/crypt/arc4random.c". Super User's BSD Cross Reference: arc4random.c. Retrieved 2016-09-07.
ChaCha based random number generator for OpenBSD.
- riastradh (Taylor Campbell), ed. (2016-03-25). "libc/gen/arc4random.c". Super User's BSD Cross Reference: arc4random.c. Retrieved 2016-09-07.
Legacy arc4random(3) API from OpenBSD reimplemented using the ChaCha20 PRF, with per-thread state.
- "kern/subr_csprng.c". Super User's BSD Cross Reference: subr_csprng.c. 2015-11-04. Retrieved 2016-09-07.
chacha_encrypt_bytes - "ChaCha Usage & Deployment". 2016-09-07. Retrieved 2016-09-07.
- "arc4random(3)". NetBSD Manual Pages. 2014-11-16. Archived from the original on 2020-07-06. Retrieved 2016-09-07.
- Corbet, Jonathan. "Replacing /dev/urandom". Linux Weekly News. Retrieved 2016-09-20.
- "Merge tag 'random_for_linus' of git.kernel.org/pub/scm/linux/kernel/git/tytso/random". Linux kernel source tree. Retrieved 2016-09-20.
random: replace non-blocking pool with a Chacha20-based CRNG
- Michael Larabel (2016-07-25). "/dev/random Seeing Improvements For Linux 4.8". Phoronix. Retrieved 2016-10-03.
- Cox, Russ; Valsorda, Filippo. "Secure Randomness in Go 1.22 - The Go Programming Language". go.dev.
- "What's the appeal of using ChaCha20 instead of AES?". Cryptography Stack Exchange. 2016-04-12.
- "AES-NI SSL Performance Study @ Calomel.org".
- Pfau, Johannes; Reuter, Maximilian; Harbaum, Tanja; Hofmann, Klaus; Becker, Jurgen (September 2019). "A Hardware Perspective on the ChaCha Ciphers: Scalable Chacha8/12/20 Implementations Ranging from 476 Slices to Bitrates of 175 Gbit/s". 2019 32nd IEEE International System-on-Chip Conference (SOCC). pp. 294–299. doi:10.1109/SOCC46988.2019.1570548289. ISBN 978-1-7281-3483-3.
- "Protocol and Cryptography". WireGuard. Jason A. Donenfeld. Retrieved 4 July 2018.
- ^ "ChaCha20 and Poly1305 for IETF protocols" (PDF). Retrieved 2017-08-07.
Changes from regular ChaCha. The nonce: block sequence number split was changed from 64:64 to 96:32 The ChaCha20 state is initialized as follows:
- Header of RFC 7539.
External links
- Snuffle 2005: the Salsa20 encryption function
- Salsa20 specification (PDF)
- Salsa20/8 and Salsa20/12 (PDF)
- The eSTREAM Project: Salsa20
- The ChaCha family of stream ciphers
- Salsa20 Usage & Deployment
- Implementation and Didactical Visualization of the ChaCha Cipher Family in CrypTool 2