In geometry, the Spieker center is a special point associated with a plane triangle. It is defined as the center of mass of the perimeter of the triangle. The Spieker center of a triangle △ABC is the center of gravity of a homogeneous wire frame in the shape of △ABC. The point is named in honor of the 19th-century German geometer Theodor Spieker. The Spieker center is a triangle center and it is listed as the point X(10) in Clark Kimberling's Encyclopedia of Triangle Centers.
Location

The following result can be used to locate the Spieker center of any triangle.
- The Spieker center of triangle △ABC is the incenter of the medial triangle of △ABC.
That is, the Spieker center of △ABC is the center of the circle inscribed in the medial triangle of △ABC. This circle is known as the Spieker circle.
The Spieker center is also located at the intersection of the three cleavers of triangle △ABC. A cleaver of a triangle is a line segment that bisects the perimeter of the triangle and has one endpoint at the midpoint of one of the three sides. Each cleaver contains the center of mass of the boundary of △ABC, so the three cleavers meet at the Spieker center.
To see that the incenter of the medial triangle coincides with the intersection point of the cleavers, consider a homogeneous wireframe in the shape of triangle △ABC consisting of three wires in the form of line segments having lengths a, b, c. The wire frame has the same center of mass as a system of three particles of masses a, b, c placed at the midpoints D, E, F of the sides BC, CA, AB. The centre of mass of the particles at E and F is the point P which divides the segment EF in the ratio c : b. The line DP is the internal bisector of ∠D. The centre of mass of the three particle system thus lies on the internal bisector of ∠D. Similar arguments show that the center mass of the three particle system lies on the internal bisectors of ∠E and ∠F also. It follows that the center of mass of the wire frame is the point of concurrence of the internal bisectors of the angles of the triangle △DEF , which is the incenter of the medial triangle △DEF .
Properties
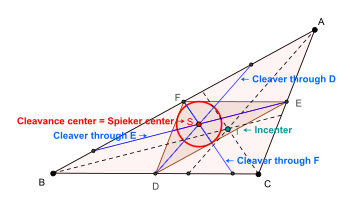
Let S be the Spieker center of triangle △ABC.
- The trilinear coordinates of S are
- The barycentric coordinates of S are
- S is the radical center of the three excircles.
- S is the cleavance center of triangle △ABC
- S is collinear with the incenter (I), the centroid (G), and the Nagel point (N) of triangle △ABC. Moreover,
- Thus on a suitably scaled and positioned number line, I = 0, G = 2, S = 3, and M = 6.
- S lies on the Kiepert hyperbola. S is the point of concurrence of the lines AX, BY, CZ where △XBC, △YCA, △ZAB are similar, isosceles and similarly situated triangles constructed on the sides of triangle △ABC as bases, having the common base angle
References
- ^ Honsberger, Ross (1995). Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Mathematical Association of America. pp. 3–4.
- Kimberling, Clark. "Spieker center". Retrieved 5 May 2012.
- Spieker, Theodor (1888). Lehrbuch der ebenen Geometrie. Potsdam, Germany.
{{cite book}}: CS1 maint: location missing publisher (link) - ^ Kimberling, Clark. "Encyclopedia of Triangle Centers". Retrieved 5 May 2012.
- Odenhal, Boris (2010), "Some triangle centers associated with the circles tangent to the excircles" (PDF), Forum Geometricorum, 10: 35–40, archived from the original (PDF) on 2021-11-14, retrieved 2014-11-30
- Bogomolny, A. "Nagel Line from Interactive Mathematics Miscellany and Puzzles". Retrieved 5 May 2012.
- Weisstein, Eric W. "Kiepert Hyperbola". MathWorld.



