In category theory, monoidal functors are functors between monoidal categories which preserve the monoidal structure. More specifically, a monoidal functor between two monoidal categories consists of a functor between the categories, along with two coherence maps—a natural transformation and a morphism that preserve monoidal multiplication and unit, respectively. Mathematicians require these coherence maps to satisfy additional properties depending on how strictly they want to preserve the monoidal structure; each of these properties gives rise to a slightly different definition of monoidal functors
- The coherence maps of lax monoidal functors satisfy no additional properties; they are not necessarily invertible.
- The coherence maps of strong monoidal functors are invertible.
- The coherence maps of strict monoidal functors are identity maps.
Although we distinguish between these different definitions here, authors may call any one of these simply monoidal functors.
Definition
Let and be monoidal categories. A lax monoidal functor from to (which may also just be called a monoidal functor) consists of a functor together with a natural transformation
between functors and a morphism
- ,
called the coherence maps or structure morphisms, which are such that for every three objects , and of the diagrams
commute in the category . Above, the various natural transformations denoted using are parts of the monoidal structure on and .
Variants
- The dual of a monoidal functor is a comonoidal functor; it is a monoidal functor whose coherence maps are reversed. Comonoidal functors may also be called opmonoidal, colax monoidal, or oplax monoidal functors.
- A strong monoidal functor is a monoidal functor whose coherence maps are invertible.
- A strict monoidal functor is a monoidal functor whose coherence maps are identities.
- A braided monoidal functor is a monoidal functor between braided monoidal categories (with braidings denoted ) such that the following diagram commutes for every pair of objects A, B in :
- A symmetric monoidal functor is a braided monoidal functor whose domain and codomain are symmetric monoidal categories.
Examples
- The underlying functor from the category of abelian groups to the category of sets. In this case, the map sends (a, b) to ; the map sends to 1.
- If is a (commutative) ring, then the free functor extends to a strongly monoidal functor (and also if is commutative).
- If is a homomorphism of commutative rings, then the restriction functor is monoidal and the induction functor is strongly monoidal.
- An important example of a symmetric monoidal functor is the mathematical model of topological quantum field theory. Let be the category of cobordisms of n-1,n-dimensional manifolds with tensor product given by disjoint union, and unit the empty manifold. A topological quantum field theory in dimension n is a symmetric monoidal functor
- The homology functor is monoidal as via the map .
Alternate notions
If and are closed monoidal categories with internal hom-functors (we drop the subscripts for readability), there is an alternative formulation
- ψAB : F(A ⇒ B) → FA ⇒ FB
of φAB commonly used in functional programming. The relation between ψAB and φAB is illustrated in the following commutative diagrams:
Properties
- If is a monoid object in , then is a monoid object in .
Monoidal functors and adjunctions
Suppose that a functor is left adjoint to a monoidal . Then has a comonoidal structure induced by , defined by
and
- .
If the induced structure on is strong, then the unit and counit of the adjunction are monoidal natural transformations, and the adjunction is said to be a monoidal adjunction; conversely, the left adjoint of a monoidal adjunction is always a strong monoidal functor.
Similarly, a right adjoint to a comonoidal functor is monoidal, and the right adjoint of a comonoidal adjunction is a strong monoidal functor.
See also
Inline citations
- Perrone (2024), pp. 360–364
- Perrone (2024), pp. 367–368
References
- Kelly, G. Max (1974). "Doctrinal adjunction". Category Seminar. Lecture Notes in Mathematics. Vol. 420. Springer. pp. 257–280. doi:10.1007/BFb0063105. ISBN 978-3-540-37270-7.
- Perrone, Paolo (2024). Starting Category Theory. World Scientific. doi:10.1142/9789811286018_0005. ISBN 978-981-12-8600-1.
| Functor types | |
|---|---|
 and
and  be monoidal categories. A lax monoidal functor from
be monoidal categories. A lax monoidal functor from  to
to  (which may also just be called a monoidal functor) consists of a
(which may also just be called a monoidal functor) consists of a  together with a
together with a 
 and a morphism
and a morphism
 ,
, ,
,  and
and  of
of 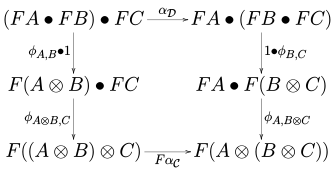


 are parts of the monoidal structure on
are parts of the monoidal structure on  are invertible.
are invertible. ) such that the following diagram commutes for every pair of objects A, B in
) such that the following diagram commutes for every pair of objects A, B in 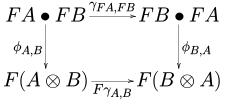
 from the category of abelian groups to the category of sets. In this case, the map
from the category of abelian groups to the category of sets. In this case, the map  sends (a, b) to
sends (a, b) to  ; the map
; the map  sends
sends  to 1.
to 1. is a (commutative) ring, then the free functor
is a (commutative) ring, then the free functor  extends to a strongly monoidal functor
extends to a strongly monoidal functor  (and also
(and also  if
if  is a homomorphism of commutative rings, then the restriction functor
is a homomorphism of commutative rings, then the restriction functor  is monoidal and the induction functor
is monoidal and the induction functor  is strongly monoidal.
is strongly monoidal. be the category of
be the category of 
 via the map
via the map  .
. (we drop the subscripts for readability), there is an alternative formulation
(we drop the subscripts for readability), there is an alternative formulation


 is a
is a  is a monoid object in
is a monoid object in  .
. . Then
. Then  has a comonoidal structure
has a comonoidal structure  induced by
induced by  , defined by
, defined by

 .
.