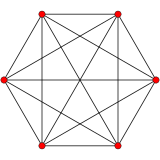
 5-simplex |
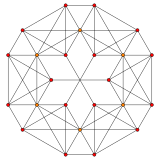 Truncated 5-simplex |
 Bitruncated 5-simplex |
| Orthogonal projections in A5 Coxeter plane | ||
|---|---|---|
In five-dimensional geometry, a truncated 5-simplex is a convex uniform 5-polytope, being a truncation of the regular 5-simplex.
There are unique 2 degrees of truncation. Vertices of the truncation 5-simplex are located as pairs on the edge of the 5-simplex. Vertices of the bitruncation 5-simplex are located on the triangular faces of the 5-simplex.
Truncated 5-simplex
| Truncated 5-simplex | ||
| Type | Uniform 5-polytope | |
| Schläfli symbol | t{3,3,3,3} | |
| Coxeter-Dynkin diagram | ||
| 4-faces | 12 | 6 {3,3,3} 6 t{3,3,3} |
| Cells | 45 | 30 {3,3} 15 t{3,3} |
| Faces | 80 | 60 {3} 20 {6} |
| Edges | 75 | |
| Vertices | 30 | |
| Vertex figure |  ( )v{3,3} | |
| Coxeter group | A5 , order 720 | |
| Properties | convex | |
The truncated 5-simplex has 30 vertices, 75 edges, 80 triangular faces, 45 cells (15 tetrahedral, and 30 truncated tetrahedron), and 12 4-faces (6 5-cell and 6 truncated 5-cells).
Alternate names
- Truncated hexateron (Acronym: tix) (Jonathan Bowers)
Coordinates
The vertices of the truncated 5-simplex can be most simply constructed on a hyperplane in 6-space as permutations of (0,0,0,0,1,2) or of (0,1,2,2,2,2). These coordinates come from facets of the truncated 6-orthoplex and bitruncated 6-cube respectively.
Images
| Ak Coxeter plane |
A5 | A4 |
|---|---|---|
| Graph | 
|

|
| Dihedral symmetry | ||
| Ak Coxeter plane |
A3 | A2 |
| Graph | 
|

|
| Dihedral symmetry |
Bitruncated 5-simplex
| bitruncated 5-simplex | ||
| Type | Uniform 5-polytope | |
| Schläfli symbol | 2t{3,3,3,3} | |
| Coxeter-Dynkin diagram | ||
| 4-faces | 12 | 6 2t{3,3,3} 6 t{3,3,3} |
| Cells | 60 | 45 {3,3} 15 t{3,3} |
| Faces | 140 | 80 {3} 60 {6} |
| Edges | 150 | |
| Vertices | 60 | |
| Vertex figure | 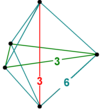 { }v{3} | |
| Coxeter group | A5 , order 720 | |
| Properties | convex | |
Alternate names
- Bitruncated hexateron (Acronym: bittix) (Jonathan Bowers)
Coordinates
The vertices of the bitruncated 5-simplex can be most simply constructed on a hyperplane in 6-space as permutations of (0,0,0,1,2,2) or of (0,0,1,2,2,2). These represent positive orthant facets of the bitruncated 6-orthoplex, and the tritruncated 6-cube respectively.
Images
| Ak Coxeter plane |
A5 | A4 |
|---|---|---|
| Graph | 
|

|
| Dihedral symmetry | ||
| Ak Coxeter plane |
A3 | A2 |
| Graph | 
|

|
| Dihedral symmetry |
Related uniform 5-polytopes
The truncated 5-simplex is one of 19 uniform 5-polytopes based on the Coxeter group, all shown here in A5 Coxeter plane orthographic projections. (Vertices are colored by projection overlap order, red, orange, yellow, green, cyan, blue, purple having progressively more vertices)
| A5 polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 t0 |
 t1 |
 t2 |
 t0,1 |
 t0,2 |
 t1,2 |
 t0,3 | |||||
 t1,3 |
 t0,4 |
 t0,1,2 |
 t0,1,3 |
 t0,2,3 |
 t1,2,3 |
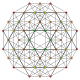 t0,1,4 | |||||
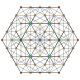 t0,2,4 |
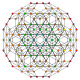 t0,1,2,3 |
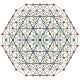 t0,1,2,4 |
 t0,1,3,4 |
 t0,1,2,3,4 | |||||||
Notes
- Klitizing, (x3x3o3o3o - tix)
- Klitizing, (o3x3x3o3o - bittix)
References
- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I,
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II,
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III,
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
- Klitzing, Richard. "5D uniform polytopes (polytera)". x3x3o3o3o - tix, o3x3x3o3o - bittix
External links
- Glossary for hyperspace, George Olshevsky.
- Polytopes of Various Dimensions, Jonathan Bowers
- Truncated uniform polytera (tix), Jonathan Bowers
- Multi-dimensional Glossary
| Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform polychoron | Pentachoron | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||