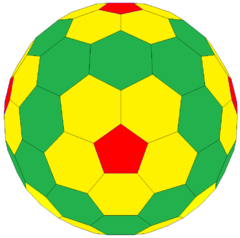
| Chamfered dodecahedron | |
|---|---|
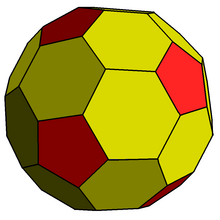 | |
| Type | Goldberg polyhedron (GV(2,0) = {5+,3}2,0) Fullerene (C80) Near-miss Johnson solid |
| Faces | 12 pentagons 30 irregular hexagons |
| Edges | 120 (2 types) |
| Vertices | 80 (2 types) |
| Vertex configuration | 60 (5.6.6) 20 (6.6.6) |
| Conway notation | cD = t5daD = dk5aD |
| Symmetry group | Icosahedral (Ih) |
| Dual polyhedron | Pentakis icosidodecahedron |
| Properties | convex, equilateral-faced |
| Net | |
 | |
In geometry, the chamfered dodecahedron is a convex polyhedron with 80 vertices, 120 edges, and 42 faces: 30 hexagons and 12 pentagons. It is constructed as a chamfer (edge-truncation) of a regular dodecahedron. The pentagons are reduced in size and new hexagonal faces are added in place of all the original edges. Its dual is the pentakis icosidodecahedron.
It is also called a truncated rhombic triacontahedron, constructed as a truncation of the rhombic triacontahedron. It can more accurately be called an order-5 truncated rhombic triacontahedron because only the order-5 vertices are truncated.
Structure
These 12 order-5 vertices can be truncated such that all edges are equal length. The original 30 rhombic faces become non-regular hexagons, and the truncated vertices become regular pentagons.
The hexagon faces can be equilateral but not regular with D2 symmetry. The angles at the two vertices with vertex configuration 6.6.6 are and at the remaining four vertices with 5.6.6, they are 121.717° each.
It is the Goldberg polyhedron GV(2,0), containing pentagonal and hexagonal faces.
It also represents the exterior envelope of a cell-centered orthogonal projection of the 120-cell, one of six convex regular 4-polytopes.
Chemistry
This is the shape of the fullerene C80; sometimes this shape is denoted C80(Ih) to describe its icosahedral symmetry and distinguish it from other less-symmetric 80-vertex fullerenes. It is one of only four fullerenes found by Deza, Deza & Grishukhin (1998) to have a skeleton that can be isometrically embeddable into an L1 space.

Related polyhedra
This polyhedron looks very similar to the uniform truncated icosahedron which has 12 pentagons, but only 20 hexagons.
-
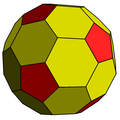 Truncated rhombic triacontahedron
Truncated rhombic triacontahedron
G(2,0) -
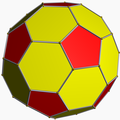 Truncated icosahedron
Truncated icosahedron
G(1,1) -
 cell-centered orthogonal projection of the 120-cell
cell-centered orthogonal projection of the 120-cell
The chamfered dodecahedron creates more polyhedra by basic Conway polyhedron notation. The zip chamfered dodecahedron makes a chamfered truncated icosahedron, and Goldberg (2,2).
| "seed" | ambo | truncate | zip | expand | bevel | snub | chamfer | whirl |
|---|---|---|---|---|---|---|---|---|
 cD = G(2,0) cD |
 acD acD |
 tcD tcD |
 zcD = G(2,2) zcD |
 ecD ecD |
 bcD bcD |
 scD scD |
 ccD = G(4,0) ccD |
 wcD = G(4,2) wcD |
| dual | join | needle | kis | ortho | medial | gyro | dual chamfer | dual whirl |
 dcD dcD |
 jcD jcD |
 ncD ncD |
 kcD kcD |
 ocD ocD |
 mcD mcD |
 gcD gcD |
 dccD dccD |
 dwcD dwcD |
Chamfered truncated icosahedron
| Chamfered truncated icosahedron | |
|---|---|
| |
| Goldberg polyhedron | GV(2,2) = {5+,3}2,2 |
| Conway notation | ctI |
| Fullerene | C240 |
| Faces | 12 pentagons 110 hexagons (3 types) |
| Edges | 360 |
| Vertices | 240 |
| Symmetry | Ih, , (*532) |
| Dual polyhedron | Hexapentakis chamfered dodecahedron |
| Properties | convex |
In geometry, the chamfered truncated icosahedron is a convex polyhedron with 240 vertices, 360 edges, and 122 faces, 110 hexagons and 12 pentagons.
It is constructed by a chamfer operation to the truncated icosahedron, adding new hexagons in place of original edges. It can also be constructed as a zip (= dk = dual of kis of) operation from the chamfered dodecahedron. In other words, raising pentagonal and hexagonal pyramids on a chamfered dodecahedron (kis operation) will yield the (2,2) geodesic polyhedron. Taking the dual of that yields the (2,2) Goldberg polyhedron, which is the chamfered truncated icosahedron, and is also Fullerene C240.
Dual
Its dual, the hexapentakis chamfered dodecahedron has 240 triangle faces (grouped as 60 (blue), 60 (red) around 12 5-fold symmetry vertices and 120 around 20 6-fold symmetry vertices), 360 edges, and 122 vertices.

Hexapentakis chamfered dodecahedron
References
- "C80 Isomers". Archived from the original on 2014-08-12. Retrieved 2014-08-05.
Bibliography
- Deza, Antoine; Deza, Michel; Grishukhin, Viatcheslav (October 1998). "Fullerenes and coordination polyhedra versus half-cube embeddings". Discrete Mathematics. 192 (1–3): 41–80. doi:10.1016/S0012-365X(98)00065-X.
- Goldberg, Michael (1937). "A class of multi-symmetric polyhedra". Tohoku Mathematical Journal. 43: 104–108.
- Hart, George (2012). "Goldberg Polyhedra". In Senechal, Marjorie (ed.). Shaping Space (2nd ed.). Springer. pp. 125–138. doi:10.1007/978-0-387-92714-5_9. ISBN 978-0-387-92713-8.
- Hart, George (June 18, 2013). "Mathematical Impressions: Goldberg Polyhedra". Simons Science News.
External links
- Vertex- and edge-truncation of the Platonic and Archimedean solids leading to vertex-transitive polyhedra Livio Zefiro
- VRML polyhedral generator (Conway polyhedron notation)
 and at the remaining four vertices with 5.6.6, they are 121.717° each.
and at the remaining four vertices with 5.6.6, they are 121.717° each.