This is an old revision of this page, as edited by 68.56.80.231 (talk) at 23:05, 11 October 2008 (→Numerical value). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.
Revision as of 23:05, 11 October 2008 by 68.56.80.231 (talk) (→Numerical value)(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff)
| List of numbers – Irrational numbers ζ(3) – √2 – √3 – √5 – φ – α – e – π – δ | |
| Binary | 11.00100100001111110110… |
| Decimal | 3.14159265358979323846… |
| Hexadecimal | 3.243F6A8885A308D31319… |
| Continued fraction | Note that this continued fraction is not periodic. |
Pi or π is a mathematical constant which represents the ratio of any circle's circumference to its diameter in Euclidean geometry, which is the same as the ratio of a circle's area to the square of its radius. It is approximately equal to 3.14159. Pi is one of the most important mathematical constants: many formulae from mathematics, science, and engineering involve π.
Pi is an irrational number, which means that it cannot be expressed as a fraction m/n, where m and n are integers. Consequently its decimal representation never ends or repeats. Beyond being irrational, it is a transcendental number, which means that no finite sequence of algebraic operations on integers (powers, roots, sums, etc.) could ever produce it. Throughout the history of mathematics, much effort has been made to determine π more accurately and understand its nature; fascination with the number has even carried over into culture at large.
The Greek letter π, often spelled out pi in text, was adopted for the number from the Greek word for perimeter "περίμετρος", probably by William Jones in 1706, and popularized by Leonhard Euler some years later. The constant is occasionally also referred to as the circular constant, Archimedes' constant (not to be confused with an Archimedes number), or Ludolph's number.
Fundamentals
The letter π

The name of the Greek letter π is pi, and this spelling is used in typographical contexts where the Greek letter is not available or where its usage could be problematic. When referring to this constant, the symbol π is always pronounced like "pie" in English, the conventional English pronunciation of the letter. In Greek, the name of this letter is pronounced /pi/.
The constant is named "π" because "π" is the first letter of the Greek words περιφέρεια (periphery) and περίμετρος (perimeter), probably referring to its use in the formula to find the circumference, or perimeter, of a circle. π is Unicode character U+03C0 ("Greek small letter pi").
Definition

In Euclidean plane geometry, π is defined as the ratio of a circle's circumference to its diameter:
Note that the ratio /d does not depend on the size of the circle. For example, if a circle has twice the diameter d of another circle it will also have twice the circumference c, preserving the ratio /d. This fact is a consequence of the similarity of all circles.
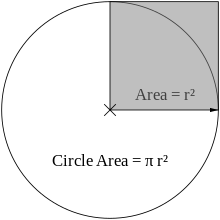
Alternatively π can be also defined as the ratio of a circle's area (A) to the area of a square whose side is equal to the radius:
The constant π may be defined in other ways that avoid the concepts of arc length and area, for example, as twice the smallest positive x for which cos(x) = 0. The formulas below illustrate other (equivalent) definitions.
Irrationality and transcendence
Main article: Proof that π is irrationalThe constant π is an irrational number; that is, it cannot be written as the ratio of two integers. This was proven in 1761 by Johann Heinrich Lambert. In the 20th century, proofs were found that require no prerequisite knowledge beyond integral calculus. One of those, due to Ivan Niven, is widely known. A somewhat earlier similar proof is by Mary Cartwright.
Furthermore, π is also transcendental, as was proven by Ferdinand von Lindemann in 1882. This means that there is no polynomial with rational coefficients of which π is a root. An important consequence of the transcendence of π is the fact that it is not constructible. Because the coordinates of all points that can be constructed with compass and straightedge are constructible numbers, it is impossible to square the circle: that is, it is impossible to construct, using compass and straightedge alone, a square whose area is equal to the area of a given circle.
Numerical value
See also: numerical approximations of πUse in mathematics and science
Main article: List of formulas involving ππ is ubiquitous in mathematics, appearing even in places that lack an obvious connection to the circles of Euclidean geometry.
Geometry and trigonometry
See also: Area of a diskFor any circle with radius r and diameter d = 2r, the circumference is πd and the area is πr. Further, π appears in formulas for areas and volumes of many other geometrical shapes based on circles, such as ellipses, spheres, cones, and tori. Accordingly, π appears in definite integrals that describe circumference, area or volume of shapes generated by circles. In the basic case, half the area of the unit disk is given by:
and
gives half the circumference of the unit circle. More complicated shapes can be integrated as solids of revolution.
From the unit-circle definition of the trigonometric functions also follows that the sine and cosine have period 2π. That is, for all x and integers n, sin(x) = sin(x + 2πn) and cos(x) = cos(x + 2πn). Because sin(0) = 0, sin(2πn) = 0 for all integers n. Also, the angle measure of 180° is equal to π radians. In other words, 1° = (π/180) radians.
In modern mathematics, π is often defined using trigonometric functions, for example as the smallest positive x for which sin x = 0, to avoid unnecessary dependence on the subtleties of Euclidean geometry and integration. Equivalently, π can be defined using the inverse trigonometric functions, for example as π = 2 arccos(0) or π = 4 arctan(1). Expanding inverse trigonometric functions as power series is the easiest way to derive infinite series for π.
Higher analysis and number theory
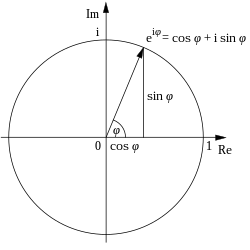
The frequent appearance of π in complex analysis can be related to the behavior of the exponential function of a complex variable, described by Euler's formula
where i is the imaginary unit satisfying i = −1 and e ≈ 2.71828 is Euler's number. This formula implies that imaginary powers of e describe rotations on the unit circle in the complex plane; these rotations have a period of 360° = 2π. In particular, the 180° rotation φ = π results in the remarkable Euler's identity
There are n different n-th roots of unity
A consequence is that the gamma function of a half-integer is a rational multiple of √π.
Physics
Although not a physical constant, π appears routinely in equations describing fundamental principles of the Universe, due in no small part to its relationship to the nature of the circle and, correspondingly, spherical coordinate systems. Using units such as Planck units can sometimes eliminate π from formulae.
- Heisenberg's uncertainty principle, which shows that the uncertainty in the measurement of a particle's position (Δx) and momentum (Δp) can not both be arbitrarily small at the same time:
- Coulomb's law for the electric force, describing the force between two electric charges (q1 and q2) separated by distance r:
- Kepler's third law constant, relating the orbital period (P) and the semimajor axis (a) to the masses (M and m) of two co-orbiting bodies:
Probability and statistics
In probability and statistics, there are many distributions whose formulas contain π, including:
- the probability density function for the normal distribution with mean μ and standard deviation σ, due to the Gaussian integral:
- the probability density function for the (standard) Cauchy distribution:
Note that since for any probability density function f(x), the above formulas can be used to produce other integral formulas for π.
Buffon's needle problem is sometimes quoted as a empirical approximation of π in "popular mathematics" works. Consider dropping a needle of length L repeatedly on a surface containing parallel lines drawn S units apart (with S > L). If the needle is dropped n times and x of those times it comes to rest crossing a line (x > 0), then one may approximate π using the Monte Carlo method:
Though this result is mathematically impeccable, it cannot be used to determine more than very few digits of π by experiment. Reliably getting just three digits (including the initial "3") right requires millions of throws, and the number of throws grows exponentially with the number of digits desired. Furthermore, any error in the measurement of the lengths L and S will transfer directly to an error in the approximated π. For example, a difference of a single atom in the length of a 10-centimeter needle would show up around the 9th digit of the result. In practice, uncertainties in determining whether the needle actually crosses a line when it appears to exactly touch it will limit the attainable accuracy to much less than 9 digits.
See also
- List of topics related to π
- Proof that 22/7 exceeds π
- Feynman point – comprising the 762nd through 767th decimal places of π, consisting of the digit 9 repeated six times.
- Indiana Pi Bill.
- Pi Day.
- Software for calculating π on personal computers.
- Mathematical constants: e and φ
- SOCR resource hands-on activity for estimation of π using needle-dropping simulation.
References
- Howard Whitley Eves (1969). An Introduction to the History of Mathematics. Holt, Rinehart & Winston.
- ^ "About Pi". Ask Dr. Math FAQ. Retrieved 2007-10-29.
- "Characters Ordered by Unicode". W3C. Retrieved 2007-10-25.
- Richmond, Bettina (1999-01-12). "Area of a Circle". Western Kentucky University. Retrieved 2007-11-04.
{{cite web}}: Check date values in:|date=(help) - Rudin, Walter (1976) . Principles of mathematical analysis (3e ed.). McGraw-Hill. p. 183. ISBN 0-07-054235-X.
- Niven, Ivan (1947). "A simple proof that π is irrational" (PDF). Bulletin of the American Mathematical Society. 53 (6): 509. doi:10.1090/S0002-9904-1947-08821-2. Retrieved 2007-11-04.
- Richter, Helmut (1999-07-28). "Pi Is Irrational". Leibniz Rechenzentrum. Retrieved 2007-11-04.
{{cite web}}: Check date values in:|date=(help) - Jeffreys, Harold (1973). Scientific Inference (3rd ed.). Cambridge University Press.
- Mayer, Steve. "The Transcendence of π". Retrieved 2007-11-04.
- "Squaring the Circle". cut-the-knot. Retrieved 2007-11-04.
- "Japanese breaks pi memory record". BBC News. 2005-07-02. Retrieved 2007-10-30.
{{cite web}}: Check date values in:|date=(help) - "Area and Circumference of a Circle by Archimedes". Penn State. Retrieved 2007-11-08.
- Weisstein, Eric W (2006-01-28). "Unit Disk Integral". MathWorld. Retrieved 2007-11-08.
{{cite web}}: Check date values in:|date=(help) - "Area and Circumference of a Circle by Archimedes". Penn State. Retrieved 2007-11-08.
- Weisstein, Eric W (2006-05-04). "Solid of Revolution". MathWorld. Retrieved 2007-11-08.
{{cite web}}: Check date values in:|date=(help) - Miller, Cole. "The Cosmological Constant" (PDF). University of Maryland. Retrieved 2007-11-08.
- Imamura, James M (2005-08-17). "Heisenberg Uncertainty Principle". University of Oregon. Retrieved 2007-11-09.
{{cite web}}: Check date values in:|date=(help) - Einstein, Albert (1916). "The Foundation of the General Theory of Relativity" (PDF). Annalen der Physik. Retrieved 2007-11-09.
-
Nave, C. Rod (2005-06-28). "Coulomb's Constant". HyperPhysics. Georgia State University. Retrieved 2007-11-09.
{{cite web}}: Check date values in:|date=(help) - "Magnetic constant". NIST. 2006 CODATA recommended values. Retrieved 2007-11-09.
{{cite web}}: Check date values in:|date=(help) - Weisstein, Eric W (2004-10-07). "Gaussian Integral". MathWorld. Retrieved 2007-11-08.
{{cite web}}: Check date values in:|date=(help) - Weisstein, Eric W (2005-10-11). "Cauchy Distribution". MathWorld. Retrieved 2007-11-08.
{{cite web}}: Check date values in:|date=(help) - Weisstein, Eric W (2003-07-02). "Probability Function". MathWorld. Retrieved 2007-11-08.
{{cite web}}: Check date values in:|date=(help) - ^ Weisstein, Eric W (2005-12-12). "Buffon's Needle Problem". MathWorld. Retrieved 2007-11-10.
{{cite web}}: Check date values in:|date=(help) - Bogomolny, Alex (2001-08). "Math Surprises: An Example". cut-the-knot. Retrieved 2007-10-28.
{{cite web}}: Check date values in:|date=(help) - Ramaley, J. F. (Oct 1969). "Buffon's Noodle Problem". The American Mathematical Monthly. 76 (8): 916–918. doi:10.2307/2317945.
- "The Monte Carlo algorithm/method". datastructures. 2007-01-09. Retrieved 2007-11-07.
{{cite web}}: Check date values in:|date=(help)
External links
- The Joy of Pi by David Blatner
- Decimal expansions of Pi and related links at the On-Line Encyclopedia of Integer Sequences
- J J O'Connor and E F Robertson: A history of pi. Mac Tutor project
- Lots of formulas for π at MathWorld
- PlanetMath: Pi
- Finding the value of π
- Determination of π at cut-the-knot
- BBC Radio Program about π
- Statistical Distribution Information on PI based on 1.2 trillion digits of PI
- The Digits of Pi — First ten thousand
- First 4 Million Digits of π - Warning - Roughly 2 megabytes will be transferred.
- One million digits of pi at piday.org
- Project Gutenberg E-Text containing a million digits of π
- Search the first 200 million digits of π for arbitrary strings of numbers
- Source code for calculating the digits of π
- π is Wrong! An opinion column on why 2π is more useful in mathematics.
- 70 Billion digits of Pi(π) downloads.
- The first 16 million digits of Pi (18 mb .txt file)
Template:Link FA Template:Link FA Template:Link FA Template:Link FA Template:Link FA Template:Link FA
Categories:
















 for any probability density function f(x), the above formulas can be used to produce other integral formulas for π.
for any probability density function f(x), the above formulas can be used to produce other integral formulas for π.
