Misplaced Pages

Family of bifrusta
Example: hexagonal bifrustum
Faces	2 n-gons 2n trapezoids
Edges	5n
Vertices	3n
Symmetry group	Dnh, , (*n22)
Surface area	${\displaystyle {\begin{aligned}&n(a+b){\sqrt {\left({\tfrac {a-b}{2}}\cot {\tfrac {\pi }{n}}\right)^{2}+h^{2}}}\\&\ \ +\ n{\frac {b^{2}}{2\tan {\frac {\pi }{n}}}}\end{aligned}}}$
Volume	${\displaystyle n{\frac {a^{2}+b^{2}+ab}{6\tan {\frac {\pi }{n}}}}h}$
Dual polyhedron	Elongated bipyramids
Properties	convex

In geometry, an n-agonal bifrustum is a polyhedron composed of three parallel planes of n-agons, with the middle plane largest and usually the top and bottom congruent.

It can be constructed as two congruent frusta combined across a plane of symmetry, and also as a bipyramid with the two polar vertices truncated.

They are duals to the family of elongated bipyramids.

Formulae

For a regular n-gonal bifrustum with the equatorial polygon sides a, bases sides b and semi-height (half the distance between the planes of bases) h, the lateral surface area A_l, total area A and volume V are: and $${\displaystyle {\begin{aligned}A_{l}&=n(a+b){\sqrt {\left({\tfrac {a-b}{2}}\cot {\tfrac {\pi }{n}}\right)^{2}+h^{2}}}\\A&=A_{l}+n{\frac {b^{2}}{2\tan {\frac {\pi }{n}}}}\\V&=n{\frac {a^{2}+b^{2}+ab}{6\tan {\frac {\pi }{n}}}}h\end{aligned}}}$$ Note that the volume V is twice the volume of a frusta.

Forms

Three bifrusta are duals to three Johnson solids, J_14-16. In general, a n-agonal bifrustum has 2n trapezoids, 2 n-agons, and is dual to the elongated dipyramids.

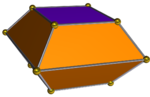
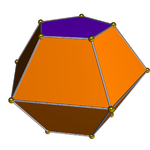
Triangular bifrustum	Square bifrustum	Pentagonal bifrustum
6 trapezoids, 2 triangles. Dual to elongated triangular bipyramid, J14	8 trapezoids, 2 squares. Dual to elongated square bipyramid, J15	10 trapezoids, 2 pentagons. Dual to elongated pentagonal bipyramid, J16

References

1. "Octagonal Bifrustum". etc.usf.edu. Retrieved 2022-06-16.
2. "Regelmäßiges Bifrustum - Rechner". RECHNERonline (in German). Retrieved 2022-06-30.
3. "mathworld pyramidal frustum".

This polyhedron-related article is a stub. You can help Misplaced Pages by expanding it.

• v
• t
• e

• Polyhedron stubs
• Polyhedra