
Cyclohexane conformations are any of several three-dimensional shapes adopted by cyclohexane. Because many compounds feature structurally similar six-membered rings, the structure and dynamics of cyclohexane are important prototypes of a wide range of compounds.
The internal angles of a regular, flat hexagon are 120°, while the preferred angle between successive bonds in a carbon chain is about 109.5°, the tetrahedral angle (the arc cosine of −1/3). Therefore, the cyclohexane ring tends to assume non-planar (warped) conformations, which have all angles closer to 109.5° and therefore a lower strain energy than the flat hexagonal shape.
Consider the carbon atoms numbered from 1 to 6 around the ring. If we hold carbon atoms 1, 2, and 3 stationary, with the correct bond lengths and the tetrahedral angle between the two bonds, and then continue by adding carbon atoms 4, 5, and 6 with the correct bond length and the tetrahedral angle, we can vary the three dihedral angles for the sequences (2,3,4), (3,4,5), and (4,5,6). The next bond, from atom 6, is also oriented by a dihedral angle, so we have four degrees of freedom. But that last bond has to end at the position of atom 1, which imposes three conditions in three-dimensional space. If the bond angle in the chain (6,1,2) should also be the tetrahedral angle then we have four conditions. In principle this means that there are no degrees of freedom of conformation, assuming all the bond lengths are equal and all the angles between bonds are equal. It turns out that, with atoms 1, 2, and 3 fixed, there are two solutions called chair, depending on whether the dihedral angle for (1,2,3,4) is positive or negative, and these two solutions are the same under a rotation. But there is also a continuum of solutions, a topological circle where angle strain is zero, including the twist boat and the boat conformations. All the conformations on this continuum have a twofold axis of symmetry running through the ring, whereas the chair conformations do not (they have D3d symmetry, with a threefold axis running through the ring). It is because of the symmetry of the conformations on this continuum that it is possible to satisfy all four constraints with a range of dihedral angles at (1,2,3,4). On this continuum the energy varies because of Pitzer strain related to the dihedral angles. The twist boat has a lower energy than the boat. In order to go from the chair conformation to a twist-boat conformation or the other chair conformation, bond angles have to be changed, leading to a high-energy half-chair conformation. So the relative stabilities are: chair > twist boat > boat > half-chair. All relative conformational energies are shown below. At room temperature the molecule can easily move among these conformations, but only chair and twist-boat can be isolated in pure form, because the others are not at local energy minima.
The boat and twist-boat conformations, as said, lie along a continuum of zero angle strain. If there are substituents that allow the different carbon atoms to be distinguished, then this continuum is like a circle with six boat conformations and six twist-boat conformations between them, three "right-handed" and three "left-handed". (Which should be called right-handed is unimportant.) But if the carbon atoms are indistinguishable, as in cyclohexane itself, then moving along the continuum takes the molecule from the boat form to a "right-handed" twist-boat, and then back to the same boat form (with a permutation of the carbon atoms), then to a "left-handed" twist-boat, and then back again to the achiral boat. The passage boat⊣twist-boat⊣boat⊣twist-boat⊣boat constitutes a pseudorotation.
Coplanar carbons
Another way to compare the stability within two molecules of cyclohexane in the same conformation is to evaluate the number of coplanar carbons in each molecule. Coplanar carbons are carbons that are all on the same plane. Increasing the number of coplanar carbons increases the number of eclipsing substituents trying to form a 120°, which is unattainable due to the overlapping hydrogens. This overlap increases the overall torsional strain and decreases the stability of the conformation. Cyclohexane diminishes the torsional strain from eclipsing substituents through adopting a conformation with a lower number of nonplanar carbons. For example, if a half-chair conformation contains four coplanar carbons and another half-chair conformation contains five coplanar carbons, the conformation with four coplanar carbons will be more stable.
Principal conformers
The different conformations are called "conformers", a blend of the words "conformation" and "isomer".
Chair conformation
The chair conformation is the most stable conformer. At 298 K (25 °C), 99.99% of all molecules in a cyclohexane solution adopt this conformation.
The symmetry group is D3d. All carbon centers are equivalent. Six hydrogen centers are poised in axial positions, roughly parallel with the C3 axis, and six hydrogen atoms are parallel with the equator of the molecule.
Each carbon bears one "up" and one "down" hydrogen. The C–H bonds in successive carbons are thus staggered so that there is little torsional strain. The chair geometry is often preserved when the hydrogen atoms are replaced by halogens or other simple groups. However, when these hydrogens are substituted for a larger group, strain is imposed upon the molecule due to diaxial interactions. This is an interaction (that is usually repulsive) between two substituents in the axial position on a cyclohexane ring.
If one thinks of a carbon atom as a point with four half-bonds sticking out towards the vertices of a tetrahedron, they can imagine them standing on a surface with one half-bond pointing straight up. Looking from right above, the other three would appear to go outwards towards the vertices of an equilateral triangle, so the bonds would appear to have an angle of 120° between them. Now consider six such atoms standing on the surface so that their non-vertical half-bonds meet up and form a perfect hexagon. If three of the atoms are then reflected to be below the surface, the result will be something very similar to chair-conformation cyclohexane. In this model, the six vertical half-bonds are exactly vertical, and the ends of the six non-vertical half-bonds that stick out from the ring are exactly on the equator (that is, on the surface). Since C–H bonds are actually longer than half a C–C bond, the "equatorial" hydrogen atoms of chair cyclohexane will actually be below the equator when attached to a carbon that is above the equator, and vice versa. This is also true of other substituents. The dihedral angle for a series of four carbon atoms going around the ring in this model alternates between exactly +60° and −60° (called gauche).
The chair conformation cannot deform without changing the bond angles or lengths. We can think of it as two chains, mirror images one of the other, containing atoms (1,2,3,4) and (1,6,5,4), with opposite dihedral angles. The distance from atom 1 to atom 4 depends on the absolute value of the dihedral angle. If these two dihedral angles change (still being opposite one of the other), it is not possible to maintain the correct bond angle at both carbon 1 and carbon 4.
Boat and twist-boat conformations
The boat conformations have higher energy than the chair conformations. The interaction between the two flagpole hydrogens, in particular, generates steric strain. Torsional strain also exists between the C2–C3 and C5–C6 bonds (carbon number 1 is one of the two on a mirror plane), which are eclipsed — that is, these two bonds are parallel one to the other across a mirror plane. Because of this strain, the boat configuration is unstable (i.e. is not a local energy minimum).
The molecular symmetry is C2v.
The boat conformations spontaneously distorts to twist-boat conformations. Here the symmetry is D2, a purely rotational point group with three twofold axes. This conformation can be derived from the boat conformation by applying a slight twist to the molecule so as to remove eclipsing of two pairs of methylene groups. The twist-boat conformation is chiral, existing in right-handed and left-handed versions.
The concentration of the twist-boat conformation at room temperature is less than 0.1%, but at 1,073 K (800 °C) it can reach 30%. Rapid cooling of a sample of cyclohexane from 1,073 K (800 °C) to 40 K (−233 °C) will freeze in a large concentration of twist-boat conformation, which will then slowly convert to the chair conformation upon heating.
Dynamics
Main article: Ring flipChair to chair
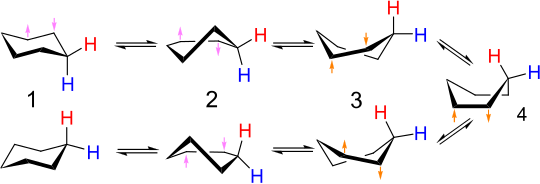
The interconversion of chair conformers is called ring flipping or chair-flipping. Carbon–hydrogen bonds that are axial in one configuration become equatorial in the other, and vice versa. At room temperature the two chair conformations rapidly equilibrate. The proton NMR spectrum of cyclohexane is a singlet at room temperature, with no separation into separate signals for axial and equatorial hydrogens.
In one chair form, the dihedral angle of the chain of carbon atoms (1,2,3,4) is positive whereas that of the chain (1,6,5,4) is negative, but in the other chair form, the situation is the opposite. So both these chains have to undergo a reversal of dihedral angle. When one of these two four-atom chains flattens to a dihedral angle of zero, we have the half-chair conformation, at a maximum energy along the conversion path. When the dihedral angle of this chain then becomes equal (in sign as well as magnitude) to that of the other four-atom chain, the molecule has reached the continuum of conformations, including the twist boat and the boat, where the bond angles and lengths can all be at their normal values and the energy is therefore relatively low. After that, the other four-carbon chain has to switch the sign of its dihedral angle in order to attain the target chair form, so again the molecule has to pass through the half-chair as the dihedral angle of this chain goes through zero. Switching the signs of the two chains sequentially in this way minimizes the maximum energy state along the way (at the half-chair state) — having the dihedral angles of both four-atom chains switch sign simultaneously would mean going through a conformation of even higher energy due to angle strain at carbons 1 and 4.
The detailed mechanism of the chair-to-chair interconversion has been the subject of much study and debate. The half-chair state (D, in figure below) is the key transition state in the interconversion between the chair and twist-boat conformations. The half-chair has C2 symmetry. The interconversion between the two chair conformations involves the following sequence: chair → half-chair → twist-boat → half-chair′ → chair′.
Twist-boat to twist-boat
The boat conformation (C, below) is a transition state, allowing the interconversion between two different twist-boat conformations. While the boat conformation is not necessary for interconversion between the two chair conformations of cyclohexane, it is often included in the reaction coordinate diagram used to describe this interconversion because its energy is considerably lower than that of the half-chair, so any molecule with enough energy to go from twist-boat to chair also has enough energy to go from twist-boat to boat. Thus, there are multiple pathways by which a molecule of cyclohexane in the twist-boat conformation can achieve the chair conformation again.

Conformations: chair (A), twist-boat (B), boat (C) and half-chair (D). Energies are 43 kJ/mol (10 kcal/mol), 25 kJ/mol (6 kcal/mol) and 21 kJ/mol (5 kcal/mol).
Substituted derivatives

In cyclohexane, the two chair conformations have the same energy. The situation becomes more complex with substituted derivatives.
Monosubstituted cyclohexanes
A monosubstituted cyclohexane is one in which there is one non-hydrogen substituent in the cyclohexane ring. The most energetically favorable conformation for a monosubstituted cyclohexane is the chair conformation with the non-hydrogen substituent in the equatorial position because it prevents high steric strain from 1,3 diaxial interactions. In methylcyclohexane the two chair conformers are not isoenergetic. The methyl group prefers the equatorial orientation. The preference of a substituent towards the equatorial conformation is measured in terms of its A value, which is the Gibbs free energy difference between the two chair conformations. A positive A value indicates preference towards the equatorial position. The magnitude of the A values ranges from nearly zero for very small substituents such as deuterium, to about 5 kcal/mol (21 kJ/mol) for very bulky substituents such as the tert-butyl group. Thus, the magnitude of the A value will also correspond to the preference for the equatorial position. Though an equatorial substituent has no 1,3 diaxial interaction that causes steric strain, it has a Gauche interaction in which an equatorial substituent repels the electron density from a neighboring equatorial substituent.
Disubstituted cyclohexanes
For 1,2- and 1,4-disubstituted cyclohexanes, a cis configuration leads to one axial and one equatorial group. Such species undergo rapid, degenerate chair flipping. For 1,2- and 1,4-disubstituted cyclohexane, a trans configuration, the diaxial conformation is effectively prevented by its high steric strain. For 1,3-disubstituted cyclohexanes, the cis form is diequatorial and the flipped conformation suffers additional steric interaction between the two axial groups. trans-1,3-Disubstituted cyclohexanes are like cis-1,2- and cis-1,4- and can flip between the two equivalent axial/equatorial forms.
Cis-1,4-Di-tert-butylcyclohexane has an axial tert-butyl group in the chair conformation and conversion to the twist-boat conformation places both groups in more favorable equatorial positions. As a result, the twist-boat conformation is more stable by 0.47 kJ/mol (0.11 kcal/mol) at 125 K (−148 °C) as measured by NMR spectroscopy.
Also, for a disubstituted cyclohexane, as well as more highly substituted molecules, the aforementioned A values are additive for each substituent. For example, if calculating the A value of a dimethylcyclohexane, any methyl group in the axial position contributes 1.70 kcal/mol- this number is specific to methyl groups and is different for each possible substituent. Therefore, the overall A value for the molecule is 1.70 kcal/mol per methyl group in the axial position.
1,3 diaxial interactions and gauche interactions
1,3 Diaxial interactions occur when the non-hydrogen substituent on a cyclohexane occupies the axial position. This axial substituent is in the eclipsed position with the axial substituents on the 3-carbons relative to itself (there will be two such carbons and thus two 1,3 diaxial interactions). This eclipsed position increases the steric strain on the cyclohexane conformation and the confirmation will shift towards a more energetically favorable equilibrium.
Gauche interactions occur when a non-hydrogen substituent on a cyclohexane occupies the equatorial position. The equatorial substituent is in a staggered position with the 2-carbons relative to itself (there will be two such carbons and thus two 1,2 gauche interactions). This creates a dihedral angle of ~60°. This staggered position is generally preferred to the eclipsed positioning.
Effects of substituent size on stability
Once again, the conformation and position of groups (ie. substituents) larger than a singular hydrogen are critical to the overall stability of the molecule. The larger the group, the less likely to prefer the axial position on its respective carbon. Maintaining said position with a larger size costs more energy from the molecule as a whole because of steric repulsion between the large groups' nonbonded electron pairs and the electrons of the smaller groups (ie. hydrogens). Such steric repulsions are absent for equatorial groups. The cyclohexane model thus assesses steric size of functional groups on the basis of gauche interactions. The gauche interaction will increase in energy as the size of the substituent involved increases. For example, a t-butyl substituent would sustain a higher energy gauche interaction as compared to a methyl group, and therefore, contribute more to the instability of the molecule as a whole.
In comparison, a staggered conformation is thus preferred; the larger groups would maintain the equatorial position and lower the energy of the entire molecule. This preference for the equatorial position among bulkier groups lowers the energy barriers between different conformations of the ring. When the molecule is activated, there will be a loss in entropy due to the stability of the larger substituents. Therefore, the preference of the equatorial positions by large molecules (such as a methyl group) inhibits the reactivity of the molecule and thus makes the molecule more stable as a whole.
Effects on conformational equilibrium
Conformational equilibrium is the tendency to favor the conformation where cyclohexane is the most stable. This equilibrium depends on the interactions between the molecules in the compound and the solvent. Polarity and nonpolarity are the main factors in determining how well a solvent interacts with a compound. Cyclohexane is considered nonpolar, meaning that there is no electronegative difference between its bonds and its overall structure is symmetrical. Due to this, when cyclohexane is immersed in a polar solvent, it will have less solvent distribution, which signifies a poor interaction between the solvent and solute. This produces a limited catalytic effect. Moreover, when cyclohexane comes into contact with a nonpolar solvent, the solvent distribution is much greater, showing a strong interaction between the solvent and solute. This strong interaction yields a heighten catalytic effect.
Heterocyclic analogs
Heterocyclic analogs of cyclohexane are pervasive in sugars, piperidines, dioxanes, etc. They exist generally follow the trends seen for cyclohexane, i.e. the chair conformer being most stable. The axial–equatorial equilibria (A values) are however strongly affected by the replacement of a methylene by O or NH. Illustrative are the conformations of the glucosides. 1,2,4,5-Tetrathiane ((SCH2)3) lacks the unfavorable 1,3-diaxial interactions of cyclohexane. Consequently its twist-boat conformation is populated; in the corresponding tetramethyl structure, 3,3,6,6-tetramethyl-1,2,4,5-tetrathiane, the twist-boat conformation dominates.
Historical background
In 1890, Hermann Sachse [de], a 28-year-old assistant in Berlin, published instructions for folding a piece of paper to represent two forms of cyclohexane he called symmetrical and asymmetrical (what we would now call chair and boat). He clearly understood that these forms had two positions for the hydrogen atoms (again, to use modern terminology, axial and equatorial), that two chairs would probably interconvert, and even how certain substituents might favor one of the chair forms (Sachse–Mohr theory [de]). Because he expressed all this in mathematical language, few chemists of the time understood his arguments. He had several attempts at publishing these ideas, but none succeeded in capturing the imagination of chemists. His death in 1893 at the age of 31 meant his ideas sank into obscurity. It was only in 1918 that Ernst Mohr [de], based on the molecular structure of diamond that had recently been solved using the then very new technique of X-ray crystallography, was able to successfully argue that Sachse's chair was the pivotal motif. Derek Barton and Odd Hassel shared the 1969 Nobel Prize in Chemistry for work on the conformations of cyclohexane and various other molecules.
Practical applications
Cyclohexane is the most stable of the cycloalkanes, due to the stability of adapting to its chair conformer. This conformer stability allows cyclohexane to be used as a standard in lab analyses. More specifically, cyclohexane is used as a standard for pharmaceutical reference in solvent analysis of pharmaceutical compounds and raw materials. This specific standard signifies that cyclohexane is used in quality analysis of food and beverages, pharmaceutical release testing, and pharmaceutical method development; these various methods test for purity, biosafety, and bioavailability of products. The stability of the chair conformer of cyclohexane gives the cycloalkane a versatile and important application when regarding the safety and properties of pharmaceuticals.
References
- Eliel, Ernest Ludwig; Wilen, Samuel H. (2008). Stereochemistry of Organic Compounds. Wiley India. ISBN 978-8126515707.
- ^ Smith, Michael B.; March, Jerry (2007), Advanced Organic Chemistry: Reactions, Mechanisms, and Structure (6th ed.), New York: Wiley-Interscience, ISBN 978-0-471-72091-1
- ^ J, Clayden (2003). Organic chemistry (2nd ed.). Oxford. p. 373. ISBN 9780191666216.
{{cite book}}: CS1 maint: location missing publisher (link) - ^ Nelson, Donna J.; Brammer, Christopher N. (2011). "Toward Consistent Terminology for Cyclohexane Conformers in Introductory Organic Chemistry". J. Chem. Educ. 88 (3): 292–294. Bibcode:2011JChEd..88..292N. doi:10.1021/ed100172k.
- "Conformations of Cyclohexane | Chair, Boat & Twist-Boat Conformation - Video & Lesson Transcript". study.com. Retrieved 2022-11-18.
- "4.3: Conformation Analysis of Cyclohexane". Chemistry LibreTexts. 2021-12-15. Retrieved 2022-11-18.
- "Illustrated Glossary of Organic Chemistry - Diaxial interaction (1,3-diaxial interaction)". www.chem.ucla.edu. Retrieved 2022-11-18.
- Squillacote, M.; Sheridan, R. S.; Chapman, O. L.; Anet, F. A. L. (1975-05-01). "Spectroscopic detection of the twist-boat conformation of cyclohexane. Direct measurement of the free energy difference between the chair and the twist-boat". J. Am. Chem. Soc. 97 (11): 3244–3246. doi:10.1021/ja00844a068.
- ^ Gill, G.; Pawar, D. M.; Noe, E. A. (2005). "Conformational Study of cis-1,4-Di-tert-butylcyclohexane by Dynamic NMR Spectroscopy and Computational Methods. Observation of Chair and Twist-Boat Conformations". J. Org. Chem. 70 (26): 10726–10731. doi:10.1021/jo051654z. PMID 16355992.
- ^ Brown, William H.; Foote, Christopher S.; Iverson, Brent L.; Anslyn, Eric V. (2013). Organic Chemistry (8th ed.). Cengage Learning. p. 93. ISBN 9781285874838.
- Allinger, Norman L.; Miller, Mary Ann (May 1961). "Conformational Analysis. XVII. 1 The 1,3-Diaxial Methyl-Methyl Interaction 2". Journal of the American Chemical Society. 83 (9): 2145–2146. doi:10.1021/ja01470a024. ISSN 0002-7863.
- Zupanek, Žiga; Tramšek, Melita; Kokalj, Anton; Tavčar, Gašper (2019-11-01). "The peculiar case of conformations in coordination compounds of group V pentahalides with N-heterocyclic carbene and synthesis of their imidazolium salts". Journal of Fluorine Chemistry. 227: 109373. doi:10.1016/j.jfluchem.2019.109373. ISSN 0022-1139. S2CID 203937568.
- Ouellette, Robert J.; Rawn, J. David (2014-01-01), Ouellette, Robert J.; Rawn, J. David (eds.), "4 - Alkanes and Cycloalkanes: Structures and Reactions", Organic Chemistry, Boston: Elsevier, pp. 111–161, doi:10.1016/b978-0-12-800780-8.00004-8, ISBN 978-0-12-800780-8, retrieved 2022-11-18
- Boiadjiev, Stefan E.; Lightner, David A. (2000-11-22). "Steric Size in Conformational Analysis. Steric Compression Analyzed by Circular Dichroism Spectroscopy". Journal of the American Chemical Society. 122 (46): 11328–11339. doi:10.1021/ja002069c. ISSN 0002-7863.
- Kang, Sunyoung; Noh, Chanwoo; Kang, Hyosik; Shin, Ji-Yeon; Kim, So-Young; Kim, Seulah; Son, Moon-Gi; Park, Eunseok; Song, Hyun Kyu; Shin, Seokmin; Lee, Sanghun; Kim, Nak-Kyoon; Jung, YounJoon; Lee, Yan (2021-11-22). "Dynamics and Entropy of Cyclohexane Rings Control pH-Responsive Reactivity". JACS Au. 1 (11): 2070–2079. doi:10.1021/jacsau.1c00354. ISSN 2691-3704. PMC 8611792. PMID 34841418.
- Turan, Haydar Taylan; Brickel, Sebastian; Meuwly, Markus (2022-03-10). "Solvent Effects on the Menshutkin Reaction". The Journal of Physical Chemistry B. 126 (9): 1951–1961. arXiv:2111.05244. doi:10.1021/acs.jpcb.1c09710. ISSN 1520-5207. PMID 35196449. S2CID 243861101.
- Bragg, W. H.; Bragg, W. L. (1913). "The structure of the diamond". Nature. 91 (2283): 557. Bibcode:1913Natur..91..557B. doi:10.1038/091557a0.
- Bragg, W. H.; Bragg, W. L. (1913). "The structure of the diamond". Proc. R. Soc. A. 89 (610): 277–291. Bibcode:1913RSPSA..89..277B. doi:10.1098/rspa.1913.0084.
- Sachse, H. (1890). "Ueber die geometrischen Isomerien der Hexamethylenderivate". Berichte der deutschen chemischen Gesellschaft (in German). 23 (1). Wiley: 1363–1370. doi:10.1002/cber.189002301216. ISSN 0365-9496.
- Sachse, H. (1892-01-01). "Über die Konfigurationen der Polymethylenringe". Zeitschrift für Physikalische Chemie. 10U (1). Walter de Gruyter GmbH: 203. doi:10.1515/zpch-1892-1013. ISSN 2196-7156. S2CID 99024270.
- Sachse, H. (1893-01-01). "Eine Deutung der Affinität". Zeitschrift für Physikalische Chemie. 11U (1). Walter de Gruyter GmbH: 185–219. doi:10.1515/zpch-1893-1114. ISSN 2196-7156. S2CID 99555387.
- Mohr, Ernst (1918-09-20). "Die Baeyersche Spannungstheorie und die Struktur des Diamanten". Journal für Praktische Chemie (in German). 98 (1). Wiley: 315–353. doi:10.1002/prac.19180980123. ISSN 0021-8383.
- Mohr, Ernst (1922-01-14). "Zur Theorie dercis-trans-Isomerie des Dekahydro-naphthalins". Berichte der deutschen chemischen Gesellschaft. 55 (1). Wiley: 230–231. doi:10.1002/cber.19220550128. ISSN 0365-9488.
- This history is nicely summarized here: Archived 2012-02-28 at the Wayback Machine.
- "Stability Studies and Testing of Pharmaceuticals: An Overview – IPA". Retrieved 2022-11-18.
- "Guide to Pharmaceutical Analytical Method Development | Rondaxe NY". Rondaxe | Drug development services for exceptional productivity. Retrieved 2022-11-18.
Further reading
- Colin A. Russell, 1975, "The Origins of Conformational Analysis," in Van 't Hoff–Le Bel Centennial, O. B. Ramsay, Ed. (ACS Symposium Series 12), Washington, D.C.: American Chemical Society, pp. 159–178.
- William Reusch, 2010, "Ring Conformations" and "Substituted Cyclohexane Compounds," in Virtual Textbook of Organic Chemistry, East Lansing, MI, USA:Michigan State University, see and , accessed 20 June 2015.
External links
- Java applets of all conformations Archived 2009-09-02 at the Wayback Machine from the University of Nijmegen
| Types of carbohydrates | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| General | |||||||||||||||
| Geometry | |||||||||||||||
| Monosaccharides |
| ||||||||||||||
| Multiple |
| ||||||||||||||