
In mathematics, an expression is a written arrangement of symbols following the context-dependent, syntactic conventions of mathematical notation. Symbols can denote numbers, variables, operations, and functions. Other symbols include punctuation marks and brackets, used for grouping where there is not a well-defined order of operations.
Expressions are commonly distinguished from formulas: expressions are a kind of mathematical object, whereas formulas are statements about mathematical objects. This is analogous to natural language, where a noun phrase refers to an object, and a whole sentence refers to a fact. For example, is an expression, while the inequality is a formula.
To evaluate an expression means to find a numerical value equivalent to the expression. Expressions can be evaluated or simplified by replacing operations that appear in them with their result. For example, the expression simplifies to , and evaluates to
An expression is often used to define a function, by taking the variables to be arguments, or inputs, of the function, and assigning the output to be the evaluation of the resulting expression. For example, and define the function that associates to each number its square plus one. An expression with no variables would define a constant function. Usually, two expressions are considered equal or equivalent if they define the same function. Such an equality is called a "semantic equality", that is, both expressions "mean the same thing."
History
For broader coverage of this topic, see History of mathematics and History of mathematical notation.Early written mathematics


 The Ishango bone at the RBINS. A Babylonian tablet approximating the square root of 2. Problem 14 from the Moscow Mathematical Papyrus.
The Ishango bone at the RBINS. A Babylonian tablet approximating the square root of 2. Problem 14 from the Moscow Mathematical Papyrus.
The earliest written mathematics likely began with tally marks, where each mark represented one unit, carved into wood or stone. An example of early counting is the Ishango bone, found near the Nile and dating back over 20,000 years ago, which is thought to show a six-month lunar calendar. Ancient Egypt developed a symbolic system using hieroglyphics, assigning symbols for powers of ten and using addition and subtraction symbols resembling legs in motion. This system, recorded in texts like the Rhind Mathematical Papyrus (c. 2000–1800 BC), influenced other Mediterranean cultures. In Mesopotamia, a similar system evolved, with numbers written in a base-60 (sexagesimal) format on clay tablets written in Cuneiform, a technique originating with the Sumerians around 3000 BC. This base-60 system persists today in measuring time and angles.
Syncopated stage
The "syncopated" stage of mathematics introduced symbolic abbreviations for commonly used operations and quantities, marking a shift from purely geometric reasoning. Ancient Greek mathematics, largely geometric in nature, drew on Egyptian numerical systems (especially Attic numerals), with little interest in algebraic symbols, until the arrival of Diophantus of Alexandria, who pioneered a form of syncopated algebra in his Arithmetica, which introduced symbolic manipulation of expressions. His notation represented unknowns and powers symbolically, but without modern symbols for relations (such as equality or inequality) or exponents. An unknown number was called . The square of was ; the cube was ; the fourth power was ; and the fifth power was . So for example, what would be written in modern notation as:Would be written in Diophantus's syncopated notation as:
In the 7th century, Brahmagupta used different colours to represent the unknowns in algebraic equations in the Brāhmasphuṭasiddhānta. Greek and other ancient mathematical advances, were often trapped in cycles of bursts of creativity, followed by long periods of stagnation, but this began to change as knowledge spread in the early modern period.
Symbolic stage and early arithmetic

The transition to fully symbolic algebra began with Ibn al-Banna' al-Marrakushi (1256–1321) and Abū al-Ḥasan ibn ʿAlī al-Qalaṣādī, (1412–1482) who introduced symbols for operations using Arabic characters. The plus sign (+) appeared around 1351 with Nicole Oresme, likely derived from the Latin et (meaning "and"), while the minus sign (−) was first used in 1489 by Johannes Widmann. Luca Pacioli included these symbols in his works, though much was based on earlier contributions by Piero della Francesca. The radical symbol (√) for square root was introduced by Christoph Rudolff in the 1500s, and parentheses for precedence by Niccolò Tartaglia in 1556. François Viète’s New Algebra (1591) formalized modern symbolic manipulation. The multiplication sign (×) was first used by William Oughtred and the division sign (÷) by Johann Rahn.
René Descartes further advanced algebraic symbolism in La Géométrie (1637), where he introduced the use of letters at the end of the alphabet (x, y, z) for variables, along with the Cartesian coordinate system, which bridged algebra and geometry. Isaac Newton and Gottfried Wilhelm Leibniz independently developed calculus in the late 17th century, with Leibniz's notation becoming the standard.
Variables and evaluation
In elementary algebra, a variable in an expression is a letter that represents a number whose value may change. To evaluate an expression with a variable means to find the value of the expression when the variable is assigned a given number. Expressions can be evaluated or simplified by replacing operations that appear in them with their result, or by combining like-terms.
For example, take the expression ; it can be evaluated at x = 3 in the following steps:
, (replace x with 3)
(use definition of exponent)
(simplify)
A term is a constant or the product of a constant and one or more variables. Some examples include The constant of the product is called the coefficient. Terms that are either constants or have the same variables raised to the same powers are called like terms. If there are like terms in an expression, one can simplify the expression by combining the like terms. One adds the coefficients and keeps the same variable.
Any variable can be classified as being either a free variable or a bound variable. For a given combination of values for the free variables, an expression may be evaluated, although for some combinations of values of the free variables, the value of the expression may be undefined. Thus an expression represents an operation over constants and free variables and whose output is the resulting value of the expression.
For a non-formalized language, that is, in most mathematical texts outside of mathematical logic, for an individual expression it is not always possible to identify which variables are free and bound. For example, in , depending on the context, the variable can be free and bound, or vice-versa, but they cannot both be free. Determining which value is assumed to be free depends on context and semantics.
Equivalence
Main article: Identity (mathematics)An expression is often used to define a function, or denote compositions of functions, by taking the variables to be arguments, or inputs, of the function, and assigning the output to be the evaluation of the resulting expression. For example, and define the function that associates to each number its square plus one. An expression with no variables would define a constant function. In this way, two expressions are said to be equivalent if, for each combination of values for the free variables, they have the same output, i.e., they represent the same function. The equivalence between two expressions is called an identity and is sometimes denoted with
For example, in the expression the variable n is bound, and the variable x is free. This expression is equivalent to the simpler expression 12 x; that is The value for x = 3 is 36, which can be denoted
Polynomial evaluation
Main article: Polynomial evaluationA polynomial consists of variables and coefficients, that involve only the operations of addition, subtraction, multiplication and exponentiation to nonnegative integer powers, and has a finite number of terms. The problem of polynomial evaluation arises frequently in practice. In computational geometry, polynomials are used to compute function approximations using Taylor polynomials. In cryptography and hash tables, polynomials are used to compute k-independent hashing.
In the former case, polynomials are evaluated using floating-point arithmetic, which is not exact. Thus different schemes for the evaluation will, in general, give slightly different answers. In the latter case, the polynomials are usually evaluated in a finite field, in which case the answers are always exact.
For evaluating the univariate polynomial the most naive method would use multiplications to compute , use multiplications to compute and so on for a total of multiplications and additions. Using better methods, such as Horner's rule, this can be reduced to multiplications and additions. If some preprocessing is allowed, even more savings are possible.
Computation
Main article: ComputationA computation is any type of arithmetic or non-arithmetic calculation that is "well-defined". The notion that mathematical statements should be 'well-defined' had been argued by mathematicians since at least the 1600s, but agreement on a suitable definition proved elusive. A candidate definition was proposed independently by several mathematicians in the 1930s. The best-known variant was formalised by the mathematician Alan Turing, who defined a well-defined statement or calculation as any statement that could be expressed in terms of the initialisation parameters of a Turing machine. Turing's definition apportioned "well-definedness" to a very large class of mathematical statements, including all well-formed algebraic statements, and all statements written in modern computer programming languages.
Despite the widespread uptake of this definition, there are some mathematical concepts that have no well-defined characterisation under this definition. This includes the halting problem and the busy beaver game. It remains an open question as to whether there exists a more powerful definition of 'well-defined' that is able to capture both computable and 'non-computable' statements. All statements characterised in modern programming languages are well-defined, including C++, Python, and Java.
Common examples of computation are basic arithmetic and the execution of computer algorithms. A calculation is a deliberate mathematical process that transforms one or more inputs into one or more outputs or results. For example, multiplying 7 by 6 is a simple algorithmic calculation. Extracting the square root or the cube root of a number using mathematical models is a more complex algorithmic calculation.
Rewriting
Expressions can be computed by means of an evaluation strategy. To illustrate, executing a function call f(a,b) may first evaluate the arguments a and b, store the results in references or memory locations ref_a and ref_b, then evaluate the function's body with those references passed in. This gives the function the ability to look up the original argument values passed in through dereferencing the parameters (some languages use specific operators to perform this), to modify them via assignment as if they were local variables, and to return values via the references. This is the call-by-reference evaluation strategy. Evaluation strategy is part of the semantics of the programming language definition. Some languages, such as PureScript, have variants with different evaluation strategies. Some declarative languages, such as Datalog, support multiple evaluation strategies. Some languages define a calling convention.
In rewriting, a reduction strategy or rewriting strategy is a relation specifying a rewrite for each object or term, compatible with a given reduction relation. A rewriting strategy specifies, out of all the reducible subterms (redexes), which one should be reduced (contracted) within a term. One of the most common systems involves lambda calculus.
Well-defined expressions
Main article: Well-defined expressionThe language of mathematics exhibits a kind of grammar (called formal grammar) about how expressions may be written. There are two considerations for well-definedness of mathematical expressions, syntax and semantics. Syntax is concerned with the rules used for constructing, or transforming the symbols of an expression without regard to any interpretation or meaning given to them. Expressions that are syntactically correct are called well-formed. Semantics is concerned with the meaning of these well-formed expressions. Expressions that are semantically correct are called well-defined.
Well-formed
The syntax of mathematical expressions can be described somewhat informally as follows: the allowed operators must have the correct number of inputs in the correct places (usually written with infix notation), the sub-expressions that make up these inputs must be well-formed themselves, have a clear order of operations, etc. Strings of symbols that conform to the rules of syntax are called well-formed, and those that are not well-formed are called, ill-formed, and are do not constitute mathematical expressions.
For example, in arithmetic, the expression 1 + 2 × 3 is well-formed, but
- .
is not.
However, being well-formed is not enough to be considered well-defined. For example in arithmetic, the expression is well-formed, but it is not well-defined. (See Division by zero). Such expressions are called undefined.
Well-defined
Semantics is the study of meaning. Formal semantics is about attaching meaning to expressions. An expression that defines a unique value or meaning is said to be well-defined. Otherwise, the expression is said to be ill defined or ambiguous. In general the meaning of expressions is not limited to designating values; for instance, an expression might designate a condition, or an equation that is to be solved, or it can be viewed as an object in its own right that can be manipulated according to certain rules. Certain expressions that designate a value simultaneously express a condition that is assumed to hold, for instance those involving the operator to designate an internal direct sum.
In algebra, an expression may be used to designate a value, which might depend on values assigned to variables occurring in the expression. The determination of this value depends on the semantics attached to the symbols of the expression. The choice of semantics depends on the context of the expression. The same syntactic expression 1 + 2 × 3 can have different values (mathematically 7, but also 9), depending on the order of operations implied by the context (See also Operations § Calculators).
For real numbers, the product is unambiguous because ; hence the notation is said to be well defined. This property, also known as associativity of multiplication, guarantees the result does not depend on the sequence of multiplications; therefore, a specification of the sequence can be omitted. The subtraction operation is non-associative; despite that, there is a convention that is shorthand for , thus it is considered "well-defined". On the other hand, Division is non-associative, and in the case of , parenthesization conventions are not well established; therefore, this expression is often considered ill-defined.
Unlike with functions, notational ambiguities can be overcome by means of additional definitions (e.g., rules of precedence, associativity of the operator). For example, in the programming language C, the operator - for subtraction is left-to-right-associative, which means that a-b-c is defined as (a-b)-c, and the operator = for assignment is right-to-left-associative, which means that a=b=c is defined as a=(b=c). In the programming language APL there is only one rule: from right to left – but parentheses first.
Formal definition
The term 'expression' is part of the language of mathematics, that is to say, it is not defined within mathematics, but taken as a primitive part of the language. To attempt to define the term would not be doing mathematics, but rather, one would be engaging in a kind of metamathematics (the metalanguage of mathematics), usually mathematical logic. Within mathematical logic, mathematics is usually described as a kind of formal language, and a well-formed expression can be defined recursively as follows:
The alphabet consists of:
- A set of individual constants: Symbols representing fixed objects in the domain of discourse, such as numerals (1, 2.5, 1/7, ...), sets (, ...), truth values (T or F), etc.
- A set of individual variables: A countably infinite amount of symbols representing variables used for representing an unspecified object in the domain. (Usually letters like x, or y)
- A set of operations: Function symbols representing operations that can be performed on elements over the domain, like addition (+), multiplication (×), or set operations like union (∪), or intersection (∩). (Functions can be understood as unary operations)
- Brackets ( )
With this alphabet, the recursive rules for forming a well-formed expression (WFE) are as follows:
- Any constant or variable as defined are the atomic expressions, the simplest well-formed expressions (WFE's). For instance, the constant or the variable are syntactically correct expressions.
- Let be a metavariable for any n-ary operation over the domain, and let be metavariables for any WFE's.
- Then is also well-formed. For the most often used operations, more convenient notations (like infix notation) have been developed over the centuries.
- For instance, if the domain of discourse is the real numbers, can denote the binary operation +, then is well-formed. Or can be the unary operation so is well-formed.
- Brackets are initially around each non-atomic expression, but they can be deleted in cases where there is a defined order of operations, or where order doesn't matter (i.e. where operations are associative).
A well-formed expression can be thought as a syntax tree. The leaf nodes are always atomic expressions. Operations and have exactly two child nodes, while operations , and have exactly one. There are countably infinitely many WFE's, however, each WFE has a finite number of nodes.
Lambda calculus
Main article: Lambda calculusFormal languages allow formalizing the concept of well-formed expressions.
In the 1930s, a new type of expression, the lambda expression, was introduced by Alonzo Church and Stephen Kleene for formalizing functions and their evaluation. The lambda operators (lambda abstraction and function application) form the basis for lambda calculus, a formal system used in mathematical logic and programming language theory.
The equivalence of two lambda expressions is undecidable (but see unification (computer science)). This is also the case for the expressions representing real numbers, which are built from the integers by using the arithmetical operations, the logarithm and the exponential (Richardson's theorem).
Types of expressions
Algebraic expression
An algebraic expression is an expression built up from algebraic constants, variables, and the algebraic operations (addition, subtraction, multiplication, division and exponentiation by a rational number). For example, 3x − 2xy + c is an algebraic expression. Since taking the square root is the same as raising to the power 1/2, the following is also an algebraic expression:
See also: Algebraic equation and Algebraic closure
Polynomial expression
A polynomial expression is an expression built with scalars (numbers of elements of some field), indeterminates, and the operators of addition, multiplication, and exponentiation to nonnegative integer powers; for example
Using associativity, commutativity and distributivity, every polynomial expression is equivalent to a polynomial, that is an expression that is a linear combination of products of integer powers of the indeterminates. For example the above polynomial expression is equivalent (denote the same polynomial as
Many author do not distinguish polynomials and polynomial expressions. In this case the expression of a polynomial expression as a linear combination is called the canonical form, normal form, or expanded form of the polynomial.
Computational expression
Main article: Expression (computer science)In computer science, an expression is a syntactic entity in a programming language that may be evaluated to determine its value or fail to terminate, in which case the expression is undefined. It is a combination of one or more constants, variables, functions, and operators that the programming language interprets (according to its particular rules of precedence and of association) and computes to produce ("to return", in a stateful environment) another value. This process, for mathematical expressions, is called evaluation. In simple settings, the resulting value is usually one of various primitive types, such as string, Boolean, or numerical (such as integer, floating-point, or complex).
In computer algebra, formulas are viewed as expressions that can be evaluated as a Boolean, depending on the values that are given to the variables occurring in the expressions. For example takes the value false if x is given a value less than 1, and the value true otherwise.
Expressions are often contrasted with statements—syntactic entities that have no value (an instruction).
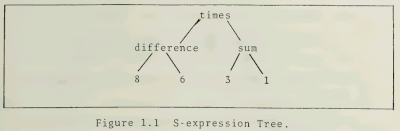
Except for numbers and variables, every mathematical expression may be viewed as the symbol of an operator followed by a sequence of operands. In computer algebra software, the expressions are usually represented in this way. This representation is very flexible, and many things that seem not to be mathematical expressions at first glance, may be represented and manipulated as such. For example, an equation is an expression with "=" as an operator, a matrix may be represented as an expression with "matrix" as an operator and its rows as operands.
See: Computer algebra expression
Logical expression
In mathematical logic, a "logical expression" can refer to either terms or formulas. A term denotes a mathematical object while a formula denotes a mathematical fact. In particular, terms appear as components of a formula.
A first-order term is recursively constructed from constant symbols, variables, and function symbols. An expression formed by applying a predicate symbol to an appropriate number of terms is called an atomic formula, which evaluates to true or false in bivalent logics, given an interpretation. For example, is a term built from the constant 1, the variable x, and the binary function symbols and ; it is part of the atomic formula which evaluates to true for each real-numbered value of x.
Formal expression
See also: Regular expressionA formal expression is a kind of string of symbols, created by the same production rules as standard expressions, however, they are used without regard to the meaning of the expression. In this way, two formal expressions are considered equal only if they are syntactically equal, that is, if they are the exact same expression. For instance, the formal expressions "2" and "1+1" are not equal.
See also
- Analytic expression
- Closed-form expression
- Formal calculation
- Functional programming
- Infinite expression
- Number sentence
- Rewriting
- Signature (logic)
Notes
- The study of non-computable statements is the field of hypercomputation.
- For a full history, see Cardone and Hindley's "History of Lambda-calculus and Combinatory Logic" (2006).
References
- Oxford English Dictionary, s.v. “Expression (n.), sense II.7,” "A group of symbols which together represent a numeric, algebraic, or other mathematical quantity or function."
- Stoll, Robert R. (1963). Set Theory and Logic. San Francisco, CA: Dover Publications. ISBN 978-0-486-63829-4.
- Oxford English Dictionary, s.v. "Evaluate (v.), sense a", "Mathematics. To work out the ‘value’ of (a quantitative expression); to find a numerical expression for (any quantitative fact or relation)."
- Oxford English Dictionary, s.v. “Simplify (v.), sense 4.a”, "To express (an equation or other mathematical expression) in a form that is easier to understand, analyse, or work with, e.g. by collecting like terms or substituting variables."
- Codd, Edgar Frank (June 1970). "A Relational Model of Data for Large Shared Data Banks" (PDF). Communications of the ACM. 13 (6): 377–387. doi:10.1145/362384.362685. S2CID 207549016. Archived (PDF) from the original on 2004-09-08. Retrieved 2020-04-29.
- Marshack, Alexander (1991). The Roots of Civilization, Colonial Hill, Mount Kisco, NY.
- Encyclopædia Americana. By Thomas Gamaliel Bradford. Pg 314
- Mathematical Excursion, Enhanced Edition: Enhanced Webassign Edition By Richard N. Aufmann, Joanne Lockwood, Richard D. Nation, Daniel K. Cleg. Pg 186
- Mathematics and Measurement By Oswald Ashton Wentworth Dilk. Pg 14
- Diophantine Equations. Submitted by: Aaron Zerhusen, Chris Rakes, & Shasta Meece. MA 330-002. Dr. Carl Eberhart. 16 February 1999.
- Boyer (1991). "Revival and Decline of Greek Mathematics". pp. 180-182. "In this respect it can be compared with the great classics of the earlier Alexandrian Age; yet it has practically nothing in common with these or, in fact, with any traditional Greek mathematics. It represents essentially a new branch and makes use of a different approach. Being divorced from geometric methods, it resembles Babylonian algebra to a large extent. But whereas Babylonian mathematicians had been concerned primarily with approximate solutions of determinate equations as far as the third degree, the Arithmetica of Diophantus (such as we have it) is almost entirely devoted to the exact solution of equations, both determinate and indeterminate. Throughout the six surviving books of Arithmetica there is a systematic use of abbreviations for powers of numbers and for relationships and operations. An unknown number is represented by a symbol resembling the Greek letter ζ {\displaystyle \zeta } (perhaps for the last letter of arithmos). It is instead a collection of some 150 problems, all worked out in terms of specific numerical examples, although perhaps generality of method was intended. There is no postulation development, nor is an effort made to find all possible solutions. In the case of quadratic equations with two positive roots, only the larger is give, and negative roots are not recognized. No clear-cut distinction is made between determinate and indeterminate problems, and even for the latter for which the number of solutions generally is unlimited, only a single answer is given. Diophantus solved problems involving several unknown numbers by skillfully expressing all unknown quantities, where possible, in terms of only one of them."
- Boyer (1991). "Revival and Decline of Greek Mathematics". p. 178. "The chief difference between Diophantine syncopation and the modern algebraic notation is the lack of special symbols for operations and relations, as well as of the exponential notation."
- A History of Greek Mathematics: From Aristarchus to Diophantus. By Sir Thomas Little Heath. Pg 456
- A History of Greek Mathematics: From Aristarchus to Diophantus. By Sir Thomas Little Heath. Pg 458
- O'Connor, John J.; Robertson, Edmund F., "al-Marrakushi ibn Al-Banna", MacTutor History of Mathematics Archive, University of St Andrews
- Gullberg, Jan (1997). Mathematics: From the Birth of Numbers. W. W. Norton. p. 298. ISBN 0-393-04002-X.
- O'Connor, John J.; Robertson, Edmund F., "Abu'l Hasan ibn Ali al Qalasadi", MacTutor History of Mathematics Archive, University of St Andrews
- Der Algorismus proportionum des Nicolaus Oresme: Zum ersten Male nach der Lesart der Handschrift R.40.2. der Königlichen Gymnasial-bibliothek zu Thorn. Nicole Oresme. S. Calvary & Company, 1868.
- Later early modern version: A New System of Mercantile Arithmetic: Adapted to the Commerce of the United States, in Its Domestic and Foreign Relations with Forms of Accounts and Other Writings Usually Occurring in Trade. By Michael Walsh. Edmund M. Blunt (proprietor.), 1801.
- Descartes 2006, p.1xiii "This short work marks the moment at which algebra and geometry ceased being separate."
- Marecek, Lynn; Mathis, Andrea Honeycutt (2020-05-06). "1.1 Use the Language of Algebra - Intermediate Algebra 2e | OpenStax". openstax.org. Retrieved 2024-10-14.
- C.C. Chang; H. Jerome Keisler (1977). Model Theory. Studies in Logic and the Foundation of Mathematics. Vol. 73. North Holland.; here: Sect.1.3
- Sobolev, S.K. (originator). Free variable. Encyclopedia of Mathematics. Springer. ISBN 1402006098.
- Codd, Edgar Frank (June 1970). "A Relational Model of Data for Large Shared Data Banks" (PDF). Communications of the ACM. 13 (6): 377–387. doi:10.1145/362384.362685. S2CID 207549016. Archived (PDF) from the original on 2004-09-08. Retrieved 2020-04-29.
- Equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Equation&oldid=32613
- Pratt, Vaughan, "Algebra", The Stanford Encyclopedia of Philosophy (Winter 2022 Edition), Edward N. Zalta & Uri Nodelman (eds.), URL: https://plato.stanford.edu/entries/algebra/#Laws
- "Definition of COMPUTATION". www.merriam-webster.com. 2024-10-11. Retrieved 2024-10-12.
- Couturat, Louis (1901). la Logique de Leibniz a'Après des Documents Inédits. Paris. ISBN 978-0343895099.
- Davis, Martin; Davis, Martin D. (2000). The Universal Computer. W. W. Norton & Company. ISBN 978-0-393-04785-1.
- Davis, Martin (1982-01-01). Computability & Unsolvability. Courier Corporation. ISBN 978-0-486-61471-7.
- Turing, A.M. (1937) . "On Computable Numbers, with an Application to the Entscheidungsproblem" (PDF). Proceedings of the London Mathematical Society. 2. Vol. 42. pp. 230–65. doi:10.1112/plms/s2-42.1.230.
- ^ Davis, Martin; Davis, Martin D. (2000). The Universal Computer. W. W. Norton & Company. ISBN 978-0-393-04785-1.
- Davis, Martin (2006). "Why there is no such discipline as hypercomputation". Applied Mathematics and Computation. 178 (1): 4–7. doi:10.1016/j.amc.2005.09.066.
- Araki, Shota; Nishizaki, Shin-ya (November 2014). "Call-by-name evaluation of RPC and RMI calculi". Theory and Practice of Computation. p. 1. doi:10.1142/9789814612883_0001. ISBN 978-981-4612-87-6. Retrieved 2021-08-21.
- Daniel P. Friedman; Mitchell Wand (2008). Essentials of Programming Languages (third ed.). Cambridge, MA: The MIT Press. ISBN 978-0262062794.
- Stoll, Robert R. (1963). Set Theory and Logic. San Francisco, CA: Dover Publications. ISBN 978-0-486-63829-4.
- Weisstein, Eric W. "Well-Defined". From MathWorld – A Wolfram Web Resource. Retrieved 2013-01-02.
- Weisstein, Eric W. "Well-Defined". From MathWorld – A Wolfram Web Resource. Retrieved 2013-01-02.
- "Operator Precedence and Associativity in C". GeeksforGeeks. 2014-02-07. Retrieved 2019-10-18.
- C.C. Chang; H. Jerome Keisler (1977). Model Theory. Studies in Logic and the Foundation of Mathematics. Vol. 73. North Holland.; here: Sect.1.3
- Hermes, Hans (1973). Introduction to Mathematical Logic. Springer London. ISBN 3540058192. ISSN 1431-4657.; here: Sect.II.1.3
- Church, Alonzo (1932). "A set of postulates for the foundation of logic". Annals of Mathematics. Series 2. 33 (2): 346–366. doi:10.2307/1968337. JSTOR 1968337.
- Morris, Christopher G. (1992). Academic Press dictionary of science and technology. Gulf Professional Publishing. p. 74.
algebraic expression over a field.
- Mitchell, J. (2002). Concepts in Programming Languages. Cambridge: Cambridge University Press, 3.4.1 Statements and Expressions, p. 26
- Maurizio Gabbrielli, Simone Martini (2010). Programming Languages - Principles and Paradigms. Springer London, 6.1 Expressions, p. 120
- Cassidy, Kevin G. (Dec 1985). The Feasibility of Automatic Storage Reclamation with Concurrent Program Execution in a LISP Environment (PDF) (Master's thesis). Naval Postgraduate School, Monterey/CA. p. 15. ADA165184.
- McCoy, Neal H. (1960). Introduction To Modern Algebra. Boston: Allyn & Bacon. p. 127. LCCN 68015225.
- Fraleigh, John B. (2003). A first course in abstract algebra. Boston : Addison-Wesley. ISBN 978-0-201-76390-4.
Works Cited
Descartes, René (2006) . A discourse on the method of correctly conducting one's reason and seeking truth in the sciences. Translated by Ian Maclean. Oxford University Press. ISBN 0-19-282514-3.
| Mathematical logic | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| General | |||||||||
| Theorems (list) and paradoxes | |||||||||
| Logics |
| ||||||||
| Set theory |
| ||||||||
| Formal systems (list), language and syntax |
| ||||||||
| Proof theory | |||||||||
| Model theory | |||||||||
| Computability theory | |||||||||
| Related | |||||||||
 is an expression, while the
is an expression, while the  is a formula.
is a formula.
 simplifies to
simplifies to  , and evaluates to
, and evaluates to 
 and
and  define the function that associates to each number its
define the function that associates to each number its  . The square of
. The square of  ; the cube was
; the cube was  ; the fourth power was
; the fourth power was  ; and the fifth power was
; and the fifth power was  . So for example, what would be written in modern notation as:
. So for example, what would be written in modern notation as: Would be written in Diophantus's syncopated notation as:
Would be written in Diophantus's syncopated notation as:

 ; it can be evaluated at x = 3 in the following steps:
; it can be evaluated at x = 3 in the following steps:
 , (replace x with 3)
, (replace x with 3)
 (use definition of
(use definition of  (simplify)
(simplify)


 The constant of the product is called the
The constant of the product is called the 
 , depending on the context, the variable
, depending on the context, the variable  can be free and
can be free and  bound, or vice-versa, but they cannot both be free. Determining which value is assumed to be free depends on context and
bound, or vice-versa, but they cannot both be free. Determining which value is assumed to be free depends on context and 
 the variable n is bound, and the variable x is free. This expression is equivalent to the simpler expression 12 x; that is
the variable n is bound, and the variable x is free. This expression is equivalent to the simpler expression 12 x; that is  The value for x = 3 is 36, which can be denoted
The value for x = 3 is 36, which can be denoted 
 the most naive method would use
the most naive method would use  multiplications to compute
multiplications to compute  , use
, use  multiplications to compute
multiplications to compute  and so on for a total of
and so on for a total of  multiplications and
multiplications and  .
. is well-formed, but it is not well-defined. (See
is well-formed, but it is not well-defined. (See  to designate an internal
to designate an internal  is unambiguous because
is unambiguous because  ; hence the notation is said to be well defined. This property, also known as
; hence the notation is said to be well defined. This property, also known as  is shorthand for
is shorthand for  , thus it is considered "well-defined". On the other hand,
, thus it is considered "well-defined". On the other hand,  , parenthesization conventions are not well established; therefore, this expression is often considered ill-defined.
, parenthesization conventions are not well established; therefore, this expression is often considered ill-defined.
 , ...),
, ...),  or the variable
or the variable  are syntactically correct expressions.
are syntactically correct expressions. be a
be a  be metavariables for any WFE's.
be metavariables for any WFE's. is also well-formed. For the most often used operations, more convenient notations (like
is also well-formed. For the most often used operations, more convenient notations (like  is well-formed. Or
is well-formed. Or  so
so  is well-formed.
is well-formed. and
and  have exactly two child nodes, while operations
have exactly two child nodes, while operations  ,
,  and
and  have exactly one. There are countably infinitely many WFE's, however, each WFE has a finite number of nodes.
have exactly one. There are countably infinitely many WFE's, however, each WFE has a finite number of nodes.



 is a term built from the constant 1, the variable x, and the binary function symbols
is a term built from the constant 1, the variable x, and the binary function symbols  ; it is part of the atomic formula
; it is part of the atomic formula  which evaluates to true for each
which evaluates to true for each