| Great stellated 120-cell | |
|---|---|
 Orthogonal projection | |
| Type | Schläfli-Hess polytope |
| Cells | 120 {5/2,3} |
| Faces | 720 {5/2} |
| Edges | 720 |
| Vertices | 120 |
| Vertex figure | {3,5} |
| Schläfli symbol | {5/2,3,5} |
| Coxeter-Dynkin diagram | |
| Symmetry group | H4, |
| Dual | Grand 120-cell |
| Properties | Regular |
In geometry, the great stellated 120-cell or great stellated polydodecahedron is a regular star 4-polytope with Schläfli symbol {5/2,3,5}. It is one of 10 regular Schläfli-Hess polytopes.
It is one of four regular star 4-polytopes discovered by Ludwig Schläfli. It is named by John Horton Conway, extending the naming system by Arthur Cayley for the Kepler-Poinsot solids.
Related polytopes
It has the same edge arrangement as the grand 600-cell, icosahedral 120-cell, and the same face arrangement as the grand stellated 120-cell.
| H3 | A2 / B3 / D4 | A3 / B2 |
|---|---|---|
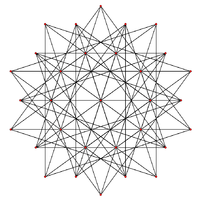
|

|

|
See also
- List of regular polytopes
- Convex regular 4-polytope
- Kepler-Poinsot solids - regular star polyhedron
- Star polygon - regular star polygons
References
- Edmund Hess, (1883) Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder .
- H. S. M. Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26, Regular Star-polytopes, pp. 404–408)
- Klitzing, Richard. "4D uniform polytopes (polychora) o5o3o5/2x - gishi".
External links
- Regular polychora Archived 2003-09-06 at the Wayback Machine
- Discussion on names
- Reguläre Polytope
- The Regular Star Polychora
- Paper model of 3D cross-section of Great Stellated 120-cell created using nets generated by Stella4D software
| Regular 4-polytopes | |||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
This 4-polytope article is a stub. You can help Misplaced Pages by expanding it. |