In science and engineering, hydraulic conductivity (K, in SI units of meters per second), is a property of porous materials, soils and rocks, that describes the ease with which a fluid (usually water) can move through the pore space, or fracture network. It depends on the intrinsic permeability (k, unit: m) of the material, the degree of saturation, and on the density and viscosity of the fluid. Saturated hydraulic conductivity, Ksat, describes water movement through saturated media. By definition, hydraulic conductivity is the ratio of volume flux to hydraulic gradient yielding a quantitative measure of a saturated soil's ability to transmit water when subjected to a hydraulic gradient.
Methods of determination
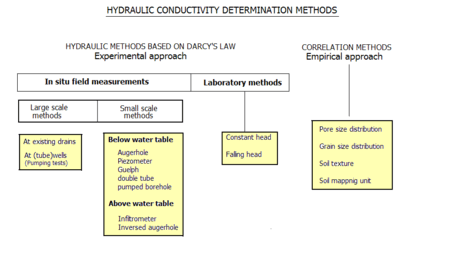
There are two broad approaches for determining hydraulic conductivity:
- In the empirical approach the hydraulic conductivity is correlated to soil properties like pore-size and particle-size (grain-size) distributions, and soil texture.
- In the experimental approach the hydraulic conductivity is determined from hydraulic experiments that are interpreted using Darcy's law.
The experimental approach is broadly classified into:
- Laboratory tests using soil samples subjected to hydraulic experiments
- Field tests (on site, in situ) that are differentiated into:
- small-scale field tests, using observations of the water level in cavities in the soil
- large-scale field tests, like pumping tests in wells or by observing the functioning of existing horizontal drainage systems.
The small-scale field tests are further subdivided into:
- infiltration tests in cavities above the water table
- slug tests in cavities below the water table
The methods of determining hydraulic conductivity and other hydraulic properties are investigated by numerous researchers and include additional empirical approaches.
Estimation by empirical approach
Estimation from grain size
Allen Hazen derived an empirical formula for approximating hydraulic conductivity from grain-size analyses:
where
- Hazen's empirical coefficient, which takes a value between 0.0 and 1.5 (depending on literature), with an average value of 1.0. A.F. Salarashayeri & M. Siosemarde indicate C is usually between 1.0 and 1.5, with D in mm and K in cm/s.
- is the diameter of the 10 percentile grain size of the material.
Pedotransfer function
A pedotransfer function (PTF) is a specialized empirical estimation method, used primarily in the soil sciences, but increasingly used in hydrogeology. There are many different PTF methods, however, they all attempt to determine soil properties, such as hydraulic conductivity, given several measured soil properties, such as soil particle size, and bulk density.
Determination by experimental approach
There are relatively simple and inexpensive laboratory tests that may be run to determine the hydraulic conductivity of a soil: constant-head method and falling-head method.
Laboratory methods
Constant-head method
The constant-head method is typically used on granular soil. This procedure allows water to move through the soil under a steady state head condition while the volume of water flowing through the soil specimen is measured over a period of time. By knowing the volume ΔV of water measured in a time Δt, over a specimen of length L and cross-sectional area A, as well as the head h, the hydraulic conductivity (K) can be derived by simply rearranging Darcy's law:
Proof: Darcy's law states that the volumetric flow depends on the pressure differential ΔP between the two sides of the sample, the permeability k and the dynamic viscosity μ as:
In a constant head experiment, the head (difference between two heights) defines an excess water mass, ρAh, where ρ is the density of water. This mass weighs down on the side it is on, creating a pressure differential of ΔP = ρgh, where g is the gravitational acceleration. Plugging this directly into the above gives
If the hydraulic conductivity is defined to be related to the hydraulic permeability as
this gives the result.
Falling-head method
In the falling-head method, the soil sample is first saturated under a specific head condition. The water is then allowed to flow through the soil without adding any water, so the pressure head declines as water passes through the specimen. The advantage to the falling-head method is that it can be used for both fine-grained and coarse-grained soils. . If the head drops from hi to hf in a time Δt, then the hydraulic conductivity is equal to
Proof: As above, Darcy's law reads
The decrease in volume is related to the falling head by ΔV = ΔhA. Plugging this relationship into the above, and taking the limit as Δt → 0, the differential equation
has the solution
Plugging in and rearranging gives the result.
In-situ (field) methods
In compare to laboratory method, field methods gives the most reliable information about the permeability of soil with minimum disturbances. In laboratory methods, the degree of disturbances affect the reliability of value of permeability of the soil.
Pumping Test
Pumping test is the most reliable method to calculate the coefficient of permeability of a soil. This test is further classified into Pumping in test and pumping out test.
Augerhole method
There are also in-situ methods for measuring the hydraulic conductivity in the field.
When the water table is shallow, the augerhole method, a slug test, can be used for determining the hydraulic conductivity below the water table.
The method was developed by Hooghoudt (1934) in The Netherlands and introduced in the US by Van Bavel en Kirkham (1948).
The method uses the following steps:
- an augerhole is perforated into the soil to below the water table
- water is bailed out from the augerhole
- the rate of rise of the water level in the hole is recorded
- the K-value is calculated from the data as:
where:
- K is the horizontal saturated hydraulic conductivity (m/day)
- H is the depth of the water level in the hole relative to the water table in the soil (cm):
- Ht = H at time t
- Ho = H at time t = 0
- t is the time (in seconds) since the first measurement of H as Ho
- F is a factor depending on the geometry of the hole:
where:
- r is the radius of the cylindrical hole (cm)
- h' is the average depth of the water level in the hole relative to the water table in the soil (cm), found as
- D is the depth of the bottom of the hole relative to the water table in the soil (cm).

The picture shows a large variation of K-values measured with the augerhole method in an area of 100 ha. The ratio between the highest and lowest values is 25. The cumulative frequency distribution is lognormal and was made with the CumFreq program.
Related magnitudes
Transmissivity
The transmissivity is a measure of how much water can be transmitted horizontally, such as to a pumping well.
- Transmissivity should not be confused with the similar word transmittance used in optics, meaning the fraction of incident light that passes through a sample.
An aquifer may consist of n soil layers. The transmissivity Ti of a horizontal flow for the ith soil layer with a saturated thickness di and horizontal hydraulic conductivity Ki is:
Transmissivity is directly proportional to horizontal hydraulic conductivity Ki and thickness di. Expressing Ki in m/day and di in m, the transmissivity Ti is found in units m/day.
The total transmissivity Tt of the aquifer is the sum of every layer's transmissivity:
The apparent horizontal hydraulic conductivity KA of the aquifer is:
where Dt, the total thickness of the aquifer, is the sum of each layer's individual thickness:
The transmissivity of an aquifer can be determined from pumping tests.
Influence of the water table
When a soil layer is above the water table, it is not saturated and does not contribute to the transmissivity. When the soil layer is entirely below the water table, its saturated thickness corresponds to the thickness of the soil layer itself. When the water table is inside a soil layer, the saturated thickness corresponds to the distance of the water table to the bottom of the layer. As the water table may behave dynamically, this thickness may change from place to place or from time to time, so that the transmissivity may vary accordingly.
In a semi-confined aquifer, the water table is found within a soil layer with a negligibly small transmissivity, so that changes of the total transmissivity (Dt) resulting from changes in the level of the water table are negligibly small.
When pumping water from an unconfined aquifer, where the water table is inside a soil layer with a significant transmissivity, the water table may be drawn down whereby the transmissivity reduces and the flow of water to the well diminishes.
Resistance
The resistance to vertical flow (Ri) of the ith soil layer with a saturated thickness di and vertical hydraulic conductivity Kvi is:
Expressing Kvi in m/day and di in m, the resistance (Ri) is expressed in days.
The total resistance (Rt) of the aquifer is the sum of each layer's resistance:
The apparent vertical hydraulic conductivity (KvA) of the aquifer is:
where Dt is the total thickness of the aquifer:
The resistance plays a role in aquifers where a sequence of layers occurs with varying horizontal permeability so that horizontal flow is found mainly in the layers with high horizontal permeability while the layers with low horizontal permeability transmit the water mainly in a vertical sense.
Anisotropy
When the horizontal and vertical hydraulic conductivity ( and ) of the soil layer differ considerably, the layer is said to be anisotropic with respect to hydraulic conductivity.
When the apparent horizontal and vertical hydraulic conductivity ( and ) differ considerably, the aquifer is said to be anisotropic with respect to hydraulic conductivity.
An aquifer is called semi-confined when a saturated layer with a relatively small horizontal hydraulic conductivity (the semi-confining layer or aquitard) overlies a layer with a relatively high horizontal hydraulic conductivity so that the flow of groundwater in the first layer is mainly vertical and in the second layer mainly horizontal.
The resistance of a semi-confining top layer of an aquifer can be determined from pumping tests.
When calculating flow to drains or to a well field in an aquifer with the aim to control the water table, the anisotropy is to be taken into account, otherwise the result may be erroneous.
Relative properties
Because of their high porosity and permeability, sand and gravel aquifers have higher hydraulic conductivity than clay or unfractured granite aquifers. Sand or gravel aquifers would thus be easier to extract water from (e.g., using a pumping well) because of their high transmissivity, compared to clay or unfractured bedrock aquifers.
Hydraulic conductivity has units with dimensions of length per time (e.g., m/s, ft/day and (gal/day)/ft ); transmissivity then has units with dimensions of length squared per time. The following table gives some typical ranges (illustrating the many orders of magnitude which are likely) for K values.
Hydraulic conductivity (K) is one of the most complex and important of the properties of aquifers in hydrogeology as the values found in nature:
- range over many orders of magnitude (the distribution is often considered to be lognormal),
- vary a large amount through space (sometimes considered to be randomly spatially distributed, or stochastic in nature),
- are directional (in general K is a symmetric second-rank tensor; e.g., vertical K values can be several orders of magnitude smaller than horizontal K values),
- are scale dependent (testing a m³ of aquifer will generally produce different results than a similar test on only a cm³ sample of the same aquifer),
- must be determined indirectly through field pumping tests, laboratory column flow tests or inverse computer simulation, (sometimes also from grain size analyses), and
- are very dependent (in a non-linear way) on the water content, which makes solving the unsaturated flow equation difficult. In fact, the variably saturated K for a single material varies over a wider range than the saturated K values for all types of materials (see chart below for an illustrative range of the latter).
Ranges of values for natural materials
Table of saturated hydraulic conductivity (K) values found in nature

Values are for typical fresh groundwater conditions — using standard values of viscosity and specific gravity for water at 20 °C and 1 atm. See the similar table derived from the same source for intrinsic permeability values.
| K (cm/s) | 10² | 10 | 10=1 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| K (ft/day) | 10 | 10,000 | 1,000 | 100 | 10 | 1 | 0.1 | 0.01 | 0.001 | 0.0001 | 10 | 10 | 10 |
| Relative Permeability | Pervious | Semi-Pervious | Impervious | ||||||||||
| Aquifer | Good | Poor | None | ||||||||||
| Unconsolidated Sand & Gravel | Well Sorted Gravel | Well Sorted Sand or Sand & Gravel | Very Fine Sand, Silt, Loess, Loam | ||||||||||
| Unconsolidated Clay & Organic | Peat | Layered Clay | Fat / Unweathered Clay | ||||||||||
| Consolidated Rocks | Highly Fractured Rocks | Oil Reservoir Rocks | Fresh Sandstone | Fresh Limestone, Dolomite | Fresh Granite | ||||||||
Source: modified from Bear, 1972
| Soil Type | Liquid Limit, LL (%) | Void Ratio at Liquid Limit, (%) | Hydraulic conductivity, cm/s |
|---|---|---|---|
| Bentonite | 330 | 9.24 | 1,28 |
| Bentonite sand | 215 | 5,91 | 2,65 |
| Natural marine soil | 106 | 2,798 | 2,56 |
| Air-dried marine soil | 84 | 2,234 | 2,42 |
| Open-dried marine soil | 60 | 1,644 | 2,63 |
| Brown soil | 62 | 1,674 | 2,83 |
See also
- Aquifer test
- Hydraulic analogy
- Pedotransfer function – for estimating hydraulic conductivities given soil properties
References
- https://www.preene.com/blog/2014/07/what-is-hydraulic-conductivity#:~:text=DEFINITIONS%20OF%20HYDRAULIC%20CONDUCTIVITY&text=In%20theoretical%20terms%2C%20hydraulic%20conductivity,the%20material%20is%20less%20permeable. Hydraulic conductivity definition
- Sahu, Sudarsan; Saha, Dipankar (2016). "Empirical Methods and Estimation of Hydraulic Conductivity of Fluvial Aquifers". Environmental & Engineering Geoscience. 22 (4): 319–340. Bibcode:2016EEGeo..22..319S. doi:10.2113/gseegeosci.22.4.319.
- Wösten, J.H.M., Pachepsky, Y.A., and Rawls, W.J. (2001). "Pedotransfer functions: bridging the gap between available basic soil data and missing soil hydraulic characteristics". Journal of Hydrology. 251 (3–4): 123–150. Bibcode:2001JHyd..251..123W. doi:10.1016/S0022-1694(01)00464-4.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Controlling capillary flow an application of Darcy's law
- Liu, Cheng "Soils and Foundations." Upper Saddle River, New Jersey: Prentice Hall, 2001 ISBN 0-13-025517-3
- S.B.Hooghoudt, 1934, in Dutch. Bijdrage tot de kennis van enige natuurkundige grootheden van de grond. Verslagen Landbouwkundig Onderzoek No. 40 B, p. 215-345.
- C.H.M. van Bavel and D. Kirkham, 1948. Field measurement of soil permeability using auger holes. Soil. Sci. Soc. Am. Proc 13:90-96.
- ^ Determination of the Saturated Hydraulic Conductivity. Chapter 12 in: H.P.Ritzema (ed., 1994) Drainage Principles and Applications, ILRI Publication 16, p.435-476. International Institute for Land Reclamation and Improvement, Wageningen (ILRI), The Netherlands. ISBN 90-70754-33-9. Free download from: , under nr. 6, or directly as PDF :
- Drainage research in farmers' fields: analysis of data. Contribution to the project “Liquid Gold” of the International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. Free download from : , under nr. 2, or directly as PDF :
- ^ J.Boonstra and R.A.L.Kselik, SATEM 2002: Software for aquifer test evaluation, 2001. Publ. 57, International Institute for Land reclamation and Improvement (ILRI), Wageningen, The Netherlands. ISBN 90-70754-54-1 On line :
- The energy balance of groundwater flow applied to subsurface drainage in anisotropic soils by pipes or ditches with entrance resistance. International Institute for Land Reclamation and Improvement, Wageningen, The Netherlands. On line: Archived 2009-02-19 at the Wayback Machine . Paper based on: R.J. Oosterbaan, J. Boonstra and K.V.G.K. Rao, 1996, “The energy balance of groundwater flow”. Published in V.P.Singh and B.Kumar (eds.), Subsurface-Water Hydrology, p. 153-160, Vol.2 of Proceedings of the International Conference on Hydrology and Water Resources, New Delhi, India, 1993. Kluwer Academic Publishers, Dordrecht, The Netherlands. ISBN 978-0-7923-3651-8. On line: . The corresponding free EnDrain program can be downloaded from:
- Subsurface drainage by (tube)wells, 9 pp. Explanation of equations used in the WellDrain model. International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. On line: . The corresponding free WellDrain program can be downloaded from :
- Bear, J. (1972). Dynamics of Fluids in Porous Media. Dover Publications. ISBN 0-486-65675-6.
- Table 4.4 James K. Mitchell, Kenichi Soga, Fundamentals of SoilBehavior, third ed., John Wiley & Sons Inc., Hoboken, NJ, 2005, 577 pp., ISBN 0-471-46302-7.
- Nagaraj, T. S., Pandian, N. S., and Narasimha Raju, P. S. R. 1991. An approach for prediction of compressibility and permeability behaviour of sand-bentonite mixes, Indian Geotechnical Journal, Vol. 21, No. 3, pp. 271–282
External links
| Physical aquifer properties used in hydrogeology | |
|---|---|
| Geotechnical engineering | |||||||
|---|---|---|---|---|---|---|---|
| Offshore geotechnical engineering | |||||||
| Investigation and instrumentation | |||||||
| Soil |
| ||||||
| Structures (Interaction) |
| ||||||
| Mechanics |
| ||||||
| Numerical analysis software | |||||||
| Related fields | |||||||

 Hazen's empirical coefficient, which takes a value between 0.0 and 1.5 (depending on literature), with an average value of 1.0. A.F. Salarashayeri & M. Siosemarde indicate C is usually between 1.0 and 1.5, with D in mm and K in cm/s.
Hazen's empirical coefficient, which takes a value between 0.0 and 1.5 (depending on literature), with an average value of 1.0. A.F. Salarashayeri & M. Siosemarde indicate C is usually between 1.0 and 1.5, with D in mm and K in cm/s. is the
is the 







 and rearranging gives the result.
and rearranging gives the result.










 and
and  ) of the
) of the  soil layer differ considerably, the layer is said to be
soil layer differ considerably, the layer is said to be  and
and  ) differ considerably, the
) differ considerably, the  (%)
(%) cm/s
cm/s
 sand
sand