In convex analysis and the calculus of variations, both branches of mathematics, a pseudoconvex function is a function that behaves like a convex function with respect to finding its local minima, but need not actually be convex. Informally, a differentiable function is pseudoconvex if it is increasing in any direction where it has a positive directional derivative. The property must hold in all of the function domain, and not only for nearby points.
Formal definition
Consider a differentiable function , defined on a (nonempty) convex open set of the finite-dimensional Euclidean space . This function is said to be pseudoconvex if the following property holds:
for all .Equivalently:
for all .Here is the gradient of , defined by:
Note that the definition may also be stated in terms of the directional derivative of , in the direction given by the vector . This is because, as is differentiable, this directional derivative is given by:
Properties
Relation to other types of "convexity"
Every convex function is pseudoconvex, but the converse is not true. For example, the function is pseudoconvex but not convex. Similarly, any pseudoconvex function is quasiconvex; but the converse is not true, since the function is quasiconvex but not pseudoconvex. This can be summarized schematically as:
convex pseudoconvex quasiconvex
To see that is not pseudoconvex, consider its derivative at : . Then, if was pseudoconvex, we should have:
In particular it should be true for . But it is not, as: .
Sufficient optimality condition
For any differentiable function, we have the Fermat's theorem necessary condition of optimality, which states that: if has a local minimum at in an open domain, then must be a stationary point of (that is: ).
Pseudoconvexity is of great interest in the area of optimization, because the converse is also true for any pseudoconvex function. That is: if is a stationary point of a pseudoconvex function , then has a global minimum at . Note also that the result guarantees a global minimum (not only local).
This last result is also true for a convex function, but it is not true for a quasiconvex function. Consider for example the quasiconvex function:
.This function is not pseudoconvex, but it is quasiconvex. Also, the point is a critical point of , as . However, does not have a global minimum at (not even a local minimum).
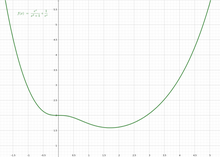
Finally, note that a pseudoconvex function may not have any critical point. Take for example the pseudoconvex function: , whose derivative is always positive: .
Examples
An example of a function that is pseudoconvex, but not convex, is: The figure shows this function for the case where . This example may be generalized to two variables as:

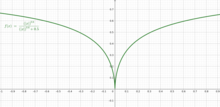
The previous example may be modified to obtain a function that is not convex, nor pseudoconvex, but is quasiconvex:
The figure shows this function for the case where . As can be seen, this function is not convex because of the concavity, and it is not pseudoconvex because it is not differentiable at .
Generalization to nondifferentiable functions
The notion of pseudoconvexity can be generalized to nondifferentiable functions as follows. Given any function , we can define the upper Dini derivative of by:
where u is any unit vector. The function is said to be pseudoconvex if it is increasing in any direction where the upper Dini derivative is positive. More precisely, this is characterized in terms of the subdifferential as follows:
For all : if is such that , then , for all ;where denotes the line segment adjoining x and y.
Related notions
A pseudoconcave function is a function whose negative is pseudoconvex. A pseudolinear function is a function that is both pseudoconvex and pseudoconcave. For example, linear–fractional programs have pseudolinear objective functions and linear–inequality constraints. These properties allow fractional-linear problems to be solved by a variant of the simplex algorithm (of George B. Dantzig).
Given a vector-valued function , there is a more general notion of -pseudoconvexity and -pseudolinearity; wherein classical pseudoconvexity and pseudolinearity pertain to the case when .
See also
Notes
- Mangasarian 1965
- Mangasarian 1965
- Floudas & Pardalos 2001
- Rapcsak 1991
- Chapter five: Craven, B. D. (1988). Fractional programming. Sigma Series in Applied Mathematics. Vol. 4. Berlin: Heldermann Verlag. p. 145. ISBN 3-88538-404-3. MR 0949209.
- Kruk, Serge; Wolkowicz, Henry (1999). "Pseudolinear programming". SIAM Review. 41 (4): 795–805. Bibcode:1999SIAMR..41..795K. doi:10.1137/S0036144598335259. JSTOR 2653207. MR 1723002.
- Mathis, Frank H.; Mathis, Lenora Jane (1995). "A nonlinear programming algorithm for hospital management". SIAM Review. 37 (2): 230–234. doi:10.1137/1037046. JSTOR 2132826. MR 1343214. S2CID 120626738.
- Ansari, Qamrul Hasan; Lalitha, C. S.; Mehta, Monika (2013). Generalized Convexity, Nonsmooth Variational Inequalities, and Nonsmooth Optimization. CRC Press. p. 107. ISBN 9781439868218. Retrieved 15 July 2019.
- Mishra, Shashi K.; Giorgi, Giorgio (2008). Invexity and Optimization. Springer Science & Business Media. p. 39. ISBN 9783540785613. Retrieved 15 July 2019.
References
- Floudas, Christodoulos A.; Pardalos, Panos M. (2001), "Generalized monotone multivalued maps", Encyclopedia of Optimization, Springer, p. 227, ISBN 978-0-7923-6932-5.
- Mangasarian, O. L. (January 1965). "Pseudo-Convex Functions". Journal of the Society for Industrial and Applied Mathematics, Series A. 3 (2): 281–290. doi:10.1137/0303020. ISSN 0363-0129..
- Rapcsak, T. (1991-02-15). "On pseudolinear functions". European Journal of Operational Research. 50 (3): 353–360. doi:10.1016/0377-2217(91)90267-Y. ISSN 0377-2217.
| Convex analysis and variational analysis | |
|---|---|
| Basic concepts | |
| Topics (list) | |
| Maps | |
| Main results (list) | |
| Sets | |
| Series | |
| Duality | |
| Applications and related | |
 , defined on a (nonempty)
, defined on a (nonempty)  of the finite-dimensional
of the finite-dimensional  . This function is said to be pseudoconvex if the following property holds:
. This function is said to be pseudoconvex if the following property holds:
 .
.
 .
.
 is the
is the  , defined by:
, defined by: 
 . This is because, as
. This is because, as 
 is pseudoconvex but not convex. Similarly, any pseudoconvex function is
is pseudoconvex but not convex. Similarly, any pseudoconvex function is  is quasiconvex but not pseudoconvex. This can be summarized schematically as:
is quasiconvex but not pseudoconvex. This can be summarized schematically as:
 pseudoconvex
pseudoconvex  :
:  . Then, if
. Then, if 
 . But it is not, as:
. But it is not, as:  .
.
 in an
in an  ).
).
 .
.
 , whose derivative is always positive:
, whose derivative is always positive:  .
.
 The figure shows this function for the case where
The figure shows this function for the case where  . This example may be generalized to two variables as:
. This example may be generalized to two variables as:


 . As can be seen, this function is not convex because of the concavity, and it is not pseudoconvex because it is not differentiable at
. As can be seen, this function is not convex because of the concavity, and it is not pseudoconvex because it is not differentiable at  , we can define the upper
, we can define the upper 
 as follows:
as follows:
 : if
: if  is such that
is such that  , then
, then  , for all
, for all  ;
;
 denotes the line segment adjoining x and y.
denotes the line segment adjoining x and y.
 , there is a more general notion of
, there is a more general notion of  .
.