In quantum computing, the quantum Fourier transform (QFT) is a linear transformation on quantum bits, and is the quantum analogue of the discrete Fourier transform. The quantum Fourier transform is a part of many quantum algorithms, notably Shor's algorithm for factoring and computing the discrete logarithm, the quantum phase estimation algorithm for estimating the eigenvalues of a unitary operator, and algorithms for the hidden subgroup problem. The quantum Fourier transform was discovered by Don Coppersmith. With small modifications to the QFT, it can also be used for performing fast integer arithmetic operations such as addition and multiplication.
The quantum Fourier transform can be performed efficiently on a quantum computer with a decomposition into the product of simpler unitary matrices. The discrete Fourier transform on amplitudes can be implemented as a quantum circuit consisting of only Hadamard gates and controlled phase shift gates, where is the number of qubits. This can be compared with the classical discrete Fourier transform, which takes gates (where is the number of bits), which is exponentially more than .
The quantum Fourier transform acts on a quantum state vector (a quantum register), and the classical Discrete Fourier transform acts on a vector. Both types of vectors can be written as lists of complex numbers. In the classical case, the vector can be represented with e.g. an array of floating point numbers, and in the quantum case it is a sequence of probability amplitudes for all the possible outcomes upon measurement (the outcomes are the basis states, or eigenstates). Because measurement collapses the quantum state to a single basis state, not every task that uses the classical Fourier transform can take advantage of the quantum Fourier transform's exponential speedup.
The best quantum Fourier transform algorithms known (as of late 2000) require only gates to achieve an efficient approximation, provided that a controlled phase gate is implemented as a native operation.
Definition
The quantum Fourier transform is the classical discrete Fourier transform applied to the vector of amplitudes of a quantum state, which has length if it is applied to a register of qubits.
The classical Fourier transform acts on a vector and maps it to the vector according to the formula:
where is an N-th root of unity.
Similarly, the quantum Fourier transform acts on a quantum state and maps it to a quantum state according to the formula:
(Conventions for the sign of the phase factor exponent vary; here the quantum Fourier transform has the same effect as the inverse discrete Fourier transform, and vice versa.)
Since is a rotation, the inverse quantum Fourier transform acts similarly but with:
In case that is a basis state, the quantum Fourier Transform can also be expressed as the map
Equivalently, the quantum Fourier transform can be viewed as a unitary matrix (or quantum gate) acting on quantum state vectors, where the unitary matrix is the DFT matrix
where . For example, in the case of and phase the transformation matrix is
Properties
Unitarity
Most of the properties of the quantum Fourier transform follow from the fact that it is a unitary transformation. This can be checked by performing matrix multiplication and ensuring that the relation holds, where is the Hermitian adjoint of . Alternately, one can check that orthogonal vectors of norm 1 get mapped to orthogonal vectors of norm 1.
From the unitary property it follows that the inverse of the quantum Fourier transform is the Hermitian adjoint of the Fourier matrix, thus . Since there is an efficient quantum circuit implementing the quantum Fourier transform, the circuit can be run in reverse to perform the inverse quantum Fourier transform. Thus both transforms can be efficiently performed on a quantum computer.
Circuit implementation
The quantum gates used in the circuit of qubits are the Hadamard gate and the dyadic rational phase gate :
The circuit is composed of gates and the controlled version of :
An orthonormal basis consists of the basis states
These basis states span all possible states of the qubits:
where, with tensor product notation , indicates that qubit is in state , with either 0 or 1. By convention, the basis state index is the binary number encoded by the , with the most significant bit.
The action of the Hadamard gate is , where the sign depends on .
The quantum Fourier transform can be written as the tensor product of a series of terms:
Using the fractional binary notation
the action of the quantum Fourier transform can be expressed in a compact manner:
To obtain this state from the circuit depicted above, a swap operation of the qubits must be performed to reverse their order. At most swaps are required.
Because the discrete Fourier transform, an operation on n qubits, can be factored into the tensor product of n single-qubit operations, it is easily represented as a quantum circuit (up to an order reversal of the output). Each of those single-qubit operations can be implemented efficiently using one Hadamard gate and a linear number of controlled phase gates. The first term requires one Hadamard gate and controlled phase gates, the next term requires one Hadamard gate and controlled phase gate, and each following term requires one fewer controlled phase gate. Summing up the number of gates, excluding the ones needed for the output reversal, gives gates, which is quadratic polynomial in the number of qubits. This value is much smaller than for the classical Fourier transformation.
The circuit-level implementation of the quantum Fourier transform on a linear nearest neighbor architecture has been studied before. The circuit depth is linear in the number of qubits.
Example
The quantum Fourier transform on three qubits, with , is represented by the following transformation:
where is an eighth root of unity satisfying .
The matrix representation of the Fourier transform on three qubits is:
The 3-qubit quantum Fourier transform can be rewritten as:
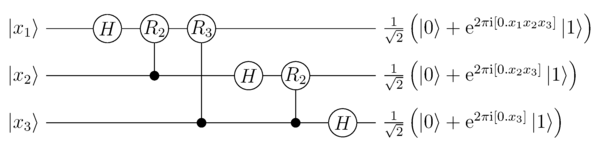
The following sketch shows the respective circuit for (with reversed order of output qubits with respect to the proper QFT):
As calculated above, the number of gates used is which is equal to , for .
Relation to quantum Hadamard transform
See also: Hadamard transform § Quantum computing applicationsUsing the generalized Fourier transform on finite (abelian) groups, there are actually two natural ways to define a quantum Fourier transform on an n-qubit quantum register. The QFT as defined above is equivalent to the DFT, which considers these n qubits as indexed by the cyclic group . However, it also makes sense to consider the qubits as indexed by the Boolean group , and in this case the Fourier transform is the Hadamard transform. This is achieved by applying a Hadamard gate to each of the n qubits in parallel. Shor's algorithm uses both types of Fourier transforms, an initial Hadamard transform as well as a QFT.
For other groups
The Fourier transform can be formulated for groups other than the cyclic group, and extended to the quantum setting. For example, consider the symmetric group . The Fourier transform can be expressed in matrix form
where is the element of the matrix representation of , is the set of paths from the root node to in the Bratteli diagram of , is the set of representations of indexed by Young diagrams, and is a permutation.
Over a finite field
The discrete Fourier transform can also be formulated over a finite field , and a quantum version can be defined. Here . Let be an arbitrary linear map (trace, for example). Then for each define
for and extend linearly.
References
- Coppersmith, D. (2002). An approximate Fourier transform useful in quantum factoring (Preprint). arXiv:quant-ph/0201067.
- Draper, Thomas G. (7 Aug 2000). "Addition on a Quantum Computer". arXiv:quant-ph/0008033.
- Ruiz-Perez, Lidia; Juan Carlos, Garcia-Escartin (2 May 2017). "Quantum arithmetic with the quantum Fourier transform". Quantum Information Processing. 16 (6): 152. arXiv:1411.5949v2. Bibcode:2017QuIP...16..152R. doi:10.1007/s11128-017-1603-1. S2CID 10948948.
- Şahin, Engin (2020). "Quantum arithmetic operations based on quantum Fourier transform on signed integers". International Journal of Quantum Information. 18 (6): 2050035. arXiv:2005.00443v3. doi:10.1142/s0219749920500355. ISSN 1793-6918.
- ^ Nielsen, Michael A.; Chuang, Isaac L. (2012). Quantum Computation and Quantum Information. doi:10.1017/CBO9780511976667. ISBN 978-1-107-00217-3.
- Hales, L.; Hallgren, S. (November 12–14, 2000). "An improved quantum Fourier transform algorithm and applications". Proceedings 41st Annual Symposium on Foundations of Computer Science. pp. 515–525. CiteSeerX 10.1.1.29.4161. doi:10.1109/SFCS.2000.892139. ISBN 0-7695-0850-2. S2CID 424297.
- Kurgalin, Sergei; Borzunov, Sergei (2021). Concise guide to quantum computing: algorithms, exercises, and implementations. Texts in computer science. Cham: Springer. ISBN 978-3-030-65054-4.
- Fowler, A.G.; Devitt, S.J.; Hollenberg, L.C.L. (July 2004). "Implementation of Shor's algorithm on a linear nearest neighbour qubit array". Quantum Information and Computation. 4 (4): 237–251. doi:10.26421/QIC4.4-1.
- Maslov, Dmitri (15 November 2007). "Linear depth stabilizer and quantum Fourier transformation circuits with no auxiliary qubits in finite-neighbor quantum architectures". Physical Review A. 76 (5): 052310. arXiv:quant-ph/0703211. Bibcode:2007PhRvA..76e2310M. doi:10.1103/PhysRevA.76.052310. S2CID 18645435.
- Fourier Analysis of Boolean Maps– A Tutorial –, pp. 12-13
- Lecture 5: Basic quantum algorithms, Rajat Mittal, pp. 4-5
- Moore, Cristopher; Rockmore, Daniel; Russell, Alexander (2003). Generic Quantum Fourier Transforms (Preprint). arXiv:quant-ph/0304064.
- Kawano, Yasuhito; Sekigawa, Hiroshi (July 2016). "Quantum Fourier transform over symmetric groups — improved result". Journal of Symbolic Computation. 75: 219–243. doi:10.1016/j.jsc.2015.11.016.
- Beals, Robert (1997). "Quantum computation of Fourier transforms over symmetric groups". Proceedings of the twenty-ninth annual ACM symposium on Theory of computing - STOC '97. pp. 48–53. doi:10.1145/258533.258548. ISBN 0-89791-888-6.
- de Beaudrap, Niel; Cleve, Richard; Waltrous, John (8 November 2002). "Sharp Quantum versus Classical Query Complexity Separations". Algorithmica. 34 (4): 449–461. doi:10.1007/s00453-002-0978-1.
Further reading
- Parthasarathy, K. R. (2006). Lectures on Quantum Computation, Quantum Error Correcting Codes and Information Theory. Tata Institute of Fundamental Research. ISBN 978-81-7319-688-1.
- Preskill, John (September 1998). "Lecture Notes for Physics 229: Quantum Information and Computation" (PDF).
External links
- Wolfram Demonstration Project: Quantum Circuit Implementing Grover's Search Algorithm
- Wolfram Demonstration Project: Quantum Circuit Implementing Quantum Fourier Transform
- Quirk online life quantum fourier transform
| Quantum information science | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| General | |||||||||
| Theorems | |||||||||
| Quantum communication |
| ||||||||
| Quantum algorithms | |||||||||
| Quantum complexity theory | |||||||||
| Quantum processor benchmarks | |||||||||
| Quantum computing models | |||||||||
| Quantum error correction | |||||||||
| Physical implementations |
| ||||||||
| Quantum programming | |||||||||
 amplitudes can be implemented as a
amplitudes can be implemented as a 
 is the number of qubits. This can be compared with the classical discrete Fourier transform, which takes
is the number of qubits. This can be compared with the classical discrete Fourier transform, which takes  gates (where
gates (where  gates to achieve an efficient approximation, provided that a
gates to achieve an efficient approximation, provided that a  if it is applied to a register of
if it is applied to a register of  and maps it to the vector
and maps it to the vector
 according to the formula:
according to the formula:

 is an N-th
is an N-th  and maps it to a quantum state
and maps it to a quantum state  according to the formula:
according to the formula:

 is a rotation, the inverse quantum Fourier transform acts similarly but with:
is a rotation, the inverse quantum Fourier transform acts similarly but with:

 is a basis state, the quantum Fourier Transform can also be expressed as the map
is a basis state, the quantum Fourier Transform can also be expressed as the map

 is the
is the 
 . For example, in the case of
. For example, in the case of  and phase
and phase  the transformation matrix is
the transformation matrix is

 holds, where
holds, where  is the
is the  . Alternately, one can check that orthogonal vectors of
. Alternately, one can check that orthogonal vectors of  . Since there is an efficient quantum circuit implementing the quantum Fourier transform, the circuit can be run in reverse to perform the inverse quantum Fourier transform. Thus both transforms can be efficiently performed on a quantum computer.
. Since there is an efficient quantum circuit implementing the quantum Fourier transform, the circuit can be run in reverse to perform the inverse quantum Fourier transform. Thus both transforms can be efficiently performed on a quantum computer.
 :
:

 gates and the
gates and the 


 ,
,  indicates that qubit
indicates that qubit  is in state
is in state  , with
, with  is the
is the  the most significant bit.
the most significant bit.
 , where the sign depends on
, where the sign depends on  .
.



 swaps are required.
swaps are required.
 controlled phase gates, the next term requires one Hadamard gate and
controlled phase gates, the next term requires one Hadamard gate and  controlled phase gate, and each following term requires one fewer controlled phase gate. Summing up the number of gates, excluding the ones needed for the output reversal, gives
controlled phase gate, and each following term requires one fewer controlled phase gate. Summing up the number of gates, excluding the ones needed for the output reversal, gives  gates, which is quadratic polynomial in the number of qubits. This value is much smaller than for the classical Fourier transformation.
gates, which is quadratic polynomial in the number of qubits. This value is much smaller than for the classical Fourier transformation.
 with
with  , is represented by the following transformation:
, is represented by the following transformation:

 is an eighth
is an eighth  .
.


 (with reversed order of output qubits with respect to the proper QFT):
(with reversed order of output qubits with respect to the proper QFT):
 which is equal to
which is equal to  , for
, for  . However, it also makes sense to consider the qubits as indexed by the
. However, it also makes sense to consider the qubits as indexed by the  , and in this case the Fourier transform is the
, and in this case the Fourier transform is the  . The Fourier transform can be expressed in matrix form
. The Fourier transform can be expressed in matrix form

 is the
is the  element of the matrix representation of
element of the matrix representation of  ,
,  is the set of paths from the root node to
is the set of paths from the root node to  in the Bratteli diagram of
in the Bratteli diagram of  is the set of representations of
is the set of representations of  is a permutation.
is a permutation.
 , and a quantum version can be defined. Here
, and a quantum version can be defined. Here  . Let
. Let  be an arbitrary linear map (trace, for example). Then for each
be an arbitrary linear map (trace, for example). Then for each  define
define

 and extend
and extend  linearly.
linearly.