 | |
| Other names | Magic Cube, Speed Cube, Puzzle Cube, Cube |
|---|---|
| Type | Combination puzzle |
| Inventor(s) | Ernő Rubik |
| Company | Rubik's Brand Ltd (Spin Master) |
| Country | Hungary |
| Availability | 1977: as Hungarian Magic Cube, first test batches released in Budapest As Rubik's Cube, worldwide, 1980–present |
| Official website | |

The Rubik's Cube is a 3D combination puzzle invented in 1974 by Hungarian sculptor and professor of architecture Ernő Rubik. Originally called the Magic Cube, the puzzle was licensed by Rubik to be sold by Pentangle Puzzles in the UK in 1978, and then by Ideal Toy Corp in 1980 via businessman Tibor Laczi and Seven Towns founder Tom Kremer. The cube was released internationally in 1980 and became one of the most recognized icons in popular culture. It won the 1980 German Game of the Year special award for Best Puzzle. As of January 2024, around 500 million cubes had been sold worldwide, making it the world's bestselling puzzle game and bestselling toy. The Rubik's Cube was inducted into the US National Toy Hall of Fame in 2014.
On the original, classic Rubik's Cube, each of the six faces was covered by nine stickers, with each face in one of six solid colours: white, red, blue, orange, green, and yellow. Some later versions of the cube have been updated to use coloured plastic panels instead. Since 1988, the arrangement of colours has been standardised, with white opposite yellow, blue opposite green, and orange opposite red, and with the red, white, and blue arranged clockwise, in that order. On early cubes, the position of the colours varied from cube to cube.
An internal pivot mechanism enables each face to turn independently, thus mixing up the colours. For the puzzle to be solved, each face must be returned to having only one colour. The Cube has inspired other designers to create a number of similar puzzles with various numbers of sides, dimensions, and mechanisms.
Although the Rubik's Cube reached the height of its mainstream popularity in the 1980s, it is still widely known and used. Many speedcubers continue to practice it and similar puzzles, and to compete for the fastest times in various categories. Since 2003, the World Cube Association (WCA), the international governing body of the Rubik's Cube, has organised competitions worldwide and has recognised world records.
History
Precursors
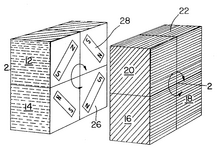
In March 1970, Larry D. Nichols invented a 2x2x2 "Puzzle with Pieces Rotatable in Groups" and filed a Canadian patent application for it. Nichols's cube was held together by magnets. Nichols was granted U.S. patent 3,655,201 on 11 April 1972, two years before Rubik invented his Cube.
On 9 April 1970, Frank Fox applied to patent an "amusement device", a type of sliding puzzle on a spherical surface with "at least two 3×3 arrays" intended to be used for the game of noughts and crosses. He received his UK patent (1344259) on 16 January 1974.
Rubik's invention
In the mid-1970s, Ernő Rubik worked at the Department of Interior Design at the Academy of Applied Arts and Crafts in Budapest. Although it is widely reported that the Cube was built as a teaching tool to help his students understand 3D objects, his actual purpose was solving the structural problem of moving the parts independently without the entire mechanism falling apart. He did not realise that he had created a puzzle until the first time he scrambled his new Cube and then tried to restore it. Rubik applied for a patent in Hungary for his "Magic Cube" (Hungarian: bűvös kocka) on 30 January 1975, and HU170062 was granted later that year.
The first test batches of the Magic Cube were produced in late 1977 and released in toy shops in Budapest. Magic Cube was held together with interlocking plastic pieces that prevented the puzzle from being easily pulled apart, unlike the magnets in Nichols's design. With Ernő Rubik's permission, businessman Tibor Laczi took a Cube to Germany's Nuremberg Toy Fair in February 1979 in an attempt to popularise it. It was noticed by Seven Towns founder Tom Kremer, and they signed a deal with Ideal Toys in September 1979 to release the Magic Cube worldwide. Ideal wanted at least a recognisable name to trademark; that arrangement put Rubik in the spotlight because the Magic Cube was renamed after its inventor in 1980.

The puzzle made its international debut at the toy fairs of London, Paris, Nuremberg, and New York in January and February 1980.
After its international debut, the progress of the Cube towards the toy shop shelves of the West was briefly halted so that it could be manufactured to Western safety and packaging specifications. A lighter Cube was produced, and Ideal decided to rename it. "The Gordian Knot" and "Inca Gold" were considered, but the company finally decided on "Rubik's Cube", and the first batch was exported from Hungary in May 1980.
The packaging had a few variations depending on the country, most popular being a clear plastic cylinder but cardboard versions were also used. The cube itself had slightly different variations in the order of the colours (Western vs. Japanese colour scheme where blue/yellow are switched) and some of the cubes did not have a white piece logo.
1980s Cube craze

After the first batches of Rubik's Cubes were released in May 1980, initial sales were modest, but Ideal began a television advertising campaign in the middle of the year which it supplemented with newspaper advertisements. At the end of 1980, Rubik's Cube won a German Game of the Year special award and won similar awards for best toy in the UK, France, and the US. By 1981, Rubik's Cube had become a craze, and it is estimated that in the period from 1980 to 1983 around 200 million Rubik's Cubes were sold worldwide. In March 1981, a speedcubing championship organised by the Guinness Book of World Records was held in Munich, and a Rubik's Cube was depicted on the front cover of Scientific American that same month. In June 1981, The Washington Post reported that Rubik's Cube is "a puzzle that's moving like fast food right now ... this year's Hoola Hoop or Bongo Board", and by September 1981, New Scientist noted that the cube had "captivated the attention of children of ages from 7 to 70 all over the world this summer."
As most people could solve only one or two sides, numerous books were published including David Singmaster's Notes on Rubik's "Magic Cube" (1980) and Patrick Bossert's You Can Do the Cube (1981). At one stage in 1981, three of the top ten best selling books in the US were books on solving Rubik's Cube, and the best-selling book of 1981 was James G. Nourse's The Simple Solution to Rubik's Cube which sold over 6 million copies. In 1981, the Museum of Modern Art in New York exhibited a Rubik's Cube, and at the 1982 World's Fair in Knoxville, Tennessee a six-foot Cube was put on display. ABC Television even developed a cartoon show called Rubik, the Amazing Cube. In June 1982, the First Rubik's Cube World Championship took place in Budapest and would become the only competition recognized as official until the championship was revived in 2003.
In October 1982, The New York Times reported that sales had fallen and that "the craze has died", and by 1983 it was clear that sales had plummeted. However, in some countries such as China and the USSR, the craze had started later and demand was still high because of a shortage of Cubes.
21st-century revival
Rubik's Cubes continued to be marketed and sold throughout the 1980s and 1990s, but it was not until the early 2000s that interest in the Cube began increasing again. In the US, sales doubled between 2001 and 2003, and The Boston Globe remarked that it was "becoming cool to own a Cube again". The 2003 World Rubik's Games Championship was the first speedcubing tournament since 1982. It was held in Toronto and was attended by 83 participants. The tournament led to the formation of the World Cube Association in 2004. Annual sales of Rubik branded cubes were said to have reached 15 million worldwide in 2008. Part of the new appeal was ascribed to the advent of Internet video sites, such as YouTube, which allowed fans to share their solving strategies. Following the expiration of Rubik's patent in 2000, other brands of cubes appeared, especially from Chinese companies. Many of these Chinese branded cubes have been engineered for speed and are favoured by speedcubers. On 27 October 2020, Spin Master said it will pay $50 million to buy the Rubik's Cube brand.
Imitations
Taking advantage of an initial shortage of cubes, many imitations and variations appeared, many of which may have violated one or more patents. In 2000 the patents expired, and since then, many Chinese companies have produced copies, modifications, and improvements upon the Rubik and V-Cube designs.
Patent history
Nichols assigned his patent to his employer Moleculon Research Corp., which sued Ideal in 1982. In 1984, Ideal lost the patent infringement suit and appealed. In 1986, the appeals court affirmed the judgment that Rubik's 2×2×2 Pocket Cube infringed Nichols's patent, but overturned the judgment on Rubik's 3×3×3 Cube.
Even while Rubik's patent application was being processed, Terutoshi Ishigi, a self-taught engineer and ironworks owner near Tokyo, filed for a Japanese patent for a nearly identical mechanism, which was granted in 1976 (Japanese patent publication JP55-008192). Until 1999, when an amended Japanese patent law was enforced, Japan's patent office granted Japanese patents for non-disclosed technology within Japan without requiring worldwide novelty. Hence, Ishigi's patent is generally accepted as an independent reinvention at that time. Rubik applied for more patents in 1980, including another Hungarian patent on 28 October. In the United States, Rubik was granted U.S. patent 4,378,116 on 29 March 1983 for the Cube. This patent expired in 2000.
Trademarks
Rubik's Brand Ltd. also holds the registered trademarks for the word "Rubik" and "Rubik's" and for the 2D and 3D visualisations of the puzzle. The trademarks were upheld by a ruling of the General Court of the European Union on 25 November 2014 in a successful defence against a German toy manufacturer seeking to invalidate them. However, European toy manufacturers are allowed to create differently shaped puzzles that have a similar rotating or twisting functionality of component parts such as for example Skewb, Pyraminx or Impossiball.
On 10 November 2016, Rubik's Cube lost a ten-year battle over a key trademark issue. The European Union's highest court, the Court of Justice, ruled that the puzzle's shape was not sufficient to grant it trademark protection.
Mechanics
| This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. Find sources: "Rubik's Cube" – news · newspapers · books · scholar · JSTOR (January 2021) (Learn how and when to remove this message) |


A standard Rubik's Cube measures 5.6 centimetres (2+1⁄4 in) on each side. The puzzle consists of 26 unique miniature cubes, also known as "cubies" or "cubelets". Each of these includes a concealed inward extension that interlocks with the other cubes while permitting them to move to different locations. However, the centre cube of each of the six faces is merely a single square façade; all six are affixed to the core mechanism. These provide structure for the other pieces to fit into and rotate around. Hence, there are 21 pieces: a single core piece consisting of three intersecting axes holding the six centre squares in place but letting them rotate, and 20 smaller plastic pieces that fit into it to form the assembled puzzle.
Each of the six centre pieces pivots on a fastener held by the centre piece, a "3D cross". A spring between each fastener and its corresponding piece tensions the piece inward, so that collectively, the whole assembly remains compact but can still be easily manipulated. The older versions of the official Cube used a screw that can be tightened or loosened to change the "feel" of the Cube. Newer official Rubik's brand cubes have rivets instead of screws and cannot be adjusted. Inexpensive clones do not have screws or springs, all they have is a plastic clip to keep the centre piece in place and freely rotate.
The Cube can be taken apart without much difficulty, typically by rotating the top layer by 45° and then prying one of its edge cubes away from the other two layers. Consequently, it is a simple process to "solve" a Cube by taking it apart and reassembling it in a solved state.
There are six central pieces that show one coloured face, twelve edge pieces that show two coloured faces, and eight corner pieces that show three coloured faces. Each piece shows a unique colour combination, but not all combinations are present (for example, if red and orange are on opposite sides of the solved Cube, there is no edge piece with both red and orange sides). The location of these cubes relative to one another can be altered by twisting an outer third of the Cube by increments of 90 degrees, but the location of the coloured sides relative to one another in the completed state of the puzzle cannot be altered; it is fixed by the relative positions of the centre squares. However, Cubes with alternative colour arrangements also exist; for example, with the yellow face opposite the green, the blue face opposite the white, and red and orange remaining opposite each other.
Douglas Hofstadter, in the July 1982 issue of Scientific American, pointed out that Cubes could be coloured in such a way as to emphasise the corners or edges, rather than the faces as the standard colouring does; but neither of these alternative colourings has ever become popular.
Mathematics
The puzzle was originally advertised as having "over 3,000,000,000 (three billion) combinations but only one solution". Depending on how combinations are counted, the actual number is significantly higher.
Permutations
Main article: Rubik's Cube group
The original (3×3×3) Rubik's Cube has eight corners and twelve edges. There are 8! (40,320) ways to arrange the corner cubes. Each corner has three possible orientations, although only seven (of eight) can be oriented independently; the orientation of the eighth (final) corner depends on the preceding seven, giving 3 (2,187) possibilities. There are 12!/2 (239,500,800) ways to arrange the edges, restricted from 12! because edges must be in an even permutation exactly when the corners are. (When arrangements of centres are also permitted, as described below, the rule is that the combined arrangement of corners, edges, and centres must be an even permutation.) Eleven edges can be flipped independently, with the flip of the twelfth depending on the preceding ones, giving 2 (2,048) possibilities.
which is approximately 43 quintillion. To put this into perspective, if one had one standard-sized Rubik's Cube for each permutation, one could cover the Earth's surface 275 times, or stack them in a tower 261 light-years high.
The preceding figure is limited to permutations that can be reached solely by turning the sides of the cube. If one considers permutations reached through disassembly of the cube, the number becomes twelve times larger:
which is approximately 519 quintillion possible arrangements of the pieces that make up the cube, but only one-twelfth of these are actually solvable. This is because there is no sequence of moves that will swap a single pair of pieces or rotate a single corner or edge cube. Thus, there are 12 possible sets of reachable configurations, sometimes called "universes" or "orbits", into which the cube can be placed by dismantling and reassembling it.
The preceding numbers assume the centre faces are in a fixed position. If one considers turning the whole cube to be a different permutation, then each of the preceding numbers should be multiplied by 24. A chosen colour can be on one of six sides, and then one of the adjacent colours can be in one of four positions; this determines the positions of all remaining colours.
Centre faces
The original Rubik's Cube had no orientation markings on the centre faces (although some carried the "Rubik's Cube" mark on the centre square of the white face), and therefore solving it does not require any attention to orienting those faces correctly. However, with marker pens, one could, for example, mark the central squares of an unscrambled Cube with four coloured marks on each edge, each corresponding to the colour of the adjacent face; a cube marked in this way is referred to as a "supercube". Some Cubes have also been produced commercially with markings on all of the squares, such as the Lo Shu magic square or playing card suits. Cubes have also been produced where the nine stickers on a face are used to make a single larger picture, and centre orientation matters on these as well. Thus one can nominally solve a Cube yet have the markings on the centres rotated; it then becomes an additional test to solve the centres as well.
Marking Rubik's Cube's centres increases its difficulty, because this expands the set of distinguishable possible configurations. There are 4/2 (2,048) ways to orient the centres since an even permutation of the corners implies an even number of quarter turns of centres as well. In particular, when the Cube is unscrambled apart from the orientations of the central squares, there will always be an even number of centre squares requiring a quarter turn. Thus orientations of centres increases the total number of possible Cube permutations from 43,252,003,274,489,856,000 (4.3×10) to 88,580,102,706,155,225,088,000 (8.9×10).
When turning a cube over is considered to be a change in permutation then we must also count arrangements of the centre faces. Nominally there are 6! ways to arrange the six centre faces of the cube, but only 24 of these are achievable without disassembly of the cube. When the orientations of centres are also counted, as above, this increases the total number of possible Cube permutations from 88,580,102,706,155,225,088,000 (8.9×10) to 2,125,922,464,947,725,402,112,000 (2.1×10).
Algorithms
In Rubik's cubers' parlance, a memorised sequence of moves that have a desired effect on the cube is called an "algorithm". This terminology is derived from the mathematical use of algorithm, meaning a list of well-defined instructions for performing a task from a given initial state, through well-defined successive states, to a desired end-state. Each method of solving the Cube employs its own set of algorithms, together with descriptions of what effect the algorithm has, and when it can be used to bring the cube closer to being solved.
Many algorithms are designed to transform only a small part of the cube without interfering with other parts that have already been solved so that they can be applied repeatedly to different parts of the cube until the whole is solved. For example, there are well-known algorithms for cycling three corners without changing the rest of the puzzle or flipping the orientation of a pair of edges while leaving the others intact.
Some algorithms do have a certain desired effect on the cube (for example, swapping two corners) but may also have the side-effect of changing other parts of the cube (such as permuting some edges). Such algorithms are often simpler than the ones without side effects and are employed early on in the solution when most of the puzzle has not yet been solved and the side effects are not important. Towards the end of the solution, the more specific (and usually more complicated) algorithms are used instead.
Relevance and application of mathematical group theory
Rubik's Cube lends itself to the application of mathematical group theory, which has been helpful for deducing certain algorithms – in particular, those which have a commutator structure, namely XYXY (where X and Y are specific moves or move-sequences and X and Y are their respective inverses), or a conjugate structure, namely XYX, often referred to by speedcubers colloquially as a "setup move". In addition, the fact that there are well-defined subgroups within the Rubik's Cube group enables the puzzle to be learned and mastered by moving up through various self-contained "levels of difficulty". For example, one such "level" could involve solving cubes that have been scrambled using only 180-degree turns. These subgroups are the principle underlying the computer cubing methods by Thistlethwaite and Kociemba, which solve the cube by further reducing it to another subgroup.
Unitary representation
The Rubik's group can be endowed with a unitary representation: such a description allows the Rubik's Cube to be mapped into a quantum system of few particles, where the rotations of its faces are implemented by unitary operators. The rotations of the faces act as generators of the Lie group.
Solutions
Singmaster notation
Many 3×3×3 Rubik's Cube enthusiasts use a notation developed by David Singmaster to denote a sequence of moves, referred to as "Singmaster notation" or simple "Cube notation". Its relative nature allows algorithms to be written in such a way that they can be applied regardless of which side is designated the top or how the colours are organised on a particular cube.
- F (Front): the side currently facing the solver
- B (Back): the side opposite the front
- U (Up): the side above or on top of the front side
- D (Down): the side opposite the top, underneath the Cube
- L (Left): the side directly to the left of the front
- R (Right): the side directly to the right of the front
- f (Front two layers): the side facing the solver and the corresponding middle layer
- b (Back two layers): the side opposite the front and the corresponding middle layer
- u (Up two layers): the top side and the corresponding middle layer
- d (Down two layers): the bottom layer and the corresponding middle layer
- l (Left two layers): the side to the left of the front and the corresponding middle layer
- r (Right two layers): the side to the right of the front and the corresponding middle layer
- x (rotate): rotate the entire Cube on R
- y (rotate): rotate the entire Cube on U
- z (rotate): rotate the entire Cube on F
When a prime symbol ( ′ ) follows a letter, it indicates an anticlockwise face turn; while a letter without a prime symbol denotes a clockwise turn. These directions are as one is looking at the specified face. A letter followed by a 2 (occasionally a superscript ) denotes two turns, or a 180-degree turn. For example, R means to turn the right side clockwise, but R′ means to turn the right side anticlockwise. The letters x, y, and z are used to indicate that the entire Cube should be turned about one of its axes, corresponding to R, U, and F turns respectively. When x, y, or z is primed, it is an indication that the cube must be rotated in the opposite direction. When x, y, or z is squared, the cube must be rotated 180 degrees.
One of the most common deviations from Singmaster notation, and in fact the current official standard, is to use "w", for "wide", instead of lowercase letters to represent moves of two layers; thus, a move of Rw is equivalent to one of r.
For methods using middle-layer turns (particularly corners-first methods), there is a generally accepted "MES" extension to the notation where letters M, E, and S denote middle layer turns. It was used e.g. in Marc Waterman's Algorithm.
- M (Middle): the layer between L and R, turn direction as L (top-down)
- E (Equator): the layer between U and D, turn direction as D (left-right)
- S (Standing): the layer between F and B, turn direction as F
The 4×4×4 and larger cubes use an extended notation to refer to the additional middle layers. Generally speaking, uppercase letters (F B U D L R) refer to the outermost portions of the cube (called faces). Lowercase letters (f b u d l r) refer to the inner portions of the cube (called slices). An asterisk (L*), a number in front of it (2L), or two layers in parentheses (Ll), means to turn the two layers at the same time (both the inner and the outer left faces) For example: (Rr)' l2 f' means to turn the two rightmost layers anticlockwise, then the left inner layer twice, and then the inner front layer anticlockwise. By extension, for cubes of 6×6×6 and larger, moves of three layers are notated by the number 3, for example, 3L.
An alternative notation, Wolstenholme notation, is designed to make memorising sequences of moves easier for novices. This notation uses the same letters for faces except it replaces U with T (top), so that all are consonants. The key difference is the use of the vowels O, A, and I for clockwise, anticlockwise, and twice (180-degree) turns, which results in word-like sequences such as LOTA RATO LATA ROTI (equivalent to LU′ R′ U L′ U′ R U2 in Singmaster notation). The addition of a C implies rotation of the entire cube, so ROC is the clockwise rotation of the cube around its right face. Middle layer moves are denoted by adding an M to the corresponding face move, so RIM means a 180-degree turn of the middle layer adjacent to the R face.
Another notation appeared in the 1981 book The Simple Solution to Rubik's Cube. Singmaster notation was not widely known at the time of publication. The faces were named Top (T), Bottom (B), Left (L), Right (R), Front (F), and Posterior (P), with + for clockwise, – for anticlockwise, and 2 for 180-degree turns.
Another notation appeared in the 1982 "The Ideal Solution" book for Rubik's Revenge. Horizontal planes were noted as tables, with table 1 or T1 starting at the top. Vertical front to back planes were noted as books, with book 1 or B1 starting from the left. Vertical left to right planes were noted as windows, with window 1 or W1 starting at the front. Using the front face as a reference view, table moves were left or right, book moves were up or down, and window moves were clockwise or anticlockwise.
Period of move sequences
The repetition of any given move sequence on a cube which is initially in solved state will eventually return the cube back to its solved state: the smallest number of iterations required is the period of the sequence. For example, the 180-degree turn of any side has period 2 (e.g. {U}); the 90-degree turn of any side has period 4 (e.g. {R}). The maximum period for a move sequence is 1260: for example, allowing for full rotations, {F x} or {R y} or {U z}; not allowing for rotations, {D R' U M}, or {B E L' F}, or {S' U' B D}; only allowing for clockwise quarter turns, {U R S U L}, or {F L E B L}, or {R U R D S}; only allowing for lateral clockwise quarter turns, {F B L F B R F U}, or {U D R U D L U F}, or {R L D R L U R F}.
Optimal solutions
Main article: Optimal solutions for Rubik's CubeAlthough there are a significant number of possible permutations for Rubik's Cube, a number of solutions have been developed which allow solving the cube in well under 100 moves.
Many general solutions for the Cube have been discovered independently. David Singmaster first published his solution in the book Notes on Rubik's "Magic Cube" in 1981. This solution involves solving the Cube layer by layer, in which one layer (designated the top) is solved first, followed by the middle layer, and then the final and bottom layer. After sufficient practice, solving the Cube layer by layer can be done in under one minute. Other general solutions include "corners first" methods or combinations of several other methods. In 1982, David Singmaster and Alexander Frey hypothesised that the number of moves needed to solve the Cube, given an ideal algorithm, might be in "the low twenties". In 2007, Daniel Kunkle and Gene Cooperman used computer search methods to demonstrate that any 3×3×3 Rubik's Cube configuration can be solved in 26 moves or fewer. In 2008, Tomas Rokicki lowered that number to 22 moves, and in July 2010, a team of researchers including Rokicki, working with computers provided by Google, proved that the so-called "God's number" for Rubik's Cube is 20. This means that all initial configurations can be solved in 20 moves or less, and some (in fact millions) require 20. More generally, it has been shown that an n×n×n Rubik's Cube can be solved optimally in Θ(n / log(n)) moves.
Speedcubing methods
A solution commonly used by speedcubers was developed by Jessica Fridrich. This method is called CFOP standing for "Cross, F2L, OLL, PLL". It is similar to the layer-by-layer method but employs the use of a large number of algorithms, especially for orienting and permuting the last layer. The cross is solved first, followed by first layer corners and second layer edges simultaneously, with each corner paired up with a second-layer edge piece, thus completing the first two layers (F2L). This is then followed by orienting the last layer, then permuting the last layer (OLL and PLL respectively). There are a total of 120 algorithms for Fridrich's method, however they are not all required to use the CFOP method. Most dedicated cubers will learn as many of these algorithms as possible, and most advanced cubers know all of them. If a cuber knows every algorithm for OLL they may be described as knowing full OLL. It is the same for PLL and F2L.
A now well-known method was developed by Lars Petrus. In this method, a 2×2×2 section is solved first, followed by a 2×2×3, and then the incorrect edges are solved using a three-move algorithm, which eliminates the need for a possible 32-move algorithm later. The principle behind this is that in layer-by-layer, one must constantly break and fix the completed layer(s); the 2×2×2 and 2×2×3 sections allow three or two layers (respectively) to be turned without ruining progress. One of the advantages of this method is that it tends to give solutions in fewer moves. For this reason, the method is also popular for fewest move competitions.
The Roux Method, developed by Gilles Roux, is similar to the Petrus method in that it relies on block building rather than layers, but derives from corners-first methods. In Roux, a 3×2×1 block is solved, followed by another 3×2×1 on the opposite side. Next, the corners of the top layer are solved. The cube can then be solved using only moves of the U layer and M slice.
Beginners' methods
Most beginner solution methods involve solving the cube one layer at a time ("layer-by-layer" method or "beginner's method"), using algorithms that preserve what has already been solved. The easiest layer by layer methods require only 3–8 algorithms.
In 1981, thirteen-year-old Patrick Bossert developed a solution for solving the cube, along with a graphical notation, designed to be easily understood by novices. It was subsequently published as You Can Do The Cube and became a best-seller.
In 1997, Denny Dedmore published a solution described using diagrammatic icons representing the moves to be made, instead of the usual notation.
Philip Marshall's The Ultimate Solution to Rubik's Cube takes a different approach, averaging only 65 twists yet requiring the memorisation of only two algorithms. The cross is solved first, followed by the remaining edges (using the Edge Piece Series FR'F'R), then five corners (using the Corner Piece Series URU'L'UR'U'L, which is the same as the typical last layer corner permutation algorithm), and finally the last three corners.
Rubik's Cube solver programs
The most move optimal online Rubik's Cube solver programs use Herbert Kociemba's two-phase algorithm which can typically determine a solution of 20 moves or fewer. The user has to set the colour configuration of the scrambled cube, and the program returns the steps required to solve it.
Competitions and records
Speedcubing competitions
Main articles: Speedcubing and World Cube AssociationSpeedcubing (or speedsolving) is the practice of trying to solve a Rubik's Cube in the shortest time possible. There are a number of speedcubing competitions that take place around the world.
A speedcubing championship organised by the Guinness Book of World Records was held in Munich on 13 March 1981. The contest used standardised scrambling and fixed inspection times, and the winners were Ronald Brinkmann and Jury Fröschl with times of 38.0 seconds. The first world championship was the 1982 World Rubik's Cube Championship held in Budapest on 5 June 1982, which was won by Minh Thai, a Vietnamese student from Los Angeles, with a time of 22.95 seconds.
Since 2003, the winner of a competition is determined by taking the average time of the middle three of five attempts. However, the single best time of all tries is also recorded. The World Cube Association maintains a history of world records. In 2004, the WCA made it mandatory to use a special timing device called a Stackmat timer.
In addition to the main 3x3x3 event, the WCA also holds events where the cube is solved in different ways:
- Blindfolded solving
- Multiple blindfolded solving, or "multi-blind", in which the contestant solves any number of cubes blindfolded in a row
- Solving the cube using a single hand, or one handed solving
- Solving the cube in the fewest possible moves
In blindfolded solving, the contestant first studies the scrambled cube (i.e., looking at it normally with no blindfold), and is then blindfolded before beginning to turn the cube's faces. Their recorded time for this event includes both the time spent memorizing the cube and the time spent manipulating it.
In multiple blindfolded solving, all of the cubes are memorised, and then all of the cubes are solved once blindfolded; thus, the main challenge is memorising many – often ten or more – separate cubes. The event is scored not by time but by the number of points achieved after the one-hour time limit has elapsed. The number of points achieved is equal to the number of cubes solved correctly, minus the number of cubes unsolved after the end of the attempt, where a greater number of points is better. If multiple competitors achieve the same number of points, rankings are assessed based on the total time of the attempt, with a shorter time being better.
In fewest moves solving, the contestant is given one hour to find a solution and must write it down.
Records
Competition records
- Single time: The world record time for solving a 3×3×3 Rubik's Cube is 3.13 seconds, held by Max Park of the United States, broken on 11 June 2023 at Pride in Long Beach.
- Average time: The world record average of the middle three of five solve times (which excludes the fastest and slowest) is 4.09 seconds, set by Yiheng Wang (王艺衡) of China on 21 September at the Xuzhou Autumn 2024 cubing competition in Xuzhou, Jiangsu, China.
- One-handed solving: The world record fastest one-handed solve is 5.66 seconds, set by Dhruva Sai Meruva of Switzerland on 6 October 2024 at Swiss Nationals 2024 in Basel, Switzerland. The world record fastest average of five one-handed solves is 8.09 seconds, set by Sean Patrick Villanueva of the Philippines on 26 May 2024 at Quezon City Open II 2024.
- Blindfold solving: The world record fastest Rubik's Cube solve blindfolded is 12.00 seconds (including memorization), set by Tommy Cherry of the United States on 11 February 2024 at Triton Tricubealon 2024 in San Diego, California, United States. The world record mean of three for blindfold solving is 14.05 seconds, set by Tommy Cherry on 28 July 2024 at the Rubik's WCA European Championship 2024 in Pamplona, Spain.
- Multiple blindfold solving: The world record for multiple Rubik's Cube solving blindfolded is 62 out of 65 cubes in 57 minutes and 47 seconds, set by Graham Siggins of the United States on 26 June 2022 at Blind Is Back LA 2022.
- Fewest moves solving: The world record of fewest moves to solve a cube, given one hour to determine one's solution, is 16, which was achieved by Sebastiano Tronto of Italy on 15 June 2019 at FMC 2019, Aeden Bryant of the USA on 23 June 2024 at Ashfield Summer Challenge 2024, and Levi Gibson of the USA on 23 June 2024 at Ashfield Summer Challenge 2024. The world record mean of three for the fewest moves challenge is 20.00, set by Wong Chong Wen (黄崇文) of Singapore on 17 September 2023 at FMC Johor Bahru.
Other records
- Non-human solving: The fastest non-human Rubik's Cube solve was performed by Rubik's Contraption, a robot made by Ben Katz and Jared Di Carlo. A YouTube video shows a 0.38-second solving time using a Nucleo with the min2phase algorithm.
- Highest order physical n×n×n cube solving: Jeremy Smith solved a 21x21x21 in 95 minutes and 55.52 seconds.
- Group solving (12 minutes): The record for most people solving a Rubik's Cube at once in twelve minutes is 134, set on 17 March 2010 by schoolboys from Dr Challoner's Grammar School, Amersham, England, breaking the previous Guinness World Record of 96 people at once.
- Group solving (30 minutes): On 21 November 2012, at the O2 Arena in London, 1414 people, mainly students from schools across London, solved Rubik's Cube in under 30 minutes, breaking the previous Guinness World Record of 937. The event was hosted by Depaul UK.
- On 4 November 2012, 3248 people, mainly students of the College of Engineering Pune, successfully solved Rubik's cube in 30 minutes on college ground. The successful attempt is recorded in the Limca Book of Records. The college will submit the relevant data, witness statements and video of the event to Guinness authorities.
Top 10 solvers by single solve
| Position | Name | Result | Nationality | Competition |
|---|---|---|---|---|
| 1 | Max Park | 3.13 | ||
| 2 | Ruihang Xu (许瑞航) | 3.24 | ||
| 3 | Yiheng Wang (王艺衡) | 3.27 | ||
| 4 | Luke Garrett | 3.44 | ||
| 5 | Aaron Huynh | 3.46 | ||
| 6 | Yusheng Du (杜宇生) | 3.47 | ||
| 7 | Xuanyi Geng (耿暄一) | 3.54 | ||
| 8 | Matty Hiroto Inaba | 3.59 | ||
| 9 | Tymon Kolasiński | 3.66 | ||
| 10 | Aidan Grainger | 3.69 |
Variations


There are many different variations of Rubik's Cubes. The most common class of variants changes the "order" of the cube, defined by the number of layers in each dimension or equivalently by the number of pieces along each edge (including corners). The 2×2×2 (Pocket/Mini Cube), the standard 3×3×3 cube, the 4×4×4 (Rubik's Revenge/Master Cube), and the 5×5×5 (Professor's Cube) are the most well known, as they are all available under the official Rubik's brand. The WCA sanctions speedsolving competitions for cube orders up to 7×7×7. These "big cubes" represent about the limit of practicality for the purpose of competitive speedsolving, as the cubes become increasingly ungainly and prone to mechanical failure (such as "popping", where one or more pieces become dislodged from the puzzle), and average solve times increase quadratically with each larger order, in proportion to the number of total "facelets" of the cube.
Even larger cubes based on the V-Cube patents are commercially available to the mass-market from non-licensed manufacturers, most of them Chinese firms which also produce popular cubes designed for speed-solving. The 17×17×17 "Over the Top" cube (available late 2011) was until December 2017 the largest commercially sold cube, and the most expensive, costing over US$2000. A mass-produced 17×17×17 was later introduced by the Chinese manufacturer YuXin. A working design for a 22×22×22 cube exists and was demonstrated in January 2016, and a 33×33×33 in December 2017, though designs this large are not currently mass-produced. Chinese manufacturer ShengShou has been producing cubes in all sizes from 2×2×2 to 15×15×15 (as of May 2020), and has also come out with a 17×17×17. The largest currently mass-produced cube is 21×21×21, made by MoYu beginning in 2021, and costing between $1100 and $1600.
There are many variations of the original cube, some of which are made by Rubik. The mechanical products include Rubik's Magic, 360, and Twist. There are electronic variants such as Rubik's Revolution and Slide that were also inspired by the original. One of the 3×3×3 Cube variants is Rubik's TouchCube. Sliding a finger across its faces causes its patterns of coloured lights to rotate the same way they would on a mechanical cube. The TouchCube also has buttons for hints and self-solving, and it includes a charging stand. The TouchCube was introduced at the American International Toy Fair in New York on 15 February 2009.
The Cube has inspired an entire category of similar puzzles, commonly referred to as twisty puzzles, which includes the cubes of different sizes mentioned above, as well as various other geometric shapes. Some such shapes include the tetrahedron (Pyraminx), the octahedron (Skewb Diamond), the dodecahedron (Megaminx), and the icosahedron (Dogic). There are also puzzles that change shape such as Rubik's Snake and the Square One.
In 2011, Guinness World Records awarded the "largest order Rubiks magic cube" to a 17×17×17 cube, made by Oskar van Deventer. On 2 December 2017, Grégoire Pfennig announced that he had broken this record, with a 33×33×33 cube, and that his claim had been submitted to Guinness for verification. On 8 April 2018, Grégoire Pfennig announced another world record, the 2x2x50 cube. Whether this is a replacement for the 33×33×33 record, or an additional record, remains to be seen.

Some puzzles have also been created in the shape of Kepler–Poinsot polyhedra, such as Alexander's Star (a great dodecahedron). Grégoire Pfennig has also created at least one puzzle in the shape of a small stellated dodecahedron.
Custom-built puzzles

Puzzles have been built resembling Rubik's Cube, or based on its inner workings. For example, a cuboid is a puzzle based on Rubik's Cube, but with different functional dimensions, such as 2×2×4, 2×3×4, and 3×3×5.
Other Rubik's Cube modifications include "shape mods", cubes that have been extended or truncated to form a new shape. An example of this is the Trabjer's Octahedron, which can be built by truncating and extending portions of a regular 3×3×3. Most shape modifications can be adapted to higher-order cubes. In the case of Tony Fisher's Rhombic Dodecahedron, there are 3×3×3, 4×4×4, 5×5×5, and 6×6×6 versions of the puzzle.
Rubik's Cube software
Puzzles, like Rubik's Cube, can be simulated by computer software to provide very large puzzles that are impractical to build, as well as virtual puzzles that cannot be physically built, such as many higher dimensional analogues of the Rubik's Cube.
-
 A 2×2×2×2 in MagicCube4D
A 2×2×2×2 in MagicCube4D
-
 A 3×3×3×3 in MagicCube4D
A 3×3×3×3 in MagicCube4D
-
 A 4×4×4×4 in MagicCube4D
A 4×4×4×4 in MagicCube4D
-
 A 3×3×3×3×3 in MagicCube5D
A 3×3×3×3×3 in MagicCube5D
Chrome Cube Lab
Google has released the Chrome Cube Lab in association with Ernő Rubik. The site has various interactive objects based on Rubik's Cube. Customised versions of Rubik's Cube can be created and uploaded.
Exhibits and art

Liberty Science Center in Jersey City, New Jersey, and Google designed an interactive exhibit based on the Rubik's Cube. It opened in April 2014 in celebration of the 40th anniversary of the Cube's invention before traveling internationally for seven years. Exhibition elements include a 35-foot-tall rooftop cube made of lights that people can manipulate with their cellphones, a $2.5 million cube made of diamonds, a giant walk-in cube displaying the inner workings of the puzzle, and cube-solving robots.
Probably from the earliest days of the Rubik's Cube craze in the 1980s people have assembled cubes to form simple art pieces, several early 'Folk Artists' are noted for their work. Rubik's Cubes have also been the subject of several pop art installations. Owing to their popularity as a children's toy several artists and groups have created large Rubik's Cubes.
Tony Rosenthal's Alamo (The Astor Place Cube) is a spinnable statue of a Cube standing in New York City. Once the cube was covered with coloured panels so that it resembled a Rubik's Cube. Similarly, the University of Michigan students covered Endover creating a large Rubik's Cube on the University of Michigan's Central Campus for April Fool's Day in 2008.
Rubik's Cubism
Beyond the Folk Art of the 1980s and 1990s, and the simple replication of a Rubik's Cube in oversized form, artists have developed a pointillist art style using the cubes. Rubik's Cube Art a.k.a. Rubik's Cubism or RubikCubism makes use of a standard Rubik's Cube, a popular puzzle toy of the 1980s.
The earliest recorded artworks appear to have been created by Fred Holly, a legally blind man in his 60s in the mid-1980s. These early pieces focus on geometrics and colour patterns. There does not appear to be other recorded art pieces until the mid-1990s by cube aficionados involved in the puzzle and game industry.

The Folk art form reached another level of its evolution with the development and maturity into a Pop art form consisting of pointillist Cube Art renderings. The street artist who uses the alias "Invader" or "Space Invader" started exhibiting pointillist pieces, including one of a man behind a desk and Mario Bros, using Rubik's Cube in June 2005 in an exhibition named 'Rubik Cubism' at Sixspace in Los Angeles. Prior to this exhibition the artist had used Rubik's Cubes to create giant Space Invaders. Another artist includes Robbie Mackinnon of Toronto Canada with earliest published work in 2007 who claims to have developed his pointillist Cube Art years earlier while being a teacher in China. Robbie Mackinnon's work has been exhibited in Ripley's Believe it or Not and focussed on using pop-art, while Space Invader has exhibited his Cube Art alongside mosaic Space Invaders in commercial and public galleries.
In 2010 artist Pete Fecteau created "Dream Big", a tribute to Martin Luther King Jr. using 4,242 officially licensed Rubik's Cubes. Fecteau also worked with the organization You Can Do The Rubik's Cube to create two separate guides designed to teach school children how to create Rubik's Cube mosaics from templates which he also created.
Music
Italian composer Maria Mannone created a cube called "CubeHarmonic" which has musical note names on its facets, creating different chord structures depending on its configuration.
Reviews
- Games
- 1980 Games 100 in Games
- 1981 Games 100 in Games
See also
- Mirror blocks
- n-dimensional sequential move puzzle
- Rubik's Domino
- Rubik's family cubes of all sizes
- Spatial ability
- V-Cube 8 (8×8×8)
- List of Rubik's Cube manufacturers
References
- ^ Evans, Pete (27 October 2020). "Canadian company that owns classic toys Etch A Sketch and Aerobie buys Rubik's Cube for $50M". CBC News.
- Fotheringham, William (2007). Fotheringham's Sporting Pastimes. Anova Books. p. 50. ISBN 978-1-86105-953-6.
- de Castella, Tom (28 April 2014). "The people who are still addicted to the Rubik's Cube". BBC News Magazine. BBC. Retrieved 28 April 2014.
- ^ "Jan. 30, 1975: Rubik Applies for Patent on Magic Cube". Wired. 30 January 2009. Retrieved 24 January 2019.
- "25th Anniversa[r]y of Erno Rubik's Magic Cube. First introduced to the Western World by Pentangle Puzzles in 1978". puzzlemuseum.com. Retrieved 29 November 2020.
- Daintith, John (1994). A Biographical Encyclopedia of Scientists. Bristol: Institute of Physics Pub. p. 771. ISBN 0-7503-0287-9.
- Michael Shanks (8 May 2005). "History of the Cube". Stanford University. Archived from the original on 20 January 2013. Retrieved 26 July 2012.
- Prakash, Prarthana. "How the Rubik's Cube has lived to 50 years—and continues to be popular among members of Gen Z and beyond". Fortune Europe. Retrieved 3 April 2024.
- Adams, William Lee (28 January 2009). "The Rubik's Cube: A Puzzling Success". Time. Archived from the original on 1 February 2009. Retrieved 5 February 2009.
- Jamieson, Alastair (31 January 2009). "Rubik's Cube inventor is back with Rubik's 360". The Daily Telegraph. London. Archived from the original on 11 January 2022. Retrieved 5 February 2009.
- "eGames, Mindscape Put International Twist on Rubik's Cube PC Game". Reuters. 6 February 2008. Archived from the original on 12 February 2009. Retrieved 6 February 2009.
- Marshall, Ray. "Squaring up to the Rubchallenge". Archived from the original on 20 January 2013. Retrieved 15 August 2005.
- "Rubik's Cube 25 years on: crazy toys, crazy times". The Independent. London. 16 August 2007. Retrieved 6 February 2009.
- "National Toy Hall Of Fame 2014 - CBS News". CBS News. 6 November 2014.
- Dempsey, Michael W. (1988). Growing up with science: The illustrated encyclopedia of invention. London: Marshall Cavendish. p. 1245. ISBN 0-87475-841-6.
- Ewing, John; Czes Kosniowski (1982). Puzzle It Out: Cubes, Groups and Puzzles. Cambridge: Press Syndicate of the University of Cambridge. p. 4. ISBN 0-521-28924-6. Retrieved 19 May 2014.
- "Patent Specification 1344259" (PDF). Retrieved 15 June 2012.
- Sagert, Kelly Boyer (2007). The 1970s (American Popular Culture Through History). Westport, Conn: Greenwood Press. p. 130. ISBN 978-0-313-33919-6.
- "Rubik's Cube". PuzzleSolver. 1 December 2006. Retrieved 20 June 2012.
- ^ Holper, Paul (2006). Inventing Millions. Orient. pp. 64–65. ISBN 8122204589.
- "History". Rubiks. 19 May 2008. Archived from the original on 26 January 2019. Retrieved 25 January 2019.
- "About". Rubiks. 25 January 2019. Archived from the original on 14 August 2018. Retrieved 25 January 2019.
- Dougherty, Philip H. (30 July 1981). "Advertising Ideal Toy's Son of Rubik Cube". The New York Times.
- ^ Carlisle, Rodney P. (2009). Encyclopedia of Play in Today's Society. Sage. p. 612. ISBN 978-1452266107.
- "Interview with Ernő Rubik". Europa. Archived from the original on 27 May 2018. Retrieved 26 October 2016.
- Singmaster, David (1994). "The Utility of Recreational Mathematics". In Guy, Richard K.; Woodrow, Robert E. (eds.). The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and Its History. Cambridge University Press. p. 340. ISBN 088385516X. Singmaster estimates the numbers sold were between 100 and 300 million. His estimate is based on sales of 50 to 100 million legitimate cubes and perhaps a higher number of imitations.
- Batchelor, Bob; Stoddart, Scott (2007). The 1980s. Greenwood. p. 97. ISBN 978-0313330001.
- Allen, Henry (10 June 1981). "The Cube". The Washington Post.
- Herman, Ros (10 September 1981). "Cubic mastery". New Scientist. Archived from the original on 19 August 2020.
- Singmaster, David (1994). "The Utility of Recreational Mathematics". In Guy, Richard K.; Woodrow, Robert E. (eds.). The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and Its History. Cambridge University Press. p. 340. ISBN 088385516X.
- Hanauer, Joan (5 January 1982). "The man who wrote the best-selling book of 1981". United Press International.
- Terrace, Vincent (2008). Encyclopedia of Television Shows, 1925 through 2010. McFarland. p. 915. ISBN 978-0786486410.
- Scheffler, Ian (2016). Cracking the Cube. Simon and Schuster. p. 88. ISBN 978-1501121944.
- "Rubik's Cube: A Craze Ends". The New York Times. 30 October 1982.
- "China facing Rubik Cube shortage". United Press International. 22 February 1982.
- Reed, Steven R. (8 December 1982). "Russians Queue for Rubik's Cube". United Press International.
- ^ Harris, Dan (2008). Speedsolving the Cube. Sterling. p. 3. ISBN 978-1402753138.
- Noonan, Erica (8 November 2003). "Let's twist again". Boston Globe.
- ^ Quenqua, Douglas (6 August 2012). "Rubik's Cube Twists Back into Limelight". The New York Times.
- ^ Hookway, James (14 December 2011). "One Cube, Many Knockoffs, Quintillions of Possibilities". The Wall Street Journal.
- "Moleculon Research Corporation v. CBS, Inc". Digital-law-online.info. Retrieved 20 June 2012.
- "Japan: Patents". 26 April 1978. Archived from the original on 12 February 2009.
- "Major Amendments to the Japanese Patent Law (since 1985)" (PDF). Archived from the original (PDF) on 16 February 2012. Retrieved 20 June 2012.
- ^ Hofstadter, Douglas R. (1985). Metamagical Themas: Questing for the Essence of Mind and Pattern. New York: Basic Books. ISBN 0-465-04566-9.
Hofstadter gives the name as 'Ishige'.
- Longridge, Mark (2004). "Rubik's Cube Chronology".
- "The History of Rubik's Cube – Erno Rubik". Inventors.about.com. 9 April 2012. Archived from the original on 23 May 2020. Retrieved 20 June 2012.
- Bodoni (25 November 2014). "Rubik's Cube Wins Trademark Toy Story at EU Court". Bloomberg L.P. Retrieved 13 December 2014.
- Smithers, Rebecca (10 November 2016). "Rubik's Cube puzzled after losing EU trademark battle". The Guardian. Retrieved 8 December 2016.
- Bandelow, C. (6 December 2012). Inside Rubik's Cube and Beyond. Springer Science & Business Media. p. 2. ISBN 978-1-4684-7779-5.
- Zeng, Da-Xing; Li, Ming; Wang, Juan-Juan; Hou, Yu-Lei; Lu, Wen-Juan; Huang, Zhen (27 August 2018). "Overview of Rubik's Cube and Reflections on Its Application in Mechanism". Chinese Journal of Mechanical Engineering. 31 (1): 77. Bibcode:2018ChJME..31...77Z. doi:10.1186/s10033-018-0269-7. ISSN 2192-8258.
- Rubik's Cube Commercial 1981. 23 October 2008. Archived from the original on 11 December 2021. Retrieved 10 October 2017 – via YouTube.
- Schönert, Martin. "Analyzing Rubik's Cube with GAP". gap-system.org. Archived from the original on 28 September 2017. Retrieved 30 December 2022.
- "The Mathematics of the Rubik's Cube" (PDF). Massachusetts Institute of Technology. 17 March 2009.
- Scott Vaughen. "Counting the Permutations of the Rubik's Cube". Montgomery County Community College. Archived from the original on 19 July 2011. Retrieved 19 January 2011.
- Hofstadter, Douglas R. (March 1981). "Metamagical themas: The Magic Cube's cubies are twiddled by cubists and solved by cubemeisters". Scientific American. 244 (3): 20–39. doi:10.1038/scientificamerican0381-20. JSTOR 24964321.; see p. 22
- ^ Singmaster, David (1981). Notes on Rubik's Magic Cube. Harmondsworth, Eng: Penguin Books. ISBN 0-907395-00-7.
- S. Corli; L. Moro; D.E. Galli; E. Prati (2021). "Solving Rubik's Cube via Quantum Mechanics and Deep Reinforcement Learning". Journal of Physics A: Mathematical and Theoretical. 54 (5): 425302. arXiv:2109.07199. Bibcode:2021JPhA...54P5302C. doi:10.1088/1751-8121/ac2596. ISSN 1751-8113. S2CID 237513509.
- ^ Joyner, David (2002). Adventures in group theory: Rubik's Cube, Merlin's machine, and Other Mathematical Toys. Baltimore: Johns Hopkins University Press. p. 7. ISBN 0-8018-6947-1.
- "World Cube Association Competition Regulations". World Cube Association. Retrieved 5 May 2012.
- Treep, Anneke; Waterman, Marc (1987). Marc Waterman's Algorithm, Part 2. Cubism For Fun 15. Nederlandse Kubus Club. p. 10.
- "Rubik's Cube - Solution and Wolstenholme Notation". topaccolades.com. Retrieved 19 February 2022.
- Frey, Alexander H. Jr.; Singmaster, David (1982). Handbook of Cubik Math. Hillside, N.J.: Enslow Publishers. ISBN 0-89490-058-7.
- Kunkle, D.; Cooperman, C. (2007). "Twenty-Six Moves Suffice for Rubik's Cube" (PDF). Proceedings of the International Symposium on Symbolic and Algebraic Computation (ISSAC '07). ACM Press.
- Rubik's cube proof cut to 25 moves. 2008.
- Julie J. Rehmeyer. "Cracking the Cube". MathTrek. Archived from the original on 11 October 2007. Retrieved 9 August 2007.
- Tom Rokicki (2008). "Twenty-Five Moves Suffice for Rubik's Cube". arXiv:0803.3435 .
- "Rubik's Cube Algorithm Cut Again, Down to 23 Moves". . 5 June 2008. Retrieved 5 June 2008.
- Rokicki, Tom. "Twenty-Two Moves Suffice". Retrieved 20 August 2008.
- ^ Fildes, Jonathan (11 August 2010). "Rubik's Cube quest for speedy solution comes to an end". BBC News.
- Flatley, Joseph F. (9 August 2010). "Rubik's Cube solved in twenty moves, 35 years of CPU time". Engadget. Retrieved 10 August 2010.
- Davidson, Morley; Dethridge, John; Kociemba, Herbert; Rokicki, Tomas. "God's Number is 20". cube20.org. Retrieved 10 August 2010.
- Demaine, Erik D.; Demaine, Martin L.; Eisenstat, Sarah; Lubiw, Anna; Winslow, Andrew (2011). "Algorithms for Solving Rubik's Cubes". arXiv:1106.5736v1 .
- "Rubik's Cube Solution - Petrus Method". lar5.com. Retrieved 8 November 2018.
- "Introduction". Grrroux.free.fr. Retrieved 20 June 2012.
- "How to solve a Rubik's Cube". how-to-solve-a-rubix-cube.com. Retrieved 28 June 2016.
- "Beginner Solution to the Rubik's Cube (available in multiple languages)". Jasmine Lee. Retrieved 17 July 2017.
- Evans, Rob (24 September 1981). "Restore your cube". New Scientist: 802. Archived from the original on 18 August 2020.
- "Rubik's Cube". Newsweek. 99: 16. 1982.
- "Website with solutions created by Denny Dedmore". Helm.lu. Retrieved 20 June 2012.
- Marshall, Philip (2005). "The Ultimate Solution to Rubik's Cube". helm.lu. Retrieved 30 December 2022.
- "Rubik's Cube solver". rubiks-cube-solver.com. Retrieved 28 June 2016.
- ^ McWhirter, Norris, ed. (1983). "Cubism". Guinness Book of Records. Guinness Publishing. p. 85. ISBN 9780851122519.
- Hanauer, Joan (26 May 1982). "Cube Contest". United Press International.
- "World Cube Association Official Results". World Cube Association. Archived from the original on 7 June 2019. Retrieved 16 February 2008.
- "Competition Regulations, Article 9: Events". World Cube Association. 9 April 2008. Retrieved 16 April 2008.
- "Rubik's 3x3x3 Cube: Blindfolded records". WorldCubeAssociation.org. Archived from the original on 10 December 2015. Retrieved 20 June 2012.
- "WCA Regulations – World Cube Association". worldcubeassociation.org. Retrieved 5 April 2018.
- "Rubik's 3x3x3 Cube: One-handed". Worldcubeassociation.org. Archived from the original on 10 December 2015. Retrieved 20 June 2012.
- "Rankings | World Cube Association". worldcubeassociation.org.
- "WCA Live". live.worldcubeassociation.org. Retrieved 12 June 2023.
- "Xuzhou Autumn 2024 | World Cube Association". www.worldcubeassociation.org. Retrieved 25 September 2024.
- "Records | World Cube Association". www.worldcubeassociation.org. Retrieved 21 October 2024.
- "Rankings | World Cube Association". www.worldcubeassociation.org. Retrieved 21 October 2024.
- "Rankings | World Cube Association". www.worldcubeassociation.org. Retrieved 21 October 2024.
- "Rankings | World Cube Association". www.worldcubeassociation.org. Retrieved 21 October 2024.
- "World Cube Association – Official Results". worldcubeassociation.org. Archived from the original on 2 July 2018. Retrieved 28 March 2018.
- "Rankings | World Cube Association". www.worldcubeassociation.org. Retrieved 21 October 2024.
- "Rubik's robot solves puzzle in 0.38 seconds". BBC News. 8 March 2018. Retrieved 8 March 2018.
- MoYu 21x21x21 M solve - 1:35:55.52, 22 February 2022, retrieved 12 March 2023
- "List of Unofficial World Records". speedsolving.com – Wiki. Retrieved 12 March 2023.
- "Pupils break Rubik's Cube Record". BBC News. 17 March 2010. Retrieved 20 June 2012.
- "Schools Smash World Record". Depaul UK. 21 November 2012. Archived from the original on 20 January 2013. Retrieved 21 November 2012.
- "CoEP sets another record, over 3,000 solve Rubik's Cube in 30 minutes". The Indian Express. 5 November 2012. Retrieved 5 November 2012.
- "Rankings | World Cube Association". worldcubeassociation.org. Retrieved 30 December 2022.
- "US7600756B2 patent". Google Patents. Retrieved 14 April 2022.
- "You Probably Won't Live Long Enough to Solve the World's Largest 22x22 Rubik's Cube". 15 January 2016. Archived from the original on 10 February 2016. Retrieved 10 February 2016.
- ^ "World Record 33x33x33 Rubik's Cube !!!!!". 2 December 2017. Archived from the original on 11 December 2021. Retrieved 10 February 2018 – via YouTube.
- "ShengShou". TheCubicle. Retrieved 23 May 2020.
- "MoYu 21x21 Cube Stickerless → MasterCubeStore". MasterCubeStore.com.
- "Variations". Rubik's. Retrieved 30 December 2012.
- "NY Toy Fair opens with new Rubik's Cube, Lego deals". Reuters. 16 February 2009. Archived from the original on 26 November 2020. Retrieved 23 March 2009.
- "Toy Fair Kicks Off at Javits Center". Archived from the original on 22 April 2009. Retrieved 23 March 2009.
- "Largest Order Rubiks / Magic Cube". Guinness World Records. Retrieved 4 January 2013.
- van Deventer, Oskar. "Over the Top – 17x17x17".
- "World Record 2x2x50 Rubik's Cube !!! :D". 8 April 2018. Archived from the original on 11 December 2021. Retrieved 13 April 2018 – via YouTube.
- Martin, W. Eric (April 2004). "Gamebits: Rubik's Cube... Cubed". Games. Vol. 28, no. 3. p. 4.
- Green, Melinda (25 June 2009). "Magic Cube 4D". Superliminal.com. Retrieved 20 June 2012.
- "Magic Cube 5D". Gravitation3d.com. Retrieved 20 June 2012.
- Armstrong, Calvin; Goldstine, Susan (September 2014). "Review: Beyond Rubik's Cube Exhibit". The College Mathematics Journal. 45: 254–256. doi:10.4169/college.math.j.45.4.254. JSTOR 10.4169/college.math.j.45.4.254. S2CID 218549192.
- "Chrome Cube Lab". Retrieved 19 May 2014.
- "Liberty Science Center". Archived from the original on 20 June 2012. Retrieved 15 November 2012.
- Shaffrey, Ted (27 April 2012). "Cubism? Rubik helps with toy's anniversary exhibit". New York. Associated Press.
- Quenqua, Douglas (6 August 2012). "Rubik's Cube Twists Back Into Limelight". The New York Times. New York.
- ^ The Rubik's Cube Designs of Fred Holly Archived 31 August 2009 at the Wayback Machine
- ^ "Jacob Davenport » Rubik's Cube Art". www.playagaingames.com.
- Moynihan, Colin (19 November 2005). "The Cube, Restored, Is Back and Turning at Astor Place". The New York Times. Retrieved 18 March 2009.
- "All Too Flat : Pranks : Cube". Retrieved 29 May 2009.
- McKinney, Todd (7 April 2008). "Photo: Blue-bik's cube". The University Record Online. The Regents of the University of Michigan. Archived from the original on 24 February 2021. Retrieved 3 December 2010.
- "Rubikcubism". Archived from the original on 7 March 2012.
- "RUBIKCUBISM / A LOGICAL EXHIBITION OF INVADER AT SIXSPACE / LA. 2005". Archived from the original on 3 March 2012.
- "Rubik Space By Invader". Archived from the original on 13 March 2012.
- "Home". Cubeworks. Archived from the original on 3 April 2011.
- "Twoguysfromtoronto.com". www.twoguysfromtoronto.com. Archived from the original on 23 April 2021. Retrieved 27 August 2023.
- "Exhibitions". Archived from the original on 23 February 2012.
- "Dream Big « Pete Fecteau". Archived from the original on 5 March 2012.
- "You Can Do The Cube Official Site". Archived from the original on 26 January 2012. Retrieved 22 January 2012.
- Roberts, Siobhan (1 July 2024). "The Rubik's Cube Turns 50". The New York Times. Retrieved 4 July 2024.
- R.M.K. (1 November 1979). "The Magic Cube". GAMES Magazine. No. 14. p. 78.
- "GAMES Magazine #20". November 1980.
Further reading
- Bizek, Hana M. (1997). Mathematics of the Rubik's Cube Design. Pittsburgh, Pa: Dorrance Pub. Co. ISBN 0805939199.
- Frey, Alexander; Singmaster, David (1982). Handbook of Cubic Math. Enslow. ISBN 0894900587.
- Rubik, Ernő; Varga, Tamas; Keri, Gerson; Marx, Gyorgy; Vekerdy, Tamas (1987). Singmaster, David (ed.). Rubik's Cubic Compendium. Oxford University Press. ISBN 0198532024.
- Slocum, Jerry; Singmaster, David; Huang, Wei-Hwa; Gebhardt, Dieter; Hellings, Geert; Rubik, Ernő (2009). The Cube: The Ultimate Guide to the World's Bestselling Puzzle. Black Dog & Leventhal. ISBN 978-1579128050.
External links
- "Rubik's Cube". Google Doodle. Archived from the original on 19 May 2014. Retrieved 19 May 2014. (Working model)
- Complete disassembly of a 3^3 classic Rubik's cube
- How to solve a Rubik's Cube on YouTube
- List of related puzzles and solutions
- Official website
- Safecracker Method: Solving Rubik's Cube with just 10 Numbers
- Speedsolving Wiki
- World Cube Association
| Rubik's Cube | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Puzzle inventors | |||||||||||||||
| Rubik's Cubes | |||||||||||||||
| Variations of the Rubik's Cube | |||||||||||||||
| Other cubic combination puzzles | |||||||||||||||
| Non-cubic combination puzzles |
| ||||||||||||||
| Virtual combination puzzles (>3D) | |||||||||||||||
| Derivatives | |||||||||||||||
| Renowned solvers |
| ||||||||||||||
| Solutions |
| ||||||||||||||
| Mathematics | |||||||||||||||
| Official organization | |||||||||||||||
| Related articles | |||||||||||||||


