| Regular hexagon | |
|---|---|
 A regular hexagon A regular hexagon | |
| Type | Regular polygon |
| Edges and vertices | 6 |
| Schläfli symbol | {6}, t{3} |
| Coxeter–Dynkin diagrams | |
| Symmetry group | Dihedral (D6), order 2×6 |
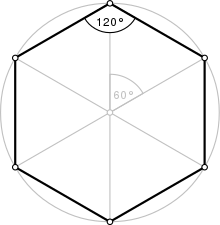
| Internal angle (degrees) | 120° |
| Properties | Convex, cyclic, equilateral, isogonal, isotoxal |
| Dual polygon | Self |
In geometry, a hexagon (from Greek ἕξ, hex, meaning "six", and γωνία, gonía, meaning "corner, angle") is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.
Regular hexagon
A regular hexagon has Schläfli symbol {6} and can also be constructed as a truncated equilateral triangle, t{3}, which alternates two types of edges.
A regular hexagon is defined as a hexagon that is both equilateral and equiangular. It is bicentric, meaning that it is both cyclic (has a circumscribed circle) and tangential (has an inscribed circle).
The common length of the sides equals the radius of the circumscribed circle or circumcircle, which equals times the apothem (radius of the inscribed circle). All internal angles are 120 degrees. A regular hexagon has six rotational symmetries (rotational symmetry of order six) and six reflection symmetries (six lines of symmetry), making up the dihedral group D6. The longest diagonals of a regular hexagon, connecting diametrically opposite vertices, are twice the length of one side. From this it can be seen that a triangle with a vertex at the center of the regular hexagon and sharing one side with the hexagon is equilateral, and that the regular hexagon can be partitioned into six equilateral triangles.
Like squares and equilateral triangles, regular hexagons fit together without any gaps to tile the plane (three hexagons meeting at every vertex), and so are useful for constructing tessellations. The cells of a beehive honeycomb are hexagonal for this reason and because the shape makes efficient use of space and building materials. The Voronoi diagram of a regular triangular lattice is the honeycomb tessellation of hexagons.
 A step-by-step animation of the construction of a regular hexagon using compass and straightedge, given by Euclid's Elements, Book IV, Proposition 15: this is possible as 6 2 × 3, a product of a power of two and distinct Fermat primes.
A step-by-step animation of the construction of a regular hexagon using compass and straightedge, given by Euclid's Elements, Book IV, Proposition 15: this is possible as 6 2 × 3, a product of a power of two and distinct Fermat primes. When the side length AB is given, drawing a circular arc from point A and point B gives the intersection M, the center of the circumscribed circle. Transfer the line segment AB four times on the circumscribed circle and connect the corner points.
When the side length AB is given, drawing a circular arc from point A and point B gives the intersection M, the center of the circumscribed circle. Transfer the line segment AB four times on the circumscribed circle and connect the corner points.
Parameters
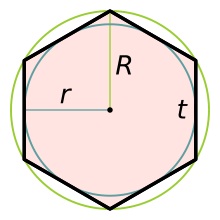
The maximal diameter (which corresponds to the long diagonal of the hexagon), D, is twice the maximal radius or circumradius, R, which equals the side length, t. The minimal diameter or the diameter of the inscribed circle (separation of parallel sides, flat-to-flat distance, short diagonal or height when resting on a flat base), d, is twice the minimal radius or inradius, r. The maxima and minima are related by the same factor:
- and, similarly,
The area of a regular hexagon
For any regular polygon, the area can also be expressed in terms of the apothem a and the perimeter p. For the regular hexagon these are given by a = r, and p, so
The regular hexagon fills the fraction of its circumscribed circle.
If a regular hexagon has successive vertices A, B, C, D, E, F and if P is any point on the circumcircle between B and C, then PE + PF = PA + PB + PC + PD.
It follows from the ratio of circumradius to inradius that the height-to-width ratio of a regular hexagon is 1:1.1547005; that is, a hexagon with a long diagonal of 1.0000000 will have a distance of 0.8660254 or cos(30°) between parallel sides.
Point in plane
For an arbitrary point in the plane of a regular hexagon with circumradius , whose distances to the centroid of the regular hexagon and its six vertices are and respectively, we have
If are the distances from the vertices of a regular hexagon to any point on its circumcircle, then
Symmetry
| Example hexagons by symmetry | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|


The regular hexagon has D6 symmetry. There are 16 subgroups. There are 8 up to isomorphism: itself (D6), 2 dihedral: (D3, D2), 4 cyclic: (Z6, Z3, Z2, Z1) and the trivial (e)
These symmetries express nine distinct symmetries of a regular hexagon. John Conway labels these by a letter and group order. r12 is full symmetry, and a1 is no symmetry. p6, an isogonal hexagon constructed by three mirrors can alternate long and short edges, and d6, an isotoxal hexagon constructed with equal edge lengths, but vertices alternating two different internal angles. These two forms are duals of each other and have half the symmetry order of the regular hexagon. The i4 forms are regular hexagons flattened or stretched along one symmetry direction. It can be seen as an elongated rhombus, while d2 and p2 can be seen as horizontally and vertically elongated kites. g2 hexagons, with opposite sides parallel are also called hexagonal parallelogons.
Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g6 subgroup has no degrees of freedom but can be seen as directed edges.
Hexagons of symmetry g2, i4, and r12, as parallelogons can tessellate the Euclidean plane by translation. Other hexagon shapes can tile the plane with different orientations.
| p6m (*632) | cmm (2*22) | p2 (2222) | p31m (3*3) | pmg (22*) | pg (××) | |
|---|---|---|---|---|---|---|
 r12 |
 i4 |
 g2 |
 d2 |
 d2 |
 p2 |
 a1 |
| Dih6 | Dih2 | Z2 | Dih1 | Z1 | ||
A2 and G2 groups
 A2 group roots |
 G2 group roots |
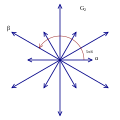
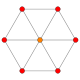
The 6 roots of the simple Lie group A2, represented by a Dynkin diagram ![]()
![]()
![]() , are in a regular hexagonal pattern. The two simple roots have a 120° angle between them.
, are in a regular hexagonal pattern. The two simple roots have a 120° angle between them.
The 12 roots of the Exceptional Lie group G2, represented by a Dynkin diagram ![]()
![]()
![]() are also in a hexagonal pattern. The two simple roots of two lengths have a 150° angle between them.
are also in a hexagonal pattern. The two simple roots of two lengths have a 150° angle between them.
Dissection
| 6-cube projection | 12 rhomb dissection | |
|---|---|---|

|

|
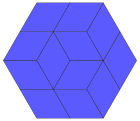
|
Coxeter states that every zonogon (a 2m-gon whose opposite sides are parallel and of equal length) can be dissected into 1⁄2m(m − 1) parallelograms. In particular this is true for regular polygons with evenly many sides, in which case the parallelograms are all rhombi. This decomposition of a regular hexagon is based on a Petrie polygon projection of a cube, with 3 of 6 square faces. Other parallelogons and projective directions of the cube are dissected within rectangular cuboids.
| Dissection of hexagons into three rhombs and parallelograms | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2D | Rhombs | Parallelograms | |||||||||

|

|

|

| ||||||||
| Regular {6} | Hexagonal parallelogons | ||||||||||
| 3D | Square faces | Rectangular faces | |||||||||

|

|

|

| ||||||||
| Cube | Rectangular cuboid | ||||||||||
Related polygons and tilings
A regular hexagon has Schläfli symbol {6}. A regular hexagon is a part of the regular hexagonal tiling, {6,3}, with three hexagonal faces around each vertex.
A regular hexagon can also be created as a truncated equilateral triangle, with Schläfli symbol t{3}. Seen with two types (colors) of edges, this form only has D3 symmetry.
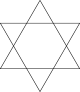
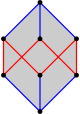
A truncated hexagon, t{6}, is a dodecagon, {12}, alternating two types (colors) of edges. An alternated hexagon, h{6}, is an equilateral triangle, {3}. A regular hexagon can be stellated with equilateral triangles on its edges, creating a hexagram. A regular hexagon can be dissected into six equilateral triangles by adding a center point. This pattern repeats within the regular triangular tiling.
A regular hexagon can be extended into a regular dodecagon by adding alternating squares and equilateral triangles around it. This pattern repeats within the rhombitrihexagonal tiling.
|

|
|

|
|
|
|
|
| Regular {6} |
Truncated t{3} = {6} |
Hypertruncated triangles | Stellated Star figure 2{3} |
Truncated t{6} = {12} |
Alternated h{6} = {3} | ||
|---|---|---|---|---|---|---|---|
|

|

|

|
|
|
|

|
| Crossed hexagon |
A concave hexagon | A self-intersecting hexagon (star polygon) | Extended Central {6} in {12} |
A skew hexagon, within cube | Dissected {6} | projection octahedron |
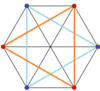
Complete graph |
|---|
Self-crossing hexagons
There are six self-crossing hexagons with the vertex arrangement of the regular hexagon:
| Dih2 | Dih1 | Dih3 | |||
|---|---|---|---|---|---|
 Figure-eight |
 Center-flip |
 Unicursal |
 Fish-tail |
 Double-tail |
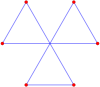 Triple-tail |
Hexagonal structures

From bees' honeycombs to the Giant's Causeway, hexagonal patterns are prevalent in nature due to their efficiency. In a hexagonal grid each line is as short as it can possibly be if a large area is to be filled with the fewest hexagons. This means that honeycombs require less wax to construct and gain much strength under compression.
Irregular hexagons with parallel opposite edges are called parallelogons and can also tile the plane by translation. In three dimensions, hexagonal prisms with parallel opposite faces are called parallelohedrons and these can tessellate 3-space by translation.
| Form | Hexagonal tiling | Hexagonal prismatic honeycomb |
|---|---|---|
| Regular | 
|

|
| Parallelogonal | 
|

|
Tesselations by hexagons
Main article: Hexagonal tilingIn addition to the regular hexagon, which determines a unique tessellation of the plane, any irregular hexagon which satisfies the Conway criterion will tile the plane.
Hexagon inscribed in a conic section
Pascal's theorem (also known as the "Hexagrammum Mysticum Theorem") states that if an arbitrary hexagon is inscribed in any conic section, and pairs of opposite sides are extended until they meet, the three intersection points will lie on a straight line, the "Pascal line" of that configuration.
Cyclic hexagon
The Lemoine hexagon is a cyclic hexagon (one inscribed in a circle) with vertices given by the six intersections of the edges of a triangle and the three lines that are parallel to the edges that pass through its symmedian point.
If the successive sides of a cyclic hexagon are a, b, c, d, e, f, then the three main diagonals intersect in a single point if and only if ace = bdf.
If, for each side of a cyclic hexagon, the adjacent sides are extended to their intersection, forming a triangle exterior to the given side, then the segments connecting the circumcenters of opposite triangles are concurrent.
If a hexagon has vertices on the circumcircle of an acute triangle at the six points (including three triangle vertices) where the extended altitudes of the triangle meet the circumcircle, then the area of the hexagon is twice the area of the triangle.
Hexagon tangential to a conic section
Let ABCDEF be a hexagon formed by six tangent lines of a conic section. Then Brianchon's theorem states that the three main diagonals AD, BE, and CF intersect at a single point.
In a hexagon that is tangential to a circle and that has consecutive sides a, b, c, d, e, and f,
Equilateral triangles on the sides of an arbitrary hexagon

If an equilateral triangle is constructed externally on each side of any hexagon, then the midpoints of the segments connecting the centroids of opposite triangles form another equilateral triangle.
Skew hexagon

A skew hexagon is a skew polygon with six vertices and edges but not existing on the same plane. The interior of such a hexagon is not generally defined. A skew zig-zag hexagon has vertices alternating between two parallel planes.
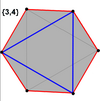
A regular skew hexagon is vertex-transitive with equal edge lengths. In three dimensions it will be a zig-zag skew hexagon and can be seen in the vertices and side edges of a triangular antiprism with the same D3d, symmetry, order 12.
The cube and octahedron (same as triangular antiprism) have regular skew hexagons as petrie polygons.
 Cube |
 Octahedron |
Petrie polygons
The regular skew hexagon is the Petrie polygon for these higher dimensional regular, uniform and dual polyhedra and polytopes, shown in these skew orthogonal projections:
| 4D | 5D | |
|---|---|---|
 3-3 duoprism |
 3-3 duopyramid |
 5-simplex |
Convex equilateral hexagon
A principal diagonal of a hexagon is a diagonal which divides the hexagon into quadrilaterals. In any convex equilateral hexagon (one with all sides equal) with common side a, there exists a principal diagonal d1 such that
and a principal diagonal d2 such that
Polyhedra with hexagons
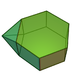
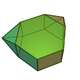
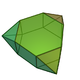
There is no Platonic solid made of only regular hexagons, because the hexagons tessellate, not allowing the result to "fold up". The Archimedean solids with some hexagonal faces are the truncated tetrahedron, truncated octahedron, truncated icosahedron (of soccer ball and fullerene fame), truncated cuboctahedron and the truncated icosidodecahedron. These hexagons can be considered truncated triangles, with Coxeter diagrams of the form ![]()
![]()
![]()
![]()
![]() and
and ![]()
![]()
![]()
![]()
![]() .
.
| Hexagons in Archimedean solids | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Tetrahedral | Octahedral | Icosahedral | |||||||||
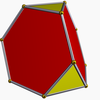 truncated tetrahedron |
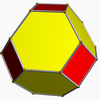 truncated octahedron |
 truncated cuboctahedron |
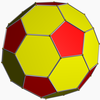 truncated icosahedron |
 truncated icosidodecahedron | |||||||
There are other symmetry polyhedra with stretched or flattened hexagons, like these Goldberg polyhedron G(2,0):
| Hexagons in Goldberg polyhedra | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Tetrahedral | Octahedral | Icosahedral | |||||||||
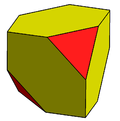 Chamfered tetrahedron |
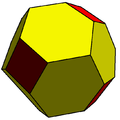 Chamfered cube |
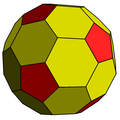 Chamfered dodecahedron | |||||||||
There are also 9 Johnson solids with regular hexagons:
| Prismoids with hexagons | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 Hexagonal prism |
 Hexagonal antiprism |
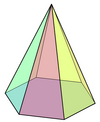 Hexagonal pyramid | |||||||||
| Tilings with regular hexagons | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Regular | 1-uniform | ||||||||||
| {6,3} |
r{6,3} |
rr{6,3} |
tr{6,3} | ||||||||

|

|

|

| ||||||||
| 2-uniform tilings | |||||||||||

|

|

|

| ||||||||
Hexagon versus Sexagon
The debate over whether hexagons should be referred to as "sexagons" has its roots in the etymology of the term. The prefix "hex-" originates from the Greek word "hex," meaning six, while "sex-" comes from the Latin "sex," also signifying six. Some linguists and mathematicians argue that since many English mathematical terms derive from Latin, the use of "sexagon" would align with this tradition. Historical discussions date back to the 19th century, when mathematicians began to standardize terminology in geometry. However, the term "hexagon" has prevailed in common usage and academic literature, solidifying its place in mathematical terminology despite the historical argument for "sexagon." The consensus remains that "hexagon" is the appropriate term, reflecting its Greek origins and established usage in mathematics. (see Numeral_prefix#Occurrences).
Gallery of natural and artificial hexagons
-
 The ideal crystalline structure of graphene is a hexagonal grid.
The ideal crystalline structure of graphene is a hexagonal grid.
-
 Assembled E-ELT mirror segments
Assembled E-ELT mirror segments
-
 A beehive honeycomb
A beehive honeycomb
-
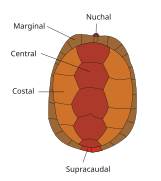 The scutes of a turtle's carapace
The scutes of a turtle's carapace
-
 Saturn's hexagon, a hexagonal cloud pattern around the north pole of the planet
Saturn's hexagon, a hexagonal cloud pattern around the north pole of the planet
-
 Micrograph of a snowflake
Micrograph of a snowflake
-
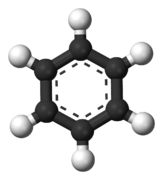 Benzene, the simplest aromatic compound with hexagonal shape.
Benzene, the simplest aromatic compound with hexagonal shape.
-
 Hexagonal order of bubbles in a foam.
Hexagonal order of bubbles in a foam.
-
 Crystal structure of a molecular hexagon composed of hexagonal aromatic rings.
Crystal structure of a molecular hexagon composed of hexagonal aromatic rings.
-
 Naturally formed basalt columns from Giant's Causeway in Northern Ireland; large masses must cool slowly to form a polygonal fracture pattern
Naturally formed basalt columns from Giant's Causeway in Northern Ireland; large masses must cool slowly to form a polygonal fracture pattern
-
 An aerial view of Fort Jefferson in Dry Tortugas National Park
An aerial view of Fort Jefferson in Dry Tortugas National Park
-
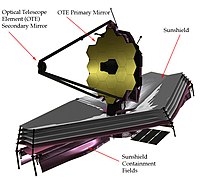 The James Webb Space Telescope mirror is composed of 18 hexagonal segments.
The James Webb Space Telescope mirror is composed of 18 hexagonal segments.
-
 In French, l'Hexagone refers to Metropolitan France for its vaguely hexagonal shape.
In French, l'Hexagone refers to Metropolitan France for its vaguely hexagonal shape.
-
Hexagonal Hanksite crystal, one of many hexagonal crystal system minerals
-
 Hexagonal barn
Hexagonal barn
-
 The Hexagon, a hexagonal theatre in Reading, Berkshire
The Hexagon, a hexagonal theatre in Reading, Berkshire
-
 Władysław Gliński's hexagonal chess
Władysław Gliński's hexagonal chess
-
 Pavilion in the Taiwan Botanical Gardens
Pavilion in the Taiwan Botanical Gardens
-
 Hexagonal window
Hexagonal window
See also
- 24-cell: a four-dimensional figure which, like the hexagon, has orthoplex facets, is self-dual and tessellates Euclidean space
- Hexagonal crystal system
- Hexagonal number
- Hexagonal tiling: a regular tiling of hexagons in a plane
- Hexagram: six-sided star within a regular hexagon
- Unicursal hexagram: single path, six-sided star, within a hexagon
- Honeycomb conjecture
- Havannah: abstract board game played on a six-sided hexagonal grid
- Central place theory
References
- Cube picture
- Wenninger, Magnus J. (1974), Polyhedron Models, Cambridge University Press, p. 9, ISBN 9780521098595, archived from the original on 2016-01-02, retrieved 2015-11-06.
- ^ Meskhishvili, Mamuka (2020). "Cyclic Averages of Regular Polygons and Platonic Solids". Communications in Mathematics and Applications. 11: 335–355. arXiv:2010.12340. doi:10.26713/cma.v11i3.1420 (inactive 1 November 2024).
{{cite journal}}: CS1 maint: DOI inactive as of November 2024 (link) - John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275–278)
- Coxeter, Mathematical recreations and Essays, Thirteenth edition, p.141
- Cartensen, Jens, "About hexagons", Mathematical Spectrum 33(2) (2000–2001), 37–40.
- Dergiades, Nikolaos (2014). "Dao's theorem on six circumcenters associated with a cyclic hexagon". Forum Geometricorum. 14: 243–246. Archived from the original on 2014-12-05. Retrieved 2014-11-17.
- Johnson, Roger A., Advanced Euclidean Geometry, Dover Publications, 2007 (orig. 1960).
- Gutierrez, Antonio, "Hexagon, Inscribed Circle, Tangent, Semiperimeter", Archived 2012-05-11 at the Wayback Machine, Accessed 2012-04-17.
- Dao Thanh Oai (2015). "Equilateral triangles and Kiepert perspectors in complex numbers". Forum Geometricorum. 15: 105–114. Archived from the original on 2015-07-05. Retrieved 2015-04-12.
- Inequalities proposed in "Crux Mathematicorum", Archived 2017-08-30 at the Wayback Machine.
External links
- Definition and properties of a hexagon with interactive animation and construction with compass and straightedge.
- An Introduction to Hexagonal Geometry on Hexnet a website devoted to hexagon mathematics.
- Hexagons are the Bestagons on YouTube – an animated internet video about hexagons by CGP Grey.
| Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform polychoron | Pentachoron | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||
| Polygons (List) | |||||||
|---|---|---|---|---|---|---|---|
| Triangles | |||||||
| Quadrilaterals | |||||||
| By number of sides |
| ||||||
| Star polygons | |||||||
| Classes | |||||||
 times the
times the  2 × 3, a product of a power of two and distinct
2 × 3, a product of a power of two and distinct  and, similarly,
and, similarly, 

 , so
, so

 of its
of its  , whose distances to the centroid of the regular hexagon and its six vertices are
, whose distances to the centroid of the regular hexagon and its six vertices are  and
and  respectively, we have
respectively, we have