| Revision as of 18:53, 9 October 2008 view sourceAlexTiefling (talk | contribs)Extended confirmed users6,225 editsm Undid revision 244187763 by 84.193.242.8 (talk) There's no such thing as 'pi exactly' as a finite string of digits.← Previous edit | Latest revision as of 18:04, 6 January 2025 view source D.Lazard (talk | contribs)Extended confirmed users33,839 edits It is not the diameter that is "approximately equal" | ||
| Line 1: | Line 1: | ||
| {{Short description|Number, approximately 3.14}} | |||
| {{pp-semi|small=yes}} | |||
| {{ |
{{About|the mathematical constant|the Greek letter|Pi (letter)|other uses|Pi (disambiguation)|and|PI (disambiguation){{!}}PI}} | ||
| {{Pp|small=yes}} | |||
| <!-- | |||
| {{Featured article}} | |||
| {{Use Oxford spelling|date=July 2020}} | |||
| {{Use dmy dates|date=July 2020|cs1-dates=l}} | |||
| {{Pi box}} | |||
| The number '''{{pi}}''' ({{IPAc-en|p|aɪ}}; spelled out as "'''pi'''") is a ], approximately equal to 3.14159, that is the ] of a ]'s ] to its ]. It appears in many formulae across ] and ], and some of these formulae are commonly used for defining {{pi}}, to avoid relying on the definition of the ]. | |||
| The number {{pi}} is an ], meaning that it cannot be expressed exactly as a ratio of two integers, although fractions such as <math>\tfrac{22}{7}</math> are commonly ]. Consequently, its ] never ends, nor ]. It is a ], meaning that it cannot be a solution of an ] involving only finite sums, products, powers, and integers. The transcendence of {{pi}} implies that it is impossible to solve the ancient challenge of ] with a ]. The decimal digits of {{pi}} appear to be ],{{efn|In particular, {{pi}} is conjectured to be a ], which implies a specific kind of statistical randomness on its digits in all bases.}} but no proof of this ] has been found. | |||
| IMPORTANT NOTICE: Please note that Misplaced Pages is not a database to store the millions of digits of π; please refrain from adding those to Misplaced Pages, as it could cause technical problems (and it makes the page unreadable, or at least unattractive, in the opinion of most readers). Instead, you could add links in the "External links" section, to other web sites containing information regarding digits of π. | |||
| For thousands of years, mathematicians have attempted to extend their understanding of {{pi}}, sometimes by computing its value to a high degree of accuracy. Ancient civilizations, including the ] and ], required fairly accurate approximations of {{pi}} for practical computations. Around 250{{Nbsp}}BC, the ] ] created an algorithm to approximate {{pi}} with arbitrary accuracy. In the 5th century AD, ] approximated {{pi}} to seven digits, while ] made a five-digit approximation, both using geometrical techniques. The first computational formula for {{pi}}, based on ], was discovered a millennium later.{{sfn|Andrews|Askey|Roy|1999|p=59}}<ref>{{Cite journal |first=R. C. |last=Gupta |title=On the remainder term in the Madhava–Leibniz's series |journal=Ganita Bharati |volume=14 |issue=1–4 |year=1992 |pages=68–71}} | |||
| This has been established by a very clear consensus and any editor adding lists of digits of pi is liable to be blocked from editing without further warning. | |||
| </ref> The earliest known use of the Greek letter ] to represent the ratio of a circle's circumference to its diameter was by the Welsh mathematician ] in 1706.<ref name=jones>{{cite book |last=Jones |first=William |author-link=William Jones (mathematician) |year=1706 |title=Synopsis Palmariorum Matheseos |place=London |publisher=J. Wale |url=https://archive.org/details/SynopsisPalmariorumMatheseosOrANewIntroductionToTheMathematics/page/n283/ |pages=, |quote-page=263 |quote=There are various other ways of finding the ''Lengths'', or ''Areas'' of particular ''Curve Lines'' or ''Planes'', which may very much facilitate the Practice; as for instance, in the ''Circle'', the Diameter is to Circumference as 1 to {{br}}<math> | |||
| \overline{\tfrac{16}5 - \tfrac4{239}} | |||
| - \tfrac13\overline{\tfrac{16}{5^3} - \tfrac4{239^3}} | |||
| + \tfrac15\overline{\tfrac{16}{5^5} - \tfrac4{239^5}} | |||
| -,\, \&c. =</math>{{br}}{{math|1=3.14159, &''c.'' = ''π''}}. This ''Series'' (among others for the same purpose, and drawn from the same Principle) I receiv'd from the Excellent Analyst, and my much Esteem'd Friend Mr. '']''; and by means thereof, '']''{{'}}s Number, or that in Art. 64.38. may be Examin'd with all desireable Ease and Dispatch. | |||
| }} | |||
| <p>Reprinted in {{cite book |last=Smith |first=David Eugene |year=1929 |title=A Source Book in Mathematics |publisher=McGraw–Hill |chapter=William Jones: The First Use of {{mvar|π}} for the Circle Ratio |chapter-url=https://archive.org/details/sourcebookinmath1929smit/page/346/ |pages=346–347 }}</p></ref> The invention of ] soon led to the calculation of hundreds of digits of {{pi}}, enough for all practical scientific computations. Nevertheless, in the 20th and 21st centuries, mathematicians and ] have pursued new approaches that, when combined with increasing computational power, extended the decimal representation of {{pi}} to many trillions of digits.<ref>{{cite web |url=http://www.pi2e.ch/ |title=π<sup>e</sup> trillion digits of π |archive-url=https://web.archive.org/web/20161206063441/http://www.pi2e.ch/ |website=pi2e.ch |archive-date=6 December 2016 |url-status=live}} <!-- – the exact number of digits increases periodically – it should not be included in this article by citing only a ]. --></ref><ref>{{Cite web |last=Haruka Iwao |first=Emma |author-link=Emma Haruka Iwao |url=https://cloud.google.com/blog/products/compute/calculating-31-4-trillion-digits-of-archimedes-constant-on-google-cloud |title=Pi in the sky: Calculating a record-breaking 31.4 trillion digits of Archimedes' constant on Google Cloud |website=] |date=14 March 2019 |access-date=12 April 2019 |archive-url=https://web.archive.org/web/20191019023120/https://cloud.google.com/blog/products/compute/calculating-31-4-trillion-digits-of-archimedes-constant-on-google-cloud |archive-date=19 October 2019 |url-status=live}}</ref> These computations are motivated by the development of efficient algorithms to calculate numeric series, as well as the human quest to break records.{{sfn|Arndt|Haenel|2006|p=17}}<ref>{{cite journal |last1=Bailey |first1=David H. |last2=Plouffe |first2=Simon M. |last3=Borwein |first3=Peter B. |last4=Borwein |first4=Jonathan M. |title=The quest for PI |journal=] |volume=19 |issue=1 |year=1997 |pages=50–56 |issn=0343-6993 |doi=10.1007/BF03024340 |citeseerx=10.1.1.138.7085|s2cid=14318695 }}</ref> The extensive computations involved have also been used to test ]s as well as stress testing consumer computer hardware. | |||
| Because it relates to a circle, {{pi}} is found in many formulae in ] and ], especially those concerning circles, ellipses and spheres. It is also found in formulae from other topics in science, such as ], ]s, ], ], and ]. It also appears in areas having little to do with geometry, such as ] and ], and in modern ] can be defined without any reference to geometry. The ubiquity of {{pi}} makes it one of the most widely known mathematical constants inside and outside of science. Several books devoted to {{pi}} have been published, and record-setting calculations of the digits of {{pi}} often result in news headlines. | |||
| --> | |||
| ] | |||
| {{TOC limit|limit=3}} | |||
| {| class="infobox" style ="width: 370px;" | |||
| | colspan="2" align="center" | ] – ]s <br> ] – ] – ] – ] – ] – ] – ] – ] – ] | |||
| == Fundamentals == | |||
| |- | |||
| |] | |||
| === Name === | |||
| | 11.00100100001111110110… | |||
| The symbol used by mathematicians to represent the ratio of a circle's circumference to its diameter is the lowercase ], sometimes spelled out as ''pi.''<ref name=firstPi/> In English, {{pi}} is ] ({{IPAc-en|p|aɪ}} {{respell|PY}}).<ref>{{cite web |url=http://dictionary.reference.com/browse/pi?s=t |title=pi |publisher=Dictionary.reference.com |date=2 March 1993 |access-date=18 June 2012|url-status=live |archive-url=https://web.archive.org/web/20140728121603/http://dictionary.reference.com/browse/pi?s=t |archive-date=28 July 2014}}</ref> In mathematical use, the lowercase letter {{pi}} is distinguished from its capitalized and enlarged counterpart {{math|Π}}, which denotes a ], analogous to how {{math|Σ}} denotes ]. | |||
| The choice of the symbol {{pi}} is discussed in the section ]. | |||
| === Definition === | |||
| ] | |||
| {{pi}} is commonly defined as the ] of a ]'s ] {{math|''C''}} to its ] {{math|''d''}}:{{sfn|Arndt|Haenel|2006|p=8}} | |||
| <math display="block"> \pi = \frac{C}{d}</math> | |||
| The ratio <math display="inline">\frac{C}{d}</math> is constant, regardless of the circle's size. For example, if a circle has twice the diameter of another circle, it will also have twice the circumference, preserving the ratio <math display="inline">\frac{C}{d}</math>. This definition of {{pi}} implicitly makes use of ]; although the notion of a circle can be extended to any ], these new circles will no longer satisfy the formula <math display="inline">\pi=\frac{C}{d}</math>.{{sfn|Arndt|Haenel|2006|p=8}} | |||
| Here, the circumference of a circle is the ] around the ] of the circle, a quantity which can be formally defined independently of geometry using ]—a concept in ].<ref>{{cite book |first=Tom |last=Apostol |author-link=Tom M. Apostol |title=Calculus|volume=1 |publisher=Wiley |edition=2nd |year=1967|page= 102|quote=From a logical point of view, this is unsatisfactory at the present stage because we have not yet discussed the concept of arc length}}</ref> For example, one may directly compute the arc length of the top half of the unit circle, given in ] by the equation <math display="inline">x^2+y^2=1</math>, as the ]:{{sfn|Remmert|2012|p=129}} | |||
| <math display=block>\pi = \int_{-1}^1 \frac{dx}{\sqrt{1-x^2}}.</math> | |||
| An integral such as this was proposed as a definition of {{pi}} by ], who defined it directly as an integral in 1841.{{efn|The specific integral that Weierstrass used was<ref>{{harvnb|Remmert|2012|p=148}}. {{pb}} {{cite book |last=Weierstrass |first=Karl |author-link=Karl Weierstrass |chapter=Darstellung einer analytischen Function einer complexen Veränderlichen, deren absoluter Betrag zwischen zwei gegebenen Grenzen liegt |trans-chapter=Representation of an analytical function of a complex variable, whose absolute value lies between two given limits |language=de |title=Mathematische Werke |volume=1 |publication-place=Berlin |publisher=Mayer & Müller |year=1841 |publication-date=1894 |pages=51–66 |chapter-url=https://archive.org/details/mathematischewer01weieuoft/page/51/ }} </ref> <math display=block>\pi=\int_{-\infty}^\infty\frac{dx}{1+x^2}.</math>}} | |||
| Integration is no longer commonly used in a first analytical definition because, as {{harvnb|Remmert|2012}} explains, ] typically precedes integral calculus in the university curriculum, so it is desirable to have a definition of {{pi}} that does not rely on the latter. One such definition, due to Richard Baltzer<ref>{{cite book |first=Richard |last=Baltzer |title=Die Elemente der Mathematik |language=de |trans-title=The Elements of Mathematics |year=1870 |page=195 |url=https://archive.org/details/dieelementederm02baltgoog |publisher=Hirzel |url-status=live |archive-url=https://web.archive.org/web/20160914204826/https://archive.org/details/dieelementederm02baltgoog |archive-date=14 September 2016}}</ref> and popularized by ],<ref>{{cite book |first=Edmund |last=Landau |author-link=Edmund Landau |title=Einführung in die Differentialrechnung und Integralrechnung |language=de |publisher=Noordoff |year=1934 |page=193}}</ref> is the following: {{pi}} is twice the smallest positive number at which the ] function equals 0.{{sfn|Arndt|Haenel|2006|p=8}}{{sfn|Remmert|2012|p=129}}<ref name="Rudin 1976">{{cite book |last=Rudin |first=Walter |title=Principles of Mathematical Analysis |url=https://archive.org/details/principlesofmath00rudi|url-access=registration |publisher=McGraw-Hill |year=1976 |isbn=978-0-07-054235-8|page=183}}</ref> {{pi}} is also the smallest positive number at which the ] function equals zero, and the difference between consecutive zeroes of the sine function. The cosine and sine can be defined independently of geometry as a ],<ref>{{cite book |last=Rudin |first=Walter |title=Real and complex analysis |publisher=McGraw-Hill |year=1986|page= 2}}</ref> or as the solution of a ].<ref name="Rudin 1976" /> | |||
| In a similar spirit, {{pi}} can be defined using properties of the ], {{math|exp ''z''}}, of a ] variable {{math|''z''}}. Like the cosine, the complex exponential can be defined in one of several ways. The set of complex numbers at which {{math|exp ''z''}} is equal to one is then an (imaginary) arithmetic progression of the form: | |||
| <math display=block>\{\dots,-2\pi i, 0, 2\pi i, 4\pi i,\dots\} = \{2\pi ki\mid k\in\mathbb Z\}</math> | |||
| and there is a unique positive real number {{pi}} with this property.{{sfn|Remmert|2012|p=129}}<ref>{{cite book |first=Lars |last=Ahlfors |author-link=Lars Ahlfors |title=Complex analysis |publisher=McGraw-Hill |year=1966 |page=46}}</ref> | |||
| A variation on the same idea, making use of sophisticated mathematical concepts of ] and ], is the following theorem:<ref>{{cite book |last=Bourbaki |first=Nicolas |author-link=Nicolas Bourbaki |title=Topologie generale |publisher=Springer |year=1981|at=§VIII.2}}</ref> there is a unique (] ]) ] ] from the ] '''R'''/'''Z''' of real numbers under addition ] integers (the ]), onto the multiplicative group of ] of ] one. The number {{pi}} is then defined as half the magnitude of the derivative of this homomorphism.<ref name="Nicolas Bourbaki">{{cite book |last=Bourbaki |first=Nicolas |author-link=Nicolas Bourbaki |title=Fonctions d'une variable réelle |language=fr |publisher=Springer |year=1979|at= §II.3}}</ref> | |||
| === Irrationality and normality === | |||
| {{pi}} is an ], meaning that it cannot be written as the ]. Fractions such as {{math|{{sfrac|22|7}}}} and {{math|{{sfrac|355|113}}}} are commonly used to approximate {{pi}}, but no ] (ratio of whole numbers) can be its exact value.{{sfn|Arndt|Haenel|2006|p=5}} Because {{pi}} is irrational, it has an infinite number of digits in its ], and does not settle into an infinitely ] of digits. There are several ]; they generally require calculus and rely on the '']'' technique. The degree to which {{pi}} can be approximated by ]s (called the ]) is not precisely known; estimates have established that the irrationality measure is larger or at least equal to the measure of {{math|''e''}} but smaller than the measure of ]s.<ref>{{cite journal |last1=Salikhov |first1=V. |year=2008 |title=On the Irrationality Measure of pi |journal=Russian Mathematical Surveys |volume=53 |issue=3 |pages=570–572 |doi=10.1070/RM2008v063n03ABEH004543 |bibcode=2008RuMaS..63..570S|s2cid=250798202 | issn = 0036-0279 }}</ref> | |||
| The digits of {{pi}} have no apparent pattern and have passed tests for ], including tests for ]; a number of infinite length is called normal when all possible sequences of digits (of any given length) appear equally often. The conjecture that {{pi}} is ] has not been proven or disproven.{{sfn|Arndt|Haenel|2006|pp=22–23}} | |||
| Since the advent of computers, a large number of digits of {{pi}} have been available on which to perform statistical analysis. ] has performed detailed statistical analyses on the decimal digits of {{pi}}, and found them consistent with normality; for example, the frequencies of the ten digits 0 to 9 were subjected to ]s, and no evidence of a pattern was found.{{sfn|Arndt|Haenel|2006|pp=22, 28–30}} Any random sequence of digits contains arbitrarily long subsequences that appear non-random, by the ]. Thus, because the sequence of {{pi}}'s digits passes statistical tests for randomness, it contains some sequences of digits that may appear non-random, such as a ] that begins at the 762nd decimal place of the decimal representation of {{pi}}.{{sfn|Arndt|Haenel|2006|p=3}} This is also called the "Feynman point" in ], after ], although no connection to Feynman is known. | |||
| === Transcendence === | |||
| {{See also|Lindemann–Weierstrass theorem}}], ] is not possible in a finite number of steps using the classical tools of ].|left]] | |||
| In addition to being irrational, {{pi}} is also a ], which means that it is not the ] of any non-constant ] with ] coefficients, such as <math display="inline">\frac{x^5}{120}-\frac{x^3}{6}+x=0</math>.{{sfn|Arndt|Haenel|2006|p=6}}{{efn|The polynomial shown is the first few terms of the ] expansion of the ] function.}} This follows from the so-called ], which also establishes the transcendence of ]. | |||
| The transcendence of {{pi}} has two important consequences: First, {{pi}} cannot be expressed using any finite combination of rational numbers and square roots or ] (such as <math>\sqrt{31}</math> or <math>\sqrt{10}</math>). Second, since no transcendental number can be ] with ], it is not possible to "]". In other words, it is impossible to construct, using compass and straightedge alone, a square whose area is exactly equal to the area of a given circle.<ref>{{harvnb|Posamentier|Lehmann|2004|p=25}}</ref> Squaring a circle was one of the important geometry problems of the ].<ref>{{harvnb|Eymard|Lafon|2004|p=129}}</ref> Amateur mathematicians in modern times have sometimes attempted to square the circle and claim success—despite the fact that it is mathematically impossible.<ref>{{cite book |last=Beckmann |first=Peter |title=History of Pi |publisher=St. Martin's Press |year=1989 |orig-year=1974 |isbn=978-0-88029-418-8 |page=37}}</ref><ref>{{cite book |last1=Schlager |first1=Neil |last2=Lauer |first2=Josh |title=Science and Its Times: Understanding the Social Significance of Scientific Discovery |publisher=Gale Group |year=2001 |isbn=978-0-7876-3933-4|url-access=registration |url=https://archive.org/details/scienceitstimesu0000unse|access-date=19 December 2019|archive-url=https://web.archive.org/web/20191213112426/https://archive.org/details/scienceitstimesu0000unse|archive-date=13 December 2019|url-status=live}}, p. 185.</ref> | |||
| An ] thus far is the question of whether or not the numbers ''{{mvar|π}}'' and ''{{mvar|e}}'' are ] ("relatively transcendental"). This would be resolved by ]<ref>{{Cite book |last1=Murty |first1=M. Ram |url=https://link.springer.com/book/10.1007/978-1-4939-0832-5 |title=Transcendental Numbers |last2=Rath |first2=Purusottam |date=2014 |publisher=Springer |language=en |doi=10.1007/978-1-4939-0832-5|isbn=978-1-4939-0831-8 }}</ref><ref>{{Cite web |last=Waldschmidt |first=Michel |date=2021 |title=Schanuel's Conjecture: algebraic independence of transcendental numbers |url=https://webusers.imj-prg.fr/~michel.waldschmidt/articles/pdf/SchanuelEn.pdf}}</ref> – a currently unproven generalization of the Lindemann–Weierstrass theorem.<ref>{{Cite web |last=Weisstein |first=Eric W. |title=Lindemann-Weierstrass Theorem |url=https://mathworld.wolfram.com/Lindemann-WeierstrassTheorem.html |access-date=2024-10-26 |website=mathworld.wolfram.com |language=en}}</ref> | |||
| === Continued fractions === | |||
| As an irrational number, {{pi}} cannot be represented as a ]. But every number, including {{pi}}, can be represented by an infinite<!--rationals have infinitely many 0's in the CF representation--> series of nested fractions, called a ]: | |||
| <math display=block> | |||
| \pi = 3+\textstyle \cfrac{1}{7+\textstyle \cfrac{1}{15+\textstyle \cfrac{1}{1+\textstyle \cfrac{1}{292+\textstyle \cfrac{1}{1+\textstyle \cfrac{1}{1+\textstyle \cfrac{1}{1+\ddots}}}}}}} | |||
| </math> | |||
| Truncating the continued fraction at any point yields a rational approximation for {{pi}}; the first four of these are {{math|3}}, {{math|{{sfrac|22|7}}}}, {{math|{{sfrac|333|106}}}}, and {{math|{{sfrac|355|113}}}}. These numbers are among the best-known and most widely used historical approximations of the constant. Each approximation generated in this way is a best rational approximation; that is, each is closer to {{pi}} than any other fraction with the same or a smaller denominator.<ref name="Eymard 1999 78">{{harvnb|Eymard|Lafon|2004|p=78}}</ref> Because {{pi}} is transcendental, it is by definition not ] and so cannot be a ]. Therefore, {{pi}} cannot have a ]. Although the simple continued fraction for {{pi}} (with numerators all 1, shown above) also does not exhibit any other obvious pattern,{{sfn|Arndt|Haenel|2006|p=33}}<ref name=mollin>{{cite journal|last=Mollin|first=R. A.|issue=3|journal=Nieuw Archief voor Wiskunde|mr=1743850|pages=383–405|title=Continued fraction gems|volume=17|year=1999}}</ref> several non-simple ]s do, such as:<ref>{{cite journal |title=An Elegant Continued Fraction for {{pi}}|first=L.J.|last=Lange|journal=]|volume=106|issue=5| date=May 1999 |pages=456–458|jstor=2589152|doi=10.2307/2589152}}</ref> | |||
| <math display=block> | |||
| \begin{align} | |||
| \pi &= 3+ \cfrac | |||
| {1^2}{6+ \cfrac | |||
| {3^2}{6+ \cfrac | |||
| {5^2}{6+ \cfrac | |||
| {7^2}{6+ \ddots}}}} | |||
| = \cfrac | |||
| {4}{1+ \cfrac | |||
| {1^2}{2+ \cfrac | |||
| {3^2}{2+ \cfrac | |||
| {5^2}{2+ \ddots}}}} | |||
| = \cfrac | |||
| {4}{1+ \cfrac | |||
| {1^2}{3+ \cfrac | |||
| {2^2}{5+ \cfrac | |||
| {3^2}{7+ \ddots}}}} | |||
| \end{align} | |||
| </math> | |||
| The middle of these is due to the mid-17th century mathematician ], see ]. | |||
| === Approximate value and digits === | |||
| Some ] include: | |||
| * '''Integers''': 3 | |||
| * '''Fractions''': Approximate fractions include (in order of increasing accuracy) {{sfrac|22|7}}, {{sfrac|333|106}}, {{sfrac|355|113}}, {{sfrac|52163|16604}}, {{sfrac|103993|33102}}, {{sfrac|104348|33215}}, and {{sfrac|245850922|78256779}}.<ref name="Eymard 1999 78" /> (List is selected terms from {{OEIS2C|id=A063674}} and {{OEIS2C|id=A063673}}.) | |||
| * '''Digits''': The first 50 decimal digits are {{gaps|3.14159|26535|89793|23846|26433|83279|50288|41971|69399|37510...}}{{sfn|Arndt|Haenel|2006|p=240}} (see {{OEIS2C|id=A000796}}) | |||
| '''Digits in other number systems''' | |||
| * The first 48 ] (] 2) digits (called ]s) are {{gaps|11.0010|0100|0011|1111|0110|1010|1000|1000|1000|0101|1010|0011...}} (see {{OEIS2C|id=A004601}}) | |||
| * The first 36 digits in ] (base 3) are {{gaps|10.010|211|012|222|010|211|002|111|110|221|222|220...}} (see {{OEIS2C|id=A004602}}) | |||
| * The first 20 digits in ] (base 16) are {{gaps|3.243F|6A88|85A3|08D3|1319...}}{{sfn|Arndt|Haenel|2006|p=242}} (see {{OEIS2C|id=A062964}}) | |||
| * The first five ] (base 60) digits are 3;8,29,44,0,47<ref>{{cite journal |title=Abu-r-Raihan al-Biruni, 973–1048 |last=Kennedy |first=E.S. |journal=Journal for the History of Astronomy |volume=9 |page=65 |bibcode=1978JHA.....9...65K |doi=10.1177/002182867800900106 |year=1978|s2cid=126383231 }} ] used a three-sexagesimal-digit approximation, and ] expanded this to nine digits; see {{cite book |last=Aaboe |first=Asger |author-link=Asger Aaboe |year=1964 |title=Episodes from the Early History of Mathematics |series=New Mathematical Library |volume=13 |publisher=Random House |location=New York |page=125 |url=https://books.google.com/books?id=5wGzF0wPFYgC&pg=PA125 |url-status=live |archive-url=https://web.archive.org/web/20161129205051/https://books.google.com/books?id=5wGzF0wPFYgC&pg=PA125 |archive-date=29 November 2016 |df=dmy-all |isbn=978-0-88385-613-0}}</ref> (see {{OEIS2C|id=A060707}}) | |||
| === Complex numbers and Euler's identity === | |||
| ] on the ] centred at the ] in the ] given by ]]] | |||
| Any ], say {{Mvar|z}}, can be expressed using a pair of ]s. In the ], one number (] or {{Mvar|r}}) is used to represent {{Mvar|z}}'s distance from the ] of the ], and the other (angle or {{Mvar|φ}}) the counter-clockwise ] from the positive real line:{{sfn|Abramson|2014|loc=}} | |||
| <math display=block>z = r\cdot(\cos\varphi + i\sin\varphi),</math> | |||
| where {{Mvar|i}} is the ] satisfying <math>i^2=-1</math>. The frequent appearance of {{pi}} in ] can be related to the behaviour of the ] of a complex variable, described by ]:<ref name="EF">{{harvnb|Bronshteĭn|Semendiaev|1971|p=592}}</ref> | |||
| <math display=block>e^{i\varphi} = \cos \varphi + i\sin \varphi,</math> | |||
| where ] is the base of the ]. This formula establishes a correspondence between imaginary powers of {{math|''e''}} and points on the ] centred at the origin of the complex plane. Setting <math>\varphi=\pi</math> in Euler's formula results in ], celebrated in mathematics due to it containing five important mathematical constants:<ref name="EF" /><ref>{{cite book|last=Maor|first=Eli|title=E: The Story of a Number|publisher=Princeton University Press|year=2009|page=160|isbn=978-0-691-14134-3}}</ref> | |||
| <math display=block>e^{i \pi} + 1 = 0.</math> | |||
| There are {{math|''n''}} different ]s {{Mvar|z}} satisfying <math>z^n=1</math>, and these are called the "{{math|''n''}}-th ]"{{sfn|Andrews|Askey|Roy|1999|p=14}} and are given by the formula: | |||
| <math display=block>e^{2 \pi i k/n} \qquad (k = 0, 1, 2, \dots, n - 1).</math> | |||
| == History == | |||
| <!-- ] links here --> | |||
| {{Main|Approximations of π{{!}}Approximations of {{pi}}}} | |||
| {{See also|Chronology of computation of π|l1=Chronology of computation of {{pi}}}} | |||
| === Antiquity === | |||
| The best-known approximations to {{pi}} dating ] were accurate to two decimal places; this was improved upon in ] in particular by the mid-first millennium, to an accuracy of seven decimal places. | |||
| After this, no further progress was made until the late medieval period. | |||
| The earliest written approximations of {{pi}} are found in ] and Egypt, both within one percent of the true value. In Babylon, a ] dated 1900–1600 BC has a geometrical statement that, by implication, treats {{pi}} as {{sfrac|25|8}} = 3.125.{{sfn|Arndt|Haenel|2006|p=167}} In Egypt, the ], dated around 1650 BC but copied from a document dated to 1850 BC, has a formula for the area of a circle that treats {{pi}} as <math display="inline">\bigl(\frac{16}{9}\bigr)^2\approx3.16</math>.<ref name=mollin/>{{sfn|Arndt|Haenel|2006|p=167}} Although some ] have theorized that the ] was built with proportions related to {{pi}}, this theory is not widely accepted by scholars.<ref>{{Cite book |pages=67–77, 165–166 |title=The Shape of the Great Pyramid |first=Roger |last=Herz-Fischler |publisher=Wilfrid Laurier University Press |year=2000 |isbn=978-0-88920-324-2 |url=https://books.google.com/books?id=066T3YLuhA0C&pg=67 |access-date=5 June 2013 |url-status=live |archive-url=https://web.archive.org/web/20161129205154/https://books.google.com/books?id=066T3YLuhA0C&pg=67 |archive-date=29 November 2016}}</ref> | |||
| In the ] of ], dating to an oral tradition from the first or second millennium BC, approximations are given which have been variously interpreted as approximately 3.08831, 3.08833, 3.004, 3, or 3.125.<ref>{{cite book|page=|title=Mathematics in India|title-link=Mathematics in India (book)|first=Kim|last=Plofker|date= 2009|publisher=Princeton University Press|isbn=978-0691120676}}</ref> | |||
| === Polygon approximation era === | |||
| ] | |||
| ] developed the polygonal approach to approximating {{pi}}.]] | |||
| The first recorded algorithm for rigorously calculating the value of {{pi}} was a geometrical approach using polygons, devised around 250 BC by the Greek mathematician ], implementing the ].{{sfn|Arndt|Haenel|2006|p=170}} This polygonal algorithm dominated for over 1,000 years, and as a result {{pi}} is sometimes referred to as Archimedes's constant.{{sfn|Arndt|Haenel|2006|pp=175, 205}} Archimedes computed upper and lower bounds of {{pi}} by drawing a regular hexagon inside and outside a circle, and successively doubling the number of sides until he reached a 96-sided regular polygon. By calculating the perimeters of these polygons, he proved that {{math|{{sfrac|223|71}} < {{pi}} < {{sfrac|22|7}}}} (that is, {{math|3.1408 < {{pi}} < 3.1429}}).<ref name=life-of-pi>{{cite book|last=Borwein|first=Jonathan M.|author-link=Jonathan Borwein|editor1-last=Sidoli|editor1-first=Nathan|editor2-last=Van Brummelen|editor2-first=Glen|contribution=The life of {{pi}}: from Archimedes to ENIAC and beyond|doi=10.1007/978-3-642-36736-6_24|location=Heidelberg|mr=3203895|pages=531–561|publisher=Springer|title=From Alexandria, through Baghdad: Surveys and studies in the ancient Greek and medieval Islamic mathematical sciences in honor of J. L. Berggren|year=2014|isbn=978-3-642-36735-9 }}</ref> Archimedes' upper bound of {{math|{{sfrac|22|7}}}} may have led to a widespread popular belief that {{pi}} is equal to {{math|{{sfrac|22|7}}}}.{{sfn|Arndt|Haenel|2006|p=171}} Around 150 AD, Greek-Roman scientist ], in his '']'', gave a value for {{pi}} of 3.1416, which he may have obtained from Archimedes or from ].{{sfn|Arndt|Haenel|2006|p=176}}{{sfn|Boyer|Merzbach|1991|p=168}}<!--may be suspect--> Mathematicians using polygonal algorithms reached 39 digits of {{pi}} in 1630, a record only broken in 1699 when infinite series were used to reach 71 digits.<ref name="ArPI">{{harvnb|Arndt|Haenel|2006|pp=15–16, 175, 184–186, 205}}. Grienberger achieved 39 digits in 1630; Sharp 71 digits in 1699.</ref> | |||
| In ], values for {{pi}} included 3.1547 (around 1 AD), <math>\sqrt{10}</math> (100 AD, approximately 3.1623), and {{math|{{sfrac|142|45}}}} (3rd century, approximately 3.1556).{{sfn|Arndt|Haenel|2006|pp=176–177}} Around 265 AD, the ] mathematician ] created a ] and used it with a 3,072-sided polygon to obtain a value of {{pi}} of 3.1416.<ref name="autogenerated202">{{harvnb|Boyer|Merzbach|1991|p=202}}</ref>{{sfn|Arndt|Haenel|2006|p=177}} Liu later invented a faster method of calculating {{pi}} and obtained a value of 3.14 with a 96-sided polygon, by taking advantage of the fact that the differences in area of successive polygons form a geometric series with a factor of 4.<ref name="autogenerated202" /> The Chinese mathematician ], around 480 AD, calculated that <math>3.1415926<\pi<3.1415927</math> and suggested the approximations <math display="inline">\pi \approx \frac{355}{113} = 3.14159292035...</math> and <math display="inline">\pi \approx \frac{22}{7} = 3.142857142857...</math>, which he termed the '']'' (<nowiki>''</nowiki>close ratio") and ''Yuelü'' ("approximate ratio"), respectively, using ] applied to a 12,288-sided polygon. With a correct value for its seven first decimal digits, this value remained the most accurate approximation of {{pi}} available for the next 800 years.{{sfn|Arndt|Haenel|2006|p=178}} | |||
| The Indian astronomer ] used a value of 3.1416 in his '']'' (499 AD).{{sfn|Arndt|Haenel|2006|p=179}} ] in {{Circa|1220}} computed 3.1418 using a polygonal method, independent of Archimedes.{{sfn|Arndt|Haenel|2006|p=180}} Italian author ] apparently employed the value <math display="inline">3+\frac{\sqrt{2}}{10} \approx 3.14142</math>.{{sfn|Arndt|Haenel|2006|p=180}} | |||
| The Persian astronomer ] produced nine ] digits, roughly the equivalent of 16 decimal digits, in 1424, using a polygon with <math display="inline">3\times 2^{28}</math> sides,<ref>{{cite journal |first1=Mohammad K. |last1=Azarian |title=al-Risāla al-muhītīyya: A Summary |journal=Missouri Journal of Mathematical Sciences |volume=22 |issue=2 |year=2010 |pages=64–85 |doi=10.35834/mjms/1312233136|doi-access=free}}</ref><ref>{{cite web |last1=O'Connor |first1=John J. |last2=Robertson |first2=Edmund F. |year=1999 |title=Ghiyath al-Din Jamshid Mas'ud al-Kashi |work=] |url=http://www-history.mcs.st-and.ac.uk/history/Biographies/Al-Kashi.html |access-date=11 August 2012 |url-status=live |archive-url=https://web.archive.org/web/20110412192025/http://www-history.mcs.st-and.ac.uk/history/Biographies/Al-Kashi.html |archive-date=12 April 2011}}</ref> which stood as the world record for about 180 years.{{sfn|Arndt|Haenel|2006|p=182}} French mathematician ] in 1579 achieved nine digits with a polygon of <math display="inline">3\times 2^{17}</math> sides.{{sfn|Arndt|Haenel|2006|p=182}} Flemish mathematician ] arrived at 15 decimal places in 1593.{{sfn|Arndt|Haenel|2006|p=182}} In 1596, Dutch mathematician ] reached 20 digits, a record he later increased to 35 digits (as a result, {{pi}} was called the "Ludolphian number" in Germany until the early 20th century).{{sfn|Arndt|Haenel|2006|pp=182–183}} Dutch scientist ] reached 34 digits in 1621,{{sfn|Arndt|Haenel|2006|p=183}} and Austrian astronomer ] arrived at 38 digits in 1630 using 10<sup>40</sup> sides.<ref>{{cite book |first=Christophorus |last=Grienbergerus |author-link=Christoph Grienberger |language=la |year=1630 |title=Elementa Trigonometrica |url=http://librarsi.comune.palermo.it/gesuiti2/06.04.01.pdf |archive-url=https://web.archive.org/web/20140201234124/http://librarsi.comune.palermo.it/gesuiti2/06.04.01.pdf |archive-date=1 February 2014}} His evaluation was 3.14159 26535 89793 23846 26433 83279 50288 4196 < {{pi}} < 3.14159 26535 89793 23846 26433 83279 50288 4199.</ref> ] was able to arrive at 10 decimal places in 1654 using a slightly different method equivalent to ].<ref>{{cite book|last=Brezinski|first=C.|contribution=Some pioneers of extrapolation methods|date=2009|url=https://www.worldscientific.com/doi/10.1142/9789812836267_0001|title=The Birth of Numerical Analysis|pages=1–22|publisher=World Scientific|doi=10.1142/9789812836267_0001|isbn=978-981-283-625-0|editor1-first=Adhemar|editor1-last=Bultheel|editor1-link=Adhemar Bultheel|editor2-first=Ronald|editor2-last=Cools}}</ref><ref>{{Cite journal|last=Yoder|first=Joella G.|author-link=Joella Yoder |date=1996|title=Following in the footsteps of geometry: The mathematical world of Christiaan Huygens|journal=De Zeventiende Eeuw|volume=12|pages=83–93|url=https://www.dbnl.org/tekst/_zev001199601_01/_zev001199601_01_0009.php|via=]}}</ref> | |||
| === Infinite series === | |||
| {{comparison_pi_infinite_series.svg}} | |||
| The calculation of {{pi}} was revolutionized by the development of ] techniques in the 16th and 17th centuries. An infinite series is the sum of the terms of an infinite ]. Infinite series allowed mathematicians to compute {{pi}} with much greater precision than ] and others who used geometrical techniques.<ref name="Ais">{{harvnb|Arndt|Haenel|2006|pp=185–191}}</ref> Although infinite series were exploited for {{pi}} most notably by European mathematicians such as ] and ], the approach also appeared in the ] sometime in the 14th or 15th century.<ref name="Roypp"/>{{sfn|Arndt|Haenel|2006|pp=185–186}} Around 1500 AD, a written description of an infinite series that could be used to compute {{pi}} was laid out in ] verse in '']'' by ].<ref name="Roypp">{{cite journal |last=Roy |first=Ranjan |year=1990 |title=The Discovery of the Series Formula for {{mvar|π}} by Leibniz, Gregory and Nilakantha |journal=Mathematics Magazine |volume=63 |number=5 |pages=291–306 |url=https://www.maa.org/sites/default/files/images/upload_library/22/Allendoerfer/1991/0025570x.di021167.02p0073q.pdf |doi=10.1080/0025570X.1990.11977541 |access-date=21 February 2023 |archive-date=14 March 2023 |archive-url=https://web.archive.org/web/20230314224252/https://www.maa.org/sites/default/files/images/upload_library/22/Allendoerfer/1991/0025570x.di021167.02p0073q.pdf |url-status=dead }}</ref> The series are presented without proof, but proofs are presented in a later work, '']'', from around 1530 AD. Several infinite series are described, including series for sine (which Nilakantha attributes to ]), cosine, and arctangent which are now sometimes referred to as ]. The series for arctangent is sometimes called ] or the Gregory–Leibniz series.<ref name="Roypp" /> Madhava used infinite series to estimate {{pi}} to 11 digits around 1400.<ref>{{cite book |last=Joseph |first=George Gheverghese |title=The Crest of the Peacock: Non-European Roots of Mathematics |publisher=Princeton University Press |year=1991 |isbn=978-0-691-13526-7 |url=https://books.google.com/books?id=c-xT0KNJp0cC&pg=PA264 |page=264}}<!-- This ISBN is for the third edition from 2011! --></ref> | |||
| In 1593, ] published what is now known as ], an ] (rather than an ], which is more typically used in {{pi}} calculations):{{sfn|Arndt|Haenel|2006|p=187}}<ref>{{OEIS2C|id=A060294}}</ref><ref>{{cite book|url=https://books.google.com/books?id=7_BCAAAAcAAJ|title=Variorum de rebus mathematicis responsorum|volume=VIII|first=Franciscus|last=Vieta|year=1593}}</ref> | |||
| <math display=block> \frac2\pi = \frac{\sqrt2}2 \cdot \frac{\sqrt{2+\sqrt2}}2 \cdot \frac{\sqrt{2+\sqrt{2+\sqrt2}}}2 \cdots</math> | |||
| In 1655, ] published what is now known as ], also an infinite product:{{sfn|Arndt|Haenel|2006|p=187}} | |||
| <math display=block> | |||
| \frac{\pi}{2} = \Big(\frac{2}{1} \cdot \frac{2}{3}\Big) \cdot \Big(\frac{4}{3} \cdot \frac{4}{5}\Big) \cdot \Big(\frac{6}{5} \cdot \frac{6}{7}\Big) \cdot \Big(\frac{8}{7} \cdot \frac{8}{9}\Big) \cdots | |||
| </math> | |||
| ] | |||
| used ] to compute {{pi}} to 15 digits, later writing "I am ashamed to tell you to how many figures I carried these computations".<ref name="Newton" />]] | |||
| In the 1660s, the English scientist ] and German mathematician ] discovered ], which led to the development of many infinite series for approximating {{pi}}. Newton himself used an arcsine series to compute a 15-digit approximation of {{pi}} in 1665 or 1666, writing, "I am ashamed to tell you to how many figures I carried these computations, having no other business at the time."<ref name="Newton">{{harvnb|Arndt|Haenel|2006|p=188}}. Newton quoted by Arndt.</ref> | |||
| In 1671, ], and independently, Leibniz in 1673, discovered the ] expansion for ]:<ref name=Roypp/><ref>{{cite journal |last=Horvath |first=Miklos |title=On the Leibnizian quadrature of the circle. |journal=Annales Universitatis Scientiarum Budapestiensis (Sectio Computatorica) |volume=4 |year=1983 |pages=75–83 |url=http://ac.inf.elte.hu/Vol_004_1983/075.pdf }}</ref><ref name="LS" /> | |||
| <math display=block> | |||
| \arctan z = z - \frac {z^3} {3} +\frac {z^5} {5} -\frac {z^7} {7} +\cdots | |||
| </math> | |||
| This series, sometimes called the ], equals <math display="inline">\frac{\pi}{4}</math> when evaluated with <math>z=1</math>.<ref name="LS">{{harvnb|Eymard|Lafon|2004|pp=53–54}}</ref> But for <math>z=1</math>, ] (that is, approaches the answer very gradually), taking about ten times as many terms to calculate each additional digit.<ref>{{cite journal |last=Cooker |first=M.J. |year=2011 |title=Fast formulas for slowly convergent alternating series |journal=Mathematical Gazette |volume=95 |number=533 |pages=218–226 |doi=10.1017/S0025557200002928 |s2cid=123392772 |url=https://www.cambridge.org/core/services/aop-cambridge-core/content/view/F7C083868DEB95FE049CD44163367592/S0025557200002928a.pdf/div-class-title-fast-formulas-for-slowly-convergent-alternating-series-div.pdf |access-date=23 February 2023 |archive-date=4 May 2019 |archive-url=https://web.archive.org/web/20190504091131/https://www.cambridge.org/core/services/aop-cambridge-core/content/view/F7C083868DEB95FE049CD44163367592/S0025557200002928a.pdf/div-class-title-fast-formulas-for-slowly-convergent-alternating-series-div.pdf |url-status=deviated <!-- now paywalled --> }}</ref> | |||
| In 1699, English mathematician ] used the Gregory–Leibniz series for <math display="inline">z=\frac{1}{\sqrt{3}}</math> to compute {{pi}} to 71 digits, breaking the previous record of 39 digits, which was set with a polygonal algorithm.{{sfn|Arndt|Haenel|2006|p=189}} | |||
| In 1706, ] used the Gregory–Leibniz series to produce an algorithm that converged much faster:<ref name=jones/><ref name=tweddle>{{cite journal |last=Tweddle |first=Ian |year=1991 |title=John Machin and Robert Simson on Inverse-tangent Series for {{mvar|π}} |journal= Archive for History of Exact Sciences |volume=42 |number=1 |pages=1–14 |doi= 10.1007/BF00384331 |jstor=41133896 |s2cid=121087222 }}</ref>{{sfn|Arndt|Haenel|2006|pp=192–193}} | |||
| <math display=block> \frac{\pi}{4} = 4 \arctan \frac{1}{5} - \arctan \frac{1}{239}.</math> | |||
| Machin reached 100 digits of {{pi}} with this formula.<ref name="A72n4">{{harvnb|Arndt|Haenel|2006|pp=72–74}}</ref> Other mathematicians created variants, now known as ]e, that were used to set several successive records for calculating digits of {{pi}}.<ref>{{cite journal |last=Lehmer |first=D. H. |author-link=D. H. Lehmer |year=1938 |title=On Arccotangent Relations for {{mvar|π}} |journal=American Mathematical Monthly |volume=45 |number=10 |pages=657–664 Published by: Mathematical Association of America |jstor=2302434 |doi=10.1080/00029890.1938.11990873 |url=https://www.maa.org/sites/default/files/pdf/pubs/amm_supplements/Monthly_Reference_7.pdf |access-date=21 February 2023 |archive-date=7 March 2023 |archive-url=https://web.archive.org/web/20230307164817/https://www.maa.org/sites/default/files/pdf/pubs/amm_supplements/Monthly_Reference_7.pdf |url-status=dead }}</ref><ref name="A72n4" /> | |||
| Isaac Newton ] of the Gregory–Leibniz series in 1684 (in an unpublished work; others independently discovered the result):<ref>{{cite book |last=Roy |first=Ranjan |year=2021 |orig-year=1st ed. 2011 |title=Series and Products in the Development of Mathematics |edition=2 |volume=1 |publisher=Cambridge University Press |pages=215–216, 219–220}} | |||
| <p>{{cite book |last=Newton |first=Isaac |authorlink=Isaac Newton |year=1971 |editor-last=Whiteside |editor-first=Derek Thomas |editor-link=Tom Whiteside |title=The Mathematical Papers of Isaac Newton |volume=4, 1674–1684 |publisher=Cambridge University Press |pages=526–653 }}</p></ref> | |||
| : <math> | |||
| \arctan x | |||
| = \frac{x}{1 + x^2} + \frac23\frac{x^3}{(1 + x^2)^2} | |||
| + \frac{2\cdot 4}{3 \cdot 5}\frac{x^5}{(1 + x^2)^3} + \cdots | |||
| </math> | |||
| ] popularized this series in his 1755 differential calculus textbook, and later used it with Machin-like formulae, including <math display=inline>\tfrac\pi4 = 5\arctan\tfrac17 + 2\arctan\tfrac{3}{79},</math> with which he computed 20 digits of {{pi}} in one hour.<ref> | |||
| {{cite web |last=Sandifer |first=Ed |year=2009 |title=Estimating π |website=How Euler Did It |url=http://eulerarchive.maa.org/hedi/HEDI-2009-02.pdf }} Reprinted in {{cite book |last=Sandifer |first=Ed |display-authors=0 |year=2014 |title=How Euler Did Even More |pages=109–118 |publisher=Mathematical Association of America}} | |||
| <p>{{cite book |last=Euler |first=Leonhard |authorlink=Leonhard Euler |year=1755 |title=] |chapter=§2.2.30 |page=318 |publisher=Academiae Imperialis Scientiarium Petropolitanae |language=la |chapter-url=https://archive.org/details/institutiones-calculi-differentialis-cum-eius-vsu-in-analysi-finitorum-ac-doctri/page/318 |id=}}</p> | |||
| <p>{{cite journal |last=Euler |first=Leonhard |author-link=Leonhard Euler |year=1798 |orig-year=written 1779 |title=Investigatio quarundam serierum, quae ad rationem peripheriae circuli ad diametrum vero proxime definiendam maxime sunt accommodatae |journal=Nova Acta Academiae Scientiarum Petropolitinae |volume=11 |pages=133–149, 167–168 |url=https://archive.org/details/novaactaacademia11petr/page/133 |id= }}</p> | |||
| <p>{{cite journal |last=Chien-Lih |first=Hwang |year=2004 |title=88.38 Some Observations on the Method of Arctangents for the Calculation of {{mvar|π}} |journal=Mathematical Gazette |volume=88 |number=512 |pages=270–278 |doi=10.1017/S0025557200175060 |s2cid=123532808 }}</p> | |||
| <p>{{cite journal |last=Chien-Lih |first=Hwang |year=2005 |title=89.67 An elementary derivation of Euler's series for the arctangent function |journal=Mathematical Gazette |volume=89 |number=516 |pages=469–470 |doi=10.1017/S0025557200178404 |s2cid=123395287 }}</p> | |||
| </ref> | |||
| Machin-like formulae remained the best-known method for calculating {{pi}} well into the age of computers, and were used to set records for 250 years, culminating in a 620-digit approximation in 1946 by Daniel Ferguson – the best approximation achieved without the aid of a calculating device.{{sfn|Arndt|Haenel|2006|pp=192–196, 205}} | |||
| In 1844, a record was set by ], who employed a Machin-like formula to calculate 200 decimals of {{pi}} in his head at the behest of German mathematician ].<ref name="A194">{{harvnb|Arndt|Haenel|2006|pp=194–196}}</ref> | |||
| In 1853, British mathematician ] calculated {{pi}} to 607 digits, but made a mistake in the 528th digit, rendering all subsequent digits incorrect. Though he calculated an additional 100 digits in 1873, bringing the total up to 707, his previous mistake rendered all the new digits incorrect as well.<ref name="hayes-2014">{{cite magazine |last=Hayes |first=Brian |url=https://www.americanscientist.org/article/pencil-paper-and-pi |title=Pencil, Paper, and Pi |volume=102 |issue=5 |page=342 |magazine=] |date=September 2014 |access-date=22 January 2022 |doi=10.1511/2014.110.342}}</ref> | |||
| ==== Rate of convergence ==== | |||
| Some infinite series for {{pi}} ] faster than others. Given the choice of two infinite series for {{pi}}, mathematicians will generally use the one that converges more rapidly because faster convergence reduces the amount of computation needed to calculate {{pi}} to any given accuracy.<ref name="Aconverge">{{cite journal |last1=Borwein |first1=J.M. |last2=Borwein |first2=P.B. |title=Ramanujan and Pi |year=1988 |journal=Scientific American |volume=256 |issue=2 |pages=112–117 |bibcode=1988SciAm.258b.112B |doi=10.1038/scientificamerican0288-112}}{{br}}{{harvnb|Arndt|Haenel|2006|pp=15–17, 70–72, 104, 156, 192–197, 201–202}}</ref> A simple infinite series for {{pi}} is the ]:{{sfn|Arndt|Haenel|2006|pp=69–72}} | |||
| <math display=block> | |||
| \pi = \frac{4}{1} - \frac{4}{3} + \frac{4}{5} - \frac{4}{7} + \frac{4}{9} - \frac{4}{11} + \frac{4}{13} - \cdots | |||
| </math> | |||
| As individual terms of this infinite series are added to the sum, the total gradually gets closer to {{pi}}, and – with a sufficient number of terms – can get as close to {{pi}} as desired. It converges quite slowly, though – after 500,000 terms, it produces only five correct decimal digits of {{pi}}.<ref>{{cite journal |last1=Borwein |first1=J.M. |last2=Borwein |first2=P.B. |last3=Dilcher |first3=K. |year=1989 |title=Pi, Euler Numbers, and Asymptotic Expansions |journal=American Mathematical Monthly |volume=96 |issue=8 |pages=681–687 |doi=10.2307/2324715 |jstor=2324715|hdl=1959.13/1043679 |hdl-access=free }}</ref> | |||
| An infinite series for {{pi}} (published by Nilakantha in the 15th century) that converges more rapidly than the Gregory–Leibniz series is:{{sfn|Arndt|Haenel|2006|loc = Formula 16.10, p. 223}}<ref>{{cite book |last=Wells |first=David |page=35 |title=The Penguin Dictionary of Curious and Interesting Numbers |edition=revised |publisher=Penguin |year=1997 |isbn=978-0-14-026149-3}}</ref> | |||
| <math display=block> | |||
| \pi = 3 + \frac{4}{2\times3\times4} - \frac{4}{4\times5\times6} + \frac{4}{6\times7\times8} - \frac{4}{8\times9\times10} + \cdots | |||
| </math> | |||
| The following table compares the convergence rates of these two series: | |||
| {|class="wikitable" style="text-align: center; margin: auto;" | |||
| |- | |- | ||
| ! Infinite series for {{pi}} !! After 1st term !! After 2nd term !! After 3rd term !! After 4th term !! After 5th term !! Converges to: | |||
| | ] | |||
| | 3.14159265358979323846… | |||
| |- | |- | ||
| | <math>\pi = \frac{4}{1} - \frac{4}{3} + \frac{4}{5} - \frac{4}{7} + \frac{4}{9} - \frac{4}{11} + \frac{4}{13} + \cdots</math> | |||
| | ] | |||
| ||4.0000||2.6666 ... ||3.4666 ... ||2.8952 ... ||3.3396 ... ||rowspan=2| {{pi}} = 3.1415 ... | |||
| | 3.243F6A8885A308D31319… | |||
| |- | |- | ||
| | <math>\pi = {{3}} + \frac{{4}}{2\times3\times4} - \frac{{4}}{4\times5\times6} + \frac{{4}}{6\times7\times8} - \cdots </math> | |||
| | ] | |||
| ||3.0000||3.1666 ... ||3.1333 ... ||3.1452 ... ||3.1396 ... | |||
| | <math>3 + \cfrac{1}{7 + \cfrac{1}{15 + \cfrac{1}{1 + \cfrac{1}{292 + \ddots}}}}</math><br><small>Note that this continued fraction is not periodic.</small> | |||
| |} | |} | ||
| After five terms, the sum of the Gregory–Leibniz series is within 0.2 of the correct value of {{pi}}, whereas the sum of Nilakantha's series is within 0.002 of the correct value. Nilakantha's series converges faster and is more useful for computing digits of {{pi}}. Series that converge even faster include ] and ], the latter producing 14 correct decimal digits per term.<ref name="Aconverge" /> | |||
| '''Pi''' or '''π''' is a ] which represents the ratio of any ]'s circumference to its diameter in ], which is the same as the ratio of a circle's area to the square of its radius. It is approximately equal to 3.14159. Pi is one of the most important mathematical constants: many formulae from mathematics, ], and ] involve π.<ref>{{cite book | title = An Introduction to the History of Mathematics | author = Howard Whitley Eves | year = 1969 | publisher = Holt, Rinehart & Winston | url = http://books.google.com/books?id=LIsuAAAAIAAJ&q=%22important+numbers+in+mathematics%22&dq=%22important+numbers+in+mathematics%22&pgis=1 }}</ref> | |||
| === Irrationality and transcendence === | |||
| Pi is an ], which means that it cannot be expressed as a ] ''m''/''n'', where ''m'' and ''n'' are ]s. Consequently its ] never ends or repeats. Beyond being ], it is a ], which means that no finite sequence of algebraic operations on ]s (powers, roots, sums, etc.) could ever produce it. Throughout the history of mathematics, much effort has been made to determine π more accurately and understand its nature; fascination with the number has even carried over into culture at large. | |||
| {{See also|Proof that π is irrational{{!}}Proof that {{pi}} is irrational|Proof that π is transcendental{{!}}Proof that {{pi}} is transcendental}} | |||
| Not all mathematical advances relating to {{pi}} were aimed at increasing the accuracy of approximations. When Euler solved the ] in 1735, finding the exact value of the sum of the reciprocal squares, he established a connection between {{pi}} and the ]s that later contributed to the development and study of the ]:<ref name="Posamentier">{{harvnb|Posamentier|Lehmann|2004|p=284}}</ref> | |||
| <math display=block> \frac{\pi^2}{6} = \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots</math> | |||
| The Greek letter π, often spelled out ''pi'' in text, was adopted for the number from the Greek word for ''perimeter'' "περίμετρος", probably by ] in 1706, and popularized by ] some years later. The constant is occasionally also referred to as the '''circular constant''', ''']' constant''' (not to be confused with an ]), or ''']'s number'''. | |||
| Swiss scientist ] in 1768 proved that {{pi}} is ], meaning it is not equal to the quotient of any two integers.{{sfn|Arndt|Haenel|2006|p=5}} ] exploited a continued-fraction representation of the tangent function.<ref>Lambert, Johann, "Mémoire sur quelques propriétés remarquables des quantités transcendantes circulaires et logarithmiques", reprinted in {{harvnb|Berggren|Borwein|Borwein|1997|pp=129–140}}</ref> French mathematician ] proved in 1794 that {{pi}}<sup>2</sup> is also irrational. In 1882, German mathematician ] proved that {{pi}} is ],<ref>{{cite journal | last=Lindemann | first=F. | author-link=Ferdinand Lindemann | year=1882 | title=Über die Ludolph'sche Zahl | journal=Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin | volume=2 | pages=679–682 | url=https://archive.org/details/sitzungsberichte1882deutsch/page/679 }}</ref> confirming a conjecture made by both ] and Euler.{{sfn|Arndt|Haenel|2006|p=196}}<ref>Hardy and Wright 1938 and 2000: 177 footnote § 11.13–14 references Lindemann's proof as appearing at ''Math. Ann''. 20 (1882), 213–225.</ref> Hardy and Wright states that "the proofs were afterwards modified and simplified by Hilbert, Hurwitz, and other writers".<ref>cf Hardy and Wright 1938 and 2000:177 footnote § 11.13–14. The proofs that e and π are transcendental can be found on pp. 170–176. They cite two sources of the proofs at Landau 1927 or Perron 1910; see the "List of Books" at pp. 417–419 for full citations.</ref> | |||
| ==Fundamentals== | |||
| === The letter π === | |||
| ] | |||
| {{main|pi (letter)}} | |||
| The name of the ] is ''pi'', and this spelling is used in ] contexts where the Greek letter is not available or where its usage could be problematic. When referring to this constant, the symbol π is always pronounced like "pie" in ], the conventional ''English'' pronunciation of the letter.<!--only state this fact, try not to justify here: see Talk page --> In Greek, the name of this letter is ] {{IPA|/pi/}}. | |||
| === Adoption of the symbol {{pi}} === | |||
| The ] is named "π" because "π" is the first letter of the ] words περιφέρεια (periphery) and περίμετρος (perimeter), probably referring to its use in the formula to find the circumference, or perimeter, of a circle.<ref name="adm">{{cite web|url=http://mathforum.org/dr.math/faq/faq.pi.html|title=About Pi|work=Ask Dr. Math FAQ|accessdate=2007-10-29}}</ref> π is ] ] U+03C0 ("]").<ref>{{cite web|url=http://www.w3.org/TR/MathML2/bycodes.html|title=Characters Ordered by Unicode|publisher=]|accessdate=2007-10-25}}</ref> | |||
| {{Multiple image | |||
| | image1 = William Jones, the Mathematician.jpg | |||
| | caption1 = The earliest known use of the Greek letter π to represent the ratio of a circle's circumference to its diameter was by Welsh mathematician ] in 1706 | |||
| | caption2 = ] popularized the use of the Greek letter π in works he published in 1736 and 1748. | |||
| | total_width = 300 | |||
| | image2 = Leonhard Euler.jpg | |||
| | align = left | |||
| }} | |||
| In the earliest usages, the ] was used to denote the ] (''semiperipheria'' in Latin) of a circle<ref name=firstPi>{{Cite book |url=https://books.google.com/books?id=KTgPAAAAQAAJ&pg=PP3 |title=Theorematum in libris Archimedis de sphaera et cylindro declarario |last=Oughtred |first=William |date=1652 |publisher=Excudebat L. Lichfield, Veneunt apud T. Robinson |language=la |quote={{math|''δ''.''π''}} :: semidiameter. semiperipheria}}</ref> and was combined in ratios with ] (for ] or semidiameter) or ] (for ]) to form circle constants.<ref name="Cajori-2007">{{Cite book |url=https://books.google.com/books?id=bT5suOONXlgC&pg=PA9 |title=A History of Mathematical Notations: Vol. II |last=Cajori |first=Florian |date=2007 |publisher=Cosimo, Inc. |isbn=978-1-60206-714-1 |pages=8–13 |language=en |quote=the ratio of the length of a circle to its diameter was represented in the fractional form by the use of two letters ... J.A. Segner ... in 1767, he represented {{math|3.14159...}} by {{math|''δ'':''π''}}, as did Oughtred more than a century earlier}}</ref><ref>{{wikicite |ref={{harvid|Schepler|1950}} |reference = Schepler, H.C. (1950) "The Chronology of Pi" ''Mathematics Magazine''. '''23'''.{{br}}Part 1. Jan/Feb. (3): 165–170. ]:.{{br}}Part 2. Mar/Apr. (4): 216-228. ]:.{{br}}Part 3. May/Jun. (5): 279-283. ]:.}}{{br}}See p. 220: ] used the letter {{pi}} to represent the periphery (that is, the circumference) of a circle.</ref><ref name="Smith-1958">{{Cite book |url=https://books.google.com/books?id=uTytJGnTf1kC&pg=PA312 |title=History of Mathematics |last=Smith |first=David E. |date=1958 |publisher=Courier Corporation |isbn=978-0-486-20430-7 |page=312 |language=en}}</ref><ref>{{Cite journal|last=Archibald|first=R.C.|date=1921|title=Historical Notes on the Relation {{math|1=''e''<sup>−(''π''/2)</sup> = ''i''<sup>''i''</sup>}}|jstor=2972388|journal=The American Mathematical Monthly|volume=28|issue=3|pages=116–121|doi=10.2307/2972388|quote=It is noticeable that these letters are ''never'' used separately, that is, {{pi}} is ''not'' used for 'Semiperipheria'}}</ref> (Before then, mathematicians sometimes used letters such as {{mvar|c}} or {{mvar|p}} instead.{{sfn|Arndt|Haenel|2006|p=166}}) The first recorded use is ] {{nobr|"<math>\delta . \pi</math>"}}, to express the ratio of periphery and diameter in the 1647 and later editions of {{lang|la|Clavis Mathematicae|italic=yes}}.<ref>See, for example, {{cite book |url=https://archive.org/details/bub_gb_ddMxgr27tNkC |title=Clavis Mathematicæ |last=Oughtred |first=William |date=1648 |publisher=Thomas Harper |location=London |page= |language=la|trans-title=The key to mathematics}} (English translation: {{Cite book |url=https://books.google.com/books?id=S50yAQAAMAAJ&pg=PA99 |title=Key of the Mathematics |last=Oughtred |first=William |date=1694 |publisher=J. Salusbury |language=en}})</ref>{{sfn|Arndt|Haenel|2006|p=166}} ] likewise used {{nobr|"<math display=inline>\frac \pi \delta</math>"}} to represent the constant {{math|3.14...}},<ref>{{Cite book|chapter-url=https://archive.org/stream/mathematicalwor00whewgoog#page/n405/mode/1up |title=The mathematical works of Isaac Barrow |last=Barrow |first=Isaac |date=1860 |publisher=Cambridge University press |others=Harvard University |editor-last=Whewell|editor-first=William |pages=381 |language=la |chapter=Lecture XXIV}}</ref> while ] instead used {{nobr|"<math display=inline>\frac \pi \rho</math>"}} to represent {{math|6.28... }}.<ref>{{Cite journal |last=Gregorius |first=David |date=1695 |title=Ad Reverendum Virum D. Henricum Aldrich S.T.T. Decanum Aedis Christi Oxoniae |jstor=102382 |journal=Philosophical Transactions |language=la |volume=19 |issue=231 |pages=637–652 |doi=10.1098/rstl.1695.0114 |bibcode=1695RSPT...19..637G|doi-access=free|url=https://archive.org/download/crossref-pre-1909-scholarly-works/10.1098%252Frstl.1684.0084.zip/10.1098%252Frstl.1695.0114.pdf}}</ref><ref name="Smith-1958" /> | |||
| The earliest known use of the Greek letter {{pi}} alone to represent the ratio of a circle's circumference to its diameter was by Welsh mathematician ] in his 1706 work ''{{lang|la|Synopsis Palmariorum Matheseos|italic=unset}}; or, a New Introduction to the Mathematics''.<ref name=jones/>{{sfn|Arndt|Haenel|2006|p=165|ps=: A facsimile of Jones' text is in {{harvnb|Berggren|Borwein|Borwein|1997|pp=108–109}}.}} The Greek letter appears on p. 243 in the phrase "<math display=inline>\tfrac12</math> Periphery ({{pi}})", calculated for a circle with radius one. However, Jones writes that his equations for {{pi}} are from the "ready pen of the truly ingenious Mr. ]", leading to speculation that Machin may have employed the Greek letter before Jones.{{sfn|Arndt|Haenel|2006|p=166}} Jones' notation was not immediately adopted by other mathematicians, with the fraction notation still being used as late as 1767.<ref name="Cajori-2007" /><ref>{{Cite book |url=https://books.google.com/books?id=NmYVAAAAQAAJ&pg=PA282 |title=Cursus Mathematicus |last=Segner |first=Joannes Andreas |date=1756 |publisher=Halae Magdeburgicae |page=282 |language=la|access-date=15 October 2017|archive-url=https://web.archive.org/web/20171015150340/https://books.google.co.uk/books?id=NmYVAAAAQAAJ&pg=PA282|archive-date=15 October 2017|url-status=live}}</ref> | |||
| ===Definition=== | |||
| ] | |||
| In ], π is defined as the ] of a ]'s ] to its ]:<ref name="adm"/> | |||
| ] started using the single-letter form beginning with his 1727 ''Essay Explaining the Properties of Air'', though he used {{math|1=''π'' = 6.28...}}, the ratio of periphery to radius, in this and some later writing.<ref>{{Cite journal |last=Euler |first=Leonhard |date=1727 |title=Tentamen explicationis phaenomenorum aeris|url=http://eulerarchive.maa.org/docs/originals/E007.pdf#page=5 |journal=Commentarii Academiae Scientiarum Imperialis Petropolitana |language=la |volume=2 |page=351 |id= |quote=Sumatur pro ratione radii ad peripheriem, {{math|I : π}} |access-date=15 October 2017|archive-url=https://web.archive.org/web/20160401072718/http://eulerarchive.maa.org/docs/originals/E007.pdf#page=5|archive-date=1 April 2016|url-status=live}} {{Webarchive|url=https://web.archive.org/web/20160610172054/http://www.17centurymaths.com/contents/euler/e007tr.pdf#page=3 |date=10 June 2016 }}: "{{mvar|π}} is taken for the ratio of the radius to the periphery "</ref><ref>{{Cite book |url=https://books.google.com/books?id=3C1iHFBXVEcC&pg=PA139 |title=Lettres inédites d'Euler à d'Alembert |last=Euler |first=Leonhard |series=Bullettino di Bibliografia e di Storia delle Scienze Matematiche e Fisiche |year=1747 |editor-last=Henry|editor-first=Charles |volume=19 |publication-date=1886 |page=139 |language=fr |id= |quote=Car, soit π la circonference d'un cercle, dout le rayon est {{math|{{=}} 1}}}} English translation in {{Cite journal |last=Cajori |first=Florian |date=1913 |title=History of the Exponential and Logarithmic Concepts |jstor=2973441 |journal=The American Mathematical Monthly |volume=20 |issue=3 |pages=75–84 |doi=10.2307/2973441 |quote=Letting {{pi}} be the circumference (!) of a circle of unit radius}}</ref> Euler first used {{nowrap|1={{pi}} = 3.14...}} in his 1736 work '']'',<ref>{{Cite book|last=Euler|first=Leonhard|title=Mechanica sive motus scientia analytice exposita. (cum tabulis)|date=1736|publisher=Academiae scientiarum Petropoli|volume=1|page=113|language=la|chapter=Ch. 3 Prop. 34 Cor. 1|id=|quote=Denotet {{math|1 : ''π''}} rationem diametri ad peripheriam|chapter-url=https://books.google.com/books?id=jgdTAAAAcAAJ&pg=PA113}} {{Webarchive|url=https://web.archive.org/web/20160610183753/http://www.17centurymaths.com/contents/euler/mechvol1/ch3a.pdf#page=26|date=10 June 2016}} : "Let {{math|1 : ''π''}} denote the ratio of the diameter to the circumference"</ref> and continued in his widely read 1748 work {{lang|la|]|italic=yes}} (he wrote: "for the sake of brevity we will write this number as {{pi}}; thus {{pi}} is equal to half the circumference of a circle of radius {{math|1}}").<ref>{{Cite book |url=http://gallica.bnf.fr/ark:/12148/bpt6k69587/f155 |title=Leonhardi Euleri opera omnia. 1, Opera mathematica. Volumen VIII, Leonhardi Euleri introductio in analysin infinitorum. Tomus primus / ediderunt Adolf Krazer et Ferdinand Rudio |last=Euler |first=Leonhard |date=1922 |publisher=B.G. Teubneri |location=Lipsae |pages=133–134 |language=la |id=|access-date=15 October 2017|archive-url=https://web.archive.org/web/20171016022758/http://gallica.bnf.fr/ark:/12148/bpt6k69587/f155|archive-date=16 October 2017|url-status=live}}</ref> Because Euler corresponded heavily with other mathematicians in Europe, the use of the Greek letter spread rapidly, and the practice was universally adopted thereafter in the ],{{sfn|Arndt|Haenel|2006|p=166}} though the definition still varied between {{math|3.14...}} and {{math|6.28...}} as late as 1761.<ref>{{Cite book |url=https://books.google.com/books?id=P-hEAAAAcAAJ&pg=PA374 |title=Cursus Mathematicus: Elementorum Analyseos Infinitorum Elementorum Analyseos Infinitorvm |last=Segner |first=Johann Andreas von |date=1761 |publisher=Renger |page=374 |language=la |quote=Si autem {{pi}} notet peripheriam circuli, cuius diameter eſt {{math|2}}}}</ref> | |||
| :<math> \pi = \frac{c}{d}. </math> | |||
| == Modern quest for more digits == | |||
| Note that the ratio <sup>''c''</sup>/<sub>''d''</sub> does not depend on the size of the circle. For example, if a circle has twice the diameter ''d'' of another circle it will also have twice the circumference ''c'', preserving the ratio <sup>''c''</sup>/<sub>''d''</sub>. This fact is a consequence of the ] of all circles. | |||
| === Computer era and iterative algorithms === | |||
| ] | |||
| {{quote box|quote= | |||
| Alternatively π can be also defined as the ratio of a circle's ] (A) to the area of a square whose side is equal to the ]:<ref name="adm"/><ref>{{cite web|url=http://www.wku.edu/~tom.richmond/Pir2.html|title=Area of a Circle|first=Bettina|last=Richmond|publisher=]|date=]|accessdate=2007-11-04}}</ref> | |||
| The ]:{{br}}Initialize | |||
| <math display=block>\textstyle a_0 = 1, \quad b_0 = \frac{1}{\sqrt 2}, \quad t_0 = \frac{1}{4}, \quad p_0 = 1.</math> | |||
| Iterate | |||
| <math display=block>\textstyle a_{n+1} = \frac{a_n+b_n}{2}, \quad \quad b_{n+1} = \sqrt{a_n b_n},</math> | |||
| <math display=block>\textstyle t_{n+1} = t_n - p_n (a_n-a_{n+1})^2, \quad \quad p_{n+1} = 2 p_n.</math> | |||
| Then an estimate for {{pi}} is given by | |||
| <math display=block>\textstyle \pi \approx \frac{(a_n + b_n)^2}{4 t_n}.</math> | |||
| |fontsize=90%|qalign=left}} | |||
| The development of computers in the mid-20th century again revolutionized the hunt for digits of {{pi}}. Mathematicians ] and Levi Smith reached 1,120 digits in 1949 using a desk calculator.{{sfn|Arndt|Haenel|2006|p=205}} Using an ] (arctan) infinite series, a team led by George Reitwiesner and ] that same year achieved 2,037 digits with a calculation that took 70 hours of computer time on the ] computer.{{sfn|Arndt|Haenel|2006|p=197}}<ref>{{cite journal |last=Reitwiesner |first=George |title=An ENIAC Determination of pi and e to 2000 Decimal Places |journal=Mathematical Tables and Other Aids to Computation |year=1950 |volume=4 |issue=29 |pages=11–15 |doi=10.2307/2002695 |jstor=2002695}}</ref> The record, always relying on an arctan series, was broken repeatedly (3089 digits in 1955,<ref>{{cite journal|first1=J. C.|last1=Nicholson| first2=J. |last2=Jeenel|journal=Math. Tabl. Aids. Comp.|volume=9|number=52|year=1955|doi=10.2307/2002052|jstor=2002052|title=Some comments on a NORC Computation of π|pages=162–164}}</ref> 7,480 digits in 1957; 10,000 digits in 1958; 100,000 digits in 1961) until 1 million digits was reached in 1973.{{sfn|Arndt|Haenel|2006|p=197}} | |||
| :<math> \pi = \frac{A}{r^2}. </math> | |||
| Two additional developments around 1980 once again accelerated the ability to compute {{pi}}. First, the discovery of new ]s for computing {{pi}}, which were much faster than the infinite series; and second, the invention of ] that could multiply large numbers very rapidly.{{sfn|Arndt|Haenel|2006|pp=15–17}} Such algorithms are particularly important in modern {{pi}} computations because most of the computer's time is devoted to multiplication.{{sfn|Arndt|Haenel|2006|p=131}} They include the ], ], and ].{{sfn|Arndt|Haenel|2006|pp=132, 140}} | |||
| The constant π may be defined in other ways that avoid the concepts of ] length and area, for example, as twice the smallest positive ''x'' for which ](''x'') = 0.<ref>{{cite book |last=Rudin |first=Walter |authorlink=Walter Rudin |title=Principles of mathematical analysis |edition=3e |year=1976 |origyear=1953 |publisher=McGraw-Hill |id=ISBN 0-07-054235-X | pages = 183}}</ref> The formulas below illustrate other (equivalent) definitions. | |||
| The iterative algorithms were independently published in 1975–1976 by physicist ] and scientist ].{{sfn|Arndt|Haenel|2006|p=87}} These avoid reliance on infinite series. An iterative algorithm repeats a specific calculation, each iteration using the outputs from prior steps as its inputs, and produces a result in each step that converges to the desired value. The approach was actually invented over 160 years earlier by ], in what is now termed the ] (AGM method) or ].{{sfn|Arndt|Haenel|2006|p=87}} As modified by Salamin and Brent, it is also referred to as the Brent–Salamin algorithm. | |||
| ===Irrationality and transcendence=== | |||
| {{main|Proof that π is irrational}} | |||
| The constant π is an ]; that is, it cannot be written as the ratio of two ]s. This was proven in ] by ].<ref name="adm"/> In the 20th century, proofs were found that require no prerequisite knowledge beyond integral calculus. One of those, due to ], is widely known.<ref>{{cite journal|title=A simple proof that π is irrational|first=Ivan|last=Niven|authorlink=Ivan Niven|journal=]|volume=53|number=6|pages=509|year=1947|url=http://www.ams.org/bull/1947-53-06/S0002-9904-1947-08821-2/S0002-9904-1947-08821-2.pdf|format=]|accessdate=2007-11-04|doi=10.1090/S0002-9904-1947-08821-2}}</ref><ref>{{cite web|first=Helmut|last=Richter|url=http://www.lrz-muenchen.de/~hr/numb/pi-irr.html|title=Pi Is Irrational|date=]|publisher=Leibniz Rechenzentrum|accessdate=2007-11-04}}</ref> A somewhat earlier similar proof is by ].<ref>{{cite book|first=Harold|last=Jeffreys|authorlink=Harold Jeffreys|title=Scientific Inference|edition=3rd|publisher=]|year=1973}}</ref> | |||
| The iterative algorithms were widely used after 1980 because they are faster than infinite series algorithms: whereas infinite series typically increase the number of correct digits additively in successive terms, iterative algorithms generally ''multiply'' the number of correct digits at each step. For example, the Brent–Salamin algorithm doubles the number of digits in each iteration. In 1984, brothers ] and ] produced an iterative algorithm that quadruples the number of digits in each step; and in 1987, one that increases the number of digits five times in each step.<ref>{{harvnb|Arndt|Haenel|2006|pp=111 (5 times); pp. 113–114 (4 times)}}. For details of algorithms, see {{cite book |last1=Borwein |first1=Jonathan|last2=Borwein |first2=Peter|title=Pi and the AGM: a Study in Analytic Number Theory and Computational Complexity |publisher=Wiley |year=1987 |isbn=978-0-471-31515-5 }}</ref> Iterative methods were used by Japanese mathematician ] to set several records for computing {{pi}} between 1995 and 2002.<ref name="Background" /> This rapid convergence comes at a price: the iterative algorithms require significantly more memory than infinite series.<ref name="Background">{{cite web |last=Bailey |first=David H. |url=http://crd-legacy.lbl.gov/~dhbailey/dhbpapers/dhb-kanada.pdf |title=Some Background on Kanada's Recent Pi Calculation |date=16 May 2003 |access-date=12 April 2012|url-status=live |archive-url=https://web.archive.org/web/20120415102439/http://crd-legacy.lbl.gov/~dhbailey/dhbpapers/dhb-kanada.pdf |archive-date=15 April 2012}}</ref> | |||
| Furthermore, π is also ], as was proven by ] in ]. This means that there is no ] with ] coefficients of which π is a ].<ref name="ttop">{{cite web|first=Steve|last=Mayer|url=http://dialspace.dial.pipex.com/town/way/po28/maths/docs/pi.html|title=The Transcendence of π|accessdate=2007-11-04}}</ref> An important consequence of the transcendence of π is the fact that it is not ]. Because the coordinates of all points that can be constructed with ] are constructible numbers, it is impossible to ]: that is, it is impossible to construct, using compass and straightedge alone, a square whose area is equal to the area of a given circle.<ref>{{cite web|url=http://www.cut-the-knot.org/impossible/sq_circle.shtml|title=Squaring the Circle|publisher=]|accessdate=2007-11-04}}</ref> | |||
| === Motives for computing {{pi}} === | |||
| ===Numerical value=== | |||
| ].|left|300x300px]] | |||
| {{seealso|numerical approximations of π}} | |||
| For most numerical calculations involving {{pi}}, a handful of digits provide sufficient precision. According to Jörg Arndt and Christoph Haenel, thirty-nine digits are sufficient to perform most ] calculations, because that is the accuracy necessary to calculate the circumference of the ] with a precision of one atom. Accounting for additional digits needed to compensate for computational ]s, Arndt concludes that a few hundred digits would suffice for any scientific application. Despite this, people have worked strenuously to compute {{pi}} to thousands and millions of digits.<ref>{{harvnb|Arndt|Haenel|2006|pp=17–19}}</ref> This effort may be partly ascribed to the human compulsion to break records, and such achievements with {{pi}} often make headlines around the world.<ref name="MSNBC">{{cite news |title=John W. Wrench, Jr.: Mathematician Had a Taste for Pi |first=Matt |last=Schudel |newspaper=The Washington Post |date=25 March 2009 |page=B5}}</ref><ref name="independent.co.uk">{{cite news |title=The Big Question: How close have we come to knowing the precise value of pi? |url=https://www.independent.co.uk/news/science/the-big-question-how-close-have-we-come-to-knowing-the-precise-value-of-pi-1861197.html |newspaper=The Independent |date=8 January 2010 |access-date=14 April 2012 |location=London |first=Steve |last=Connor|url-status=live |archive-url=https://web.archive.org/web/20120402220803/http://www.independent.co.uk/news/science/the-big-question-how-close-have-we-come-to-knowing-the-precise-value-of-pi-1861197.html |archive-date=2 April 2012}}</ref> They also have practical benefits, such as testing ]s, testing numerical analysis algorithms (including ]); and within pure mathematics itself, providing data for evaluating the randomness of the digits of {{pi}}.{{sfn|Arndt|Haenel|2006|p=18}} | |||
| <!-- IMPORTANT NOTICE: Please note that Misplaced Pages is not a database to store millions of digits of π; please refrain from adding those to Misplaced Pages, as it could cause technical problems (and it makes the page unreadable or at least unattractive in the opinion of most readers). Instead, you could add links in the "External links" section, to other web sites containing information regarding digits of π.--> | |||
| The numerical value of π ] to 53 ] is:<ref>{{cite web|url=http://www.research.att.com/~njas/sequences/A000796|title=A000796: Decimal expansion of Pi|publisher=]|accessdate=2007-11-04}}</ref> | |||
| === Rapidly convergent series === | |||
| :<!--Please discuss any changes to this on the Talk page.-->3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 582 | |||
| ], working in isolation in India, produced many innovative series for computing {{pi}}.]] | |||
| :''See ] and those at sequence ] in ] for more digits.'' | |||
| Modern {{pi}} calculators do not use iterative algorithms exclusively. New infinite series were discovered in the 1980s and 1990s that are as fast as iterative algorithms, yet are simpler and less memory intensive.<ref name="Background" /> The fast iterative algorithms were anticipated in 1914, when Indian mathematician ] published dozens of innovative new formulae for {{pi}}, remarkable for their elegance, mathematical depth and rapid convergence.<ref>{{harvnb|Arndt|Haenel|2006|pp=103–104}}</ref> One of his formulae, based on ]s, is | |||
| <math display=block> | |||
| \frac{1}{\pi} = \frac{2 \sqrt 2}{9801} \sum_{k=0}^\infty \frac{(4k)!(1103+26390k)}{k!^4\left(396^{4k}\right)}. | |||
| </math> | |||
| This series converges much more rapidly than most arctan series, including Machin's formula.<ref>{{harvnb|Arndt|Haenel|2006|p=104}}</ref> ] was the first to use it for advances in the calculation of {{pi}}, setting a record of 17 million digits in 1985.<ref>{{harvnb|Arndt|Haenel|2006|pp=104, 206}}</ref> Ramanujan's formulae anticipated the modern algorithms developed by the Borwein brothers (] and ]) and the ].<ref>{{harvnb|Arndt|Haenel|2006|pp=110–111}}</ref> The ] developed in 1987 is | |||
| While the value of pi has been computed to more than a ] (10<sup>12</sup>) digits,<ref>{{cite web |url=http://www.super-computing.org/pi_current.html |title=Current publicized world record of pi |accessdate=2007-10-14}}</ref> elementary applications, such as calculating the circumference of a circle, will rarely require more than a dozen decimal places. For example, a value truncated to 11 decimal places is accurate enough to calculate the circumference of the earth with a precision of a millimeter, and one truncated to 39 decimal places is sufficient to compute the circumference of any circle that fits in the ] to a precision comparable to the size of a ].<ref>{{cite book |title=Excursions in Calculus |last=Young |first=Robert M. |year=1992 |publisher=Mathematical Association of America (MAA)|location=Washington |isbn=0883853175 |pages=417 | url = http://books.google.com/books?id=iEMmV9RWZ4MC&pg=PA238&dq=intitle:Excursions+intitle:in+intitle:Calculus+39+digits&lr=&as_brr=0&ei=AeLrSNKJOYWQtAPdt5DeDQ&sig=ACfU3U0NSYsF9kVp6om4Zyw3a7F82QCofQ }}</ref><ref>{{cite web |url=http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=AJPIAS000067000004000298000001&idtype=cvips&gifs=yes |title=Statistical estimation of pi using random vectors |accessdate=2007-08-12 |format= |work=}}</ref> | |||
| <math display=block> | |||
| \frac{1}{\pi} = \frac{\sqrt{10005}}{4270934400} \sum_{k=0}^\infty \frac{(6k)! (13591409 + 545140134k)}{(3k)!\,k!^3 (-640320)^{3k}}. | |||
| </math> | |||
| It produces about 14 digits of {{pi}} per term<ref>{{harvnb|Eymard|Lafon|2004|p=254}}</ref> and has been used for several record-setting {{pi}} calculations, including the first to surpass 1 billion (10<sup>9</sup>) digits in 1989 by the Chudnovsky brothers, 10 trillion (10<sup>13</sup>) digits in 2011 by Alexander Yee and Shigeru Kondo,<ref name="NW">{{cite book|last1=Bailey|first1=David H.|author1-link=David H. Bailey (mathematician)|last2=Borwein|first2=Jonathan M.|author2-link=Jonathan Borwein|contribution=15.2 Computational records|contribution-url=https://books.google.com/books?id=K26zDAAAQBAJ&pg=PA469|doi=10.1007/978-3-319-32377-0|page=469|publisher=Springer International Publishing|title=Pi: The Next Generation, A Sourcebook on the Recent History of Pi and Its Computation|year=2016|isbn=978-3-319-32375-6 }}</ref> and 100 trillion digits by ] in 2022.<ref>{{Cite magazine |url=https://thenewstack.io/how-googles-emma-haruka-iwao-helped-set-a-new-record-for-pi/ |title=How Google's Emma Haruka Iwao Helped Set a New Record for Pi |date=11 June 2022|magazine=The New Stack|first=David|last=Cassel}}</ref> For similar formulae, see also the ]. | |||
| Because π is an ], its decimal expansion never ends and does not ]. This infinite sequence of digits has fascinated mathematicians and laymen alike, and much effort over the last few centuries has been put into computing more digits and investigating the number's properties.<ref>{{MathWorld|urlname=PiDigits|title=Pi Digits}}</ref> Despite much analytical work, and ] calculations that have determined over 1 ] digits of π, no simple pattern in the digits has ever been found.<ref>{{cite news|first=Chad|last=Boutin|url=http://www.purdue.edu/UNS/html4ever/2005/050426.Fischbach.pi.html|title=Pi seems a good random number generator - but not always the best|publisher=]|date=]|accessdate=2007-11-04}}</ref> Digits of π are available on many web pages, and there is ] to billions of digits on any ]. | |||
| In 2006, mathematician ] used the PSLQ ]<ref>PSLQ means Partial Sum of Least Squares.</ref> to generate several new formulae for {{pi}}, conforming to the following template: | |||
| ===Calculating π=== | |||
| <math display=block> | |||
| {{main|Computing π}} | |||
| \pi^k = \sum_{n=1}^\infty \frac{1}{n^k} \left(\frac{a}{q^n-1} + \frac{b}{q^{2n}-1} + \frac{c}{q^{4n}-1}\right), | |||
| </math> | |||
| where {{math|''q''}} is {{math|]}} (Gelfond's constant), {{math|''k''}} is an ], and {{math|''a'', ''b'', ''c''}} are certain rational numbers that Plouffe computed.<ref>{{cite web |first=Simon |last=Plouffe |author-link=Simon Plouffe |title=Identities inspired by Ramanujan's Notebooks (part 2) |date=April 2006 |url=<!-- http://www.lacim.uqam.ca/~plouffe/inspired2.pdf -->http://plouffe.fr/simon/inspired2.pdf |access-date=10 April 2009|url-status=live |archive-url=https://web.archive.org/web/20120114101641/http://www.plouffe.fr/simon/inspired2.pdf |archive-date=14 January 2012}}</ref> | |||
| === Monte Carlo methods === | |||
| π can be empirically estimated by drawing a large circle, then measuring its diameter and circumference and dividing the circumference by the diameter. Another geometry-based approach, due to ]<ref name="NOVA">{{cite web|first=Rick|last=Groleau|url=http://www.pbs.org/wgbh/nova/archimedes/pi.html|title=Infinite Secrets: Approximating Pi|publisher=NOVA|date=09-2003|accessdate=2007-11-04}}</ref>, is to calculate the ], ''P<sub>n</sub> ,'' of a ] with ''n'' sides ]d around a circle with diameter ''d.'' Then | |||
| {{multiple image | |||
| | direction = horizontal | |||
| | image1 = Buffon needle.svg | |||
| | caption1 = ]. Needles ''a'' and ''b'' are dropped randomly. | |||
| | alt1 = Needles of length ''ℓ'' scattered on stripes with width ''t'' | |||
| | image2 = Pi 30K.gif | |||
| | caption2 = Random dots are placed on a square and a circle inscribed inside. | |||
| | alt2 = Thousands of dots randomly covering a square and a circle inscribed in the square. | |||
| | align = left | |||
| | total_width = 225 | |||
| }} | |||
| ], which evaluate the results of multiple random trials, can be used to create approximations of {{pi}}.<ref>{{harvnb|Arndt|Haenel|2006|p=39}}</ref> ] is one such technique: If a needle of length {{math|''ℓ''}} is dropped {{math|''n''}} times on a surface on which parallel lines are drawn {{math|''t''}} units apart, and if {{math|''x''}} of those times it comes to rest crossing a line ({{math|''x''}} > 0), then one may approximate {{pi}} based on the counts:<ref name="bn">{{cite journal |last=Ramaley |first=J.F. |title=Buffon's Noodle Problem |jstor=2317945 |journal=The American Mathematical Monthly |volume=76 |issue=8 |date=October 1969 |pages=916–918 |doi=10.2307/2317945}}</ref> | |||
| <math display=block>\pi \approx \frac{2n\ell}{xt}.</math> | |||
| Another Monte Carlo method for computing {{pi}} is to draw a circle inscribed in a square, and randomly place dots in the square. The ratio of dots inside the circle to the total number of dots will approximately equal {{math|π/4}}.<ref>{{harvnb|Arndt|Haenel|2006|pp=39–40}}{{br}}{{harvnb|Posamentier|Lehmann|2004|p=105}}</ref> | |||
| :<math>\pi = \lim_{n \to \infty}\frac{P_{n}}{d}</math> | |||
| ] | |||
| That is, the more sides the polygon has, the closer the approximation approaches π. Archimedes determined the accuracy of this approach by comparing the perimeter of the circumscribed polygon with the perimeter of a regular polygon with the same number of sides ] inside the circle. Using a polygon with 96 sides, he computed the fractional range: <math>\begin{smallmatrix}3\frac{10}{71}\ <\ \pi\ <\ 3\frac{1}{7}\end{smallmatrix}</math>.<ref>{{cite book | |||
| Another way to calculate {{pi}} using probability is to start with a ], generated by a sequence of (fair) coin tosses: independent ]s {{math|''X<sub>k</sub>''}} such that {{math|''X<sub>k</sub>'' ∈ {{mset|−1,1}}}} with equal probabilities. The associated random walk is | |||
| | first=Petr | last=Beckmann | |||
| <math display=block>W_n = \sum_{k=1}^n X_k</math> | |||
| | year=1989 | |||
| so that, for each {{mvar|n}}, {{math|''W<sub>n</sub>''}} is drawn from a shifted and scaled ]. As {{mvar|n}} varies, {{math|''W<sub>n</sub>''}} defines a (discrete) ]. Then {{pi}} can be calculated by<ref>{{cite journal |last=Grünbaum |first=B. |author-link=Branko Grünbaum |title=Projection Constants |journal=] |volume=95 |issue=3 |pages=451–465 |year=1960 |doi=10.1090/s0002-9947-1960-0114110-9|doi-access=free}}</ref> | |||
| | title=A History of Pi | |||
| <math display=block>\pi = \lim_{n\to\infty} \frac{2n}{E^2}.</math> | |||
| | publisher=Barnes & Noble Publishing | |||
| | isbn=0880294183 }}</ref> | |||
| This Monte Carlo method is independent of any relation to circles, and is a consequence of the ], discussed ]. | |||
| π can also be calculated using purely mathematical methods. Most formulas used for calculating the value of π have desirable mathematical properties, but are difficult to understand without a background in ] and ]. However, some are quite simple, such as this form of the ]:<ref>{{cite book |first=Pierre |last=Eymard |coauthors=Jean-Pierre Lafon |others=Stephen S. Wilson (translator)|title=The Number π|url=http://books.google.com/books?id=qZcCSskdtwcC&pg=PA53&dq=leibniz+pi&ei=uFsuR5fOAZTY7QLqouDpCQ&sig=k8VlN5VTxcX9a6Ewc71OCGe_5jk |accessdate=2007-11-04 |year=2004 |month=02 |publisher=American Mathematical Society |isbn=0821832468 |pages=53 |chapter=2.6 }}</ref> | |||
| These Monte Carlo methods for approximating {{pi}} are very slow compared to other methods, and do not provide any information on the exact number of digits that are obtained. Thus they are never used to approximate {{pi}} when speed or accuracy is desired.<ref>{{harvnb|Arndt|Haenel|2006|pp=43}}{{br}}{{harvnb|Posamentier|Lehmann|2004|pp=105–108}}</ref> | |||
| :<math>\pi = \frac{4}{1}-\frac{4}{3}+\frac{4}{5}-\frac{4}{7}+\frac{4}{9}-\frac{4}{11}\cdots\! </math>. | |||
| === Spigot algorithms === | |||
| While that series is easy to write and calculate, it is not immediately obvious why it yields π. In addition, this series converges so slowly that 300 terms are not sufficient to calculate '''π''' correctly to 2 decimal places.<ref>{{cite journal|url=http://www.scm.org.co/Articulos/832.pdf|format=]|title=Even from Gregory-Leibniz series π could be computed: an example of how convergence of series can be accelerated|journal=Lecturas Mathematicas|volume=27|year=2006|pages=21–25|first=Vito|last=Lampret, Spanish|accessdate=2007-11-04}}</ref> However, by computing this series in a somewhat more clever way by taking the midpoints of partial sums, it can be made to converge much faster. Let | |||
| Two algorithms were discovered in 1995 that opened up new avenues of research into {{pi}}. They are called ]s because, like water dripping from a ], they produce single digits of {{pi}} that are not reused after they are calculated.{{sfn|Arndt|Haenel|2006|pp=77–84}}<ref name="Gibbons">{{cite journal|last=Gibbons|first=Jeremy|author-link=Jeremy Gibbons|doi=10.2307/27641917|issue=4|journal=]|jstor=27641917|mr=2211758|pages=318–328|title=Unbounded spigot algorithms for the digits of pi|url=https://www.cs.ox.ac.uk/jeremy.gibbons/publications/spigot.pdf|volume=113|year=2006}}</ref> This is in contrast to infinite series or iterative algorithms, which retain and use all intermediate digits until the final result is produced.{{sfn|Arndt|Haenel|2006|pp=77–84}} | |||
| Mathematicians ] and Stanley Rabinowitz produced a simple spigot algorithm in 1995.<ref name="Gibbons" />{{sfn|Arndt|Haenel|2006|p=77}}<ref>{{cite journal |first1=Stanley |last1=Rabinowitz |last2=Wagon |first2=Stan |date=March 1995 |title=A spigot algorithm for the digits of Pi |journal=American Mathematical Monthly |volume=102 |issue=3 |pages=195–203 |doi=10.2307/2975006 |jstor=2975006}}</ref> Its speed is comparable to arctan algorithms, but not as fast as iterative algorithms.{{sfn|Arndt|Haenel|2006|p=77}} | |||
| <math>\pi_{0,1} = \frac{4}{1}, \pi_{0,2} =\frac{4}{1}-\frac{4}{3}, \pi_{0,3} =\frac{4}{1}-\frac{4}{3}+\frac{4}{5}, \pi_{0,4} =\frac{4}{1}-\frac{4}{3}+\frac{4}{5}-\frac{4}{7}, \cdots\! </math> | |||
| Another spigot algorithm, the ] ], was discovered in 1995 by Simon Plouffe:{{sfn|Arndt|Haenel|2006|pp=117, 126–128}}<ref name="bbpf">{{cite journal |last1=Bailey |first1=David H. |author-link=David H. Bailey (mathematician) |last2=Borwein |first2=Peter B. |author2-link=Peter Borwein |last3=Plouffe |first3=Simon |author3-link=Simon Plouffe |date=April 1997 |title=On the Rapid Computation of Various Polylogarithmic Constants |journal=Mathematics of Computation |volume=66 |issue=218 |pages=903–913 |url=<!-- http://crd.lbl.gov/~dhbailey/dhbpapers/digits.pdf -->http://crd-legacy.lbl.gov/~dhbailey/dhbpapers/digits.pdf |doi=10.1090/S0025-5718-97-00856-9 |url-status=live |archive-url=https://web.archive.org/web/20120722015837/http://crd-legacy.lbl.gov/~dhbailey/dhbpapers/digits.pdf |archive-date=22 July 2012 |citeseerx=10.1.1.55.3762 |bibcode=1997MaCom..66..903B|s2cid=6109631 }}</ref> | |||
| and then define | |||
| <math display=block> \pi = \sum_{k=0}^\infty \frac{1}{16^k} \left( \frac{4}{8k + 1} - \frac{2}{8k + 4} - \frac{1}{8k + 5} - \frac{1}{8k + 6}\right).</math> | |||
| This formula, unlike others before it, can produce any individual ] digit of {{pi}} without calculating all the preceding digits.{{sfn|Arndt|Haenel|2006|pp=117, 126–128}} Individual binary digits may be extracted from individual hexadecimal digits, and ] digits can be extracted from one or two hexadecimal digits. An important application of digit extraction algorithms is to validate new claims of record {{pi}} computations: After a new record is claimed, the decimal result is converted to hexadecimal, and then a digit extraction algorithm is used to calculate several randomly selected hexadecimal digits near the end; if they match, this provides a measure of confidence that the entire computation is correct.<ref name="NW" /> | |||
| <math>\pi_{i,j} = \frac{\pi_{i-1,j}+\pi_{i-1,j+1}}{2}</math> for all <math>i,j\ge 1</math> | |||
| Between 1998 and 2000, the ] project ] used ] (a modification of the BBP algorithm) to compute the quadrillionth (10<sup>15</sup>th) bit of {{pi}}, which turned out to be 0.<ref>{{harvnb|Arndt|Haenel|2006|p=20}}{{br}}Bellards formula in: {{cite web |url=http://fabrice.bellard.free.fr/pi/pi_bin/pi_bin.html |title=A new formula to compute the n<sup>th</sup> binary digit of pi |first=Fabrice |last=Bellard |author-link=Fabrice Bellard |access-date=27 October 2007 |archive-url=https://web.archive.org/web/20070912084453/http://fabrice.bellard.free.fr/pi/pi_bin/pi_bin.html <!-- http://www.lacim.uqam.ca/~plouffe/inspired2.pdf --> |archive-date=12 September 2007}}</ref> In September 2010, a ] employee used the company's ] application on one thousand computers over a 23-day period to compute 256 ]s of {{pi}} at the two-quadrillionth (2×10<sup>15</sup>th) bit, which also happens to be zero.<ref>{{cite news |title=Pi record smashed as team finds two-quadrillionth digit |last=Palmer |first=Jason |newspaper=BBC News |date=16 September 2010 |url=https://www.bbc.co.uk/news/technology-11313194 |access-date=26 March 2011 |url-status=live |archive-url=https://web.archive.org/web/20110317170643/http://www.bbc.co.uk/news/technology-11313194 |archive-date=17 March 2011}}</ref> | |||
| then computing <math>\pi_{10,10}</math> will take similar computation time to computing 150 terms of the original series in a brute force manner, and <math>\pi_{10,10}=3.141592653\cdots</math>, correct to 9 decimal places. This computation is an example of the ].<ref>A. van Wijngaarden, in: Cursus: Wetenschappelijk Rekenen B, Process Analyse, Stichting Mathematisch Centrum, (Amsterdam, 1965) pp. 51-60.</ref> | |||
| In 2022, Plouffe found a base-10 algorithm for calculating digits of {{pi}}.<ref>{{cite arXiv |last=Plouffe |first=Simon |year=2022 |eprint=2201.12601 |title=A formula for the {{mvar|n}}th decimal digit or binary of {{mvar|π}} and powers of {{mvar|π}} |class=math.NT }}</ref> | |||
| ==History== | |||
| {{seealso|Chronology of computation of π|Numerical approximations of π}} | |||
| The history of π parallels the development of mathematics as a whole.<ref>{{cite book |last=Beckmann |first=Petr |authorlink=Petr Beckmann |title=A History of π |year=1976 |publisher=] |id=ISBN 0-312-38185-9}}</ref> Some authors divide progress into three periods: the ancient period during which π was studied geometrically, the classical era following the development of calculus in Europe around the 17th century, and the age of digital computers.<ref>{{cite web|url=http://numbers.computation.free.fr/Constants/Pi/pi.html|title=Archimedes' constant π|accessdate=2007-11-04}}</ref> | |||
| == Role and characterizations in mathematics == | |||
| ===Geometrical period=== | |||
| Because {{pi}} is closely related to the circle, it is found in ] from the fields of geometry and trigonometry, particularly those concerning circles, spheres, or ellipses. Other branches of science, such as statistics, physics, ], and number theory, also include {{pi}} in some of their important formulae. | |||
| === Geometry and trigonometry === | |||
| That the ratio of the circumference to the diameter of a circle is the same for all circles, and that it is slightly more than 3, was known to ancient Egyptian, Babylonian, Indian and Greek geometers. The earliest known approximations date from around 1900 BC; they are 25/8 (Babylonia) and 256/81 (Egypt), both within 1% of the true value.<ref name="adm"/> The Indian text '']'' gives π as 339/108 ≈ 3.139. The ] appears to suggest, in the Book of ], that π = 3, which is notably worse than other estimates available at the time of writing (600 BC). The interpretation of the passage is disputed,<ref>{{cite web|first=H. Peter|last=Aleff|url=http://www.recoveredscience.com/const303solomonpi.htm|title=Ancient Creation Stories told by the Numbers: Solomon's Pi|publisher=recoveredscience.com|accessdate=2007-10-30}}</ref><ref name="ahop">{{cite web|first=J J|last=O'Connor|coauthors=E F Robertson|url=http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Pi_through_the_ages.html|title=A history of Pi|date=2001-08|accessdate=2007-10-30}}</ref> as some believe the ratio of 3:1 is of an exterior circumference to an interior diameter of a thinly walled basin, which could indeed be an accurate ratio, depending on the thickness of the walls (See: ]). | |||
| ] is {{pi}}.]] | |||
| {{pi}} appears in formulae for areas and volumes of geometrical shapes based on circles, such as ]s, ]s, ], and ]. Below are some of the more common formulae that involve {{pi}}.<ref>{{harvnb|Bronshteĭn|Semendiaev|1971|pp=200, 209}}</ref> | |||
| ] (287-212 BC) was the first to estimate π rigorously. He realized that its magnitude can be bounded from below and above by inscribing circles in ]s and calculating the outer and inner polygons' respective perimeters:<ref name="ahop"/> | |||
| * The circumference of a circle with radius {{math|''r''}} is {{math|2π''r''}}. | |||
| * The ] with radius {{math|''r''}} is {{math|π''r''<sup>2</sup>}}. | |||
| * The area of an ellipse with semi-major axis {{math|''a''}} and semi-minor axis {{math|''b''}} is {{math|π''ab''}}. | |||
| * The volume of a sphere with radius {{math|''r''}} is {{math|{{sfrac|4|3}}π''r''<sup>3</sup>}}. | |||
| * The surface area of a sphere with radius {{math|''r''}} is {{math|4π''r''<sup>2</sup>}}. | |||
| Some of the formulae above are special cases of the volume of the ] and the surface area of its boundary, the ], given ]. | |||
| Apart from circles, there are other ]. By ], every curve of constant width has perimeter {{pi}} times its width. The ] (formed by the intersection of three circles with the sides of an ] as their radii) has the smallest possible area for its width and the circle the largest. There also exist non-circular ] and even ]s of constant width.<ref>{{cite book|last1=Martini|first1=Horst|last2=Montejano|first2=Luis|last3=Oliveros|first3=Déborah|author3-link=Déborah Oliveros|doi=10.1007/978-3-030-03868-7|isbn=978-3-030-03866-3|mr=3930585|publisher=Birkhäuser|s2cid=127264210|title=Bodies of Constant Width: An Introduction to Convex Geometry with Applications|year=2019}}{{pb}} | |||
| ] | |||
| See Barbier's theorem, Corollary 5.1.1, p. 98; Reuleaux triangles, pp. 3, 10; smooth curves such as an analytic curve due to Rabinowitz, § 5.3.3, pp. 111–112.</ref> | |||
| ] | |||
| By using the equivalent of 96-sided polygons, he proved that 223/71 < π < 22/7.<ref name="ahop"/> Taking the average of these values yields 3.1419. | |||
| ] that describe circumference, area, or volume of shapes generated by circles typically have values that involve {{pi}}. For example, an integral that specifies half the area of a circle of radius one is given by:<ref>{{cite book|last1=Herman|first1=Edwin|last2=Strang|first2=Gilbert|author2-link=Gilbert Strang|contribution=Section 5.5, Exercise 316|contribution-url=https://openstax.org/books/calculus-volume-1/pages/5-5-substitution|page=594|publisher=]|title=Calculus|volume=1|year=2016}}</ref> | |||
| In the following centuries further development took place in India and China. Around 265, the ] mathematician ] provided a simple and rigorous ] to calculate π to any degree of accuracy. He himself carried through the calculation to 3072-gon and obtained an approximate value for π of 3.1416. | |||
| <math display=block>\int_{-1}^1 \sqrt{1-x^2}\,dx = \frac{\pi}{2}.</math> | |||
| : <math> | |||
| \begin{align} | |||
| \pi \approx A_{3072} & {} = 768 \sqrt{2 - \sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2+1}}}}}}}}} \\ | |||
| & {} \approx 3.14159. | |||
| \end{align} | |||
| </math> | |||
| In that integral, the function <math>\sqrt{1-x^2}</math> represents the height over the <math>x</math>-axis of a ] (the ] is a consequence of the ]), and the integral computes the area below the semicircle. | |||
| Later, Liu Hui invented a ] and obtained an approximate value of 3.1416 with only a 96-gon, by taking advantage of the fact that the difference in area of successive polygons forms a geometric series with a factor of 4. | |||
| The existence of such integrals makes {{pi}} an ].<ref>{{Citation |last1=Kontsevich |first1=Maxim |title=Periods |date=2001 |work=Mathematics Unlimited — 2001 and Beyond |pages=771–808 |editor-last=Engquist |editor-first=Björn |url=https://link.springer.com/chapter/10.1007/978-3-642-56478-9_39 |access-date=2024-09-23 |place=Berlin, Heidelberg |publisher=Springer |language=en |doi=10.1007/978-3-642-56478-9_39 |isbn=978-3-642-56478-9 |last2=Zagier |first2=Don |editor2-last=Schmid |editor2-first=Wilfried}}</ref> | |||
| Around 480, the Chinese mathematician ] demonstrated that π ≈ 355/113, and showed that 3.1415926 < π < 3.1415927 using Liu Hui's algorithm applied to a 12288-gon. This value would stand as the most accurate approximation of π over the next 900 years. | |||
| === |
=== Units of angle === | ||
| {{Main|Units of angle measure}} | |||
| ] and ] functions repeat with period 2{{pi}}.|left]]The ]s rely on angles, and mathematicians generally use ]s as units of measurement. {{pi}} plays an important role in angles measured in radians, which are defined so that a complete circle spans an angle of 2{{pi}} radians. The angle measure of 180° is equal to {{pi}} radians, and {{nowrap|1=1° = {{pi}}/180 radians}}.{{sfn|Abramson|2014|loc=}} | |||
| Common trigonometric functions have periods that are multiples of {{pi}}; for example, sine and cosine have period 2{{pi}},<ref name="WCS">{{harvnb|Bronshteĭn|Semendiaev|1971|pp=210–211}}</ref> so for any angle {{math|''θ''}} and any integer {{math|''k''}},<ref name="WCS" /> | |||
| Until the ], π was known to fewer than 10 decimal digits. The next major advancement in the study of π came with the development of ], and in particular the discovery of ] which in principle permit calculating π to any desired accuracy by adding sufficiently many terms. Around 1400, ] found the first known such series: | |||
| <math display=block> \sin\theta = \sin\left(\theta + 2\pi k \right) \text{ and } \cos\theta = \cos\left(\theta + 2\pi k \right).</math> | |||
| === Eigenvalues === | |||
| :<math>\frac{\pi}{4} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \cdots\!</math> | |||
| ]s of a vibrating string are ]s of the second derivative, and form a ]. The associated eigenvalues form the ] of integer multiples of {{pi}}.]] | |||
| Many of the appearances of {{pi}} in the formulae of mathematics and the sciences have to do with its close relationship with geometry. However, {{pi}} also appears in many natural situations having apparently nothing to do with geometry. | |||
| In many applications, it plays a distinguished role as an ]. For example, an idealized ] can be modelled as the graph of a function {{math|''f''}} on the unit interval {{closed-closed|0, 1}}, with ] {{math|1=''f''(0) = ''f''(1) = 0}}. The modes of vibration of the string are solutions of the ] <math>f''(x) + \lambda f(x) = 0</math>, or <math>f''(t) = -\lambda f(x)</math>. Thus {{math|λ}} is an eigenvalue of the second derivative ] <math>f \mapsto f''</math>, and is constrained by ] to take on only certain specific values. It must be positive, since the operator is ], so it is convenient to write {{math|1=''λ'' = ''ν''<sup>2</sup>}}, where {{math|''ν'' > 0}} is called the ]. Then {{math|1=''f''(''x'') = sin(''π'' ''x'')}} satisfies the boundary conditions and the differential equation with {{math|1=''ν'' = ''π''}}.<ref>{{cite book |last1=Hilbert |first1=David |author1-link=David Hilbert |last2=Courant |first2=Richard |author2-link=Richard Courant |title=Methods of mathematical physics, volume 1 |pages=286–290 |year=1966 |publisher=Wiley}}</ref> | |||
| This is now known as the ]<ref>{{citation|title=Special Functions|last=George E. Andrews, Richard Askey|first=Ranjan Roy|publisher=]|year=1999|isbn=0521789885|page=58}}</ref><ref>{{citation|first=R. C.|last=Gupta|title=On the remainder term in the Madhava-Leibniz's series|journal=Ganita Bharati|volume=14|issue=1-4|year=1992|pages=68-71}}</ref> or Gregory-Leibniz series since it was rediscovered by ] and ] in the 17th century. Unfortunately, the rate of convergence is too slow to calculate many digits in practice; about 4,000 terms must be summed to improve upon Archimedes' estimate. However, by transforming the series into | |||
| The value {{pi}} is, in fact, the ''least'' such value of the wavenumber, and is associated with the ] of vibration of the string. One way to show this is by estimating the ], which satisfies ]:{{sfn|Dym|McKean|1972|page=47}} for a function <math>f : \to \Complex</math> with {{math|1=''f''(0) = ''f''(1) = 0}} and {{math|''f''}}, {{math|''f''{{′}}}} both ], we have: | |||
| :<math>\pi = \sqrt{12} \, \left(1-\frac{1}{3 \cdot 3} + \frac{1}{5 \cdot 3^2} - \frac{1}{7 \cdot 3^3} + \cdots\right)\!</math> | |||
| <math display=block>\pi^2\int_0^1|f(x)|^2\,dx\le \int_0^1|f'(x)|^2\,dx,</math> | |||
| with equality precisely when {{math|''f''}} is a multiple of {{math|sin(π ''x'')}}. Here {{pi}} appears as an optimal constant in Wirtinger's inequality, and it follows that it is the smallest wavenumber, using the ] of the eigenvalue. As a consequence, {{pi}} is the smallest ] of the derivative operator on the space of functions on {{closed-closed|0, 1}} vanishing at both endpoints (the ] <math>H^1_0</math>). | |||
| === Inequalities === | |||
| ] was able to calculate π as 3.14159265359, correct to 11 decimal places. The record was beaten in 1424 by the ], ], who determined 16 decimals of π. | |||
| ] was the solution to an isoperimetric problem, according to a legend recounted by ]:<ref>{{cite journal |first=William |last=Thompson |author-link=Lord Kelvin |title=Isoperimetrical problems |year=1894 |journal=Nature Series: Popular Lectures and Addresses |volume=II |pages=571–592}}</ref> those lands bordering the sea that ] could enclose on all other sides within a single given oxhide, cut into strips.|left]] | |||
| The number {{pi}} serves appears in similar eigenvalue problems in higher-dimensional analysis. As mentioned ], it can be characterized via its role as the best constant in the ]: the area {{mvar|A}} enclosed by a plane ] of perimeter {{mvar|P}} satisfies the inequality | |||
| The first major European contribution since Archimedes was made by the German mathematician ] (1540–1610), who used a geometrical method to compute 35 decimals of π. He was so proud of the calculation, which required the greater part of his life, that he had the digits engraved into his tombstone.<ref>{{cite book | title = Mathematical Tables; Containing the Common, Hyperbolic, and Logistic Logarithms... | author = Charles Hutton | publisher = London: Rivington | year = 1811 | pages = p.13 | url = http://books.google.com/books?id=zDMAAAAAQAAJ&pg=PA13&dq=snell+descartes+date:0-1837&lr=&as_brr=1&ei=rqPgR7yeNqiwtAPDvNEV }}</ref> | |||
| <math display=block>4\pi A\le P^2,</math> | |||
| and equality is clearly achieved for the circle, since in that case {{math|1=''A'' = π''r''{{sup|2}}}} and {{math|1=''P'' = 2π''r''}}.<ref>{{cite book |first=Isaac |last=Chavel |title=Isoperimetric inequalities |publisher=Cambridge University Press |year=2001}}</ref> | |||
| Ultimately, as a consequence of the isoperimetric inequality, {{pi}} appears in the optimal constant for the critical ] in ''n'' dimensions, which thus characterizes the role of {{pi}} in many physical phenomena as well, for example those of classical ].<ref>{{cite journal |last=Talenti|first= Giorgio |title=Best constant in Sobolev inequality |journal=Annali di Matematica Pura ed Applicata |volume=110 |number=1 |pages=353–372 |issn=1618-1891 |doi=10.1007/BF02418013 |citeseerx=10.1.1.615.4193 |year=1976|s2cid=16923822 }}</ref><ref>{{cite arXiv |title=Best constants in Poincaré inequalities for convex domains |eprint=1110.2960 |author1=L. Esposito |author2=C. Nitsch |author3=C. Trombetti |year=2011 |class=math.AP}}</ref><ref>{{cite journal |title=Best constants for Gagliardo–Nirenberg inequalities and applications to nonlinear diffusions |first1=M.|last1=Del Pino |first2=J.|last2= Dolbeault |journal=Journal de Mathématiques Pures et Appliquées |year=2002 |volume=81 |issue=9 |pages=847–875 |doi=10.1016/s0021-7824(02)01266-7 |citeseerx=10.1.1.57.7077|s2cid=8409465 }}</ref> In two dimensions, the critical Sobolev inequality is | |||
| Around the same time, the methods of calculus and determination of infinite series and products for geometrical quantities began to emerge in Europe. The first such representation was the ], | |||
| <math display=block>2\pi\|f\|_2 \le \|\nabla f\|_1</math> | |||
| :<math>\frac2\pi = \frac{\sqrt2}2 \cdot \frac{\sqrt{2+\sqrt2}}2 \cdot \frac{\sqrt{2+\sqrt{2+\sqrt2}}}2 \cdot \cdots\!</math> | |||
| for ''f'' a smooth function with compact support in {{math|'''R'''<sup>2</sup>}}, <math>\nabla f</math> is the ] of ''f'', and <math>\|f\|_2</math> and <math>\|\nabla f\|_1</math> refer respectively to the ]. The Sobolev inequality is equivalent to the isoperimetric inequality (in any dimension), with the same best constants. | |||
| Wirtinger's inequality also generalizes to higher-dimensional ] that provide best constants for the ] of an ''n''-dimensional membrane. Specifically, {{pi}} is the greatest constant such that | |||
| found by ] in 1593. Another famous result is ], | |||
| <math display=block> | |||
| \pi \le \frac{\left (\int_G |\nabla u|^2\right)^{1/2}}{\left (\int_G|u|^2\right)^{1/2}} | |||
| </math> | |||
| for all ] subsets {{math|''G''}} of {{math|'''R'''<sup>''n''</sup>}} of diameter 1, and square-integrable functions ''u'' on {{math|''G''}} of mean zero.<ref>{{cite journal |last1=Payne |first1=L.E. |last2=Weinberger |first2=H.F. |title=An optimal Poincaré inequality for convex domains |year=1960 |journal=Archive for Rational Mechanics and Analysis |volume=5 |issue=1 |issn=0003-9527 |pages=286–292 |doi=10.1007/BF00252910 |bibcode=1960ArRMA...5..286P|s2cid=121881343 }}</ref> Just as Wirtinger's inequality is the ] form of the ] problem in one dimension, the Poincaré inequality is the variational form of the ] eigenvalue problem, in any dimension. | |||
| === Fourier transform and Heisenberg uncertainty principle === | |||
| :<math>\frac{\pi}{2} = \frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \cdots\!</math> | |||
| ]]] | |||
| The constant {{pi}} also appears as a critical spectral parameter in the ]. This is the ], that takes a complex-valued integrable function {{math|''f''}} on the real line to the function defined as: | |||
| <math display=block>\hat{f}(\xi) = \int_{-\infty}^\infty f(x) e^{-2\pi i x\xi}\,dx.</math> | |||
| Although there are several different conventions for the Fourier transform and its inverse, any such convention must involve {{pi}} ''somewhere''. The above is the most canonical definition, however, giving the unique unitary operator on {{math|''L''{{sup|2}}}} that is also an algebra homomorphism of {{math|''L''{{sup|1}}}} to {{math|''L''{{sup|∞}}}}.<ref>{{cite book |title=Harmonic analysis in phase space |first=Gerald|last= Folland |publisher=Princeton University Press |year=1989 |page=5|author-link=Gerald Folland}}</ref> | |||
| written down by ] in 1655. ] himself derived a series for π and calculated 15 digits, although he later confessed: "I am ashamed to tell you to how many figures I carried these computations, having no other business at the time." <ref></ref> | |||
| The ] also contains the number {{pi}}. The uncertainty principle gives a sharp lower bound on the extent to which it is possible to localize a function both in space and in frequency: with our conventions for the Fourier transform, | |||
| In 1706 ] was the first to compute 100 decimals of π, using the formula | |||
| <math display=block> | |||
| \left(\int_{-\infty}^\infty x^2|f(x)|^2\,dx\right) | |||
| \left(\int_{-\infty}^\infty \xi^2|\hat{f}(\xi)|^2\,d\xi\right) | |||
| \ge | |||
| \left(\frac{1}{4\pi}\int_{-\infty}^\infty |f(x)|^2\,dx\right)^2. | |||
| </math> | |||
| The physical consequence, about the uncertainty in simultaneous position and momentum observations of a ] system, is ]. The appearance of {{pi}} in the formulae of Fourier analysis is ultimately a consequence of the ], asserting the uniqueness of the ] of the ].<ref name=howe>{{cite journal |first=Roger |last=Howe |title=On the role of the Heisenberg group in harmonic analysis |journal=] |volume=3 |pages=821–844 |number=2 |year=1980 |doi=10.1090/S0273-0979-1980-14825-9 |mr=578375|doi-access=free}}</ref> | |||
| :<math>\frac{\pi}{4} = 4 \, \arctan \frac{1}{5} - \arctan \frac{1}{239}\!</math> | |||
| === Gaussian integrals === | |||
| with | |||
| ] {{math|1=''ƒ''(''x'') = ''e''{{sup|−''x''{{sup|2}}}}}}. The coloured region between the function and the ''x''-axis has area {{math|{{sqrt|π}}}}.|left]] | |||
| The fields of ] and ] frequently use the ] as a simple model for complex phenomena; for example, scientists generally assume that the observational error in most experiments follows a normal distribution.<ref>Feller, W. ''An Introduction to Probability Theory and Its Applications, Vol. 1'', Wiley, 1968, pp. 174–190.</ref> The ], which is the ] of the normal distribution with ] {{math|μ}} and ] {{math|σ}}, naturally contains {{pi}}:<ref name="GaussProb">{{harvnb|Bronshteĭn|Semendiaev|1971|pp=106–107, 744, 748}}</ref> | |||
| :<math>\arctan \, x = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \cdots\!</math> | |||
| <math display=block>f(x) = {1 \over \sigma\sqrt{2\pi} }\,e^{-(x-\mu )^2/(2\sigma^2)}.</math> | |||
| The factor of <math>\tfrac{1}{\sqrt{2\pi}}</math> makes the area under the graph of {{math|''f''}} equal to one, as is required for a probability distribution. This follows from a ] in the ]:<ref name="GaussProb" /> | |||
| Formulas of this type, now known as ]s, were used to set several successive records and remained the best known method for calculating π well into the age of computers. A remarkable record was set by the calculating prodigy ], who in 1844 employed a Machin-like formula to calculate 200 decimals of π in his head. The best value at the end of the 19th century was due to ], who took 15 years to calculate π with 707 digits, although due to a mistake only the first 527 were correct. (To avoid such errors, modern record calculations of any kind are often performed twice, with two different formulas. If the results are the same, they are likely to be correct.) | |||
| <math display=block>\int_{-\infty}^\infty e^{-u^2} \, du=\sqrt{\pi}</math> | |||
| which says that the area under the basic ] in the figure is equal to the square root of {{pi}}. | |||
| The ] explains the central role of normal distributions, and thus of {{pi}}, in probability and statistics. This theorem is ultimately connected with the ] of {{pi}} as the eigenvalue associated with the Heisenberg uncertainty principle, and the fact that equality holds in the uncertainty principle only for the Gaussian function.{{sfn|Dym|McKean|1972|loc=Section 2.7}} Equivalently, {{pi}} is the unique constant making the Gaussian normal distribution {{math|''e''{{sup|−π''x''{{sup|2}}}}}} equal to its own Fourier transform.<ref>{{cite book |first1=Elias|last1=Stein |first2=Guido|last2=Weiss |title=Fourier analysis on Euclidean spaces |year=1971 |publisher=Princeton University Press |page=6|author1-link=Elias Stein}}; Theorem 1.13.</ref> Indeed, according to {{harvtxt|Howe|1980}}, the "whole business" of establishing the fundamental theorems of Fourier analysis reduces to the Gaussian integral.<ref name=howe/> | |||
| Theoretical advances in the 18th century led to insights about π's nature that could not be achieved through numerical calculation alone. ] proved the irrationality of π in 1761, and ] proved in 1794 that also π<sup>2</sup> is irrational. When ] in 1735 solved the famous ] – finding the exact value of | |||
| === Topology === | |||
| :<math>\frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots\!</math> | |||
| ] of the ], a surface of ] three and Euler characteristic −4, as a quotient of the ] by the ] ] of the ]. The hyperbolic area of a fundamental domain is {{math|8π}}, by Gauss–Bonnet.]] | |||
| The constant {{pi}} appears in the ] which relates the ] to their ]. Specifically, if a ] surface {{math|Σ}} has ] ''K'', then | |||
| <math display=block>\int_\Sigma K\,dA = 2\pi \chi(\Sigma)</math> | |||
| where {{math|''χ''(Σ)}} is the ], which is an integer.<ref>{{cite book |title=A Comprehensive Introduction to Differential Geometry |volume=3 |first=Michael|last= Spivak |year=1999 |publisher=Publish or Perish Press|author-link=Michael Spivak}}; Chapter 6.</ref> An example is the surface area of a sphere ''S'' of curvature 1 (so that its ], which coincides with its radius, is also 1.) The Euler characteristic of a sphere can be computed from its ]s and is found to be equal to two. Thus we have | |||
| <math display=block>A(S) = \int_S 1\,dA = 2\pi\cdot 2 = 4\pi</math> | |||
| reproducing the formula for the surface area of a sphere of radius 1. | |||
| The constant appears in many other integral formulae in topology, in particular, those involving ]es via the ].<ref>{{cite book |last1=Kobayashi |first1=Shoshichi |last2=Nomizu |first2=Katsumi |title=Foundations of Differential Geometry |volume=2 |publisher=] |year=1996 |edition=New |page=293|title-link=Foundations of Differential Geometry}}; Chapter XII ''Characteristic classes''</ref> | |||
| which is π<sup>2</sup>/6, he established a deep connection between π and the ]s. Both Legendre and Leonhard Euler speculated that π might be ], a fact that was proved in 1882 by ]. | |||
| === Cauchy's integral formula === | |||
| ]' book ''A New Introduction to Mathematics'' from ] is cited as the first text where the ] was used for this constant, but this notation became particularly popular after ] adopted it in 1737.<ref>{{cite web|url=http://www.famousWelsh.com/cgibin/getmoreinf.cgi?pers_id=737|title=About: William Jones|work=Famous Welsh|accessdate=2007-10-27}}</ref> He wrote: | |||
| ] | |||
| {{cquote|<nowiki>There are various other ways of finding the Lengths or Areas of particular Curve Lines, or Planes, which may very much facilitate the Practice; as for instance, in the Circle, the Diameter is to the Circumference as 1 to (16/5 - 4/239) - 1/3(16/5^3 - 4/239^3) + ... = 3.14159... = π</nowiki><ref name="adm"/>}} | |||
| {{seealso|history of mathematical notation}} | |||
| One of the key tools in ] is ] of a function over a positively oriented (]) ] {{math|''γ''}}. A form of ] states that if a point {{math|''z''<sub>0</sub>}} is interior to {{math|''γ''}}, then<ref>{{cite book |first=Lars|last= Ahlfors |title=Complex analysis |publisher=McGraw-Hill |year=1966 |page=115|author-link=Lars Ahlfors}}</ref> | |||
| ===Computation in the computer age=== | |||
| <math display=block>\oint_\gamma \frac{dz}{z-z_0} = 2\pi i.</math> | |||
| Although the curve {{math|''γ''}} is not a circle, and hence does not have any obvious connection to the constant {{pi}}, a standard proof of this result uses ], which implies that the integral is invariant under ] of the curve, so that it can be deformed to a circle and then integrated explicitly in polar coordinates. More generally, it is true that if a rectifiable closed curve {{math|γ}} does not contain {{math|''z''<sub>0</sub>}}, then the above integral is {{math|2π''i''}} times the ] of the curve. | |||
| The advent of digital computers in the 20th century led to an increased rate of new π calculation records. ] used ] to compute 2037 digits of π in 1949, a calculation that took 70 hours. Additional thousands of decimal places were obtained in the following decades, with the million-digit milestone passed in 1973. Progress was not only due to faster hardware, but also new algorithms. One of the most significant developments was the discovery of the ] (FFT) in the 1960s, which allows computers to perform arithmetic on extremely large numbers quickly. | |||
| The general form of Cauchy's integral formula establishes the relationship between the values of a ] {{math|''f''(''z'')}} on the Jordan curve {{math|''γ''}} and the value of {{math|''f''(''z'')}} at any interior point {{math|''z''<sub>0</sub>}} of {{math|γ}}:<ref>{{cite book|last=Joglekar|first=S. D.|title=Mathematical Physics|publisher=Universities Press|year=2005|page=166|isbn=978-81-7371-422-1}}</ref> | |||
| In the beginning of the 20th century, the Indian mathematician ] found many new formulas for π, some remarkable for their elegance and mathematical depth.<ref name="rad">{{cite web|url=http://numbers.computation.free.fr/Constants/Pi/piramanujan.html|title=The constant π: Ramanujan type formulas|accessdate=2007-11-04}}</ref> Two of his most famous formulas are the series | |||
| <math display=block>\oint_\gamma { f(z) \over z-z_0 }\,dz = 2\pi i f (z_{0})</math> | |||
| provided {{math|''f''(''z'')}} is analytic in the region enclosed by {{math|''γ''}} and extends continuously to {{math|''γ''}}. Cauchy's integral formula is a special case of the ], that if {{math|''g''(''z'')}} is a ] the region enclosed by {{math|''γ''}} and is continuous in a neighbourhood of {{math|''γ''}}, then | |||
| <math display=block>\oint_\gamma g(z)\, dz =2\pi i \sum \operatorname{Res}( g, a_k ) </math> | |||
| where the sum is of the ] at the ] of {{math|''g''(''z'')}}. | |||
| === Vector calculus and physics === | |||
| :<math>\frac{1}{\pi} = \frac{2 \sqrt 2}{9801} \sum_{k=0}^\infty \frac{(4k)!(1103+26390k)}{(k!)^4 396^{4k}}\!</math> | |||
| The constant {{pi}} is ubiquitous in ] and ], for example in ],<ref>{{cite book|first=H. M.|last=Schey|year=1996|title=Div, Grad, Curl, and All That: An Informal Text on Vector Calculus|publisher=W.W. Norton |isbn=0-393-96997-5}}</ref> ], ], and even the ].<ref>{{cite book|last=Yeo|first=Adrian|title=The pleasures of pi, e and other interesting numbers|publisher=World Scientific Pub.|year=2006|page=21|isbn=978-981-270-078-0}}</ref><ref>{{cite book|last=Ehlers|first=Jürgen|title=Einstein's Field Equations and Their Physical Implications|publisher=Springer|year=2000|page=7|isbn=978-3-540-67073-5}}</ref> Perhaps the simplest example of this is the two-dimensional ], representing the potential of a point source at the origin, whose associated field has unit outward ] through any smooth and oriented closed surface enclosing the source: | |||
| and | |||
| <math display="block">\Phi(\mathbf x) = \frac{1}{2\pi}\log|\mathbf x|.</math> | |||
| :<math>\frac{426880 \sqrt{10005}}{\pi} = \sum_{k=0}^\infty \frac{(6k)! (13591409 + 545140134k)}{(3k)!(k!)^3 (-640320)^{3k}}\!</math> | |||
| The factor of <math>1/2\pi</math> is necessary to ensure that <math>\Phi</math> is the ] of the ] in <math>\mathbb R^2</math>:<ref name="Elliptic PDE2">{{citation|first1=D.|last1=Gilbarg|first2=Neil|last2=Trudinger|authorlink2=Neil Trudinger|title=Elliptic Partial Differential Equations of Second Order|publisher=Springer|publication-place=New York|year=1983|isbn=3-540-41160-7}}</ref> | |||
| <math display="block">\Delta\Phi = \delta</math> | |||
| where <math>\delta</math> is the ]. | |||
| In higher dimensions, factors of {{pi}} are present because of a normalization by the n-dimensional volume of the unit ]. For example, in three dimensions, the Newtonian potential is:<ref name="Elliptic PDE2"/> | |||
| which deliver 14 digits per term.<ref name="rad"/> The Chudnovsky brothers used this formula to set several π computing records in the end of the 1980s, including the first calculation of over one billion (1,011,196,691) decimals in 1989. It remains the formula of choice for π calculating software that runs on personal computers, as opposed to the ]s used to set modern records. | |||
| <math display="block">\Phi(\mathbf x) = -\frac{1}{4\pi|\mathbf x|},</math> | |||
| which has the 2-dimensional volume (i.e., the area) of the unit 2-sphere in the denominator. | |||
| === Total curvature === | |||
| Whereas series typically increase the accuracy with a fixed amount for each added term, there exist iterative algorithms that ''multiply'' the number of correct digits at each step, with the downside that each step generally requires an expensive calculation. A breakthrough was made in 1975, when ] and ] independently discovered the ], which uses only arithmetic to double the number of correct digits at each step.<ref name="brent">{{Citation | last=Brent | first=Richard | author-link=Richard Brent (scientist) | year=1975 | title=Multiple-precision zero-finding methods and the complexity of elementary function evaluation | periodical=Analytic Computational Complexity | publication-place=New York | publisher=Academic Press | editor-last=Traub | editor-first=J F | pages=151–176 | url=http://wwwmaths.anu.edu.au/~brent/pub/pub028.html | accessdate=2007-09-08}}</ref> The algorithm consists of setting | |||
| {{excerpt|Total curvature}} | |||
| === The gamma function and Stirling's approximation === | |||
| :<math>a_0 = 1 \quad \quad \quad b_0 = \frac{1}{\sqrt 2} \quad \quad \quad t_0 = \frac{1}{4} \quad \quad \quad p_0 = 1\!</math> | |||
| ] | |||
| The ] function <math>n!</math> is the product of all of the positive integers through {{math|''n''}}. The ] extends the concept of ] (normally defined only for non-negative integers) to all complex numbers, except the negative real integers, with the identity <math>\Gamma(n)=(n-1)!</math>. When the gamma function is evaluated at half-integers, the result contains {{pi}}. For example, <math> \Gamma(1/2) = \sqrt{\pi} </math> and <math display="inline">\Gamma(5/2) = \frac {3 \sqrt{\pi}} {4}</math>.<ref>{{harvnb|Bronshteĭn|Semendiaev|1971|pp=191–192}}</ref> | |||
| The gamma function is defined by its ] development:<ref>{{cite book |title=The Gamma Function |first=Emil|last= Artin |publisher=Holt, Rinehart and Winston |year=1964 |series=Athena series; selected topics in mathematics |edition=1st|author-link= Emil Artin}}</ref> | |||
| and iterating | |||
| <math display=block>\Gamma(z) = \frac{e^{-\gamma z}}{z}\prod_{n=1}^\infty \frac{e^{z/n}}{1+z/n}</math> | |||
| where {{math|γ}} is the ]. Evaluated at {{math|''z'' {{=}} 1/2}} and squared, the equation {{math|Γ(1/2)<sup>2</sup> {{=}} π}} reduces to the Wallis product formula. The gamma function is also connected to the ] and identities for the ], in which the constant {{pi}} ]. | |||
| The gamma function is used to calculate the volume {{math|''V''<sub>''n''</sub>(''r'')}} of the ] of radius ''r'' in Euclidean ''n''-dimensional space, and the surface area {{math|''S''<sub>''n''−1</sub>(''r'')}} of its boundary, the ]:<ref>{{cite book |first=Lawrence|last= Evans |title=Partial Differential Equations |publisher=AMS |year=1997 |page=615}}</ref> | |||
| :<math>a_{n+1} = \frac{a_n+b_n}{2} \quad \quad \quad b_{n+1} = \sqrt{a_n b_n}\!</math> | |||
| <math display=block>V_n(r) = \frac{\pi^{n/2}}{\Gamma\left(\frac{n}{2}+1\right)}r^n,</math> | |||
| <math display=block>S_{n-1}(r) = \frac{n\pi^{n/2}}{\Gamma\left(\frac{n}{2}+1\right)}r^{n-1}.</math> | |||
| Further, it follows from the ] that | |||
| until ''a<sub>n</sub>'' and ''b<sub>n</sub>'' are close enough. Then the estimate for π is given by | |||
| <math display=block>2\pi r = \frac{S_{n+1}(r)}{V_n(r)}.</math> | |||
| The gamma function can be used to create a simple approximation to the factorial function {{math|''n''!}} for large {{math|''n''}}: <math display="inline"> n! \sim \sqrt{2 \pi n} \left(\frac{n}{e}\right)^n</math> which is known as ].<ref>{{harvnb|Bronshteĭn|Semendiaev|1971|p=190}}</ref> Equivalently, | |||
| :<math>\pi \approx \frac{(a_n + b_n)^2}{4 t_n}\!</math>. | |||
| <math display=block>\pi = \lim_{n\to\infty} \frac{e^{2n}n!^2}{2 n^{2n+1}}.</math> | |||
| As a geometrical application of Stirling's approximation, let {{math|Δ<sub>''n''</sub>}} denote the ] in ''n''-dimensional Euclidean space, and {{math|(''n'' + 1)Δ<sub>''n''</sub>}} denote the simplex having all of its sides scaled up by a factor of {{math|''n'' + 1}}. Then | |||
| Using this scheme, 25 iterations suffice to reach 45 million correct decimals. A similar algorithm that quadruples the accuracy in each step has been found by ] and ].<ref>{{cite book|first=Jonathan M|last=Borwein|authorlink=Jonathan Borwein|coauthors=Borwein, Peter, Berggren, Lennart|date=2004|title=Pi: A Source Book|publisher=Springer|isbn=0387205713}}</ref> The methods have been used by ] and team to set most of the π calculation records since 1980, up to a calculation of 206,158,430,000 decimals of π in 1999. The current record is 1,241,100,000,000 decimals, set by Kanada and team in 2002. Although most of Kanada's previous records were set using the Brent-Salamin algorithm, the 2002 calculation made use of two Machin-like formulas that were slower but crucially reduced memory consumption. The calculation was performed on a 64-node Hitachi supercomputer with 1 ] of main memory, capable of carrying out 2 trillion operations per second. | |||
| <math display=block>\operatorname{Vol}((n+1)\Delta_n) = \frac{(n+1)^n}{n!} \sim \frac{e^{n+1}}{\sqrt{2\pi n}}.</math> | |||
| ] is that this is the (optimal) upper bound on the volume of a ] containing only one ].<ref>{{cite journal |author1=Benjamin Nill |author2=Andreas Paffenholz |title=On the equality case in Erhart's volume conjecture |year=2014 |arxiv=1205.1270 |journal=Advances in Geometry |volume=14 |issue=4 |pages=579–586 |issn=1615-7168 |doi=10.1515/advgeom-2014-0001|s2cid=119125713 }}</ref> | |||
| An important recent development was the ] (BBP formula), discovered by ] and named after the authors of the paper in which the formula was first published, ], ], and Plouffe.<ref name="bbpf">{{cite journal | |||
| | author = ], ], and ] | |||
| | year =1997 | month = April | |||
| | title = On the Rapid Computation of Various Polylogarithmic Constants | |||
| | journal = Mathematics of Computation | |||
| | volume = 66 | issue = 218 | pages = 903–913 | |||
| | url = http://crd.lbl.gov/~dhbailey/dhbpapers/digits.pdf | |||
| | format = ] | |||
| | doi = 10.1090/S0025-5718-97-00856-9 | |||
| }}</ref> The formula, | |||
| === Number theory and Riemann zeta function === | |||
| :<math>\pi = \sum_{k=0}^\infty \frac{1}{16^k} \left( \frac{4}{8k + 1} - \frac{2}{8k + 4} - \frac{1}{8k + 5} - \frac{1}{8k + 6}\right),</math> | |||
| ], which are arithmetic localizations of the circle. The ]s of analytic number theory are also localized in each prime ''p''.]] | |||
| ]: the value of {{math|''ζ''(2)}} is the ] area of a fundamental domain of the ], times {{math|{{pi}}/2}}.]] | |||
| The ] {{math|''ζ''(''s'')}} is used in many areas of mathematics. When evaluated at {{math|1=''s'' = 2}} it can be written as | |||
| <math display=block>\zeta(2) = \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \cdots</math> | |||
| Finding a ] for this infinite series was a famous problem in mathematics called the ]. ] solved it in 1735 when he showed it was equal to {{math|π<sup>2</sup>/6}}.<ref name="Posamentier" /> Euler's result leads to the ] result that the probability of two random numbers being ] (that is, having no shared factors) is equal to {{math|6/π<sup>2</sup>}}.<ref>{{harvnb|Arndt|Haenel|2006|pp=41–43}}</ref><ref>This theorem was proved by ] in 1881. For a more rigorous proof than the intuitive and informal one given here, see {{cite book|last=Hardy|first=G. H.|title=An Introduction to the Theory of Numbers|publisher=Oxford University Press|year=2008|isbn=978-0-19-921986-5|at=Theorem 332}}</ref> This probability is based on the observation that the probability that any number is ] by a prime {{math|''p''}} is {{math|1/''p''}} (for example, every 7th integer is divisible by 7.) Hence the probability that two numbers are both divisible by this prime is {{math|1/''p''<sup>2</sup>}}, and the probability that at least one of them is not is {{math|1 − 1/''p''<sup>2</sup>}}. For distinct primes, these divisibility events are mutually independent; so the probability that two numbers are relatively prime is given by a product over all primes:<ref>{{cite book|author1-link=C. Stanley Ogilvy|last1=Ogilvy|first1=C. S.|last2=Anderson|first2=J. T.|title=Excursions in Number Theory|publisher=Dover Publications Inc.|year=1988|pages=29–35|isbn=0-486-25778-9}}</ref> | |||
| is remarkable because it allows extracting any individual ] or ] digit of π without calculating all the preceding ones.<ref name="bbpf"/> Between 1998 and 2000, the ] project ] used a modification of the BBP formula due to ] to compute the ] (1,000,000,000,000,000:th) bit of π, which turned out to be 0.<ref>{{cite web|url=http://fabrice.bellard.free.fr/pi/pi_bin/pi_bin.html|title=A new formula to compute the n<sup>th</sup> binary digit of pi|first=Fabrice|last=Bellard|authorlink=Fabrice Bellard|accessdate=2007-10-27}}</ref> | |||
| <math display=block>\begin{align} | |||
| \prod_p^\infty \left(1-\frac{1}{p^2}\right) &= \left( \prod_p^\infty \frac{1}{1-p^{-2}} \right)^{-1}\\ | |||
| &= \frac{1}{1 + \frac{1}{2^2} + \frac{1}{3^2} + \cdots }\\ | |||
| &= \frac{1}{\zeta(2)} = \frac{6}{\pi^2} \approx 61\%. | |||
| \end{align}</math> | |||
| This probability can be used in conjunction with a ] to approximate {{pi}} using a Monte Carlo approach.<ref>{{harvnb|Arndt|Haenel|2006|p=43}}</ref> | |||
| ===Memorizing digits=== | |||
| {{main|Piphilology}} | |||
| ] | |||
| The solution to the Basel problem implies that the geometrically derived quantity {{pi}} is connected in a deep way to the distribution of prime numbers. This is a special case of ], which asserts the equality of similar such infinite products of ''arithmetic'' quantities, localized at each prime ''p'', and a ''geometrical'' quantity: the reciprocal of the volume of a certain ]. In the case of the Basel problem, it is the ] {{math|]/]}}.<ref>{{cite book |title=Algebraic Groups and Number Theory |first1=Vladimir|last1=Platonov |first2=Andrei |last2=Rapinchuk |publisher=Academic Press |year=1994 |pages=262–265}}</ref> | |||
| Even long before computers have calculated ''π'', memorizing a ''record'' number of digits became an obsession for some people. | |||
| In 2006, ], a retired Japanese engineer, claimed to have recited 100,000 decimal places.<ref name="japantimes">{{cite news|first=Tomoko|last=Otake|url=http://search.japantimes.co.jp/print/fl20061217x1.html|title=How can anyone remember 100,000 numbers?|work=]|date=]|accessdate=2007-10-27}}</ref> This, however, has yet to be verified by ]. The Guinness-recognized record for remembered digits of ''π'' is 67,890 digits, held by ], a 24-year-old graduate student from ].<ref>{{cite web|url=http://www.pi-world-ranking-list.com/news/index.htm|title=Pi World Ranking List|accessdate=2007-10-27}}</ref> It took him 24 hours and 4 minutes to recite to the 67,890th decimal place of ''π'' without an error.<ref>{{cite news|url=http://www.newsgd.com/culture/peopleandlife/200611280032.htm|title=Chinese student breaks Guiness record by reciting 67,890 digits of pi|work=News Guangdong|date=]|accessdate=2007-10-27}}</ref> | |||
| The zeta function also satisfies Riemann's functional equation, which involves {{pi}} as well as the gamma function: | |||
| There are many ways to memorize ''π'', including the use of "piems", which are poems that represent ''π'' in a way such that the length of each word (in letters) represents a digit. Here is an example of a piem: ''How I need a drink, alcoholic in nature'' (or: ''of course'')'', after the heavy lectures involving quantum mechanics.''<ref>{{cite web|first=Jonathan M|last=Borwein|authorlink=Jonathan Borwein|url=http://users.cs.dal.ca/~jborwein/pi-culture.pdf|format=]|title=The Life of Pi: From Archimedes to Eniac and Beyond|publisher=] Computer Science|date=]|accessdate=2007-10-29}}</ref> Notice how the first word has 3 letters, the second word has 1, the third has 4, the fourth has 1, the fifth has 5, and so on. The '']'' contains the first 3834 digits of ''π'' in this manner.<ref>{{cite web|first=Mike|last=Keith|authorlink=Mike Keith (mathematician)|url=http://users.aol.com/s6sj7gt/solution.htm|title=Cadaeic Cadenza: Solution & Commentary|date=1996|accessdate=2007-10-30}}</ref> Piems are related to the entire field of humorous yet serious study that involves the use of ] to remember the digits of ''π'', known as ]. See ] for examples. In other languages there are similar methods of memorization. However, this method proves inefficient for large memorizations of pi. Other methods include remembering patterns in the numbers.<ref>{{cite web|first=Yicong|last=Liu|url=http://silverchips.mbhs.edu/inside.php?sid=3577|title=Oh my, memorizing so many digits of pi.|publisher=Silver Chips Online|date=]|accessdate=2007-11-04}}</ref> | |||
| <math display=block>\zeta(s) = 2^s\pi^{s-1}\ \sin\left(\frac{\pi s}{2}\right)\ \Gamma(1-s)\ \zeta(1-s).</math> | |||
| Furthermore, the derivative of the zeta function satisfies | |||
| ==Advanced properties== | |||
| <math display=block>\exp(-\zeta'(0)) = \sqrt{2\pi}.</math> | |||
| ===Numerical approximations=== | |||
| {{main|History of numerical approximations of π}} | |||
| Due to the transcendental nature of ''π'', there are no closed form expressions for the number in terms of algebraic numbers and functions.<ref name="ttop"/> Formulas for calculating ''π'' using elementary arithmetic typically include ] or ] (such as "..."), which indicates that the formula is really a formula for an infinite sequence of approximations to ''π''.<ref>{{cite web|url=http://mathworld.wolfram.com/PiFormulas.html|title=Pi Formulas|first=Eric W|last=Weisstein|authorlink=Eric W. Weisstein|publisher=]|date=]|accessdate=2007-11-10}}</ref> The more terms included in a calculation, the closer to ''π'' the result will get. | |||
| A consequence is that {{pi}} can be obtained from the ] of the ]. This functional determinant can be computed via a product expansion, and is equivalent to the Wallis product formula.<ref>{{cite journal |last=Sondow|first= J. |title=Analytic continuation of Riemann's zeta function and values at negative integers via Euler's transformation of series |journal=] |volume=120 |issue=2 |pages=421–424 |year=1994 |doi=10.1090/s0002-9939-1994-1172954-7 |citeseerx=10.1.1.352.5774|s2cid= 122276856 }}</ref> The calculation can be recast in ], specifically the ] to the ].<ref>{{cite journal |doi=10.1063/1.4930800 |author1=T. Friedmann |author2=C.R. Hagen |title=Quantum mechanical derivation of the Wallis formula for pi |journal=Journal of Mathematical Physics |volume=56 |issue=11 |pages=112101 |year=2015 |arxiv=1510.07813 |bibcode=2015JMP....56k2101F|s2cid=119315853 }}</ref> | |||
| Consequently, numerical calculations must use ]s of ''π''. For many purposes, 3.14 or ] is close enough, although engineers often use 3.1416 (5 ]) or 3.14159 (6 significant figures) for more precision. The approximations <sup>22</sup>/<sub>7</sub> and <sup>355</sup>/<sub>113</sub>, with 3 and 7 significant figures respectively, are obtained from the simple ] expansion of ''π''. The approximation ] (3.1415929…) is the best one that may be expressed with a three-digit or four-digit ].<ref>{{cite news|language=Chinese|author=韩雪涛|title=数学科普:常识性谬误流传令人忧|publisher=中华读书报|date=]|url=http://www.xys.org/~xys/xys/ebooks/others/science/dajia/shuxuekepu.txt|accessdate=2006-10-06}}</ref><ref>{{cite web|url=http://www.kaidy.com/PiReward.htm|title=Magic of 355 ÷ 113|publisher=Kaidy Educational Resources|accessdate=2007-11-08}}</ref><ref>{{cite web|url=http://numbers.computation.free.fr/Constants/Pi/piApprox.html|title=Collection of approximations for π|publisher=Numbers, constants and computation|first=Xavier|last=Gourdon|coauthors=Pascal Sebah|accessdate=2007-11-08}}</ref> | |||
| === Fourier series === | |||
| The earliest numerical approximation of ''π'' is almost certainly the value {{num|3}}.<ref name="ahop"/> In cases where little precision is required, it may be an acceptable substitute. That 3 is an underestimate follows from the fact that it is the ratio of the ] of an ] ] ] to the ] of the ]. | |||
| ] (shown), which are elements of a ]. ] makes heavy use of this machinery.<ref>{{cite conference |last1=Tate |first1=John T. |editor1-first=J. W. S. |editor1-last=Cassels|editor2-first=A.|editor2-last=Fröhlich|title=Algebraic Number Theory (Proc. Instructional Conf., Brighton, 1965) |publisher=Thompson, Washington, DC |isbn=978-0-9502734-2-6 |mr=0217026 |year=1950 |contribution=Fourier analysis in number fields, and Hecke's zeta-functions |pages=305–347}}</ref>|left]] | |||
| The constant {{pi}} also appears naturally in ] of ]s. Periodic functions are functions on the group {{math|'''T''' {{=}}'''R'''/'''Z'''}} of fractional parts of real numbers. The Fourier decomposition shows that a complex-valued function {{math|''f''}} on {{math|'''T'''}} can be written as an infinite linear superposition of ]s of {{math|'''T'''}}. That is, continuous ]s from {{math|'''T'''}} to the ] {{math|''U''(1)}} of unit modulus complex numbers. It is a theorem that every character of {{math|'''T'''}} is one of the complex exponentials <math>e_n(x)= e^{2\pi i n x}</math>. | |||
| There is a unique character on {{math|'''T'''}}, up to complex conjugation, that is a group isomorphism. Using the ] on the circle group, the constant {{pi}} is half the magnitude of the ] of this character. The other characters have derivatives whose magnitudes are positive integral multiples of 2{{pi}}.<ref name="Nicolas Bourbaki" /> As a result, the constant {{pi}} is the unique number such that the group '''T''', equipped with its Haar measure, is ] to the ] of integral multiples of 2{{pi}}.{{sfn|Dym|McKean|1972|loc=Chapter 4}} This is a version of the one-dimensional ]. | |||
| ===Open questions=== | |||
| The most pressing open question about ''π'' is whether it is a ] — whether any digit block occurs in the expansion of ''π'' just as often as one would statistically expect if the digits had been produced completely "randomly", and that this is true in ''every'' base, not just base 10.<ref>{{cite web|url=http://mathworld.wolfram.com/NormalNumber.html|title=Normal Number|first=Eric W|last=Weisstein|authorlink=Eric W. Weisstein|publisher=]|date=]|accessdate=2007-11-10}}</ref> Current knowledge on this point is very weak; e.g., it is not even known which of the digits 0,…,9 occur infinitely often in the decimal expansion of ''π''.<ref>{{cite news|url=http://www.lbl.gov/Science-Articles/Archive/pi-random.html|title=Are The Digits of Pi Random? Lab Researcher May Hold The Key|first=Paul|last=Preuss|authorlink=Paul Preuss|publisher=]|date=]|accessdate=2007-11-10}}</ref> | |||
| === Modular forms and theta functions === | |||
| Bailey and Crandall showed in ] that the existence of the above mentioned ] and similar formulas imply that the normality in base 2 of ''π'' and various other constants can be reduced to a plausible ] of ].<ref>{{cite news|url=http://www.sciencenews.org/articles/20010901/bob9.asp|title=Pi à la Mode: Mathematicians tackle the seeming randomness of pi's digits|first=Ivars|last=Peterson|authorlink=Ivars Peterson|work=Science News Online|date=]|accessdate=2007-11-10}}</ref> | |||
| ] of periods of an elliptic curve.]] | |||
| The constant {{pi}} is connected in a deep way with the theory of ]s and ]s. For example, the ] involves in an essential way the ] of an ]. | |||
| It is also unknown whether ''π'' and ] are ], although ] proved the algebraic independence of {π, ], ](1/4)} in 1996.<ref>{{cite journal|author=Nesterenko, Yuri V|authorlink=Yuri Valentinovich Nesterenko|title=Modular Functions and Transcendence Problems|journal=] Série 1|volume=322|number=10|pages=909–914|year=1996}}</ref> However it is known that at least one of ''πe'' and ''π'' + ''e'' is ] (see ]).<!-- redundant wikilink intentional: specifically relevant to this section--> | |||
| ]s are ]s in the ] characterized by their transformation properties under the ] <math>\mathrm{SL}_2(\mathbb Z)</math> (or its various subgroups), a lattice in the group <math>\mathrm{SL}_2(\mathbb R)</math>. An example is the ] | |||
| ==Use in mathematics and science== | |||
| <math display=block>\theta(z,\tau) = \sum_{n=-\infty}^\infty e^{2\pi i nz + i\pi n^2\tau}</math> | |||
| {{main|List of formulas involving π}} | |||
| which is a kind of modular form called a ].<ref name="Mumford 1983 1–117">{{cite book |first=David |last=Mumford |author-link=David Mumford |title=Tata Lectures on Theta I |year=1983 |publisher=Birkhauser |location=Boston |isbn=978-3-7643-3109-2 |pages=1–117}}</ref> This is sometimes written in terms of the ] <math>q=e^{\pi i \tau}</math>. | |||
| π is ubiquitous in mathematics, appearing even in places that lack an obvious connection to the circles of Euclidean geometry.<ref>{{cite web|url=http://news.bbc.co.uk/1/hi/world/asia-pacific/4644103.stm|title=Japanese breaks pi memory record|work=]|date=]|accessdate=2007-10-30}}</ref> | |||
| The constant {{pi}} is the unique constant making the Jacobi theta function an ], which means that it transforms in a specific way. Certain identities hold for all automorphic forms. An example is | |||
| ===Geometry and trigonometry=== | |||
| <math display=block>\theta(z+\tau,\tau) = e^{-\pi i\tau -2\pi i z}\theta(z,\tau),</math> | |||
| {{seealso|Area of a disk}} | |||
| which implies that {{math|θ}} transforms as a representation under the discrete ]. General modular forms and other ]s also involve {{pi}}, once again because of the ].<ref name="Mumford 1983 1–117" /> | |||
| For any circle with radius ''r'' and diameter ''d'' = 2''r'', the circumference is π''d'' and the area is π''r''<sup>2</sup>. Further, π appears in formulas for areas and volumes of many other geometrical shapes based on circles, such as ]s, ]s, ]s, and ].<ref>{{cite web|url=http://www.math.psu.edu/courses/maserick/circle/circleapplet.html|title=Area and Circumference of a Circle by Archimedes|publisher=]|accessdate=2007-11-08}}</ref> Accordingly, π appears in ] that describe circumference, area or volume of shapes generated by circles. In the basic case, half the area of the ] is given by:<ref name="udi">{{cite web|url=http://mathworld.wolfram.com/UnitDiskIntegral.html|title=Unit Disk Integral|publisher=]|first=Eric W|last=Weisstein|authorlink=Eric W. Weisstein|date=]|accessdate=2007-11-08}}</ref> | |||
| :<math>\int_{-1}^1 \sqrt{1-x^2}\,dx = \frac{\pi}{2}</math> | |||
| and | |||
| :<math>\int_{-1}^1\frac{1}{\sqrt{1-x^2}}\,dx = \pi</math> | |||
| gives half the circumference of the ].<ref>{{cite web|url=http://www.math.psu.edu/courses/maserick/circle/circleapplet.html|title=Area and Circumference of a Circle by Archimedes|publisher=]|accessdate=2007-11-08}}</ref> More complicated shapes can be integrated as ].<ref>{{cite web|url=http://mathworld.wolfram.com/SolidofRevolution.html|title=Solid of Revolution|publisher=]|first=Eric W|last=Weisstein|authorlink=Eric W. Weisstein|date=]|accessdate=2007-11-08}}</ref> | |||
| === Cauchy distribution and potential theory === | |||
| From the unit-circle definition of the ]s also follows that the sine and cosine have period 2π. That is, for all ''x'' and integers ''n'', sin(''x'') = sin(''x'' + 2π''n'') and cos(''x'') = cos(''x'' + 2π''n''). Because sin(0) = 0, sin(2π''n'') = 0 for all integers ''n''. Also, the angle measure of 180° is equal to π radians. In other words, 1° = (π/180) radians. | |||
| ], named for ] (1718–1799), is a geometrical construction of the graph of the Cauchy distribution.|left]] | |||
| ] through a membrane.]] | |||
| The ] | |||
| <math display=block>g(x)=\frac{1}{\pi}\cdot\frac{1}{x^2+1}</math> | |||
| is a ]. The total probability is equal to one, owing to the integral: | |||
| <math display=block>\int_{-\infty }^{\infty } \frac{1}{x^2+1} \, dx = \pi.</math> | |||
| The ] of the Cauchy distribution is equal to {{math|ln(4π)}}, which also involves {{pi}}. | |||
| In modern mathematics, π is often ''defined'' using trigonometric functions, for example as the smallest positive ''x'' for which sin ''x'' = 0, to avoid unnecessary dependence on the subtleties of Euclidean geometry and integration. Equivalently, π can be defined using the ]s, for example as π = 2 arccos(0) or π = 4 arctan(1). Expanding inverse trigonometric functions as ] is the easiest way to derive infinite series for π. | |||
| The Cauchy distribution plays an important role in ] because it is the simplest ], the classical ] associated with a ] in a half-plane.<ref>{{cite book |first1=Sidney|last1= Port |first2=Charles|last2= Stone |title=Brownian motion and classical potential theory |publisher=Academic Press |year=1978 |page=29}}</ref> ]s and so also the ] are associated with the asymptotics of the Poisson kernel. The Hilbert transform ''H'' is the integral transform given by the ] of the ] | |||
| ===Higher analysis and number theory=== | |||
| <math display=block>Hf(t) = \frac{1}{\pi}\int_{-\infty}^\infty \frac{f(x)\,dx}{x-t}.</math> | |||
| The constant {{pi}} is the unique (positive) normalizing factor such that ''H'' defines a ] on the Hilbert space of square-integrable real-valued functions on the real line.<ref>{{cite book |last=Titchmarsh |first=E. |author-link=Edward Charles Titchmarsh |title=Introduction to the Theory of Fourier Integrals |isbn=978-0-8284-0324-5 |year=1948 |edition=2nd|publication-date=1986 |publisher=Clarendon Press |location=Oxford University}}</ref> The Hilbert transform, like the Fourier transform, can be characterized purely in terms of its transformation properties on the Hilbert space {{math|L<sup>2</sup>('''R''')}}: up to a normalization factor, it is the unique bounded linear operator that commutes with positive dilations and anti-commutes with all reflections of the real line.<ref>{{cite book |first=Elias |last=Stein |author-link=Elias Stein |title=Singular Integrals and Differentiability Properties of Functions |publisher=Princeton University Press |year=1970}}; Chapter II.</ref> The constant {{pi}} is the unique normalizing factor that makes this transformation unitary. | |||
| ] | |||
| === In the Mandelbrot set=== | |||
| The frequent appearance of π in ] can be related to the behavior of the ] of a complex variable, described by ] | |||
| ] can be used to approximate {{pi}}.]] | |||
| An occurrence of {{pi}} in the ] called the ] was discovered by David Boll in 1991.<ref name="KA">{{cite journal |last1=Klebanoff |first1=Aaron |year=2001 |title=Pi in the Mandelbrot set |journal=Fractals |volume=9 |issue=4 |pages=393–402 |url=http://home.comcast.net/~davejanelle/mandel.pdf |archive-url=https://web.archive.org/web/20111027155739/http://home.comcast.net/~davejanelle/mandel.pdf |archive-date=27 October 2011 |access-date=14 April 2012 |doi=10.1142/S0218348X01000828 |url-status=dead }}</ref> He examined the behaviour of the Mandelbrot set near the "neck" at {{math|(−0.75, 0)}}. When the number of iterations until divergence for the point {{math|(−0.75, ''ε'')}} is multiplied by {{mvar|ε}}, the result approaches {{pi}} as {{mvar|ε}} approaches zero. The point {{math|(0.25 + ''ε'', 0)}} at the cusp of the large "valley" on the right side of the Mandelbrot set behaves similarly: the number of iterations until divergence multiplied by the square root of {{mvar|ε}} tends to {{pi}}.<ref name="KA" /><ref>{{cite book|last=Peitgen|first=Heinz-Otto|title=Chaos and fractals: new frontiers of science|publisher=Springer|year=2004|pages=801–803|isbn=978-0-387-20229-7}}</ref> | |||
| :<math>e^{i\varphi} = \cos \varphi + i\sin \varphi \!</math> | |||
| === Projective geometry === | |||
| where ''i'' is the ] satisfying ''i''<sup>2</sup> = −1 and ''e'' ≈ 2.71828 is ]. This formula implies that imaginary powers of ''e'' describe rotations on the ] in the complex plane; these rotations have a period of 360° = 2π. In particular, the 180° rotation ''φ'' = π results in the remarkable ] | |||
| Let {{math|''V''}} be the set of all twice differentiable real functions <math>f:\mathbb R\to\mathbb R</math> that satisfy the ] <math>f''(x)+f(x)=0</math>. Then {{math|''V''}} is a two-dimensional real ], with two parameters corresponding to a pair of ] for the differential equation. For any <math>t\in\mathbb R</math>, let <math>e_t:V\to\mathbb R</math> be the evaluation functional, which associates to each <math>f\in V</math> the value <math>e_t(f)=f(t)</math> of the function {{math|''f''}} at the real point {{math|''t''}}. Then, for each ''t'', the ] of <math>e_t</math> is a one-dimensional linear subspace of {{math|''V''}}. Hence <math>t\mapsto\ker e_t</math> defines a function from <math>\mathbb R\to\mathbb P(V)</math> from the real line to the ]. This function is periodic, and the quantity {{pi}} can be characterized as the period of this map.<ref>{{cite book |title=Projective Differential Geometry Old and New: From the Schwarzian Derivative to the Cohomology of Diffeomorphism Groups |series=Cambridge Tracts in Mathematics |publisher=Cambridge University Press |year=2004 |isbn=978-0-521-83186-4 |first1=V.|last1=Ovsienko|first2=S.|last2=Tabachnikov|contribution=Section 1.3}}</ref> This is notable in that the constant {{pi}}, rather than 2{{pi}}, appears naturally in this context. | |||
| == Outside mathematics == | |||
| :<math>e^{i \pi} = -1.\!</math> | |||
| === Describing physical phenomena === | |||
| There are ''n'' different ''n''-th ] | |||
| Although not a ], {{pi}} appears routinely in equations describing fundamental principles of the universe, often because of {{pi}}'s relationship to the circle and to ]s. A simple formula from the field of ] gives the approximate period {{math|''T''}} of a simple ] of length {{math|''L''}}, swinging with a small amplitude ({{math|''g''}} is the ]):<ref>{{cite book|last1=Halliday|first1=David|last2=Resnick|first2=Robert|last3=Walker|first3=Jearl|title=Fundamentals of Physics|edition=5th|publisher=John Wiley & Sons|year=1997|page=381|isbn=0-471-14854-7}}</ref> | |||
| :<math>e^{2 \pi i k/n} \qquad (k = 0, 1, 2, \dots, n - 1).</math> | |||
| <math display=block>T \approx 2\pi \sqrt\frac{L}{g}.</math> | |||
| One of the key formulae of ] is ], which shows that the uncertainty in the measurement of a particle's position (Δ{{math|''x''}}) and ] (Δ{{math|''p''}}) cannot both be arbitrarily small at the same time (where {{math|''h''}} is the ]):<ref>{{cite book|title=College Physics 2e|contribution=29.7 Probability: The Heisenberg Uncertainty Principle|contribution-url=https://openstax.org/books/college-physics-2e/pages/29-7-probability-the-heisenberg-uncertainty-principle|publisher=]|first1=Paul Peter|last1=Urone|first2=Roger|last2=Hinrichs|year=2022}}</ref> | |||
| The ] | |||
| <math display=block> \Delta x\, \Delta p \ge \frac{h}{4\pi}.</math> | |||
| The fact that {{pi}} is approximately equal to 3 plays a role in the relatively long lifetime of ]. The inverse lifetime to lowest order in the ] {{math|''α''}} is<ref>{{cite book |last1=Itzykson |first1=C. |author-link1=Claude Itzykson |last2=Zuber |first2=J.-B. |author-link2=Jean-Bernard Zuber |title=Quantum Field Theory |date=1980 |publisher=Dover Publications |location=Mineola, NY |isbn=978-0-486-44568-7 |edition=2005 |url=https://books.google.com/books?id=4MwsAwAAQBAJ |lccn=2005053026 |oclc=61200849}}</ref> | |||
| :<math>\int_{-\infty}^{\infty}e^{-x^2}dx=\sqrt{\pi}.</math> | |||
| <math display=block>\frac{1}{\tau} = 2\frac{\pi^2 - 9}{9\pi}m_\text{e}\alpha^{6},</math> | |||
| where {{math|''m''<sub>e</sub>}} is the mass of the electron. | |||
| {{pi}} is present in some structural engineering formulae, such as the ] formula derived by Euler, which gives the maximum axial load {{math|''F''}} that a long, slender column of length {{math|''L''}}, ] {{math|''E''}}, and ] {{math|''I''}} can carry without buckling:<ref>{{cite book|last=Low|first=Peter|title=Classical Theory of Structures Based on the Differential Equation|publisher=Cambridge University Press|year=1971|pages=116–118|isbn=978-0-521-08089-7}}</ref> | |||
| A consequence is that the ] of a half-integer is a rational multiple of √π. | |||
| <math display=block>F =\frac{\pi^2EI}{L^2}.</math> | |||
| <!-- need some prose here on the zeta function and primes --> | |||
| The field of ] contains {{pi}} in ], which approximates the ] {{math|''F''}} exerted on small, ] objects of radius {{math|''R''}}, moving with velocity {{math|''v''}} in a ] with ] {{math|''η''}}:<ref>{{cite book|last=Batchelor|first=G. K.|title=An Introduction to Fluid Dynamics|publisher=Cambridge University Press|year=1967|page=233|isbn=0-521-66396-2}}</ref> | |||
| ===Physics=== | |||
| <math display=block>F =6\pi\eta Rv.</math> | |||
| Although not a ], ''π'' appears routinely in equations describing fundamental principles of the Universe, due in no small part to its relationship to the nature of the circle and, correspondingly, ]s. Using units such as ] can sometimes eliminate ''π'' from formulae. | |||
| In electromagnetics, the ] constant ''μ''<sub>0</sub> appears in ], which describe the properties of ] and ] fields and ]. Before 20 May 2019, it was defined as exactly | |||
| *The ]:<ref>{{cite web|first=Cole|last=Miller|url=http://www.astro.umd.edu/~miller/teaching/astr422/lecture12.pdf|format=]|title=The Cosmological Constant|publisher=]|accessdate=2007-11-08}}</ref> | |||
| <math display=block>\mu_0 = 4 \pi \times 10^{-7}\text{ H/m} \approx 1.2566370614 \ldots \times 10 ^{-6} \text{ N/A}^2. </math> | |||
| *], which shows that the uncertainty in the measurement of a particle's position (Δ''x'') and ] (Δ''p'') can not both be arbitrarily small at the same time:<ref>{{cite web|first=James M|last=Imamura|url=http://zebu.uoregon.edu/~imamura/208/jan27/hup.html|title=Heisenberg Uncertainty Principle|publisher=]|date=]|accessdate=2007-11-09}}</ref> | |||
| ::<math> \Delta x\, \Delta p \ge \frac{h}{4\pi} </math> | |||
| *] of ]:<ref name = ein>{{cite journal| last = Einstein| first = Albert| authorlink = Albert Einstein | title = The Foundation of the General Theory of Relativity| journal = ] |date=1916| url = http://www.alberteinstein.info/gallery/gtext3.html| format = ] | id = | accessdate = 2007-11-09 }}</ref> | |||
| ::<math> R_{ik} - {g_{ik} R \over 2} + \Lambda g_{ik} = {8 \pi G \over c^4} T_{ik} </math> | |||
| *] for the ], describing the force between two ]s (''q<sub>1</sub>'' and ''q<sub>2</sub>'') separated by distance ''r'':<ref> | |||
| {{cite web|first=C. Rod|last=Nave|url=http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elefor.html#c3|title=Coulomb's Constant|work=]|publisher=]|date=]|accessdate=2007-11-09}}</ref> | |||
| ::<math> F = \frac{\left|q_1q_2\right|}{4 \pi \varepsilon_0 r^2}</math> | |||
| *]:<ref>{{cite web |url=http://physics.nist.gov/cgi-bin/cuu/Value?mu0 |title=Magnetic constant |accessdate=2007-11-09 |date=2006 ] recommended values |publisher=] }}</ref> | |||
| ::<math> \mu_0 = 4 \pi \cdot 10^{-7}\,\mathrm{N/A^2}\,</math> | |||
| *], relating the ] (''P'') and the ] (''a'') to the ]es (''M'' and ''m'') of two co-orbiting bodies: | |||
| ::<math>\frac{P^2}{a^3}={(2\pi)^2 \over G (M+m)} </math> | |||
| === Memorizing digits === | |||
| ===Probability and statistics=== | |||
| {{Main|Piphilology}} | |||
| In ] and ], there are many ] whose formulas contain ''π'', including: | |||
| ] is the practice of memorizing large numbers of digits of {{pi}},<ref name="A445">{{harvnb|Arndt|Haenel|2006|pp=44–45}}</ref> and world-records are kept by the '']''. The record for memorizing digits of {{pi}}, certified by Guinness World Records, is 70,000 digits, recited in India by Rajveer Meena in 9 hours and 27 minutes on 21 March 2015.<ref> {{webarchive|url=https://web.archive.org/web/20160214205333/http://www.guinnessworldrecords.com/world-records/most-pi-places-memorised |date=14 February 2016 }}, Guinness World Records.</ref> In 2006, ], a retired Japanese engineer, claimed to have recited 100,000 decimal places, but the claim was not verified by Guinness World Records.<ref name="japantimes">{{cite news |first=Tomoko |last=Otake |url=<!-- http://www.lacim.uqam.ca/~plouffe/inspired2.pdf -->http://www.japantimes.co.jp/life/2006/12/17/general/how-can-anyone-remember-100000-numbers/ |title=How can anyone remember 100,000 numbers? |work=] |date=17 December 2006 |access-date=27 October 2007|url-status=live |archive-url=https://web.archive.org/web/20130818004142/http://www.japantimes.co.jp/life/2006/12/17/life/how-can-anyone-remember-100000-numbers/ |archive-date=18 August 2013}}</ref> | |||
| *the ] for the ] with ] μ and ] σ, due to the ]:<ref>{{cite web|url=http://mathworld.wolfram.com/GaussianIntegral.html|title=Gaussian Integral|publisher=]|first=Eric W|last=Weisstein|authorlink=Eric W. Weisstein|date=]|accessdate=2007-11-08}}</ref> | |||
| One common technique is to memorize a story or poem in which the word lengths represent the digits of {{pi}}: The first word has three letters, the second word has one, the third has four, the fourth has one, the fifth has five, and so on. Such memorization aids are called ]s. An early example of a mnemonic for pi, originally devised by English scientist ], is "How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics."<ref name="A445" /> When a poem is used, it is sometimes referred to as a ''piem''.<ref>{{cite book|last=Danesi|first=Marcel|chapter=Chapter 4: Pi in Popular Culture|date=January 2021|doi=10.1163/9789004433397|page=|publisher=Brill|title=Pi ({{pi}}) in Nature, Art, and Culture|isbn=9789004433373 |s2cid=224869535 }}</ref> Poems for memorizing {{pi}} have been composed in several languages in addition to English.<ref name="A445" /> Record-setting {{pi}} memorizers typically do not rely on poems, but instead use methods such as remembering number patterns and the ].<ref>{{cite journal |last1=Raz |first1=A. |last2=Packard |first2=M.G. |year=2009 |title=A slice of pi: An exploratory neuroimaging study of digit encoding and retrieval in a superior memorist |journal=Neurocase |volume=15 |issue=5 |pages=361–372 |doi=10.1080/13554790902776896 |pmid=19585350 |pmc=4323087}}</ref> | |||
| :<math>f(x) = {1 \over \sigma\sqrt{2\pi} }\,e^{-(x-\mu )^2/(2\sigma^2)}</math> | |||
| *the probability density function for the (standard) ]:<ref>{{cite web|url=http://mathworld.wolfram.com/CauchyDistribution.html|title=Cauchy Distribution|publisher=]|first=Eric W|last=Weisstein|authorlink=Eric W. Weisstein|date=]|accessdate=2007-11-08}}</ref> | |||
| A few authors have used the digits of {{pi}} to establish a new form of ], where the word lengths are required to represent the digits of {{pi}}. The '']'' contains the first 3835 digits of {{pi}} in this manner,<ref>{{cite web |first=Mike |last=Keith |author-link=Mike Keith (mathematician) |url=http://www.cadaeic.net/comments.htm |title=Cadaeic Cadenza Notes & Commentary |access-date=29 July 2009|url-status=live |archive-url=https://web.archive.org/web/20090118060210/http://cadaeic.net/comments.htm |archive-date=18 January 2009}}</ref> and the full-length book ''Not a Wake'' contains 10,000 words, each representing one digit of {{pi}}.<ref name=KeithNAW>{{cite book |last=Keith |first=Michael |title=Not A Wake: A dream embodying (pi)'s digits fully for 10,000 decimals |publisher=Vinculum Press |isbn=978-0-9630097-1-5 |author2=Diana Keith |date=17 February 2010}}</ref> | |||
| :<math>f(x) = \frac{1}{\pi (1 + x^2)}.</math> | |||
| === In popular culture === | |||
| Note that since <math>\int_{-\infty}^{\infty} f(x)\,dx = 1</math> for any probability density function ''f''(''x''), the above formulas can be used to produce other integral formulas for ''π''.<ref>{{cite web|url=http://mathworld.wolfram.com/ProbabilityFunction.html|title=Probability Function|publisher=]|first=Eric W|last=Weisstein|authorlink=Eric W. Weisstein|date=]|accessdate=2007-11-08}}</ref> | |||
| ] are circular, and "pie" and {{pi}} are ], making pie a frequent subject of pi ]s.]] | |||
| Perhaps because of the simplicity of its definition and its ubiquitous presence in formulae, {{pi}} has been represented in popular culture more than other mathematical constructs.<ref>For instance, Pickover calls π "the most famous mathematical constant of all time", and Peterson writes, "Of all known mathematical constants, however, pi continues to attract the most attention", citing the ] π perfume, ], and ] as examples. See: {{cite book |title=Keys to Infinity |first=Clifford A. |last=Pickover |author-link=Clifford A. Pickover |publisher=Wiley & Sons |year=1995 |isbn=978-0-471-11857-2 |page= |url=https://archive.org/details/keystoinfinity00clif/page/59}} {{cite book |title=Mathematical Treks: From Surreal Numbers to Magic Circles |series=MAA spectrum |first=Ivars |last=Peterson |author-link=Ivars Peterson |publisher=Mathematical Association of America |year=2002 |isbn=978-0-88385-537-9 |page=17 |url=https://books.google.com/books?id=4gWSAraVhtAC&pg=PA17|url-status=live |archive-url=https://web.archive.org/web/20161129190818/https://books.google.com/books?id=4gWSAraVhtAC&pg=PA17 |archive-date=29 November 2016}}</ref> | |||
| ] problem is sometimes quoted as a empirical approximation of ''π'' in "popular mathematics" works. Consider dropping a needle of length ''L'' repeatedly on a surface containing parallel lines drawn ''S'' units apart (with ''S'' > ''L''). If the needle is dropped ''n'' times and ''x'' of those times it comes to rest crossing a line (''x'' > 0), then one may approximate ''π'' using the ]:<ref name="bn">{{cite web|url=http://mathworld.wolfram.com/BuffonsNeedleProblem.html|title=Buffon's Needle Problem|first=Eric W|last=Weisstein|authorlink=Eric W. Weisstein|publisher=]|date=]|accessdate=2007-11-10}}</ref><ref>{{cite web|first=Alex|last=Bogomolny|url=http://www.cut-the-knot.org/ctk/August2001.shtml|title=Math Surprises: An Example|work=]|date=2001-08|accessdate=2007-10-28}}</ref><ref>{{cite journal|last = Ramaley|first = J. F.|title = Buffon's Noodle Problem|journal = The American Mathematical Monthly|volume = 76|issue = 8|date=Oct 1969|pages = 916–918|doi = 10.2307/2317945}}</ref><ref>{{cite web|url=http://www.datastructures.info/the-monte-carlo-algorithmmethod/|title=The Monte Carlo algorithm/method|work=datastructures|date=]|accessdate=2007-11-07}}</ref> | |||
| :<math>\pi \approx \frac{2nL}{xS}.</math> | |||
| Though this result is mathematically impeccable, it cannot be used to determine more than very few digits of ''π'' ''by experiment''. Reliably getting just three digits (including the initial "3") right requires millions of throws,<ref name="bn"/> and the number of throws grows ] with the number of digits desired. Furthermore, any error in the measurement of the lengths ''L'' and ''S'' will transfer directly to an error in the approximated ''π''. For example, a difference of a single ] in the length of a 10-centimeter needle would show up around the 9th digit of the result. In practice, uncertainties in determining whether the needle actually crosses a line when it appears to exactly touch it will limit the attainable accuracy to much less than 9 digits. | |||
| In the ] (a science museum in Paris) there is a circular room known as the ''pi room''. On its wall are inscribed 707 digits of {{pi}}. The digits are large wooden characters attached to the dome-like ceiling. The digits were based on an 1873 calculation by English mathematician ], which included an error beginning at the 528th digit. The error was detected in 1946 and corrected in 1949.<ref>{{harvnb|Posamentier|Lehmann|2004|p=118}}{{br}}{{harvnb|Arndt|Haenel|2006|p=50}}</ref> | |||
| ==See also== | |||
| *] | |||
| In ]'s 1985 novel '']'' it is suggested that the creator of the universe buried a message deep within the digits of {{pi}}. This part of the story was omitted from the ] adaptation of the novel.<ref>{{harvnb|Arndt|Haenel|2006|p=14}}</ref><ref>{{cite book|first1=Burkard |last1=Polster |first2=Marty |last2=Ross |author-link1=Burkard Polster |title=Math Goes to the Movies |year=2012 |isbn=978-1-421-40484-4 |publisher=Johns Hopkins University Press |pages=56–57}}</ref> The digits of {{pi}} have also been incorporated into the lyrics of the song "Pi" from the 2005 album '']'' by ].<ref>{{cite journal |title=Review of Aerial |first=Andy |last=Gill |journal=] |date=4 November 2005 |url=http://gaffa.org/reaching/rev_aer_UK5.html |quote=the almost autistic satisfaction of the obsessive-compulsive mathematician fascinated by 'Pi' (which affords the opportunity to hear Bush slowly sing vast chunks of the number in question, several dozen digits long)|url-status=live |archive-url=https://web.archive.org/web/20061015122229/http://gaffa.org/reaching/rev_aer_UK5.html |archive-date=15 October 2006}}</ref> In the 1967 '']'' episode "]", an out-of-control computer is contained by being instructed to "Compute to the last digit the value of {{pi}}".<ref name=life-of-pi/> | |||
| *] | |||
| *] – comprising the 762nd through 767th decimal places of π, consisting of the digit 9 repeated six times. | |||
| In the United States, ] falls on 14 March (written 3/14 in the US style), and is popular among students.<ref name=life-of-pi/> {{pi}} and its digital representation are often used by self-described "math ]s" for ]s among mathematically and technologically minded groups. A ] variously attributed to the ] or the ] includes "3.14159".<ref>{{cite journal|last=Rubillo|first=James M.|date=January 1989|issue=1|journal=]|jstor=27966082|page=10|title=Disintegrate 'em|volume=82}}</ref><ref>{{cite book|last=Petroski|first=Henry|author-link=Henry Petroski|isbn=978-1-139-50530-7|page=47|publisher=Cambridge University Press|title=Title An Engineer's Alphabet: Gleanings from the Softer Side of a Profession|url=https://books.google.com/books?id=oVXzxvS3MLUC&pg=PA47|year=2011}}</ref> Pi Day in 2015 was particularly significant because the date and time 3/14/15 9:26:53 reflected many more digits of pi.<ref>{{cite news |url=https://www.usatoday.com/story/news/nation-now/2015/03/14/pi-day-kids-videos/24753169/ |title=Happy Pi Day! Watch these stunning videos of kids reciting 3.14 |newspaper=USAToday.com |date=14 March 2015 |access-date=14 March 2015 |url-status=live |archive-url=https://web.archive.org/web/20150315005038/http://www.usatoday.com/story/news/nation-now/2015/03/14/pi-day-kids-videos/24753169/ |archive-date=15 March 2015}}</ref><ref>{{Cite journal |url=http://probability.ca/jeff/writing/PiInstant.html |title=Pi Instant |last=Rosenthal |first=Jeffrey S. |date=February 2015 |page=22 |journal=Math Horizons|volume=22 |issue=3 |doi=10.4169/mathhorizons.22.3.22 |s2cid=218542599 }}</ref> In parts of the world where dates are commonly noted in day/month/year format, 22 July represents "Pi Approximation Day", as 22/7 = 3.142857.<ref>{{cite news |last1=Griffin |first1=Andrew |title=Pi Day: Why some mathematicians refuse to celebrate 14 March and won't observe the dessert-filled day |url=https://www.independent.co.uk/news/science/pi-day-march-14-maths-google-doodle-pie-baking-celebrate-30-anniversary-a8254036.html |website=The Independent |access-date=2 February 2019 |archive-url=https://web.archive.org/web/20190424151944/https://www.independent.co.uk/news/science/pi-day-march-14-maths-google-doodle-pie-baking-celebrate-30-anniversary-a8254036.html |archive-date=24 April 2019 |url-status=live}}</ref> | |||
| *]. | |||
| *]. | |||
| {{anchor|tau}} <!-- (was) used in the redirect ] --> | |||
| *] on personal computers. | |||
| Some have proposed replacing {{pi}} by ],<ref>{{cite book|last1=Freiberger|first1=Marianne|last2=Thomas|first2=Rachel|contribution=Tau – the new {{pi}}|contribution-url=https://books.google.com/books?id=IbR-BAAAQBAJ&pg=PT133|isbn=978-1-62365-411-5|page=159|publisher=Quercus|title=Numericon: A Journey through the Hidden Lives of Numbers|year=2015}}</ref> arguing that {{mvar|τ}}, as the number of radians in one ] or the ratio of a circle's circumference to its radius, is more natural than {{pi}} and simplifies many formulae.<ref>{{cite journal |last=Abbott |first=Stephen |title=My Conversion to Tauism |journal=Math Horizons |date=April 2012 |volume=19 |issue=4 |page=34 |doi=10.4169/mathhorizons.19.4.34 |s2cid=126179022 |url=http://www.maa.org/sites/default/files/pdf/Mathhorizons/apr12_aftermath.pdf|url-status=live |archive-url=https://web.archive.org/web/20130928095819/http://www.maa.org/sites/default/files/pdf/Mathhorizons/apr12_aftermath.pdf |archive-date=28 September 2013}}</ref><ref>{{cite journal |last=Palais |first=Robert |title={{pi}} Is Wrong!|journal=The Mathematical Intelligencer|year=2001|volume=23|issue=3|pages=7–8|doi=10.1007/BF03026846|s2cid=120965049 |url=http://www.math.utah.edu/~palais/pi.pdf|url-status=live|archive-url=https://web.archive.org/web/20120622070009/http://www.math.utah.edu/~palais/pi.pdf|archive-date=22 June 2012}}</ref> This use of {{math|τ}} has not made its way into mainstream mathematics,<ref>{{cite journal |url=http://www.telegraphindia.com/1110630/jsp/nation/story_14178997.jsp |title=Life of pi in no danger – Experts cold-shoulder campaign to replace with tau |journal=Telegraph India |date=30 June 2011|url-status=dead |archive-url=https://web.archive.org/web/20130713084345/http://www.telegraphindia.com/1110630/jsp/nation/story_14178997.jsp |archive-date=13 July 2013}}</ref> but since 2010 this has led to people celebrating Two Pi Day or Tau Day on June 28.<ref>{{Cite web |title=Forget Pi Day. We should be celebrating Tau Day {{!}} Science News |url=https://www.sciencenews.org/blog/science-the-public/forget-pi-day-we-should-be-celebrating-tau-day |access-date=2023-05-02 |language=en-US}}</ref> | |||
| *]s: ] and ] | |||
| * ] resource . | |||
| In 1897, an amateur mathematician attempted to persuade the ] to pass the ], which described a method to ] and contained text that implied various incorrect values for {{pi}}, including 3.2. The bill is notorious as an attempt to establish a value of mathematical constant by legislative fiat. The bill was passed by the Indiana House of Representatives, but rejected by the Senate, and thus it did not become a law.<ref>{{harvnb|Arndt|Haenel|2006|pp=211–212}}{{br}}{{harvnb|Posamentier|Lehmann|2004|pp=36–37}}{{br}}{{cite journal |last1=Hallerberg |first1=Arthur |date=May 1977 |title=Indiana's squared circle |journal=Mathematics Magazine |volume=50 |issue=3 |pages=136–140 |jstor=2689499 |doi=10.2307/2689499}}</ref> | |||
| === In computer culture === | |||
| In contemporary ], individuals and organizations frequently pay homage to the number {{pi}}. For instance, the ] ] let the version numbers of his program ] approach {{pi}}. The versions are 3, 3.1, 3.14, and so forth.<ref>{{cite journal |url=http://www.ntg.nl/maps/05/34.pdf |title=The Future of TeX and Metafont |first=Donald |last=Knuth |author-link=Donald Knuth |journal=TeX Mag |volume=5 |issue=1 |page=145 |date=3 October 1990 |access-date=17 February 2017|url-status=live |archive-url=https://web.archive.org/web/20160413230304/http://www.ntg.nl/maps/05/34.pdf |archive-date=13 April 2016}}</ref> | |||
| Many ]s include {{pi}} for use in programs. Similarly, ''{{mvar|τ}}'' has been added to several programming languages as a predefined constant.<ref>{{cite web| url = https://www.python.org/dev/peps/pep-0628/| title = PEP 628 – Add math.tau}}</ref><ref>{{cite web |url=https://docs.rs/tau/latest/tau/ |title=Crate tau |access-date=2022-12-06}}</ref> | |||
| == See also == | |||
| * ] | |||
| * ] | |||
| * ] | |||
| == References == | == References == | ||
| === Explanatory notes === | |||
| {{notelist}} | |||
| === Citations === | |||
| {{reflist|3}} | |||
| {{reflist}} | |||
| === General and cited sources === | |||
| ==External links== | |||
| {{refbegin|30em|indent=yes}} | |||
| {{commonscat}} | |||
| * {{cite book|last=Abramson|first=Jay|title=Precalculus|publisher=]|year=2014|url=https://openstax.org/details/books/precalculus}} | |||
| * | |||
| * {{cite book |last1=Andrews |first1=George E. |last2=Askey |first2=Richard |last3=Roy |first3=Ranjan |title=Special Functions |url=https://books.google.com/books?id=kGshpCa3eYwC&pg=PA59 |year=1999 |publisher=University Press |location=Cambridge |isbn=978-0-521-78988-2}} | |||
| * at the ] | |||
| * {{cite book |last1=Arndt |first1=Jörg |last2=Haenel |first2=Christoph |title=Pi Unleashed |publisher=Springer-Verlag |year=2006 |isbn=978-3-540-66572-4 <!--isbn only volume 1--> |url=https://books.google.com/books?id=QwwcmweJCDQC |access-date=5 June 2013}} English translation by Catriona and David Lischka. | |||
| * | |||
| * {{cite book |last1=Berggren |first1=Lennart |last2=Borwein |first2=Jonathan|author2-link=Jonathan Borwein |last3=Borwein |first3=Peter|author3-link=Peter Borwein |title=Pi: a Source Book |publisher=Springer-Verlag |year=1997 |isbn=978-0-387-20571-7 }} | |||
| * at ] | |||
| * {{cite book |last1=Boyer |first1=Carl B. |last2=Merzbach |first2=Uta C.|author2-link= Uta Merzbach |year=1991 |title=A History of Mathematics |url=https://archive.org/details/historyofmathema00boye|url-access=registration |edition=2 |publisher=Wiley |isbn=978-0-471-54397-8 }}<!-- Year from ISBN. Original citatation was just to Boyer. Possible that edition is wrong and therefore page is wrong. Editions: Boyer 1968, Boyer/Merzbach 1989, Boyer/Merzbach 1991, Merzbach/Boyer 2010, Merzbach/Boyer 2011. Verify second: Hui and 3072-sided polygon is on cited p. 202 of 1991 edition; p. 228 of 1968 edition. Google snippet has a hit for 3.1456 on p. 168 for 1991, but does not show the number. --> | |||
| * | |||
| * {{cite book |last1=Bronshteĭn |first1=Ilia |last2=Semendiaev |first2=K.A. |title=A Guide Book to Mathematics |publisher=] |year=1971 |isbn=978-3-87144-095-3 |title-link=A Guide Book to Mathematics}} | |||
| * | |||
| * {{cite book |first1=H. |last1=Dym |first2=H. P. |last2=McKean |title=Fourier series and integrals |publisher=Academic Press |year=1972 }} | |||
| * at ] | |||
| * {{wikicite |ref={{harvid|Eymard|Lafon|2004}} |reference={{cite book |ref=none |last1=Eymard |first1=Pierre |last2=Lafon |first2=Jean Pierre |title=The Number {{pi}} |publisher=American Mathematical Society |year=2004 |isbn=978-0-8218-3246-2 |translator-last=Wilson |translator-first=Stephen }} English translation of {{cite book |ref=none |display-authors=0 |last1=Eymard |first1=Pierre |last2=Lafon |first2=Jean Pierre |title=Autour du nombre {{pi}} |language=fr |publisher=Hermann |year=1999 }} }} | |||
| * | |||
| * {{cite book |last1=Posamentier |first1=Alfred S. |last2=Lehmann |first2=Ingmar |title={{pi}}: A Biography of the World's Most Mysterious Number |url=https://archive.org/details/pi00alfr_0|url-access=registration |publisher=Prometheus Books |year=2004 |isbn=978-1-59102-200-8 }} | |||
| * based on 1.2 trillion digits of PI | |||
| * {{cite book |last=Remmert |first=Reinhold |editor1=Heinz-Dieter Ebbinghaus |editor2=Hans Hermes |editor3=Friedrich Hirzebruch |editor4=Max Koecher |editor5=Klaus Mainzer |editor6=Jürgen Neukirch |editor7=Alexander Prestel |editor8=Reinhold Remmert |title=Numbers|chapter-url=https://books.google.com/books?id=Z53SBwAAQBAJ&pg=PA123 |chapter=Ch. 5 What is π? |date=2012 |publisher=Springer |isbn=978-1-4612-1005-4}} | |||
| * | |||
| {{refend}} | |||
| * - ''Warning'' - Roughly 2 ]s will be transferred. | |||
| * | |||
| * | |||
| * | |||
| * | |||
| * | |||
| * | |||
| * (18 mb .txt file) | |||
| == Further reading == | |||
| ] | |||
| {{refbegin|indent=yes}} | |||
| ] | |||
| * {{cite book |last=Blatner |first=David |title=The Joy of {{pi}} |publisher=Walker & Company |year=1999 |isbn=978-0-8027-7562-7 }} | |||
| ] | |||
| * {{cite book |author-link=Jean-Paul Delahaye |last=Delahaye |first=Jean-Paul |title=Le fascinant nombre {{pi}} |location=Paris |publisher=Bibliothèque Pour la Science |date=1997 |isbn=2-902918-25-9}} | |||
| ] | |||
| {{refend}} | |||
| == External links == | |||
| {{Link FA|de}} | |||
| {{ |
{{Commons category|Pi}} | ||
| * {{mathworld|title=Pi|urlname=Pi}} | |||
| {{Link FA|sr}} | |||
| * Demonstration by Lambert (1761) of irrationality of {{pi}}, {{Webarchive|url=https://web.archive.org/web/20141231045534/https://www.bibnum.education.fr/mathematiques/theorie-des-nombres/lambert-et-l-irrationalite-de-p-1761 |date=31 December 2014 }} and analysed '' {{Webarchive|url=https://web.archive.org/web/20150402115151/https://www.bibnum.education.fr/sites/default/files/24-lambert-analysis.pdf |date=2 April 2015 }}'' (PDF). | |||
| {{Link FA|af}} | |||
| * 2 billion searchable digits of {{pi}}, {{mvar|e}} and {{radic|2}} | |||
| {{Link FA|nl}} | |||
| * and (interactive illustrations) | |||
| {{Link FA|eo}} | |||
| {{Irrational number}} | |||
| ] | |||
| {{Authority control}} | |||
| ] | |||
| ] | |||
| ] | ] | ||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
Latest revision as of 18:04, 6 January 2025
Number, approximately 3.14 This article is about the mathematical constant. For the Greek letter, see Pi (letter). For other uses, see Pi (disambiguation) and PI.
| Part of a series of articles on the |
| mathematical constant π |
|---|
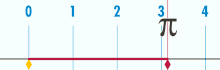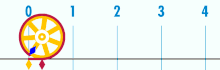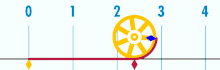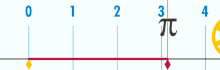 |
| 3.1415926535897932384626433... |
| Uses |
| Properties |
| Value |
| People |
| History |
| In culture |
| Related topics |
The number π (/paɪ/; spelled out as "pi") is a mathematical constant, approximately equal to 3.14159, that is the ratio of a circle's circumference to its diameter. It appears in many formulae across mathematics and physics, and some of these formulae are commonly used for defining π, to avoid relying on the definition of the length of a curve.
The number π is an irrational number, meaning that it cannot be expressed exactly as a ratio of two integers, although fractions such as are commonly used to approximate it. Consequently, its decimal representation never ends, nor enters a permanently repeating pattern. It is a transcendental number, meaning that it cannot be a solution of an algebraic equation involving only finite sums, products, powers, and integers. The transcendence of π implies that it is impossible to solve the ancient challenge of squaring the circle with a compass and straightedge. The decimal digits of π appear to be randomly distributed, but no proof of this conjecture has been found.
For thousands of years, mathematicians have attempted to extend their understanding of π, sometimes by computing its value to a high degree of accuracy. Ancient civilizations, including the Egyptians and Babylonians, required fairly accurate approximations of π for practical computations. Around 250 BC, the Greek mathematician Archimedes created an algorithm to approximate π with arbitrary accuracy. In the 5th century AD, Chinese mathematicians approximated π to seven digits, while Indian mathematicians made a five-digit approximation, both using geometrical techniques. The first computational formula for π, based on infinite series, was discovered a millennium later. The earliest known use of the Greek letter π to represent the ratio of a circle's circumference to its diameter was by the Welsh mathematician William Jones in 1706. The invention of calculus soon led to the calculation of hundreds of digits of π, enough for all practical scientific computations. Nevertheless, in the 20th and 21st centuries, mathematicians and computer scientists have pursued new approaches that, when combined with increasing computational power, extended the decimal representation of π to many trillions of digits. These computations are motivated by the development of efficient algorithms to calculate numeric series, as well as the human quest to break records. The extensive computations involved have also been used to test supercomputers as well as stress testing consumer computer hardware.
Because it relates to a circle, π is found in many formulae in trigonometry and geometry, especially those concerning circles, ellipses and spheres. It is also found in formulae from other topics in science, such as cosmology, fractals, thermodynamics, mechanics, and electromagnetism. It also appears in areas having little to do with geometry, such as number theory and statistics, and in modern mathematical analysis can be defined without any reference to geometry. The ubiquity of π makes it one of the most widely known mathematical constants inside and outside of science. Several books devoted to π have been published, and record-setting calculations of the digits of π often result in news headlines.
Fundamentals
Name
The symbol used by mathematicians to represent the ratio of a circle's circumference to its diameter is the lowercase Greek letter π, sometimes spelled out as pi. In English, π is pronounced as "pie" (/paɪ/ PY). In mathematical use, the lowercase letter π is distinguished from its capitalized and enlarged counterpart Π, which denotes a product of a sequence, analogous to how Σ denotes summation.
The choice of the symbol π is discussed in the section Adoption of the symbol π.
Definition

π is commonly defined as the ratio of a circle's circumference C to its diameter d:
The ratio is constant, regardless of the circle's size. For example, if a circle has twice the diameter of another circle, it will also have twice the circumference, preserving the ratio . This definition of π implicitly makes use of flat (Euclidean) geometry; although the notion of a circle can be extended to any curve (non-Euclidean) geometry, these new circles will no longer satisfy the formula .
Here, the circumference of a circle is the arc length around the perimeter of the circle, a quantity which can be formally defined independently of geometry using limits—a concept in calculus. For example, one may directly compute the arc length of the top half of the unit circle, given in Cartesian coordinates by the equation , as the integral:
An integral such as this was proposed as a definition of π by Karl Weierstrass, who defined it directly as an integral in 1841.
Integration is no longer commonly used in a first analytical definition because, as Remmert 2012 explains, differential calculus typically precedes integral calculus in the university curriculum, so it is desirable to have a definition of π that does not rely on the latter. One such definition, due to Richard Baltzer and popularized by Edmund Landau, is the following: π is twice the smallest positive number at which the cosine function equals 0. π is also the smallest positive number at which the sine function equals zero, and the difference between consecutive zeroes of the sine function. The cosine and sine can be defined independently of geometry as a power series, or as the solution of a differential equation.
In a similar spirit, π can be defined using properties of the complex exponential, exp z, of a complex variable z. Like the cosine, the complex exponential can be defined in one of several ways. The set of complex numbers at which exp z is equal to one is then an (imaginary) arithmetic progression of the form: and there is a unique positive real number π with this property.
A variation on the same idea, making use of sophisticated mathematical concepts of topology and algebra, is the following theorem: there is a unique (up to automorphism) continuous isomorphism from the group R/Z of real numbers under addition modulo integers (the circle group), onto the multiplicative group of complex numbers of absolute value one. The number π is then defined as half the magnitude of the derivative of this homomorphism.
Irrationality and normality
π is an irrational number, meaning that it cannot be written as the ratio of two integers. Fractions such as 22/7 and 355/113 are commonly used to approximate π, but no common fraction (ratio of whole numbers) can be its exact value. Because π is irrational, it has an infinite number of digits in its decimal representation, and does not settle into an infinitely repeating pattern of digits. There are several proofs that π is irrational; they generally require calculus and rely on the reductio ad absurdum technique. The degree to which π can be approximated by rational numbers (called the irrationality measure) is not precisely known; estimates have established that the irrationality measure is larger or at least equal to the measure of e but smaller than the measure of Liouville numbers.
The digits of π have no apparent pattern and have passed tests for statistical randomness, including tests for normality; a number of infinite length is called normal when all possible sequences of digits (of any given length) appear equally often. The conjecture that π is normal has not been proven or disproven.
Since the advent of computers, a large number of digits of π have been available on which to perform statistical analysis. Yasumasa Kanada has performed detailed statistical analyses on the decimal digits of π, and found them consistent with normality; for example, the frequencies of the ten digits 0 to 9 were subjected to statistical significance tests, and no evidence of a pattern was found. Any random sequence of digits contains arbitrarily long subsequences that appear non-random, by the infinite monkey theorem. Thus, because the sequence of π's digits passes statistical tests for randomness, it contains some sequences of digits that may appear non-random, such as a sequence of six consecutive 9s that begins at the 762nd decimal place of the decimal representation of π. This is also called the "Feynman point" in mathematical folklore, after Richard Feynman, although no connection to Feynman is known.
Transcendence
See also: Lindemann–Weierstrass theorem
In addition to being irrational, π is also a transcendental number, which means that it is not the solution of any non-constant polynomial equation with rational coefficients, such as . This follows from the so-called Lindemann–Weierstrass theorem, which also establishes the transcendence of the constant e.
The transcendence of π has two important consequences: First, π cannot be expressed using any finite combination of rational numbers and square roots or n-th roots (such as or ). Second, since no transcendental number can be constructed with compass and straightedge, it is not possible to "square the circle". In other words, it is impossible to construct, using compass and straightedge alone, a square whose area is exactly equal to the area of a given circle. Squaring a circle was one of the important geometry problems of the classical antiquity. Amateur mathematicians in modern times have sometimes attempted to square the circle and claim success—despite the fact that it is mathematically impossible.
An unsolved problem thus far is the question of whether or not the numbers π and e are algebraically independent ("relatively transcendental"). This would be resolved by Schanuel's conjecture – a currently unproven generalization of the Lindemann–Weierstrass theorem.
Continued fractions
As an irrational number, π cannot be represented as a common fraction. But every number, including π, can be represented by an infinite series of nested fractions, called a simple continued fraction:
Truncating the continued fraction at any point yields a rational approximation for π; the first four of these are 3, 22/7, 333/106, and 355/113. These numbers are among the best-known and most widely used historical approximations of the constant. Each approximation generated in this way is a best rational approximation; that is, each is closer to π than any other fraction with the same or a smaller denominator. Because π is transcendental, it is by definition not algebraic and so cannot be a quadratic irrational. Therefore, π cannot have a periodic continued fraction. Although the simple continued fraction for π (with numerators all 1, shown above) also does not exhibit any other obvious pattern, several non-simple continued fractions do, such as:
The middle of these is due to the mid-17th century mathematician William Brouncker, see § Brouncker's formula.
Approximate value and digits
Some approximations of pi include:
- Integers: 3
- Fractions: Approximate fractions include (in order of increasing accuracy) 22/7, 333/106, 355/113, 52163/16604, 103993/33102, 104348/33215, and 245850922/78256779. (List is selected terms from OEIS: A063674 and OEIS: A063673.)
- Digits: The first 50 decimal digits are 3.14159265358979323846264338327950288419716939937510... (see OEIS: A000796)
Digits in other number systems
- The first 48 binary (base 2) digits (called bits) are 11.001001000011111101101010100010001000010110100011... (see OEIS: A004601)
- The first 36 digits in ternary (base 3) are 10.010211012222010211002111110221222220... (see OEIS: A004602)
- The first 20 digits in hexadecimal (base 16) are 3.243F6A8885A308D31319... (see OEIS: A062964)
- The first five sexagesimal (base 60) digits are 3;8,29,44,0,47 (see OEIS: A060707)
Complex numbers and Euler's identity

Any complex number, say z, can be expressed using a pair of real numbers. In the polar coordinate system, one number (radius or r) is used to represent z's distance from the origin of the complex plane, and the other (angle or φ) the counter-clockwise rotation from the positive real line: where i is the imaginary unit satisfying . The frequent appearance of π in complex analysis can be related to the behaviour of the exponential function of a complex variable, described by Euler's formula: where the constant e is the base of the natural logarithm. This formula establishes a correspondence between imaginary powers of e and points on the unit circle centred at the origin of the complex plane. Setting in Euler's formula results in Euler's identity, celebrated in mathematics due to it containing five important mathematical constants:
There are n different complex numbers z satisfying , and these are called the "n-th roots of unity" and are given by the formula:
History
Main article: Approximations of π See also: Chronology of computation of πAntiquity
The best-known approximations to π dating before the Common Era were accurate to two decimal places; this was improved upon in Chinese mathematics in particular by the mid-first millennium, to an accuracy of seven decimal places. After this, no further progress was made until the late medieval period.
The earliest written approximations of π are found in Babylon and Egypt, both within one percent of the true value. In Babylon, a clay tablet dated 1900–1600 BC has a geometrical statement that, by implication, treats π as 25/8 = 3.125. In Egypt, the Rhind Papyrus, dated around 1650 BC but copied from a document dated to 1850 BC, has a formula for the area of a circle that treats π as . Although some pyramidologists have theorized that the Great Pyramid of Giza was built with proportions related to π, this theory is not widely accepted by scholars. In the Shulba Sutras of Indian mathematics, dating to an oral tradition from the first or second millennium BC, approximations are given which have been variously interpreted as approximately 3.08831, 3.08833, 3.004, 3, or 3.125.
Polygon approximation era

The first recorded algorithm for rigorously calculating the value of π was a geometrical approach using polygons, devised around 250 BC by the Greek mathematician Archimedes, implementing the method of exhaustion. This polygonal algorithm dominated for over 1,000 years, and as a result π is sometimes referred to as Archimedes's constant. Archimedes computed upper and lower bounds of π by drawing a regular hexagon inside and outside a circle, and successively doubling the number of sides until he reached a 96-sided regular polygon. By calculating the perimeters of these polygons, he proved that 223/71 < π < 22/7 (that is, 3.1408 < π < 3.1429). Archimedes' upper bound of 22/7 may have led to a widespread popular belief that π is equal to 22/7. Around 150 AD, Greek-Roman scientist Ptolemy, in his Almagest, gave a value for π of 3.1416, which he may have obtained from Archimedes or from Apollonius of Perga. Mathematicians using polygonal algorithms reached 39 digits of π in 1630, a record only broken in 1699 when infinite series were used to reach 71 digits.
In ancient China, values for π included 3.1547 (around 1 AD), (100 AD, approximately 3.1623), and 142/45 (3rd century, approximately 3.1556). Around 265 AD, the Wei Kingdom mathematician Liu Hui created a polygon-based iterative algorithm and used it with a 3,072-sided polygon to obtain a value of π of 3.1416. Liu later invented a faster method of calculating π and obtained a value of 3.14 with a 96-sided polygon, by taking advantage of the fact that the differences in area of successive polygons form a geometric series with a factor of 4. The Chinese mathematician Zu Chongzhi, around 480 AD, calculated that and suggested the approximations and , which he termed the Milü (''close ratio") and Yuelü ("approximate ratio"), respectively, using Liu Hui's algorithm applied to a 12,288-sided polygon. With a correct value for its seven first decimal digits, this value remained the most accurate approximation of π available for the next 800 years.
The Indian astronomer Aryabhata used a value of 3.1416 in his Āryabhaṭīya (499 AD). Fibonacci in c. 1220 computed 3.1418 using a polygonal method, independent of Archimedes. Italian author Dante apparently employed the value .
The Persian astronomer Jamshīd al-Kāshī produced nine sexagesimal digits, roughly the equivalent of 16 decimal digits, in 1424, using a polygon with sides, which stood as the world record for about 180 years. French mathematician François Viète in 1579 achieved nine digits with a polygon of sides. Flemish mathematician Adriaan van Roomen arrived at 15 decimal places in 1593. In 1596, Dutch mathematician Ludolph van Ceulen reached 20 digits, a record he later increased to 35 digits (as a result, π was called the "Ludolphian number" in Germany until the early 20th century). Dutch scientist Willebrord Snellius reached 34 digits in 1621, and Austrian astronomer Christoph Grienberger arrived at 38 digits in 1630 using 10 sides. Christiaan Huygens was able to arrive at 10 decimal places in 1654 using a slightly different method equivalent to Richardson extrapolation.
Infinite series

The calculation of π was revolutionized by the development of infinite series techniques in the 16th and 17th centuries. An infinite series is the sum of the terms of an infinite sequence. Infinite series allowed mathematicians to compute π with much greater precision than Archimedes and others who used geometrical techniques. Although infinite series were exploited for π most notably by European mathematicians such as James Gregory and Gottfried Wilhelm Leibniz, the approach also appeared in the Kerala school sometime in the 14th or 15th century. Around 1500 AD, a written description of an infinite series that could be used to compute π was laid out in Sanskrit verse in Tantrasamgraha by Nilakantha Somayaji. The series are presented without proof, but proofs are presented in a later work, Yuktibhāṣā, from around 1530 AD. Several infinite series are described, including series for sine (which Nilakantha attributes to Madhava of Sangamagrama), cosine, and arctangent which are now sometimes referred to as Madhava series. The series for arctangent is sometimes called Gregory's series or the Gregory–Leibniz series. Madhava used infinite series to estimate π to 11 digits around 1400.
In 1593, François Viète published what is now known as Viète's formula, an infinite product (rather than an infinite sum, which is more typically used in π calculations):
In 1655, John Wallis published what is now known as Wallis product, also an infinite product:

In the 1660s, the English scientist Isaac Newton and German mathematician Gottfried Wilhelm Leibniz discovered calculus, which led to the development of many infinite series for approximating π. Newton himself used an arcsine series to compute a 15-digit approximation of π in 1665 or 1666, writing, "I am ashamed to tell you to how many figures I carried these computations, having no other business at the time."
In 1671, James Gregory, and independently, Leibniz in 1673, discovered the Taylor series expansion for arctangent:
This series, sometimes called the Gregory–Leibniz series, equals when evaluated with . But for , it converges impractically slowly (that is, approaches the answer very gradually), taking about ten times as many terms to calculate each additional digit.
In 1699, English mathematician Abraham Sharp used the Gregory–Leibniz series for to compute π to 71 digits, breaking the previous record of 39 digits, which was set with a polygonal algorithm.
In 1706, John Machin used the Gregory–Leibniz series to produce an algorithm that converged much faster:
Machin reached 100 digits of π with this formula. Other mathematicians created variants, now known as Machin-like formulae, that were used to set several successive records for calculating digits of π.
Isaac Newton accelerated the convergence of the Gregory–Leibniz series in 1684 (in an unpublished work; others independently discovered the result):
Leonhard Euler popularized this series in his 1755 differential calculus textbook, and later used it with Machin-like formulae, including with which he computed 20 digits of π in one hour.
Machin-like formulae remained the best-known method for calculating π well into the age of computers, and were used to set records for 250 years, culminating in a 620-digit approximation in 1946 by Daniel Ferguson – the best approximation achieved without the aid of a calculating device.
In 1844, a record was set by Zacharias Dase, who employed a Machin-like formula to calculate 200 decimals of π in his head at the behest of German mathematician Carl Friedrich Gauss.
In 1853, British mathematician William Shanks calculated π to 607 digits, but made a mistake in the 528th digit, rendering all subsequent digits incorrect. Though he calculated an additional 100 digits in 1873, bringing the total up to 707, his previous mistake rendered all the new digits incorrect as well.
Rate of convergence
Some infinite series for π converge faster than others. Given the choice of two infinite series for π, mathematicians will generally use the one that converges more rapidly because faster convergence reduces the amount of computation needed to calculate π to any given accuracy. A simple infinite series for π is the Gregory–Leibniz series:
As individual terms of this infinite series are added to the sum, the total gradually gets closer to π, and – with a sufficient number of terms – can get as close to π as desired. It converges quite slowly, though – after 500,000 terms, it produces only five correct decimal digits of π.
An infinite series for π (published by Nilakantha in the 15th century) that converges more rapidly than the Gregory–Leibniz series is:
The following table compares the convergence rates of these two series:
| Infinite series for π | After 1st term | After 2nd term | After 3rd term | After 4th term | After 5th term | Converges to: |
|---|---|---|---|---|---|---|
| 4.0000 | 2.6666 ... | 3.4666 ... | 2.8952 ... | 3.3396 ... | π = 3.1415 ... | |
| 3.0000 | 3.1666 ... | 3.1333 ... | 3.1452 ... | 3.1396 ... |
After five terms, the sum of the Gregory–Leibniz series is within 0.2 of the correct value of π, whereas the sum of Nilakantha's series is within 0.002 of the correct value. Nilakantha's series converges faster and is more useful for computing digits of π. Series that converge even faster include Machin's series and Chudnovsky's series, the latter producing 14 correct decimal digits per term.
Irrationality and transcendence
See also: Proof that π is irrational and Proof that π is transcendentalNot all mathematical advances relating to π were aimed at increasing the accuracy of approximations. When Euler solved the Basel problem in 1735, finding the exact value of the sum of the reciprocal squares, he established a connection between π and the prime numbers that later contributed to the development and study of the Riemann zeta function:
Swiss scientist Johann Heinrich Lambert in 1768 proved that π is irrational, meaning it is not equal to the quotient of any two integers. Lambert's proof exploited a continued-fraction representation of the tangent function. French mathematician Adrien-Marie Legendre proved in 1794 that π is also irrational. In 1882, German mathematician Ferdinand von Lindemann proved that π is transcendental, confirming a conjecture made by both Legendre and Euler. Hardy and Wright states that "the proofs were afterwards modified and simplified by Hilbert, Hurwitz, and other writers".
Adoption of the symbol π
 The earliest known use of the Greek letter π to represent the ratio of a circle's circumference to its diameter was by Welsh mathematician William Jones in 1706
The earliest known use of the Greek letter π to represent the ratio of a circle's circumference to its diameter was by Welsh mathematician William Jones in 1706 Leonhard Euler popularized the use of the Greek letter π in works he published in 1736 and 1748.
Leonhard Euler popularized the use of the Greek letter π in works he published in 1736 and 1748.
In the earliest usages, the Greek letter π was used to denote the semiperimeter (semiperipheria in Latin) of a circle and was combined in ratios with δ (for diameter or semidiameter) or ρ (for radius) to form circle constants. (Before then, mathematicians sometimes used letters such as c or p instead.) The first recorded use is Oughtred's "", to express the ratio of periphery and diameter in the 1647 and later editions of Clavis Mathematicae. Barrow likewise used "" to represent the constant 3.14..., while Gregory instead used "" to represent 6.28... .
The earliest known use of the Greek letter π alone to represent the ratio of a circle's circumference to its diameter was by Welsh mathematician William Jones in his 1706 work Synopsis Palmariorum Matheseos; or, a New Introduction to the Mathematics. The Greek letter appears on p. 243 in the phrase " Periphery (π)", calculated for a circle with radius one. However, Jones writes that his equations for π are from the "ready pen of the truly ingenious Mr. John Machin", leading to speculation that Machin may have employed the Greek letter before Jones. Jones' notation was not immediately adopted by other mathematicians, with the fraction notation still being used as late as 1767.
Euler started using the single-letter form beginning with his 1727 Essay Explaining the Properties of Air, though he used π = 6.28..., the ratio of periphery to radius, in this and some later writing. Euler first used π = 3.14... in his 1736 work Mechanica, and continued in his widely read 1748 work Introductio in analysin infinitorum (he wrote: "for the sake of brevity we will write this number as π; thus π is equal to half the circumference of a circle of radius 1"). Because Euler corresponded heavily with other mathematicians in Europe, the use of the Greek letter spread rapidly, and the practice was universally adopted thereafter in the Western world, though the definition still varied between 3.14... and 6.28... as late as 1761.
Modern quest for more digits
Computer era and iterative algorithms
The Gauss–Legendre iterative algorithm:
Initialize Iterate Then an estimate for π is given by
The development of computers in the mid-20th century again revolutionized the hunt for digits of π. Mathematicians John Wrench and Levi Smith reached 1,120 digits in 1949 using a desk calculator. Using an inverse tangent (arctan) infinite series, a team led by George Reitwiesner and John von Neumann that same year achieved 2,037 digits with a calculation that took 70 hours of computer time on the ENIAC computer. The record, always relying on an arctan series, was broken repeatedly (3089 digits in 1955, 7,480 digits in 1957; 10,000 digits in 1958; 100,000 digits in 1961) until 1 million digits was reached in 1973.
Two additional developments around 1980 once again accelerated the ability to compute π. First, the discovery of new iterative algorithms for computing π, which were much faster than the infinite series; and second, the invention of fast multiplication algorithms that could multiply large numbers very rapidly. Such algorithms are particularly important in modern π computations because most of the computer's time is devoted to multiplication. They include the Karatsuba algorithm, Toom–Cook multiplication, and Fourier transform-based methods.
The iterative algorithms were independently published in 1975–1976 by physicist Eugene Salamin and scientist Richard Brent. These avoid reliance on infinite series. An iterative algorithm repeats a specific calculation, each iteration using the outputs from prior steps as its inputs, and produces a result in each step that converges to the desired value. The approach was actually invented over 160 years earlier by Carl Friedrich Gauss, in what is now termed the arithmetic–geometric mean method (AGM method) or Gauss–Legendre algorithm. As modified by Salamin and Brent, it is also referred to as the Brent–Salamin algorithm.
The iterative algorithms were widely used after 1980 because they are faster than infinite series algorithms: whereas infinite series typically increase the number of correct digits additively in successive terms, iterative algorithms generally multiply the number of correct digits at each step. For example, the Brent–Salamin algorithm doubles the number of digits in each iteration. In 1984, brothers John and Peter Borwein produced an iterative algorithm that quadruples the number of digits in each step; and in 1987, one that increases the number of digits five times in each step. Iterative methods were used by Japanese mathematician Yasumasa Kanada to set several records for computing π between 1995 and 2002. This rapid convergence comes at a price: the iterative algorithms require significantly more memory than infinite series.
Motives for computing π

For most numerical calculations involving π, a handful of digits provide sufficient precision. According to Jörg Arndt and Christoph Haenel, thirty-nine digits are sufficient to perform most cosmological calculations, because that is the accuracy necessary to calculate the circumference of the observable universe with a precision of one atom. Accounting for additional digits needed to compensate for computational round-off errors, Arndt concludes that a few hundred digits would suffice for any scientific application. Despite this, people have worked strenuously to compute π to thousands and millions of digits. This effort may be partly ascribed to the human compulsion to break records, and such achievements with π often make headlines around the world. They also have practical benefits, such as testing supercomputers, testing numerical analysis algorithms (including high-precision multiplication algorithms); and within pure mathematics itself, providing data for evaluating the randomness of the digits of π.
Rapidly convergent series

Modern π calculators do not use iterative algorithms exclusively. New infinite series were discovered in the 1980s and 1990s that are as fast as iterative algorithms, yet are simpler and less memory intensive. The fast iterative algorithms were anticipated in 1914, when Indian mathematician Srinivasa Ramanujan published dozens of innovative new formulae for π, remarkable for their elegance, mathematical depth and rapid convergence. One of his formulae, based on modular equations, is
This series converges much more rapidly than most arctan series, including Machin's formula. Bill Gosper was the first to use it for advances in the calculation of π, setting a record of 17 million digits in 1985. Ramanujan's formulae anticipated the modern algorithms developed by the Borwein brothers (Jonathan and Peter) and the Chudnovsky brothers. The Chudnovsky formula developed in 1987 is
It produces about 14 digits of π per term and has been used for several record-setting π calculations, including the first to surpass 1 billion (10) digits in 1989 by the Chudnovsky brothers, 10 trillion (10) digits in 2011 by Alexander Yee and Shigeru Kondo, and 100 trillion digits by Emma Haruka Iwao in 2022. For similar formulae, see also the Ramanujan–Sato series.
In 2006, mathematician Simon Plouffe used the PSLQ integer relation algorithm to generate several new formulae for π, conforming to the following template: where q is e (Gelfond's constant), k is an odd number, and a, b, c are certain rational numbers that Plouffe computed.
Monte Carlo methods
 Buffon's needle. Needles a and b are dropped randomly.
Buffon's needle. Needles a and b are dropped randomly. Random dots are placed on a square and a circle inscribed inside.
Random dots are placed on a square and a circle inscribed inside.
Monte Carlo methods, which evaluate the results of multiple random trials, can be used to create approximations of π. Buffon's needle is one such technique: If a needle of length ℓ is dropped n times on a surface on which parallel lines are drawn t units apart, and if x of those times it comes to rest crossing a line (x > 0), then one may approximate π based on the counts:
Another Monte Carlo method for computing π is to draw a circle inscribed in a square, and randomly place dots in the square. The ratio of dots inside the circle to the total number of dots will approximately equal π/4.

Another way to calculate π using probability is to start with a random walk, generated by a sequence of (fair) coin tosses: independent random variables Xk such that Xk ∈ {−1,1} with equal probabilities. The associated random walk is so that, for each n, Wn is drawn from a shifted and scaled binomial distribution. As n varies, Wn defines a (discrete) stochastic process. Then π can be calculated by
This Monte Carlo method is independent of any relation to circles, and is a consequence of the central limit theorem, discussed below.
These Monte Carlo methods for approximating π are very slow compared to other methods, and do not provide any information on the exact number of digits that are obtained. Thus they are never used to approximate π when speed or accuracy is desired.
Spigot algorithms
Two algorithms were discovered in 1995 that opened up new avenues of research into π. They are called spigot algorithms because, like water dripping from a spigot, they produce single digits of π that are not reused after they are calculated. This is in contrast to infinite series or iterative algorithms, which retain and use all intermediate digits until the final result is produced.
Mathematicians Stan Wagon and Stanley Rabinowitz produced a simple spigot algorithm in 1995. Its speed is comparable to arctan algorithms, but not as fast as iterative algorithms.
Another spigot algorithm, the BBP digit extraction algorithm, was discovered in 1995 by Simon Plouffe:
This formula, unlike others before it, can produce any individual hexadecimal digit of π without calculating all the preceding digits. Individual binary digits may be extracted from individual hexadecimal digits, and octal digits can be extracted from one or two hexadecimal digits. An important application of digit extraction algorithms is to validate new claims of record π computations: After a new record is claimed, the decimal result is converted to hexadecimal, and then a digit extraction algorithm is used to calculate several randomly selected hexadecimal digits near the end; if they match, this provides a measure of confidence that the entire computation is correct.
Between 1998 and 2000, the distributed computing project PiHex used Bellard's formula (a modification of the BBP algorithm) to compute the quadrillionth (10th) bit of π, which turned out to be 0. In September 2010, a Yahoo! employee used the company's Hadoop application on one thousand computers over a 23-day period to compute 256 bits of π at the two-quadrillionth (2×10th) bit, which also happens to be zero.
In 2022, Plouffe found a base-10 algorithm for calculating digits of π.
Role and characterizations in mathematics
Because π is closely related to the circle, it is found in many formulae from the fields of geometry and trigonometry, particularly those concerning circles, spheres, or ellipses. Other branches of science, such as statistics, physics, Fourier analysis, and number theory, also include π in some of their important formulae.
Geometry and trigonometry
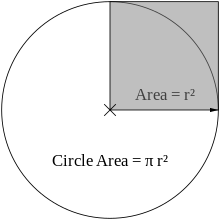
π appears in formulae for areas and volumes of geometrical shapes based on circles, such as ellipses, spheres, cones, and tori. Below are some of the more common formulae that involve π.
- The circumference of a circle with radius r is 2πr.
- The area of a circle with radius r is πr.
- The area of an ellipse with semi-major axis a and semi-minor axis b is πab.
- The volume of a sphere with radius r is 4/3πr.
- The surface area of a sphere with radius r is 4πr.
Some of the formulae above are special cases of the volume of the n-dimensional ball and the surface area of its boundary, the (n−1)-dimensional sphere, given below.
Apart from circles, there are other curves of constant width. By Barbier's theorem, every curve of constant width has perimeter π times its width. The Reuleaux triangle (formed by the intersection of three circles with the sides of an equilateral triangle as their radii) has the smallest possible area for its width and the circle the largest. There also exist non-circular smooth and even algebraic curves of constant width.
Definite integrals that describe circumference, area, or volume of shapes generated by circles typically have values that involve π. For example, an integral that specifies half the area of a circle of radius one is given by:
In that integral, the function represents the height over the -axis of a semicircle (the square root is a consequence of the Pythagorean theorem), and the integral computes the area below the semicircle.
The existence of such integrals makes π an algebraic period.
Units of angle
Main article: Units of angle measure
The trigonometric functions rely on angles, and mathematicians generally use radians as units of measurement. π plays an important role in angles measured in radians, which are defined so that a complete circle spans an angle of 2π radians. The angle measure of 180° is equal to π radians, and 1° = π/180 radians.
Common trigonometric functions have periods that are multiples of π; for example, sine and cosine have period 2π, so for any angle θ and any integer k,
Eigenvalues
Many of the appearances of π in the formulae of mathematics and the sciences have to do with its close relationship with geometry. However, π also appears in many natural situations having apparently nothing to do with geometry.
In many applications, it plays a distinguished role as an eigenvalue. For example, an idealized vibrating string can be modelled as the graph of a function f on the unit interval [0, 1], with fixed ends f(0) = f(1) = 0. The modes of vibration of the string are solutions of the differential equation , or . Thus λ is an eigenvalue of the second derivative operator , and is constrained by Sturm–Liouville theory to take on only certain specific values. It must be positive, since the operator is negative definite, so it is convenient to write λ = ν, where ν > 0 is called the wavenumber. Then f(x) = sin(π x) satisfies the boundary conditions and the differential equation with ν = π.
The value π is, in fact, the least such value of the wavenumber, and is associated with the fundamental mode of vibration of the string. One way to show this is by estimating the energy, which satisfies Wirtinger's inequality: for a function with f(0) = f(1) = 0 and f, f′ both square integrable, we have: with equality precisely when f is a multiple of sin(π x). Here π appears as an optimal constant in Wirtinger's inequality, and it follows that it is the smallest wavenumber, using the variational characterization of the eigenvalue. As a consequence, π is the smallest singular value of the derivative operator on the space of functions on [0, 1] vanishing at both endpoints (the Sobolev space ).
Inequalities

The number π serves appears in similar eigenvalue problems in higher-dimensional analysis. As mentioned above, it can be characterized via its role as the best constant in the isoperimetric inequality: the area A enclosed by a plane Jordan curve of perimeter P satisfies the inequality and equality is clearly achieved for the circle, since in that case A = πr and P = 2πr.
Ultimately, as a consequence of the isoperimetric inequality, π appears in the optimal constant for the critical Sobolev inequality in n dimensions, which thus characterizes the role of π in many physical phenomena as well, for example those of classical potential theory. In two dimensions, the critical Sobolev inequality is for f a smooth function with compact support in R, is the gradient of f, and and refer respectively to the L and L-norm. The Sobolev inequality is equivalent to the isoperimetric inequality (in any dimension), with the same best constants.
Wirtinger's inequality also generalizes to higher-dimensional Poincaré inequalities that provide best constants for the Dirichlet energy of an n-dimensional membrane. Specifically, π is the greatest constant such that for all convex subsets G of R of diameter 1, and square-integrable functions u on G of mean zero. Just as Wirtinger's inequality is the variational form of the Dirichlet eigenvalue problem in one dimension, the Poincaré inequality is the variational form of the Neumann eigenvalue problem, in any dimension.
Fourier transform and Heisenberg uncertainty principle

The constant π also appears as a critical spectral parameter in the Fourier transform. This is the integral transform, that takes a complex-valued integrable function f on the real line to the function defined as:
Although there are several different conventions for the Fourier transform and its inverse, any such convention must involve π somewhere. The above is the most canonical definition, however, giving the unique unitary operator on L that is also an algebra homomorphism of L to L.
The Heisenberg uncertainty principle also contains the number π. The uncertainty principle gives a sharp lower bound on the extent to which it is possible to localize a function both in space and in frequency: with our conventions for the Fourier transform,
The physical consequence, about the uncertainty in simultaneous position and momentum observations of a quantum mechanical system, is discussed below. The appearance of π in the formulae of Fourier analysis is ultimately a consequence of the Stone–von Neumann theorem, asserting the uniqueness of the Schrödinger representation of the Heisenberg group.
Gaussian integrals

The fields of probability and statistics frequently use the normal distribution as a simple model for complex phenomena; for example, scientists generally assume that the observational error in most experiments follows a normal distribution. The Gaussian function, which is the probability density function of the normal distribution with mean μ and standard deviation σ, naturally contains π:
The factor of makes the area under the graph of f equal to one, as is required for a probability distribution. This follows from a change of variables in the Gaussian integral: which says that the area under the basic bell curve in the figure is equal to the square root of π.
The central limit theorem explains the central role of normal distributions, and thus of π, in probability and statistics. This theorem is ultimately connected with the spectral characterization of π as the eigenvalue associated with the Heisenberg uncertainty principle, and the fact that equality holds in the uncertainty principle only for the Gaussian function. Equivalently, π is the unique constant making the Gaussian normal distribution e equal to its own Fourier transform. Indeed, according to Howe (1980), the "whole business" of establishing the fundamental theorems of Fourier analysis reduces to the Gaussian integral.
Topology

The constant π appears in the Gauss–Bonnet formula which relates the differential geometry of surfaces to their topology. Specifically, if a compact surface Σ has Gauss curvature K, then where χ(Σ) is the Euler characteristic, which is an integer. An example is the surface area of a sphere S of curvature 1 (so that its radius of curvature, which coincides with its radius, is also 1.) The Euler characteristic of a sphere can be computed from its homology groups and is found to be equal to two. Thus we have reproducing the formula for the surface area of a sphere of radius 1.
The constant appears in many other integral formulae in topology, in particular, those involving characteristic classes via the Chern–Weil homomorphism.
Cauchy's integral formula

One of the key tools in complex analysis is contour integration of a function over a positively oriented (rectifiable) Jordan curve γ. A form of Cauchy's integral formula states that if a point z0 is interior to γ, then
Although the curve γ is not a circle, and hence does not have any obvious connection to the constant π, a standard proof of this result uses Morera's theorem, which implies that the integral is invariant under homotopy of the curve, so that it can be deformed to a circle and then integrated explicitly in polar coordinates. More generally, it is true that if a rectifiable closed curve γ does not contain z0, then the above integral is 2πi times the winding number of the curve.
The general form of Cauchy's integral formula establishes the relationship between the values of a complex analytic function f(z) on the Jordan curve γ and the value of f(z) at any interior point z0 of γ: provided f(z) is analytic in the region enclosed by γ and extends continuously to γ. Cauchy's integral formula is a special case of the residue theorem, that if g(z) is a meromorphic function the region enclosed by γ and is continuous in a neighbourhood of γ, then where the sum is of the residues at the poles of g(z).
Vector calculus and physics
The constant π is ubiquitous in vector calculus and potential theory, for example in Coulomb's law, Gauss's law, Maxwell's equations, and even the Einstein field equations. Perhaps the simplest example of this is the two-dimensional Newtonian potential, representing the potential of a point source at the origin, whose associated field has unit outward flux through any smooth and oriented closed surface enclosing the source: The factor of is necessary to ensure that is the fundamental solution of the Poisson equation in : where is the Dirac delta function.
In higher dimensions, factors of π are present because of a normalization by the n-dimensional volume of the unit n sphere. For example, in three dimensions, the Newtonian potential is: which has the 2-dimensional volume (i.e., the area) of the unit 2-sphere in the denominator.
Total curvature
This section is an excerpt from Total curvature.
In mathematical study of the differential geometry of curves, the total curvature of an immersed plane curve is the integral of curvature along a curve taken with respect to arc length:
The gamma function and Stirling's approximation

The factorial function is the product of all of the positive integers through n. The gamma function extends the concept of factorial (normally defined only for non-negative integers) to all complex numbers, except the negative real integers, with the identity . When the gamma function is evaluated at half-integers, the result contains π. For example, and .
The gamma function is defined by its Weierstrass product development: where γ is the Euler–Mascheroni constant. Evaluated at z = 1/2 and squared, the equation Γ(1/2) = π reduces to the Wallis product formula. The gamma function is also connected to the Riemann zeta function and identities for the functional determinant, in which the constant π plays an important role.
The gamma function is used to calculate the volume Vn(r) of the n-dimensional ball of radius r in Euclidean n-dimensional space, and the surface area Sn−1(r) of its boundary, the (n−1)-dimensional sphere:
Further, it follows from the functional equation that
The gamma function can be used to create a simple approximation to the factorial function n! for large n: which is known as Stirling's approximation. Equivalently,
As a geometrical application of Stirling's approximation, let Δn denote the standard simplex in n-dimensional Euclidean space, and (n + 1)Δn denote the simplex having all of its sides scaled up by a factor of n + 1. Then
Ehrhart's volume conjecture is that this is the (optimal) upper bound on the volume of a convex body containing only one lattice point.
Number theory and Riemann zeta function


The Riemann zeta function ζ(s) is used in many areas of mathematics. When evaluated at s = 2 it can be written as
Finding a simple solution for this infinite series was a famous problem in mathematics called the Basel problem. Leonhard Euler solved it in 1735 when he showed it was equal to π/6. Euler's result leads to the number theory result that the probability of two random numbers being relatively prime (that is, having no shared factors) is equal to 6/π. This probability is based on the observation that the probability that any number is divisible by a prime p is 1/p (for example, every 7th integer is divisible by 7.) Hence the probability that two numbers are both divisible by this prime is 1/p, and the probability that at least one of them is not is 1 − 1/p. For distinct primes, these divisibility events are mutually independent; so the probability that two numbers are relatively prime is given by a product over all primes:
This probability can be used in conjunction with a random number generator to approximate π using a Monte Carlo approach.
The solution to the Basel problem implies that the geometrically derived quantity π is connected in a deep way to the distribution of prime numbers. This is a special case of Weil's conjecture on Tamagawa numbers, which asserts the equality of similar such infinite products of arithmetic quantities, localized at each prime p, and a geometrical quantity: the reciprocal of the volume of a certain locally symmetric space. In the case of the Basel problem, it is the hyperbolic 3-manifold SL2(R)/SL2(Z).
The zeta function also satisfies Riemann's functional equation, which involves π as well as the gamma function:
Furthermore, the derivative of the zeta function satisfies
A consequence is that π can be obtained from the functional determinant of the harmonic oscillator. This functional determinant can be computed via a product expansion, and is equivalent to the Wallis product formula. The calculation can be recast in quantum mechanics, specifically the variational approach to the spectrum of the hydrogen atom.
Fourier series

The constant π also appears naturally in Fourier series of periodic functions. Periodic functions are functions on the group T =R/Z of fractional parts of real numbers. The Fourier decomposition shows that a complex-valued function f on T can be written as an infinite linear superposition of unitary characters of T. That is, continuous group homomorphisms from T to the circle group U(1) of unit modulus complex numbers. It is a theorem that every character of T is one of the complex exponentials .
There is a unique character on T, up to complex conjugation, that is a group isomorphism. Using the Haar measure on the circle group, the constant π is half the magnitude of the Radon–Nikodym derivative of this character. The other characters have derivatives whose magnitudes are positive integral multiples of 2π. As a result, the constant π is the unique number such that the group T, equipped with its Haar measure, is Pontrjagin dual to the lattice of integral multiples of 2π. This is a version of the one-dimensional Poisson summation formula.
Modular forms and theta functions

The constant π is connected in a deep way with the theory of modular forms and theta functions. For example, the Chudnovsky algorithm involves in an essential way the j-invariant of an elliptic curve.
Modular forms are holomorphic functions in the upper half plane characterized by their transformation properties under the modular group (or its various subgroups), a lattice in the group . An example is the Jacobi theta function which is a kind of modular form called a Jacobi form. This is sometimes written in terms of the nome .
The constant π is the unique constant making the Jacobi theta function an automorphic form, which means that it transforms in a specific way. Certain identities hold for all automorphic forms. An example is which implies that θ transforms as a representation under the discrete Heisenberg group. General modular forms and other theta functions also involve π, once again because of the Stone–von Neumann theorem.
Cauchy distribution and potential theory


The Cauchy distribution is a probability density function. The total probability is equal to one, owing to the integral:
The Shannon entropy of the Cauchy distribution is equal to ln(4π), which also involves π.
The Cauchy distribution plays an important role in potential theory because it is the simplest Furstenberg measure, the classical Poisson kernel associated with a Brownian motion in a half-plane. Conjugate harmonic functions and so also the Hilbert transform are associated with the asymptotics of the Poisson kernel. The Hilbert transform H is the integral transform given by the Cauchy principal value of the singular integral
The constant π is the unique (positive) normalizing factor such that H defines a linear complex structure on the Hilbert space of square-integrable real-valued functions on the real line. The Hilbert transform, like the Fourier transform, can be characterized purely in terms of its transformation properties on the Hilbert space L(R): up to a normalization factor, it is the unique bounded linear operator that commutes with positive dilations and anti-commutes with all reflections of the real line. The constant π is the unique normalizing factor that makes this transformation unitary.
In the Mandelbrot set

An occurrence of π in the fractal called the Mandelbrot set was discovered by David Boll in 1991. He examined the behaviour of the Mandelbrot set near the "neck" at (−0.75, 0). When the number of iterations until divergence for the point (−0.75, ε) is multiplied by ε, the result approaches π as ε approaches zero. The point (0.25 + ε, 0) at the cusp of the large "valley" on the right side of the Mandelbrot set behaves similarly: the number of iterations until divergence multiplied by the square root of ε tends to π.
Projective geometry
Let V be the set of all twice differentiable real functions that satisfy the ordinary differential equation . Then V is a two-dimensional real vector space, with two parameters corresponding to a pair of initial conditions for the differential equation. For any , let be the evaluation functional, which associates to each the value of the function f at the real point t. Then, for each t, the kernel of is a one-dimensional linear subspace of V. Hence defines a function from from the real line to the real projective line. This function is periodic, and the quantity π can be characterized as the period of this map. This is notable in that the constant π, rather than 2π, appears naturally in this context.
Outside mathematics
Describing physical phenomena
Although not a physical constant, π appears routinely in equations describing fundamental principles of the universe, often because of π's relationship to the circle and to spherical coordinate systems. A simple formula from the field of classical mechanics gives the approximate period T of a simple pendulum of length L, swinging with a small amplitude (g is the earth's gravitational acceleration):
One of the key formulae of quantum mechanics is Heisenberg's uncertainty principle, which shows that the uncertainty in the measurement of a particle's position (Δx) and momentum (Δp) cannot both be arbitrarily small at the same time (where h is the Planck constant):
The fact that π is approximately equal to 3 plays a role in the relatively long lifetime of orthopositronium. The inverse lifetime to lowest order in the fine-structure constant α is where me is the mass of the electron.
π is present in some structural engineering formulae, such as the buckling formula derived by Euler, which gives the maximum axial load F that a long, slender column of length L, modulus of elasticity E, and area moment of inertia I can carry without buckling:
The field of fluid dynamics contains π in Stokes' law, which approximates the frictional force F exerted on small, spherical objects of radius R, moving with velocity v in a fluid with dynamic viscosity η:
In electromagnetics, the vacuum permeability constant μ0 appears in Maxwell's equations, which describe the properties of electric and magnetic fields and electromagnetic radiation. Before 20 May 2019, it was defined as exactly
Memorizing digits
Main article: PiphilologyPiphilology is the practice of memorizing large numbers of digits of π, and world-records are kept by the Guinness World Records. The record for memorizing digits of π, certified by Guinness World Records, is 70,000 digits, recited in India by Rajveer Meena in 9 hours and 27 minutes on 21 March 2015. In 2006, Akira Haraguchi, a retired Japanese engineer, claimed to have recited 100,000 decimal places, but the claim was not verified by Guinness World Records.
One common technique is to memorize a story or poem in which the word lengths represent the digits of π: The first word has three letters, the second word has one, the third has four, the fourth has one, the fifth has five, and so on. Such memorization aids are called mnemonics. An early example of a mnemonic for pi, originally devised by English scientist James Jeans, is "How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics." When a poem is used, it is sometimes referred to as a piem. Poems for memorizing π have been composed in several languages in addition to English. Record-setting π memorizers typically do not rely on poems, but instead use methods such as remembering number patterns and the method of loci.
A few authors have used the digits of π to establish a new form of constrained writing, where the word lengths are required to represent the digits of π. The Cadaeic Cadenza contains the first 3835 digits of π in this manner, and the full-length book Not a Wake contains 10,000 words, each representing one digit of π.
In popular culture

Perhaps because of the simplicity of its definition and its ubiquitous presence in formulae, π has been represented in popular culture more than other mathematical constructs.
In the Palais de la Découverte (a science museum in Paris) there is a circular room known as the pi room. On its wall are inscribed 707 digits of π. The digits are large wooden characters attached to the dome-like ceiling. The digits were based on an 1873 calculation by English mathematician William Shanks, which included an error beginning at the 528th digit. The error was detected in 1946 and corrected in 1949.
In Carl Sagan's 1985 novel Contact it is suggested that the creator of the universe buried a message deep within the digits of π. This part of the story was omitted from the film adaptation of the novel. The digits of π have also been incorporated into the lyrics of the song "Pi" from the 2005 album Aerial by Kate Bush. In the 1967 Star Trek episode "Wolf in the Fold", an out-of-control computer is contained by being instructed to "Compute to the last digit the value of π".
In the United States, Pi Day falls on 14 March (written 3/14 in the US style), and is popular among students. π and its digital representation are often used by self-described "math geeks" for inside jokes among mathematically and technologically minded groups. A college cheer variously attributed to the Massachusetts Institute of Technology or the Rensselaer Polytechnic Institute includes "3.14159". Pi Day in 2015 was particularly significant because the date and time 3/14/15 9:26:53 reflected many more digits of pi. In parts of the world where dates are commonly noted in day/month/year format, 22 July represents "Pi Approximation Day", as 22/7 = 3.142857.
Some have proposed replacing π by τ = 2π, arguing that τ, as the number of radians in one turn or the ratio of a circle's circumference to its radius, is more natural than π and simplifies many formulae. This use of τ has not made its way into mainstream mathematics, but since 2010 this has led to people celebrating Two Pi Day or Tau Day on June 28.
In 1897, an amateur mathematician attempted to persuade the Indiana legislature to pass the Indiana Pi Bill, which described a method to square the circle and contained text that implied various incorrect values for π, including 3.2. The bill is notorious as an attempt to establish a value of mathematical constant by legislative fiat. The bill was passed by the Indiana House of Representatives, but rejected by the Senate, and thus it did not become a law.
In computer culture
In contemporary internet culture, individuals and organizations frequently pay homage to the number π. For instance, the computer scientist Donald Knuth let the version numbers of his program TeX approach π. The versions are 3, 3.1, 3.14, and so forth.
Many programming languages include π for use in programs. Similarly, τ has been added to several programming languages as a predefined constant.
See also
References
Explanatory notes
- In particular, π is conjectured to be a normal number, which implies a specific kind of statistical randomness on its digits in all bases.
- The specific integral that Weierstrass used was
- The polynomial shown is the first few terms of the Taylor series expansion of the sine function.
Citations
- Andrews, Askey & Roy 1999, p. 59.
- Gupta, R. C. (1992). "On the remainder term in the Madhava–Leibniz's series". Ganita Bharati. 14 (1–4): 68–71.
- ^ Jones, William (1706). Synopsis Palmariorum Matheseos. London: J. Wale. pp. 243, 263. p. 263:
There are various other ways of finding the Lengths, or Areas of particular Curve Lines or Planes, which may very much facilitate the Practice; as for instance, in the Circle, the Diameter is to Circumference as 1 to
3.14159, &c. = π. This Series (among others for the same purpose, and drawn from the same Principle) I receiv'd from the Excellent Analyst, and my much Esteem'd Friend Mr. John Machin; and by means thereof, Van Ceulen's Number, or that in Art. 64.38. may be Examin'd with all desireable Ease and Dispatch.Reprinted in Smith, David Eugene (1929). "William Jones: The First Use of π for the Circle Ratio". A Source Book in Mathematics. McGraw–Hill. pp. 346–347.
- "π trillion digits of π". pi2e.ch. Archived from the original on 6 December 2016.
- Haruka Iwao, Emma (14 March 2019). "Pi in the sky: Calculating a record-breaking 31.4 trillion digits of Archimedes' constant on Google Cloud". Google Cloud Platform. Archived from the original on 19 October 2019. Retrieved 12 April 2019.
- Arndt & Haenel 2006, p. 17.
- Bailey, David H.; Plouffe, Simon M.; Borwein, Peter B.; Borwein, Jonathan M. (1997). "The quest for PI". The Mathematical Intelligencer. 19 (1): 50–56. CiteSeerX 10.1.1.138.7085. doi:10.1007/BF03024340. ISSN 0343-6993. S2CID 14318695.
- ^ Oughtred, William (1652). Theorematum in libris Archimedis de sphaera et cylindro declarario (in Latin). Excudebat L. Lichfield, Veneunt apud T. Robinson.
δ.π :: semidiameter. semiperipheria
- "pi". Dictionary.reference.com. 2 March 1993. Archived from the original on 28 July 2014. Retrieved 18 June 2012.
- ^ Arndt & Haenel 2006, p. 8.
- Apostol, Tom (1967). Calculus. Vol. 1 (2nd ed.). Wiley. p. 102.
From a logical point of view, this is unsatisfactory at the present stage because we have not yet discussed the concept of arc length
- ^ Remmert 2012, p. 129.
- Remmert 2012, p. 148. Weierstrass, Karl (1841). "Darstellung einer analytischen Function einer complexen Veränderlichen, deren absoluter Betrag zwischen zwei gegebenen Grenzen liegt" [Representation of an analytical function of a complex variable, whose absolute value lies between two given limits]. Mathematische Werke (in German). Vol. 1. Berlin: Mayer & Müller (published 1894). pp. 51–66.
- Baltzer, Richard (1870). Die Elemente der Mathematik [The Elements of Mathematics] (in German). Hirzel. p. 195. Archived from the original on 14 September 2016.
- Landau, Edmund (1934). Einführung in die Differentialrechnung und Integralrechnung (in German). Noordoff. p. 193.
- ^ Rudin, Walter (1976). Principles of Mathematical Analysis. McGraw-Hill. p. 183. ISBN 978-0-07-054235-8.
- Rudin, Walter (1986). Real and complex analysis. McGraw-Hill. p. 2.
- Ahlfors, Lars (1966). Complex analysis. McGraw-Hill. p. 46.
- Bourbaki, Nicolas (1981). Topologie generale. Springer. §VIII.2.
- ^ Bourbaki, Nicolas (1979). Fonctions d'une variable réelle (in French). Springer. §II.3.
- ^ Arndt & Haenel 2006, p. 5.
- Salikhov, V. (2008). "On the Irrationality Measure of pi". Russian Mathematical Surveys. 53 (3): 570–572. Bibcode:2008RuMaS..63..570S. doi:10.1070/RM2008v063n03ABEH004543. ISSN 0036-0279. S2CID 250798202.
- Arndt & Haenel 2006, pp. 22–23.
- Arndt & Haenel 2006, pp. 22, 28–30.
- Arndt & Haenel 2006, p. 3.
- Arndt & Haenel 2006, p. 6.
- Posamentier & Lehmann 2004, p. 25
- Eymard & Lafon 2004, p. 129
- Beckmann, Peter (1989) . History of Pi. St. Martin's Press. p. 37. ISBN 978-0-88029-418-8.
- Schlager, Neil; Lauer, Josh (2001). Science and Its Times: Understanding the Social Significance of Scientific Discovery. Gale Group. ISBN 978-0-7876-3933-4. Archived from the original on 13 December 2019. Retrieved 19 December 2019., p. 185.
- Murty, M. Ram; Rath, Purusottam (2014). Transcendental Numbers. Springer. doi:10.1007/978-1-4939-0832-5. ISBN 978-1-4939-0831-8.
- Waldschmidt, Michel (2021). "Schanuel's Conjecture: algebraic independence of transcendental numbers" (PDF).
- Weisstein, Eric W. "Lindemann-Weierstrass Theorem". mathworld.wolfram.com. Retrieved 26 October 2024.
- ^ Eymard & Lafon 2004, p. 78
- Arndt & Haenel 2006, p. 33.
- ^ Mollin, R. A. (1999). "Continued fraction gems". Nieuw Archief voor Wiskunde. 17 (3): 383–405. MR 1743850.
- Lange, L.J. (May 1999). "An Elegant Continued Fraction for π". The American Mathematical Monthly. 106 (5): 456–458. doi:10.2307/2589152. JSTOR 2589152.
- Arndt & Haenel 2006, p. 240.
- Arndt & Haenel 2006, p. 242.
- Kennedy, E.S. (1978). "Abu-r-Raihan al-Biruni, 973–1048". Journal for the History of Astronomy. 9: 65. Bibcode:1978JHA.....9...65K. doi:10.1177/002182867800900106. S2CID 126383231. Ptolemy used a three-sexagesimal-digit approximation, and Jamshīd al-Kāshī expanded this to nine digits; see Aaboe, Asger (1964). Episodes from the Early History of Mathematics. New Mathematical Library. Vol. 13. New York: Random House. p. 125. ISBN 978-0-88385-613-0. Archived from the original on 29 November 2016.
- Abramson 2014, Section 8.5: Polar form of complex numbers.
- ^ Bronshteĭn & Semendiaev 1971, p. 592
- Maor, Eli (2009). E: The Story of a Number. Princeton University Press. p. 160. ISBN 978-0-691-14134-3.
- Andrews, Askey & Roy 1999, p. 14.
- ^ Arndt & Haenel 2006, p. 167.
- Herz-Fischler, Roger (2000). The Shape of the Great Pyramid. Wilfrid Laurier University Press. pp. 67–77, 165–166. ISBN 978-0-88920-324-2. Archived from the original on 29 November 2016. Retrieved 5 June 2013.
- Plofker, Kim (2009). Mathematics in India. Princeton University Press. p. 27. ISBN 978-0691120676.
- Arndt & Haenel 2006, p. 170.
- Arndt & Haenel 2006, pp. 175, 205.
- ^ Borwein, Jonathan M. (2014). "The life of π: from Archimedes to ENIAC and beyond". In Sidoli, Nathan; Van Brummelen, Glen (eds.). From Alexandria, through Baghdad: Surveys and studies in the ancient Greek and medieval Islamic mathematical sciences in honor of J. L. Berggren. Heidelberg: Springer. pp. 531–561. doi:10.1007/978-3-642-36736-6_24. ISBN 978-3-642-36735-9. MR 3203895.
- Arndt & Haenel 2006, p. 171.
- Arndt & Haenel 2006, p. 176.
- Boyer & Merzbach 1991, p. 168.
- Arndt & Haenel 2006, pp. 15–16, 175, 184–186, 205. Grienberger achieved 39 digits in 1630; Sharp 71 digits in 1699.
- Arndt & Haenel 2006, pp. 176–177.
- ^ Boyer & Merzbach 1991, p. 202
- Arndt & Haenel 2006, p. 177.
- Arndt & Haenel 2006, p. 178.
- Arndt & Haenel 2006, p. 179.
- ^ Arndt & Haenel 2006, p. 180.
- Azarian, Mohammad K. (2010). "al-Risāla al-muhītīyya: A Summary". Missouri Journal of Mathematical Sciences. 22 (2): 64–85. doi:10.35834/mjms/1312233136.
- O'Connor, John J.; Robertson, Edmund F. (1999). "Ghiyath al-Din Jamshid Mas'ud al-Kashi". MacTutor History of Mathematics archive. Archived from the original on 12 April 2011. Retrieved 11 August 2012.
- ^ Arndt & Haenel 2006, p. 182.
- Arndt & Haenel 2006, pp. 182–183.
- Arndt & Haenel 2006, p. 183.
- Grienbergerus, Christophorus (1630). Elementa Trigonometrica (PDF) (in Latin). Archived from the original (PDF) on 1 February 2014. His evaluation was 3.14159 26535 89793 23846 26433 83279 50288 4196 < π < 3.14159 26535 89793 23846 26433 83279 50288 4199.
- Brezinski, C. (2009). "Some pioneers of extrapolation methods". In Bultheel, Adhemar; Cools, Ronald (eds.). The Birth of Numerical Analysis. World Scientific. pp. 1–22. doi:10.1142/9789812836267_0001. ISBN 978-981-283-625-0.
- Yoder, Joella G. (1996). "Following in the footsteps of geometry: The mathematical world of Christiaan Huygens". De Zeventiende Eeuw. 12: 83–93 – via Digital Library for Dutch Literature.
- Arndt & Haenel 2006, pp. 185–191
- ^ Roy, Ranjan (1990). "The Discovery of the Series Formula for π by Leibniz, Gregory and Nilakantha" (PDF). Mathematics Magazine. 63 (5): 291–306. doi:10.1080/0025570X.1990.11977541. Archived from the original (PDF) on 14 March 2023. Retrieved 21 February 2023.
- Arndt & Haenel 2006, pp. 185–186.
- Joseph, George Gheverghese (1991). The Crest of the Peacock: Non-European Roots of Mathematics. Princeton University Press. p. 264. ISBN 978-0-691-13526-7.
- ^ Arndt & Haenel 2006, p. 187.
- OEIS: A060294
- Vieta, Franciscus (1593). Variorum de rebus mathematicis responsorum. Vol. VIII.
- ^ Arndt & Haenel 2006, p. 188. Newton quoted by Arndt.
- Horvath, Miklos (1983). "On the Leibnizian quadrature of the circle" (PDF). Annales Universitatis Scientiarum Budapestiensis (Sectio Computatorica). 4: 75–83.
- ^ Eymard & Lafon 2004, pp. 53–54
- Cooker, M.J. (2011). "Fast formulas for slowly convergent alternating series" (PDF). Mathematical Gazette. 95 (533): 218–226. doi:10.1017/S0025557200002928. S2CID 123392772. Archived from the original (PDF) on 4 May 2019. Retrieved 23 February 2023.
- Arndt & Haenel 2006, p. 189.
- Tweddle, Ian (1991). "John Machin and Robert Simson on Inverse-tangent Series for π". Archive for History of Exact Sciences. 42 (1): 1–14. doi:10.1007/BF00384331. JSTOR 41133896. S2CID 121087222.
- Arndt & Haenel 2006, pp. 192–193.
- ^ Arndt & Haenel 2006, pp. 72–74
- Lehmer, D. H. (1938). "On Arccotangent Relations for π" (PDF). American Mathematical Monthly. 45 (10): 657–664 Published by: Mathematical Association of America. doi:10.1080/00029890.1938.11990873. JSTOR 2302434. Archived from the original (PDF) on 7 March 2023. Retrieved 21 February 2023.
- Roy, Ranjan (2021) . Series and Products in the Development of Mathematics. Vol. 1 (2 ed.). Cambridge University Press. pp. 215–216, 219–220.
Newton, Isaac (1971). Whiteside, Derek Thomas (ed.). The Mathematical Papers of Isaac Newton. Vol. 4, 1674–1684. Cambridge University Press. pp. 526–653.
-
Sandifer, Ed (2009). "Estimating π" (PDF). How Euler Did It. Reprinted in How Euler Did Even More. Mathematical Association of America. 2014. pp. 109–118.
Euler, Leonhard (1755). "§2.2.30". Institutiones Calculi Differentialis (in Latin). Academiae Imperialis Scientiarium Petropolitanae. p. 318. E 212.
Euler, Leonhard (1798) . "Investigatio quarundam serierum, quae ad rationem peripheriae circuli ad diametrum vero proxime definiendam maxime sunt accommodatae". Nova Acta Academiae Scientiarum Petropolitinae. 11: 133–149, 167–168. E 705.
Chien-Lih, Hwang (2004). "88.38 Some Observations on the Method of Arctangents for the Calculation of π". Mathematical Gazette. 88 (512): 270–278. doi:10.1017/S0025557200175060. S2CID 123532808.
Chien-Lih, Hwang (2005). "89.67 An elementary derivation of Euler's series for the arctangent function". Mathematical Gazette. 89 (516): 469–470. doi:10.1017/S0025557200178404. S2CID 123395287.
- Arndt & Haenel 2006, pp. 192–196, 205.
- Arndt & Haenel 2006, pp. 194–196
- Hayes, Brian (September 2014). "Pencil, Paper, and Pi". American Scientist. Vol. 102, no. 5. p. 342. doi:10.1511/2014.110.342. Retrieved 22 January 2022.
- ^ Borwein, J.M.; Borwein, P.B. (1988). "Ramanujan and Pi". Scientific American. 256 (2): 112–117. Bibcode:1988SciAm.258b.112B. doi:10.1038/scientificamerican0288-112.
Arndt & Haenel 2006, pp. 15–17, 70–72, 104, 156, 192–197, 201–202 - Arndt & Haenel 2006, pp. 69–72.
- Borwein, J.M.; Borwein, P.B.; Dilcher, K. (1989). "Pi, Euler Numbers, and Asymptotic Expansions". American Mathematical Monthly. 96 (8): 681–687. doi:10.2307/2324715. hdl:1959.13/1043679. JSTOR 2324715.
- Arndt & Haenel 2006, Formula 16.10, p. 223.
- Wells, David (1997). The Penguin Dictionary of Curious and Interesting Numbers (revised ed.). Penguin. p. 35. ISBN 978-0-14-026149-3.
- ^ Posamentier & Lehmann 2004, p. 284
- Lambert, Johann, "Mémoire sur quelques propriétés remarquables des quantités transcendantes circulaires et logarithmiques", reprinted in Berggren, Borwein & Borwein 1997, pp. 129–140
- Lindemann, F. (1882). "Über die Ludolph'sche Zahl". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin. 2: 679–682.
- Arndt & Haenel 2006, p. 196.
- Hardy and Wright 1938 and 2000: 177 footnote § 11.13–14 references Lindemann's proof as appearing at Math. Ann. 20 (1882), 213–225.
- cf Hardy and Wright 1938 and 2000:177 footnote § 11.13–14. The proofs that e and π are transcendental can be found on pp. 170–176. They cite two sources of the proofs at Landau 1927 or Perron 1910; see the "List of Books" at pp. 417–419 for full citations.
- ^ Cajori, Florian (2007). A History of Mathematical Notations: Vol. II. Cosimo, Inc. pp. 8–13. ISBN 978-1-60206-714-1.
the ratio of the length of a circle to its diameter was represented in the fractional form by the use of two letters ... J.A. Segner ... in 1767, he represented 3.14159... by δ:π, as did Oughtred more than a century earlier
- Schepler, H.C. (1950) "The Chronology of Pi" Mathematics Magazine. 23.
Part 1. Jan/Feb. (3): 165–170. doi:10.2307/3029284.
Part 2. Mar/Apr. (4): 216-228. doi:10.2307/3029832.
Part 3. May/Jun. (5): 279-283. doi:10.2307/3029000.
See p. 220: William Oughtred used the letter π to represent the periphery (that is, the circumference) of a circle. - ^ Smith, David E. (1958). History of Mathematics. Courier Corporation. p. 312. ISBN 978-0-486-20430-7.
- Archibald, R.C. (1921). "Historical Notes on the Relation e = i". The American Mathematical Monthly. 28 (3): 116–121. doi:10.2307/2972388. JSTOR 2972388.
It is noticeable that these letters are never used separately, that is, π is not used for 'Semiperipheria'
- ^ Arndt & Haenel 2006, p. 166.
- See, for example, Oughtred, William (1648). Clavis Mathematicæ [The key to mathematics] (in Latin). London: Thomas Harper. p. 69. (English translation: Oughtred, William (1694). Key of the Mathematics. J. Salusbury.)
- Barrow, Isaac (1860). "Lecture XXIV". In Whewell, William (ed.). The mathematical works of Isaac Barrow (in Latin). Harvard University. Cambridge University press. p. 381.
- Gregorius, David (1695). "Ad Reverendum Virum D. Henricum Aldrich S.T.T. Decanum Aedis Christi Oxoniae" (PDF). Philosophical Transactions (in Latin). 19 (231): 637–652. Bibcode:1695RSPT...19..637G. doi:10.1098/rstl.1695.0114. JSTOR 102382.
- Arndt & Haenel 2006, p. 165: A facsimile of Jones' text is in Berggren, Borwein & Borwein 1997, pp. 108–109.
- Segner, Joannes Andreas (1756). Cursus Mathematicus (in Latin). Halae Magdeburgicae. p. 282. Archived from the original on 15 October 2017. Retrieved 15 October 2017.
- Euler, Leonhard (1727). "Tentamen explicationis phaenomenorum aeris" (PDF). Commentarii Academiae Scientiarum Imperialis Petropolitana (in Latin). 2: 351. E007. Archived (PDF) from the original on 1 April 2016. Retrieved 15 October 2017.
Sumatur pro ratione radii ad peripheriem, I : π
English translation by Ian Bruce Archived 10 June 2016 at the Wayback Machine: "π is taken for the ratio of the radius to the periphery " - Euler, Leonhard (1747). Henry, Charles (ed.). Lettres inédites d'Euler à d'Alembert. Bullettino di Bibliografia e di Storia delle Scienze Matematiche e Fisiche (in French). Vol. 19 (published 1886). p. 139. E858.
Car, soit π la circonference d'un cercle, dout le rayon est = 1
English translation in Cajori, Florian (1913). "History of the Exponential and Logarithmic Concepts". The American Mathematical Monthly. 20 (3): 75–84. doi:10.2307/2973441. JSTOR 2973441.Letting π be the circumference (!) of a circle of unit radius
- Euler, Leonhard (1736). "Ch. 3 Prop. 34 Cor. 1". Mechanica sive motus scientia analytice exposita. (cum tabulis) (in Latin). Vol. 1. Academiae scientiarum Petropoli. p. 113. E015.
Denotet 1 : π rationem diametri ad peripheriam
English translation by Ian Bruce Archived 10 June 2016 at the Wayback Machine : "Let 1 : π denote the ratio of the diameter to the circumference" - Euler, Leonhard (1922). Leonhardi Euleri opera omnia. 1, Opera mathematica. Volumen VIII, Leonhardi Euleri introductio in analysin infinitorum. Tomus primus / ediderunt Adolf Krazer et Ferdinand Rudio (in Latin). Lipsae: B.G. Teubneri. pp. 133–134. E101. Archived from the original on 16 October 2017. Retrieved 15 October 2017.
- Segner, Johann Andreas von (1761). Cursus Mathematicus: Elementorum Analyseos Infinitorum Elementorum Analyseos Infinitorvm (in Latin). Renger. p. 374.
Si autem π notet peripheriam circuli, cuius diameter eſt 2
- Arndt & Haenel 2006, p. 205.
- ^ Arndt & Haenel 2006, p. 197.
- Reitwiesner, George (1950). "An ENIAC Determination of pi and e to 2000 Decimal Places". Mathematical Tables and Other Aids to Computation. 4 (29): 11–15. doi:10.2307/2002695. JSTOR 2002695.
- Nicholson, J. C.; Jeenel, J. (1955). "Some comments on a NORC Computation of π". Math. Tabl. Aids. Comp. 9 (52): 162–164. doi:10.2307/2002052. JSTOR 2002052.
- Arndt & Haenel 2006, pp. 15–17.
- Arndt & Haenel 2006, p. 131.
- Arndt & Haenel 2006, pp. 132, 140.
- ^ Arndt & Haenel 2006, p. 87.
- Arndt & Haenel 2006, pp. 111 (5 times), pp. 113–114 (4 times). For details of algorithms, see Borwein, Jonathan; Borwein, Peter (1987). Pi and the AGM: a Study in Analytic Number Theory and Computational Complexity. Wiley. ISBN 978-0-471-31515-5.
- ^ Bailey, David H. (16 May 2003). "Some Background on Kanada's Recent Pi Calculation" (PDF). Archived (PDF) from the original on 15 April 2012. Retrieved 12 April 2012.
- Arndt & Haenel 2006, pp. 17–19
- Schudel, Matt (25 March 2009). "John W. Wrench, Jr.: Mathematician Had a Taste for Pi". The Washington Post. p. B5.
- Connor, Steve (8 January 2010). "The Big Question: How close have we come to knowing the precise value of pi?". The Independent. London. Archived from the original on 2 April 2012. Retrieved 14 April 2012.
- Arndt & Haenel 2006, p. 18.
- Arndt & Haenel 2006, pp. 103–104
- Arndt & Haenel 2006, p. 104
- Arndt & Haenel 2006, pp. 104, 206
- Arndt & Haenel 2006, pp. 110–111
- Eymard & Lafon 2004, p. 254
- ^ Bailey, David H.; Borwein, Jonathan M. (2016). "15.2 Computational records". Pi: The Next Generation, A Sourcebook on the Recent History of Pi and Its Computation. Springer International Publishing. p. 469. doi:10.1007/978-3-319-32377-0. ISBN 978-3-319-32375-6.
- Cassel, David (11 June 2022). "How Google's Emma Haruka Iwao Helped Set a New Record for Pi". The New Stack.
- PSLQ means Partial Sum of Least Squares.
- Plouffe, Simon (April 2006). "Identities inspired by Ramanujan's Notebooks (part 2)" (PDF). Archived (PDF) from the original on 14 January 2012. Retrieved 10 April 2009.
- Arndt & Haenel 2006, p. 39
- Ramaley, J.F. (October 1969). "Buffon's Noodle Problem". The American Mathematical Monthly. 76 (8): 916–918. doi:10.2307/2317945. JSTOR 2317945.
- Arndt & Haenel 2006, pp. 39–40
Posamentier & Lehmann 2004, p. 105 - Grünbaum, B. (1960). "Projection Constants". Transactions of the American Mathematical Society. 95 (3): 451–465. doi:10.1090/s0002-9947-1960-0114110-9.
- Arndt & Haenel 2006, pp. 43
Posamentier & Lehmann 2004, pp. 105–108 - ^ Arndt & Haenel 2006, pp. 77–84.
- ^ Gibbons, Jeremy (2006). "Unbounded spigot algorithms for the digits of pi" (PDF). The American Mathematical Monthly. 113 (4): 318–328. doi:10.2307/27641917. JSTOR 27641917. MR 2211758.
- ^ Arndt & Haenel 2006, p. 77.
- Rabinowitz, Stanley; Wagon, Stan (March 1995). "A spigot algorithm for the digits of Pi". American Mathematical Monthly. 102 (3): 195–203. doi:10.2307/2975006. JSTOR 2975006.
- ^ Arndt & Haenel 2006, pp. 117, 126–128.
- Bailey, David H.; Borwein, Peter B.; Plouffe, Simon (April 1997). "On the Rapid Computation of Various Polylogarithmic Constants" (PDF). Mathematics of Computation. 66 (218): 903–913. Bibcode:1997MaCom..66..903B. CiteSeerX 10.1.1.55.3762. doi:10.1090/S0025-5718-97-00856-9. S2CID 6109631. Archived (PDF) from the original on 22 July 2012.
- Arndt & Haenel 2006, p. 20
Bellards formula in: Bellard, Fabrice. "A new formula to compute the n binary digit of pi". Archived from the original on 12 September 2007. Retrieved 27 October 2007. - Palmer, Jason (16 September 2010). "Pi record smashed as team finds two-quadrillionth digit". BBC News. Archived from the original on 17 March 2011. Retrieved 26 March 2011.
- Plouffe, Simon (2022). "A formula for the nth decimal digit or binary of π and powers of π". arXiv:2201.12601 .
- Bronshteĭn & Semendiaev 1971, pp. 200, 209
- Martini, Horst; Montejano, Luis; Oliveros, Déborah (2019). Bodies of Constant Width: An Introduction to Convex Geometry with Applications. Birkhäuser. doi:10.1007/978-3-030-03868-7. ISBN 978-3-030-03866-3. MR 3930585. S2CID 127264210.
See Barbier's theorem, Corollary 5.1.1, p. 98; Reuleaux triangles, pp. 3, 10; smooth curves such as an analytic curve due to Rabinowitz, § 5.3.3, pp. 111–112.
- Herman, Edwin; Strang, Gilbert (2016). "Section 5.5, Exercise 316". Calculus. Vol. 1. OpenStax. p. 594.
- Kontsevich, Maxim; Zagier, Don (2001), Engquist, Björn; Schmid, Wilfried (eds.), "Periods", Mathematics Unlimited — 2001 and Beyond, Berlin, Heidelberg: Springer, pp. 771–808, doi:10.1007/978-3-642-56478-9_39, ISBN 978-3-642-56478-9, retrieved 23 September 2024
- Abramson 2014, Section 5.1: Angles.
- ^ Bronshteĭn & Semendiaev 1971, pp. 210–211
- Hilbert, David; Courant, Richard (1966). Methods of mathematical physics, volume 1. Wiley. pp. 286–290.
- Dym & McKean 1972, p. 47.
- Thompson, William (1894). "Isoperimetrical problems". Nature Series: Popular Lectures and Addresses. II: 571–592.
- Chavel, Isaac (2001). Isoperimetric inequalities. Cambridge University Press.
- Talenti, Giorgio (1976). "Best constant in Sobolev inequality". Annali di Matematica Pura ed Applicata. 110 (1): 353–372. CiteSeerX 10.1.1.615.4193. doi:10.1007/BF02418013. ISSN 1618-1891. S2CID 16923822.
- L. Esposito; C. Nitsch; C. Trombetti (2011). "Best constants in Poincaré inequalities for convex domains". arXiv:1110.2960 .
- Del Pino, M.; Dolbeault, J. (2002). "Best constants for Gagliardo–Nirenberg inequalities and applications to nonlinear diffusions". Journal de Mathématiques Pures et Appliquées. 81 (9): 847–875. CiteSeerX 10.1.1.57.7077. doi:10.1016/s0021-7824(02)01266-7. S2CID 8409465.
- Payne, L.E.; Weinberger, H.F. (1960). "An optimal Poincaré inequality for convex domains". Archive for Rational Mechanics and Analysis. 5 (1): 286–292. Bibcode:1960ArRMA...5..286P. doi:10.1007/BF00252910. ISSN 0003-9527. S2CID 121881343.
- Folland, Gerald (1989). Harmonic analysis in phase space. Princeton University Press. p. 5.
- ^ Howe, Roger (1980). "On the role of the Heisenberg group in harmonic analysis". Bulletin of the American Mathematical Society. 3 (2): 821–844. doi:10.1090/S0273-0979-1980-14825-9. MR 0578375.
- Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 1, Wiley, 1968, pp. 174–190.
- ^ Bronshteĭn & Semendiaev 1971, pp. 106–107, 744, 748
- Dym & McKean 1972, Section 2.7.
- Stein, Elias; Weiss, Guido (1971). Fourier analysis on Euclidean spaces. Princeton University Press. p. 6.; Theorem 1.13.
- Spivak, Michael (1999). A Comprehensive Introduction to Differential Geometry. Vol. 3. Publish or Perish Press.; Chapter 6.
- Kobayashi, Shoshichi; Nomizu, Katsumi (1996). Foundations of Differential Geometry. Vol. 2 (New ed.). Wiley Interscience. p. 293.; Chapter XII Characteristic classes
- Ahlfors, Lars (1966). Complex analysis. McGraw-Hill. p. 115.
- Joglekar, S. D. (2005). Mathematical Physics. Universities Press. p. 166. ISBN 978-81-7371-422-1.
- Schey, H. M. (1996). Div, Grad, Curl, and All That: An Informal Text on Vector Calculus. W.W. Norton. ISBN 0-393-96997-5.
- Yeo, Adrian (2006). The pleasures of pi, e and other interesting numbers. World Scientific Pub. p. 21. ISBN 978-981-270-078-0.
- Ehlers, Jürgen (2000). Einstein's Field Equations and Their Physical Implications. Springer. p. 7. ISBN 978-3-540-67073-5.
- ^ Gilbarg, D.; Trudinger, Neil (1983), Elliptic Partial Differential Equations of Second Order, New York: Springer, ISBN 3-540-41160-7
- Bronshteĭn & Semendiaev 1971, pp. 191–192
- Artin, Emil (1964). The Gamma Function. Athena series; selected topics in mathematics (1st ed.). Holt, Rinehart and Winston.
- Evans, Lawrence (1997). Partial Differential Equations. AMS. p. 615.
- Bronshteĭn & Semendiaev 1971, p. 190
- Benjamin Nill; Andreas Paffenholz (2014). "On the equality case in Erhart's volume conjecture". Advances in Geometry. 14 (4): 579–586. arXiv:1205.1270. doi:10.1515/advgeom-2014-0001. ISSN 1615-7168. S2CID 119125713.
- Arndt & Haenel 2006, pp. 41–43
- This theorem was proved by Ernesto Cesàro in 1881. For a more rigorous proof than the intuitive and informal one given here, see Hardy, G. H. (2008). An Introduction to the Theory of Numbers. Oxford University Press. Theorem 332. ISBN 978-0-19-921986-5.
- Ogilvy, C. S.; Anderson, J. T. (1988). Excursions in Number Theory. Dover Publications Inc. pp. 29–35. ISBN 0-486-25778-9.
- Arndt & Haenel 2006, p. 43
- Platonov, Vladimir; Rapinchuk, Andrei (1994). Algebraic Groups and Number Theory. Academic Press. pp. 262–265.
- Sondow, J. (1994). "Analytic continuation of Riemann's zeta function and values at negative integers via Euler's transformation of series". Proceedings of the American Mathematical Society. 120 (2): 421–424. CiteSeerX 10.1.1.352.5774. doi:10.1090/s0002-9939-1994-1172954-7. S2CID 122276856.
- T. Friedmann; C.R. Hagen (2015). "Quantum mechanical derivation of the Wallis formula for pi". Journal of Mathematical Physics. 56 (11): 112101. arXiv:1510.07813. Bibcode:2015JMP....56k2101F. doi:10.1063/1.4930800. S2CID 119315853.
- Tate, John T. (1950). "Fourier analysis in number fields, and Hecke's zeta-functions". In Cassels, J. W. S.; Fröhlich, A. (eds.). Algebraic Number Theory (Proc. Instructional Conf., Brighton, 1965). Thompson, Washington, DC. pp. 305–347. ISBN 978-0-9502734-2-6. MR 0217026.
- Dym & McKean 1972, Chapter 4.
- ^ Mumford, David (1983). Tata Lectures on Theta I. Boston: Birkhauser. pp. 1–117. ISBN 978-3-7643-3109-2.
- Port, Sidney; Stone, Charles (1978). Brownian motion and classical potential theory. Academic Press. p. 29.
- Titchmarsh, E. (1948). Introduction to the Theory of Fourier Integrals (2nd ed.). Oxford University: Clarendon Press (published 1986). ISBN 978-0-8284-0324-5.
- Stein, Elias (1970). Singular Integrals and Differentiability Properties of Functions. Princeton University Press.; Chapter II.
- ^ Klebanoff, Aaron (2001). "Pi in the Mandelbrot set" (PDF). Fractals. 9 (4): 393–402. doi:10.1142/S0218348X01000828. Archived from the original (PDF) on 27 October 2011. Retrieved 14 April 2012.
- Peitgen, Heinz-Otto (2004). Chaos and fractals: new frontiers of science. Springer. pp. 801–803. ISBN 978-0-387-20229-7.
- Ovsienko, V.; Tabachnikov, S. (2004). "Section 1.3". Projective Differential Geometry Old and New: From the Schwarzian Derivative to the Cohomology of Diffeomorphism Groups. Cambridge Tracts in Mathematics. Cambridge University Press. ISBN 978-0-521-83186-4.
- Halliday, David; Resnick, Robert; Walker, Jearl (1997). Fundamentals of Physics (5th ed.). John Wiley & Sons. p. 381. ISBN 0-471-14854-7.
- Urone, Paul Peter; Hinrichs, Roger (2022). "29.7 Probability: The Heisenberg Uncertainty Principle". College Physics 2e. OpenStax.
- Itzykson, C.; Zuber, J.-B. (1980). Quantum Field Theory (2005 ed.). Mineola, NY: Dover Publications. ISBN 978-0-486-44568-7. LCCN 2005053026. OCLC 61200849.
- Low, Peter (1971). Classical Theory of Structures Based on the Differential Equation. Cambridge University Press. pp. 116–118. ISBN 978-0-521-08089-7.
- Batchelor, G. K. (1967). An Introduction to Fluid Dynamics. Cambridge University Press. p. 233. ISBN 0-521-66396-2.
- ^ Arndt & Haenel 2006, pp. 44–45
- "Most Pi Places Memorized" Archived 14 February 2016 at the Wayback Machine, Guinness World Records.
- Otake, Tomoko (17 December 2006). "How can anyone remember 100,000 numbers?". The Japan Times. Archived from the original on 18 August 2013. Retrieved 27 October 2007.
- Danesi, Marcel (January 2021). "Chapter 4: Pi in Popular Culture". Pi (π) in Nature, Art, and Culture. Brill. p. 97. doi:10.1163/9789004433397. ISBN 9789004433373. S2CID 224869535.
- Raz, A.; Packard, M.G. (2009). "A slice of pi: An exploratory neuroimaging study of digit encoding and retrieval in a superior memorist". Neurocase. 15 (5): 361–372. doi:10.1080/13554790902776896. PMC 4323087. PMID 19585350.
- Keith, Mike. "Cadaeic Cadenza Notes & Commentary". Archived from the original on 18 January 2009. Retrieved 29 July 2009.
- Keith, Michael; Diana Keith (17 February 2010). Not A Wake: A dream embodying (pi)'s digits fully for 10,000 decimals. Vinculum Press. ISBN 978-0-9630097-1-5.
- For instance, Pickover calls π "the most famous mathematical constant of all time", and Peterson writes, "Of all known mathematical constants, however, pi continues to attract the most attention", citing the Givenchy π perfume, Pi (film), and Pi Day as examples. See: Pickover, Clifford A. (1995). Keys to Infinity. Wiley & Sons. p. 59. ISBN 978-0-471-11857-2. Peterson, Ivars (2002). Mathematical Treks: From Surreal Numbers to Magic Circles. MAA spectrum. Mathematical Association of America. p. 17. ISBN 978-0-88385-537-9. Archived from the original on 29 November 2016.
- Posamentier & Lehmann 2004, p. 118
Arndt & Haenel 2006, p. 50 - Arndt & Haenel 2006, p. 14
- Polster, Burkard; Ross, Marty (2012). Math Goes to the Movies. Johns Hopkins University Press. pp. 56–57. ISBN 978-1-421-40484-4.
- Gill, Andy (4 November 2005). "Review of Aerial". The Independent. Archived from the original on 15 October 2006.
the almost autistic satisfaction of the obsessive-compulsive mathematician fascinated by 'Pi' (which affords the opportunity to hear Bush slowly sing vast chunks of the number in question, several dozen digits long)
- Rubillo, James M. (January 1989). "Disintegrate 'em". The Mathematics Teacher. 82 (1): 10. JSTOR 27966082.
- Petroski, Henry (2011). Title An Engineer's Alphabet: Gleanings from the Softer Side of a Profession. Cambridge University Press. p. 47. ISBN 978-1-139-50530-7.
- "Happy Pi Day! Watch these stunning videos of kids reciting 3.14". USAToday.com. 14 March 2015. Archived from the original on 15 March 2015. Retrieved 14 March 2015.
- Rosenthal, Jeffrey S. (February 2015). "Pi Instant". Math Horizons. 22 (3): 22. doi:10.4169/mathhorizons.22.3.22. S2CID 218542599.
- Griffin, Andrew. "Pi Day: Why some mathematicians refuse to celebrate 14 March and won't observe the dessert-filled day". The Independent. Archived from the original on 24 April 2019. Retrieved 2 February 2019.
- Freiberger, Marianne; Thomas, Rachel (2015). "Tau – the new π". Numericon: A Journey through the Hidden Lives of Numbers. Quercus. p. 159. ISBN 978-1-62365-411-5.
- Abbott, Stephen (April 2012). "My Conversion to Tauism" (PDF). Math Horizons. 19 (4): 34. doi:10.4169/mathhorizons.19.4.34. S2CID 126179022. Archived (PDF) from the original on 28 September 2013.
- Palais, Robert (2001). "π Is Wrong!" (PDF). The Mathematical Intelligencer. 23 (3): 7–8. doi:10.1007/BF03026846. S2CID 120965049. Archived (PDF) from the original on 22 June 2012.
- "Life of pi in no danger – Experts cold-shoulder campaign to replace with tau". Telegraph India. 30 June 2011. Archived from the original on 13 July 2013.
- "Forget Pi Day. We should be celebrating Tau Day | Science News". Retrieved 2 May 2023.
- Arndt & Haenel 2006, pp. 211–212
Posamentier & Lehmann 2004, pp. 36–37
Hallerberg, Arthur (May 1977). "Indiana's squared circle". Mathematics Magazine. 50 (3): 136–140. doi:10.2307/2689499. JSTOR 2689499. - Knuth, Donald (3 October 1990). "The Future of TeX and Metafont" (PDF). TeX Mag. 5 (1): 145. Archived (PDF) from the original on 13 April 2016. Retrieved 17 February 2017.
- "PEP 628 – Add math.tau".
- "Crate tau". Retrieved 6 December 2022.
General and cited sources
- Abramson, Jay (2014). Precalculus. OpenStax.
- Andrews, George E.; Askey, Richard; Roy, Ranjan (1999). Special Functions. Cambridge: University Press. ISBN 978-0-521-78988-2.
- Arndt, Jörg; Haenel, Christoph (2006). Pi Unleashed. Springer-Verlag. ISBN 978-3-540-66572-4. Retrieved 5 June 2013. English translation by Catriona and David Lischka.
- Berggren, Lennart; Borwein, Jonathan; Borwein, Peter (1997). Pi: a Source Book. Springer-Verlag. ISBN 978-0-387-20571-7.
- Boyer, Carl B.; Merzbach, Uta C. (1991). A History of Mathematics (2 ed.). Wiley. ISBN 978-0-471-54397-8.
- Bronshteĭn, Ilia; Semendiaev, K.A. (1971). A Guide Book to Mathematics. Verlag Harri Deutsch. ISBN 978-3-87144-095-3.
- Dym, H.; McKean, H. P. (1972). Fourier series and integrals. Academic Press.
- Eymard, Pierre; Lafon, Jean Pierre (2004). The Number π. Translated by Wilson, Stephen. American Mathematical Society. ISBN 978-0-8218-3246-2. English translation of Autour du nombre π (in French). Hermann. 1999.
- Posamentier, Alfred S.; Lehmann, Ingmar (2004). π: A Biography of the World's Most Mysterious Number. Prometheus Books. ISBN 978-1-59102-200-8.
- Remmert, Reinhold (2012). "Ch. 5 What is π?". In Heinz-Dieter Ebbinghaus; Hans Hermes; Friedrich Hirzebruch; Max Koecher; Klaus Mainzer; Jürgen Neukirch; Alexander Prestel; Reinhold Remmert (eds.). Numbers. Springer. ISBN 978-1-4612-1005-4.
Further reading
- Blatner, David (1999). The Joy of π. Walker & Company. ISBN 978-0-8027-7562-7.
- Delahaye, Jean-Paul (1997). Le fascinant nombre π. Paris: Bibliothèque Pour la Science. ISBN 2-902918-25-9.
External links
- Weisstein, Eric W. "Pi". MathWorld.
- Demonstration by Lambert (1761) of irrationality of π, online Archived 31 December 2014 at the Wayback Machine and analysed BibNum Archived 2 April 2015 at the Wayback Machine (PDF).
- π Search Engine 2 billion searchable digits of π, e and √2
- approximation von π by lattice points and approximation of π with rectangles and trapezoids (interactive illustrations)
| Irrational numbers | ||
|---|---|---|
|  | |
 are commonly
are commonly 
 is constant, regardless of the circle's size. For example, if a circle has twice the diameter of another circle, it will also have twice the circumference, preserving the ratio
is constant, regardless of the circle's size. For example, if a circle has twice the diameter of another circle, it will also have twice the circumference, preserving the ratio  .
.
 , as the
, as the 
 and there is a unique positive real number π with this property.
and there is a unique positive real number π with this property.
 . This follows from the so-called
. This follows from the so-called  or
or  ). Second, since no transcendental number can be
). Second, since no transcendental number can be 

 where i is the
where i is the  . The frequent appearance of π in
. The frequent appearance of π in  where
where  in Euler's formula results in
in Euler's formula results in 
 , and these are called the "n-th
, and these are called the "n-th 
 . Although some
. Although some  and suggested the approximations
and suggested the approximations  and
and  , which he termed the
, which he termed the  .
.
 sides, which stood as the world record for about 180 years. French mathematician
sides, which stood as the world record for about 180 years. French mathematician  sides. Flemish mathematician
sides. Flemish mathematician 


 when evaluated with
when evaluated with  . But for
. But for  to compute π to 71 digits, breaking the previous record of 39 digits, which was set with a polygonal algorithm.
to compute π to 71 digits, breaking the previous record of 39 digits, which was set with a polygonal algorithm.


 with which he computed 20 digits of π in one hour.
with which he computed 20 digits of π in one hour.





 ", to express the ratio of periphery and diameter in the 1647 and later editions of Clavis Mathematicae.
", to express the ratio of periphery and diameter in the 1647 and later editions of Clavis Mathematicae.  " to represent the constant 3.14..., while
" to represent the constant 3.14..., while  " to represent 6.28... .
" to represent 6.28... .
 Periphery (π)", calculated for a circle with radius one. However, Jones writes that his equations for π are from the "ready pen of the truly ingenious Mr.
Periphery (π)", calculated for a circle with radius one. However, Jones writes that his equations for π are from the "ready pen of the truly ingenious Mr.  Iterate
Iterate

 Then an estimate for π is given by
Then an estimate for π is given by



 where q is
where q is 
 so that, for each n, Wn is drawn from a shifted and scaled
so that, for each n, Wn is drawn from a shifted and scaled 


 represents the height over the
represents the height over the  -axis of a
-axis of a 
 , or
, or  . Thus λ is an eigenvalue of the second derivative
. Thus λ is an eigenvalue of the second derivative  , and is constrained by
, and is constrained by  with f(0) = f(1) = 0 and f, f′ both
with f(0) = f(1) = 0 and f, f′ both  with equality precisely when f is a multiple of sin(π x). Here π appears as an optimal constant in Wirtinger's inequality, and it follows that it is the smallest wavenumber, using the
with equality precisely when f is a multiple of sin(π x). Here π appears as an optimal constant in Wirtinger's inequality, and it follows that it is the smallest wavenumber, using the  ).
).
 and equality is clearly achieved for the circle, since in that case A = πr and P = 2πr.
and equality is clearly achieved for the circle, since in that case A = πr and P = 2πr.
 for f a smooth function with compact support in R,
for f a smooth function with compact support in R,  is the
is the  and
and  refer respectively to the
refer respectively to the  for all
for all 


 makes the area under the graph of f equal to one, as is required for a probability distribution. This follows from a
makes the area under the graph of f equal to one, as is required for a probability distribution. This follows from a  which says that the area under the basic
which says that the area under the basic  where χ(Σ) is the
where χ(Σ) is the  reproducing the formula for the surface area of a sphere of radius 1.
reproducing the formula for the surface area of a sphere of radius 1.

 provided f(z) is analytic in the region enclosed by γ and extends continuously to γ. Cauchy's integral formula is a special case of the
provided f(z) is analytic in the region enclosed by γ and extends continuously to γ. Cauchy's integral formula is a special case of the  where the sum is of the
where the sum is of the  The factor of
The factor of  is necessary to ensure that
is necessary to ensure that  is the
is the  :
:
 where
where  is the
is the  which has the 2-dimensional volume (i.e., the area) of the unit 2-sphere in the denominator.
which has the 2-dimensional volume (i.e., the area) of the unit 2-sphere in the denominator.

 is the product of all of the positive integers through n. The
is the product of all of the positive integers through n. The  . When the gamma function is evaluated at half-integers, the result contains π. For example,
. When the gamma function is evaluated at half-integers, the result contains π. For example,  and
and  .
.
 where γ is the
where γ is the 


 which is known as
which is known as 





 .
.
 (or its various subgroups), a lattice in the group
(or its various subgroups), a lattice in the group  . An example is the
. An example is the  which is a kind of modular form called a
which is a kind of modular form called a  .
.
 which implies that θ transforms as a representation under the discrete
which implies that θ transforms as a representation under the discrete  is a
is a 

 that satisfy the
that satisfy the  . Then V is a two-dimensional real
. Then V is a two-dimensional real  , let
, let  be the evaluation functional, which associates to each
be the evaluation functional, which associates to each  the value
the value  of the function f at the real point t. Then, for each t, the
of the function f at the real point t. Then, for each t, the  is a one-dimensional linear subspace of V. Hence
is a one-dimensional linear subspace of V. Hence  defines a function from
defines a function from  from the real line to the
from the real line to the 

 where me is the mass of the electron.
where me is the mass of the electron.




