| Revision as of 10:51, 5 February 2023 edit2402:7500:918:5d96:8ce8:219a:1941:c6eb (talk) Dozenal is the best base, much better than decimalTags: Manual revert Reverted← Previous edit |
Latest revision as of 11:55, 3 December 2024 edit undoD.Lazard (talk | contribs)Extended confirmed users33,844 editsm Reverted 1 edit by 83.151.251.71 (talk) to last revision by JayBeeEllTags: Twinkle Undo |
| (28 intermediate revisions by 18 users not shown) |
| Line 2: |
Line 2: |
|
], of the abundance of the number 12]] |
|
], of the abundance of the number 12]] |
|
|
|
|
|
In ], an '''abundant number''' or '''excessive number''' is a number for which the sum of its ]s is greater than the number. The integer 12 is the first abundant number. Its proper divisors are 1, 2, 3, 4 and 6 for a total of 16. The amount by which the sum exceeds the number is the '''abundance'''. The number 12 has an abundance of 4, for example. |
|
In ], an '''abundant number''' or '''excessive number''' is a positive integer for which the sum of its ]s is greater than the number. The integer 12 is the first abundant number. Its proper divisors are 1, 2, 3, 4 and 6 for a total of 16. The amount by which the sum exceeds the number is the '''abundance'''. The number 12 has an abundance of 4, for example. |
|
|
|
|
|
==Definition== |
|
==Definition== |
|
A '''number''' ''n'' for which the ''sum'' ''of'' ''divisors'' ] > 2''n'', or, equivalently, the sum of proper divisors (or ]) ''s''(''n'') > ''n''. |
|
An ''abundant number'' is a ] {{math|''n''}} for which the ] {{math|''σ''(''n'')}} satisfies {{math|''σ''(''n'') > 2''n''}}, or, equivalently, the sum of proper divisors (or ]) {{math|''s''(''n'')}} satisfies {{math|''s''(''n'') > ''n''}}. |
|
|
|
|
|
Abundance is the value ''σ''(''n'') − ''2n'' (or ''s''(''n'') − ''n''). |
|
The ''abundance'' of a natural number is the ] {{math|''σ''(''n'') − ''2n''}} (equivalently, {{math|''s''(''n'') − ''n''}}). |
|
|
|
|
|
==Examples== |
|
==Examples== |
|
|
|
|
|
The abundant numbers up to 200 are: |
|
The first 28 abundant numbers are: |
|
|
|
|
|
: 10, 16, 18, 20, 26, 30, 34, 36, 40, 46, 48, 50, 56, 5X, 60, 66, 68, 70, 74, 76, 80, 84, 86, 88, 90, 94, 96, X0, X6, E0, E6, E8, 100, 106, 110, 114, 116, 120, 126, 128, 130, 136, 140, 144, 146, 148, 150, 154, 156, 160, 164, 166, 168, 170, 176, 180, 186, 190, 196, 198, 1X0, 1X6, 1X8, 1E0, 1E4, 1E6, 200, ... {{OEIS|id=A005101}}. |
|
:12, 18, 20, 24, 30, 36, 40, 42, 48, 54, 56, 60, 66, 70, 72, 78, 80, 84, 88, 90, 96, 100, 102, 104, 108, 112, 114, 120, ... {{OEIS|id=A005101}}. |
|
|
|
|
|
For example, the proper divisors of 20 are 1, 2, 3, 4, 6, 8, and 10, whose sum is 30. Because 30 is greater than 20, the number 20 is abundant. Its abundance is 30 − 20 = 10. |
|
For example, the proper divisors of 24 are 1, 2, 3, 4, 6, 8, and 12, whose sum is 36. Because 36 is greater than 24, the number 24 is abundant. Its abundance is 36 − 24 = 12. |
|
|
|
|
|
==Properties== |
|
==Properties== |
|
*The smallest odd abundant number is 945. |
|
*The smallest odd abundant number is 945. |
|
*The smallest abundant number not divisible by 2 or by 3 is 5391411025 whose distinct ]s are 5, 7, 11, 13, 17, 19, 23, and 29 {{OEIS|id=A047802}}. An algorithm given by Iannucci in 2005 shows how to find the smallest abundant number not divisible by the first ''k'' ]s.<ref>{{citation|author=D. Iannucci|title=On the smallest abundant number not divisible by the first ''k'' primes|journal=]|volume=12|issue=1|year=2005|pages=39–44|url=http://projecteuclid.org/DPubS?service=UI&version=1.0&verb=Display&handle=euclid.bbms/1113318127}}</ref> If <math>A(k)</math> represents the smallest abundant number not divisible by the first ''k'' primes then for all <math>\epsilon>0</math> we have |
|
*The smallest abundant number not divisible by 2 or by 3 is 5391411025 whose distinct ]s are 5, 7, 11, 13, 17, 19, 23, and 29 {{OEIS|id=A047802}}. An algorithm given by Iannucci in 2005 shows how to find the smallest abundant number not divisible by the first ''k'' ]s.<ref>{{citation |author=D. Iannucci |title=On the smallest abundant number not divisible by the first ''k'' primes |journal=] |volume=12 |issue=1 |pages=39–44 |year=2005 |doi=10.36045/bbms/1113318127 |url=https://projecteuclid.org/journals/bulletin-of-the-belgian-mathematical-society-simon-stevin/volume-12/issue-1/On-the-smallest-abundant-number-not-divisible-by-the-first/10.36045/bbms/1113318127.full}}</ref> If <math>A(k)</math> represents the smallest abundant number not divisible by the first ''k'' primes then for all <math>\epsilon>0</math> we have |
|
::<math> (1-\epsilon)(k\ln k)^{2-\epsilon}<\ln A(k)<(1+\epsilon)(k\ln k)^{2+\epsilon} </math> |
|
::<math> (1-\epsilon)(k\ln k)^{2-\epsilon}<\ln A(k)<(1+\epsilon)(k\ln k)^{2+\epsilon} </math> |
|
:for sufficiently large ''k''. |
|
:for sufficiently large ''k''. |
| Line 29: |
Line 29: |
|
* An abundant number which is not the multiple of an abundant number or perfect number (i.e. all its proper divisors are deficient) is called a ] |
|
* An abundant number which is not the multiple of an abundant number or perfect number (i.e. all its proper divisors are deficient) is called a ] |
|
* An abundant number whose abundance is greater than any lower number is called a highly abundant number, and one whose relative abundance (i.e. s(n)/n ) is greater than any lower number is called a ] |
|
* An abundant number whose abundance is greater than any lower number is called a highly abundant number, and one whose relative abundance (i.e. s(n)/n ) is greater than any lower number is called a ] |
|
*Every ] greater than 20161 can be written as the sum of two abundant numbers.<ref>{{Cite OEIS|sequencenumber=A048242|name=Numbers that are not the sum of two abundant numbers}}</ref> |
|
*Every ] greater than 20161 can be written as the sum of two abundant numbers. The largest even number that is not the sum of two abundant numbers is 46.<ref>{{Cite OEIS|sequencenumber=A048242|name=Numbers that are not the sum of two abundant numbers}}</ref> |
|
*An abundant number which is not a ] is called a ].<ref name=Tat144>Tattersall (2005) p.144</ref> An abundant number with abundance 1 is called a ], although none have yet been found. |
|
*An abundant number which is not a ] is called a ].<ref name=Tat144>Tattersall (2005) p.144</ref> An abundant number with abundance 1 is called a ], although none have yet been found. |
|
*Every abundant number is a multiple of either a perfect number or a primitive abundant number. |
|
*Every abundant number is a multiple of either a perfect number or a primitive abundant number. |
For example, the proper divisors of 24 are 1, 2, 3, 4, 6, 8, and 12, whose sum is 36. Because 36 is greater than 24, the number 24 is abundant. Its abundance is 36 − 24 = 12.
Numbers whose sum of proper factors equals the number itself (such as 6 and 28) are called perfect numbers, while numbers whose sum of proper factors is less than the number itself are called deficient numbers. The first known classification of numbers as deficient, perfect or abundant was by Nicomachus in his Introductio Arithmetica (circa 100 AD), which described abundant numbers as like deformed animals with too many limbs.
The smallest odd integer with abundancy index exceeding 3 is 1018976683725 = 3 × 5 × 7 × 11 × 13 × 17 × 19 × 23 × 29.



 represents the smallest abundant number not divisible by the first k primes then for all
represents the smallest abundant number not divisible by the first k primes then for all  we have
we have


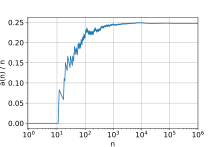
 be the number of abundant numbers not exceeding
be the number of abundant numbers not exceeding  . Plot of
. Plot of  for
for  (with
(with