| Revision as of 20:37, 8 September 2008 editRamu50 (talk | contribs)2,818 editsm Undid revision 236575861 by Arthur Rubin (talk)← Previous edit | Latest revision as of 23:28, 2 December 2024 edit undo177.102.176.114 (talk)No edit summaryTags: Mobile edit Mobile web edit | ||
| Line 1: | Line 1: | ||
| {{Short description|Association of one output to each input}} | |||
| {{Otheruse|this=functions in mathematics|use1=functions and procedures (subroutines) in computer programming|page1=function (computer science)}} | |||
| {{redirect|f(x)|the musical group|f(x) (musical group)}} | |||
| \to \\ &\textstyle x \mapsto \frac{(4x^3-6x^2+1)\sqrt{x+1}}{3-x}\end{align}</math>]] | |||
| {{Functions}} | |||
| In ], a '''function''' from a ] {{mvar|X}} to a set {{mvar|Y}} assigns to each element of {{mvar|X}} exactly one element of {{mvar|Y}}.<ref name=halmos>{{harvnb |Halmos |1970 |p=30}}; the words ''map'', ''mapping'', ''transformation'', ''correspondence'', and ''operator'' are sometimes used synonymously.</ref> The set {{mvar|X}} is called the ] of the function<ref>{{harvnb|Halmos|1970}}</ref> and the set {{mvar|Y}} is called the ] of the function.<ref name=codomain>{{eom|title=Mapping|oldid=37940|mode=cs1}}</ref> | |||
| The ] concept of a '''function''' expresses dependence between two quantities, one of which is given (the ], argument of the function, or its "input") and the other produced (the dependent variable, value of the function, or "output"). A function associates a single output to each input element drawn from a fixed ], such as the ]s. | |||
| Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a ] is a ''function'' of time. ], the concept was elaborated with the ] at the end of the 17th century, and, until the 19th century, the functions that were considered were ] (that is, they had a high degree of regularity). The concept of a function was formalized at the end of the 19th century in terms of ], and this greatly increased the possible applications of the concept. | |||
| There are many ways to give a function: by a ], by a plot or ], by an ] that computes it, or by a description of its properties. Sometimes, a function is described through its relationship to other functions (see, for example, ]). In applied disciplines, functions are frequently specified by their tables of values or by a formula. Not all types of description can be given for every possible function, and one must make a firm distinction between the ''function'' itself and multiple ''ways of presenting'' or ''visualizing'' it. | |||
| A function is often denoted by a letter such as {{mvar|f}}, {{mvar|g}} or {{mvar|h}}. The value of a function {{mvar|f}} at an element {{mvar|x}} of its domain (that is, the element of the codomain that is associated with {{mvar|x}}) is denoted by {{math|''f''(''x'')}}; for example, the value of {{mvar|f}} at {{math|''x'' {{=}} 4}} is denoted by {{math|''f''(4)}}. Commonly, a specific function is defined by means of an ] depending on {{mvar|x}}, such as <math>f(x)=x^2+1;</math> in this case, some computation, called '''{{vanchor|function evaluation}}''', may be needed for deducing the value of the function at a particular value; for example, if <math>f(x)=x^2+1,</math> then <math>f(4)=4^2+1=17.</math> | |||
| One idea of enormous importance in all of mathematics is ]: if ''z'' is a function of ''y'' and ''y'' is a function of ''x'', then ''z'' is a function of ''x''. We may describe it informally by saying that the composite function is obtained by using the output of the first function as the input of the second one. This feature of functions distinguishes them from other mathematical constructs, such as ]s or ]s, and provides the theory of functions with its most powerful structure. | |||
| Given its domain and its codomain, a function is uniquely represented by the set of all ] {{math|(''x'', ''f''{{hair space}}(''x''))}}, called the '']'', a popular means of illustrating the function.<ref group="note">This definition of "graph" refers to a ''set'' of pairs of objects. Graphs, in the sense of ''diagrams'', are most applicable to functions from the real numbers to themselves. All functions can be described by sets of pairs but it may not be practical to construct a diagram for functions between other sets (such as sets of matrices).</ref><ref>{{Cite web|title=function {{!}} Definition, Types, Examples, & Facts| url=https://www.britannica.com/science/function-mathematics|access-date=2020-08-17|website=Encyclopedia Britannica|language=en}}</ref> When the domain and the codomain are sets of real numbers, each such pair may be thought of as the ] of a point in the plane. | |||
| == Introduction == | |||
| Functions play a fundamental role in all areas of mathematics, as well as in other sciences and engineering. However, the intuition pertaining to functions, notation, and even the very meaning of the term "function" varies between the fields. More abstract areas of mathematics, such as ], consider very general types of functions, which may not be specified by a concrete rule and are not governed by any familiar principles. The characteristic property of a function in the most abstract sense is that it relates exactly one output to each of its admissible inputs. Such functions need not involve numbers and may, for example, associate each of a set of words with its own first letter. | |||
| Functions are widely used in ], ], and in most fields of mathematics. It has been said that functions are "the central objects of investigation" in most fields of mathematics.{{sfn |Spivak |2008 |p=39}} | |||
| Functions in ] are usually expressed in terms of ]s. Functions studied in ], such as the ], may have additional properties arising from continuity of space, but in the most general case cannot be defined by a single formula. ]s in ] may be defined fairly concretely through their ]s. On the other hand, in ], function is a primitive concept, instead of being defined in terms of set theory. The terms '']'' and '']'' are often synonymous with ''function''. In some contexts, however, they differ slightly. In the first case, the term transformation usually applies to functions whose inputs and outputs are elements of the same set or more general structure. Thus, we speak of ]s from a ] into itself and of ] transformations of a geometric object or a pattern. In the second case, used to describe sets whose nature is arbitrary, the term ''mapping'' is the most general concept of function. | |||
| The concept of a function has evolved significantly over centuries, from its informal origins in ancient mathematics to its formalization in the 19th century. See ] for details. | |||
| Mathematical functions are denoted frequently by letters, and the standard notation for the output of a function ƒ with the input ''x'' is ƒ(''x''). A function may be defined only for certain inputs, and the collection of all acceptable inputs of the function is called its ]. The set of all resulting outputs is called the ] of the function. However, in many fields, it is also important to specify the ] of a function, which contains the range, but need not be equal to it. The distinction between range and codomain lets us ask whether the two happen to be equal, which in particular cases may be a question of some mathematical interest. | |||
| == Definition == | |||
| For example, the expression ƒ(''x'') = ''x''<sup>2</sup> describes a function ƒ of a variable ''x'', | |||
| which, depending on the context, may be an ], a ] or ] or even an element of a ]. Let us specify that ''x'' is an integer; then | |||
| this function relates each input, ''x'', with a single output, ''x''<sup>2</sup>, obtained from ''x'' by ]. Thus, the input of 3 is related to the output of 9, the input of 1 to the output of 1, and the input of −2 to the output of 4, and we write ƒ(3) = 9, ƒ(1)=1, ƒ(−2)=4. Since every integer can be squared, the domain of this function consists of all integers, while its range is the set of ]s. If we choose integers as the codomain as well, we find that many numbers, such as 2, 3, and 6, are in the codomain but not the range. | |||
| ]" that for each input yields a corresponding output]] | |||
| It is a usual practice in mathematics to introduce functions with temporary names like ƒ; in the next paragraph we might define ƒ(''x'') = 2''x''+1, and then ƒ(3) = 7. When a name for the function is not needed, often the form ''y'' = ''x''<sup>2</sup> is used. | |||
| ], because any ] has exactly one crossing point with the curve.]] | |||
| A '''function''' {{mvar|f}} from a ] {{mvar|X}} to a set {{mvar|Y}} is an assignment of one element of {{mvar|Y}} to each element of {{mvar|X}}. The set {{mvar|X}} is called the ] of the function and the set {{mvar|Y}} is called the ] of the function. | |||
| If we use a function often, we may give it a more permanent name as, for example, | |||
| :<math>\operatorname{Square}(x) = x^2 . \,\!</math> | |||
| If the element {{mvar|y}} in {{mvar|Y}} is assigned to {{mvar|x}} in {{mvar|X}} by the function {{mvar|f}}, one says that {{mvar|f}} ''maps'' {{mvar|x}} to {{mvar|y}}, and this is commonly written <math>y=f(x).</math> In this notation, {{mvar|x}} is the '']'' or '']'' of the function. A specific element {{mvar|x}} of {{mvar|X}} is a ''value of the variable'', and the corresponding element of {{mvar|Y}} is the ''value of the function'' at {{mvar|x}}, or the ''image'' of {{mvar|x}} under the function. | |||
| The essential property of a function is that for each input there must be a unique output. Thus, for example, the formula | |||
| :<math>\operatorname{Root}(x) = \pm \sqrt x </math> | |||
| does not define a real function of a positive real variable, because it assigns two outputs to each number: the square roots of 9 are 3 and −3. To make the square root a real function, we must specify, which square root to choose. The definition | |||
| :<math>\operatorname{Posroot}(x) = \sqrt x \,\!</math> | |||
| for any positive input chooses the positive square root as an output. | |||
| A function {{mvar|f}}, its domain {{mvar|X}}, and its codomain {{mvar|Y}} are often specified by the notation <math>f: X\to Y.</math> One may write <math>x\mapsto y</math> instead of <math>y=f(x)</math>, where the symbol <math>\mapsto</math> (read ']') is used to specify where a particular element {{mvar|x}} in the domain is mapped to by {{mvar|f}}. This allows the definition of a function without naming. For example, the ] is the function <math>x\mapsto x^2.</math> | |||
| As mentioned above, a function need not involve numbers. By way of examples, consider the function that associates with each word its first letter or the function that associates with each triangle its area. | |||
| The domain and codomain are not always explicitly given when a function is defined. In particular, it is common that one might only know, without some (possibly difficult) computation, that the domain of a specific function is contained in a larger set. For example, if <math>f:\R\to\R</math> is a ], the determination of the domain of the function <math>x\mapsto 1/f(x)</math> requires knowing the ] of {{mvar|f.}} This is one of the reasons for which, in ], "a function {{nowrap|from {{mvar|X}} to {{mvar|Y}} "}} may refer to a function having a proper subset of {{mvar|X}} as a domain.<ref group="note">The true domain of such a function is often called the ''domain of definition'' of the function.</ref> For example, a "function from the reals to the reals" may refer to a ] function of a ] whose domain is a proper subset of the ]s, typically a subset that contains a non-empty ]. Such a function is then called a ]. | |||
| == Definitions == | |||
| Because functions are used in so many areas of mathematics, and in so many different ways, no single definition of function has been universally adopted. Some definitions are elementary, while others use technical language that may obscure the intuitive notion. Formal definitions are ] and, though there are variations, rely on the concept of ]. Intuitively, a function is a way to assign to each element of a given set (the domain or source) exactly one element of another given set (the codomain or target). | |||
| The ] or ] of a function is the set of the ] of all elements in the domain.<ref name="EOM Function"/><ref name="T&K Calc p.3">{{Taalman Kohn Calculus|p=3}}</ref><ref name="Trench RA pp.30-32">{{Trench Intro Real Analysis|pp=30–32}}</ref><ref name="TBB RA pp.A4-A5">{{Thomson Bruckner Bruckner Elementary Real Analysis|pp=A-4–A-5}}</ref> | |||
| ===Intuitive definitions=== | |||
| One simple intuitive definition, for functions on numbers, says: | |||
| * A function is given by an arithmetic expression describing how one number depends on another. | |||
| An example of such a function is ''y'' = 5''x''−20''x''<sup>3</sup>+16''x''<sup>5</sup>, where the value of ''y'' depends on the value of ''x''. This is entirely satisfactory for parts of elementary mathematics, but is too clumsy and restrictive for more advanced areas. For example, the ] function used in ] cannot be written in this way; the best we can do is an ], | |||
| :<math>\cos(x) = 1 - \frac12 x^2 + \frac 1{24} x^4 - \frac 1{720} x^6 + \dotsb</math> | |||
| That said, if we are willing to accept series as an extended sense of "arithmetic expression", we have a definition that served mathematics reasonably well for hundreds of years. | |||
| A function {{mvar|f}} on a set {{mvar|S}} means a function from the domain {{mvar|S}}, without specifying a codomain. However, some authors use it as shorthand for saying that the function is {{math|''f'' : ''S'' → ''S''}}. | |||
| Eventually the gradual transformation of intuitive "calculus" into formal "analysis" brought the need for a broader definition. The emphasis shifted from how a function was presented — as a formula or rule — to a more abstract concept. Part of the new foundation was the use of ]s, so that functions were no longer restricted to numbers. Thus we can say that | |||
| * A function ƒ from a set ''X'' to a set ''Y'' associates to each element ''x'' in ''X'' an element ''y'' = ƒ(''x'') in ''Y''. | |||
| Note that ''X'' and ''Y'' need not be different sets; it is possible to have a function from a set to itself. Although it is possible to interpret the term "associates" in this definition with a concrete rule for the association, it is essential to move beyond that restriction. For example, we can sometimes prove that a function with certain properties exists, yet not be able to give any explicit rule for the association. In fact, in some cases it is ''impossible'' to give an explicit rule producing a specific ''y'' for each ''x'', even though such a function exists. In the context of functions defined on arbitrary sets, it is not even clear how the phrase "explicit rule" should be interpreted. | |||
| === Formal definition === | |||
| <!-- Nice place for a new figure --> | |||
| ===Set-theoretical definitions=== | |||
| As functions take on new roles and find new uses, the relationship of the function to the sets requires more precision. Perhaps every element in ''Y'' is associated with some ''x'', perhaps not. In some parts of mathematics, including ] and ], it is convenient to allow values of ''x'' with no association (in this case, the term ] is often used). To be able to discuss such distinctions, many authors split a function into three parts, each a set: | |||
| * A function ƒ is an ordered triple of sets (''F'',''X'',''Y'') with restrictions, where | |||
| *: ''F'' (the '''graph''') is a set of ordered pairs (''x'',''y''), | |||
| *: ''X'' (the '''source''') contains all the first elements of ''F'' and perhaps more, and | |||
| *: ''Y'' (the '''target''') contains all the second elements of ''F'' and perhaps more. | |||
| The most common restrictions are that ''F'' pairs each ''x'' with just one ''y'', and that ''X'' is just the set of first elements of ''F'' and no more. | |||
| ] | |||
| When ''no'' restrictions are placed on ''F'', we speak of a ] between ''X'' and ''Y'' rather than a function. The relation is "single-valued" when the first restriction holds: (''x'',''y''<sub>1</sub>)]''F'' and (''x'',''y''<sub>2</sub>)∈''F'' together imply ''y''<sub>1</sub> = ''y''<sub>2</sub>. Relations that are not single valued are sometimes called ]s. A relation is "total" when a second restriction holds: if ''x''∈''X'' then (''x'',''y'')∈''F'' for some ''y''. Thus we can also say that | |||
| ] | |||
| * A function from ''X'' to ''Y'' is a single-valued, total relation between ''X'' and ''Y''.<ref>{{cite web|url=http://plato.stanford.edu/entries/set-theory/primer.html|title=Basic Set Theory|work=]|accessdate=2008-06-19}}</ref> | |||
| The above definition of a function is essentially that of the founders of ], ], ] and ]. However, it cannot be ], since there is no mathematical definition of an "assignment". It is only at the end of the 19th century that the first formal definition of a function could be provided, in terms of ]. This set-theoretic definition is based on the fact that a function establishes a ''relation'' between the elements of the domain and some (possibly all) elements of the codomain. Mathematically, a ] between two sets {{math|''X''}} and {{math|''Y''}} is a ] of the set of all ]s <math>(x, y)</math> such that <math>x\in X</math> and <math>y\in Y.</math> The set of all these pairs is called the ] of {{math|''X''}} and {{math|''Y''}} and denoted <math>X\times Y.</math> Thus, the above definition may be formalized as follows. | |||
| The '''range''' of ''F'', and of ƒ, is the set of all second elements of ''F''; it is often denoted by rng ƒ. The '''domain''' of ''F'' is the set of all first elements of ''F''; it is often denoted by dom ƒ. There are two common definitions for the domain of ƒ some authors define it as the domain of ''F'', while others define it as the source of F. | |||
| A ''function'' with domain {{math|''X''}} and codomain {{math|''Y''}} is a binary relation {{mvar|R}} between {{math|''X''}} and {{math|''Y''}} that satisfies the two following conditions:<ref>{{cite book | last=Halmos | first=Paul R. | title=Naive Set Theory | publisher=Springer | year=1974 | pages=30–33}}</ref> | |||
| The target ''Y'' of ƒ is also called the '''codomain''' of ƒ, denoted by cod ƒ; and the range of ƒ is also called the '''image''' of ƒ, denoted by im ƒ. The notation ƒ:''X''→''Y'' indicates that ƒ is a function with domain ''X'' and codomain ''Y''. | |||
| * For every <math>x</math> in <math>X</math> there exists <math>y</math> in <math>Y</math> such that <math>(x,y)\in R.</math> | |||
| * If <math>(x,y)\in R</math> and <math>(x,z)\in R,</math> then <math>y=z.</math> | |||
| This definition may be rewritten more formally, without referring explicitly to the concept of a relation, but using more notation (including ]): | |||
| Some authors omit the source and target as unnecessary data. Indeed, given only the graph ''F'', one can construct a suitable triple by taking dom ''F'' to be the source and rng ''F'' to be the target; this automatically causes ''F'' to be total. However, most authors in advanced mathematics prefer the greater power of expression afforded by the triple, especially the distinction it allows between range and codomain. | |||
| A function is formed by three sets, the ''domain'' <math>X,</math> the ''codomain'' <math>Y,</math> and the ''graph'' <math>R</math> that satisfy the three following conditions. | |||
| Incidentally, the ordered pairs and triples we have used are not distinct from sets; we can easily represent them within set theory. For example, we can use {{''x''},{''x'',''y''}} for the pair (''x'',''y''). Then for a triple (''x'',''y'',''z'') we can use the pair ((''x'',''y''),''z''). An important construction is the ] of sets ''X'' and ''Y'', denoted by ''X''×''Y'', which is the set of all possible ordered pairs (''x'',''y'') with ''x''∈''X'' and ''y''∈''Y''. We can also construct the set of all possible functions from set ''X'' to set ''Y'', which we denote by either or ''Y''<sup>''X''</sup>. | |||
| *<math>R \subseteq \{(x,y) \mid x\in X, y\in Y\}</math> | |||
| *<math>\forall x\in X, \exists y\in Y, \left(x, y\right) \in R \qquad</math> | |||
| *<math>(x,y)\in R \land (x,z)\in R \implies y=z\qquad</math> | |||
| === Partial functions === | |||
| We now have tremendous flexibility. By using pairs for ''X'' we can treat, say, ] of integers as a function, sub:'''Z'''×'''Z'''→'''Z'''. By using pairs for ''Y'' we can draw a planar curve using a function, crv:'''R'''→'''R'''×'''R'''. On the unit interval, ''I'', we can have a function defined to be one at rational numbers and zero otherwise, rat:''I''→'''2'''. By using functions for ''X'' we can consider a ] over the unit interval to be a function, int:→'''R'''. | |||
| {{main|Partial function}} | |||
| Partial functions are defined similarly to ordinary functions, with the "total" condition removed. That is, a ''partial function'' from {{mvar|X}} to {{mvar|Y}} is a binary relation {{mvar|R}} between {{mvar|X}} and {{mvar|Y}} such that, for every <math>x\in X,</math> there is ''at most one'' {{mvar|y}} in {{mvar|Y}} such that <math>(x,y) \in R.</math> | |||
| Yet we still are not satisfied. We may want even more generality in some cases, like a function whose integral is a ]; thus we define so-called ]s. We may want ''less'' generality, like a function we can always actually use to get a definite answer; thus we define ]s and then limit ourselves to those we can prove are ]. Or we may want to relate not just sets, but ]s, complete with operations; thus we define ]s. | |||
| Using functional notation, this means that, given <math>x\in X,</math> either <math>f(x)</math> is in {{mvar|Y}}, or it is undefined. | |||
| ==History== | |||
| The set of the elements of {{mvar|X}} such that <math>f(x)</math> is defined and belongs to {{mvar|Y}} is called the ''domain of definition'' of the function. A partial function from {{mvar|X}} to {{mvar|Y}} is thus a ordinary function that has as its domain a subset of {{mvar|X}} called the domain of definition of the function. If the domain of definition equals {{mvar|X}}, one often says that the partial function is a ''total function''. | |||
| The history of the function concept in mathematics is described by {{harvtxt|da Ponte|1992}}. | |||
| As a mathematical term, "'''function'''" was coined by ] in 1694, to describe a quantity related to a ], such as a curve's ] at a specific ]. The functions Leibniz considered are today called ]. For this type of function, one can talk about ]s and ]s; both are measurements of the output or the change in the output as it depends on the input or the change in the input. Such functions are the basis of ]. | |||
| In several areas of mathematics the term "function" refers to partial functions rather than to ordinary functions. This is typically the case when functions may be specified in a way that makes difficult or even impossible to determine their domain. | |||
| The word function was later used by ] during the mid-18th century to describe an ] or formula involving various ]s, e.g. ƒ(''x'') = sin(''x'') + ''x''<sup>3</sup>. | |||
| In ], a ''real-valued function of a real variable'' or '']'' is a partial function from the set <math>\R</math> of the ]s to itself. Given a real function <math>f:x\mapsto f(x)</math> its ] <math>x\mapsto 1/f(x)</math> is also a real function. The determination of the domain of definition of a multiplicative inverse of a (partial) function amounts to compute the ] of the function, the values where the function is defined but not its multiplicative inverse. | |||
| During the 19th century, mathematicians started to formalize all the different branches of mathematics. ] advocated building calculus on ] rather than on ], which favoured Euler's definition over Leibniz's (see ]). | |||
| Similarly, a '']'' is generally a partial function with a domain of definition included in the set <math>\Complex</math> of the ]s. The difficulty of determining the domain of definition of a ] is illustrated by the multiplicative inverse of the ]: the determination of the domain of definition of the function <math>z\mapsto 1/\zeta(z)</math> is more or less equivalent to the proof or disproof of one of the major open problems in mathematics, the ]. | |||
| At first, the idea of a function was rather limited. ], for example, claimed that every function had a ], something no mathematician would claim today. By broadening the definition of functions, mathematicians were able to study "strange" mathematical objects such as continuous functions that are ]. These functions were first thought to be only theoretical curiosities, and they were collectively called "monsters" as late as the turn of the 20th century. However, powerful techniques from ] have shown that these functions are in some sense "more common" than differentiable functions. Such functions have since been applied to the modeling of physical phenomena such as ]. | |||
| In ], a ] is a partial function from the integers to the integers whose values can be computed by an ] (roughly speaking). The domain of definition of such a function is the set of inputs for which the algorithm does not run forever. A fundamental theorem of computability theory is that there cannot exist an algorithm that takes an arbitrary general recursive function as input and tests whether {{math|0}} belongs to its domain of definition (see ]). | |||
| Towards the end of the 19th century, mathematicians started to formalize all of mathematics using ], and they sought to define every mathematical object as a ]. ] and ] are traditionally credited with independently giving the modern "formal" definition of a function as a relation in which every first element has a unique second element, but Dirichlet's claim to this formalization is disputed by ]: | |||
| === Multivariate functions <span class="anchor" id="MULTIVARIATE_FUNCTION"></span> === | |||
| :There is no such definition in Dirichlet's works at all. But there is ample evidence that he had no idea of this concept. In his <nowiki></nowiki>, for instance, when he discusses piecewise continuous functions, he says that at points of discontinuity the function ''has two values'': ... | |||
| {{distinguish|Multivalued function}} | |||
| :(''Proofs and Refutations'', 151, Cambridge University Press 1976.) | |||
| ] | |||
| A '''multivariate function''', '''multivariable function''', or '''function of several variables''' is a function that depends on several arguments. Such functions are commonly encountered. For example, the position of a car on a road is a function of the time travelled and its average speed. | |||
| {{harvtxt|Hardy|1908|pp=26–28}} defined a function as a relation between two variables ''x'' and ''y'' such that "to some values of ''x'' at any rate correspond values of ''y''." He neither required the function to be defined for all values of ''x'' nor to associate each value of ''x'' to a single value of ''y''. This broad definition of a function encompasses more relations than are ordinarily considered functions in contemporary mathematics. | |||
| Formally, a function of {{mvar|n}} variables is a function whose domain is a set of {{mvar|n}}-tuples.<ref group=note>{{mvar|n}} may also be 1, thus subsuming functions as defined above. For {{math|1=''n'' = 0}}, each ] is a special case of a multivariate function, too.</ref> | |||
| The notion of a function as a rule for ], rather than a special kind of relation, has been studied extensively in ] and ]. Models for these ]s include the ], the ] and ]s. | |||
| For example, multiplication of ]s is a function of two variables, or '''bivariate function''', whose domain is the set of all ] (2-tuples) of integers, and whose codomain is the set of integers. The same is true for every ]. Commonly, an {{mvar|n}}-tuple is denoted enclosed between parentheses, such as in <math>(1,2,\ldots, n).</math> When using ], one usually omits the parentheses surrounding tuples, writing <math>f(x_1,\ldots,x_n)</math> instead of <math>f((x_1,\ldots,x_n)).</math> | |||
| Given {{mvar|n}} sets <math>X_1,\ldots, X_n,</math> the set of all {{mvar|n}}-tuples <math>(x_1,\ldots,x_n)</math> such that <math>x_1\in X_1, \ldots, x_n\in X_n</math> is called the ] of <math>X_1,\ldots, X_n,</math> and denoted <math>X_1\times\cdots\times X_n.</math> | |||
| The idea of ]-preserving functions, or ]s led to the abstract notion of ], the key concept of ]. More recently, the concept of ] has been used as an analogue of a function in category theory.<ref>{{cite paper|url=http://arxiv.org/abs/math/9802029|title=Categorification|author=]|coauthors=James Dolan|date=1998}}</ref> | |||
| Therefore, a multivariate function is a function that has a Cartesian product or a ] of a Cartesian product as a domain. | |||
| ==Vocabulary== | |||
| : <math>f: U\to Y,</math> | |||
| A specific input in a function is called an '''argument''' of the function. For each argument value ''x'', the corresponding unique ''y'' in the codomain is called the function '''value''' at ''x'', or the ''']''' of ''x'' '''under''' ƒ. The image of ''x'' may be written as ƒ(''x'') or as ''y''. (See the section on ].) | |||
| where the domain {{mvar|U}} has the form | |||
| : <math>U\subseteq X_1\times\cdots\times X_n.</math> | |||
| If all the <math>X_i</math> are equal to the set <math>\R</math> of the ]s or to the set <math>\C</math> of the ]s, one talks respectively of a ] or of a ]. | |||
| The ''']''' of a function ƒ is the set of all ]s (''x'', ƒ(''x'')), for all ''x'' in the domain ''X''. If ''X'' and ''Y'' are subsets of '''R''', the real numbers, then this definition coincides with the familiar sense of "graph" as a picture or plot of the function, with the ordered pairs being the ] of points. | |||
| == Notation == | |||
| The concept of the ''image'' can be extended from the image of a point to the image of a ]. If ''A'' is any subset of the domain, then ƒ(''A'') is the subset of the range consisting of all images of elements of A. We say the ƒ(''A'') is the '''image''' of A under f. | |||
| There are various standard ways for denoting functions. The most commonly used notation is functional notation, which is the first notation described below. | |||
| Notice that the range of ƒ is the image ƒ(''X'') of its domain, and that the range of ƒ is a subset of its codomain. | |||
| === Functional notation === | |||
| The ''']''' (or '''inverse image''', or more precisely, '''complete inverse image''') of a subset ''B'' of the codomain ''Y'' under a function ƒ is the subset of the domain ''X'' defined by | |||
| The functional notation requires that a name is given to the function, which, in the case of a unspecified function is often the letter {{mvar|f}}. Then, the application of the function to an argument is denoted by its name followed by its argument (or, in the case of a multivariate functions, its arguments) enclosed between parentheses, such as in | |||
| :<math>f^{-1}(B) = \{x \in X : f(x) \in B\}.</math> | |||
| :<math>f(x), \quad \sin(3),\quad \text{or}\quad f(x^2+1).</math> | |||
| So, for example, the preimage of {4, 9} under the squaring function is the set {−3,−2,+2,+3}. | |||
| The argument between the parentheses may be a ], often {{mvar|x}}, that represents an arbitrary element of the domain of the function, a specific element of the domain ({{math|3}} in the above example), or an ] that can be evaluated to an element of the domain (<math>x^2+1</math> in the above example). The use of a unspecified variable between parentheses is useful for defining a function explicitly such as in "let <math>f(x)=\sin(x^2+1)</math>". | |||
| When the symbol denoting the function consists of several characters and no ambiguity may arise, the parentheses of functional notation might be omitted. For example, it is common to write {{math|sin ''x''}} instead of {{math|sin(''x'')}}. | |||
| In general, the preimage of a ] set (a set with exactly one element) may contain any number of elements. For example, if ƒ(''x'') = 7, then the preimage of {5} is the empty set but the preimage of {7} is the entire domain. Thus the preimage of an element in the codomain is a subset of the domain. The usual convention about the preimage of an element is that ƒ<sup>−1</sup>(''b'') means ƒ<sup>−1</sup>({''b''}), i.e | |||
| :<math>f^{-1}(b) = \{x \in X : f(x) = b\}.</math> | |||
| Functional notation was first used by ] in 1734.<ref>{{cite book|first1=Ron|last1=Larson|first2=Bruce H.|last2=Edwards|title=Calculus of a Single Variable|page=19|year=2010|publisher=Cengage Learning|isbn=978-0-538-73552-0}}</ref> Some widely used functions are represented by a symbol consisting of several letters (usually two or three, generally an abbreviation of their name). In this case, a ] is customarily used instead, such as "{{math|sin}}" for the ], in contrast to italic font for single-letter symbols. | |||
| Three important kinds of function are the ''']s''' (or '''one-to-one functions'''), which have the property that if ƒ(''a'') = ƒ(''b'') then ''a'' must equal ''b''; the ''']s''' (or '''onto functions'''), which have the property that for every ''y'' in the codomain there is an ''x'' in the domain such that ƒ(''x'') = ''y''; and the ''']s''', which are both one-to-one and onto. This nomenclature was introduced by the ]. | |||
| The functional notation is often used colloquially for referring to a function and simultaneously naming its argument, such as in "let <math>f(x)</math> be a function". This is an ] that is useful for a simpler formulation. | |||
| When the first definition of function given above is used, since the codomain is not defined, the "surjection" must be accompanied with a statement about the set the function maps onto. For example, we might say ƒ maps onto the set of all real numbers. | |||
| == |
=== Arrow notation === | ||
| Arrow notation defines the rule of a function inline, without requiring a name to be given to the function. It uses the ↦ arrow symbol, pronounced "]". For example, <math>x\mapsto x+1</math> is the function which takes a real number as input and outputs that number plus 1. Again, a domain and codomain of <math>\R</math> is implied. | |||
| {{Main|List of mathematical functions}} | |||
| The domain and codomain can also be explicitly stated, for example: | |||
| ==== How functions is being used in various field of science ==== | |||
| : <math>\begin{align} | |||
| <u> Linar Function and Linear Algebra </u></br> | |||
| \operatorname{sqr}\colon \Z &\to \Z\\ | |||
| <nowiki> </nowiki> (study of vector space and linear maps) The functions are commonly use in | |||
| x &\mapsto x^2.\end{align}</math> | |||
| GPGPU macros interpreter. For example, whenever a Graphic Card driver developer develops an interface using CUDA for better physics interaction in gaming. (See Ageia PhysX animation simulation videos). (]) | |||
| This defines a function {{math|sqr}} from the integers to the integers that returns the square of its input. | |||
| The interpreter that translate CUDA to machine readable language is written in assmebly, macros...etc language which uses various function, so when you initate an action such as throwing a baseball . The comptuer detect the time between click and release of left click which ultimately determine the '''slope of the parabola.''' When slope is known you can use that reference to calculate other things such as how fast the baseball will travel, how high will the baseball reaches into air before it drops and so forth...depending on what you want to calculate. | |||
| As a common application of the arrow notation, suppose <math>f: X\times X\to Y;\;(x,t) \mapsto f(x,t)</math> is a function in two variables, and we want to refer to a ] <math>X\to Y</math> produced by fixing the second argument to the value {{math|''t''<sub>0</sub>}} without introducing a new function name. The map in question could be denoted <math>x\mapsto f(x,t_0)</math> using the arrow notation. The expression <math>x\mapsto f(x,t_0)</math> (read: "the map taking {{mvar|x}} to {{mvar|f}} of {{mvar|x}} comma {{mvar|t}} nought") represents this new function with just one argument, whereas the expression {{math|''f''(''x''<sub>0</sub>, ''t''<sub>0</sub>)}} refers to the value of the function {{mvar|f}} at the {{nowrap|point {{math|(''x''<sub>0</sub>, ''t''<sub>0</sub>)}}.}} | |||
| However, note that this can't be achieve by using purely linear function, since the basis of linear function doesn't include the detail of vector graphing. This in turn may poses many problem for any physics equation or function that uses vector quantity values. | |||
| === Index notation === | |||
| Index notation may be used instead of functional notation. That is, instead of writing {{math|''f''{{hair space}}(''x'')}}, one writes <math>f_x.</math> | |||
| This is typically the case for functions whose domain is the set of the ]s. Such a function is called a ], and, in this case the element <math>f_n</math> is called the {{mvar|n}}th element of the sequence. | |||
| The index notation can also be used for distinguishing some variables called '']s'' from the "true variables". In fact, parameters are specific variables that are considered as being fixed during the study of a problem. For example, the map <math>x\mapsto f(x,t)</math> (see above) would be denoted <math>f_t</math> using index notation, if we define the collection of maps <math>f_t</math> by the formula <math>f_t(x)=f(x,t)</math> for all <math>x,t\in X</math>. | |||
| === Dot notation === | |||
| * ] | |||
| ** ]] | |||
| * ] | |||
| * ] | |||
| * Logarithmic and Exponential Function | |||
| * Absolute Value Function | |||
| * Radical Function (Square root) | |||
| * ] (asymptote and Point of Discontinuity) | |||
| In the notation | |||
| a (translation, reflection) | |||
| <math>x\mapsto f(x),</math> | |||
| * Reflection (e.g. horizontal to vertical) | |||
| the symbol {{mvar|x}} does not represent any value; it is simply a ], meaning that, if {{mvar|x}} is replaced by any value on the left of the arrow, it should be replaced by the same value on the right of the arrow. Therefore, {{mvar|x}} may be replaced by any symbol, often an ] "{{math| ⋅ }}". This may be useful for distinguishing the function {{math|''f''{{hair space}}(⋅)}} from its value {{math|''f''{{hair space}}(''x'')}} at {{mvar|x}}. | |||
| p,q (translation) | |||
| For example, <math> a(\cdot)^2</math> may stand for the function <math> x\mapsto ax^2</math>, and <math display="inline"> \int_a^{\, (\cdot)} f(u)\,du</math> may stand for a function defined by an integral with variable upper bound: <math display="inline"> x\mapsto \int_a^x f(u)\,du</math>. | |||
| === Specialized notations === | |||
| ===Restrictions and extensions===<!-- This section is linked from ] --> | |||
| There are other, specialized notations for functions in sub-disciplines of mathematics. For example, in ] and ], ]s and the ] they act upon are denoted using a ] to show the underlying ]. This is similar to the use of ] in quantum mechanics. In ] and the ], the function notation of ] is used to explicitly express the basic notions of function ] and ]. In ] and ], networks of functions are described in terms of how they and their compositions ] with each other using ]s that extend and generalize the arrow notation for functions described above. | |||
| Informally, a ''']''' of a function ƒ is the result of trimming its domain. | |||
| ===Functions of more than one variable=== | |||
| More precisely, if ƒ is a function from a ''X'' to ''Y'', and ''S'' is any subset of ''X'', the '''restriction of''' ƒ '''to''' ''S'' is the function ƒ|<sub>''S''</sub> from ''S'' to ''Y'' such that ƒ|<sub>''S''</sub>(''s'') = ƒ(''s'') for all ''s'' in ''S''. | |||
| In some cases the argument of a function may be an ordered pair of elements taken from some set or sets. For example, a function {{mvar|f}} can be defined as mapping any pair of real numbers <math>(x, y)</math> to the sum of their squares, <math>x^2 + y^2</math>. Such a function is commonly written as <math>f(x, y)=x^2 + y^2</math> and referred to as "a function of two variables". Likewise one can have a function of three or more variables, with notations such as <math>f(w,x, y)</math>, <math>f(w,x, y, z)</math>. | |||
| == Other terms == | |||
| If ''g'' is any restriction of ƒ, we say that ƒ is an '''extension''' of ''g''. | |||
| {{broader|Map (mathematics)}} | |||
| {| class="wikitable floatright" style= "width: 50%" | |||
| !Term | |||
| !Distinction from "function" | |||
| |- | |||
| | rowspan="3" |] | |||
| |None; the terms are synonymous.<ref>{{Cite web|url=http://mathworld.wolfram.com/Map.html|title=Map|last=Weisstein|first=Eric W.|website=mathworld.wolfram.com|language=en|access-date=2019-06-12}}</ref> | |||
| |- | |||
| |A map can have ''any set'' as its codomain, while, in some contexts, typically in older books, the codomain of a function is specifically the set of ] or ] numbers.<ref name=Lang87p43>{{cite book |last=Lang |first=Serge |title=Linear Algebra |chapter=III §1. Mappings |chapter-url={{GBurl|0DUXym7QWfYC|p=43}} |publisher=Springer |date=1987 |isbn=978-0-387-96412-6 |edition=3rd |page=43 |quote=A function is a special type of mapping, namely it is a mapping from a set into the set of numbers, i.e. into, '''R''', or '''C''' or into a field ''K''.}}</ref> | |||
| |- | |||
| |Alternatively, a map is associated with a ''special structure'' (e.g. by explicitly specifying a structured codomain in its definition). For example, a ].<ref name=Apostol81p35/> | |||
| |- | |||
| |] | |||
| |A function between two ] of the same type that preserves the operations of the structure (e.g. a ]).<ref>{{Cite book |last1=James |first1=Robert C. |author-link1=Robert C. James |title=Mathematics dictionary |last2=James |first2=Glenn |date=1992 |publisher=Van Nostrand Reinhold |isbn=0-442-00741-8 |edition=5th |page=202 |oclc=25409557}}</ref> | |||
| |- | |||
| |] | |||
| |A generalisation of homomorphisms to any ], even when the objects of the category are not sets (for example, a ] defines a category with only one object, which has the elements of the group as morphisms; see {{slink|Category (mathematics)|Examples}} for this example and other similar ones).<ref>{{harvnb|James|James|1992|p=48}}</ref> | |||
| |} | |||
| A function may also be called a '''map''' or a '''mapping''', but some authors make a distinction between the term "map" and "function". For example, the term "map" is often reserved for a "function" with some sort of special structure (e.g. ]). In particular ''map'' may be used in place of ''homomorphism'' for the sake of succinctness (e.g., ] or ''map from {{mvar|G}} to {{mvar|H}}'' instead of ''] from {{mvar|G}} to {{mvar|H}}''). Some authors<ref name=Apostol81p35>{{cite book |first=T.M. |last=Apostol |title=Mathematical Analysis|year=1981 |publisher=Addison-Wesley |page=35 |isbn=978-0-201-00288-1 |oclc=928947543 |edition=2nd}}</ref> reserve the word ''mapping'' for the case where the structure of the codomain belongs explicitly to the definition of the function. | |||
| Some authors, such as ],<ref name=Lang87p43/> use "function" only to refer to maps for which the ] is a subset of the ] or ] numbers, and use the term ''mapping'' for more general functions. | |||
| ==Notation== | |||
| It is common to omit the parentheses around the argument when there is little chance of ambiguity, thus: sin ''x''. In some formal settings, use of ], ''x'' ƒ, eliminates the need for any parentheses; and, for example, the ] function is always written ''n''!, even though its generalization, the ], is written Γ(''n''). | |||
| In the theory of ]s, a map denotes an ] used to create ]. See also ]. | |||
| Formal description of a function typically involves the function's name, its domain, its codomain, and a rule of correspondence. Thus we frequently see a two-part notation, an example being | |||
| : <math>\begin{align} | |||
| f\colon \mathbb{N} &\to \mathbb{R} \\ | |||
| n &\mapsto \frac{n}{\pi} | |||
| \end{align}</math> | |||
| where the first part is read: | |||
| * "ƒ is a function from '''N''' to '''R'''" (one often writes informally "Let ƒ: ''X'' → ''Y''" to mean "Let ƒ be a function from ''X'' to ''Y''"), or | |||
| * "ƒ is a function on '''N''' into '''R'''", or | |||
| * "ƒ is a '''R'''-valued function of an '''N'''-valued variable", | |||
| and the second part is read: | |||
| * <math> n \,</math> maps to <math> \frac{n}{\pi} \,\! </math> | |||
| Whichever definition of ''map'' is used, related terms like '']'', '']'', '']'', '']'' have the same meaning as for a function. | |||
| Here the function named "ƒ" has the ]s as domain, the ]s as codomain, and maps ''n'' to itself divided by π. Less formally, this long form might be abbreviated | |||
| : <math> f(n) = \frac{n}{\pi} , \,\! </math> | |||
| though with some loss of information; we no longer are explicitly given the domain and codomain. Even the long form here abbreviates the fact that the ''n'' on the right-hand side is silently treated as a real number using the standard embedding. | |||
| == Specifying a function == | |||
| An alternative to the colon notation, convenient when functions are being composed, writes the function name above the arrow. For example, if ƒ is followed by ''g'', where ''g'' produces the ] ''e''<sup>'''i'''''x''</sup>, we may write | |||
| Given a function <math>f</math>, by definition, to each element <math>x</math> of the domain of the function <math>f</math>, there is a unique element associated to it, the value <math>f(x)</math> of <math>f</math> at <math>x</math>. There are several ways to specify or describe how <math>x</math> is related to <math>f(x)</math>, both explicitly and implicitly. Sometimes, a theorem or an ] asserts the existence of a function having some properties, without describing it more precisely. Often, the specification or description is referred to as the definition of the function <math>f</math>. | |||
| : <math> \mathbb{N} \xrightarrow{f} \mathbb{R} \xrightarrow{g} \mathbb{C} . \,\! </math> | |||
| A more elaborate form of this is the ]. | |||
| === By listing function values === | |||
| Use of ƒ(''A'') to denote the image of a subset ''A''⊆''X'' is consistent so long as no subset of the domain is also an element of the domain. In some fields (e.g. in set theory, where ]s are also sets of ordinals) it is convenient or even necessary to distinguish the two concepts; the customary notation is ƒ for the set { ƒ(''x''): x ∈ ''A'' }; some authors write ƒ`''x'' instead of ƒ(''x''), and ƒ``''A'' instead of ƒ. | |||
| On a finite set a function may be defined by listing the elements of the codomain that are associated to the elements of the domain. For example, if <math>A = \{ 1, 2, 3 \}</math>, then one can define a function <math>f: A \to \mathbb{R}</math> by <math>f(1) = 2, f(2) = 3, f(3) = 4.</math> | |||
| === By a formula === | |||
| == Function composition == | |||
| Functions are often defined by an ] that describes a combination of ] and previously defined functions; such a formula allows computing the value of the function from the value of any element of the domain. | |||
| For example, in the above example, <math>f</math> can be defined by the formula <math>f(n) = n+1</math>, for <math>n\in\{1,2,3\}</math>. | |||
| When a function is defined this way, the determination of its domain is sometimes difficult. If the formula that defines the function contains divisions, the values of the variable for which a denominator is zero must be excluded from the domain; thus, for a complicated function, the determination of the domain passes through the computation of the ] of auxiliary functions. Similarly, if ]s occur in the definition of a function from <math>\mathbb{R}</math> to <math>\mathbb{R},</math> the domain is included in the set of the values of the variable for which the arguments of the square roots are nonnegative. | |||
| For example, <math>f(x)=\sqrt{1+x^2}</math> defines a function <math>f: \mathbb{R} \to \mathbb{R}</math> whose domain is <math>\mathbb{R},</math> because <math>1+x^2</math> is always positive if {{mvar|x}} is a real number. On the other hand, <math>f(x)=\sqrt{1-x^2}</math> defines a function from the reals to the reals whose domain is reduced to the interval {{closed-closed|−1, 1}}. (In old texts, such a domain was called the ''domain of definition'' of the function.) | |||
| Functions can be classified by the nature of formulas that define them: | |||
| * A ] is a function that may be written <math>f(x) = ax^2+bx+c,</math> where {{math|''a'', ''b'', ''c''}} are ]. | |||
| * More generally, a ] is a function that can be defined by a formula involving only additions, subtractions, multiplications, and ] to nonnegative integer powers. For example, <math>f(x) = x^3-3x-1</math> and <math>f(x) = (x-1)(x^3+1) +2x^2 -1</math> are polynomial functions of <math>x</math>. | |||
| * A ] is the same, with divisions also allowed, such as <math>f(x) = \frac{x-1}{x+1},</math> and <math>f(x) = \frac 1{x+1}+\frac 3x-\frac 2{x-1}.</math> | |||
| * An ] is the same, with ] and ] also allowed. | |||
| * An ]<ref group=note>Here "elementary" has not exactly its common sense: although most functions that are encountered in elementary courses of mathematics are elementary in this sense, some elementary functions are not elementary for the common sense, for example, those that involve roots of polynomials of high degree.</ref> is the same, with ]s and ] allowed. | |||
| === Inverse and implicit functions === | |||
| A function <math>f : X\to Y,</math> with domain {{mvar|X}} and codomain {{mvar|Y}}, is ], if for every {{mvar|y}} in {{mvar|Y}}, there is one and only one element {{mvar|x}} in {{mvar|X}} such that {{math|1=''y'' = ''f''(''x'')}}. In this case, the ] of {{mvar|f}} is the function <math>f^{-1} : Y \to X</math> that maps <math>y\in Y</math> to the element <math>x\in X</math> such that {{math|1=''y'' = ''f''(''x'')}}. For example, the ] is a bijective function from the positive real numbers to the real numbers. It thus has an inverse, called the ], that maps the real numbers onto the positive numbers. | |||
| If a function <math>f: X\to Y</math> is not bijective, it may occur that one can select subsets <math>E\subseteq X</math> and <math>F\subseteq Y</math> such that the ] of {{mvar|f}} to {{mvar|E}} is a bijection from {{mvar|E}} to {{mvar|F}}, and has thus an inverse. The ] are defined this way. For example, the ] induces, by restriction, a bijection from the ] {{closed-closed|0, ''π''}} onto the interval {{closed-closed|−1, 1}}, and its inverse function, called ], maps {{closed-closed|−1, 1}} onto {{closed-closed|0, ''π''}}. The other inverse trigonometric functions are defined similarly. | |||
| More generally, given a ] {{mvar|R}} between two sets {{mvar|X}} and {{mvar|Y}}, let {{mvar|E}} be a subset of {{mvar|X}} such that, for every <math>x\in E,</math> there is some <math>y\in Y</math> such that {{math|''x R y''}}. If one has a criterion allowing selecting such a {{mvar|y}} for every <math>x\in E,</math> this defines a function <math>f: E\to Y,</math> called an ], because it is implicitly defined by the relation {{mvar|R}}. | |||
| For example, the equation of the ] <math>x^2+y^2=1</math> defines a relation on real numbers. If {{math|−1 < ''x'' < 1}} there are two possible values of {{mvar|y}}, one positive and one negative. For {{math|1=''x'' = ± 1}}, these two values become both equal to 0. Otherwise, there is no possible value of {{mvar|y}}. This means that the equation defines two implicit functions with domain {{closed-closed|−1, 1}} and respective codomains {{closed-open|0, +∞}} and {{open-closed|−∞, 0}}. | |||
| In this example, the equation can be solved in {{mvar|y}}, giving <math>y=\pm \sqrt{1-x^2},</math> but, in more complicated examples, this is impossible. For example, the relation <math>y^5+y+x=0</math> defines {{mvar|y}} as an implicit function of {{mvar|x}}, called the ], which has <math>\mathbb R</math> as domain and range. The Bring radical cannot be expressed in terms of the four arithmetic operations and ]. | |||
| The ] provides mild ] conditions for existence and uniqueness of an implicit function in the neighborhood of a point. | |||
| === Using differential calculus === | |||
| Many functions can be defined as the ] of another function. This is the case of the ], which is the antiderivative of {{math|1/''x''}} that is 0 for {{math|1=''x'' = 1}}. Another common example is the ]. | |||
| More generally, many functions, including most ]s, can be defined as solutions of ]s. The simplest example is probably the ], which can be defined as the unique function that is equal to its derivative and takes the value 1 for {{math|1=''x'' = 0}}. | |||
| ] can be used to define functions on the domain in which they converge. For example, the ] is given by <math display="inline">e^x = \sum_{n=0}^{\infty} {x^n \over n!}</math>. However, as the coefficients of a series are quite arbitrary, a function that is the sum of a convergent series is generally defined otherwise, and the sequence of the coefficients is the result of some computation based on another definition. Then, the power series can be used to enlarge the domain of the function. Typically, if a function for a real variable is the sum of its ] in some interval, this power series allows immediately enlarging the domain to a subset of the ]s, the ] of the series. Then ] allows enlarging further the domain for including almost the whole ]. This process is the method that is generally used for defining the ], the ] and the ] of a complex number. | |||
| === By recurrence === | |||
| {{main|Recurrence relation}} | |||
| Functions whose domain are the nonnegative integers, known as ]s, are sometimes defined by ]s. | |||
| The ] function on the nonnegative integers (<math>n\mapsto n!</math>) is a basic example, as it can be defined by the recurrence relation | |||
| : <math>n!=n(n-1)!\quad\text{for}\quad n>0,</math> | |||
| and the initial condition | |||
| : <math>0!=1.</math> | |||
| == Representing a function == | |||
| A ] is commonly used to give an intuitive picture of a function. As an example of how a graph helps to understand a function, it is easy to see from its graph whether a function is increasing or decreasing. Some functions may also be represented by ]s. | |||
| === Graphs and plots === | |||
| {{main|Graph of a function}} | |||
| ]]] | |||
| ] | |||
| Given a function <math>f : X\to Y,</math> its ''graph'' is, formally, the set | |||
| : <math>G=\{(x,f(x))\mid x\in X\}.</math> | |||
| In the frequent case where {{mvar|X}} and {{mvar|Y}} are subsets of the ]s (or may be identified with such subsets, e.g. ]), an element <math>(x,y)\in G</math> may be identified with a point having coordinates {{math|''x'', ''y''}} in a 2-dimensional coordinate system, e.g. the ]. Parts of this may create a ] that represents (parts of) the function. The use of plots is so ubiquitous that they too are called the ''graph of the function''. Graphic representations of functions are also possible in other coordinate systems. For example, the graph of the ] | |||
| : <math>x\mapsto x^2,</math> | |||
| consisting of all points with coordinates <math>(x, x^2)</math> for <math>x\in \R,</math> yields, when depicted in Cartesian coordinates, the well known ]. If the same quadratic function <math>x\mapsto x^2,</math> with the same formal graph, consisting of pairs of numbers, is plotted instead in ] <math>(r,\theta) =(x,x^2),</math> the plot obtained is ]. | |||
| === Tables === | |||
| {{Main|Mathematical table}} | |||
| A function can be represented as a table of values. If the domain of a function is finite, then the function can be completely specified in this way. For example, the multiplication function <math>f:\{1,\ldots,5\}^2 \to \mathbb{R}</math> defined as <math>f(x,y)=xy</math> can be represented by the familiar ] | |||
| {| class="wikitable" style="text-align: center;" | |||
| ! {{diagonal split header|{{mvar|x}}|{{mvar|y}}}} | |||
| ! 1 !! 2 !! 3 !! 4 !! 5 | |||
| |- | |||
| ! 1 | |||
| | 1 || 2 || 3 || 4 || 5 | |||
| |- | |||
| ! 2 | |||
| | 2 || 4 ||6 || 8 || 10 | |||
| |- | |||
| ! 3 | |||
| | 3 || 6 || 9 || 12 || 15 | |||
| |- | |||
| ! 4 | |||
| | 4 || 8 || 12 || 16 || 20 | |||
| |- | |||
| ! 5 | |||
| | 5 || 10 || 15 || 20 || 25 | |||
| |} | |||
| On the other hand, if a function's domain is continuous, a table can give the values of the function at specific values of the domain. If an intermediate value is needed, ] can be used to estimate the value of the function. For example, a portion of a table for the sine function might be given as follows, with values rounded to 6 decimal places: | |||
| {| class="wikitable" style="text-align: center;" | |||
| ! {{mvar|x}} !! {{math|sin ''x''}} | |||
| |- | |||
| |1.289 || 0.960557 | |||
| |- | |||
| |1.290 || 0.960835 | |||
| |- | |||
| |1.291 || 0.961112 | |||
| |- | |||
| |1.292 || 0.961387 | |||
| |- | |||
| |1.293 || 0.961662 | |||
| |} | |||
| Before the advent of handheld calculators and personal computers, such tables were often compiled and published for functions such as logarithms and trigonometric functions. | |||
| === Bar chart === | |||
| {{main|Bar chart}} | |||
| A bar chart can represent a function whose domain is a finite set, the ]s, or the ]s. In this case, an element {{mvar|x}} of the domain is represented by an ] of the {{mvar|x}}-axis, and the corresponding value of the function, {{math|''f''(''x'')}}, is represented by a ] whose base is the interval corresponding to {{mvar|x}} and whose height is {{math|''f''(''x'')}} (possibly negative, in which case the bar extends below the {{mvar|x}}-axis). | |||
| == General properties == | |||
| This section describes general properties of functions, that are independent of specific properties of the domain and the codomain. | |||
| === Standard functions === | |||
| There are a number of standard functions that occur frequently: | |||
| * For every set {{mvar|X}}, there is a unique function, called the '''{{vanchor|empty function}}''', or '''empty map''', from the ] to {{mvar|X}}. The graph of an empty function is the empty set.<ref group=note>By definition, the graph of the empty function to {{mvar|X}} is a subset of the Cartesian product {{math|∅ × ''X''}}, and this product is empty.</ref> The existence of empty functions is needed both for the coherency of the theory and for avoiding exceptions concerning the empty set in many statements. Under the usual set-theoretic definition of a function as an ] (or equivalent ones), there is exactly one empty function for each set, thus the empty function <math>\varnothing \to X</math> is not equal to <math>\varnothing \to Y</math> if and only if <math>X\ne Y</math>, although their graphs are both the ]. | |||
| * For every set {{mvar|X}} and every ] {{math|{{mset|''s''}}}}, there is a unique function from {{mvar|X}} to {{math|{{mset|''s''}}}}, which maps every element of {{mvar|X}} to {{mvar|s}}. This is a surjection (see below) unless {{mvar|X}} is the empty set. | |||
| * Given a function <math>f: X\to Y,</math> the ''canonical surjection'' of {{mvar|f}} onto its image <math>f(X)=\{f(x)\mid x\in X\}</math> is the function from {{mvar|X}} to {{math|''f''(''X'')}} that maps {{mvar|x}} to {{math|''f''(''x'')}}. | |||
| * For every ] {{mvar|A}} of a set {{mvar|X}}, the ] of {{mvar|A}} into {{mvar|X}} is the injective (see below) function that maps every element of {{mvar|A}} to itself. | |||
| * The ] on a set {{mvar|X}}, often denoted by {{math|id<sub>''X''</sub>}}, is the inclusion of {{mvar|X}} into itself. | |||
| === Function composition === | |||
| {{Main|Function composition}} | {{Main|Function composition}} | ||
| The '''function composition''' of two or more functions uses the output of one function as the input of another. The functions ƒ: ''X'' → ''Y'' and ''g'': ''Y'' → ''Z'' can be ''composed'' by first applying ƒ to an argument ''x'' to obtain ''y'' = ƒ(''x'') and then applying ''g'' to ''y'' to obtain ''z'' = ''g''(''y''). The composite function formed in this way from general ƒ and ''g'' may be written | |||
| Given two functions <math>f: X\to Y</math> and <math>g: Y\to Z</math> such that the domain of {{mvar|g}} is the codomain of {{mvar|f}}, their ''composition'' is the function <math>g \circ f: X \rightarrow Z</math> defined by | |||
| : <math>(g \circ f)(x) = g(f(x)).</math> | |||
| That is, the value of <math>g \circ f</math> is obtained by first applying {{math|''f''}} to {{math|''x''}} to obtain {{math|1=''y'' = ''f''(''x'')}} and then applying {{math|''g''}} to the result {{mvar|y}} to obtain {{math|1=''g''(''y'') = ''g''(''f''(''x''))}}. In this notation, the function that is applied first is always written on the right. | |||
| The composition <math>g\circ f</math> is an ] on functions that is defined only if the codomain of the first function is the domain of the second one. Even when both <math>g \circ f</math> and <math>f \circ g</math> satisfy these conditions, the composition is not necessarily ], that is, the functions <math>g \circ f</math> and <math> f \circ g</math> need not be equal, but may deliver different values for the same argument. For example, let {{math|1=''f''(''x'') = ''x''<sup>2</sup>}} and {{math|1=''g''(''x'') = ''x'' + 1}}, then <math>g(f(x))=x^2+1</math> and <math> f(g(x)) = (x+1)^2</math> agree just for <math>x=0.</math> | |||
| The function composition is ] in the sense that, if one of <math>(h\circ g)\circ f</math> and <math>h\circ (g\circ f)</math> is defined, then the other is also defined, and they are equal, that is, <math>(h\circ g)\circ f = h\circ (g\circ f).</math> Therefore, it is usual to just write <math>h\circ g\circ f.</math> | |||
| The ]s <math>\operatorname{id}_X</math> and <math>\operatorname{id}_Y</math> are respectively a ] and a ] for functions from {{mvar|X}} to {{mvar|Y}}. That is, if {{mvar|f}} is a function with domain {{mvar|X}}, and codomain {{mvar|Y}}, one has | |||
| <math>f\circ \operatorname{id}_X = \operatorname{id}_Y \circ f = f.</math> | |||
| <gallery widths="250" heights="300"> | |||
| File:Function machine5.svg|A composite function ''g''(''f''(''x'')) can be visualized as the combination of two "machines". | |||
| File:Example for a composition of two functions.svg|A simple example of a function composition | |||
| File:Compfun.svg|Another composition. In this example, {{math|1=(''g'' ∘ ''f'' )(c) = #}}. | |||
| </gallery> | |||
| === Image and preimage === | |||
| {{Main|Image (mathematics)}} | |||
| Let <math>f: X\to Y.</math> The ''image'' under {{mvar|f}} of an element {{mvar|x}} of the domain {{mvar|X}} is {{math|''f''(''x'')}}.<ref name="EOM Function"/> If {{math|''A''}} is any subset of {{math|''X''}}, then the ''image'' of {{mvar|A}} under {{mvar|f}}, denoted {{math|''f''(''A'')}}, is the subset of the codomain {{math|''Y''}} consisting of all images of elements of {{mvar|A}},<ref name="EOM Function"/> that is, | |||
| : <math>f(A)=\{f(x)\mid x\in A\}.</math> | |||
| The ''image'' of {{math|''f''}} is the image of the whole domain, that is, {{math|''f''(''X'')}}.{{r|PCM p.11}} It is also called the ] of {{mvar|f}},{{r|EOM Function|T&K Calc p.3|Trench RA pp.30-32|TBB RA pp.A4-A5}} although the term ''range'' may also refer to the codomain.{{r|TBB RA pp.A4-A5|PCM p.11}}<ref name = "standard">''Quantities and Units - Part 2: Mathematical signs and symbols to be used in the natural sciences and technology'', p. 15. ISO 80000-2 (ISO/IEC 2009-12-01)</ref> | |||
| On the other hand, the '']'' or '']'' under {{mvar|f}} of an element {{mvar|y}} of the codomain {{mvar|Y}} is the set of all elements of the domain {{math|''X''}} whose images under {{mvar|f}} equal {{mvar|y}}.<ref name="EOM Function"/> In symbols, the preimage of {{mvar|y}} is denoted by <math>f^{-1}(y)</math> and is given by the equation | |||
| : <math>f^{-1}(y) = \{x \in X \mid f(x) = y\}.</math> | |||
| Likewise, the preimage of a subset {{math|''B''}} of the codomain {{math|''Y''}} is the set of the preimages of the elements of {{math|''B''}}, that is, it is the subset of the domain {{math|''X''}} consisting of all elements of {{math|''X''}} whose images belong to {{math|''B''}}.<ref name="EOM Function"/> It is denoted by <math>f^{-1}(B)</math> and is given by the equation | |||
| : <math>f^{-1}(B) = \{x \in X \mid f(x) \in B\}.</math> | |||
| For example, the preimage of <math>\{4, 9\}</math> under the ] is the set <math>\{-3,-2,2,3\}</math>. | |||
| By definition of a function, the image of an element {{math|''x''}} of the domain is always a single element of the codomain. However, the preimage <math>f^{-1}(y)</math> of an element {{mvar|y}} of the codomain may be ] or contain any number of elements. For example, if {{mvar|f}} is the function from the integers to themselves that maps every integer to 0, then <math>f^{-1}(0) = \mathbb{Z}</math>. | |||
| If <math>f : X\to Y</math> is a function, {{math|''A''}} and {{math|''B''}} are subsets of {{math|''X''}}, and {{math|''C''}} and {{math|''D''}} are subsets of {{math|''Y''}}, then one has the following properties: | |||
| * <math>A\subseteq B \Longrightarrow f(A)\subseteq f(B)</math> | |||
| * <math>C\subseteq D \Longrightarrow f^{-1}(C)\subseteq f^{-1}(D)</math> | |||
| * <math>A \subseteq f^{-1}(f(A))</math> | |||
| * <math>C \supseteq f(f^{-1}(C))</math> | |||
| * <math>f(f^{-1}(f(A)))=f(A)</math> | |||
| * <math>f^{-1}(f(f^{-1}(C)))=f^{-1}(C)</math> | |||
| The preimage by {{mvar|f}} of an element {{mvar|y}} of the codomain is sometimes called, in some contexts, the ] of {{math|''y''}} under {{mvar|''f''}}. | |||
| If a function {{mvar|f}} has an inverse (see below), this inverse is denoted <math>f^{-1}.</math> In this case <math>f^{-1}(C)</math> may denote either the image by <math>f^{-1}</math> or the preimage by {{mvar|f}} of {{mvar|C}}. This is not a problem, as these sets are equal. The notation <math>f(A)</math> and <math>f^{-1}(C)</math> may be ambiguous in the case of sets that contain some subsets as elements, such as <math>\{x, \{x\}\}.</math> In this case, some care may be needed, for example, by using square brackets <math>f, f^{-1}</math> for images and preimages of subsets and ordinary parentheses for images and preimages of elements. | |||
| === Injective, surjective and bijective functions === | |||
| {{main|Bijection, injection and surjection}} | |||
| Let <math>f : X\to Y</math> be a function. | |||
| The function {{mvar|f}} is '']'' (or ''one-to-one'', or is an ''injection'') if {{math|''f''(''a'') ≠ ''f''(''b'')}} for every two different elements {{math|''a''}} and {{mvar|''b''}} of {{mvar|X}}.<ref name="PCM p.11">{{Princeton Companion to Mathematics|p=11}}</ref><ref name="EOM Injection">{{eom |title=Injection |oldid=30986 |author-first=O.A. |author-last=Ivanova|mode=cs1}}</ref> Equivalently, {{mvar|f}} is injective if and only if, for every <math>y\in Y,</math> the preimage <math>f^{-1}(y)</math> contains at most one element. An empty function is always injective. If {{mvar|X}} is not the empty set, then {{mvar|f}} is injective if and only if there exists a function <math>g: Y\to X</math> such that <math>g\circ f=\operatorname{id}_X,</math> that is, if {{mvar|f}} has a ].<ref name="EOM Injection"/> ''Proof'': If {{mvar|f}} is injective, for defining {{mvar|g}}, one chooses an element <math>x_0</math> in {{mvar|X}} (which exists as {{mvar|X}} is supposed to be nonempty),<ref group=note>The ] is not needed here, as the choice is done in a single set.</ref> and one defines {{mvar|g}} by <math>g(y)=x</math> if <math>y=f(x)</math> and <math>g(y)=x_0</math> if <math>y\not\in f(X).</math> Conversely, if <math>g\circ f=\operatorname{id}_X,</math> and <math>y=f(x),</math> then <math>x=g(y),</math> and thus <math>f^{-1}(y)=\{x\}.</math> | |||
| The function {{mvar|f}} is '']'' (or ''onto'', or is a ''surjection'') if its range <math>f(X)</math> equals its codomain <math>Y</math>, that is, if, for each element <math>y</math> of the codomain, there exists some element <math>x</math> of the domain such that <math>f(x) = y</math> (in other words, the preimage <math>f^{-1}(y)</math> of every <math>y\in Y</math> is nonempty).<ref name="PCM p.11"/><ref name="EOM Surjection">{{eom |title=Surjection |oldid=35689 |author-first=O.A. |author-last=Ivanova|mode=cs1}}</ref> If, as usual in modern mathematics, the ] is assumed, then {{mvar|f}} is surjective if and only if there exists a function <math>g: Y\to X</math> such that <math>f\circ g=\operatorname{id}_Y,</math> that is, if {{mvar|f}} has a ].<ref name="EOM Surjection"/> The axiom of choice is needed, because, if {{mvar|f}} is surjective, one defines {{mvar|g}} by <math>g(y)=x,</math> where <math>x</math> is an ''arbitrarily chosen'' element of <math>f^{-1}(y).</math> | |||
| The function {{mvar|f}} is '']'' (or is a ''bijection'' or a ''one-to-one correspondence'') if it is both injective and surjective.<ref name="PCM p.11"/><ref name="EOM Bijection">{{eom |title=Bijection |oldid=30987 |author-first=O.A. |author-last=Ivanova|mode=cs1}}</ref> That is, {{mvar|f}} is bijective if, for every <math>y\in Y,</math> the preimage <math>f^{-1}(y)</math> contains exactly one element. The function {{mvar|f}} is bijective if and only if it admits an ], that is, a function <math>g : Y\to X</math> such that <math>g\circ f=\operatorname{id}_X</math> and <math>f\circ g=\operatorname{id}_Y.</math><ref name="EOM Bijection"/> (Contrarily to the case of surjections, this does not require the axiom of choice; the proof is straightforward). | |||
| Every function <math>f: X\to Y</math> may be ] as the composition <math>i\circ s</math> of a surjection followed by an injection, where {{mvar|s}} is the canonical surjection of {{mvar|X}} onto {{math|''f''(''X'')}} and {{mvar|i}} is the canonical injection of {{math|''f''(''X'')}} into {{mvar|Y}}. This is the ''canonical factorization'' of {{mvar|f}}. | |||
| "One-to-one" and "onto" are terms that were more common in the older English language literature; "injective", "surjective", and "bijective" were originally coined as French words in the second quarter of the 20th century by the ] and imported into English.<ref>{{Cite web |last=Hartnett |first=Kevin |date=9 November 2020 |title=Inside the Secret Math Society Known Simply as Nicolas Bourbaki |url=https://www.quantamagazine.org/inside-the-secret-math-society-known-as-nicolas-bourbaki-20201109/ |access-date=2024-06-05 |website=Quanta Magazine}}</ref> As a word of caution, "a one-to-one function" is one that is injective, while a "one-to-one correspondence" refers to a bijective function. Also, the statement "{{math|''f''}} maps {{math|''X''}} ''onto'' {{math|''Y''}}" differs from "{{math|''f''}} maps {{math|''X''}} ''into'' {{math|''B''}}", in that the former implies that {{math|''f''}} is surjective, while the latter makes no assertion about the nature of {{math|''f''}}. In a complicated reasoning, the one letter difference can easily be missed. Due to the confusing nature of this older terminology, these terms have declined in popularity relative to the Bourbakian terms, which have also the advantage of being more symmetrical. | |||
| === Restriction and extension <span class="anchor" id="Restrictions and extensions"></span> === | |||
| <!-- This section is linked from ], ], ] --> | |||
| {{main|Restriction (mathematics)}} | |||
| If <math>f : X \to Y</math> is a function and {{math|''S''}} is a subset of {{math|''X''}}, then the ''restriction'' of <math>f</math> to ''S'', denoted <math>f|_S</math>, is the function from {{math|''S''}} to {{math|''Y''}} defined by | |||
| : <math>f|_S(x) = f(x)</math> | |||
| for all {{math|''x''}} in {{math|''S''}}. Restrictions can be used to define partial ]s: if there is a ] {{math|''S''}} of the domain of a function <math>f</math> such that <math>f|_S</math> is injective, then the canonical surjection of <math>f|_S</math> onto its image <math>f|_S(S) = f(S)</math> is a bijection, and thus has an inverse function from <math>f(S)</math> to {{math|''S''}}. One application is the definition of ]. For example, the ] function is injective when restricted to the ] {{closed-closed|0, ''π''}}. The image of this restriction is the interval {{closed-closed|−1, 1}}, and thus the restriction has an inverse function from {{closed-closed|−1, 1}} to {{closed-closed|0, ''π''}}, which is called ] and is denoted {{math|arccos}}. | |||
| Function restriction may also be used for "gluing" functions together. Let <math display="inline"> X=\bigcup_{i\in I}U_i</math> be the decomposition of {{mvar|X}} as a ] of subsets, and suppose that a function <math>f_i : U_i \to Y</math> is defined on each <math>U_i</math> such that for each pair <math>i, j</math> of indices, the restrictions of <math>f_i</math> and <math>f_j</math> to <math>U_i \cap U_j</math> are equal. Then this defines a unique function <math>f : X \to Y</math> such that <math>f|_{U_i} = f_i</math> for all {{mvar|i}}. This is the way that functions on ]s are defined. | |||
| An ''extension'' of a function {{mvar|f}} is a function {{mvar|g}} such that {{mvar|f}} is a restriction of {{mvar|g}}. A typical use of this concept is the process of ], that allows extending functions whose domain is a small part of the ] to functions whose domain is almost the whole complex plane. | |||
| Here is another classical example of a function extension that is encountered when studying ] of the ]. A ''homography'' is a function <math>h(x)=\frac{ax+b}{cx+d}</math> such that {{math|''ad'' − ''bc'' ≠ 0}}. Its domain is the set of all ]s different from <math>-d/c,</math> and its image is the set of all real numbers different from <math>a/c.</math> If one extends the real line to the ] by including {{math|∞}}, one may extend {{mvar|h}} to a bijection from the extended real line to itself by setting <math>h(\infty)=a/c</math> and <math>h(-d/c)=\infty</math>. | |||
| == In calculus == | |||
| {{further|History of the function concept}} | |||
| The idea of function, starting in the 17th century, was fundamental to the new ]. At that time, only ] functions of a ] were considered, and all functions were assumed to be ]. But the definition was soon extended to ] and to ]. In the second half of the 19th century, the mathematically rigorous definition of a function was introduced, and functions with arbitrary domains and codomains were defined. | |||
| Functions are now used throughout all areas of mathematics. In introductory ], when the word ''function'' is used without qualification, it means a real-valued function of a single real variable. The more general definition of a function is usually introduced to second or third year college students with ] majors, and in their senior year they are introduced to calculus in a larger, more rigorous setting in courses such as ] and ]. | |||
| === Real function === | |||
| {{see also|Real analysis}} | |||
| ] | |||
| ] | |||
| ] and ].]] | |||
| A ''real function'' is a ] ], that is, a function whose codomain is the ] and whose domain is a set of ]s that contains an ]. In this section, these functions are simply called ''functions''. | |||
| The functions that are most commonly considered in mathematics and its applications have some regularity, that is they are ], ], and even ]. This regularity insures that these functions can be visualized by their ]. In this section, all functions are differentiable in some interval. | |||
| Functions enjoy ]s, that is, if {{mvar|f}} and {{mvar|g}} are functions, their sum, difference and product are functions defined by | |||
| : <math>\begin{align} | : <math>\begin{align} | ||
| (f+g)(x)&=f(x)+g(x)\\ | |||
| g\circ f\colon X &\to Z \\ | |||
| (f-g)(x)&=f(x)-g(x)\\ | |||
| (f\cdot g)(x)&=f(x)\cdot g(x)\\ | |||
| \end{align}</math> | |||
| \end{align}.</math> | |||
| The function on the right acts first and the function on the left acts second, reversing English reading order. We remember the order by reading the notation as "''g'' of ƒ". The order is important, because rarely do we get the same result both ways. For example, suppose ƒ(''x'') = ''x''<sup>2</sup> and ''g''(''x'') = ''x''+1. Then ''g''(ƒ(''x'')) = ''x''<sup>2</sup>+1, while ƒ(''g''(''x'')) = (''x''+1)<sup>2</sup>, which is ''x''<sup>2</sup>+2''x''+1, a different function. | |||
| The domains of the resulting functions are the ] of the domains of {{mvar|f}} and {{mvar|g}}. The quotient of two functions is defined similarly by | |||
| : <math>\frac fg(x)=\frac{f(x)}{g(x)},</math> | |||
| but the domain of the resulting function is obtained by removing the ] of {{mvar|g}} from the intersection of the domains of {{mvar|f}} and {{mvar|g}}. | |||
| The ]s are defined by ]s, and their domain is the whole set of real numbers. They include ]s, ]s and ]s. ]s are quotients of two polynomial functions, and their domain is the real numbers with a finite number of them removed to avoid ]. The simplest rational function is the function <math>x\mapsto \frac 1x,</math> whose graph is a ], and whose domain is the whole ] except for 0. | |||
| In a similar way, the function given above by the formula ''y'' = 5''x''−20''x''<sup>3</sup>+16''x''<sup>5</sup> can be obtained by composing several functions, namely the ], ], and multiplication of real numbers. | |||
| The ] of a real differentiable function is a real function. An ] of a continuous real function is a real function that has the original function as a derivative. For example, the function <math display="inline">x\mapsto\frac 1x</math> is continuous, and even differentiable, on the positive real numbers. Thus one antiderivative, which takes the value zero for {{math|1=''x'' = 1}}, is a differentiable function called the ]. | |||
| == Identity function == | |||
| {{Main|Identity function}} | |||
| The unique function over a set ''X'' that maps each element to itself is called the '''identity function''' for ''X'', and typically denoted by id<sub>''X''</sub>. Each set has its own identity function, so the subscript cannot be omitted unless the set can be inferred from context. Under composition, an identity function is "neutral": if ƒ is any function from ''X'' to ''Y'', then | |||
| :<math>\begin{align} | |||
| f \circ \mathrm{id}_X &= f , \\ | |||
| \mathrm{id}_Y \circ f &= f . | |||
| \end{align}</math> | |||
| A real function {{mvar|f}} is ] in an interval if the sign of <math>\frac{f(x)-f(y)}{x-y}</math> does not depend of the choice of {{mvar|x}} and {{mvar|y}} in the interval. If the function is differentiable in the interval, it is monotonic if the sign of the derivative is constant in the interval. If a real function {{mvar|f}} is monotonic in an interval {{mvar|I}}, it has an ], which is a real function with domain {{math|''f''(''I'')}} and image {{mvar|I}}. This is how ] are defined in terms of ], where the trigonometric functions are monotonic. Another example: the natural logarithm is monotonic on the positive real numbers, and its image is the whole real line; therefore it has an inverse function that is a ] between the real numbers and the positive real numbers. This inverse is the ]. | |||
| == Inverse function == | |||
| {{Main|Inverse function}} | |||
| If ƒ is a function from ''X'' to ''Y'' then an '''inverse function''' for ƒ, denoted by ƒ<sup>−1</sup>, is a function in the opposite direction, from ''Y'' to ''X'', with the property that a round trip (a ]) returns each element to itself. Not every function has an inverse; those that do are called '''invertible'''. | |||
| Many other real functions are defined either by the ] (the inverse function is a particular instance) or as solutions of ]s. For example, the ] and the ] functions are the solutions of the ] | |||
| As a simple example, if ƒ converts a temperature in degrees ] to degrees ], the function converting degrees ] to degrees ] would be a suitable ƒ<sup>−1</sup>. | |||
| :<math> |
: <math>y''+y=0</math> | ||
| such that | |||
| f(C) &= \tfrac95 C + 32 \\ | |||
| : <math>\sin 0=0, \quad \cos 0=1, \quad\frac{\partial \sin x}{\partial x}(0)=1, \quad\frac{\partial \cos x}{\partial x}(0)=0.</math> | |||
| f^{-1}(F) &= \tfrac59 (F - 32) | |||
| \end{align}</math> | |||
| === Vector-valued function === | |||
| The notation for composition reminds us of multiplication; in fact, sometimes we denote it using juxtaposition, ''g''ƒ, without an intervening circle. Under this analogy, identity functions are like 1, and inverse functions are like ]s (hence the notation). | |||
| {{main|Vector-valued function|Vector field}} | |||
| When the elements of the codomain of a function are ], the function is said to be a vector-valued function. These functions are particularly useful in applications, for example modeling physical properties. For example, the function that associates to each point of a fluid its ] is a vector-valued function. | |||
| ==Specifying a function== | |||
| A function can be defined by any mathematical condition relating each argument to the corresponding output value. If the domain is finite, a function ƒ may be defined by simply tabulating all the arguments ''x'' and their corresponding function values ƒ(''x''). More commonly, a function is defined by a ], or (more generally) an ] — a recipe that tells how to compute the value of ƒ(''x'') given any ''x'' in the domain. | |||
| Some vector-valued functions are defined on a subset of <math>\mathbb{R}^n</math> or other spaces that share geometric or ] properties of <math>\mathbb{R}^n</math>, such as ]. These vector-valued functions are given the name ''vector fields''. | |||
| There are many other ways of defining functions. Examples include ], algebraic or ] ], ], ], infinite ], and as solutions to ] and ]s. The ] provides a powerful and flexible ] for defining and combining functions of several variables. | |||
| == Function space == | |||
| ===Computability=== | |||
| {{Main|Function space|Functional analysis}} | |||
| {{main|computable function}} | |||
| In ], and more specifically in ], a '''function space''' is a set of ] or ]s, which share a specific property and form a ]. For example, the real ]s with a ] (that is, they are zero outside some ]) form a function space that is at the basis of the theory of ]. | |||
| Functions that send integers to integers, or finite strings to finite strings, can sometimes be defined by an ], which gives a precise description of a set of steps for computing the output of the function from its input. Functions definable by an algorithm are called ''']s'''. For example, the ] gives a precise process to compute the ] of two positive integers. Many of the functions studied in the context of ] are computable. | |||
| Function spaces play a fundamental role in advanced mathematical analysis, by allowing the use of their algebraic and ] properties for studying properties of functions. For example, all theorems of existence and uniqueness of solutions of ] or ]s result of the study of function spaces. | |||
| Fundamental results of ] show that there are functions that can be precisely defined but are not computable. Moreover, in the sense of ], almost all functions from the integers to integers are not computable. The number of computable functions from integers to integers is ], because the number of possible algorithms is. The number of all functions from integers to integers is higher: the same as the cardinality of the ]s. Thus most functions from integers to integers are not computable. Specific examples of uncomputable functions are known, including the ] and functions related to the ] and other ]. | |||
| == Multi-valued functions == | |||
| ===Functions with multiple inputs and outputs=== | |||
| {{main|Multi-valued function}} | |||
| The concept of function can be extended to an object that takes a combination of two (or more) argument values to a single result. This intuitive concept is formalized by a function whose domain is the ] of two or more sets. | |||
| ] | |||
| ] | |||
| Several methods for specifying functions of real or complex variables start from a local definition of the function at a point or on a ] of a point, and then extend by continuity the function to a much larger domain. Frequently, for a starting point <math>x_0,</math> there are several possible starting values for the function. | |||
| For example, in defining the ] as the inverse function of the square function, for any positive real number <math>x_0,</math> there are two choices for the value of the square root, one of which is positive and denoted <math>\sqrt {x_0},</math> and another which is negative and denoted <math>-\sqrt {x_0}.</math> These choices define two continuous functions, both having the nonnegative real numbers as a domain, and having either the nonnegative or the nonpositive real numbers as images. When looking at the graphs of these functions, one can see that, together, they form a single ]. It is therefore often useful to consider these two square root functions as a single function that has two values for positive {{mvar|x}}, one value for 0 and no value for negative {{mvar|x}}. | |||
| For example, consider the ] function that associates two ]s to their product: ƒ(''x'', ''y'') = ''x''·''y''. This function can be defined formally as having domain '''Z'''×'''Z''' , the set of all integer pairs; codomain '''Z'''; and, for graph, the set of all pairs ((''x'',''y''), ''x''·''y''). Note that the first component of any such pair is itself a pair (of integers), while the second component is a single integer. | |||
| In the preceding example, one choice, the positive square root, is more natural than the other. This is not the case in general. For example, let consider the ] that maps {{mvar|y}} to a ] {{mvar|x}} of <math>x^3-3x-y =0</math> (see the figure on the right). For {{math|1=''y'' = 0}} one may choose either <math>0, \sqrt 3,\text{ or } -\sqrt 3</math> for {{mvar|x}}. By the ], each choice defines a function; for the first one, the (maximal) domain is the interval {{closed-closed|−2, 2}} and the image is {{closed-closed|−1, 1}}; for the second one, the domain is {{closed-open|−2, ∞}} and the image is {{closed-open|1, ∞}}; for the last one, the domain is {{open-closed|−∞, 2}} and the image is {{open-closed|−∞, −1}}. As the three graphs together form a smooth curve, and there is no reason for preferring one choice, these three functions are often considered as a single ''multi-valued function'' of {{mvar|y}} that has three values for {{math|−2 < ''y'' < 2}}, and only one value for {{math|''y'' ≤ −2}} and {{math|''y'' ≥ −2}}. | |||
| The function value of the pair (''x'',''y'') is ƒ((''x'',''y'')). However, it is customary to drop one set of parentheses and consider ƒ(''x'',''y'') a '''function of two variables''' (or with two arguments), ''x'' and ''y''. | |||
| Usefulness of the concept of multi-valued functions is clearer when considering complex functions, typically ]s. The domain to which a complex function may be extended by ] generally consists of almost the whole ]. However, when extending the domain through two different paths, one often gets different values. For example, when extending the domain of the square root function, along a path of complex numbers with positive imaginary parts, one gets {{mvar|i}} for the square root of −1; while, when extending through complex numbers with negative imaginary parts, one gets {{math|−''i''}}. There are generally two ways of solving the problem. One may define a function that is not ] along some curve, called a ]. Such a function is called the ] of the function. The other way is to consider that one has a ''multi-valued function'', which is analytic everywhere except for isolated singularities, but whose value may "jump" if one follows a closed loop around a singularity. This jump is called the ]. | |||
| The concept can still further be extended by considering a function that also produces output that is expressed as several variables. For example consider the function mirror(''x'', ''y'') = (''y'', ''x'') with domain '''R'''×'''R''' and codomain '''R'''×'''R''' as well. The pair (''y'', ''x'') is a single value in the codomain seen as a cartesian product. | |||
| == In the foundations of mathematics == | |||
| There is an alternative approach: one could instead interpret a function of two variables as sending each element of A to a function from B to C, this is known as ]. The equivalence of these approaches is expressed by the ] between the function spaces <math>C^{A \times B}</math> and <math>(C^B)^A</math>. | |||
| The definition of a function that is given in this article requires the concept of ], since the domain and the codomain of a function must be a set. This is not a problem in usual mathematics, as it is generally not difficult to consider only functions whose domain and codomain are sets, which are well defined, even if the domain is not explicitly defined. However, it is sometimes useful to consider more general functions. | |||
| ====Binary operations==== | |||
| The familiar ]s of ], ] and ], can be viewed as functions from '''R'''×'''R''' to '''R'''. This view is generalized in ], where ''n''-ary functions are used to model the operations of arbitrary algebraic structures. For example, an abstract ] is defined as a set ''X'' and a function ƒ from ''X''×''X'' to ''X'' that satisfies certain properties. | |||
| For example, the ] may be considered as a function <math>x\mapsto \{x\}.</math> Its domain would include all sets, and therefore would not be a set. In usual mathematics, one avoids this kind of problem by specifying a domain, which means that one has many singleton functions. However, when establishing foundations of mathematics, one may have to use functions whose domain, codomain or both are not specified, and some authors, often logicians, give precise definitions for these weakly specified functions.<ref>{{harvnb |Gödel |1940 |p=16}}; {{harvnb |Jech |2003 |p=11}}; {{harvnb |Cunningham |2016 |p=57}}</ref> | |||
| Traditionally, addition and multiplication are written in the ] notation: ''x''+''y'' and ''x''×''y'' instead of +(''x'', ''y'') and ×(''x'', ''y''). | |||
| These generalized functions may be critical in the development of a formalization of the ]. For example, ], is an extension of the set theory in which the collection of all sets is a ]. This theory includes the ], which may be stated as: If {{mvar|X}} is a set and {{mvar|F}} is a function, then {{math|''F''}} is a set. | |||
| ==Function spaces== | |||
| The set of all functions from a set ''X'' to a set ''Y'' is denoted by ''X'' → ''Y'', by , or by ''Y''<sup>''X''</sup>. | |||
| In alternative formulations of the foundations of mathematics using ] rather than set theory, functions are taken as ]s rather than defined from other kinds of object. They are the inhabitants of ]s, and may be constructed using expressions in the ].<ref> | |||
| The latter notation is motivated by the fact that, when ''X'' and ''Y'' are finite, of ] |''X''| and |''Y''| respectively, then the number of functions ''X'' → ''Y'' is |''Y''<sup>''X''</sup>| = |''Y''|<sup>|''X''|</sup>. This is an example of ] that provides notations for sets based on their cardinalities. Other examples are the multiplication sign ''X''×''Y'' used for the ] where |''X''×''Y''| = |''X''|·|''Y''| , and the ] sign ''X''! used for the set of ]s where |''X''!| = |''X''|! , and the ] sign <math>\tbinom X n</math> used for the set of ''n''-element subsets where <math>|\tbinom X n | = \tbinom {|X|} n.</math> | |||
| {{cite book | |||
| | last = Klev | first = Ansten | |||
| | editor1-last = Centrone | editor1-first = Stefania | |||
| | editor2-last = Kant | editor2-first = Deborah | |||
| | editor3-last = Sarikaya | editor3-first = Deniz | |||
| | contribution = A comparison of type theory with set theory | |||
| | doi = 10.1007/978-3-030-15655-8_12 | |||
| | isbn = 978-3-030-15654-1 | |||
| | location = Cham | |||
| | mr = 4352345 | |||
| | pages = 271–292 | |||
| | publisher = Springer | |||
| | series = Synthese Library | |||
| | title = Reflections on the Foundations of Mathematics: Univalent Foundations, Set Theory and General Thoughts | |||
| | volume = 407 | |||
| | year = 2019}}</ref> | |||
| == In computer science == | |||
| We may interpret ƒ: ''X'' → ''Y'' to mean ƒ ∈ ; that is, "ƒ is a function from ''X'' to ''Y''". | |||
| {{main|Function (computer programming)|Lambda calculus}} | |||
| In ], a ] is, in general, a piece of a ], which ] the abstract concept of function. That is, it is a program unit that produces an output for each input. However, in many ]s every ] is called a function, even when there is no output, and when the functionality consists simply of modifying some data in the ]. | |||
| ] is the ] consisting of building programs by using only subroutines that behave like mathematical functions. For example, <code>if_then_else</code> is a function that takes three functions as arguments, and, depending on the result of the first function (''true'' or ''false''), returns the result of either the second or the third function. An important advantage of functional programming is that it makes easier ]s, as being based on a well founded theory, the ] (see below). | |||
| ==Pointwise operations== | |||
| If ƒ: ''X'' → ''R'' and ''g'': ''X'' → ''R'' are functions with common domain ''X'' and common codomain a ] ''R'', then one can define the sum function ƒ + ''g'': ''X'' → ''R'' and the product function ƒ ⋅ ''g'': ''X'' → ''R'' as follows: | |||
| :<math>\begin{align} | |||
| (f+g)(x) &= f(x)+g(x) , \\ | |||
| (f\cdot g)(x) &= f(x) \cdot g(x) , | |||
| \end{align}</math> | |||
| for all ''x'' in ''X''. | |||
| Except for computer-language terminology, "function" has the usual mathematical meaning in ]. In this area, a property of major interest is the ] of a function. For giving a precise meaning to this concept, and to the related concept of ], several ] have been introduced, the old ones being ]s, ] and ]. The fundamental theorem of ] is that these three models of computation define the same set of computable functions, and that all the other models of computation that have ever been proposed define the same set of computable functions or a smaller one. The ] is the claim that every philosophically acceptable definition of a ''computable function'' defines also the same functions. | |||
| This turns the set of all such functions into a ring. The binary operations in that ring have as domain ordered pairs of functions, and as codomain functions. This is an example of climbing up in abstraction, to functions of more complex types. | |||
| General recursive functions are ]s from integers to integers that can be defined from | |||
| By taking some other ] ''A'' in the place of ''R'', we can turn the set of all functions from ''X'' to ''A'' into an algebraic structure of the same type in an analogous way. | |||
| * ]s, | |||
| * ], and | |||
| * ] functions | |||
| via the operators | |||
| * ], | |||
| * ], and | |||
| * ]. | |||
| Although defined only for functions from integers to integers, they can model any computable function as a consequence of the following properties: | |||
| * a computation is the manipulation of finite sequences of symbols (digits of numbers, formulas, ...), | |||
| * every sequence of symbols may be coded as a sequence of ]s, | |||
| * a bit sequence can be interpreted as the ] of an integer. | |||
| ] is a theory that defines computable functions without using ], and is the theoretical background of functional programming. It consists of ''terms'' that are either variables, function definitions (''{{lambda}}''-terms), or applications of functions to terms. Terms are manipulated through some rules, (the {{math|''α''}}-equivalence, the {{mvar|β}}-reduction, and the {{mvar|η}}-conversion), which are the ]s of the theory and may be interpreted as rules of computation. | |||
| ==Other properties== | |||
| There are many other special classes of functions that are important to particular branches of mathematics, or particular applications. | |||
| Here is a partial list: | |||
| <div style="-moz-column-count:3; column-count:3;"> | |||
| *], or individually: | |||
| ** ], ], and ] | |||
| *] | |||
| *], ] | |||
| *], ], ] | |||
| *], ] | |||
| *] | |||
| *] | |||
| *] | |||
| *], ], ] | |||
| *], ], ] | |||
| *] | |||
| *] | |||
| </div> | |||
| In its original form, lambda calculus does not include the concepts of domain and codomain of a function. Roughly speaking, they have been introduced in the theory under the name of ''type'' in ]. Most kinds of typed lambda calculi can define fewer functions than untyped lambda calculus. | |||
| ==See also== | |||
| <div class="references-small" style="-moz-column-count:3; column-count:3;"> | |||
| *] | |||
| *] | |||
| *] | |||
| *] | |||
| *] | |||
| *] | |||
| *] | |||
| *] | |||
| *] | |||
| </div> | |||
| == |
== See also == | ||
| === |
=== Subpages === | ||
| {{div col|colwidth=22em}} | |||
| {{reflist}} | |||
| * ] | |||
| ===Sources=== | |||
| * ] | |||
| * {{citation |last=Anton |first=Howard |title=Calculus with Analytical Geometry |year=1980 |publisher=] |isbn=978-0-471-03248-9}} | |||
| * ] | |||
| * {{citation |last=Bartle |first=Robert G. |title=The Elements of Real Analysis |edition=2nd |year=1976 |publisher=] |isbn=978-0-471-05464-1}} | |||
| * ] | |||
| * {{citation |last=Hardy |first=Godfrey Harold |title=A Course of Pure Mathematics |year=1908 |publication-date=1993 |publisher=] |isbn=978-0-521-09227-2}} | |||
| * ] | |||
| * {{citation |last=Husch |first=Lawrence S. |title=Visual Calculus |year=2001 |publisher=] |url=http://archives.math.utk.edu/visual.calculus/ |accessdate=2007-09-27}} | |||
| {{div col end}} | |||
| * {{citation |last=da Ponte |first=João Pedro |title=The history of the concept of function and some educational implications |journal=The Mathematics Educator |year=1992 |volume=3 |number=2 |pages=3–8 |issn=1062-9017 |url=http://math.coe.uga.edu/TME/Issues/v03n2/v3n2.PonteAbs.html}} | |||
| * {{citation |last1=Thomas |first1=George B. |last2=Finney |first2=Ross L. |title=Calculus and Analytic Geometry |edition=9th |year=1995 |publisher=] |isbn=978-0-201-53174-9}} | |||
| *{{citation|title=The concept of function up to the middle of the 19th century|first=A. P.|last=Youschkevitch|journal=Archive for History of Exact Sciences|volume=16|issue=1|year=1976|pages=37–85|doi=10.1007/BF00348305}}. | |||
| *{{citation|title=The concept of function in the 19th and 20th centuries, in particular with regard to the discussions between Baire, Borel and Lebesgue|first=A. F.|last=Monna|journal=Archive for History of Exact Sciences|volume=9|issue=1|year=1972|pages=57–84|doi=10.1007/BF00348540}}. | |||
| *{{citation|title=Evolution of the Function Concept: A Brief Survey|first=Israel|last=Kleiner|journal=The College Mathematics Journal|volume=20|issue=4|year=1989|pages=282–300|doi=10.2307/2686848}}. | |||
| *{{citation|last=Ruthing|first=D.|title=Some definitions of the concept of function from Bernoulli, Joh. to Bourbaki, N.|journal=Mathematical Intelligencer|volume=6|issue=4|pages=72–77|year=1984}}. | |||
| *{{citation|title=The Concept of Function: Aspects of Epistemology and Pedagogy|publisher=Mathematical Association of America|year=1992|first1=Ed|last1=Dubinsky|first2=Guershon|last2=Harel|isbn=0883850818}}. | |||
| *{{citation|title=Historical and pedagogical aspects of the definition of function|last=Malik|first=M. A.|journal=International Journal of Mathematical Education in Science and Technology|volume=11|issue=4|year=1980|pages=489–492|doi=10.1080/0020739800110404}}. | |||
| == |
=== Generalizations === | ||
| {{div col|colwidth=22em}} | |||
| {{commonscat|Functions}} | |||
| * ] | |||
| * gives formulae and visualizations of many mathematical functions. | |||
| * ] | |||
| * , interactive Java applet for graphing and exploring functions. | |||
| * ] | |||
| * , a Java applet for exploring functions graphically. | |||
| * ] | |||
| * , online drawing program for mathematical functions. | |||
| * ] | |||
| * from ]. | |||
| * ] | |||
| * . | |||
| {{div col end}} | |||
| * | |||
| === Related topics === | |||
| ] | |||
| {{div col|colwidth=22em}} | |||
| ] | |||
| * ] | |||
| ] | |||
| * ]<!-- a function may or may not be defined by closed form --> | |||
| ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| {{div col end}} | |||
| == Notes == | |||
| {{reflist|group=note}} | |||
| == References == | |||
| {{reflist|refs= | |||
| <ref name="EOM Function">{{eom |title=Function |oldid=36823 |author-first=L.D. |author-last=Kudryavtsev|mode=cs1}}</ref> | |||
| }} | |||
| == Sources == | |||
| {{refbegin}} | |||
| * {{cite book |last=Bartle |first=Robert |author-link=Robert G. Bartle |title=The Elements of Real Analysis |publisher=Wiley |isbn=978-0-471-05465-8 |date=1976 |edition=2nd |oclc=465115030}} | |||
| * {{cite book |last=Bloch |first=Ethan D. |title=Proofs and Fundamentals: A First Course in Abstract Mathematics |publisher=Springer |year=2011|isbn=978-1-4419-7126-5 |url=https://books.google.com/books?id=QJ_537n8zKYC}} | |||
| * {{cite book |last=Cunningham |first=Daniel W. |title=Set theory: A First Course |publisher=Cambridge University Press |year=2016 |isbn=978-1-107-12032-7}} | |||
| * {{cite book |last=Gödel |first=Kurt | author-link=Kurt Gödel|title=The Consistency of the Continuum Hypothesis |publisher=Princeton University Press |year=1940 |isbn=978-0-691-07927-1}} | |||
| * {{cite book |last=Halmos |first=Paul R. |author-link=Paul Halmos |year=1970 |title=Naive Set Theory |publisher=Springer-Verlag |isbn=978-0-387-90092-6 |url=https://books.google.com/books?id=x6cZBQ9qtgoC}} | |||
| * {{cite book |last=Jech | first=Thomas| author-link=Thomas Jech| title=Set theory| edition=3rd |publisher=]| year=2003| isbn=978-3-540-44085-7}} | |||
| * {{cite book |title=Calculus |first=Michael |last=Spivak |author-link=Michael Spivak |edition=4th |year=2008 |publisher=Publish or Perish |isbn=978-0-914098-91-1 |url=https://books.google.com/books?id=7JKVu_9InRUC}} | |||
| {{refend}} | |||
| == Further reading == | |||
| {{refbegin}} | |||
| * {{cite book |last=Anton |first=Howard |title=Calculus with Analytical Geometry |url=https://archive.org/details/studentssolution00anto |url-access=registration |year=1980 |publisher=] |isbn=978-0-471-03248-9}} | |||
| * {{cite book |last=Bartle |first=Robert G. |title=The Elements of Real Analysis |edition=2nd |year=1976 |publisher=Wiley |isbn=978-0-471-05464-1}} | |||
| * {{Cite book |title=The Concept of Function: Aspects of Epistemology and Pedagogy|publisher=Mathematical Association of America |year=1992 |first1=Ed |last1=Dubinsky |first2=Guershon |last2=Harel |isbn=978-0-88385-081-7}} | |||
| * {{cite book |last=Hammack |first=Richard |title=Book of Proof |year=2009 |publisher=] |url=https://www.people.vcu.edu/~rhammack/BookOfProof/ |chapter=12. Functions |chapter-url=https://www.people.vcu.edu/~rhammack/BookOfProof/Main.pdf#page=235 |access-date=2012-08-01}} | |||
| * {{cite book |last=Husch |first=Lawrence S. |title=Visual Calculus |year=2001 |publisher=] |url=http://archives.math.utk.edu/visual.calculus/ |access-date=2007-09-27}} | |||
| * {{cite book |last=Katz |first=Robert |title=Axiomatic Analysis |year=1964 |publisher=]}} | |||
| * {{cite journal |title=Evolution of the Function Concept: A Brief Survey |first=Israel |last=Kleiner |journal=The College Mathematics Journal |volume=20 |issue=4 |year=1989 |pages=282–300 |doi=10.2307/2686848|jstor=2686848 |citeseerx=10.1.1.113.6352 }} | |||
| * {{cite book |title=The Cambridge History of Science: The modern physical and mathematical sciences |chapter=Between rigor and applications: Developments in the concept of function in mathematical analysis |first=Jesper |last=Lützen |chapter-url=https://books.google.com/books?id=B3WvWhJTTX8C&pg=PA468 |editor-first=Roy|editor-last=Porter |publisher=Cambridge University Press |year=2003 |isbn=978-0-521-57199-9}} An approachable and diverting historical presentation. | |||
| * {{cite journal |title=Historical and pedagogical aspects of the definition of function |last=Malik |first=M. A. |journal=International Journal of Mathematical Education in Science and Technology |volume=11 |issue=4 |year=1980 |pages=489–492 |doi=10.1080/0020739800110404}} | |||
| * {{cite book |last=Reichenbach |first=Hans |date=1947 |title=Elements of Symbolic Logic |publisher=Dover |isbn=0-486-24004-5}} | |||
| * {{cite journal |last=Ruthing |first=D. |title=Old Intelligencer: Some definitions of the concept of function from Bernoulli, Joh. to Bourbaki, N. |journal=Mathematical Intelligencer |volume=6 |issue=4 |pages=71–78 |year=1984 |doi=10.1007/BF03026743|s2cid=189883712 }} | |||
| * {{cite book |last1=Thomas |first1=George B. |last2=Finney |first2=Ross L. |title=Calculus and Analytic Geometry |url=https://archive.org/details/calculusanalytic00geor_0 |url-access=registration |edition=9th |year=1995 |publisher=] |isbn=978-0-201-53174-9}} | |||
| {{refend}} | |||
| == External links == | |||
| {{Commons category|Functions (mathematics)}} | |||
| * – website giving formulae and visualizations of many mathematical functions | |||
| * | |||
| {{ |
{{Analysis-footer}} | ||
| {{Authority control}} | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
Latest revision as of 23:28, 2 December 2024
Association of one output to each input "f(x)" redirects here. For the musical group, see f(x) (musical group).| Function |
|---|
| x ↦ f (x) |
| History of the function concept |
| Types by domain and codomain |
| Classes/properties |
| Constructions |
| Generalizations |
| List of specific functions |
In mathematics, a function from a set X to a set Y assigns to each element of X exactly one element of Y. The set X is called the domain of the function and the set Y is called the codomain of the function.
Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a function of time. Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of the 19th century in terms of set theory, and this greatly increased the possible applications of the concept.
A function is often denoted by a letter such as f, g or h. The value of a function f at an element x of its domain (that is, the element of the codomain that is associated with x) is denoted by f(x); for example, the value of f at x = 4 is denoted by f(4). Commonly, a specific function is defined by means of an expression depending on x, such as in this case, some computation, called function evaluation, may be needed for deducing the value of the function at a particular value; for example, if then
Given its domain and its codomain, a function is uniquely represented by the set of all pairs (x, f (x)), called the graph of the function, a popular means of illustrating the function. When the domain and the codomain are sets of real numbers, each such pair may be thought of as the Cartesian coordinates of a point in the plane.
Functions are widely used in science, engineering, and in most fields of mathematics. It has been said that functions are "the central objects of investigation" in most fields of mathematics.
The concept of a function has evolved significantly over centuries, from its informal origins in ancient mathematics to its formalization in the 19th century. See History of the function concept for details.
Definition

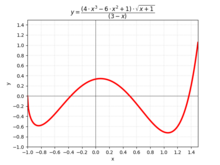
A function f from a set X to a set Y is an assignment of one element of Y to each element of X. The set X is called the domain of the function and the set Y is called the codomain of the function.
If the element y in Y is assigned to x in X by the function f, one says that f maps x to y, and this is commonly written In this notation, x is the argument or variable of the function. A specific element x of X is a value of the variable, and the corresponding element of Y is the value of the function at x, or the image of x under the function.
A function f, its domain X, and its codomain Y are often specified by the notation One may write instead of , where the symbol (read 'maps to') is used to specify where a particular element x in the domain is mapped to by f. This allows the definition of a function without naming. For example, the square function is the function
The domain and codomain are not always explicitly given when a function is defined. In particular, it is common that one might only know, without some (possibly difficult) computation, that the domain of a specific function is contained in a larger set. For example, if is a real function, the determination of the domain of the function requires knowing the zeros of f. This is one of the reasons for which, in mathematical analysis, "a function from X to Y " may refer to a function having a proper subset of X as a domain. For example, a "function from the reals to the reals" may refer to a real-valued function of a real variable whose domain is a proper subset of the real numbers, typically a subset that contains a non-empty open interval. Such a function is then called a partial function.
The range or image of a function is the set of the images of all elements in the domain.
A function f on a set S means a function from the domain S, without specifying a codomain. However, some authors use it as shorthand for saying that the function is f : S → S.
Formal definition
The above definition of a function is essentially that of the founders of calculus, Leibniz, Newton and Euler. However, it cannot be formalized, since there is no mathematical definition of an "assignment". It is only at the end of the 19th century that the first formal definition of a function could be provided, in terms of set theory. This set-theoretic definition is based on the fact that a function establishes a relation between the elements of the domain and some (possibly all) elements of the codomain. Mathematically, a binary relation between two sets X and Y is a subset of the set of all ordered pairs such that and The set of all these pairs is called the Cartesian product of X and Y and denoted Thus, the above definition may be formalized as follows.
A function with domain X and codomain Y is a binary relation R between X and Y that satisfies the two following conditions:
- For every in there exists in such that
- If and then
This definition may be rewritten more formally, without referring explicitly to the concept of a relation, but using more notation (including set-builder notation):
A function is formed by three sets, the domain the codomain and the graph that satisfy the three following conditions.
Partial functions
Main article: Partial functionPartial functions are defined similarly to ordinary functions, with the "total" condition removed. That is, a partial function from X to Y is a binary relation R between X and Y such that, for every there is at most one y in Y such that
Using functional notation, this means that, given either is in Y, or it is undefined.
The set of the elements of X such that is defined and belongs to Y is called the domain of definition of the function. A partial function from X to Y is thus a ordinary function that has as its domain a subset of X called the domain of definition of the function. If the domain of definition equals X, one often says that the partial function is a total function.
In several areas of mathematics the term "function" refers to partial functions rather than to ordinary functions. This is typically the case when functions may be specified in a way that makes difficult or even impossible to determine their domain.
In calculus, a real-valued function of a real variable or real function is a partial function from the set of the real numbers to itself. Given a real function its multiplicative inverse is also a real function. The determination of the domain of definition of a multiplicative inverse of a (partial) function amounts to compute the zeros of the function, the values where the function is defined but not its multiplicative inverse.
Similarly, a function of a complex variable is generally a partial function with a domain of definition included in the set of the complex numbers. The difficulty of determining the domain of definition of a complex function is illustrated by the multiplicative inverse of the Riemann zeta function: the determination of the domain of definition of the function is more or less equivalent to the proof or disproof of one of the major open problems in mathematics, the Riemann hypothesis.
In computability theory, a general recursive function is a partial function from the integers to the integers whose values can be computed by an algorithm (roughly speaking). The domain of definition of such a function is the set of inputs for which the algorithm does not run forever. A fundamental theorem of computability theory is that there cannot exist an algorithm that takes an arbitrary general recursive function as input and tests whether 0 belongs to its domain of definition (see Halting problem).
Multivariate functions
Not to be confused with Multivalued function.
A multivariate function, multivariable function, or function of several variables is a function that depends on several arguments. Such functions are commonly encountered. For example, the position of a car on a road is a function of the time travelled and its average speed.
Formally, a function of n variables is a function whose domain is a set of n-tuples. For example, multiplication of integers is a function of two variables, or bivariate function, whose domain is the set of all ordered pairs (2-tuples) of integers, and whose codomain is the set of integers. The same is true for every binary operation. Commonly, an n-tuple is denoted enclosed between parentheses, such as in When using functional notation, one usually omits the parentheses surrounding tuples, writing instead of
Given n sets the set of all n-tuples such that is called the Cartesian product of and denoted
Therefore, a multivariate function is a function that has a Cartesian product or a proper subset of a Cartesian product as a domain.
where the domain U has the form
If all the are equal to the set of the real numbers or to the set of the complex numbers, one talks respectively of a function of several real variables or of a function of several complex variables.
Notation
There are various standard ways for denoting functions. The most commonly used notation is functional notation, which is the first notation described below.
Functional notation
The functional notation requires that a name is given to the function, which, in the case of a unspecified function is often the letter f. Then, the application of the function to an argument is denoted by its name followed by its argument (or, in the case of a multivariate functions, its arguments) enclosed between parentheses, such as in
The argument between the parentheses may be a variable, often x, that represents an arbitrary element of the domain of the function, a specific element of the domain (3 in the above example), or an expression that can be evaluated to an element of the domain ( in the above example). The use of a unspecified variable between parentheses is useful for defining a function explicitly such as in "let ".
When the symbol denoting the function consists of several characters and no ambiguity may arise, the parentheses of functional notation might be omitted. For example, it is common to write sin x instead of sin(x).
Functional notation was first used by Leonhard Euler in 1734. Some widely used functions are represented by a symbol consisting of several letters (usually two or three, generally an abbreviation of their name). In this case, a roman type is customarily used instead, such as "sin" for the sine function, in contrast to italic font for single-letter symbols.
The functional notation is often used colloquially for referring to a function and simultaneously naming its argument, such as in "let be a function". This is an abuse of notation that is useful for a simpler formulation.
Arrow notation
Arrow notation defines the rule of a function inline, without requiring a name to be given to the function. It uses the ↦ arrow symbol, pronounced "maps to". For example, is the function which takes a real number as input and outputs that number plus 1. Again, a domain and codomain of is implied.
The domain and codomain can also be explicitly stated, for example:
This defines a function sqr from the integers to the integers that returns the square of its input.
As a common application of the arrow notation, suppose is a function in two variables, and we want to refer to a partially applied function produced by fixing the second argument to the value t0 without introducing a new function name. The map in question could be denoted using the arrow notation. The expression (read: "the map taking x to f of x comma t nought") represents this new function with just one argument, whereas the expression f(x0, t0) refers to the value of the function f at the point (x0, t0).
Index notation
Index notation may be used instead of functional notation. That is, instead of writing f (x), one writes
This is typically the case for functions whose domain is the set of the natural numbers. Such a function is called a sequence, and, in this case the element is called the nth element of the sequence.
The index notation can also be used for distinguishing some variables called parameters from the "true variables". In fact, parameters are specific variables that are considered as being fixed during the study of a problem. For example, the map (see above) would be denoted using index notation, if we define the collection of maps by the formula for all .
Dot notation
In the notation the symbol x does not represent any value; it is simply a placeholder, meaning that, if x is replaced by any value on the left of the arrow, it should be replaced by the same value on the right of the arrow. Therefore, x may be replaced by any symbol, often an interpunct " ⋅ ". This may be useful for distinguishing the function f (⋅) from its value f (x) at x.
For example, may stand for the function , and may stand for a function defined by an integral with variable upper bound: .
Specialized notations
There are other, specialized notations for functions in sub-disciplines of mathematics. For example, in linear algebra and functional analysis, linear forms and the vectors they act upon are denoted using a dual pair to show the underlying duality. This is similar to the use of bra–ket notation in quantum mechanics. In logic and the theory of computation, the function notation of lambda calculus is used to explicitly express the basic notions of function abstraction and application. In category theory and homological algebra, networks of functions are described in terms of how they and their compositions commute with each other using commutative diagrams that extend and generalize the arrow notation for functions described above.
Functions of more than one variable
In some cases the argument of a function may be an ordered pair of elements taken from some set or sets. For example, a function f can be defined as mapping any pair of real numbers to the sum of their squares, . Such a function is commonly written as and referred to as "a function of two variables". Likewise one can have a function of three or more variables, with notations such as , .
Other terms
For broader coverage of this topic, see Map (mathematics).| Term | Distinction from "function" |
|---|---|
| Map/Mapping | None; the terms are synonymous. |
| A map can have any set as its codomain, while, in some contexts, typically in older books, the codomain of a function is specifically the set of real or complex numbers. | |
| Alternatively, a map is associated with a special structure (e.g. by explicitly specifying a structured codomain in its definition). For example, a linear map. | |
| Homomorphism | A function between two structures of the same type that preserves the operations of the structure (e.g. a group homomorphism). |
| Morphism | A generalisation of homomorphisms to any category, even when the objects of the category are not sets (for example, a group defines a category with only one object, which has the elements of the group as morphisms; see Category (mathematics) § Examples for this example and other similar ones). |
A function may also be called a map or a mapping, but some authors make a distinction between the term "map" and "function". For example, the term "map" is often reserved for a "function" with some sort of special structure (e.g. maps of manifolds). In particular map may be used in place of homomorphism for the sake of succinctness (e.g., linear map or map from G to H instead of group homomorphism from G to H). Some authors reserve the word mapping for the case where the structure of the codomain belongs explicitly to the definition of the function.
Some authors, such as Serge Lang, use "function" only to refer to maps for which the codomain is a subset of the real or complex numbers, and use the term mapping for more general functions.
In the theory of dynamical systems, a map denotes an evolution function used to create discrete dynamical systems. See also Poincaré map.
Whichever definition of map is used, related terms like domain, codomain, injective, continuous have the same meaning as for a function.
Specifying a function
Given a function , by definition, to each element of the domain of the function , there is a unique element associated to it, the value of at . There are several ways to specify or describe how is related to , both explicitly and implicitly. Sometimes, a theorem or an axiom asserts the existence of a function having some properties, without describing it more precisely. Often, the specification or description is referred to as the definition of the function .
By listing function values
On a finite set a function may be defined by listing the elements of the codomain that are associated to the elements of the domain. For example, if , then one can define a function by
By a formula
Functions are often defined by an expression that describes a combination of arithmetic operations and previously defined functions; such a formula allows computing the value of the function from the value of any element of the domain. For example, in the above example, can be defined by the formula , for .
When a function is defined this way, the determination of its domain is sometimes difficult. If the formula that defines the function contains divisions, the values of the variable for which a denominator is zero must be excluded from the domain; thus, for a complicated function, the determination of the domain passes through the computation of the zeros of auxiliary functions. Similarly, if square roots occur in the definition of a function from to the domain is included in the set of the values of the variable for which the arguments of the square roots are nonnegative.
For example, defines a function whose domain is because is always positive if x is a real number. On the other hand, defines a function from the reals to the reals whose domain is reduced to the interval [−1, 1]. (In old texts, such a domain was called the domain of definition of the function.)
Functions can be classified by the nature of formulas that define them:
- A quadratic function is a function that may be written where a, b, c are constants.
- More generally, a polynomial function is a function that can be defined by a formula involving only additions, subtractions, multiplications, and exponentiation to nonnegative integer powers. For example, and are polynomial functions of .
- A rational function is the same, with divisions also allowed, such as and
- An algebraic function is the same, with nth roots and roots of polynomials also allowed.
- An elementary function is the same, with logarithms and exponential functions allowed.
Inverse and implicit functions
A function with domain X and codomain Y, is bijective, if for every y in Y, there is one and only one element x in X such that y = f(x). In this case, the inverse function of f is the function that maps to the element such that y = f(x). For example, the natural logarithm is a bijective function from the positive real numbers to the real numbers. It thus has an inverse, called the exponential function, that maps the real numbers onto the positive numbers.
If a function is not bijective, it may occur that one can select subsets and such that the restriction of f to E is a bijection from E to F, and has thus an inverse. The inverse trigonometric functions are defined this way. For example, the cosine function induces, by restriction, a bijection from the interval [0, π] onto the interval [−1, 1], and its inverse function, called arccosine, maps [−1, 1] onto [0, π]. The other inverse trigonometric functions are defined similarly.
More generally, given a binary relation R between two sets X and Y, let E be a subset of X such that, for every there is some such that x R y. If one has a criterion allowing selecting such a y for every this defines a function called an implicit function, because it is implicitly defined by the relation R.
For example, the equation of the unit circle defines a relation on real numbers. If −1 < x < 1 there are two possible values of y, one positive and one negative. For x = ± 1, these two values become both equal to 0. Otherwise, there is no possible value of y. This means that the equation defines two implicit functions with domain [−1, 1] and respective codomains [0, +∞) and (−∞, 0].
In this example, the equation can be solved in y, giving but, in more complicated examples, this is impossible. For example, the relation defines y as an implicit function of x, called the Bring radical, which has as domain and range. The Bring radical cannot be expressed in terms of the four arithmetic operations and nth roots.
The implicit function theorem provides mild differentiability conditions for existence and uniqueness of an implicit function in the neighborhood of a point.
Using differential calculus
Many functions can be defined as the antiderivative of another function. This is the case of the natural logarithm, which is the antiderivative of 1/x that is 0 for x = 1. Another common example is the error function.
More generally, many functions, including most special functions, can be defined as solutions of differential equations. The simplest example is probably the exponential function, which can be defined as the unique function that is equal to its derivative and takes the value 1 for x = 0.
Power series can be used to define functions on the domain in which they converge. For example, the exponential function is given by . However, as the coefficients of a series are quite arbitrary, a function that is the sum of a convergent series is generally defined otherwise, and the sequence of the coefficients is the result of some computation based on another definition. Then, the power series can be used to enlarge the domain of the function. Typically, if a function for a real variable is the sum of its Taylor series in some interval, this power series allows immediately enlarging the domain to a subset of the complex numbers, the disc of convergence of the series. Then analytic continuation allows enlarging further the domain for including almost the whole complex plane. This process is the method that is generally used for defining the logarithm, the exponential and the trigonometric functions of a complex number.
By recurrence
Main article: Recurrence relationFunctions whose domain are the nonnegative integers, known as sequences, are sometimes defined by recurrence relations.
The factorial function on the nonnegative integers () is a basic example, as it can be defined by the recurrence relation
and the initial condition
Representing a function
A graph is commonly used to give an intuitive picture of a function. As an example of how a graph helps to understand a function, it is easy to see from its graph whether a function is increasing or decreasing. Some functions may also be represented by bar charts.
Graphs and plots
Main article: Graph of a function
Given a function its graph is, formally, the set
In the frequent case where X and Y are subsets of the real numbers (or may be identified with such subsets, e.g. intervals), an element may be identified with a point having coordinates x, y in a 2-dimensional coordinate system, e.g. the Cartesian plane. Parts of this may create a plot that represents (parts of) the function. The use of plots is so ubiquitous that they too are called the graph of the function. Graphic representations of functions are also possible in other coordinate systems. For example, the graph of the square function
consisting of all points with coordinates for yields, when depicted in Cartesian coordinates, the well known parabola. If the same quadratic function with the same formal graph, consisting of pairs of numbers, is plotted instead in polar coordinates the plot obtained is Fermat's spiral.
Tables
Main article: Mathematical tableA function can be represented as a table of values. If the domain of a function is finite, then the function can be completely specified in this way. For example, the multiplication function defined as can be represented by the familiar multiplication table
| yx | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 |
| 2 | 2 | 4 | 6 | 8 | 10 |
| 3 | 3 | 6 | 9 | 12 | 15 |
| 4 | 4 | 8 | 12 | 16 | 20 |
| 5 | 5 | 10 | 15 | 20 | 25 |
On the other hand, if a function's domain is continuous, a table can give the values of the function at specific values of the domain. If an intermediate value is needed, interpolation can be used to estimate the value of the function. For example, a portion of a table for the sine function might be given as follows, with values rounded to 6 decimal places:
| x | sin x |
|---|---|
| 1.289 | 0.960557 |
| 1.290 | 0.960835 |
| 1.291 | 0.961112 |
| 1.292 | 0.961387 |
| 1.293 | 0.961662 |
Before the advent of handheld calculators and personal computers, such tables were often compiled and published for functions such as logarithms and trigonometric functions.
Bar chart
Main article: Bar chartA bar chart can represent a function whose domain is a finite set, the natural numbers, or the integers. In this case, an element x of the domain is represented by an interval of the x-axis, and the corresponding value of the function, f(x), is represented by a rectangle whose base is the interval corresponding to x and whose height is f(x) (possibly negative, in which case the bar extends below the x-axis).
General properties
This section describes general properties of functions, that are independent of specific properties of the domain and the codomain.
Standard functions
There are a number of standard functions that occur frequently:
- For every set X, there is a unique function, called the empty function, or empty map, from the empty set to X. The graph of an empty function is the empty set. The existence of empty functions is needed both for the coherency of the theory and for avoiding exceptions concerning the empty set in many statements. Under the usual set-theoretic definition of a function as an ordered triplet (or equivalent ones), there is exactly one empty function for each set, thus the empty function is not equal to if and only if , although their graphs are both the empty set.
- For every set X and every singleton set {s}, there is a unique function from X to {s}, which maps every element of X to s. This is a surjection (see below) unless X is the empty set.
- Given a function the canonical surjection of f onto its image is the function from X to f(X) that maps x to f(x).
- For every subset A of a set X, the inclusion map of A into X is the injective (see below) function that maps every element of A to itself.
- The identity function on a set X, often denoted by idX, is the inclusion of X into itself.
Function composition
Main article: Function compositionGiven two functions and such that the domain of g is the codomain of f, their composition is the function defined by
That is, the value of is obtained by first applying f to x to obtain y = f(x) and then applying g to the result y to obtain g(y) = g(f(x)). In this notation, the function that is applied first is always written on the right.
The composition is an operation on functions that is defined only if the codomain of the first function is the domain of the second one. Even when both and satisfy these conditions, the composition is not necessarily commutative, that is, the functions and need not be equal, but may deliver different values for the same argument. For example, let f(x) = x and g(x) = x + 1, then and agree just for
The function composition is associative in the sense that, if one of and is defined, then the other is also defined, and they are equal, that is, Therefore, it is usual to just write
The identity functions and are respectively a right identity and a left identity for functions from X to Y. That is, if f is a function with domain X, and codomain Y, one has
-
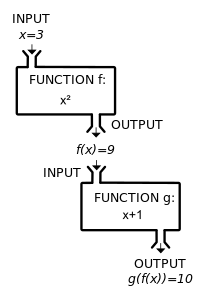 A composite function g(f(x)) can be visualized as the combination of two "machines".
A composite function g(f(x)) can be visualized as the combination of two "machines".
-
 A simple example of a function composition
A simple example of a function composition
-
 Another composition. In this example, (g ∘ f )(c) = #.
Another composition. In this example, (g ∘ f )(c) = #.
Image and preimage
Main article: Image (mathematics)Let The image under f of an element x of the domain X is f(x). If A is any subset of X, then the image of A under f, denoted f(A), is the subset of the codomain Y consisting of all images of elements of A, that is,
The image of f is the image of the whole domain, that is, f(X). It is also called the range of f, although the term range may also refer to the codomain.
On the other hand, the inverse image or preimage under f of an element y of the codomain Y is the set of all elements of the domain X whose images under f equal y. In symbols, the preimage of y is denoted by and is given by the equation
Likewise, the preimage of a subset B of the codomain Y is the set of the preimages of the elements of B, that is, it is the subset of the domain X consisting of all elements of X whose images belong to B. It is denoted by and is given by the equation
For example, the preimage of under the square function is the set .
By definition of a function, the image of an element x of the domain is always a single element of the codomain. However, the preimage of an element y of the codomain may be empty or contain any number of elements. For example, if f is the function from the integers to themselves that maps every integer to 0, then .
If is a function, A and B are subsets of X, and C and D are subsets of Y, then one has the following properties:
The preimage by f of an element y of the codomain is sometimes called, in some contexts, the fiber of y under f.
If a function f has an inverse (see below), this inverse is denoted In this case may denote either the image by or the preimage by f of C. This is not a problem, as these sets are equal. The notation and may be ambiguous in the case of sets that contain some subsets as elements, such as In this case, some care may be needed, for example, by using square brackets for images and preimages of subsets and ordinary parentheses for images and preimages of elements.
Injective, surjective and bijective functions
Main article: Bijection, injection and surjectionLet be a function.
The function f is injective (or one-to-one, or is an injection) if f(a) ≠ f(b) for every two different elements a and b of X. Equivalently, f is injective if and only if, for every the preimage contains at most one element. An empty function is always injective. If X is not the empty set, then f is injective if and only if there exists a function such that that is, if f has a left inverse. Proof: If f is injective, for defining g, one chooses an element in X (which exists as X is supposed to be nonempty), and one defines g by if and if Conversely, if and then and thus
The function f is surjective (or onto, or is a surjection) if its range equals its codomain , that is, if, for each element of the codomain, there exists some element of the domain such that (in other words, the preimage of every is nonempty). If, as usual in modern mathematics, the axiom of choice is assumed, then f is surjective if and only if there exists a function such that that is, if f has a right inverse. The axiom of choice is needed, because, if f is surjective, one defines g by where is an arbitrarily chosen element of
The function f is bijective (or is a bijection or a one-to-one correspondence) if it is both injective and surjective. That is, f is bijective if, for every the preimage contains exactly one element. The function f is bijective if and only if it admits an inverse function, that is, a function such that and (Contrarily to the case of surjections, this does not require the axiom of choice; the proof is straightforward).
Every function may be factorized as the composition of a surjection followed by an injection, where s is the canonical surjection of X onto f(X) and i is the canonical injection of f(X) into Y. This is the canonical factorization of f.
"One-to-one" and "onto" are terms that were more common in the older English language literature; "injective", "surjective", and "bijective" were originally coined as French words in the second quarter of the 20th century by the Bourbaki group and imported into English. As a word of caution, "a one-to-one function" is one that is injective, while a "one-to-one correspondence" refers to a bijective function. Also, the statement "f maps X onto Y" differs from "f maps X into B", in that the former implies that f is surjective, while the latter makes no assertion about the nature of f. In a complicated reasoning, the one letter difference can easily be missed. Due to the confusing nature of this older terminology, these terms have declined in popularity relative to the Bourbakian terms, which have also the advantage of being more symmetrical.
Restriction and extension
Main article: Restriction (mathematics)If is a function and S is a subset of X, then the restriction of to S, denoted , is the function from S to Y defined by
for all x in S. Restrictions can be used to define partial inverse functions: if there is a subset S of the domain of a function such that is injective, then the canonical surjection of onto its image is a bijection, and thus has an inverse function from to S. One application is the definition of inverse trigonometric functions. For example, the cosine function is injective when restricted to the interval [0, π]. The image of this restriction is the interval [−1, 1], and thus the restriction has an inverse function from [−1, 1] to [0, π], which is called arccosine and is denoted arccos.
Function restriction may also be used for "gluing" functions together. Let be the decomposition of X as a union of subsets, and suppose that a function is defined on each such that for each pair of indices, the restrictions of and to are equal. Then this defines a unique function such that for all i. This is the way that functions on manifolds are defined.
An extension of a function f is a function g such that f is a restriction of g. A typical use of this concept is the process of analytic continuation, that allows extending functions whose domain is a small part of the complex plane to functions whose domain is almost the whole complex plane.
Here is another classical example of a function extension that is encountered when studying homographies of the real line. A homography is a function such that ad − bc ≠ 0. Its domain is the set of all real numbers different from and its image is the set of all real numbers different from If one extends the real line to the projectively extended real line by including ∞, one may extend h to a bijection from the extended real line to itself by setting and .
In calculus
Further information: History of the function conceptThe idea of function, starting in the 17th century, was fundamental to the new infinitesimal calculus. At that time, only real-valued functions of a real variable were considered, and all functions were assumed to be smooth. But the definition was soon extended to functions of several variables and to functions of a complex variable. In the second half of the 19th century, the mathematically rigorous definition of a function was introduced, and functions with arbitrary domains and codomains were defined.
Functions are now used throughout all areas of mathematics. In introductory calculus, when the word function is used without qualification, it means a real-valued function of a single real variable. The more general definition of a function is usually introduced to second or third year college students with STEM majors, and in their senior year they are introduced to calculus in a larger, more rigorous setting in courses such as real analysis and complex analysis.
Real function
See also: Real analysis

A real function is a real-valued function of a real variable, that is, a function whose codomain is the field of real numbers and whose domain is a set of real numbers that contains an interval. In this section, these functions are simply called functions.
The functions that are most commonly considered in mathematics and its applications have some regularity, that is they are continuous, differentiable, and even analytic. This regularity insures that these functions can be visualized by their graphs. In this section, all functions are differentiable in some interval.
Functions enjoy pointwise operations, that is, if f and g are functions, their sum, difference and product are functions defined by
The domains of the resulting functions are the intersection of the domains of f and g. The quotient of two functions is defined similarly by
but the domain of the resulting function is obtained by removing the zeros of g from the intersection of the domains of f and g.
The polynomial functions are defined by polynomials, and their domain is the whole set of real numbers. They include constant functions, linear functions and quadratic functions. Rational functions are quotients of two polynomial functions, and their domain is the real numbers with a finite number of them removed to avoid division by zero. The simplest rational function is the function whose graph is a hyperbola, and whose domain is the whole real line except for 0.
The derivative of a real differentiable function is a real function. An antiderivative of a continuous real function is a real function that has the original function as a derivative. For example, the function is continuous, and even differentiable, on the positive real numbers. Thus one antiderivative, which takes the value zero for x = 1, is a differentiable function called the natural logarithm.
A real function f is monotonic in an interval if the sign of does not depend of the choice of x and y in the interval. If the function is differentiable in the interval, it is monotonic if the sign of the derivative is constant in the interval. If a real function f is monotonic in an interval I, it has an inverse function, which is a real function with domain f(I) and image I. This is how inverse trigonometric functions are defined in terms of trigonometric functions, where the trigonometric functions are monotonic. Another example: the natural logarithm is monotonic on the positive real numbers, and its image is the whole real line; therefore it has an inverse function that is a bijection between the real numbers and the positive real numbers. This inverse is the exponential function.
Many other real functions are defined either by the implicit function theorem (the inverse function is a particular instance) or as solutions of differential equations. For example, the sine and the cosine functions are the solutions of the linear differential equation
such that
Vector-valued function
Main articles: Vector-valued function and Vector fieldWhen the elements of the codomain of a function are vectors, the function is said to be a vector-valued function. These functions are particularly useful in applications, for example modeling physical properties. For example, the function that associates to each point of a fluid its velocity vector is a vector-valued function.
Some vector-valued functions are defined on a subset of or other spaces that share geometric or topological properties of , such as manifolds. These vector-valued functions are given the name vector fields.
Function space
Main articles: Function space and Functional analysisIn mathematical analysis, and more specifically in functional analysis, a function space is a set of scalar-valued or vector-valued functions, which share a specific property and form a topological vector space. For example, the real smooth functions with a compact support (that is, they are zero outside some compact set) form a function space that is at the basis of the theory of distributions.
Function spaces play a fundamental role in advanced mathematical analysis, by allowing the use of their algebraic and topological properties for studying properties of functions. For example, all theorems of existence and uniqueness of solutions of ordinary or partial differential equations result of the study of function spaces.
Multi-valued functions
Main article: Multi-valued function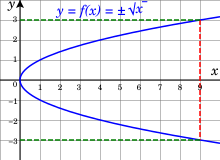

Several methods for specifying functions of real or complex variables start from a local definition of the function at a point or on a neighbourhood of a point, and then extend by continuity the function to a much larger domain. Frequently, for a starting point there are several possible starting values for the function.
For example, in defining the square root as the inverse function of the square function, for any positive real number there are two choices for the value of the square root, one of which is positive and denoted and another which is negative and denoted These choices define two continuous functions, both having the nonnegative real numbers as a domain, and having either the nonnegative or the nonpositive real numbers as images. When looking at the graphs of these functions, one can see that, together, they form a single smooth curve. It is therefore often useful to consider these two square root functions as a single function that has two values for positive x, one value for 0 and no value for negative x.
In the preceding example, one choice, the positive square root, is more natural than the other. This is not the case in general. For example, let consider the implicit function that maps y to a root x of (see the figure on the right). For y = 0 one may choose either for x. By the implicit function theorem, each choice defines a function; for the first one, the (maximal) domain is the interval [−2, 2] and the image is [−1, 1]; for the second one, the domain is [−2, ∞) and the image is [1, ∞); for the last one, the domain is (−∞, 2] and the image is (−∞, −1]. As the three graphs together form a smooth curve, and there is no reason for preferring one choice, these three functions are often considered as a single multi-valued function of y that has three values for −2 < y < 2, and only one value for y ≤ −2 and y ≥ −2.
Usefulness of the concept of multi-valued functions is clearer when considering complex functions, typically analytic functions. The domain to which a complex function may be extended by analytic continuation generally consists of almost the whole complex plane. However, when extending the domain through two different paths, one often gets different values. For example, when extending the domain of the square root function, along a path of complex numbers with positive imaginary parts, one gets i for the square root of −1; while, when extending through complex numbers with negative imaginary parts, one gets −i. There are generally two ways of solving the problem. One may define a function that is not continuous along some curve, called a branch cut. Such a function is called the principal value of the function. The other way is to consider that one has a multi-valued function, which is analytic everywhere except for isolated singularities, but whose value may "jump" if one follows a closed loop around a singularity. This jump is called the monodromy.
In the foundations of mathematics
The definition of a function that is given in this article requires the concept of set, since the domain and the codomain of a function must be a set. This is not a problem in usual mathematics, as it is generally not difficult to consider only functions whose domain and codomain are sets, which are well defined, even if the domain is not explicitly defined. However, it is sometimes useful to consider more general functions.
For example, the singleton set may be considered as a function Its domain would include all sets, and therefore would not be a set. In usual mathematics, one avoids this kind of problem by specifying a domain, which means that one has many singleton functions. However, when establishing foundations of mathematics, one may have to use functions whose domain, codomain or both are not specified, and some authors, often logicians, give precise definitions for these weakly specified functions.
These generalized functions may be critical in the development of a formalization of the foundations of mathematics. For example, Von Neumann–Bernays–Gödel set theory, is an extension of the set theory in which the collection of all sets is a class. This theory includes the replacement axiom, which may be stated as: If X is a set and F is a function, then F is a set.
In alternative formulations of the foundations of mathematics using type theory rather than set theory, functions are taken as primitive notions rather than defined from other kinds of object. They are the inhabitants of function types, and may be constructed using expressions in the lambda calculus.
In computer science
Main articles: Function (computer programming) and Lambda calculusIn computer programming, a function is, in general, a piece of a computer program, which implements the abstract concept of function. That is, it is a program unit that produces an output for each input. However, in many programming languages every subroutine is called a function, even when there is no output, and when the functionality consists simply of modifying some data in the computer memory.
Functional programming is the programming paradigm consisting of building programs by using only subroutines that behave like mathematical functions. For example, if_then_else is a function that takes three functions as arguments, and, depending on the result of the first function (true or false), returns the result of either the second or the third function. An important advantage of functional programming is that it makes easier program proofs, as being based on a well founded theory, the lambda calculus (see below).
Except for computer-language terminology, "function" has the usual mathematical meaning in computer science. In this area, a property of major interest is the computability of a function. For giving a precise meaning to this concept, and to the related concept of algorithm, several models of computation have been introduced, the old ones being general recursive functions, lambda calculus and Turing machine. The fundamental theorem of computability theory is that these three models of computation define the same set of computable functions, and that all the other models of computation that have ever been proposed define the same set of computable functions or a smaller one. The Church–Turing thesis is the claim that every philosophically acceptable definition of a computable function defines also the same functions.
General recursive functions are partial functions from integers to integers that can be defined from
- constant functions,
- successor, and
- projection functions
via the operators
Although defined only for functions from integers to integers, they can model any computable function as a consequence of the following properties:
- a computation is the manipulation of finite sequences of symbols (digits of numbers, formulas, ...),
- every sequence of symbols may be coded as a sequence of bits,
- a bit sequence can be interpreted as the binary representation of an integer.
Lambda calculus is a theory that defines computable functions without using set theory, and is the theoretical background of functional programming. It consists of terms that are either variables, function definitions (𝜆-terms), or applications of functions to terms. Terms are manipulated through some rules, (the α-equivalence, the β-reduction, and the η-conversion), which are the axioms of the theory and may be interpreted as rules of computation.
In its original form, lambda calculus does not include the concepts of domain and codomain of a function. Roughly speaking, they have been introduced in the theory under the name of type in typed lambda calculus. Most kinds of typed lambda calculi can define fewer functions than untyped lambda calculus.
See also
Subpages
- History of the function concept
- List of types of functions
- List of functions
- Function fitting
- Implicit function
Generalizations
Related topics
- Associative array
- Closed-form expression
- Elementary function
- Functional
- Functional decomposition
- Functional predicate
- Functional programming
- Parametric equation
- Set function
- Simple function
Notes
- This definition of "graph" refers to a set of pairs of objects. Graphs, in the sense of diagrams, are most applicable to functions from the real numbers to themselves. All functions can be described by sets of pairs but it may not be practical to construct a diagram for functions between other sets (such as sets of matrices).
- The true domain of such a function is often called the domain of definition of the function.
- n may also be 1, thus subsuming functions as defined above. For n = 0, each constant is a special case of a multivariate function, too.
- Here "elementary" has not exactly its common sense: although most functions that are encountered in elementary courses of mathematics are elementary in this sense, some elementary functions are not elementary for the common sense, for example, those that involve roots of polynomials of high degree.
- By definition, the graph of the empty function to X is a subset of the Cartesian product ∅ × X, and this product is empty.
- The axiom of choice is not needed here, as the choice is done in a single set.
References
- Halmos 1970, p. 30; the words map, mapping, transformation, correspondence, and operator are sometimes used synonymously.
- Halmos 1970
- "Mapping". Encyclopedia of Mathematics. EMS Press. 2001 .
- "function | Definition, Types, Examples, & Facts". Encyclopedia Britannica. Retrieved 2020-08-17.
- Spivak 2008, p. 39.
- ^ Kudryavtsev, L.D. (2001) . "Function". Encyclopedia of Mathematics. EMS Press.
- ^ Taalman, Laura; Kohn, Peter (2014). Calculus. New York City: W. H. Freeman and Company. p. 3. ISBN 978-1-4292-4186-1. LCCN 2012947365. OCLC 856545590. OL 27544563M.
- ^ Trench, William F. (2013) . Introduction to Real Analysis (2.04th ed.). Pearson Education (originally; self-republished by the author). pp. 30–32. ISBN 0-13-045786-8. LCCN 2002032369. OCLC 953799815. Zbl 1204.00023.
- ^ Thomson, Brian S.; Bruckner, Judith B.; Bruckner, Andrew M. (2008) . Elementary Real Analysis (PDF) (2nd ed.). Prentice Hall (originally; 2nd ed. self-republished by the authors). pp. A-4 – A-5. ISBN 978-1-4348-4367-8. OCLC 1105855173. OL 31844948M. Zbl 0872.26001.
- Halmos, Paul R. (1974). Naive Set Theory. Springer. pp. 30–33.
- Larson, Ron; Edwards, Bruce H. (2010). Calculus of a Single Variable. Cengage Learning. p. 19. ISBN 978-0-538-73552-0.
- Weisstein, Eric W. "Map". mathworld.wolfram.com. Retrieved 2019-06-12.
- ^ Lang, Serge (1987). "III §1. Mappings". Linear Algebra (3rd ed.). Springer. p. 43. ISBN 978-0-387-96412-6.
A function is a special type of mapping, namely it is a mapping from a set into the set of numbers, i.e. into, R, or C or into a field K.
- ^ Apostol, T.M. (1981). Mathematical Analysis (2nd ed.). Addison-Wesley. p. 35. ISBN 978-0-201-00288-1. OCLC 928947543.
- James, Robert C.; James, Glenn (1992). Mathematics dictionary (5th ed.). Van Nostrand Reinhold. p. 202. ISBN 0-442-00741-8. OCLC 25409557.
- James & James 1992, p. 48
- ^ Gowers, Timothy; Barrow-Green, June; Leader, Imre, eds. (2008). The Princeton Companion to Mathematics. Princeton, New Jersey: Princeton University Press. p. 11. doi:10.1515/9781400830398. ISBN 978-0-691-11880-2. JSTOR j.ctt7sd01. LCCN 2008020450. MR 2467561. OCLC 227205932. OL 19327100M. Zbl 1242.00016.
- Quantities and Units - Part 2: Mathematical signs and symbols to be used in the natural sciences and technology, p. 15. ISO 80000-2 (ISO/IEC 2009-12-01)
- ^ Ivanova, O.A. (2001) . "Injection". Encyclopedia of Mathematics. EMS Press.
- ^ Ivanova, O.A. (2001) . "Surjection". Encyclopedia of Mathematics. EMS Press.
- ^ Ivanova, O.A. (2001) . "Bijection". Encyclopedia of Mathematics. EMS Press.
- Hartnett, Kevin (9 November 2020). "Inside the Secret Math Society Known Simply as Nicolas Bourbaki". Quanta Magazine. Retrieved 2024-06-05.
- Gödel 1940, p. 16; Jech 2003, p. 11; Cunningham 2016, p. 57
- Klev, Ansten (2019). "A comparison of type theory with set theory". In Centrone, Stefania; Kant, Deborah; Sarikaya, Deniz (eds.). Reflections on the Foundations of Mathematics: Univalent Foundations, Set Theory and General Thoughts. Synthese Library. Vol. 407. Cham: Springer. pp. 271–292. doi:10.1007/978-3-030-15655-8_12. ISBN 978-3-030-15654-1. MR 4352345.
Sources
- Bartle, Robert (1976). The Elements of Real Analysis (2nd ed.). Wiley. ISBN 978-0-471-05465-8. OCLC 465115030.
- Bloch, Ethan D. (2011). Proofs and Fundamentals: A First Course in Abstract Mathematics. Springer. ISBN 978-1-4419-7126-5.
- Cunningham, Daniel W. (2016). Set theory: A First Course. Cambridge University Press. ISBN 978-1-107-12032-7.
- Gödel, Kurt (1940). The Consistency of the Continuum Hypothesis. Princeton University Press. ISBN 978-0-691-07927-1.
- Halmos, Paul R. (1970). Naive Set Theory. Springer-Verlag. ISBN 978-0-387-90092-6.
- Jech, Thomas (2003). Set theory (3rd ed.). Springer-Verlag. ISBN 978-3-540-44085-7.
- Spivak, Michael (2008). Calculus (4th ed.). Publish or Perish. ISBN 978-0-914098-91-1.
Further reading
- Anton, Howard (1980). Calculus with Analytical Geometry. Wiley. ISBN 978-0-471-03248-9.
- Bartle, Robert G. (1976). The Elements of Real Analysis (2nd ed.). Wiley. ISBN 978-0-471-05464-1.
- Dubinsky, Ed; Harel, Guershon (1992). The Concept of Function: Aspects of Epistemology and Pedagogy. Mathematical Association of America. ISBN 978-0-88385-081-7.
- Hammack, Richard (2009). "12. Functions" (PDF). Book of Proof. Virginia Commonwealth University. Retrieved 2012-08-01.
- Husch, Lawrence S. (2001). Visual Calculus. University of Tennessee. Retrieved 2007-09-27.
- Katz, Robert (1964). Axiomatic Analysis. D. C. Heath and Company.
- Kleiner, Israel (1989). "Evolution of the Function Concept: A Brief Survey". The College Mathematics Journal. 20 (4): 282–300. CiteSeerX 10.1.1.113.6352. doi:10.2307/2686848. JSTOR 2686848.
- Lützen, Jesper (2003). "Between rigor and applications: Developments in the concept of function in mathematical analysis". In Porter, Roy (ed.). The Cambridge History of Science: The modern physical and mathematical sciences. Cambridge University Press. ISBN 978-0-521-57199-9. An approachable and diverting historical presentation.
- Malik, M. A. (1980). "Historical and pedagogical aspects of the definition of function". International Journal of Mathematical Education in Science and Technology. 11 (4): 489–492. doi:10.1080/0020739800110404.
- Reichenbach, Hans (1947). Elements of Symbolic Logic. Dover. ISBN 0-486-24004-5.
- Ruthing, D. (1984). "Old Intelligencer: Some definitions of the concept of function from Bernoulli, Joh. to Bourbaki, N.". Mathematical Intelligencer. 6 (4): 71–78. doi:10.1007/BF03026743. S2CID 189883712.
- Thomas, George B.; Finney, Ross L. (1995). Calculus and Analytic Geometry (9th ed.). Addison-Wesley. ISBN 978-0-201-53174-9.
External links
- The Wolfram Functions – website giving formulae and visualizations of many mathematical functions
- NIST Digital Library of Mathematical Functions
| Major topics in mathematical analysis | |
|---|---|
| Mathematics portal |
 in this case, some computation, called function evaluation, may be needed for deducing the value of the function at a particular value; for example, if
in this case, some computation, called function evaluation, may be needed for deducing the value of the function at a particular value; for example, if  then
then 
 In this notation, x is the
In this notation, x is the  One may write
One may write  instead of
instead of  , where the symbol
, where the symbol  (read '
(read '
 is a
is a  requires knowing the
requires knowing the  such that
such that  and
and  The set of all these pairs is called the
The set of all these pairs is called the  Thus, the above definition may be formalized as follows.
Thus, the above definition may be formalized as follows.
 in
in  there exists
there exists  in
in  such that
such that 
 and
and  then
then 
 the codomain
the codomain  and the graph
and the graph  that satisfy the three following conditions.
that satisfy the three following conditions.



 there is at most one y in Y such that
there is at most one y in Y such that  is in Y, or it is undefined.
is in Y, or it is undefined.
 of the
of the  its
its  of the
of the  is more or less equivalent to the proof or disproof of one of the major open problems in mathematics, the
is more or less equivalent to the proof or disproof of one of the major open problems in mathematics, the  .
. When using
When using  instead of
instead of 
 the set of all n-tuples
the set of all n-tuples  such that
such that  is called the
is called the 


 are equal to the set
are equal to the set 
 in the above example). The use of a unspecified variable between parentheses is useful for defining a function explicitly such as in "let
in the above example). The use of a unspecified variable between parentheses is useful for defining a function explicitly such as in "let  ".
".
 is the function which takes a real number as input and outputs that number plus 1. Again, a domain and codomain of
is the function which takes a real number as input and outputs that number plus 1. Again, a domain and codomain of 
 is a function in two variables, and we want to refer to a
is a function in two variables, and we want to refer to a  produced by fixing the second argument to the value t0 without introducing a new function name. The map in question could be denoted
produced by fixing the second argument to the value t0 without introducing a new function name. The map in question could be denoted  using the arrow notation. The expression
using the arrow notation. The expression 
 is called the nth element of the sequence.
is called the nth element of the sequence.
 (see above) would be denoted
(see above) would be denoted  using index notation, if we define the collection of maps
using index notation, if we define the collection of maps  for all
for all  .
.
 the symbol x does not represent any value; it is simply a
the symbol x does not represent any value; it is simply a  may stand for the function
may stand for the function  , and
, and  may stand for a function defined by an integral with variable upper bound:
may stand for a function defined by an integral with variable upper bound:  .
.
 . Such a function is commonly written as
. Such a function is commonly written as  and referred to as "a function of two variables". Likewise one can have a function of three or more variables, with notations such as
and referred to as "a function of two variables". Likewise one can have a function of three or more variables, with notations such as  ,
,  .
.
 , by definition, to each element
, by definition, to each element  , then one can define a function
, then one can define a function  by
by 
 , for
, for  .
.
 the domain is included in the set of the values of the variable for which the arguments of the square roots are nonnegative.
the domain is included in the set of the values of the variable for which the arguments of the square roots are nonnegative.
 defines a function
defines a function  is always positive if x is a real number. On the other hand,
is always positive if x is a real number. On the other hand,  defines a function from the reals to the reals whose domain is reduced to the interval [−1, 1]. (In old texts, such a domain was called the domain of definition of the function.)
defines a function from the reals to the reals whose domain is reduced to the interval [−1, 1]. (In old texts, such a domain was called the domain of definition of the function.)
 where a, b, c are
where a, b, c are  and
and  are polynomial functions of
are polynomial functions of  and
and 
 with domain X and codomain Y, is
with domain X and codomain Y, is  that maps
that maps  to the element
to the element  is not bijective, it may occur that one can select subsets
is not bijective, it may occur that one can select subsets  and
and  such that the
such that the  there is some
there is some  called an
called an  defines a relation on real numbers. If −1 < x < 1 there are two possible values of y, one positive and one negative. For x = ± 1, these two values become both equal to 0. Otherwise, there is no possible value of y. This means that the equation defines two implicit functions with domain [−1, 1] and respective codomains [0, +∞) and (−∞, 0].
defines a relation on real numbers. If −1 < x < 1 there are two possible values of y, one positive and one negative. For x = ± 1, these two values become both equal to 0. Otherwise, there is no possible value of y. This means that the equation defines two implicit functions with domain [−1, 1] and respective codomains [0, +∞) and (−∞, 0].
 but, in more complicated examples, this is impossible. For example, the relation
but, in more complicated examples, this is impossible. For example, the relation  defines y as an implicit function of x, called the
defines y as an implicit function of x, called the  . However, as the coefficients of a series are quite arbitrary, a function that is the sum of a convergent series is generally defined otherwise, and the sequence of the coefficients is the result of some computation based on another definition. Then, the power series can be used to enlarge the domain of the function. Typically, if a function for a real variable is the sum of its
. However, as the coefficients of a series are quite arbitrary, a function that is the sum of a convergent series is generally defined otherwise, and the sequence of the coefficients is the result of some computation based on another definition. Then, the power series can be used to enlarge the domain of the function. Typically, if a function for a real variable is the sum of its  ) is a basic example, as it can be defined by the recurrence relation
) is a basic example, as it can be defined by the recurrence relation



 may be identified with a point having coordinates x, y in a 2-dimensional coordinate system, e.g. the
may be identified with a point having coordinates x, y in a 2-dimensional coordinate system, e.g. the 
 for
for  yields, when depicted in Cartesian coordinates, the well known
yields, when depicted in Cartesian coordinates, the well known  the plot obtained is
the plot obtained is  defined as
defined as  can be represented by the familiar
can be represented by the familiar  is not equal to
is not equal to  if and only if
if and only if  , although their graphs are both the
, although their graphs are both the  is the function from X to f(X) that maps x to f(x).
is the function from X to f(X) that maps x to f(x). such that the domain of g is the codomain of f, their composition is the function
such that the domain of g is the codomain of f, their composition is the function  defined by
defined by

 is obtained by first applying f to x to obtain y = f(x) and then applying g to the result y to obtain g(y) = g(f(x)). In this notation, the function that is applied first is always written on the right.
is obtained by first applying f to x to obtain y = f(x) and then applying g to the result y to obtain g(y) = g(f(x)). In this notation, the function that is applied first is always written on the right.
 satisfy these conditions, the composition is not necessarily
satisfy these conditions, the composition is not necessarily  and
and  agree just for
agree just for 
 and
and  is defined, then the other is also defined, and they are equal, that is,
is defined, then the other is also defined, and they are equal, that is,  Therefore, it is usual to just write
Therefore, it is usual to just write 
 and
and  are respectively a
are respectively a 

 and is given by the equation
and is given by the equation

 and is given by the equation
and is given by the equation

 under the
under the  .
.
 .
.






 In this case
In this case  may denote either the image by
may denote either the image by  or the preimage by f of C. This is not a problem, as these sets are equal. The notation
or the preimage by f of C. This is not a problem, as these sets are equal. The notation  and
and  In this case, some care may be needed, for example, by using square brackets
In this case, some care may be needed, for example, by using square brackets  for images and preimages of subsets and ordinary parentheses for images and preimages of elements.
for images and preimages of subsets and ordinary parentheses for images and preimages of elements.
 the preimage
the preimage  such that
such that  that is, if f has a
that is, if f has a  in X (which exists as X is supposed to be nonempty), and one defines g by
in X (which exists as X is supposed to be nonempty), and one defines g by  if
if  if
if  Conversely, if
Conversely, if  then
then  and thus
and thus 
 equals its codomain
equals its codomain  (in other words, the preimage
(in other words, the preimage  that is, if f has a
that is, if f has a  where
where 
 and
and  (Contrarily to the case of surjections, this does not require the axiom of choice; the proof is straightforward).
(Contrarily to the case of surjections, this does not require the axiom of choice; the proof is straightforward).
 of a surjection followed by an injection, where s is the canonical surjection of X onto f(X) and i is the canonical injection of f(X) into Y. This is the canonical factorization of f.
of a surjection followed by an injection, where s is the canonical surjection of X onto f(X) and i is the canonical injection of f(X) into Y. This is the canonical factorization of f.
 , is the function from S to Y defined by
, is the function from S to Y defined by

 is a bijection, and thus has an inverse function from
is a bijection, and thus has an inverse function from  to S. One application is the definition of
to S. One application is the definition of  be the decomposition of X as a
be the decomposition of X as a  is defined on each
is defined on each  such that for each pair
such that for each pair  of indices, the restrictions of
of indices, the restrictions of  and
and  to
to  are equal. Then this defines a unique function
are equal. Then this defines a unique function  for all i. This is the way that functions on
for all i. This is the way that functions on  such that ad − bc ≠ 0. Its domain is the set of all
such that ad − bc ≠ 0. Its domain is the set of all  and its image is the set of all real numbers different from
and its image is the set of all real numbers different from  If one extends the real line to the
If one extends the real line to the  and
and  .
.


 whose graph is a
whose graph is a  is continuous, and even differentiable, on the positive real numbers. Thus one antiderivative, which takes the value zero for x = 1, is a differentiable function called the
is continuous, and even differentiable, on the positive real numbers. Thus one antiderivative, which takes the value zero for x = 1, is a differentiable function called the  does not depend of the choice of x and y in the interval. If the function is differentiable in the interval, it is monotonic if the sign of the derivative is constant in the interval. If a real function f is monotonic in an interval I, it has an
does not depend of the choice of x and y in the interval. If the function is differentiable in the interval, it is monotonic if the sign of the derivative is constant in the interval. If a real function f is monotonic in an interval I, it has an 

 or other spaces that share geometric or
or other spaces that share geometric or  there are several possible starting values for the function.
there are several possible starting values for the function.
 and another which is negative and denoted
and another which is negative and denoted  These choices define two continuous functions, both having the nonnegative real numbers as a domain, and having either the nonnegative or the nonpositive real numbers as images. When looking at the graphs of these functions, one can see that, together, they form a single
These choices define two continuous functions, both having the nonnegative real numbers as a domain, and having either the nonnegative or the nonpositive real numbers as images. When looking at the graphs of these functions, one can see that, together, they form a single  (see the figure on the right). For y = 0 one may choose either
(see the figure on the right). For y = 0 one may choose either  for x. By the
for x. By the  Its domain would include all sets, and therefore would not be a set. In usual mathematics, one avoids this kind of problem by specifying a domain, which means that one has many singleton functions. However, when establishing foundations of mathematics, one may have to use functions whose domain, codomain or both are not specified, and some authors, often logicians, give precise definitions for these weakly specified functions.
Its domain would include all sets, and therefore would not be a set. In usual mathematics, one avoids this kind of problem by specifying a domain, which means that one has many singleton functions. However, when establishing foundations of mathematics, one may have to use functions whose domain, codomain or both are not specified, and some authors, often logicians, give precise definitions for these weakly specified functions.