| Revision as of 15:52, 2 April 2015 editGlrx (talk | contribs)Extended confirmed users, Pending changes reviewers, Rollbackers29,700 edits →Practical challenges: split author← Previous edit | Latest revision as of 23:22, 15 November 2024 edit undoXOR'easter (talk | contribs)Extended confirmed users32,744 edits →Kochen–Specker theorem (1967): title-link | ||
| (942 intermediate revisions by more than 100 users not shown) | |||
| Line 1: | Line 1: | ||
| {{Short description|Theorem in physics}} | |||
| '''Bell's theorem''' is a ‘]’ that draws an important distinction between ] (QM) and the world as described by ]. In its simplest form, Bell's theorem states:<ref name="C.B. Parker 1994 542">{{cite book | author = C.B. Parker | title = McGraw-Hill Encyclopaedia of Physics | edition = 2nd | page = 542 | year= 1994 | publisher = McGraw-Hill | isbn = 0-07-051400-3 }}</ref> | |||
| {{Redirect|Bell inequality|the related experiments|Bell test}} | |||
| {{quotation|No physical theory of ] can ever reproduce all of the predictions of quantum mechanics.}} | |||
| '''Bell's theorem''' is a term encompassing a number of closely related results in ], all of which determine that ] is incompatible with ], given some basic assumptions about the nature of measurement. "Local" here refers to the ], the idea that a ] can only be influenced by its immediate surroundings, and that interactions mediated by ] cannot propagate faster than the ]. "]" are supposed properties of quantum particles that are not included in quantum theory but nevertheless affect the outcome of experiments. In the words of physicist ], for whom this family of results is named, "If is local it will not agree with quantum mechanics, and if it agrees with quantum mechanics it will not be local."<ref>{{cite book | first = John S. | last = Bell | author-link = John Stewart Bell | title = Speakable and Unspeakable in Quantum Mechanics | publisher = Cambridge University Press | date = 1987 | page = 65 | isbn = 9780521368698 | oclc = 15053677}}</ref> | |||
| ] solid-state physicist ] has described the various appraisals of the importance of Bell's theorem within the physics community as ranging from "indifference" to "wild extravagance".<ref>{{cite journal|authorlink=David Mermin| first=David| last=Mermin| title=Is the moon there when nobody looks? Reality and the quantum theory|journal=Physics Today|date=April 1985|pages=38–47| url=http://cp3.irmp.ucl.ac.be/~maltoni/PHY1222/mermin_moon.pdf}}</ref> ] particle physicist ] declared: "Bell's theorem is the most profound discovery of science."<ref>{{cite journal|authorlink=Henry P. Stapp|first=Henry P.|last=Stapp|title=Bell's Theorem and World Process|journal=]|volume=29B|issue=2|page=270|year=1975|url=http://link.springer.com/article/10.1007/BF02728310|doi=10.1007/BF02728310}} (Quote on p. 271)</ref> | |||
| The first such result was introduced by Bell in 1964, building upon the ], which had called attention to the phenomenon of ]. Bell deduced that if measurements are performed independently on the two separated particles of an entangled pair, then the assumption that the outcomes depend upon hidden variables within each half implies a mathematical constraint on how the outcomes on the two measurements are correlated. Such a constraint would later be named a '''Bell inequality'''. Bell then showed that quantum physics predicts correlations that violate this ]. Multiple variations on Bell's theorem were put forward in the following years, using different assumptions and obtaining different Bell (or "Bell-type") inequalities. | |||
| Bell's theorem rules out ]s as a viable explanation of quantum mechanics (though it still leaves the door open for non-local hidden variables). Bell concluded: | |||
| The first rudimentary experiment designed to test Bell's theorem was performed in 1972 by ] and ].<ref>{{cite press release |url=https://www.nobelprize.org/prizes/physics/2022/press-release/ |title=The Nobel Prize in Physics 2022 |date=October 4, 2022 |work=] |publisher=] |access-date=6 October 2022}}</ref> More advanced experiments, known collectively as '']s'', have been performed many times since. Often, these experiments have had the goal of "closing loopholes", that is, ameliorating problems of experimental design or set-up that could in principle affect the validity of the findings of earlier Bell tests. Bell tests have consistently found that physical systems obey quantum mechanics and violate Bell inequalities; which is to say that the results of these experiments are incompatible with local hidden-variable theories.<ref name="NAT-20180509">{{cite journal |author=The BIG Bell Test Collaboration |title=Challenging local realism with human choices |date=9 May 2018 |journal=] |volume=557 |issue=7704 |pages=212–216 |doi=10.1038/s41586-018-0085-3 |pmid=29743691 |bibcode=2018Natur.557..212B |arxiv=1805.04431 |s2cid=13665914 }}</ref><ref>{{Cite web |url=https://www.quantamagazine.org/20170207-bell-test-quantum-loophole/ |title=Experiment Reaffirms Quantum Weirdness |last=Wolchover |first=Natalie |author-link=Natalie Wolchover |date=2017-02-07 |work=] |language=en-US |access-date=2020-02-08}}</ref> | |||
| {{quotation|In a theory in which parameters are added to quantum mechanics to determine the results of individual measurements, without changing the statistical predictions, there must be a mechanism whereby the setting of one measuring device can influence the reading of another instrument, however remote. Moreover, the signal involved must propagate instantaneously, so that a theory could not be ].<ref name=Bell1964/>}} | |||
| The exact nature of the assumptions required to prove a Bell-type constraint on correlations has been debated by physicists and by ]. While the significance of Bell's theorem is not in doubt, different ] disagree about what exactly it implies. | |||
| ] summarized one of the least popular solutions, of ], to the theorem in a 1985 BBC Radio interview, which may be convincing because it avoids having to assume that quantum mechanics and classical mechanics work in fundamentally different ways: | |||
| {{quotation|“There is a way to escape the inference of ] speeds and spooky action at a distance. But it involves absolute ] in the universe, the complete absence of ]. Suppose the world is super-deterministic, with not just inanimate nature running on behind-the-scenes clockwork, but with our behavior, including our belief that we are free to choose to do one experiment rather than another, absolutely predetermined, including the ‘decision’ by the experimenter to carry out one set of measurements rather than another, the difficulty disappears. There is no need for a faster-than-light signal to tell particle A what measurement has been carried out on particle ''B'', because the universe, including particle ''A'', already ‘knows’ what that measurement, and its outcome, will be.”<ref>The quotation is an adaptation from the edited transcript of the radio interview with John Bell of 1985. See , by Paul C. W. Davies and Julian R. Brown, 1986/1993, </ref>}} | |||
| ==Theorem== | |||
| == Historical background == | |||
| There are many variations on the basic idea, some employing stronger mathematical assumptions than others.<ref name="Stanford">{{Cite SEP|bell-theorem|title=Bell's Theorem|first = Abner | last = Shimony|author-link=Abner Shimony}}</ref> Significantly, Bell-type theorems do not refer to any particular theory of local hidden variables, but instead show that quantum physics violates general assumptions behind classical pictures of nature. The original theorem proved by Bell in 1964 is not the most amenable to experiment, and it is convenient to introduce the genre of Bell-type inequalities with a later example.<ref name="mike-and-ike"/> | |||
| In the early 1930s, the philosophical implications of the current interpretations of quantum theory troubled many prominent physicists of the day, including ]. In a well-known 1935 paper, Einstein and co-authors ] and ] (collectively "EPR") sought to demonstrate by a ] that QM was incomplete. This provided hope that a more-complete (and less-troubling) theory might one day be discovered. But that conclusion rested on the seemingly reasonable assumptions of ''locality'' and ''realism'' (together called "local realism" or "]", often interchangeably). In the vernacular of Einstein: ] meant no instantaneous ]; realism meant the moon is there even when not being observed. These assumptions were hotly debated within the physics community, notably between Nobel laureates Einstein and ]. | |||
| Hypothetical characters ] stand in widely separated locations. Their colleague Victor prepares a pair of particles and sends one to Alice and the other to Bob. When Alice receives her particle, she chooses to perform one of two possible measurements (perhaps by flipping a coin to decide which). Denote these measurements by <math>A_0</math> and <math>A_1</math>. Both <math>A_0</math> and <math>A_1</math> are ''binary'' measurements: the result of <math>A_0</math> is either <math>+1</math> or <math>-1</math>, and likewise for <math>A_1</math>. When Bob receives his particle, he chooses one of two measurements, <math>B_0</math> and <math>B_1</math>, which are also both binary. | |||
| In his groundbreaking 1964 paper, "On the Einstein Podolsky Rosen paradox",<ref name=Bell1964/><ref name=BellJS/> physicist ] presented an analogy (based on spin measurements on pairs of entangled electrons) to EPR's hypothetical paradox. Using their reasoning, he said, a choice of measurement setting here should not affect the outcome of a measurement there (and vice versa). After providing a mathematical formulation of locality and realism based on this, he showed specific cases where this would be inconsistent with the predictions of QM theory. | |||
| Suppose that each measurement reveals a property that the particle already possessed. For instance, if Alice chooses to measure <math>A_0</math> and obtains the result <math>+1</math>, then the particle she received carried a value of <math>+1</math> for a property <math>a_0</math>.{{refn|group=note|We are for convenience assuming that the response of the detector to the underlying property is deterministic. This assumption can be replaced; it is equivalent to postulating a joint probability distribution over all the observables of the experiment.<ref>{{Cite journal |last=Fine |first=Arthur |date=1982-02-01 |title=Hidden Variables, Joint Probability, and the Bell Inequalities |url=https://link.aps.org/doi/10.1103/PhysRevLett.48.291 |journal=] |language=en |volume=48 |issue=5 |pages=291–295 |doi=10.1103/PhysRevLett.48.291 |bibcode=1982PhRvL..48..291F |issn=0031-9007}}</ref><ref>{{Cite journal |last1=Braunstein |first1=Samuel L. |last2=Caves |first2=Carlton M. |author-link2=Carlton M. Caves |date=August 1990 |title=Wringing out better Bell inequalities |journal=] |language=en |volume=202 |issue=1 |pages=22–56 |doi=10.1016/0003-4916(90)90339-P|bibcode=1990AnPhy.202...22B }}</ref>}} Consider the combination<math display="block">a_0b_0 + a_0b_1 + a_1b_0-a_1b_1 = (a_0+a_1)b_0 + (a_0-a_1)b_1 \, .</math>Because both <math>a_0</math> and <math>a_1</math> take the values <math>\pm 1</math>, then either <math>a_0 = a_1</math> or <math>a_0 = -a_1</math>. In the former case, the quantity <math>(a_0-a_1)b_1</math> must equal 0, while in the latter case, <math>(a_0+a_1)b_0 = 0</math>. So, one of the terms on the right-hand side of the above expression will vanish, and the other will equal <math>\pm 2</math>. Consequently, if the experiment is repeated over many trials, with Victor preparing new pairs of particles, the absolute value of the average of the combination <math>a_0b_0 + a_0b_1 + a_1b_0-a_1b_1</math> across all the trials will be less than or equal to 2. No ''single'' trial can measure this quantity, because Alice and Bob can only choose one measurement each, but on the assumption that the underlying properties exist, the average value of the sum is just the sum of the averages for each term. Using angle brackets to denote averages<math display="block">| \langle A_0B_0 \rangle + \langle A_0B_1 \rangle + \langle A_1B_0 \rangle - \langle A_1B_1 \rangle | \leq 2 \, .</math> | |||
| In experimental tests following Bell's example, now using ] of photons instead of electrons, ] and Stuart Freedman (1972) and ] ''et al''. (1981) demonstrated that the predictions of QM are correct in this regard, although relying on additional unverifiable assumptions that open ] for local realism. | |||
| This is a Bell inequality, specifically, the ].<ref name="mike-and-ike">{{Cite book|last1=Nielsen|first1=Michael A.|last2=Chuang|first2=Isaac L.|title=Quantum Computation and Quantum Information|author-link1=Michael Nielsen |author-link2=Isaac Chuang |title-link=Quantum Computation and Quantum Information |publisher=Cambridge University Press|location=Cambridge|year=2010|edition=2nd|oclc=844974180|isbn=978-1-107-00217-3}}</ref>{{Rp|115}} Its derivation here depends upon two assumptions: first, that the underlying physical properties <math>a_0, a_1, b_0,</math> and <math>b_1</math> exist independently of being observed or measured (sometimes called the assumption of ''realism''); and second, that Alice's choice of action cannot influence Bob's result or vice versa (often called the assumption of ''locality'').<ref name="mike-and-ike" />{{Rp|117}} | |||
| Quantum mechanics can violate the CHSH inequality, as follows. Victor prepares a pair of ]s which he describes by the ]<math display="block">|\psi\rangle = \frac{|0\rangle \otimes |1\rangle - |1\rangle \otimes |0\rangle}{\sqrt{2}} ,</math> | |||
| The present status is that no conclusive, loophole-free Bell test has been performed. While a loophole-free Bell test would not demonstrate QM is complete, one would be forced to reject at least one of the principles of locality, realism, or ] (the last leads to alternative ] theories).{{citation needed|date=July 2014}} Two of these logical possibilities, non-locality and non-realism, correspond to well-developed interpretations of quantum mechanics, and have many supporters; this is not the case for the third logical possibility, non-freedom. Conclusive experimental evidence of the violation of Bell's inequality would drastically reduce the class of acceptable deterministic theories but would not falsify absolute determinism, which was described by Bell himself as “... not just inanimate nature running on behind-the-scenes clockwork, but with our behaviour, including our belief that we are free to choose to do one experiment rather than another, absolutely predetermined.” However, Bell himself considered absolute determinism an implausible solution. | |||
| where <math>|0\rangle</math> and <math>|1\rangle</math> are the eigenstates of one of the ],<math display="block">\sigma_z = \begin{pmatrix}1 & 0 \\ 0 & -1\end{pmatrix}.</math> | |||
| Victor then passes the first qubit to Alice and the second to Bob. Alice and Bob's choices of possible ] are also defined in terms of the Pauli matrices. Alice measures either of the two observables <math>\sigma_z</math> and <math>\sigma_x</math>:<math display="block">A_0 = \sigma_z,\ A_1 = \sigma_x = \begin{pmatrix}0 & 1 \\ 1 & 0 \end{pmatrix};</math> | |||
| and Bob measures either of the two observables<math display="block">B_0 = -\frac{\sigma_x + \sigma_z}{\sqrt{2}},\ B_1 = \frac{\sigma_x - \sigma_z}{\sqrt{2}} .</math> | |||
| Victor can calculate the quantum expectation values for pairs of these observables using the ]:<math display="block">\langle A_0 \otimes B_0 \rangle = \frac{1}{\sqrt{2}}, \langle A_0 \otimes B_1 \rangle = \frac{1}{\sqrt{2}}, \langle A_1 \otimes B_0 \rangle = \frac{1}{\sqrt{2}}, \langle A_1 \otimes B_1 \rangle = -\frac{1}{\sqrt{2}} \, . </math> | |||
| While only one of these four measurements can be made in a single trial of the experiment, the sum<math display="block">\langle A_0 \otimes B_0 \rangle + \langle A_0 \otimes B_1 \rangle + \langle A_1 \otimes B_0 \rangle - \langle A_1 \otimes B_1 \rangle = 2\sqrt{2} </math> | |||
| gives the sum of the average values that Victor expects to find across multiple trials. This value exceeds the classical upper bound of 2 that was deduced from the hypothesis of local hidden variables.<ref name="mike-and-ike"/>{{Rp|116}} The value <math>2\sqrt{2}</math> is in fact the largest that quantum physics permits for this combination of expectation values, making it a ].<ref>{{Cite book |last=Rau |first=Jochen |url=https://www.worldcat.org/oclc/1256446911 |title=Quantum theory : an information processing approach |date=2021 |publisher=Oxford University Press |isbn=978-0-192-65027-6 |oclc=1256446911}}</ref>{{Rp|page=140}} | |||
| ] | |||
| == Overview == | |||
| The CHSH inequality can also be thought of as ].<ref>{{cite book|last1=Cleve |first1=R. |author-link1=Richard Cleve |last2=Hoyer |first2=P. |last3=Toner |first3=B. |last4=Watrous |first4=J. |author-link4=John Watrous (computer scientist) |year=2004 |chapter=Consequences and limits of nonlocal strategies |title=Proceedings. 19th IEEE Annual Conference on Computational Complexity, 2004. |pages=236–249 |publisher=] |doi=10.1109/CCC.2004.1313847 |isbn=0-7695-2120-7 |oclc=55954993 |arxiv=quant-ph/0404076 |bibcode=2004quant.ph..4076C|s2cid=8077237 }}</ref><ref>{{Cite journal|last1=Barnum|first1=H.|last2=Beigi|first2=S.|last3=Boixo|first3=S.|last4=Elliott|first4=M. B.|last5=Wehner|first5=S.|date=2010-04-06|title=Local Quantum Measurement and No-Signaling Imply Quantum Correlations|journal=]|language=en|volume=104|issue=14|pages=140401|arxiv=0910.3952|bibcode=2010PhRvL.104n0401B|doi=10.1103/PhysRevLett.104.140401|pmid=20481921|s2cid=17298392|issn=0031-9007}}</ref> Victor prepares two bits, <math>x</math> and <math>y</math>, independently and at random. He sends bit <math>x</math> to Alice and bit <math>y</math> to Bob. Alice and Bob win if they return answer bits <math>a</math> and <math>b</math> to Victor, satisfying | |||
| Bell's theorem states that any physical theory that incorporates ] cannot reproduce all the predictions of quantum mechanical theory. Because numerous experiments agree with the predictions of quantum mechanical theory, and show differences between correlations that could not be explained by local hidden variables, the experimental results have been taken by many as refuting the concept of local realism as an explanation of the physical phenomena under test. For a hidden variable theory, if Bell's conditions are correct, the results that agree with quantum mechanical theory appear to indicate ] effects, in contradiction to the principle of locality. | |||
| <math display="block">x y = a + b \mod 2 \, .</math> | |||
| Or, equivalently, Alice and Bob win if the ] of <math>x</math> and <math>y</math> is the ] of <math>a</math> and <math>b</math>. Alice and Bob can agree upon any strategy they desire before the game, but they cannot communicate once the game begins. In any theory based on local hidden variables, Alice and Bob's probability of winning is no greater than <math>3/4</math>, regardless of what strategy they agree upon beforehand. However, if they share an entangled quantum state, their probability of winning can be as large as<math display="block">\frac{2+\sqrt{2}}{4} \approx 0.85 \, .</math> | |||
| ==Variations and related results== | |||
| These three key concepts – locality, realism, freedom – are highly technical and much debated. In particular, the concept of ''realism'' is now somewhat different from what it was in discussions in the 1930s. It is more precisely called '']''; it means that we may think of outcomes of measurements that were not actually performed as being just as much part of reality as those that were made. ''Locality'' is short for ''local relativistic causality''. ''Freedom'' refers to the physical possibility to determine settings on measurement devices independently of the internal state of the physical system being measured. | |||
| ===Bell (1964)=== | |||
| Bell's 1964 paper points out that under restricted conditions, local hidden-variable models can reproduce the predictions of quantum mechanics. He then demonstrates that this cannot hold true in general.<ref name=Bell1964>{{cite journal | last1 = Bell | first1 = J. S. | author-link = John Stewart Bell | year = 1964 | title = On the Einstein Podolsky Rosen Paradox | url = https://cds.cern.ch/record/111654/files/vol1p195-200_001.pdf | journal = ] | volume = 1 | issue = 3| pages = 195–200 | doi = 10.1103/PhysicsPhysiqueFizika.1.195 }}</ref> Bell considers a refinement by ] of the Einstein–Podolsky–Rosen (EPR) thought experiment. In this scenario, a pair of particles are formed together in such a way that they are described by a ] (which is an example of an entangled state). The particles then move apart in opposite directions. Each particle is measured by a ], a measuring instrument that can be oriented in different directions and that reports one of two possible outcomes, representable by <math>+1</math> and <math>-1</math>. The configuration of each measuring instrument is represented by a unit ], and the quantum-mechanical prediction for the ] between two detectors with settings <math>\vec{a}</math> and <math>\vec{b}</math> is | |||
| <math display="block">P(\vec{a}, \vec{b}) = -\vec{a} \cdot \vec{b}.</math> | |||
| In particular, if the orientation of the two detectors is the same (<math>\vec{a} = \vec{b}</math>), then the outcome of one measurement is certain to be the negative of the outcome of the other, giving <math>P(\vec{a}, \vec{a}) = -1</math>. And if the orientations of the two detectors are orthogonal (<math>\vec{a} \cdot \vec{b} = 0</math>), then the outcomes are uncorrelated, and <math>P(\vec{a}, \vec{b}) = 0</math>. Bell proves by example that these special cases ''can'' be explained in terms of hidden variables, then proceeds to show that the full range of possibilities involving intermediate angles ''cannot''. | |||
| Bell posited that a local hidden-variable model for these correlations would explain them in terms of an integral over the possible values of some hidden parameter <math>\lambda</math>:<math display="block">P(\vec{a}, \vec{b}) = \int d\lambda\, \rho(\lambda) A(\vec{a}, \lambda) B(\vec{b}, \lambda),</math> | |||
| ] pair, one particle is sent to one location, and the other is sent to another location. A ] of the entangled property is performed at various angles at each location. The scheme for measurements on ] looks very similar: the quantum state is different but has very similar properties.]] | |||
| where <math>\rho(\lambda)</math> is a ]. The two functions <math>A(\vec{a}, \lambda)</math> and <math>B(\vec{b}, \lambda)</math> provide the responses of the two detectors given the orientation vectors and the hidden variable:<math display="block">A(\vec{a}, \lambda) = \pm 1, \, B(\vec{b}, \lambda) = \pm 1.</math> | |||
| Crucially, the outcome of detector <math>A</math> does not depend upon <math>\vec{b}</math>, and likewise the outcome of <math>B</math> does not depend upon <math>\vec{a}</math>, because the two detectors are physically separated. Now we suppose that the experimenter has a ''choice'' of settings for the second detector: it can be set either to <math>\vec{b}</math> or to <math>\vec{c}</math>. Bell proves that the difference in correlation between these two choices of detector setting must satisfy the inequality<math display="block">|P(\vec{a}, \vec{b}) - P(\vec{a}, \vec{c})| \leq 1 + P(\vec{b}, \vec{c}).</math> | |||
| However, it is easy to find situations where quantum mechanics violates the Bell inequality.<ref>{{Cite book |last=Griffiths |first=David J. |author-link=David J. Griffiths |title=Introduction to Quantum Mechanics |title-link=Introduction to Quantum Mechanics (book) |date=2005 |publisher=Pearson Prentice Hall |isbn=0-13-111892-7 |edition=2nd |location=Upper Saddle River, NJ |oclc=53926857}}</ref>{{Rp|425–426}} For example, let the vectors <math>\vec{a}</math> and <math>\vec{b}</math> be orthogonal, and let <math>\vec{c}</math> lie in their plane at a 45° angle from both of them. Then<math display="block">P(\vec{a}, \vec{b}) = 0,</math> | |||
| while | |||
| <math display="block">P(\vec{a}, \vec{c}) = P(\vec{b}, \vec{c}) = -\frac{\sqrt{2}}{2},</math> | |||
| but | |||
| <math display="block">\frac{\sqrt{2}}{2} \nleq 1 - \frac{\sqrt{2}}{2}.</math> | |||
| Therefore, there is no local hidden-variable model that can reproduce the predictions of quantum mechanics for all choices of <math>\vec{a}</math>, <math>\vec{b}</math>, and <math>\vec{c}.</math> Experimental results contradict the classical curves and match the curve predicted by quantum mechanics as long as experimental shortcomings are accounted for.<ref name="Stanford"/> | |||
| Bell's 1964 theorem requires the possibility of perfect anti-correlations: the ability to make a probability-1 prediction about the result from the second detector, knowing the result from the first. This is related to the "EPR criterion of reality", a concept introduced in the 1935 paper by Einstein, Podolsky, and Rosen. This paper posits: "If, without in any way disturbing a system, we can predict with certainty (i.e., with probability equal to unity) the value of a physical quantity, then there exists an element of reality corresponding to that quantity."<ref name="EPR">{{cite journal | title = Can Quantum-Mechanical Description of Physical Reality be Considered Complete? | date = 1935-05-15 | first1 = A. | last1 = Einstein |first2=B. |last2 = Podolsky |first3=N. |last3 = Rosen | author-link1 = Albert Einstein | author-link2 = Boris Podolsky | author-link3 = Nathan Rosen | journal = ] | volume = 47 | issue = 10 | pages = 777–780 | bibcode = 1935PhRv...47..777E |doi = 10.1103/PhysRev.47.777 | doi-access = free }}</ref> | |||
| The theorem is usually proved by consideration of a quantum system of two ] ]s. The most common examples concern systems of particles that are entangled in ] or ]. Quantum mechanics allows predictions of correlations that would be observed if these two particles have their spin or polarization measured in different directions. Bell showed that if a local hidden variable theory holds, then these correlations would have to satisfy certain constraints, called '''Bell inequalities'''. However, for the quantum correlations arising in the specific example considered, those constraints are not satisfied, hence the phenomenon being studied cannot be explained by a local hidden variables theory. | |||
| ===GHZ–Mermin (1990)=== | |||
| Following the argument in the ] paper (but using the example of spin, as in ]'s version of the EPR argument<ref name="Bell1964">{{cite journal |last=Bell |first=John |year=1964 |title=On the Einstein Podolsky Rosen Paradox |url=http://www.drchinese.com/David/Bell_Compact.pdf |journal=] |volume=1 |issue=3 |pages=195–200}}</ref><ref>{{cite book|last=Bohm|first=David|title=Quantum Theory|authorlink=David Bohm|publisher=Prentice−Hall|year=1951}}</ref>), Bell considered an experiment in which there are "a pair of spin one-half particles formed somehow in the ] and moving freely in opposite directions."<ref name=Bell1964/> The two particles travel away from each other to two distant locations, at which measurements of spin are performed, along axes that are independently chosen. Each measurement yields a result of either spin-up (+) or spin-down (−); it means, spin in the positive or negative direction of the chosen axis. | |||
| {{main|GHZ experiment}} | |||
| ], ], and ] presented a four-particle thought experiment in 1990, which ] then simplified to use only three particles.<ref name="GHZ1990">{{cite journal |first1=D. |last1=Greenberger |author-link1=Daniel Greenberger |first2=M. |last2=Horne |author-link2=Michael A. Horne |first3=A. |last3=Shimony |author-link3=Abner Shimony |first4=A. |last4=Zeilinger |author-link4=Anton Zeilinger |title=Bell's theorem without inequalities |journal=] |volume=58 |issue=12 |pages=1131 |year=1990|bibcode = 1990AmJPh..58.1131G |doi = 10.1119/1.16243 |doi-access=free }}</ref><ref name="mermin1990">{{cite journal |first=N. David |last=Mermin |author-link=N. David Mermin |title=Quantum mysteries revisited |journal=] |volume=58 |issue=8 |pages=731–734 |year=1990|bibcode = 1990AmJPh..58..731M |doi = 10.1119/1.16503}}</ref> In this thought experiment, Victor generates a set of three spin-1/2 particles described by the quantum state<math display="block">|\psi\rangle = \frac{1}{\sqrt{2}}(|000\rangle - |111\rangle) \, , </math> | |||
| The probability of the same result being obtained at the two locations varies, depending on the relative angles at which the two spin measurements are made, and is strictly between zero and one for all relative angles other than perfectly parallel alignments (0° or 180°). Bell's theorem is concerned with correlations defined in terms of averages taken over very many trials of the experiment. The ] of two binary variables is usually defined in quantum physics as the average of the product of the two outcomes of the pairs of measurements. Note that this is different from the usual definition of ] in statistics. The quantum physicist's "correlation" is the statistician's "raw (uncentered, unnormalized) product ]". They are similar in that, with either definition, if the pairs of outcomes are always the same, the correlation is +1, no matter which same value each pair of outcomes have.{{clarify|reason=In order for the outcomes' product's average to have this property, only +1 and -1 are allowed as possible outcomes. If I'm right, this requirement should be stated explicitly.|date=January 2015}} If the pairs of outcomes are always opposite, the correlation is -1. Finally, if the pairs of outcomes are perfectly balanced, being 50% of the times in accordance, and 50% of the times opposite, the correlation, being an average, is 0. The correlation is related in a simple way to the probability of equal outcomes, namely it is equal to twice this probability, minus one. | |||
| where as above, <math>|0\rangle</math> and <math>|1\rangle</math> are the eigenvectors of the Pauli matrix <math>\sigma_z</math>. Victor then sends a particle each to Alice, Bob, and Charlie, who wait at widely separated locations. Alice measures either <math>\sigma_x</math> or <math>\sigma_y</math> on her particle, and so do Bob and Charlie. The result of each measurement is either <math>+1</math> or <math>-1</math>. Applying the Born rule to the three-qubit state <math>|\psi\rangle</math>, Victor predicts that whenever the three measurements include one <math>\sigma_x</math> and two <math>\sigma_y</math>'s, the product of the outcomes will always be <math>+1</math>. This follows because <math>|\psi\rangle</math> is an eigenvector of <math>\sigma_x \otimes \sigma_y \otimes \sigma_y</math> with eigenvalue <math>+1</math>, and likewise for <math>\sigma_y \otimes \sigma_x \otimes \sigma_y</math> and <math>\sigma_y \otimes \sigma_y \otimes \sigma_x</math>. Therefore, knowing Alice's result for a <math>\sigma_x</math> measurement and Bob's result for a <math>\sigma_y</math> measurement, Victor can predict with probability 1 what result Charlie will return for a <math>\sigma_y</math> measurement. According to the EPR criterion of reality, there would be an "element of reality" corresponding to the outcome of a <math>\sigma_y</math> measurement upon Charlie's qubit. Indeed, this same logic applies to both measurements and all three qubits. Per the EPR criterion of reality, then, each particle contains an "instruction set" that determines the outcome of a <math>\sigma_x</math> or <math>\sigma_y</math> measurement upon it. The set of all three particles would then be described by the instruction set<math display="block">(a_x,a_y,b_x,b_y,c_x,c_y) \, , </math> | |||
| with each entry being either <math>-1</math> or <math>+1</math>, and each <math>\sigma_x</math> or <math>\sigma_y</math> measurement simply returning the appropriate value. | |||
| If Alice, Bob, and Charlie all perform the <math>\sigma_x</math> measurement, then the product of their results would be <math>a_x b_x c_x</math>. This value can be deduced from<math display="block">(a_x b_y c_y) (a_y b_x c_y) (a_y b_y c_x) = a_x b_x c_x a_y^2 b_y^2 c_y^2 = a_x b_x c_x \, , </math> | |||
| ] of these entangled particles along anti-parallel directions—i.e., along the same axis but in opposite directions, the set of all results is perfectly correlated. On the other hand, if measurements are performed along parallel directions they always yield opposite results, and the set of measurements shows perfect anti-correlation. Finally, measurement at perpendicular directions has a 50% chance of matching, and the total set of measurements is uncorrelated. These basic cases are illustrated in the table below. | |||
| because the square of either <math>-1</math> or <math>+1</math> is <math>1</math>. Each factor in parentheses equals <math>+1</math>, so<math display="block">a_x b_x c_x = +1 \, , </math> | |||
| and the product of Alice, Bob, and Charlie's results will be <math>+1</math> with probability unity. But this is inconsistent with quantum physics: Victor can predict using the state <math>|\psi\rangle</math> that the measurement <math>\sigma_x \otimes \sigma_x \otimes \sigma_x</math> will instead yield <math>-1</math> with probability unity. | |||
| This thought experiment can also be recast as a traditional Bell inequality or, equivalently, as a nonlocal game in the same spirit as the CHSH game.<ref name="Brassard 2004">{{Cite journal|arxiv = quant-ph/0408052|last1 = Brassard|first1 = Gilles|title = Recasting Mermin's multi-player game into the framework of pseudo-telepathy|last2 = Broadbent|first2 = Anne|last3 = Tapp|first3 = Alain|year = 2005 |journal=Quantum Information and Computation |volume=5 |issue=7 |pages=538–550|doi = 10.26421/QIC5.7-2|bibcode = 2004quant.ph..8052B |author-link1 = Gilles Brassard |author-link2 = Anne Broadbent }}</ref> In it, Alice, Bob, and Charlie receive bits <math>x,y,z</math> from Victor, promised to always have an even number of ones, that is, <math>x\oplus y\oplus z = 0</math>, and send him back bits <math>a,b,c</math>. They win the game if <math>a,b,c</math> have an odd number of ones for all inputs except <math>x=y=z=0</math>, when they need to have an even number of ones. That is, they win the game iff <math>a \oplus b \oplus c = x \lor y \lor z</math>. With local hidden variables the highest probability of victory they can have is 3/4, whereas using the quantum strategy above they win it with certainty. This is an example of ]. | |||
| {| style="float:center" | |||
| |- style="text-align:left" | |||
| ! Anti-parallel || Pair 1 || Pair 2 || Pair 3 || Pair 4 || … || ''Pair n'' || | |||
| |- | |||
| | ], 0° || + || − || + || + || … || − || | |||
| |- | |||
| | ], 180° || + || − || + || + || … || − || | |||
| |- style="text-align:left" | |||
| ! Correlation = <span style="float:right"></span>(|| +1 || +1 || +1 || +1 || … || +1 || ) / ''n'' = +1 | |||
| |- | |||
| | || || || || || || || <small>(100% identical)</small> | |||
| |- style="text-align:left" | |||
| ! Parallel || Pair 1 || Pair 2 || Pair 3 || Pair 4 || … || ''Pair n'' || | |||
| |- | |||
| | ], 0° || + || − || − || + || … || + || | |||
| |- | |||
| | ], 0° or 360° || − || + || + || − || … || − || | |||
| |- style="text-align:left" | |||
| ! Correlation = <span style="float:right"></span>(|| -1 || -1 || -1 || -1 || … || -1 || ) / ''n'' = -1 | |||
| |- | |||
| | || || || || || || || <small>(100% opposite)</small> | |||
| |- style="text-align:left" | |||
| ! Orthogonal || Pair 1 || Pair 2 || Pair 3 || Pair 4 || … || ''Pair n'' || | |||
| |- | |||
| | Alice, 0° || + || − || + || − || … || − || | |||
| |- | |||
| | Bob, 90° or 270° || − || − || + || + || … || − || | |||
| |- style="text-align:left" | |||
| ! Correlation = <span style="float:right"></span>( || −1 || +1 || +1 || −1 || … || +1 || ) / ''n'' = 0 | |||
| |- | |||
| | || || || || || || || <small>(50% identical, 50% opposite)</small> | |||
| |} | |||
| ===Kochen–Specker theorem (1967)=== | |||
| ] | |||
| {{main|Kochen–Specker theorem}} | |||
| In quantum theory, orthonormal bases for a ] represent measurements that can be performed upon a system having that Hilbert space. Each vector in a basis represents a possible outcome of that measurement.{{refn|group=note|In more detail, as developed by ],<ref>{{cite book|first=Paul Adrien Maurice |last=Dirac |author-link=Paul Dirac |title=The Principles of Quantum Mechanics |title-link=The Principles of Quantum Mechanics |publisher=Clarendon Press |location=Oxford |year=1930}}</ref> ],<ref>{{cite book|first=David |last=Hilbert |author-link=David Hilbert |title=Lectures on the Foundations of Physics 1915–1927: Relativity, Quantum Theory and Epistemology |publisher=Springer |doi=10.1007/b12915 |editor-first1=Tilman |editor-last1=Sauer |editor-first2=Ulrich |editor-last2=Majer |year=2009 |isbn=978-3-540-20606-4 |oclc=463777694}}</ref> ],<ref>{{cite book|first=John |last=von Neumann |author-link=John von Neumann |title=Mathematische Grundlagen der Quantenmechanik |publisher=Springer |location=Berlin |year=1932}} English translation: {{cite book|title=Mathematical Foundations of Quantum Mechanics |title-link=Mathematical Foundations of Quantum Mechanics |publisher=Princeton University Press |year=1955 |translator-first=Robert T. |translator-last=Beyer |translator-link=Robert T. Beyer}}</ref> and ],<ref>{{cite book|first=Hermann |last=Weyl |author-link=Hermann Weyl |title=The Theory of Groups and Quantum Mechanics |title-link=Gruppentheorie und Quantenmechanik |orig-year=1931 |publisher=Dover |year=1950 |isbn=978-0-486-60269-1 |translator-first=H. P. |translator-last=Robertson |translator-link=Howard P. Robertson}} Translated from the German {{cite book |title=Gruppentheorie und Quantenmechanik |year=1931 |edition=2nd |publisher={{ill|S. Hirzel Verlag|de}}}}</ref> the state of a quantum mechanical system is a vector <math>|\psi\rangle</math> belonging to a (]) Hilbert space <math>\mathcal H</math>. Physical quantities of interest — position, momentum, energy, spin — are represented by "observables", which are ] linear ]s acting on the Hilbert space. When an observable is measured, the result will be one of its eigenvalues with probability given by the ]: in the simplest case the eigenvalue <math>\eta</math> is non-degenerate and the probability is given by <math>|\langle \eta|\psi\rangle|^2</math>, where <math>|\eta\rangle</math> is its associated eigenvector. More generally, the eigenvalue is degenerate and the probability is given by <math>\langle \psi|P_\eta\psi\rangle</math>, where <math>P_\eta</math> is the projector onto its associated eigenspace. For the purposes of this discussion, we can take the eigenvalues to be non-degenerate.}} Suppose that a hidden variable <math>\lambda</math> exists, so that knowing the value of <math>\lambda</math> would imply certainty about the outcome of any measurement. Given a value of <math>\lambda</math>, each measurement outcome – that is, each vector in the Hilbert space – is either ''impossible'' or ''guaranteed.'' A Kochen–Specker configuration is a finite set of vectors made of multiple interlocking bases, with the property that a vector in it will always be ''impossible'' when considered as belonging to one basis and ''guaranteed'' when taken as belonging to another. In other words, a Kochen–Specker configuration is an "uncolorable set" that demonstrates the inconsistency of assuming a hidden variable <math>\lambda</math> can be controlling the measurement outcomes.<ref>{{cite book|first=Asher |last=Peres |author-link=Asher Peres |title=Quantum Theory: Concepts and Methods |title-link=Quantum Theory: Concepts and Methods |year=1993 |publisher=] |isbn=0-7923-2549-4 |oclc=28854083}}</ref>{{Rp|196–201}} | |||
| ===Free will theorem=== | |||
| With the measurements oriented at intermediate angles between these basic cases, the existence of local hidden variables could agree with a linear dependence of the ] in the angle but, according to Bell's inequality (see below), could not agree with the dependence predicted by quantum mechanical theory, namely, that the correlation is the negative ] of the angle. Experimental results match the curve predicted by quantum mechanics.<ref name="C.B. Parker 1994 542"/> | |||
| {{main|Free will theorem}} | |||
| The Kochen–Specker type of argument, using configurations of interlocking bases, can be combined with the idea of measuring entangled pairs that underlies Bell-type inequalities. This was noted beginning in the 1970s by Kochen,<ref>{{Cite journal |last1=Redhead |first1=Michael |author-link1=Michael Redhead |last2=Brown |first2=Harvey |author-link2=Harvey R. Brown |date=1991-07-01 |title=Nonlocality in Quantum Mechanics |journal=] |language=en |volume=65 |issue=1 |pages=119–160 |doi=10.1093/aristoteliansupp/65.1.119 |issn=0309-7013 |jstor=4106773 |quote=A similar approach was arrived at independently by Simon Kochen, although never published (private communication).}}</ref> Heywood and Redhead,<ref>{{Cite journal|last1=Heywood|first1=Peter|last2=Redhead|first2=Michael L. G. |author-link2=Michael Redhead |date=May 1983|title=Nonlocality and the Kochen–Specker paradox |journal=] |language=en|volume=13|issue=5|pages=481–499|doi=10.1007/BF00729511|bibcode=1983FoPh...13..481H |s2cid=120340929|issn=0015-9018}}</ref> Stairs,<ref>{{Cite journal|last=Stairs|first=Allen|date=December 1983|title=Quantum Logic, Realism, and Value Definiteness|journal=] |language=en|volume=50|issue=4|pages=578–602|doi=10.1086/289140|s2cid=122885859|issn=0031-8248}}</ref> and Brown and Svetlichny.<ref>{{Cite journal|last1=Brown |first1=H. R. |author-link1=Harvey Brown (philosopher) |last2=Svetlichny|first2=G.|date=November 1990|title=Nonlocality and Gleason's lemma. Part I. Deterministic theories|journal=] |language=en|volume=20|issue=11|pages=1379–1387|doi=10.1007/BF01883492|bibcode=1990FoPh...20.1379B |s2cid=122868901 |issn=0015-9018}}</ref> As EPR pointed out, obtaining a measurement outcome on one half of an entangled pair implies certainty about the outcome of a corresponding measurement on the other half. The "EPR criterion of reality" posits that because the second half of the pair was not disturbed, that certainty must be due to a physical property belonging to it.<ref>{{Cite journal|last1=Glick|first1=David|last2=Boge|first2=Florian J.|date=2019-10-22|title=Is the Reality Criterion Analytic?|journal=]|language=en|volume=86|issue=6|pages=1445–1451|arxiv=1909.11893|bibcode=2019arXiv190911893G|doi=10.1007/s10670-019-00163-w|s2cid=202889160|issn=0165-0106}}</ref> In other words, by this criterion, a hidden variable <math>\lambda</math> must exist within the second, as-yet unmeasured half of the pair. No contradiction arises if only one measurement on the first half is considered. However, if the observer has a choice of multiple possible measurements, and the vectors defining those measurements form a Kochen–Specker configuration, then some outcome on the second half will be simultaneously impossible and guaranteed. | |||
| This type of argument gained attention when an instance of it was advanced by ] and ] under the name of the ].<ref>{{cite journal | last1 = Conway | first1 = John |first2=Simon |last2=Kochen | author-link1=John Horton Conway | author-link2=Simon B. Kochen |year = 2006 | title = The Free Will Theorem | journal = ] | volume = 36 | issue = 10 | pages = 1441 | doi = 10.1007/s10701-006-9068-6 |arxiv = quant-ph/0604079 |bibcode = 2006FoPh...36.1441C | s2cid = 12999337 }}</ref><ref>{{Cite web |last=Rehmeyer |first=Julie |date=2008-08-15 |title=Do subatomic particles have free will? |url=https://www.sciencenews.org/article/do-subatomic-particles-have-free-will |access-date=2022-04-23 |website=] |language=en-US}}</ref><ref>{{Cite web |last=Thomas |first=Rachel |date=2011-12-27 |title=John Conway – discovering free will (part I) |url=https://plus.maths.org/content/john-conway-discovering-free-will-part-i |access-date=2022-04-23 |website=] |language=en}}</ref> The Conway–Kochen theorem uses a pair of entangled ]s and a Kochen–Specker configuration discovered by ].<ref>{{cite journal |last1=Conway |first1=John H. |first2=Simon |last2=Kochen | author-link1=John Horton Conway | author-link2=Simon B. Kochen |title=The strong free will theorem |journal= ] |volume=56 |issue=2 |year=2009 |pages=226–232 |url=http://www.ams.org/notices/200902/rtx090200226p.pdf}}</ref> | |||
| Over the years, Bell's theorem has undergone a wide variety of experimental tests. However, various ] have been identified, including the ''detection loophole''<ref name="Stanford"> by Abner Shimony in the ], (2004).</ref> and the ''communication loophole''.<ref name="Stanford"/> Over the years experiments have been gradually improved to better address these loopholes, but no experiment to date has simultaneously fully addressed all of them.<ref name="Stanford"/> However, scientists generally expect that someone will conduct such an experiment in a few years, and it is expected to confirm yet again quantum predictions.<ref name=Zukowski>{{cite journal|last=Merali |first=Z.| title=Quantum Mechanics Braces for the Ultimate Test| journal=Science |year=2011|volume=331| issue=6023|pages=1380–1382 | doi=10.1126/science.331.6023.1380| url=http://www.sciencemag.org/content/331/6023/1380.summary?sid=3ffedc8a-df87-47c9-99f1-28c17c41e84f|accessdate=12 September 2013|bibcode = 2011Sci...331.1380M }}</ref> For example, ] has commented: | |||
| ===Quasiclassical entanglement=== | |||
| <blockquote> no single existing experiment has simultaneously blocked all of the so-called ''loopholes'', each one of those loopholes has been blocked in at least one experiment. Thus, to maintain a local hidden variable theory in the face of the existing experiments would appear to require belief in a very peculiar conspiracy of nature.<ref name="Leggett 2003">{{cite journal |last=Leggett |first=Anthony |year=2003 |title=Nonlocal Hidden-Variable Theories and Quantum Mechanics: An Incompatibility Theorem |url= |journal=Foundations of Physics |volume=33 |issue=10 |pages=1469–1493 |doi=10.1023/A:1026096313729}}</ref></blockquote> | |||
| {{main|Spekkens toy model|Werner state}} | |||
| As Bell pointed out, some predictions of quantum mechanics can be replicated in local hidden-variable models, including special cases of correlations produced from entanglement. This topic has been studied systematically in the years since Bell's theorem. In 1989, ] introduced what are now called ]s, joint quantum states for a pair of systems that yield EPR-type correlations but also admit a hidden-variable model.<ref>{{Cite journal |last=Werner |first=Reinhard F. |author-link=Reinhard F. Werner |date=1989-10-01 |title=Quantum states with Einstein–Podolsky–Rosen correlations admitting a hidden-variable model |journal=] |language=en |volume=40 |issue=8 |pages=4277–4281 |bibcode=1989PhRvA..40.4277W |doi=10.1103/PhysRevA.40.4277 |pmid=9902666 |issn=0556-2791}}</ref> Werner states are bipartite quantum states that are invariant under ] of symmetric ] form: <math display="block">\rho_{AB} = (U \otimes U) \rho_{AB} (U^\dagger \otimes U^\dagger).</math> | |||
| In 2004, ] introduced a ] that starts with the premise of local, discretized degrees of freedom and then imposes a "knowledge balance principle" that restricts how much an observer can know about those degrees of freedom, thereby making them into hidden variables. The allowed states of knowledge ("epistemic states") about the underlying variables ("ontic states") mimic some features of quantum states. Correlations in the toy model can emulate some aspects of entanglement, like ], but by construction, the toy model can never violate a Bell inequality.<ref>{{Cite journal |author1-link=Robert Spekkens |last=Spekkens |first=Robert W. |date=2007-03-19 |title=Evidence for the epistemic view of quantum states: A toy theory |journal=] |language=en |volume=75 |issue=3 |pages=032110 |arxiv=quant-ph/0401052 |bibcode=2007PhRvA..75c2110S |doi=10.1103/PhysRevA.75.032110 |s2cid=117284016 |issn=1050-2947}}</ref><ref>{{Cite journal |last1=Catani |first1=Lorenzo |last2=Browne |first2=Dan E. |date=2017-07-27 |title=Spekkens' toy model in all dimensions and its relationship with stabiliser quantum mechanics |journal=] |volume=19 |issue=7 |pages=073035 |doi=10.1088/1367-2630/aa781c |bibcode=2017NJPh...19g3035C |s2cid=119428107 |issn=1367-2630 |doi-access=free |arxiv=1701.07801 }}</ref> | |||
| ==History== | |||
| To date, Bell's theorem is generally regarded as supported by a substantial body of evidence and there are few supporters of local hidden variables, though the theorem is continually subject of study, criticism, and refinement.<ref>{{cite book |last=Griffiths |first=David J. |year=1998 |title=Introduction to Quantum Mechanics |edition=2nd |publisher=]/] |pages=423}}</ref><ref>{{cite book | |||
| ===Background=== | |||
| |last=Merzbacher |first=Eugene |year=2005 |title=Quantum Mechanics |edition=3rd |publisher=] |pages=18, 362}}</ref> | |||
| {{main|EPR paradox|History of quantum mechanics}} | |||
| The question of whether quantum mechanics can be "completed" by hidden variables dates to the early years of quantum theory. In his ], the Hungarian-born polymath ] presented what he claimed to be a proof that there could be no "hidden parameters". The validity and definitiveness of von Neumann's proof were questioned by ], in more detail by ], and possibly in conversation though not in print by Albert Einstein.{{refn|group=note|See Reichenbach<ref>{{cite book|first=Hans |last=Reichenbach |author-link=Hans Reichenbach |title=Philosophic Foundations of Quantum Mechanics |year=1944 |publisher=University of California Press |page=14 |oclc=872622725}}</ref> and Jammer,<ref name="jammer1974">{{cite book|last=Jammer|first=Max|title=The Philosophy of Quantum Mechanics|publisher=John Wiley and Sons|year=1974|isbn=0-471-43958-4|author-link=Max Jammer}}</ref>{{Rp|276}} Mermin and Schack,<ref>{{cite journal|title=Homer nodded: von Neumann's surprising oversight |journal=] |volume=48 |issue=9 |pages=1007–1020 |year=2018 |arxiv=1805.10311 |last1=Mermin |first1=N. David |last2=Schack |first2=Rüdiger |author-link1=N. David Mermin|doi=10.1007/s10701-018-0197-5 |bibcode=2018FoPh...48.1007M |s2cid=118951033 }}</ref> and for Einstein's remarks, Clauser and Shimony<ref>{{cite journal | last1 = Clauser | first1 = J. F. | last2 = Shimony | first2 = A. | title = Bell's theorem: Experimental tests and implications | url = http://www.physics.oregonstate.edu/~ostroveo/COURSES/ph651/Supplements_Phys651/RPP1978_Bell.pdf | journal = Reports on Progress in Physics | volume = 41 | issue = 12 | pages = 1881–1927 | year = 1978 | doi = 10.1088/0034-4885/41/12/002 | bibcode = 1978RPPh...41.1881C | citeseerx = 10.1.1.482.4728 | s2cid = 250885175 | access-date = 2017-10-28 | archive-date = 2017-09-23 | archive-url = https://web.archive.org/web/20170923004338/http://physics.oregonstate.edu/~ostroveo/COURSES/ph651/Supplements_Phys651/RPP1978_Bell.pdf | url-status = live }}</ref> and Wick.<ref name=":1"/>{{Rp|286}}}} (] and ] rejected von Neumann's key assumption as early as 1961, but did not publish a criticism of it until 1967.<ref>{{Cite book |author-first1=John |author-last1=Conway |author-link1=John Horton Conway |author-first2=Simon |author-last2=Kochen |author-link2=Simon B. Kochen |chapter=The Geometry of the Quantum Paradoxes |pages=257–269 |title=Quantum speakables: From Bell to Quantum Information |date=2002 |publisher=Springer |editor-first1=Reinhold A. |editor-last1=Bertlmann |editor-link1=Reinhold Bertlmann |editor-first2=Anton |editor-last2=Zeilinger |editor-link2=Anton Zeilinger |isbn=3-540-42756-2 |location=Berlin |oclc=49404213}}</ref>) | |||
| ==Importance of the theorem== | |||
| '''Bell's theorem''', derived in his seminal 1964 paper titled ''On the Einstein Podolsky Rosen paradox'',<ref name=Bell1964/> has been called, on the assumption that the theory is correct, "the most profound in science".<ref>Stapp, 1975</ref> Perhaps of equal importance is Bell's deliberate effort to encourage and bring legitimacy to work on the completeness issues, which had fallen into disrepute.<ref name="Bell 1982">{{cite journal|last=Bell|first=JS|title=On the impossible pilot wave|url=http://prac.us.edu.pl/~ztpce/QM/Bell_pilot_wave.pdf|journal=Foundations of Physics|year=1982|volume=12|pages=989–99|doi=10.1007/bf01889272|bibcode = 1982FoPh...12..989B }} Reprinted in ''Speakable and unspeakable in quantum mechanics: collected papers on quantum philosophy''. CUP, 2004, p. 160.</ref> Later in his life, Bell expressed his hope that such work would "continue to inspire those who suspect that what is proved by the impossibility proofs is lack of imagination."<ref name="Bell 1982"/> | |||
| Einstein argued persistently that quantum mechanics could not be a complete theory. His preferred argument relied on a principle of locality: | |||
| The title of Bell's seminal article refers to the 1935 paper by ]<ref>{{cite journal |doi=10.1103/PhysRev.47.777 |title=Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? |year=1935 |last1=Einstein |first1=A. |last2=Podolsky |first2=B. |last3=Rosen |first3=N. |journal=Physical Review |volume=47 |issue=10 |pages=777|bibcode = 1935PhRv...47..777E|url=http://www.drchinese.com/David/EPR.pdf}}</ref> that challenged the completeness of quantum mechanics. In his paper, Bell started from the same two assumptions as did EPR, namely (i) ''reality'' (that microscopic objects have real properties determining the outcomes of quantum mechanical measurements), and (ii) ''locality'' (that reality in one location is not influenced by measurements performed simultaneously at a distant location). Bell was able to derive from those two assumptions an important result, namely '''Bell's inequality''', implying that at least one of the assumptions must be false. | |||
| :Consider a mechanical system constituted of two partial systems ''A'' and ''B'' which have interaction with each other only during limited time. Let the ψ function before their interaction be given. Then the ] will furnish the ψ function after their interaction has taken place. Let us now determine the physical condition of the partial system ''A'' as completely as possible by measurements. Then the quantum mechanics allows us to determine the ψ function of the partial system ''B'' from the measurements made, and from the ψ function of the total system. This determination, however, gives a result which depends upon ''which'' of the determining magnitudes specifying the condition of ''A'' has been measured (for instance coordinates ''or'' momenta). Since there can be only ''one'' physical condition of ''B'' after the interaction and which can reasonably not be considered as dependent on the particular measurement we perform on the system ''A'' separated from ''B'' it may be concluded that the ψ function is not unambiguously coordinated with the physical condition. This coordination of several ψ functions with the same physical condition of system ''B'' shows again that the ψ function cannot be interpreted as a (complete) description of a physical condition of a unit system.<ref>{{cite journal|first=Albert |last=Einstein |author-link=Albert Einstein |title=Physics and reality |journal=Journal of the Franklin Institute |volume=221 |number=3 |date=March 1936 |pages=349–382 |doi=10.1016/S0016-0032(36)91047-5 |bibcode=1936FrInJ.221..349E}}</ref> | |||
| The EPR thought experiment is similar, also considering two separated systems ''A'' and ''B'' described by a joint wave function. However, the EPR paper adds the idea later known as the EPR criterion of reality, according to which the ability to predict with probability 1 the outcome of a measurement upon ''B'' implies the existence of an "element of reality" within ''B''.<ref>{{cite journal|first1=Nicholas |last1=Harrigan |first2=Robert W. |last2=Spekkens |title=Einstein, incompleteness, and the epistemic view of quantum states |journal=] |volume=40 |issue=2 |pages=125 |year=2010 |doi=10.1007/s10701-009-9347-0 |arxiv=0706.2661|bibcode=2010FoPh...40..125H |s2cid=32755624 }}</ref> | |||
| In two respects Bell's 1964 paper was a step forward compared to the EPR paper: firstly, it considered more ] than merely the ] in the EPR paper; and Bell's inequality was, in part, liable to be experimentally tested, thus raising the possibility of testing the local realism hypothesis. Limitations on such tests to date are noted below. Whereas Bell's paper deals only with deterministic hidden variable theories, Bell's theorem was later generalized to ] theories<ref name="Clauser–Horne">{{cite journal|doi=10.1103/PhysRevD.10.526|title=Experimental consequences of objective local theories| year=1974| last1=Clauser| first1=John F.|journal=Physical Review D|volume=10|issue=2|pages=526|bibcode = 1974PhRvD..10..526C| url=http://www.philoscience.unibe.ch/documents/physics/Clauser1974/Clauser1974.pdf}}</ref> as well, and it was also realised<ref>{{cite journal |last= Eberhard |first=P. H. |year=1977 |title=Bell's theorem without hidden variables |journal=] |volume=38 |pages=75–80 |doi= 10.1007/BF02726212 |url= http://www.iaea.org/inis/collection/NCLCollectionStore/_Public/08/282/8282046.pdf|bibcode = 1977NCimB..38...75E }}</ref> that the theorem is not so much about hidden variables, as about the outcomes of measurements that could have been taken instead of the one actually taken. Existence of these variables is called the assumption of realism, or the assumption of ]. | |||
| In 1951, ] proposed a variant of the EPR thought experiment in which the measurements have discrete ranges of possible outcomes, unlike the position and momentum measurements considered by EPR.<ref>{{cite book|last=Bohm |first=David |author-link=David Bohm |year=1989 |orig-date=1951 |title=Quantum Theory |publisher=Prentice-Hall |edition=Dover reprint |isbn=978-0-486-65969-5 |oclc=1103789975 |pages=614–623}}</ref> The year before, ] and Irving Shaknov had successfully measured polarizations of photons produced in entangled pairs, thereby making the Bohm version of the EPR thought experiment practically feasible.<ref>{{cite journal |last1=Wu |first1=C.-S. |author-link=Chien-Shiung Wu |last2=Shaknov |first2=I. |year=1950 |title=The Angular Correlation of Scattered Annihilation Radiation |journal=] |volume=77 |issue=1 |pages=136 |bibcode=1950PhRv...77..136W |doi=10.1103/PhysRev.77.136}}</ref> | |||
| After the EPR paper, quantum mechanics was in an unsatisfactory position: either it was incomplete, in the sense that it failed to account for some elements of physical reality, or it violated the principle of a finite propagation speed of physical effects. In a modified version of the EPR thought experiment, two hypothetical ], now commonly referred to as ], perform independent measurements of spin on a pair of electrons, prepared at a source in a special state called a ''] state''. It is the conclusion of EPR that once Alice measures spin in one direction (e.g. on the ''x'' axis), Bob's measurement in that direction is determined with certainty, as being the opposite outcome to that of Alice, whereas immediately before Alice's measurement Bob's outcome was only statistically determined (i.e., was only a probability, not a certainty); thus, either the spin in each direction is an ''element of physical reality'', or the effects travel from Alice to Bob instantly. | |||
| By the late 1940s, the mathematician ] had grown interested in the foundations of quantum physics, and in 1957 he drew up a list of postulates that he took to be a precise definition of quantum mechanics.<ref>{{Cite journal |last=Mackey |first=George W. |author-link=George Mackey |title=Quantum Mechanics and Hilbert Space |journal=] |year=1957 |volume=64 |number=8P2 |pages=45–57 |doi=10.1080/00029890.1957.11989120 |jstor=2308516}}</ref> Mackey conjectured that one of the postulates was redundant, and shortly thereafter, ] proved that it was indeed deducible from the other postulates.<ref name="gleason1957">{{cite journal|first=Andrew M.|author-link=Andrew M. Gleason|year = 1957|title = Measures on the closed subspaces of a Hilbert space|url = http://www.iumj.indiana.edu/IUMJ/FULLTEXT/1957/6/56050|journal = ]|volume = 6|issue=4|pages = 885–893|doi=10.1512/iumj.1957.6.56050|mr=0096113|last = Gleason|doi-access = free}}</ref><ref name="chernoff2009">{{Cite journal|last=Chernoff |first=Paul R. |author-link=Paul Chernoff |title=Andy Gleason and Quantum Mechanics |journal=] |volume=56 |number=10 |pages=1253–1259 |url=https://www.ams.org/notices/200910/rtx091001236p.pdf}}</ref> ] provided an argument that a broad class of hidden-variable theories are incompatible with quantum mechanics.{{refn|group=note|A hidden-variable theory that is ] implies that the probability of a given outcome is ''always'' either 0 or 1. For example, a Stern–Gerlach measurement on a ] atom will report that the atom's angular momentum along the chosen axis is one of three possible values, which can be designated <math>-</math>, <math>0</math> and <math>+</math>. In a deterministic hidden-variable theory, there exists an underlying physical property that fixes the result found in the measurement. Conditional on the value of the underlying physical property, any given outcome (for example, a result of <math>+</math>) must be either impossible or guaranteed. But Gleason's theorem implies that there can be no such deterministic probability measure, because it proves that any probability measure must take the form of a mapping <math>u \to \langle \rho u, u \rangle</math> for some density operator <math>\rho</math>. This mapping is continuous on the ] of the Hilbert space, and since this unit sphere is ], no continuous probability measure on it can be deterministic.<ref name="wilce2017">{{cite book|last=Wilce |first=A. |year=2017 |chapter-url=https://plato.stanford.edu/entries/qt-quantlog/ |chapter=Quantum Logic and Probability Theory |title=Stanford Encyclopedia of Philosophy |title-link=Stanford Encyclopedia of Philosophy|publisher=Metaphysics Research Lab, Stanford University }}</ref>{{rp|§1.3}}}} More specifically, Gleason's theorem rules out hidden-variable models that are "noncontextual". Any hidden-variable model for quantum mechanics must, in order to avoid the implications of Gleason's theorem, involve hidden variables that are not properties belonging to the measured system alone but also dependent upon the external context in which the measurement is made. This type of dependence is often seen as contrived or undesirable; in some settings, it is inconsistent with ].<ref name = "ND Mermin 1993-07">{{cite journal | last = Mermin |first = N. David |author-link=N. David Mermin |title = Hidden Variables and the Two Theorems of John Bell | journal = ] | volume = 65 |pages = 803–815 | number = 3| date = July 1993 | url = http://cqi.inf.usi.ch/qic/Mermin1993.pdf |arxiv=1802.10119 |doi = 10.1103/RevModPhys.65.803 |bibcode = 1993RvMP...65..803M |s2cid = 119546199 }}</ref><ref>{{Cite journal|last=Shimony |first=Abner |author-link=Abner Shimony |title=Contextual Hidden Variable Theories and Bell's Inequalities |journal=] |year=1984 |volume=35 |number=1 |pages=25–45 |doi=10.1093/bjps/35.1.25}}</ref> The Kochen–Specker theorem refines this statement by constructing a specific finite subset of rays on which no such probability measure can be defined.<ref name="ND Mermin 1993-07" /><ref>{{Cite journal|last=Peres|first=Asher|author-link=Asher Peres|date=1991|title=Two simple proofs of the Kochen-Specker theorem|url=http://stacks.iop.org/0305-4470/24/i=4/a=003|journal=]|language=en|volume=24|issue=4|pages=L175–L178|doi=10.1088/0305-4470/24/4/003|issn=0305-4470|bibcode=1991JPhA...24L.175P}}</ref> | |||
| In QM, predictions are formulated in terms of ] — for example, the probability that an ] will be detected in a particular place, or the probability that its spin is up or down. The idea persisted, however, that the electron in fact has a ''definite'' position and spin, and that QM's weakness is its inability to predict those values precisely. The possibility existed that some unknown theory, such as a ''hidden variables theory'', might be able to predict those quantities exactly, while at the same time also being in complete agreement with the probabilities predicted by QM. If such a hidden variables theory exists, then because the hidden variables are not described by QM the latter would be an incomplete theory. | |||
| ] came close to deriving Bell's theorem in 1960. He considered events where two ]s were produced traveling in opposite directions, and came to the conclusion that hidden variables could not explain the correlations that could be obtained in such situations. However, complications arose due to the fact that kaons decay, and he did not go so far as to deduce a Bell-type inequality.<ref name="jammer1974"/>{{Rp|308}} | |||
| == Bell inequalities == | |||
| Bell inequalities concern measurements made by observers on pairs of particles that have interacted and then separated. Assuming local realism, certain constraints must hold on the relationships between the correlations between subsequent measurements of the particles under various possible measurement settings. | |||
| === |
===Bell's publications=== | ||
| Bell chose to publish his theorem in a comparatively obscure journal because it did not require ]s, in fact paying the authors who published there at the time. Because the journal did not provide free reprints of articles for the authors to distribute, however, Bell had to spend the money he received to buy copies that he could send to other physicists.<ref name=":0">{{Cite book|last=Whitaker|first=Andrew|url=https://books.google.com/books?id=3Rg9DAAAQBAJ&q=fizika|title=John Stewart Bell and Twentieth Century Physics: Vision and Integrity|date=2016|publisher=Oxford University Press|isbn=978-0-19-874299-9|language=en}}</ref> While the articles printed in the journal themselves listed the publication's name simply as ''Physics'', the covers carried the trilingual version '']'' to reflect that it would print articles in English, French and Russian.<ref name=":1">{{cite book|last=Wick|first=David|chapter=Bell's Theorem |pages=92–100 |year=1995|title=The Infamous Boundary: Seven Decades of Heresy in Quantum Physics |publisher=Springer |location=New York|doi=10.1007/978-1-4612-4030-3_11|isbn=978-0-387-94726-6}}</ref>{{Rp|92–100, 289}} | |||
| The inequality that Bell derived can be written as:<ref name=Bell1964/> | |||
| Prior to proving his 1964 result, Bell also proved a result equivalent to the Kochen–Specker theorem (hence the latter is sometimes also known as the Bell–Kochen–Specker or Bell–KS theorem). However, publication of this theorem was inadvertently delayed until 1966.<ref name="ND Mermin 1993-07" /><ref name="Bell1966">{{cite journal | last1 = Bell | first1 = J. S. | title = On the problem of hidden variables in quantum mechanics | journal = Reviews of Modern Physics | volume = 38 | issue = 3 | pages = 447–452 | year = 1966 | doi = 10.1103/revmodphys.38.447 |bibcode = 1966RvMP...38..447B | osti = 1444158 }}</ref> In that paper, Bell argued that because an explanation of quantum phenomena in terms of hidden variables would require nonlocality, the EPR paradox "is resolved in the way which Einstein would have liked least."<ref name="Bell1966"/> | |||
| : <math> \rho(a, c) -\rho(b, a) - \rho(b, c) \le 1,</math> | |||
| ==Experiments== | |||
| where {{mvar|ρ}} is the ] between measurements of the spins of the pair of particles and {{mvar|a, b}} and ''c'' refer to three arbitrary settings of the two analysers. This inequality is however restricted in its application to the rather special case in which the outcomes on both sides of the experiment are always exactly anticorrelated whenever the analysers are parallel. The advantage of restricting attention to this special case is the resulting simplicity of the derivation. In experimental work the inequality is not very useful because it is hard, if not impossible, to create ''perfect'' anti-correlation. | |||
| ] | |||
| {{main|Bell test}} | |||
| In 1967, the unusual title ''Physics Physique Физика'' caught the attention of ], who then discovered Bell's paper and began to consider how to perform a ] in the laboratory.<ref>{{Cite web|url=https://www.scientificamerican.com/article/how-the-hippies-saved-physics-science-counterculture-and-quantum-revival-excerpt/|title=How the Hippies Saved Physics: Science, Counterculture, and the Quantum Revival |last=Kaiser|first=David|author-link=David Kaiser (physicist)|date=2012-01-30|website=]|language=en|access-date=2020-02-11}}</ref> Clauser and ] would go on to perform a Bell test in 1972.<ref>{{cite journal|last1=Freedman|first1=S. J.|author-link=Stuart Freedman|last2=Clauser|first2=J. F.|author-link2=John Clauser|year=1972|title=Experimental test of local hidden-variable theories|url=https://www.rpi.edu/dept/phys/Courses/PHYS4100/S06/BellsInequ1972.pdf|journal=]|volume=28|issue=938|pages=938–941|bibcode=1972PhRvL..28..938F|doi=10.1103/PhysRevLett.28.938}}</ref><ref>{{cite thesis|url=https://escholarship.org/content/qt2f18n5nk/qt2f18n5nk.pdf?t=p2au19 |title=Experimental test of local hidden-variable theories |first=Stuart Jay |last=Freedman |date=1972-05-05 |type=PhD |publisher=University of California, Berkeley}}</ref> This was only a limited test, because the choice of detector settings was made before the photons had left the source. In 1982, ] and collaborators performed the ] to remove this limitation.<ref>{{cite journal |first1=Alain |last1=Aspect |author-link1=Alain Aspect |first2=Jean |last2=Dalibard |first3=Gérard |last3=Roger |year=1982 |title=Experimental Test of Bell's Inequalities Using Time-Varying Analyzers |journal=] |volume=49 |issue=25 |pages=1804–7 |doi=10.1103/PhysRevLett.49.1804|bibcode = 1982PhRvL..49.1804A|doi-access=free }}</ref> This began a trend of progressively more stringent Bell tests. The GHZ thought experiment was implemented in practice, using entangled triplets of photons, in 2000.<ref name="GHZ2000">{{cite journal |first1=Jian-Wei |last1=Pan |first2=D. |last2=Bouwmeester |first3=M. |last3=Daniell |first4=H. |last4=Weinfurter |first5=A. |last5=Zeilinger |author-link5=Anton Zeilinger |year=2000 |title=Experimental test of quantum nonlocality in three-photon GHZ entanglement |journal=] |volume=403 |issue=6769 |pages=515–519 |bibcode=2000Natur.403..515P |doi=10.1038/35000514 |pmid=10676953|s2cid=4309261 }}</ref> By 2002, testing the CHSH inequality was feasible in undergraduate laboratory courses.<ref>{{cite journal|title=Entangled photons, nonlocality, and Bell inequalities in the undergraduate laboratory |first1=Dietrich |last1=Dehlinger |first2=M. W. |last2=Mitchell |journal=] |volume=70 |pages=903–910 |year=2002 |issue=9 |doi=10.1119/1.1498860|arxiv=quant-ph/0205171 |bibcode=2002AmJPh..70..903D |s2cid=49487096 }}</ref> | |||
| This simple form does have the virtue of being quite intuitive. It is easily seen to be equivalent to the following elementary result from probability theory. Consider three (highly correlated, and possibly biased) coin-flips {{mvar|X, Y}}, and ''Z'', with the property that: | |||
| #''X'' and ''Y'' give the same outcome (both heads or both tails) 99% of the time | |||
| #''Y'' and ''Z'' also give the same outcome 99% of the time, | |||
| In Bell tests, there may be problems of experimental design or set-up that affect the validity of the experimental findings. These problems are often referred to as "loopholes". The purpose of the experiment is to test whether nature can be described by ], which would contradict the predictions of quantum mechanics. | |||
| then ''X'' and ''Z'' must also yield the same outcome at least 98% of the time. The number of mismatches between ''X'' and ''Y'' (1/100) plus the number of mismatches between ''Y'' and ''Z'' (1/100) are together the ''maximum possible'' number of mismatches between ''X'' and ''Z'' (a simple ]). | |||
| The most prevalent loopholes in real experiments are the ''detection'' and ''locality'' loopholes.<ref name=larsson14>{{cite journal |last1=Larsson |first1=Jan-Åke |title=Loopholes in Bell inequality tests of local realism |journal=Journal of Physics A: Mathematical and Theoretical |date=2014 |volume=47 |issue=42 |page=424003 |doi=10.1088/1751-8113/47/42/424003 |arxiv=1407.0363 |bibcode=2014JPhA...47P4003L |s2cid=40332044 }}</ref> The detection loophole is opened when a small fraction of the particles (usually photons) are detected in the experiment, making it possible to explain the data with local hidden variables by assuming that the detected particles are an unrepresentative sample. The locality loophole is opened when the detections are not done with a ], making it possible for the result of one measurement to influence the other without contradicting relativity. In some experiments there may be additional defects that make local-hidden-variable explanations of Bell test violations possible.<ref>{{cite journal|first1=I. |last1=Gerhardt |first2=Q. |last2=Liu |first3=A. |last3=Lamas-Linares |first4=J. |last4=Skaar |first5=V. |last5=Scarani |first6=V. |last6=Makarov |first7=C. |last7=Kurtsiefer |display-authors=5|year=2011 |title=Experimentally faking the violation of Bell's inequalities |journal=] |volume=107 |issue=17 |page=170404 |arxiv=1106.3224 |doi=10.1103/PhysRevLett.107.170404 |bibcode=2011PhRvL.107q0404G |pmid=22107491|s2cid=16306493 }}</ref> | |||
| Imagine a pair of particles that can be measured at distant locations. Suppose that the measurement devices have settings, which are angles—e.g., the devices measure something called spin in some direction. The experimenter chooses the directions, one for each particle, separately. Suppose the measurement outcome is binary (e.g., spin up, spin down). Suppose the two particles are perfectly anti-correlated—in the sense that whenever both measured in the same direction, one gets identically opposite outcomes, when both measured in opposite directions they always give the same outcome. The only way to imagine how this works is that both particles leave their common source with, somehow, the outcomes they will deliver when measured in any possible direction. (How else could particle 1 know how to deliver the same answer as particle 2 when measured in the same direction? They don't know in advance how they are going to be measured...). The measurement on particle 2 (after switching its sign) can be thought of as telling us what the same measurement on particle 1 would have given. | |||
| Although both the locality and detection loopholes had been closed in different experiments, a long-standing challenge was to close both simultaneously in the same experiment. This was finally achieved in three experiments in 2015.<ref>{{cite journal|title=Quantum 'spookiness' passes toughest test yet|journal=] |date=27 August 2015|first=Zeeya|last=Merali|volume=525 |issue=7567|pages=14–15|doi=10.1038/nature.2015.18255 |pmid=26333448|bibcode=2015Natur.525...14M |s2cid=4409566|doi-access=free}}</ref><ref name="NYT-20151021">{{cite news |last=Markoff |first=Jack |title=Sorry, Einstein. Quantum Study Suggests 'Spooky Action' Is Real. |url=https://www.nytimes.com/2015/10/22/science/quantum-theory-experiment-said-to-prove-spooky-interactions.html |date=21 October 2015 |work=] |accessdate=21 October 2015 }}</ref><ref name="NTR-20151021">{{cite journal |author=Hensen, B. |title=Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres |date=21 October 2015 |journal=] |doi=10.1038/nature15759 |display-authors=etal |volume=526 |issue=7575 |pages=682–686 |bibcode=2015Natur.526..682H |pmid=26503041|arxiv=1508.05949 |s2cid=205246446 }}</ref><ref name="PRL115-250402">{{cite journal |last=Shalm |first=L. K. |title=Strong Loophole-Free Test of Local Realism|date=16 December 2015|journal=] |display-authors=etal |volume=115|issue=25|page= 250402| doi=10.1103/PhysRevLett.115.250402 |bibcode=2015PhRvL.115y0402S |pmid=26722906|pmc=5815856|arxiv=1511.03189}}</ref><ref name="PRL115-250401">{{cite journal |last=Giustina |first=M. |title=Significant-Loophole-Free Test of Bell's Theorem with Entangled Photons|date=16 December 2015|journal=] |display-authors=etal |volume=115|issue=25|page= 250401| doi=10.1103/PhysRevLett.115.250401 |pmid=26722905|arxiv=1511.03190|bibcode=2015PhRvL.115y0401G|s2cid=13789503}}</ref> | |||
| Start with one setting exactly opposite to the other. All the pairs of particles give the same outcome (each pair is either both spin up or both spin down). Now shift Alice's setting by one degree relative to Bob's. They are now one degree off being exactly opposite to one another. A small fraction of the pairs, say ''f'', now give different outcomes. If instead we had left Alice's setting unchanged but shifted Bob's by one degree (in the opposite direction), then again a fraction ''f'' of the pairs of particles turns out to give different outcomes. Finally consider what happens when both shifts are implemented at the same time: the two settings are now exactly two degrees away from being opposite to one another. By the mismatch argument, the chance of a mismatch at two degrees can't be more than twice the chance of a mismatch at one degree: it cannot be more than 2''f''. | |||
| Regarding these results, ] writes that "no experiment ... can be said to be totally loophole-free," but he says the experiments "remove the last doubts that we should renounce" local hidden variables, and refers to examples of remaining loopholes as being "far fetched" and "foreign to the usual way of reasoning in physics."<ref>{{cite journal |last=Aspect |first=Alain |author-link=Alain Aspect |date=December 16, 2015 |title=Closing the Door on Einstein and Bohr's Quantum Debate |journal=] |volume=8 |pages=123 |bibcode=2015PhyOJ...8..123A |doi=10.1103/Physics.8.123 |doi-access=free}}</ref> | |||
| These efforts to experimentally validate violations of the Bell inequalities would later result in Clauser, Aspect, and ] being awarded the 2022 ].<ref>{{Cite news |last1=Ahlander |first1=Johan |last2=Burger |first2=Ludwig |last3=Pollard |first3=Niklas |date=2022-10-04 |title=Nobel physics prize goes to sleuths of 'spooky' quantum science |language=en |work=Reuters |url=https://www.reuters.com/world/aspect-clauser-zeilinger-win-2022-nobel-prize-physics-2022-10-04/ |access-date=2022-10-04}}</ref> | |||
| Compare this with the predictions from quantum mechanics for the singlet state. For a small angle {{mvar|θ}}, measured in radians, the chance of a different outcome is approximately <math>f=\theta^2/2</math>.{{clarify|reason=Give a wikilink to an appropriate quantum theory article or section.|date=January 2015}} At two times this small angle, the chance of a mismatch is therefore about 4 times larger, since <math>2^2=4</math>. But we just argued that it cannot be more than 2 times as large. | |||
| == Interpretations == | |||
| This intuitive formulation is due to ]. The small-angle limit is discussed in Bell's original article, and therefore goes right back to the origin of the Bell inequalities. | |||
| {{main|Interpretations of quantum mechanics}} | |||
| Reactions to Bell's theorem have been many and varied. Maximilian Schlosshauer, Johannes Kofler, and Zeilinger write that Bell inequalities provide "a wonderful example of how we can have a rigorous theoretical result tested by numerous experiments, and yet disagree about the implications."<ref>{{Cite journal| arxiv=1301.1069 | |||
| | title=A Snapshot of Foundational Attitudes Toward Quantum Mechanics | |||
| | journal=Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics | |||
| | volume=44 | |||
| | issue=3 | |||
| | pages=222–230 | |||
| | date=2013-01-06 | |||
| | last1=Schlosshauer | |||
| | first1=Maximilian | |||
| | last2=Kofler | |||
| | first2=Johannes | |||
| | last3=Zeilinger | |||
| | first3=Anton | |||
| | author-link3=Anton Zeilinger | |||
| | doi=10.1016/j.shpsb.2013.04.004 | |||
| | bibcode=2013SHPMP..44..222S | |||
| | s2cid=55537196 | |||
| }}</ref> | |||
| === The Copenhagen interpretation === | |||
| ===CHSH inequality=== | |||
| ] generally take the violation of Bell inequalities as grounds to reject the assumption often called ] or "realism", which is not necessarily the same as abandoning realism in a broader philosophical sense.<ref>{{Cite journal|last=Werner|first=Reinhard F. |author-link=Reinhard F. Werner |date=2014-10-24|title=Comment on 'What Bell did'|journal=]|volume=47|issue=42|pages=424011|doi=10.1088/1751-8113/47/42/424011|issn=1751-8113 |bibcode=2014JPhA...47P4011W|s2cid=122180759 }}</ref><ref>{{cite book|last=Żukowski|first=Marek|title=Quantum [Un]Speakables II |chapter=Bell's Theorem Tells Us Not What Quantum Mechanics is, but What Quantum Mechanics is Not |date=2017|series=The Frontiers Collection|pages=175–185|editor-last=Bertlmann|editor-first=Reinhold|place=Cham|publisher=Springer International Publishing|doi=10.1007/978-3-319-38987-5_10|isbn=978-3-319-38985-1|editor2-last=Zeilinger|editor2-first=Anton |editor-link2=Anton Zeilinger |arxiv=1501.05640|s2cid=119214547}}</ref> For example, ] argues for the rejection of hidden variables and concludes that "quantum mechanics is probably as realistic as any theory of its scope and maturity ever will be".<ref name="omnes">{{cite book|first=R. |last=Omnès |author-link=Roland Omnès |title=The Interpretation of Quantum Mechanics |publisher=Princeton University Press |year=1994 |isbn=978-0-691-03669-4 |oclc=439453957 }}</ref>{{Rp|531}} Likewise, ] took the message of Bell's theorem to be that, because the premise of locality is physically reasonable, "hidden variables cannot be introduced without abandoning some of the results of quantum mechanics".<ref>{{cite book|last=Peierls |first=Rudolf |author-link=Rudolf Peierls |title=Surprises in Theoretical Physics |pages=26–29 |publisher=Princeton University Press |year=1979 |isbn=0-691-08241-3}}</ref><ref>{{cite journal|last=Mermin |first=N. D. |author-link=N. David Mermin |title=What Do These Correlations Know About Reality? Nonlocality and the Absurd |journal=] |volume=29 |year=1999 |issue=4 |pages=571–587 |arxiv=quant-ph/9807055 |bibcode=1998quant.ph..7055M |doi=10.1023/A:1018864225930}}</ref> | |||
| {{Main|CHSH inequality}} | |||
| Generalizing Bell's original inequality,<ref name=Bell1964/> ], Michael Horne, ] and R. A. Holt,<ref name="Clauser 1969">{{cite journal |doi=10.1103/PhysRevLett.23.880 |title=Proposed Experiment to Test Local Hidden-Variable Theories |year=1969 |last1=Clauser |first1=John |last2=Horne |first2=Michael |last3=Shimony |first3=Abner |last4=Holt |first4=Richard |journal=Physical Review Letters |volume=23 |issue=15 |pages=880|bibcode = 1969PhRvL..23..880C |url= ftp://ftp.phy.pku.edu.cn/pub/Books/%CE%EF%C0%ED/%BE%AD%B5%E4%D6%F8%D7%F7/Phy%20Rev%20100%C4%EA%BE%AB%D1%A1/pdf/14/022.pdf}}</ref> introduced the ],<ref name="Clauser 1969"/> which puts classical limits on the set of four correlations in Alice and Bob's experiment, without any assumption of perfect correlations (or anti-correlations) at equal settings | |||
| This is also the route taken by interpretations that descend from the Copenhagen tradition, such as ] (often advertised as "Copenhagen done right"),<ref>{{Cite journal|last=Hohenberg|first=P. C.|author-link=Pierre Hohenberg|date=2010-10-05|title=Colloquium : An introduction to consistent quantum theory|journal=] |language=en |volume=82 |issue=4 |pages=2835–2844 |arxiv=0909.2359 |doi=10.1103/RevModPhys.82.2835 |issn=0034-6861 |bibcode=2010RvMP...82.2835H|s2cid=20551033}}</ref>{{rp|2839|q=CQT most definitely opts for retaining locality (EPR2) and rejecting classical realism (EPR1)}} as well as ].<ref>{{Cite book|chapter-url=https://plato.stanford.edu/entries/quantum-bayesian/|title=] |last=Healey|first=Richard|publisher=Metaphysics Research Lab, Stanford University|year=2016|editor-last=Zalta|editor-first=Edward N.|chapter=Quantum-Bayesian and Pragmatist Views of Quantum Theory|access-date=2021-09-16|archive-date=2021-08-17|archive-url=https://web.archive.org/web/20210817204745/https://plato.stanford.edu/entries/quantum-bayesian/|url-status=live}}</ref> | |||
| :<math>(1) \quad \rho(a,b) + \rho(a,b') + \rho(a',b) - \rho(a',b') \leq 2</math>, | |||
| === Many-worlds interpretation of quantum mechanics === | |||
| where {{mvar|ρ}} denotes correlation in the quantum physicist's sense: the expected value of the product of the two binary (+/-1 valued) outcomes. | |||
| The ], also known as the ] interpretation, is dynamically local, meaning that it does not call for ],<ref name=BrownTimpson/>{{rp|17}} and deterministic, because it consists of the unitary part of quantum mechanics without collapse. It can generate correlations that violate a Bell inequality because it violates an implicit assumption by Bell that measurements have a single outcome. In fact, Bell's theorem can be proven in the Many-Worlds framework from the assumption that a measurement has a single outcome. Therefore, a violation of a Bell inequality can be interpreted as a demonstration that measurements have multiple outcomes.<ref>{{cite journal |first1=David |last1=Deutsch |author-link1=David Deutsch |first2=Patrick |last2=Hayden |author-link2=Patrick Hayden (scientist) |title=Information flow in entangled quantum systems |journal=] |date=2000 |volume=456 |issue=1999 |pages=1759–1774 |doi=10.1098/rspa.2000.0585|arxiv=quant-ph/9906007|bibcode=2000RSPSA.456.1759D |s2cid=13998168 }}</ref> | |||
| Making the special choice <math>a'=a+\pi</math>, denoting <math>b'=c</math>, and assuming perfect anti-correlation at equal settings, perfect correlation at opposite settings, therefore <math>\rho(a,a+\pi)=1</math> and <math>\rho(b,a+\pi)=-\rho(b,a)</math>, the CHSH inequality reduces to the original Bell inequality. Nowadays, (1) is also often simply called "the Bell inequality", but sometimes more completely "the Bell-CHSH inequality". | |||
| The explanation it provides for the Bell correlations is that when Alice and Bob make their measurements, they split into local branches. From the point of view of each copy of Alice, there are multiple copies of Bob experiencing different results, so Bob cannot have a definite result, and the same is true from the point of view of each copy of Bob. They will obtain a mutually well-defined result only when their future light cones overlap. At this point we can say that the Bell correlation starts existing, but it was produced by a purely local mechanism. Therefore, the violation of a Bell inequality cannot be interpreted as a proof of non-locality.<ref name=BrownTimpson>{{Cite book|first1=Harvey R. |last1=Brown |author-link1=Harvey R. Brown |first2 = Christopher G. |last2=Timpson|chapter=Bell on Bell's Theorem: The Changing Face of Nonlocality|title=Quantum Nonlocality and Reality: 50 years of Bell's theorem |editor-first1=Mary |editor-last1=Bell |editor-first2=Shan |editor-last2=Gao |publisher=Cambridge University Press|year=2016|pages = 91–123|arxiv=1501.03521|doi=10.1017/CBO9781316219393.008|isbn = 9781316219393|s2cid = 118686956}}</ref>{{rp|28|q=In our discussion of locality in the Everett interpretation we have sought to provide a constructive example illustrating precisely how a theory can be dynamically local, whilst violating local causality}} | |||
| ==Local realism== | |||
| To prove Bell's theorem via a derivation of the Bell-CHSH inequality, we first have to formalize local realism. A common approach is the following: | |||
| # There is a ] {{math|Λ}} and the observed outcomes by both Alice and Bob result by random sampling of the (unknown, "hidden") parameter {{math|''λ'' ∈ Λ}}. | |||
| # The values observed by Alice or Bob are functions of the local detector settings and the hidden parameter only. Thus | |||
| #*Value observed by Alice with detector setting {{mvar|a}} is <math>\scriptstyle A(a,\lambda)</math> | |||
| #*Value observed by Bob with detector setting {{mvar|b}} is <math>\scriptstyle B(b,\lambda)</math> | |||
| === Non-local hidden variables === | |||
| Implicit in assumption 1) above, the hidden parameter space {{math|Λ}} has a ] {{mvar|ρ}} and the ] of a random variable {{mvar|X}} on {{math|Λ}} with respect to {{mvar|ρ}} is written | |||
| Most advocates of the hidden-variables idea believe that experiments have ruled out local hidden variables.{{refn|group=note|] was one exception,<ref name="E.T. Jaynes 1989">{{Cite book |year=1989 |last1=Jaynes |first1=E. T. |title=Maximum Entropy and Bayesian Methods |chapter=Clearing up Mysteries — the Original Goal |pages=1–27 |url=http://bayes.wustl.edu/etj/articles/cmystery.pdf |doi=10.1007/978-94-015-7860-8_1 |isbn=978-90-481-4044-2 |citeseerx=10.1.1.46.1264 |access-date=2011-10-18 |archive-date=2011-10-28 |archive-url=https://web.archive.org/web/20111028131916/http://bayes.wustl.edu/etj/articles/cmystery.pdf |url-status=live }}</ref> but Jaynes' arguments have not generally been found persuasive.<ref name="Gill2002">{{cite book|chapter=Time, Finite Statistics, and Bell's Fifth Position|first=Richard D.|last=Gill|pages=179–206|title=Proceedings of the Conference Foundations of Probability and Physics - 2 : Växjö (Soland), Sweden, June 2-7, 2002 |volume=5|publisher=Växjö University Press|date=2002|arxiv=quant-ph/0301059 }}</ref>}} They are ready to give up locality, explaining the violation of Bell's inequality by means of a non-local ], in which the particles exchange information about their states. This is the basis of the ] of quantum mechanics, which requires that all particles in the universe be able to instantaneously exchange information with all others. One challenge for non-local hidden variable theories is to explain why this instantaneous communication can exist at the level of the hidden variables, but it cannot be used to send signals.<ref>{{Cite journal |last1=Wood |first1=Christopher J. |last2=Spekkens |first2=Robert W. |author-link2=Robert Spekkens |date=2015-03-03 |title=The lesson of causal discovery algorithms for quantum correlations: causal explanations of Bell-inequality violations require fine-tuning |url=https://iopscience.iop.org/article/10.1088/1367-2630/17/3/033002 |journal=] |volume=17 |issue=3 |pages=033002 |arxiv=1208.4119 |bibcode=2015NJPh...17c3002W |doi=10.1088/1367-2630/17/3/033002 |s2cid=118518558 |issn=1367-2630}}</ref> A 2007 experiment ruled out a large class of non-Bohmian non-local hidden variable theories, though not Bohmian mechanics itself.<ref>{{cite journal |doi=10.1038/nature05677 |title=An experimental test of non-local realism |year=2007 |last1=Gröblacher |first1=Simon |last2=Paterek |first2=Tomasz |last3=Kaltenbaek |first3=Rainer |last4=Brukner |first4=Časlav |author-link4=Časlav Brukner |last5=Żukowski |first5=Marek |last6=Aspelmeyer |first6=Markus |last7=Zeilinger |first7=Anton |author-link7=Anton Zeilinger |journal=] |volume=446 |issue=7138 |pages=871–5 |pmid=17443179|bibcode = 2007Natur.446..871G | arxiv= 0704.2529 |s2cid=4412358 }}</ref> | |||
| :<math> \operatorname{E}(X) = \int_\Lambda X(\lambda) \rho(\lambda) d \lambda </math> | |||
| The ], which postulates waves traveling both backwards and forwards in time, is likewise non-local.<ref>{{Cite journal|last=Kastner|first=Ruth E.|date=May 2010|title=The quantum liar experiment in Cramer's transactional interpretation|url=https://linkinghub.elsevier.com/retrieve/pii/S135521981000002X|journal=] |language=en|volume=41|issue=2|pages=86–92|arxiv=0906.1626|bibcode=2010SHPMP..41...86K|doi=10.1016/j.shpsb.2010.01.001|s2cid=16242184|access-date=2021-09-16|archive-date=2018-06-24|archive-url=https://web.archive.org/web/20180624053010/https://linkinghub.elsevier.com/retrieve/pii/S135521981000002X|url-status=live}}</ref> | |||
| where for accessibility of notation we assume that the probability measure has a density {{mvar|ρ}} that therefore is nonnegative and integrates to 1. The hidden parameter is often thought of as being associated with source but it can just as well also contain components associated with the two measurement devices. | |||
| ===Superdeterminism=== | |||
| === Derivation of CHSH inequality=== | |||
| {{Main|Superdeterminism}} | |||
| Given this formalization of what is meant by local realism, or by a hidden variables theory, the CHSH inequality can be derived as follows. | |||
| A necessary assumption to derive Bell's theorem is that the hidden variables are not correlated with the measurement settings. This assumption has been justified on the grounds that the experimenter has "]" to choose the settings, and that it is necessary to do science in the first place. A (hypothetical) theory where the choice of measurement is necessarily correlated with the system being measured is known as ''superdeterministic''.<ref name=larsson14/> | |||
| A few advocates of deterministic models have not given up on local hidden variables. For example, ] has argued that superdeterminism cannot be dismissed.<ref>{{cite book |last='t Hooft |first=Gerard |author-link=Gerard 't Hooft |title=The Cellular Automaton Interpretation of Quantum Mechanics |volume=185 |publisher=Springer |year=2016 |doi=10.1007/978-3-319-41285-6 |isbn=978-3-319-41284-9 |oclc=951761277 |series=Fundamental Theories of Physics |s2cid=7779840 |url=http://www.oapen.org/search?identifier=1002003 |access-date=2020-08-27 |archive-date=2021-12-29 |archive-url=https://web.archive.org/web/20211229062338/https://library.oapen.org/handle/20.500.12657/27994 |url-status=live }}</ref> | |||
| The subsequent derivation is clearer if we use the following abbreviated notation: <math>A=A(a, \lambda), A'=A(a', \lambda), B=B(b, \lambda), B'=B(b', \lambda)</math>. Thus each of these four quantities is {{math|±1}} and each depends on {{mvar|λ}}. It follows that for any {{math|''λ'' ∈ Λ}}, one of <math>B+B'</math> and <math>B-B'</math> is zero, and the other is {{math|±2}}. From this it follows that | |||
| :<math>AB + AB' + A'B - A'B'= A(B+B') + A'(B-B')\leq 2</math> | |||
| and therefore | |||
| :<math>\begin{align} | |||
| \rho(a,b) + \rho(a,b') + \rho(a',b) - \rho(a',b')&= \int_\Lambda AB\rho +\int_\Lambda AB'\rho +\int_\Lambda A'B\rho -\int_\Lambda A'B'\rho \\ | |||
| &= \int_\Lambda (AB+AB'+A'B-A'B')\rho\\ | |||
| &= \int_\Lambda (A(B+B') + A'(B-B')) \rho\\ | |||
| &\leq 2 | |||
| \end{align}</math> | |||
| At the heart of this derivation is a simple algebraic inequality concerning four variables, <math>A, A', B, B'</math>, which take the values {{math|±1}} only: | |||
| :<math>AB+AB'+A'B-A'B'= A(B+B')+A'(B-B') \le 2.</math> | |||
| The CHSH inequality is seen to depend only on the following three key features of a local hidden variables theory: (1) realism: alongside of the outcomes of actually performed measurements, the outcomes of potentially performed measurements also exist at the same time; (2) locality, the outcomes of measurements on Alice's particle don't depend on which measurement Bob chooses to perform on the other particle; (3) freedom: Alice and Bob can indeed choose freely which measurements to perform. | |||
| The ''realism'' assumption is actually somewhat idealistic, and Bell's theorem only proves non-locality with respect to variables that only ''exist'' for metaphysical reasons. However, before the discovery of quantum mechanics, both realism and locality were completely uncontroversial features of physical theories. | |||
| ==Bell inequalities are violated by quantum mechanical predictions== | |||
| The measurements performed by Alice and Bob are spin measurements on electrons. Alice can choose between two detector settings labeled ''a'' and ''a''′; these settings correspond to measurement of spin along the ''z'' or the ''x'' axis. Bob can choose between two detector settings labeled ''b'' and ''b''′; these correspond to measurement of spin along the ''z''′ or ''x''′ axis, where the {{math|''x''′ − ''z''′}} coordinate system is rotated 135° relative to the {{math|''x'' − ''z''}} coordinate system. The spin observables are represented by the 2 × 2 self-adjoint matrices: | |||
| :<math> S_x = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}, \quad S_z = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}</math> | |||
| These are the ] normalized so that the corresponding eigenvalues are {{math|±1}}. As is customary, we use the ] to denote the eigenvectors of {{mvar|S<sub>x</sub>}} by | |||
| :<math> \left|+x\right\rang, \quad |-x\rang. </math> | |||
| Let <math>\phi</math> be the spin singlet state for a pair of electrons discussed in the EPR paradox. This is a specially constructed state described by the following vector in the tensor product | |||
| :<math>|\phi\rang = \frac{1}{\sqrt{2}} \left(|+x\rang \otimes |-x\rang -|-x\rang \otimes |+x\rang \right)</math> | |||
| Now let us apply the CHSH formalism to the measurements that can be performed by Alice and Bob. | |||
| :<math>\begin{align} | |||
| A(a) &= S_z \otimes I\\ | |||
| A(a') &= S_x \otimes I\\ | |||
| B(b) &= -\frac{1}{\sqrt{2}} \ I \otimes (S_z + S_x)\\ | |||
| B(b') &= \frac{1}{\sqrt{2}} \ I \otimes (S_z - S_x) | |||
| \end{align}</math> | |||
| The operators <math>\scriptstyle B(b'), B(b)</math> correspond to Bob's spin measurements along ''x''′ and ''z''′. Note that the {{mvar|A}} operators commute with the {{mvar|B}} operators, so we can apply our calculation for the correlation. In this case, we can show that the CHSH inequality fails. In fact, a straightforward calculation shows that {{Citation needed|date=August 2014}} | |||
| :<math>\langle A(a) B(b) \rangle = \langle A(a') B(b) \rangle = \langle A(a') B(b') \rangle = \tfrac{1}{\sqrt{2}}</math> | |||
| :<math>\langle A(a) B(b')\rangle = -\tfrac{1}{\sqrt{2}} </math> | |||
| so that | |||
| :<math>\langle A(a) B(b) \rangle + \langle A(a') B(b') \rangle + \langle A(a') B(b) \rangle - \langle A(a) B(b') \rangle = \tfrac{4}{\sqrt{2}} = 2 \sqrt{2} > 2</math> | |||
| Bell's Theorem: If the quantum mechanical formalism is correct, then the system consisting of a pair of entangled electrons cannot satisfy the principle of local realism. Note that {{math|2{{sqrt|2}}}} is indeed the upper bound for quantum mechanics called ]. The operators giving this maximal value are always ] to the Pauli matrices. | |||
| ==Practical experiments testing Bell's theorem== | |||
| ] | |||
| {{Main|Bell test experiments}} | |||
| Experimental tests can determine whether the Bell inequalities required by local realism hold up to the empirical evidence. | |||
| Actually, most experiments have been performed using polarization of photons rather than spin of electrons (or other spin-half particles). The quantum state of the pair of entangled photons is not the singlet state, and the correspondence between angles and outcomes is different from that in the spin-half set-up. The polarization of a photon is measured in a pair of perpendicular directions. Relative to a given orientation, polarization is either vertical (denoted by V or by +) or horizontal (denoted by H or by -). The photon pairs are generated in the quantum state | |||
| :<math> \tfrac{1}{\sqrt{2}} \left (|V\rangle\otimes |V\rangle+|H\rangle\otimes|H\rangle \right)</math> | |||
| where <math>|V\rangle</math> and <math>|H\rangle</math> denotes the state of a single vertically or horizontally polarized photon, respectively (relative to a fixed and common reference direction for both particles). | |||
| When the polarization of both photons is measured in the same direction, both give the same outcome: perfect correlation. When measured at directions making an angle 45 degrees with one another, the outcomes are completely random (uncorrelated). Measuring at directions at 90 degrees to one another, the two are perfectly anti-correlated. In general, when the polarizers are at an angle {{mvar|θ}} to one another, the correlation is {{math|cos(2''θ'')}}. So relative to the correlation function for the singlet state of spin half particles, we have a positive rather than a negative cosine function, and angles are halved: the correlation is periodic with period {{mvar|π}} instead of {{math|2''π''}}. | |||
| Bell's inequalities are tested by "coincidence counts" from a Bell test experiment such as the optical one shown in the diagram. Pairs of particles are emitted as a result of a quantum process, analysed with respect to some key property such as polarisation direction, then detected. The setting (orientations) of the analysers are selected by the experimenter. | |||
| Bell test experiments to date overwhelmingly violate Bell's inequality. | |||
| ===Two classes of Bell inequalities=== | |||
| The ''fair sampling'' problem was faced openly in the 1970s. In early designs of their 1973 experiment, Freedman and Clauser<ref name="Clauser–Freedman">{{cite journal |doi=10.1103/PhysRevLett.28.938 |title=Experimental Test of Local Hidden-Variable Theories |year=1972 |last1=Freedman |first1=Stuart J. |last2=Clauser |first2=John F. |journal=Physical Review Letters |volume=28 |issue=14 |pages=938|bibcode = 1972PhRvL..28..938F |url= http://dieumsnh.qfb.umich.mx/archivoshistoricosMQ/ModernaHist/Freedman.pdf }}</ref> used ''fair sampling'' in the form of the Clauser–Horne–Shimony–Holt (CHSH<ref name="Clauser 1969"/>) hypothesis. However, shortly afterwards Clauser and Horne<ref name="Clauser–Horne"/> made the important distinction between inhomogeneous (IBI) and homogeneous (HBI) Bell inequalities. Testing an IBI requires that we compare certain coincidence rates in two separated detectors with the singles rates of the two detectors. Nobody needed to perform the experiment, because singles rates with all detectors in the 1970s were at least ten times all the coincidence rates. So, taking into account this low detector efficiency, the QM prediction actually satisfied the IBI. To arrive at an experimental design in which the QM prediction violates IBI we require detectors whose efficiency exceeds 82.8% for singlet states,<ref name="Garg & Mermin, 1987">{{citation |author=Anupam Garg, N.D. Mermin |year=1987 |title=Detector inefficiencies in the Einstein-Podolsky-Rosen experiment |journal=Phys. Rev. D |volume=25 |issue=12 |pages=3831–5 |doi=10.1103/PhysRevD.35.3831|bibcode = 1987PhRvD..35.3831G }}</ref> but have very low dark rate and short dead and resolving times. This is now within reach. | |||
| ===Practical challenges=== | |||
| {{Main|Loopholes in Bell test experiments}} | |||
| Because, at that time, even the best detectors didn't detect a large fraction of all photons, Clauser and Horne<ref name="Clauser–Horne"/> recognized that testing Bell's inequality required some extra assumptions. They introduced the ''No Enhancement Hypothesis'' (NEH): | |||
| {{quote|A light signal, originating in an ] for example, has a certain probability of activating a detector. Then, if a polarizer is interposed between the cascade and the detector, the detection probability cannot increase.}} | |||
| Given this assumption, there is a Bell inequality between the coincidence rates with polarizers and coincidence rates without polarizers. | |||
| The experiment was performed by Freedman and Clauser,<ref name="Clauser–Freedman"/> who found that the Bell's inequality was violated. So the no-enhancement hypothesis cannot be true in a local hidden variables model. | |||
| While early experiments used atomic cascades, later experiments have used parametric down-conversion, following a suggestion by Reid and Walls<ref>{{cite journal|author1-link=Margaret D. Reid |first1=M. D. |last1=Reid |first2=D. F. |last2=Walls |title= Violations of classical inequalities in quantum optics|journal=]|volume=34|page=1260|year=1986|url=http://journals.aps.org/pra/abstract/10.1103/PhysRevA.34.1260|doi=10.1103/PhysRevA.34.1260}} </ref> | |||
| , giving improved generation and detection properties. As a result, the most recent experiments with photons no longer suffer from the detection loophole (see ]). This makes the photon the first experimental system for which all main experimental loopholes have been surmounted, albeit presently only in separate experiments (Giustina et al. (2013), ''Bell violation using entangled photons without the fair-sampling assumption'', Nature 497, 227–230; B.G. Christensen et al. (2013), ''Detection-Loophole-Free Test of Quantum Nonlocality, and Applications'', arXiv:1306.5772). | |||
| == Metaphysical aspects == | |||
| Most advocates of the hidden-variables idea believe that experiments have ruled out local hidden variables. They are ready to give up locality, explaining the violation of Bell's inequality by means of a non-local ], in which the particles exchange information about their states. This is the basis of the ] of quantum mechanics, which requires that all particles in the universe be able to instantaneously exchange information with all others. A 2007 experiment ruled out a large class of non-Bohmian non-local hidden variable theories.<ref>{{cite journal |doi=10.1038/nature05677 |title=An experimental test of non-local realism |year=2007 |last1=Gröblacher |first1=Simon |last2=Paterek |first2=Tomasz |last3=Kaltenbaek |first3=Rainer |last4=Brukner |first4=Časlav |last5=Żukowski |first5=Marek |last6=Aspelmeyer |first6=Markus |last7=Zeilinger |first7=Anton |journal=Nature |volume=446 |issue=7138 |pages=871–5 |pmid=17443179|bibcode = 2007Natur.446..871G | arxiv= 0704.2529 }}</ref> | |||
| If the hidden variables can communicate with each other faster than light, Bell's inequality can easily be violated. Once one particle is measured, it can communicate the necessary correlations to the other particle. Since in relativity the notion of simultaneity is not absolute, this is unattractive. One idea is to replace instantaneous communication with a process that travels backwards in time along the past ]. This is the idea behind a ] of quantum mechanics, which interprets the statistical emergence of a quantum history as a gradual coming to agreement between histories that go both forward and backward in time.<ref>{{cite journal|doi=10.1103/RevModPhys.58.647|title=The transactional interpretation of quantum mechanics|year=1986|last1=Cramer|first1=John|journal=Reviews of Modern Physics| volume=58| issue=3| pages=647| bibcode = 1986RvMP...58..647C }}</ref> | |||
| A few advocates of deterministic models have not given up on local hidden variables. For example, ] has argued that the ] loophole cannot be dismissed.<ref>{{cite arXiv|eprint=0908.3408|author1=Gerard 't Hooft|title=Entangled quantum states in a local deterministic theory|class=quant-ph|year=2009}}</ref><ref>{{cite arXiv|eprint=quant-ph/0701097|author1=Gerard 't Hooft|title=The Free-Will Postulate in Quantum Mechanics|class=quant-ph|year=2007}}</ref> | |||
| A radical solution is offered by the ] of quantum mechanics. According to this, not only is collapse of the wave function illusory: also, the apparent random branching of possible futures when quantum systems interact with the macroscopic world is an illusion too. Measurement does not lead to a random choice of possible outcome: the only ingredient of quantum mechanics is the unitary evolution of the wave function. All possibilities co-exist forever and the only reality is the quantum mechanical wave function. According to this view, two distant observers both split into superpositions when measuring a spin. The Bell inequality violations are no longer counterintuitive, because it is not clear which copy of the observer B observer A will see when going to compare notes. If reality includes all the different outcomes, locality in physical space (not outcome space) places no restrictions on how the split observers can meet up. | |||
| This point underlines the fact that the argument that realism is incompatible with quantum mechanics and locality depends on a particular formalization of the concept of realism. The assumption, in its weakest form, is called ]. This is the assumption that outcomes of measurements not performed are just as real as those of measurements that were performed. Counterfactual definiteness is an uncontroversial property of all classical physical theories prior to quantum theory, due to their determinism. Many worlds interpretations are not only counterfactually indefinite, they are factually indefinite. The results of all experiments, even ones that have been performed, are not uniquely determined. | |||
| If one chooses to reject counterfactual definiteness, reality has been made smaller, and there is no non-locality problem. On the other hand, one is thereby introducing irreducible or intrinsic randomness into our picture of the world: randomness that cannot be "explained" as merely the reflection of our ignorance of underlying, variable, physical quantities. Non-determinism becomes a fundamental property of nature. | |||
| Assuming counterfactual definiteness, reality has been enlarged, and there is a non-locality problem. On the other hand, in the many-worlds interpretation of quantum mechanics, reality consists only of a deterministically evolving wave function, non-locality is a non-issue. | |||
| There have also been repeated claims that Bell's arguments are irrelevant because they depend on hidden assumptions that, in fact, are questionable—though none of these claims have ever achieved much support. For example, ]<ref>{{cite journal |title=Clearing up Mysteries—The Original Goal |year=1989 |last1=Jaynes |first1=E. T. |journal=Maximum Entropy and Bayesian Methods |pages=12 | url=http://bayes.wustl.edu/etj/articles/cmystery.pdf}}</ref> claimed in 1989 that there are two hidden assumptions in Bell's theorem that could limit its generality. According to him: | |||
| # Bell interpreted conditional probability P(X|Y) as a causal inference, i.e. Y exerted a causal inference on X in reality. However, P(X|Y) actually only means logical inference (deduction). Causes cannot travel faster than light or backward in time, but deduction can. | |||
| # Bell's inequality does not apply to some possible hidden variable theories. It only applies to a certain class of local hidden variable theories. In fact, it might have just missed the kind of hidden variable theories that Einstein is most interested in. | |||
| However, ] has argued that Jaynes misunderstood Bell's analysis. Gill points out that in the same conference volume in which Jaynes argues against Bell, Jaynes confesses to being extremely impressed by a short proof by ] presented at the same conference, that the singlet correlations could not be reproduced by a computer simulation of a local hidden variables theory.<ref>{{cite journal |title=Time, Finite Statistics, and Bell's Fifth Position |year=2003 |last1=Gill |first1=Richard D. |journal=Proc. of "Foundations of Probability and Physics - 2", Ser. Math. Modelling in Phys., Engin., and Cogn. Sc. |volume=5/2002| publisher=Växjö Univ. Press | pages=179–206 |arxiv= quant-ph/0301059}}</ref> According to Jaynes (writing nearly 30 years after Bell's landmark contributions), it would probably take us another 30 years to fully appreciate Gull's stunning result. | |||
| A recent flurry of activity about implications for determinism arose with the paper: ]<ref name=Conway/> which stated "the response of a spin 1 particle to a triple experiment is free—that is to say, is not a function of properties of that part of the universe that is earlier than this response with respect to any given inertial frame."<ref name=Conway2/> This theorem raised awareness of a tension between determinism on the one hand governing an experiment, while on the other hand Alice and Bob are free to choose any settings they like for their observations.<ref name=Cator/><ref name=Esfeld/> The philosopher David Hodgson supports this theorem as showing determinism is ''unscientific'', that quantum mechanics allows observers (at least in some instances) the freedom to make observations of their choosing, and so leaves the door open for free will.<ref name=Hodgson/> | |||
| ==Final remarks== | |||
| The violations of Bell's inequalities, due to quantum entanglement, just provide the definite demonstration of something that was already strongly suspected, that quantum physics cannot be represented by any version of the classical picture of physics.<ref>{{cite book| author = Roger Penrose | title = The Road to Reality | edition = | page = 583 | year= 2007 | publisher = Vintage books | isbn = 0-679-77631-1}}</ref> Some earlier elements that had seemed incompatible with classical pictures included ] and ]. The Bell violations show that no resolution of such issues can avoid the ultimate strangeness of quantum behavior.<ref>{{cite book| author = E. Abers | title = Quantum Mechanics | edition = | pages = 193–195 | year= 2004 | publisher = Addison Wesley | isbn = 9780131461000 }}</ref> | |||
| The EPR paper "pinpointed" the unusual properties of the ''entangled states'', e.g. the above-mentioned singlet state, which is the foundation for present-day applications of quantum physics, such as ]; one application involves the measurement of quantum entanglement as a physical source of bits for ] ] protocol. This non-locality was originally supposed to be illusory, because the standard interpretation could easily do away with action-at-a-distance by simply assigning to each particle definite spin-states for all possible spin directions. The EPR argument was: therefore these definite states exist, therefore quantum theory is incomplete, since they do not appear in the theory. Bell's theorem showed that the "entangledness" prediction of quantum mechanics has a degree of non-locality that cannot be explained away by any local theory. | |||
| In well-defined '']'' (see the paragraph on "test experiments") one can now falsify either quantum mechanics or Einstein's quasi-classical assumptions: currently many experiments of this kind have been performed, and the experimental results support quantum mechanics, though some point out that it is theoretically possible that detectors give a biased sample of photons, so that until the relative number of "unpaired" photons is small enough, the final word has not yet been spoken. According to Marek Zukowski, quoted in Science Magazine (2011),<ref name="Zukowski"/> experimenters expect the first loophole free experiment to be done in five years. According to one of the foremost experimentalists in this field, ] (2013), the goal of a loophole free experiment is very close and will be a major achievement. According to Gregor Weihs (University of Innsbruck and conducted a ]) at least four major experimental groups around the world are in the race to be first. In 2014, Jason Gallicchio, Andrew Friedman, and ] published a paper in Physical Review letters proposing an experiment to close the free will loophole that uses light from quasars at opposite directions in the sky (which have therefore not had any contact or communication since the Big Bang) to decide on the settings of particle detectors. As Kaiser explains it, an experiment would go something like this: A laboratory setup would consist of a particle generator, such as a radioactive atom that emits pairs of entangled particles. One detector measures a property of particle A, while another detector does the same for particle B. A split second after the particles are generated, but just before the detectors are set, scientists would use telescopic observations of distant quasars to determine which properties each detector will measure of a respective particle. In other words, quasar A determines the settings to detect particle A, and quasar B sets the detector for particle B.<ref>{{cite web |url= http://www.sciencedaily.com/releases/2014/02/140220112515.htm |title= Closing the 'free will' loophole: Using distant quasars to test Bell's theorem| format=MIT |date= 20 February 2014|website= Science Daily|publisher= Science Daily| accessdate=12 March 2014}}</ref> | |||
| What is powerful about Bell's theorem is that it doesn't refer to any particular physical theory. It shows that nature violates the most general assumptions behind classical pictures, not just details of some particular models. No combination of local deterministic and local random variables can reproduce the phenomena predicted by quantum mechanics and repeatedly observed in experiments.<ref>{{cite book| author = R.G. Lerner, G.L. Trigg | title = Encyclopaedia of Physics | edition = 2nd | page = 495 | year= 1991 | publisher = VHC publishers | isbn =0-89573-752-3}}</ref> | |||
| ==See also== | ==See also== | ||
| {{portal|physics}} | |||
| * ] | |||
| {{cols|colwidth=20em}} | |||
| * ] | |||
| * ] | * ] | ||
| * ] | |||
| * ] | |||
| * '']'' | * '']'' | ||
| * ] | |||
| * ] | * ] | ||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | * ] | ||
| * ] | * ] | ||
| * ] | |||
| * ] | |||
| * ] | * ] | ||
| * ] | |||
| * ] | * ] | ||
| * ] | * ] | ||
| * ] | * ] | ||
| * ] | * ] | ||
| {{colend}} | |||
| ==Notes== | ==Notes== | ||
| {{reflist|group=note}} | |||
| {{Reflist|colwidth=30em|refs= | |||
| <ref name=BellJS> | |||
| Reprinted in {{cite book |title=Speakable and Unspeakable in Quantum Mechanics: Collected Papers on Quantum Philosophy |author=JS Bell |chapter=Chapter 2:On the Einstein-Podolsky-Rosen paradox |url=https://books.google.com/books?id=mwAhAwAAQBAJ&pg=PT8 |isbn=978-0521523387 |year=2004 |publisher=Cambridge University Press |edition=Alain Aspect introduction to 1987 |pages=14-21}} | |||
| </ref> | |||
| <ref name=Cator> | |||
| {{cite journal |author=Cator, Eric, and Klaas Landsman |title=Constraints on determinism: Bell versus Conway–Kochen |journal=Foundations of Physics |volume=44 |issue=7 |year=2014 |pages=781-791 |url=http://arxiv.org/pdf/1402.1972}} | |||
| </ref> | |||
| <ref name=Conway> | |||
| {{cite journal | last = Conway | first = John |author2=Simon Kochen | year = 2006 | title = The Free Will Theorem | journal = Foundations of Physics | volume = 36 | issue = 10 | pages = 1441 | doi = 10.1007/s10701-006-9068-6 |arxiv = quant-ph/0604079 |bibcode = 2006FoPh...36.1441C }} | |||
| </ref> | |||
| <ref name=Conway2> | |||
| {{cite journal |author=Conway, John H., and Simon Kochen |title=The strong free will theorem |journal= Notices of the AMS |volume=56 |issue=2 |year=2009 |pages=226-232 |url=http://www.ams.org/notices/200902/rtx090200226p.pdf?q=will&sa=U&ei=k71jU8X7DoypyASw9YGoCA&ved=0CCAQFjAB&usg=AFQjCNE7L-k87yWE32ru0rDjkLOdg12LRQ}}</ref> | |||
| <ref name=Esfeld> | |||
| {{cite journal |author=Esfeld, Michael |title=Bell’s Theorem and the Issue of Determinism and Indeterminism |journal= Foundations of Physics |year=2015 |pages=1-12 |url=http://arxiv.org/pdf/1503.00660}} | |||
| </ref> | |||
| <ref name=Hodgson> | |||
| {{cite book |author=David Hodgson |title=Rationality + Consciousness = Free Will |chapter=Chapter 7: Science and determinism |isbn=9780199845309 |year=2012 |publisher=Oxford University Press |url=https://books.google.com/books?id=4SGsmowYARsC&pg=PA121&dq=%22Conway+and+Kochen+call+the+free+will+theorem%22&hl=en&sa=X&ei=UiMYVeTBII3woATFkoKAAQ&ved=0CB4Q6AEwAA#v=onepage&q=%22Conway%20and%20Kochen%20call%20the%20free%20will%20theorem%22&f=false}} | |||
| </ref> | |||
| }} | |||
| ==References== | ==References== | ||
| {{Reflist}} | |||
| {{Refbegin|colwidth=60em}} | |||
| * {{cite journal | last1 = Aspect | first1 = A. ''et al.'' | year = | title = Experimental Tests of Realistic Local Theories via Bell's Theorem | url = | journal = , Phys. Rev. Lett. '''47' | volume = 460 | issue = | page = 1981 }} | |||
| * {{cite journal | last1 = Aspect | first1 = A. ''et al.'' | year = | title = Experimental Realization of Einstein–Podolsky–Rosen–Bohm Gedankenexperiment: A New Violation of Bell's Inequalities | url = | journal = , Phys. Rev. Lett. '''49' | volume = 91 | issue = | page = 1982 }} | |||
| * {{cite journal | last1 = Aspect | first1 = A. ''et al.'' | year = | title = Experimental Test of Bell's Inequalities Using Time-Varying Analyzers | url = | journal = , Phys. Rev. Lett. '''49' | volume = 1804 | issue = | page = 1982 }} | |||
| * {{cite journal | last1 = Aspect | first1 = A. | last2 = Grangier | first2 = P. | year = | title = About resonant scattering and other hypothetical effects in the Orsay atomic-cascade experiment tests of Bell inequalities: a discussion and some new experimental data | url = | journal = , Lettere al Nuovo Cimento '''43' | volume = 345 | issue = | page = 1985 }} | |||
| * {{cite journal | last1 = D'Espagnat | first1 = B. | year = | title = | url = | journal = 241' | volume = 158 | issue = | page = 1979 }} | |||
| * {{cite journal | last1 = Bell | first1 = J. S. | year = | title = On the problem of hidden variables in quantum mechanics | url = | journal = , Rev. Mod. Phys. '''38' | volume = 447 | issue = | page = 1966 }} | |||
| * {{cite journal | last1 = Bell | first1 = J. S. | year = 1964 | title = On the Einstein Podolsky Rosen Paradox | url = | journal = Physics | volume = 1 | issue = 3| pages = 195–200 }} | |||
| * J. S. Bell, ''Introduction to the hidden variable question'', Proceedings of the International School of Physics 'Enrico Fermi', Course IL, Foundations of Quantum Mechanics (1971) 171–81 | |||
| * J. S. Bell, ''Bertlmann's socks and the nature of reality'', Journal de Physique, Colloque C2, suppl. au numero 3, Tome '''42''' (1981) pp C2 41–61 | |||
| * J. S. Bell, ''Speakable and Unspeakable in Quantum Mechanics'' (Cambridge University Press 1987) | |||
| * {{cite journal | last1 = Clauser | first1 = J. F. | last2 = Shimony | first2 = A. | year = | title = Bell's theorem: experimental tests and implications | url = | journal = , Reports on Progress in Physics '''41' | volume = 1881 | issue = | page = 1978 }} | |||
| * J. F. Clauser and M. A. Horne, Phys. Rev D '''10''', 526–535 (1974) | |||
| * {{cite journal | last1 = Fry | first1 = E. S. | last2 = Walther | first2 = T. | last3 = Li | first3 = S. | year = | title = Proposal for a loophole-free test of the Bell inequalities | url = | journal = , Phys. Rev. A '''52' | volume = 4381 | issue = | page = 1995 }} | |||
| * E. S. Fry, and T. Walther, ''Atom based tests of the Bell Inequalities — the legacy of John Bell continues'', pp 103–117 of ''Quantum speakables'', R.A. Bertlmann and A. Zeilinger (eds.) (Springer, Berlin-Heidelberg-New York, 2002) | |||
| * R. B. Griffiths, ''Consistent Quantum Theory''', Cambridge University Press (2002). | |||
| * L. Hardy, ''Nonlocality for 2 particles without inequalities for almost all entangled states''. ''Physical Review Letters'' '''71''' (11) 1665–1668 (1993) | |||
| * M. A. Nielsen and I. L. Chuang, ''Quantum Computation and Quantum Information'', Cambridge University Press (2000) | |||
| * P. Pearle, ''Hidden-Variable Example Based upon Data Rejection'', Physical Review D '''2''', 1418–25 (1970) | |||
| * A. Peres, ''Quantum Theory: Concepts and Methods'', Kluwer, Dordrecht, 1993. | |||
| * P. Pluch, ''Theory of Quantum Probability'', PhD Thesis, University of Klagenfurt, 2006. | |||
| * B. C. van Frassen, ''Quantum Mechanics'', Clarendon Press, 1991. | |||
| * M.A. Rowe, D. Kielpinski, V. Meyer, C.A. Sackett, W.M. Itano, C. Monroe, and D.J. Wineland, ''Experimental violation of Bell's inequalities with efficient detection'', (Nature, 409, 791–794, 2001). | |||
| * S. Sulcs, ''The Nature of Light and Twentieth Century Experimental Physics'', Foundations of Science '''8''', 365–391 (2003) | |||
| * S. Gröblacher et al., ''An experimental test of non-local realism'', (Nature, 446, 871–875, 2007). | |||
| * D. N. Matsukevich, P. Maunz, D. L. Moehring, S. Olmschenk, and C. Monroe, ''Bell Inequality Violation with Two Remote Atomic Qubits'', Phys. Rev. Lett. 100, 150404 (2008). | |||
| * The comic '']'', by ], refers to Bell's Theorem in the and strips. | |||
| {{Refend}} | |||
| == Further reading == | == Further reading == | ||
| The following are intended for general audiences. | The following are intended for general audiences. | ||
| * {{cite book|first=Amir D. |last=Aczel |author-link=Amir Aczel |title=Entanglement: The greatest mystery in physics |publisher=Four Walls Eight Windows |location=New York |year=2001}} | |||
| * {{cite book|first1=A. |last1=Afriat |first2=F. |last2=Selleri |title=The Einstein, Podolsky and Rosen Paradox |publisher=Plenum Press |location=New York and London |year=1999}} | |||
| * {{cite book|first1=J. |last1=Baggott |author-link=Jim Baggott |title=The Meaning of Quantum Theory |publisher=Oxford University Press |year=1992}} | |||
| * {{cite book|first=Louisa |last=Gilder |title=The Age of Entanglement: When Quantum Physics Was Reborn |location=New York |publisher=Alfred A. Knopf |year=2008}} | |||
| * {{cite book|first=Brian |last=Greene |author-link=Brian Greene |title=The Fabric of the Cosmos |title-link=The Fabric of the Cosmos |publisher=Vintage |year=2004 |isbn=0-375-72720-5}} | |||
| * {{cite journal |doi=10.1119/1.12594 |title=Bringing home the atomic world: Quantum mysteries for anybody |year=1981 |last1=Mermin |first1=N. David |author-link=N. David Mermin |s2cid=122724592 |journal=American Journal of Physics |volume=49 |issue=10 |pages=940–943|bibcode = 1981AmJPh..49..940M }} | |||
| * {{cite journal|first=N. David |last=Mermin |author-link= |title=Is the moon there when nobody looks? Reality and the quantum theory |journal=Physics Today |date=April 1985 |volume=38 |issue=4 |pages=38–47 |doi=10.1063/1.880968 |bibcode=1985PhT....38d..38M}} | |||
| The following are more technically oriented. | |||
| * Amir D. Aczel, ''Entanglement: The greatest mystery in physics'' (Four Walls Eight Windows, New York, 2001). | |||
| {{Refbegin|colwidth=60em}} | |||
| * A. Afriat and F. Selleri, ''The Einstein, Podolsky and Rosen Paradox'' (Plenum Press, New York and London, 1999) | |||
| * {{cite journal | last1 = Aspect | first1 = A. | author-link=Alain Aspect | title = Experimental Tests of Realistic Local Theories via Bell's Theorem | journal = Phys. Rev. Lett. | volume = 47 | pages = 460–463 | issue = 7| year = 1981 |display-authors=etal | doi=10.1103/physrevlett.47.460|bibcode = 1981PhRvL..47..460A | doi-access = free }} | |||
| * J. Baggott, ''The Meaning of Quantum Theory'' (Oxford University Press, 1992) | |||
| * {{cite journal | last1 = Aspect | first1 = A. | title = Experimental Realization of Einstein–Podolsky–Rosen–Bohm Gedankenexperiment: A New Violation of Bell's Inequalities | journal = Phys. Rev. Lett. | volume = 49 | issue = 2 | pages = 91–94 | year = 1982 |display-authors=etal | doi=10.1103/physrevlett.49.91|bibcode = 1982PhRvL..49...91A | doi-access = free }} | |||
| * N. David Mermin, "Is the moon there when nobody looks? Reality and the quantum theory", in ''Physics Today'', April 1985, pp. 38–47. | |||
| * {{cite journal | last1 = Aspect | first1 = A. | last2 = Grangier | first2 = P. | title = About resonant scattering and other hypothetical effects in the Orsay atomic-cascade experiment tests of Bell inequalities: a discussion and some new experimental data | journal = Lettere al Nuovo Cimento | volume = 43 | issue = 8 | pages = 345–348 | year = 1985 | doi=10.1007/bf02746964| s2cid = 120840672 }} | |||
| * Louisa Gilder, ''The Age of Entanglement: When Quantum Physics Was Reborn'' (New York: Alfred A. Knopf, 2008) | |||
| * {{cite book|first=J. S. |last=Bell |author-link=John Stewart Bell |chapter=Introduction to the hidden variable question |title=Proceedings of the International School of Physics 'Enrico Fermi', Course IL, Foundations of Quantum Mechanics |year=1971 |pages=171–81}} | |||
| * Brian Greene, ''The Fabric of the Cosmos'' (Vintage, 2004, ISBN 0-375-72720-5) | |||
| * {{cite book|first=J. S. |last=Bell |chapter=Bertlmann's Socks and the Nature of Reality |title=Speakable and Unspeakable in Quantum Mechanics |publisher=Cambridge University Press |pages=139–158 |year=2004}} | |||
| * Nick Herbert, ''Quantum Reality: Beyond the New Physics'' (Anchor, 1987, ISBN 0-385-23569-0) | |||
| * {{cite journal | last1 = D'Espagnat | first1 = B. | author-link=Bernard d'Espagnat | year = 1979 | title = The Quantum Theory and Reality | url = http://www.sciam.com/media/pdf/197911_0158.pdf | journal = Scientific American | volume = 241 | issue = 5 | pages = 158–181 | doi = 10.1038/scientificamerican1179-158 | bibcode = 1979SciAm.241e.158D | access-date = 2009-03-18 | archive-date = 2009-03-27 | archive-url = https://web.archive.org/web/20090327023619/http://www.sciam.com/media/pdf/197911_0158.pdf | url-status = live }} | |||
| * D. Wick, ''The infamous boundary: seven decades of controversy in quantum physics'' (Birkhauser, Boston 1995) | |||
| * {{cite journal | last1 = Fry | first1 = E. S. | last2 = Walther | first2 = T. | last3 = Li | first3 = S. | title = Proposal for a loophole-free test of the Bell inequalities | url = http://oaktrust.library.tamu.edu/bitstream/1969.1/126533/1/PhysRevA.52.4381.pdf | journal = Phys. Rev. A | volume = 52 | issue = 6 | pages = 4381–4395 | year = 1995 | doi = 10.1103/physreva.52.4381 | pmid = 9912775 | bibcode = 1995PhRvA..52.4381F | hdl = 1969.1/126533 | hdl-access = free | access-date = 2018-03-19 | archive-date = 2021-12-29 | archive-url = https://web.archive.org/web/20211229062332/http://oaktrust.library.tamu.edu/bitstream/handle/1969.1/126533/PhysRevA.52.4381.pdf;jsessionid=50AFAA1E4F54828C672C8FF01C56B167?sequence=1 | url-status = live }} | |||
| * R. Anton Wilson, ''Prometheus Rising'' (New Falcon Publications, 1997, ISBN 1-56184-056-4) | |||
| * {{cite book|first1=E. S. |last1=Fry |first2=T. |last2=Walther |chapter=Atom based tests of the Bell Inequalities — the legacy of John Bell continues |pages=103–117 |title=Quantum speakables |editor-first1=R. A. |editor-last1=Bertlmann |editor-first2=A. |editor-last2=Zeilinger |editor-link2=Anton Zeilinger |publisher=Springer |location=Berlin-Heidelberg-New York |year=2002}} | |||
| * ] "]" (Perennial Classics, 2001, ISBN 0-06-095968-1) | |||
| * {{cite journal | last1 = Goldstein | first1 = Sheldon | display-authors = etal | year = 2011| title = Bell's theorem | journal = ] | volume = 6 | issue = 10| page = 8378 | doi = 10.4249/scholarpedia.8378 |bibcode = 2011SchpJ...6.8378G | doi-access = free }} | |||
| * {{cite book|first=R. B. |last=Griffiths |title=Consistent Quantum Theory |publisher=Cambridge University Press |year=2001 |isbn=978-0-521-80349-6 |oclc=1180958776}} | |||
| * {{cite journal | last1 = Hardy | first1 = L. | author-link = Lucien Hardy | s2cid = 11839894 | year = 1993 | title = Nonlocality for 2 particles without inequalities for almost all entangled states | journal = Physical Review Letters | volume = 71 | issue = 11| pages = 1665–1668 | doi=10.1103/physrevlett.71.1665|bibcode = 1993PhRvL..71.1665H | pmid=10054467}} | |||
| * {{cite journal | last1 = Matsukevich | first1 = D. N. | last2 = Maunz | first2 = P. | last3 = Moehring | first3 = D. L. | last4 = Olmschenk | first4 = S. | last5 = Monroe | first5 = C. | year = 2008 | title = Bell Inequality Violation with Two Remote Atomic Qubits | journal = Phys. Rev. Lett. | volume = 100 | issue = 15| page = 150404 | doi=10.1103/physrevlett.100.150404|arxiv = 0801.2184 |bibcode = 2008PhRvL.100o0404M | pmid=18518088| s2cid = 11536757 }} | |||
| * {{Cite book|title-link= Quantum Computing: A Gentle Introduction |title=Quantum Computing: A Gentle Introduction|last1=Rieffel|first1=Eleanor G.|last2=Polak|first2=Wolfgang H.|date=4 March 2011|publisher=MIT Press|isbn=978-0-262-01506-6|language=en|author-link=Eleanor Rieffel |chapter=4.4 EPR Paradox and Bell's Theorem |pages=60–65}} | |||
| * {{cite journal | last1 = Sulcs | first1 = S. | year = 2003 | title = The Nature of Light and Twentieth Century Experimental Physics | doi = 10.1023/A:1026323203487 | journal = Foundations of Science | volume = 8 | issue = 4| pages = 365–391 | s2cid = 118769677 }} | |||
| * {{cite book|first=B. C. |last=van Fraassen |author-link=Bas van Fraassen |title=Quantum Mechanics: An Empiricist View |publisher=Clarendon Press |year=1991 |isbn=978-0-198-24861-3 |oclc=22906474}} | |||
| * {{Cite journal |last1=Wharton |first1=K. B. |last2=Argaman |first2=N. |date=2020-05-18 |title=Colloquium : Bell's theorem and locally mediated reformulations of quantum mechanics |url=https://link.aps.org/doi/10.1103/RevModPhys.92.021002 |journal=Reviews of Modern Physics |language=en |volume=92 |issue=2 |page=021002 |doi=10.1103/RevModPhys.92.021002 |issn=0034-6861|arxiv=1906.04313 |bibcode=2020RvMP...92b1002W }} | |||
| {{Refend}} | |||
| ==External links== | ==External links== | ||
| {{wikibooks |Quantum_Mechanics }} | |||
| * "", Bell's original paper. | |||
| {{wikiversity |Bell's_theorem }} | |||
| * . | |||
| {{Commons category|Bell's theorem}} | |||
| * , based on N. D. Mermin's article, {{cite journal |doi=10.1119/1.12594 |title=Bringing home the atomic world: Quantum mysteries for anybody |year=1981 |last1=Mermin |first1=N. D. |journal=American Journal of Physics |volume=49 |issue=10 |pages=940|bibcode = 1981AmJPh..49..940M }} | |||
| * | * . | ||
| * {{cite IEP |url-id=epr |title=Bell's theorem}} | |||
| * Includes a simple explanation of Bell's Inequality. | |||
| * {{springer|title=Bell inequalities|id=p/b110230 |mode=cs1}} | |||
| * | |||
| * | |||
| {{Quantum mechanics topics}} | |||
| * | |||
| {{Quantum information}} | |||
| * | |||
| {{Authority control}} | |||
| * {{IEP|epr}} | |||
| {{DEFAULTSORT:Bell's Theorem}} | |||
| ] | |||
| ] | ] | ||
| ] | ] | ||
| ] | ] | ||
| ] | |||
| ] | ] | ||
| ] | ] | ||
| ] | |||
| ] | |||
Latest revision as of 23:22, 15 November 2024
Theorem in physics "Bell inequality" redirects here. For the related experiments, see Bell test.Bell's theorem is a term encompassing a number of closely related results in physics, all of which determine that quantum mechanics is incompatible with local hidden-variable theories, given some basic assumptions about the nature of measurement. "Local" here refers to the principle of locality, the idea that a particle can only be influenced by its immediate surroundings, and that interactions mediated by physical fields cannot propagate faster than the speed of light. "Hidden variables" are supposed properties of quantum particles that are not included in quantum theory but nevertheless affect the outcome of experiments. In the words of physicist John Stewart Bell, for whom this family of results is named, "If is local it will not agree with quantum mechanics, and if it agrees with quantum mechanics it will not be local."
The first such result was introduced by Bell in 1964, building upon the Einstein–Podolsky–Rosen paradox, which had called attention to the phenomenon of quantum entanglement. Bell deduced that if measurements are performed independently on the two separated particles of an entangled pair, then the assumption that the outcomes depend upon hidden variables within each half implies a mathematical constraint on how the outcomes on the two measurements are correlated. Such a constraint would later be named a Bell inequality. Bell then showed that quantum physics predicts correlations that violate this inequality. Multiple variations on Bell's theorem were put forward in the following years, using different assumptions and obtaining different Bell (or "Bell-type") inequalities.
The first rudimentary experiment designed to test Bell's theorem was performed in 1972 by John Clauser and Stuart Freedman. More advanced experiments, known collectively as Bell tests, have been performed many times since. Often, these experiments have had the goal of "closing loopholes", that is, ameliorating problems of experimental design or set-up that could in principle affect the validity of the findings of earlier Bell tests. Bell tests have consistently found that physical systems obey quantum mechanics and violate Bell inequalities; which is to say that the results of these experiments are incompatible with local hidden-variable theories.
The exact nature of the assumptions required to prove a Bell-type constraint on correlations has been debated by physicists and by philosophers. While the significance of Bell's theorem is not in doubt, different interpretations of quantum mechanics disagree about what exactly it implies.
Theorem
There are many variations on the basic idea, some employing stronger mathematical assumptions than others. Significantly, Bell-type theorems do not refer to any particular theory of local hidden variables, but instead show that quantum physics violates general assumptions behind classical pictures of nature. The original theorem proved by Bell in 1964 is not the most amenable to experiment, and it is convenient to introduce the genre of Bell-type inequalities with a later example.
Hypothetical characters Alice and Bob stand in widely separated locations. Their colleague Victor prepares a pair of particles and sends one to Alice and the other to Bob. When Alice receives her particle, she chooses to perform one of two possible measurements (perhaps by flipping a coin to decide which). Denote these measurements by and . Both and are binary measurements: the result of is either or , and likewise for . When Bob receives his particle, he chooses one of two measurements, and , which are also both binary.
Suppose that each measurement reveals a property that the particle already possessed. For instance, if Alice chooses to measure and obtains the result , then the particle she received carried a value of for a property . Consider the combinationBecause both and take the values , then either or . In the former case, the quantity must equal 0, while in the latter case, . So, one of the terms on the right-hand side of the above expression will vanish, and the other will equal . Consequently, if the experiment is repeated over many trials, with Victor preparing new pairs of particles, the absolute value of the average of the combination across all the trials will be less than or equal to 2. No single trial can measure this quantity, because Alice and Bob can only choose one measurement each, but on the assumption that the underlying properties exist, the average value of the sum is just the sum of the averages for each term. Using angle brackets to denote averages This is a Bell inequality, specifically, the CHSH inequality. Its derivation here depends upon two assumptions: first, that the underlying physical properties and exist independently of being observed or measured (sometimes called the assumption of realism); and second, that Alice's choice of action cannot influence Bob's result or vice versa (often called the assumption of locality).
Quantum mechanics can violate the CHSH inequality, as follows. Victor prepares a pair of qubits which he describes by the Bell state where and are the eigenstates of one of the Pauli matrices, Victor then passes the first qubit to Alice and the second to Bob. Alice and Bob's choices of possible measurements are also defined in terms of the Pauli matrices. Alice measures either of the two observables and : and Bob measures either of the two observables Victor can calculate the quantum expectation values for pairs of these observables using the Born rule: While only one of these four measurements can be made in a single trial of the experiment, the sum gives the sum of the average values that Victor expects to find across multiple trials. This value exceeds the classical upper bound of 2 that was deduced from the hypothesis of local hidden variables. The value is in fact the largest that quantum physics permits for this combination of expectation values, making it a Tsirelson bound.
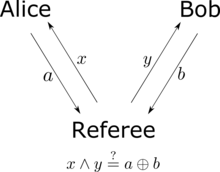
The CHSH inequality can also be thought of as a game in which Alice and Bob try to coordinate their actions. Victor prepares two bits, and , independently and at random. He sends bit to Alice and bit to Bob. Alice and Bob win if they return answer bits and to Victor, satisfying Or, equivalently, Alice and Bob win if the logical AND of and is the logical XOR of and . Alice and Bob can agree upon any strategy they desire before the game, but they cannot communicate once the game begins. In any theory based on local hidden variables, Alice and Bob's probability of winning is no greater than , regardless of what strategy they agree upon beforehand. However, if they share an entangled quantum state, their probability of winning can be as large as
Variations and related results
Bell (1964)
Bell's 1964 paper points out that under restricted conditions, local hidden-variable models can reproduce the predictions of quantum mechanics. He then demonstrates that this cannot hold true in general. Bell considers a refinement by David Bohm of the Einstein–Podolsky–Rosen (EPR) thought experiment. In this scenario, a pair of particles are formed together in such a way that they are described by a spin singlet state (which is an example of an entangled state). The particles then move apart in opposite directions. Each particle is measured by a Stern–Gerlach device, a measuring instrument that can be oriented in different directions and that reports one of two possible outcomes, representable by and . The configuration of each measuring instrument is represented by a unit vector, and the quantum-mechanical prediction for the correlation between two detectors with settings and is In particular, if the orientation of the two detectors is the same (), then the outcome of one measurement is certain to be the negative of the outcome of the other, giving . And if the orientations of the two detectors are orthogonal (), then the outcomes are uncorrelated, and . Bell proves by example that these special cases can be explained in terms of hidden variables, then proceeds to show that the full range of possibilities involving intermediate angles cannot.
Bell posited that a local hidden-variable model for these correlations would explain them in terms of an integral over the possible values of some hidden parameter : where is a probability density function. The two functions and provide the responses of the two detectors given the orientation vectors and the hidden variable: Crucially, the outcome of detector does not depend upon , and likewise the outcome of does not depend upon , because the two detectors are physically separated. Now we suppose that the experimenter has a choice of settings for the second detector: it can be set either to or to . Bell proves that the difference in correlation between these two choices of detector setting must satisfy the inequality However, it is easy to find situations where quantum mechanics violates the Bell inequality. For example, let the vectors and be orthogonal, and let lie in their plane at a 45° angle from both of them. Then while but Therefore, there is no local hidden-variable model that can reproduce the predictions of quantum mechanics for all choices of , , and Experimental results contradict the classical curves and match the curve predicted by quantum mechanics as long as experimental shortcomings are accounted for.
Bell's 1964 theorem requires the possibility of perfect anti-correlations: the ability to make a probability-1 prediction about the result from the second detector, knowing the result from the first. This is related to the "EPR criterion of reality", a concept introduced in the 1935 paper by Einstein, Podolsky, and Rosen. This paper posits: "If, without in any way disturbing a system, we can predict with certainty (i.e., with probability equal to unity) the value of a physical quantity, then there exists an element of reality corresponding to that quantity."
GHZ–Mermin (1990)
Main article: GHZ experimentDaniel Greenberger, Michael A. Horne, and Anton Zeilinger presented a four-particle thought experiment in 1990, which David Mermin then simplified to use only three particles. In this thought experiment, Victor generates a set of three spin-1/2 particles described by the quantum state where as above, and are the eigenvectors of the Pauli matrix . Victor then sends a particle each to Alice, Bob, and Charlie, who wait at widely separated locations. Alice measures either or on her particle, and so do Bob and Charlie. The result of each measurement is either or . Applying the Born rule to the three-qubit state , Victor predicts that whenever the three measurements include one and two 's, the product of the outcomes will always be . This follows because is an eigenvector of with eigenvalue , and likewise for and . Therefore, knowing Alice's result for a measurement and Bob's result for a measurement, Victor can predict with probability 1 what result Charlie will return for a measurement. According to the EPR criterion of reality, there would be an "element of reality" corresponding to the outcome of a measurement upon Charlie's qubit. Indeed, this same logic applies to both measurements and all three qubits. Per the EPR criterion of reality, then, each particle contains an "instruction set" that determines the outcome of a or measurement upon it. The set of all three particles would then be described by the instruction set with each entry being either or , and each or measurement simply returning the appropriate value.
If Alice, Bob, and Charlie all perform the measurement, then the product of their results would be . This value can be deduced from because the square of either or is . Each factor in parentheses equals , so and the product of Alice, Bob, and Charlie's results will be with probability unity. But this is inconsistent with quantum physics: Victor can predict using the state that the measurement will instead yield with probability unity.
This thought experiment can also be recast as a traditional Bell inequality or, equivalently, as a nonlocal game in the same spirit as the CHSH game. In it, Alice, Bob, and Charlie receive bits from Victor, promised to always have an even number of ones, that is, , and send him back bits . They win the game if have an odd number of ones for all inputs except , when they need to have an even number of ones. That is, they win the game iff . With local hidden variables the highest probability of victory they can have is 3/4, whereas using the quantum strategy above they win it with certainty. This is an example of quantum pseudo-telepathy.
Kochen–Specker theorem (1967)
Main article: Kochen–Specker theoremIn quantum theory, orthonormal bases for a Hilbert space represent measurements that can be performed upon a system having that Hilbert space. Each vector in a basis represents a possible outcome of that measurement. Suppose that a hidden variable exists, so that knowing the value of would imply certainty about the outcome of any measurement. Given a value of , each measurement outcome – that is, each vector in the Hilbert space – is either impossible or guaranteed. A Kochen–Specker configuration is a finite set of vectors made of multiple interlocking bases, with the property that a vector in it will always be impossible when considered as belonging to one basis and guaranteed when taken as belonging to another. In other words, a Kochen–Specker configuration is an "uncolorable set" that demonstrates the inconsistency of assuming a hidden variable can be controlling the measurement outcomes.
Free will theorem
Main article: Free will theoremThe Kochen–Specker type of argument, using configurations of interlocking bases, can be combined with the idea of measuring entangled pairs that underlies Bell-type inequalities. This was noted beginning in the 1970s by Kochen, Heywood and Redhead, Stairs, and Brown and Svetlichny. As EPR pointed out, obtaining a measurement outcome on one half of an entangled pair implies certainty about the outcome of a corresponding measurement on the other half. The "EPR criterion of reality" posits that because the second half of the pair was not disturbed, that certainty must be due to a physical property belonging to it. In other words, by this criterion, a hidden variable must exist within the second, as-yet unmeasured half of the pair. No contradiction arises if only one measurement on the first half is considered. However, if the observer has a choice of multiple possible measurements, and the vectors defining those measurements form a Kochen–Specker configuration, then some outcome on the second half will be simultaneously impossible and guaranteed.
This type of argument gained attention when an instance of it was advanced by John Conway and Simon Kochen under the name of the free will theorem. The Conway–Kochen theorem uses a pair of entangled qutrits and a Kochen–Specker configuration discovered by Asher Peres.
Quasiclassical entanglement
Main articles: Spekkens toy model and Werner stateAs Bell pointed out, some predictions of quantum mechanics can be replicated in local hidden-variable models, including special cases of correlations produced from entanglement. This topic has been studied systematically in the years since Bell's theorem. In 1989, Reinhard Werner introduced what are now called Werner states, joint quantum states for a pair of systems that yield EPR-type correlations but also admit a hidden-variable model. Werner states are bipartite quantum states that are invariant under unitaries of symmetric tensor-product form: In 2004, Robert Spekkens introduced a toy model that starts with the premise of local, discretized degrees of freedom and then imposes a "knowledge balance principle" that restricts how much an observer can know about those degrees of freedom, thereby making them into hidden variables. The allowed states of knowledge ("epistemic states") about the underlying variables ("ontic states") mimic some features of quantum states. Correlations in the toy model can emulate some aspects of entanglement, like monogamy, but by construction, the toy model can never violate a Bell inequality.
History
Background
Main articles: EPR paradox and History of quantum mechanicsThe question of whether quantum mechanics can be "completed" by hidden variables dates to the early years of quantum theory. In his 1932 textbook on quantum mechanics, the Hungarian-born polymath John von Neumann presented what he claimed to be a proof that there could be no "hidden parameters". The validity and definitiveness of von Neumann's proof were questioned by Hans Reichenbach, in more detail by Grete Hermann, and possibly in conversation though not in print by Albert Einstein. (Simon Kochen and Ernst Specker rejected von Neumann's key assumption as early as 1961, but did not publish a criticism of it until 1967.)
Einstein argued persistently that quantum mechanics could not be a complete theory. His preferred argument relied on a principle of locality:
- Consider a mechanical system constituted of two partial systems A and B which have interaction with each other only during limited time. Let the ψ function before their interaction be given. Then the Schrödinger equation will furnish the ψ function after their interaction has taken place. Let us now determine the physical condition of the partial system A as completely as possible by measurements. Then the quantum mechanics allows us to determine the ψ function of the partial system B from the measurements made, and from the ψ function of the total system. This determination, however, gives a result which depends upon which of the determining magnitudes specifying the condition of A has been measured (for instance coordinates or momenta). Since there can be only one physical condition of B after the interaction and which can reasonably not be considered as dependent on the particular measurement we perform on the system A separated from B it may be concluded that the ψ function is not unambiguously coordinated with the physical condition. This coordination of several ψ functions with the same physical condition of system B shows again that the ψ function cannot be interpreted as a (complete) description of a physical condition of a unit system.
The EPR thought experiment is similar, also considering two separated systems A and B described by a joint wave function. However, the EPR paper adds the idea later known as the EPR criterion of reality, according to which the ability to predict with probability 1 the outcome of a measurement upon B implies the existence of an "element of reality" within B.
In 1951, David Bohm proposed a variant of the EPR thought experiment in which the measurements have discrete ranges of possible outcomes, unlike the position and momentum measurements considered by EPR. The year before, Chien-Shiung Wu and Irving Shaknov had successfully measured polarizations of photons produced in entangled pairs, thereby making the Bohm version of the EPR thought experiment practically feasible.
By the late 1940s, the mathematician George Mackey had grown interested in the foundations of quantum physics, and in 1957 he drew up a list of postulates that he took to be a precise definition of quantum mechanics. Mackey conjectured that one of the postulates was redundant, and shortly thereafter, Andrew M. Gleason proved that it was indeed deducible from the other postulates. Gleason's theorem provided an argument that a broad class of hidden-variable theories are incompatible with quantum mechanics. More specifically, Gleason's theorem rules out hidden-variable models that are "noncontextual". Any hidden-variable model for quantum mechanics must, in order to avoid the implications of Gleason's theorem, involve hidden variables that are not properties belonging to the measured system alone but also dependent upon the external context in which the measurement is made. This type of dependence is often seen as contrived or undesirable; in some settings, it is inconsistent with special relativity. The Kochen–Specker theorem refines this statement by constructing a specific finite subset of rays on which no such probability measure can be defined.
Tsung-Dao Lee came close to deriving Bell's theorem in 1960. He considered events where two kaons were produced traveling in opposite directions, and came to the conclusion that hidden variables could not explain the correlations that could be obtained in such situations. However, complications arose due to the fact that kaons decay, and he did not go so far as to deduce a Bell-type inequality.
Bell's publications
Bell chose to publish his theorem in a comparatively obscure journal because it did not require page charges, in fact paying the authors who published there at the time. Because the journal did not provide free reprints of articles for the authors to distribute, however, Bell had to spend the money he received to buy copies that he could send to other physicists. While the articles printed in the journal themselves listed the publication's name simply as Physics, the covers carried the trilingual version Physics Physique Физика to reflect that it would print articles in English, French and Russian.
Prior to proving his 1964 result, Bell also proved a result equivalent to the Kochen–Specker theorem (hence the latter is sometimes also known as the Bell–Kochen–Specker or Bell–KS theorem). However, publication of this theorem was inadvertently delayed until 1966. In that paper, Bell argued that because an explanation of quantum phenomena in terms of hidden variables would require nonlocality, the EPR paradox "is resolved in the way which Einstein would have liked least."
Experiments

The source S produces pairs of "photons", sent in opposite directions. Each photon encounters a two-channel polariser whose orientation (a or b) can be set by the experimenter. Emerging signals from each channel are detected and coincidences of four types (++, −−, +− and −+) counted by the coincidence monitor.
In 1967, the unusual title Physics Physique Физика caught the attention of John Clauser, who then discovered Bell's paper and began to consider how to perform a Bell test in the laboratory. Clauser and Stuart Freedman would go on to perform a Bell test in 1972. This was only a limited test, because the choice of detector settings was made before the photons had left the source. In 1982, Alain Aspect and collaborators performed the first Bell test to remove this limitation. This began a trend of progressively more stringent Bell tests. The GHZ thought experiment was implemented in practice, using entangled triplets of photons, in 2000. By 2002, testing the CHSH inequality was feasible in undergraduate laboratory courses.
In Bell tests, there may be problems of experimental design or set-up that affect the validity of the experimental findings. These problems are often referred to as "loopholes". The purpose of the experiment is to test whether nature can be described by local hidden-variable theory, which would contradict the predictions of quantum mechanics.
The most prevalent loopholes in real experiments are the detection and locality loopholes. The detection loophole is opened when a small fraction of the particles (usually photons) are detected in the experiment, making it possible to explain the data with local hidden variables by assuming that the detected particles are an unrepresentative sample. The locality loophole is opened when the detections are not done with a spacelike separation, making it possible for the result of one measurement to influence the other without contradicting relativity. In some experiments there may be additional defects that make local-hidden-variable explanations of Bell test violations possible.
Although both the locality and detection loopholes had been closed in different experiments, a long-standing challenge was to close both simultaneously in the same experiment. This was finally achieved in three experiments in 2015. Regarding these results, Alain Aspect writes that "no experiment ... can be said to be totally loophole-free," but he says the experiments "remove the last doubts that we should renounce" local hidden variables, and refers to examples of remaining loopholes as being "far fetched" and "foreign to the usual way of reasoning in physics."
These efforts to experimentally validate violations of the Bell inequalities would later result in Clauser, Aspect, and Anton Zeilinger being awarded the 2022 Nobel Prize in Physics.
Interpretations
Main article: Interpretations of quantum mechanicsReactions to Bell's theorem have been many and varied. Maximilian Schlosshauer, Johannes Kofler, and Zeilinger write that Bell inequalities provide "a wonderful example of how we can have a rigorous theoretical result tested by numerous experiments, and yet disagree about the implications."
The Copenhagen interpretation
Copenhagen-type interpretations generally take the violation of Bell inequalities as grounds to reject the assumption often called counterfactual definiteness or "realism", which is not necessarily the same as abandoning realism in a broader philosophical sense. For example, Roland Omnès argues for the rejection of hidden variables and concludes that "quantum mechanics is probably as realistic as any theory of its scope and maturity ever will be". Likewise, Rudolf Peierls took the message of Bell's theorem to be that, because the premise of locality is physically reasonable, "hidden variables cannot be introduced without abandoning some of the results of quantum mechanics".
This is also the route taken by interpretations that descend from the Copenhagen tradition, such as consistent histories (often advertised as "Copenhagen done right"), as well as QBism.
Many-worlds interpretation of quantum mechanics
The Many-worlds interpretation, also known as the Everett interpretation, is dynamically local, meaning that it does not call for action at a distance, and deterministic, because it consists of the unitary part of quantum mechanics without collapse. It can generate correlations that violate a Bell inequality because it violates an implicit assumption by Bell that measurements have a single outcome. In fact, Bell's theorem can be proven in the Many-Worlds framework from the assumption that a measurement has a single outcome. Therefore, a violation of a Bell inequality can be interpreted as a demonstration that measurements have multiple outcomes.
The explanation it provides for the Bell correlations is that when Alice and Bob make their measurements, they split into local branches. From the point of view of each copy of Alice, there are multiple copies of Bob experiencing different results, so Bob cannot have a definite result, and the same is true from the point of view of each copy of Bob. They will obtain a mutually well-defined result only when their future light cones overlap. At this point we can say that the Bell correlation starts existing, but it was produced by a purely local mechanism. Therefore, the violation of a Bell inequality cannot be interpreted as a proof of non-locality.
Non-local hidden variables
Most advocates of the hidden-variables idea believe that experiments have ruled out local hidden variables. They are ready to give up locality, explaining the violation of Bell's inequality by means of a non-local hidden variable theory, in which the particles exchange information about their states. This is the basis of the Bohm interpretation of quantum mechanics, which requires that all particles in the universe be able to instantaneously exchange information with all others. One challenge for non-local hidden variable theories is to explain why this instantaneous communication can exist at the level of the hidden variables, but it cannot be used to send signals. A 2007 experiment ruled out a large class of non-Bohmian non-local hidden variable theories, though not Bohmian mechanics itself.
The transactional interpretation, which postulates waves traveling both backwards and forwards in time, is likewise non-local.
Superdeterminism
Main article: SuperdeterminismA necessary assumption to derive Bell's theorem is that the hidden variables are not correlated with the measurement settings. This assumption has been justified on the grounds that the experimenter has "free will" to choose the settings, and that it is necessary to do science in the first place. A (hypothetical) theory where the choice of measurement is necessarily correlated with the system being measured is known as superdeterministic.
A few advocates of deterministic models have not given up on local hidden variables. For example, Gerard 't Hooft has argued that superdeterminism cannot be dismissed.
See also
- Einstein's thought experiments
- Epistemological Letters
- Fundamental Fysiks Group
- Leggett inequality
- Leggett–Garg inequality
- Mermin's device
- Mott problem
- PBR theorem
- Quantum contextuality
- Quantum nonlocality
- Renninger negative-result experiment
Notes
- We are for convenience assuming that the response of the detector to the underlying property is deterministic. This assumption can be replaced; it is equivalent to postulating a joint probability distribution over all the observables of the experiment.
- In more detail, as developed by Paul Dirac, David Hilbert, John von Neumann, and Hermann Weyl, the state of a quantum mechanical system is a vector belonging to a (separable) Hilbert space . Physical quantities of interest — position, momentum, energy, spin — are represented by "observables", which are self-adjoint linear operators acting on the Hilbert space. When an observable is measured, the result will be one of its eigenvalues with probability given by the Born rule: in the simplest case the eigenvalue is non-degenerate and the probability is given by , where is its associated eigenvector. More generally, the eigenvalue is degenerate and the probability is given by , where is the projector onto its associated eigenspace. For the purposes of this discussion, we can take the eigenvalues to be non-degenerate.
- See Reichenbach and Jammer, Mermin and Schack, and for Einstein's remarks, Clauser and Shimony and Wick.
- A hidden-variable theory that is deterministic implies that the probability of a given outcome is always either 0 or 1. For example, a Stern–Gerlach measurement on a spin-1 atom will report that the atom's angular momentum along the chosen axis is one of three possible values, which can be designated , and . In a deterministic hidden-variable theory, there exists an underlying physical property that fixes the result found in the measurement. Conditional on the value of the underlying physical property, any given outcome (for example, a result of ) must be either impossible or guaranteed. But Gleason's theorem implies that there can be no such deterministic probability measure, because it proves that any probability measure must take the form of a mapping for some density operator . This mapping is continuous on the unit sphere of the Hilbert space, and since this unit sphere is connected, no continuous probability measure on it can be deterministic.
- E. T. Jaynes was one exception, but Jaynes' arguments have not generally been found persuasive.
References
- Bell, John S. (1987). Speakable and Unspeakable in Quantum Mechanics. Cambridge University Press. p. 65. ISBN 9780521368698. OCLC 15053677.
- "The Nobel Prize in Physics 2022". Nobel Prize (Press release). The Royal Swedish Academy of Sciences. October 4, 2022. Retrieved 6 October 2022.
- The BIG Bell Test Collaboration (9 May 2018). "Challenging local realism with human choices". Nature. 557 (7704): 212–216. arXiv:1805.04431. Bibcode:2018Natur.557..212B. doi:10.1038/s41586-018-0085-3. PMID 29743691. S2CID 13665914.
- Wolchover, Natalie (2017-02-07). "Experiment Reaffirms Quantum Weirdness". Quanta Magazine. Retrieved 2020-02-08.
- ^ Shimony, Abner. "Bell's Theorem". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy.
- ^ Nielsen, Michael A.; Chuang, Isaac L. (2010). Quantum Computation and Quantum Information (2nd ed.). Cambridge: Cambridge University Press. ISBN 978-1-107-00217-3. OCLC 844974180.
- Fine, Arthur (1982-02-01). "Hidden Variables, Joint Probability, and the Bell Inequalities". Physical Review Letters. 48 (5): 291–295. Bibcode:1982PhRvL..48..291F. doi:10.1103/PhysRevLett.48.291. ISSN 0031-9007.
- Braunstein, Samuel L.; Caves, Carlton M. (August 1990). "Wringing out better Bell inequalities". Annals of Physics. 202 (1): 22–56. Bibcode:1990AnPhy.202...22B. doi:10.1016/0003-4916(90)90339-P.
- Rau, Jochen (2021). Quantum theory : an information processing approach. Oxford University Press. ISBN 978-0-192-65027-6. OCLC 1256446911.
- Cleve, R.; Hoyer, P.; Toner, B.; Watrous, J. (2004). "Consequences and limits of nonlocal strategies". Proceedings. 19th IEEE Annual Conference on Computational Complexity, 2004. IEEE. pp. 236–249. arXiv:quant-ph/0404076. Bibcode:2004quant.ph..4076C. doi:10.1109/CCC.2004.1313847. ISBN 0-7695-2120-7. OCLC 55954993. S2CID 8077237.
- Barnum, H.; Beigi, S.; Boixo, S.; Elliott, M. B.; Wehner, S. (2010-04-06). "Local Quantum Measurement and No-Signaling Imply Quantum Correlations". Physical Review Letters. 104 (14): 140401. arXiv:0910.3952. Bibcode:2010PhRvL.104n0401B. doi:10.1103/PhysRevLett.104.140401. ISSN 0031-9007. PMID 20481921. S2CID 17298392.
- Bell, J. S. (1964). "On the Einstein Podolsky Rosen Paradox" (PDF). Physics Physique Физика. 1 (3): 195–200. doi:10.1103/PhysicsPhysiqueFizika.1.195.
- Griffiths, David J. (2005). Introduction to Quantum Mechanics (2nd ed.). Upper Saddle River, NJ: Pearson Prentice Hall. ISBN 0-13-111892-7. OCLC 53926857.
- Einstein, A.; Podolsky, B.; Rosen, N. (1935-05-15). "Can Quantum-Mechanical Description of Physical Reality be Considered Complete?". Physical Review. 47 (10): 777–780. Bibcode:1935PhRv...47..777E. doi:10.1103/PhysRev.47.777.
- Greenberger, D.; Horne, M.; Shimony, A.; Zeilinger, A. (1990). "Bell's theorem without inequalities". American Journal of Physics. 58 (12): 1131. Bibcode:1990AmJPh..58.1131G. doi:10.1119/1.16243.
- Mermin, N. David (1990). "Quantum mysteries revisited". American Journal of Physics. 58 (8): 731–734. Bibcode:1990AmJPh..58..731M. doi:10.1119/1.16503.
- Brassard, Gilles; Broadbent, Anne; Tapp, Alain (2005). "Recasting Mermin's multi-player game into the framework of pseudo-telepathy". Quantum Information and Computation. 5 (7): 538–550. arXiv:quant-ph/0408052. Bibcode:2004quant.ph..8052B. doi:10.26421/QIC5.7-2.
- Dirac, Paul Adrien Maurice (1930). The Principles of Quantum Mechanics. Oxford: Clarendon Press.
- Hilbert, David (2009). Sauer, Tilman; Majer, Ulrich (eds.). Lectures on the Foundations of Physics 1915–1927: Relativity, Quantum Theory and Epistemology. Springer. doi:10.1007/b12915. ISBN 978-3-540-20606-4. OCLC 463777694.
- von Neumann, John (1932). Mathematische Grundlagen der Quantenmechanik. Berlin: Springer. English translation: Mathematical Foundations of Quantum Mechanics. Translated by Beyer, Robert T. Princeton University Press. 1955.
- Weyl, Hermann (1950) . The Theory of Groups and Quantum Mechanics. Translated by Robertson, H. P. Dover. ISBN 978-0-486-60269-1. Translated from the German Gruppentheorie und Quantenmechanik (2nd ed.). S. Hirzel Verlag [de]. 1931.
- Peres, Asher (1993). Quantum Theory: Concepts and Methods. Kluwer. ISBN 0-7923-2549-4. OCLC 28854083.
- Redhead, Michael; Brown, Harvey (1991-07-01). "Nonlocality in Quantum Mechanics". Proceedings of the Aristotelian Society, Supplementary Volumes. 65 (1): 119–160. doi:10.1093/aristoteliansupp/65.1.119. ISSN 0309-7013. JSTOR 4106773.
A similar approach was arrived at independently by Simon Kochen, although never published (private communication).
- Heywood, Peter; Redhead, Michael L. G. (May 1983). "Nonlocality and the Kochen–Specker paradox". Foundations of Physics. 13 (5): 481–499. Bibcode:1983FoPh...13..481H. doi:10.1007/BF00729511. ISSN 0015-9018. S2CID 120340929.
- Stairs, Allen (December 1983). "Quantum Logic, Realism, and Value Definiteness". Philosophy of Science. 50 (4): 578–602. doi:10.1086/289140. ISSN 0031-8248. S2CID 122885859.
- Brown, H. R.; Svetlichny, G. (November 1990). "Nonlocality and Gleason's lemma. Part I. Deterministic theories". Foundations of Physics. 20 (11): 1379–1387. Bibcode:1990FoPh...20.1379B. doi:10.1007/BF01883492. ISSN 0015-9018. S2CID 122868901.
- Glick, David; Boge, Florian J. (2019-10-22). "Is the Reality Criterion Analytic?". Erkenntnis. 86 (6): 1445–1451. arXiv:1909.11893. Bibcode:2019arXiv190911893G. doi:10.1007/s10670-019-00163-w. ISSN 0165-0106. S2CID 202889160.
- Conway, John; Kochen, Simon (2006). "The Free Will Theorem". Foundations of Physics. 36 (10): 1441. arXiv:quant-ph/0604079. Bibcode:2006FoPh...36.1441C. doi:10.1007/s10701-006-9068-6. S2CID 12999337.
- Rehmeyer, Julie (2008-08-15). "Do subatomic particles have free will?". Science News. Retrieved 2022-04-23.
- Thomas, Rachel (2011-12-27). "John Conway – discovering free will (part I)". Plus Magazine. Retrieved 2022-04-23.
- Conway, John H.; Kochen, Simon (2009). "The strong free will theorem" (PDF). Notices of the AMS. 56 (2): 226–232.
- Werner, Reinhard F. (1989-10-01). "Quantum states with Einstein–Podolsky–Rosen correlations admitting a hidden-variable model". Physical Review A. 40 (8): 4277–4281. Bibcode:1989PhRvA..40.4277W. doi:10.1103/PhysRevA.40.4277. ISSN 0556-2791. PMID 9902666.
- Spekkens, Robert W. (2007-03-19). "Evidence for the epistemic view of quantum states: A toy theory". Physical Review A. 75 (3): 032110. arXiv:quant-ph/0401052. Bibcode:2007PhRvA..75c2110S. doi:10.1103/PhysRevA.75.032110. ISSN 1050-2947. S2CID 117284016.
- Catani, Lorenzo; Browne, Dan E. (2017-07-27). "Spekkens' toy model in all dimensions and its relationship with stabiliser quantum mechanics". New Journal of Physics. 19 (7): 073035. arXiv:1701.07801. Bibcode:2017NJPh...19g3035C. doi:10.1088/1367-2630/aa781c. ISSN 1367-2630. S2CID 119428107.
- Reichenbach, Hans (1944). Philosophic Foundations of Quantum Mechanics. University of California Press. p. 14. OCLC 872622725.
- ^ Jammer, Max (1974). The Philosophy of Quantum Mechanics. John Wiley and Sons. ISBN 0-471-43958-4.
- Mermin, N. David; Schack, Rüdiger (2018). "Homer nodded: von Neumann's surprising oversight". Foundations of Physics. 48 (9): 1007–1020. arXiv:1805.10311. Bibcode:2018FoPh...48.1007M. doi:10.1007/s10701-018-0197-5. S2CID 118951033.
- Clauser, J. F.; Shimony, A. (1978). "Bell's theorem: Experimental tests and implications" (PDF). Reports on Progress in Physics. 41 (12): 1881–1927. Bibcode:1978RPPh...41.1881C. CiteSeerX 10.1.1.482.4728. doi:10.1088/0034-4885/41/12/002. S2CID 250885175. Archived (PDF) from the original on 2017-09-23. Retrieved 2017-10-28.
- ^ Wick, David (1995). "Bell's Theorem". The Infamous Boundary: Seven Decades of Heresy in Quantum Physics. New York: Springer. pp. 92–100. doi:10.1007/978-1-4612-4030-3_11. ISBN 978-0-387-94726-6.
- Conway, John; Kochen, Simon (2002). "The Geometry of the Quantum Paradoxes". In Bertlmann, Reinhold A.; Zeilinger, Anton (eds.). Quantum speakables: From Bell to Quantum Information. Berlin: Springer. pp. 257–269. ISBN 3-540-42756-2. OCLC 49404213.
- Einstein, Albert (March 1936). "Physics and reality". Journal of the Franklin Institute. 221 (3): 349–382. Bibcode:1936FrInJ.221..349E. doi:10.1016/S0016-0032(36)91047-5.
- Harrigan, Nicholas; Spekkens, Robert W. (2010). "Einstein, incompleteness, and the epistemic view of quantum states". Foundations of Physics. 40 (2): 125. arXiv:0706.2661. Bibcode:2010FoPh...40..125H. doi:10.1007/s10701-009-9347-0. S2CID 32755624.
- Bohm, David (1989) . Quantum Theory (Dover reprint ed.). Prentice-Hall. pp. 614–623. ISBN 978-0-486-65969-5. OCLC 1103789975.
- Wu, C.-S.; Shaknov, I. (1950). "The Angular Correlation of Scattered Annihilation Radiation". Physical Review. 77 (1): 136. Bibcode:1950PhRv...77..136W. doi:10.1103/PhysRev.77.136.
- Mackey, George W. (1957). "Quantum Mechanics and Hilbert Space". The American Mathematical Monthly. 64 (8P2): 45–57. doi:10.1080/00029890.1957.11989120. JSTOR 2308516.
- Gleason, Andrew M. (1957). "Measures on the closed subspaces of a Hilbert space". Indiana University Mathematics Journal. 6 (4): 885–893. doi:10.1512/iumj.1957.6.56050. MR 0096113.
- Chernoff, Paul R. "Andy Gleason and Quantum Mechanics" (PDF). Notices of the AMS. 56 (10): 1253–1259.
- Wilce, A. (2017). "Quantum Logic and Probability Theory". Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University.
- ^ Mermin, N. David (July 1993). "Hidden Variables and the Two Theorems of John Bell" (PDF). Reviews of Modern Physics. 65 (3): 803–815. arXiv:1802.10119. Bibcode:1993RvMP...65..803M. doi:10.1103/RevModPhys.65.803. S2CID 119546199.
- Shimony, Abner (1984). "Contextual Hidden Variable Theories and Bell's Inequalities". British Journal for the Philosophy of Science. 35 (1): 25–45. doi:10.1093/bjps/35.1.25.
- Peres, Asher (1991). "Two simple proofs of the Kochen-Specker theorem". Journal of Physics A: Mathematical and General. 24 (4): L175 – L178. Bibcode:1991JPhA...24L.175P. doi:10.1088/0305-4470/24/4/003. ISSN 0305-4470.
- Whitaker, Andrew (2016). John Stewart Bell and Twentieth Century Physics: Vision and Integrity. Oxford University Press. ISBN 978-0-19-874299-9.
- ^ Bell, J. S. (1966). "On the problem of hidden variables in quantum mechanics". Reviews of Modern Physics. 38 (3): 447–452. Bibcode:1966RvMP...38..447B. doi:10.1103/revmodphys.38.447. OSTI 1444158.
- Kaiser, David (2012-01-30). "How the Hippies Saved Physics: Science, Counterculture, and the Quantum Revival [Excerpt]". Scientific American. Retrieved 2020-02-11.
- Freedman, S. J.; Clauser, J. F. (1972). "Experimental test of local hidden-variable theories" (PDF). Physical Review Letters. 28 (938): 938–941. Bibcode:1972PhRvL..28..938F. doi:10.1103/PhysRevLett.28.938.
- Freedman, Stuart Jay (1972-05-05). Experimental test of local hidden-variable theories (PDF) (PhD). University of California, Berkeley.
- Aspect, Alain; Dalibard, Jean; Roger, Gérard (1982). "Experimental Test of Bell's Inequalities Using Time-Varying Analyzers". Physical Review Letters. 49 (25): 1804–7. Bibcode:1982PhRvL..49.1804A. doi:10.1103/PhysRevLett.49.1804.
- Pan, Jian-Wei; Bouwmeester, D.; Daniell, M.; Weinfurter, H.; Zeilinger, A. (2000). "Experimental test of quantum nonlocality in three-photon GHZ entanglement". Nature. 403 (6769): 515–519. Bibcode:2000Natur.403..515P. doi:10.1038/35000514. PMID 10676953. S2CID 4309261.
- Dehlinger, Dietrich; Mitchell, M. W. (2002). "Entangled photons, nonlocality, and Bell inequalities in the undergraduate laboratory". American Journal of Physics. 70 (9): 903–910. arXiv:quant-ph/0205171. Bibcode:2002AmJPh..70..903D. doi:10.1119/1.1498860. S2CID 49487096.
- ^ Larsson, Jan-Åke (2014). "Loopholes in Bell inequality tests of local realism". Journal of Physics A: Mathematical and Theoretical. 47 (42): 424003. arXiv:1407.0363. Bibcode:2014JPhA...47P4003L. doi:10.1088/1751-8113/47/42/424003. S2CID 40332044.
- Gerhardt, I.; Liu, Q.; Lamas-Linares, A.; Skaar, J.; Scarani, V.; et al. (2011). "Experimentally faking the violation of Bell's inequalities". Physical Review Letters. 107 (17): 170404. arXiv:1106.3224. Bibcode:2011PhRvL.107q0404G. doi:10.1103/PhysRevLett.107.170404. PMID 22107491. S2CID 16306493.
- Merali, Zeeya (27 August 2015). "Quantum 'spookiness' passes toughest test yet". Nature News. 525 (7567): 14–15. Bibcode:2015Natur.525...14M. doi:10.1038/nature.2015.18255. PMID 26333448. S2CID 4409566.
- Markoff, Jack (21 October 2015). "Sorry, Einstein. Quantum Study Suggests 'Spooky Action' Is Real". New York Times. Retrieved 21 October 2015.
- Hensen, B.; et al. (21 October 2015). "Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres". Nature. 526 (7575): 682–686. arXiv:1508.05949. Bibcode:2015Natur.526..682H. doi:10.1038/nature15759. PMID 26503041. S2CID 205246446.
- Shalm, L. K.; et al. (16 December 2015). "Strong Loophole-Free Test of Local Realism". Physical Review Letters. 115 (25): 250402. arXiv:1511.03189. Bibcode:2015PhRvL.115y0402S. doi:10.1103/PhysRevLett.115.250402. PMC 5815856. PMID 26722906.
- Giustina, M.; et al. (16 December 2015). "Significant-Loophole-Free Test of Bell's Theorem with Entangled Photons". Physical Review Letters. 115 (25): 250401. arXiv:1511.03190. Bibcode:2015PhRvL.115y0401G. doi:10.1103/PhysRevLett.115.250401. PMID 26722905. S2CID 13789503.
- Aspect, Alain (December 16, 2015). "Closing the Door on Einstein and Bohr's Quantum Debate". Physics. 8: 123. Bibcode:2015PhyOJ...8..123A. doi:10.1103/Physics.8.123.
- Ahlander, Johan; Burger, Ludwig; Pollard, Niklas (2022-10-04). "Nobel physics prize goes to sleuths of 'spooky' quantum science". Reuters. Retrieved 2022-10-04.
- Schlosshauer, Maximilian; Kofler, Johannes; Zeilinger, Anton (2013-01-06). "A Snapshot of Foundational Attitudes Toward Quantum Mechanics". Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics. 44 (3): 222–230. arXiv:1301.1069. Bibcode:2013SHPMP..44..222S. doi:10.1016/j.shpsb.2013.04.004. S2CID 55537196.
- Werner, Reinhard F. (2014-10-24). "Comment on 'What Bell did'". Journal of Physics A: Mathematical and Theoretical. 47 (42): 424011. Bibcode:2014JPhA...47P4011W. doi:10.1088/1751-8113/47/42/424011. ISSN 1751-8113. S2CID 122180759.
- Żukowski, Marek (2017). "Bell's Theorem Tells Us Not What Quantum Mechanics is, but What Quantum Mechanics is Not". In Bertlmann, Reinhold; Zeilinger, Anton (eds.). Quantum [Un]Speakables II. The Frontiers Collection. Cham: Springer International Publishing. pp. 175–185. arXiv:1501.05640. doi:10.1007/978-3-319-38987-5_10. ISBN 978-3-319-38985-1. S2CID 119214547.
- Omnès, R. (1994). The Interpretation of Quantum Mechanics. Princeton University Press. ISBN 978-0-691-03669-4. OCLC 439453957.
- Peierls, Rudolf (1979). Surprises in Theoretical Physics. Princeton University Press. pp. 26–29. ISBN 0-691-08241-3.
- Mermin, N. D. (1999). "What Do These Correlations Know About Reality? Nonlocality and the Absurd". Foundations of Physics. 29 (4): 571–587. arXiv:quant-ph/9807055. Bibcode:1998quant.ph..7055M. doi:10.1023/A:1018864225930.
- Hohenberg, P. C. (2010-10-05). "Colloquium : An introduction to consistent quantum theory". Reviews of Modern Physics. 82 (4): 2835–2844. arXiv:0909.2359. Bibcode:2010RvMP...82.2835H. doi:10.1103/RevModPhys.82.2835. ISSN 0034-6861. S2CID 20551033.
- Healey, Richard (2016). "Quantum-Bayesian and Pragmatist Views of Quantum Theory". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Archived from the original on 2021-08-17. Retrieved 2021-09-16.
- ^ Brown, Harvey R.; Timpson, Christopher G. (2016). "Bell on Bell's Theorem: The Changing Face of Nonlocality". In Bell, Mary; Gao, Shan (eds.). Quantum Nonlocality and Reality: 50 years of Bell's theorem. Cambridge University Press. pp. 91–123. arXiv:1501.03521. doi:10.1017/CBO9781316219393.008. ISBN 9781316219393. S2CID 118686956.
- Deutsch, David; Hayden, Patrick (2000). "Information flow in entangled quantum systems". Proceedings of the Royal Society A. 456 (1999): 1759–1774. arXiv:quant-ph/9906007. Bibcode:2000RSPSA.456.1759D. doi:10.1098/rspa.2000.0585. S2CID 13998168.
- Jaynes, E. T. (1989). "Clearing up Mysteries — the Original Goal". Maximum Entropy and Bayesian Methods (PDF). pp. 1–27. CiteSeerX 10.1.1.46.1264. doi:10.1007/978-94-015-7860-8_1. ISBN 978-90-481-4044-2. Archived (PDF) from the original on 2011-10-28. Retrieved 2011-10-18.
- Gill, Richard D. (2002). "Time, Finite Statistics, and Bell's Fifth Position". Proceedings of the Conference Foundations of Probability and Physics - 2 : Växjö (Soland), Sweden, June 2-7, 2002. Vol. 5. Växjö University Press. pp. 179–206. arXiv:quant-ph/0301059.
- Wood, Christopher J.; Spekkens, Robert W. (2015-03-03). "The lesson of causal discovery algorithms for quantum correlations: causal explanations of Bell-inequality violations require fine-tuning". New Journal of Physics. 17 (3): 033002. arXiv:1208.4119. Bibcode:2015NJPh...17c3002W. doi:10.1088/1367-2630/17/3/033002. ISSN 1367-2630. S2CID 118518558.
- Gröblacher, Simon; Paterek, Tomasz; Kaltenbaek, Rainer; Brukner, Časlav; Żukowski, Marek; Aspelmeyer, Markus; Zeilinger, Anton (2007). "An experimental test of non-local realism". Nature. 446 (7138): 871–5. arXiv:0704.2529. Bibcode:2007Natur.446..871G. doi:10.1038/nature05677. PMID 17443179. S2CID 4412358.
- Kastner, Ruth E. (May 2010). "The quantum liar experiment in Cramer's transactional interpretation". Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics. 41 (2): 86–92. arXiv:0906.1626. Bibcode:2010SHPMP..41...86K. doi:10.1016/j.shpsb.2010.01.001. S2CID 16242184. Archived from the original on 2018-06-24. Retrieved 2021-09-16.
- 't Hooft, Gerard (2016). The Cellular Automaton Interpretation of Quantum Mechanics. Fundamental Theories of Physics. Vol. 185. Springer. doi:10.1007/978-3-319-41285-6. ISBN 978-3-319-41284-9. OCLC 951761277. S2CID 7779840. Archived from the original on 2021-12-29. Retrieved 2020-08-27.
Further reading
The following are intended for general audiences.
- Aczel, Amir D. (2001). Entanglement: The greatest mystery in physics. New York: Four Walls Eight Windows.
- Afriat, A.; Selleri, F. (1999). The Einstein, Podolsky and Rosen Paradox. New York and London: Plenum Press.
- Baggott, J. (1992). The Meaning of Quantum Theory. Oxford University Press.
- Gilder, Louisa (2008). The Age of Entanglement: When Quantum Physics Was Reborn. New York: Alfred A. Knopf.
- Greene, Brian (2004). The Fabric of the Cosmos. Vintage. ISBN 0-375-72720-5.
- Mermin, N. David (1981). "Bringing home the atomic world: Quantum mysteries for anybody". American Journal of Physics. 49 (10): 940–943. Bibcode:1981AmJPh..49..940M. doi:10.1119/1.12594. S2CID 122724592.
- Mermin, N. David (April 1985). "Is the moon there when nobody looks? Reality and the quantum theory". Physics Today. 38 (4): 38–47. Bibcode:1985PhT....38d..38M. doi:10.1063/1.880968.
The following are more technically oriented.
- Aspect, A.; et al. (1981). "Experimental Tests of Realistic Local Theories via Bell's Theorem". Phys. Rev. Lett. 47 (7): 460–463. Bibcode:1981PhRvL..47..460A. doi:10.1103/physrevlett.47.460.
- Aspect, A.; et al. (1982). "Experimental Realization of Einstein–Podolsky–Rosen–Bohm Gedankenexperiment: A New Violation of Bell's Inequalities". Phys. Rev. Lett. 49 (2): 91–94. Bibcode:1982PhRvL..49...91A. doi:10.1103/physrevlett.49.91.
- Aspect, A.; Grangier, P. (1985). "About resonant scattering and other hypothetical effects in the Orsay atomic-cascade experiment tests of Bell inequalities: a discussion and some new experimental data". Lettere al Nuovo Cimento. 43 (8): 345–348. doi:10.1007/bf02746964. S2CID 120840672.
- Bell, J. S. (1971). "Introduction to the hidden variable question". Proceedings of the International School of Physics 'Enrico Fermi', Course IL, Foundations of Quantum Mechanics. pp. 171–81.
- Bell, J. S. (2004). "Bertlmann's Socks and the Nature of Reality". Speakable and Unspeakable in Quantum Mechanics. Cambridge University Press. pp. 139–158.
- D'Espagnat, B. (1979). "The Quantum Theory and Reality" (PDF). Scientific American. 241 (5): 158–181. Bibcode:1979SciAm.241e.158D. doi:10.1038/scientificamerican1179-158. Archived (PDF) from the original on 2009-03-27. Retrieved 2009-03-18.
- Fry, E. S.; Walther, T.; Li, S. (1995). "Proposal for a loophole-free test of the Bell inequalities" (PDF). Phys. Rev. A. 52 (6): 4381–4395. Bibcode:1995PhRvA..52.4381F. doi:10.1103/physreva.52.4381. hdl:1969.1/126533. PMID 9912775. Archived from the original on 2021-12-29. Retrieved 2018-03-19.
- Fry, E. S.; Walther, T. (2002). "Atom based tests of the Bell Inequalities — the legacy of John Bell continues". In Bertlmann, R. A.; Zeilinger, A. (eds.). Quantum speakables. Berlin-Heidelberg-New York: Springer. pp. 103–117.
- Goldstein, Sheldon; et al. (2011). "Bell's theorem". Scholarpedia. 6 (10): 8378. Bibcode:2011SchpJ...6.8378G. doi:10.4249/scholarpedia.8378.
- Griffiths, R. B. (2001). Consistent Quantum Theory. Cambridge University Press. ISBN 978-0-521-80349-6. OCLC 1180958776.
- Hardy, L. (1993). "Nonlocality for 2 particles without inequalities for almost all entangled states". Physical Review Letters. 71 (11): 1665–1668. Bibcode:1993PhRvL..71.1665H. doi:10.1103/physrevlett.71.1665. PMID 10054467. S2CID 11839894.
- Matsukevich, D. N.; Maunz, P.; Moehring, D. L.; Olmschenk, S.; Monroe, C. (2008). "Bell Inequality Violation with Two Remote Atomic Qubits". Phys. Rev. Lett. 100 (15): 150404. arXiv:0801.2184. Bibcode:2008PhRvL.100o0404M. doi:10.1103/physrevlett.100.150404. PMID 18518088. S2CID 11536757.
- Rieffel, Eleanor G.; Polak, Wolfgang H. (4 March 2011). "4.4 EPR Paradox and Bell's Theorem". Quantum Computing: A Gentle Introduction. MIT Press. pp. 60–65. ISBN 978-0-262-01506-6.
- Sulcs, S. (2003). "The Nature of Light and Twentieth Century Experimental Physics". Foundations of Science. 8 (4): 365–391. doi:10.1023/A:1026323203487. S2CID 118769677.
- van Fraassen, B. C. (1991). Quantum Mechanics: An Empiricist View. Clarendon Press. ISBN 978-0-198-24861-3. OCLC 22906474.
- Wharton, K. B.; Argaman, N. (2020-05-18). "Colloquium : Bell's theorem and locally mediated reformulations of quantum mechanics". Reviews of Modern Physics. 92 (2): 021002. arXiv:1906.04313. Bibcode:2020RvMP...92b1002W. doi:10.1103/RevModPhys.92.021002. ISSN 0034-6861.
External links
- Mermin: Spooky Actions At A Distance? Oppenheimer Lecture.
- "Bell's theorem". Internet Encyclopedia of Philosophy.
- "Bell inequalities". Encyclopedia of Mathematics. EMS Press. 2001 .
| Quantum information science | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| General | |||||||||
| Theorems | |||||||||
| Quantum communication |
| ||||||||
| Quantum algorithms | |||||||||
| Quantum complexity theory | |||||||||
| Quantum processor benchmarks | |||||||||
| Quantum computing models | |||||||||
| Quantum error correction | |||||||||
| Physical implementations |
| ||||||||
| Quantum programming | |||||||||
 and
and  . Both
. Both  or
or  , and likewise for
, and likewise for  and
and  , which are also both binary.
, which are also both binary.
 . Consider the combination
. Consider the combination Because both
Because both  take the values
take the values  , then either
, then either  or
or  . In the former case, the quantity
. In the former case, the quantity  must equal 0, while in the latter case,
must equal 0, while in the latter case,  . So, one of the terms on the right-hand side of the above expression will vanish, and the other will equal
. So, one of the terms on the right-hand side of the above expression will vanish, and the other will equal  . Consequently, if the experiment is repeated over many trials, with Victor preparing new pairs of particles, the absolute value of the average of the combination
. Consequently, if the experiment is repeated over many trials, with Victor preparing new pairs of particles, the absolute value of the average of the combination  across all the trials will be less than or equal to 2. No single trial can measure this quantity, because Alice and Bob can only choose one measurement each, but on the assumption that the underlying properties exist, the average value of the sum is just the sum of the averages for each term. Using angle brackets to denote averages
across all the trials will be less than or equal to 2. No single trial can measure this quantity, because Alice and Bob can only choose one measurement each, but on the assumption that the underlying properties exist, the average value of the sum is just the sum of the averages for each term. Using angle brackets to denote averages This is a Bell inequality, specifically, the
This is a Bell inequality, specifically, the  and
and  exist independently of being observed or measured (sometimes called the assumption of realism); and second, that Alice's choice of action cannot influence Bob's result or vice versa (often called the assumption of locality).
exist independently of being observed or measured (sometimes called the assumption of realism); and second, that Alice's choice of action cannot influence Bob's result or vice versa (often called the assumption of locality).
 where
where  and
and  are the eigenstates of one of the
are the eigenstates of one of the  Victor then passes the first qubit to Alice and the second to Bob. Alice and Bob's choices of possible
Victor then passes the first qubit to Alice and the second to Bob. Alice and Bob's choices of possible  and
and  :
: and Bob measures either of the two observables
and Bob measures either of the two observables Victor can calculate the quantum expectation values for pairs of these observables using the
Victor can calculate the quantum expectation values for pairs of these observables using the  While only one of these four measurements can be made in a single trial of the experiment, the sum
While only one of these four measurements can be made in a single trial of the experiment, the sum gives the sum of the average values that Victor expects to find across multiple trials. This value exceeds the classical upper bound of 2 that was deduced from the hypothesis of local hidden variables. The value
gives the sum of the average values that Victor expects to find across multiple trials. This value exceeds the classical upper bound of 2 that was deduced from the hypothesis of local hidden variables. The value  is in fact the largest that quantum physics permits for this combination of expectation values, making it a
is in fact the largest that quantum physics permits for this combination of expectation values, making it a  and
and  , independently and at random. He sends bit
, independently and at random. He sends bit  and
and  to Victor, satisfying
to Victor, satisfying
 Or, equivalently, Alice and Bob win if the
Or, equivalently, Alice and Bob win if the  , regardless of what strategy they agree upon beforehand. However, if they share an entangled quantum state, their probability of winning can be as large as
, regardless of what strategy they agree upon beforehand. However, if they share an entangled quantum state, their probability of winning can be as large as
 and
and  is
is
 In particular, if the orientation of the two detectors is the same (
In particular, if the orientation of the two detectors is the same ( ), then the outcome of one measurement is certain to be the negative of the outcome of the other, giving
), then the outcome of one measurement is certain to be the negative of the outcome of the other, giving  . And if the orientations of the two detectors are orthogonal (
. And if the orientations of the two detectors are orthogonal ( ), then the outcomes are uncorrelated, and
), then the outcomes are uncorrelated, and  . Bell proves by example that these special cases can be explained in terms of hidden variables, then proceeds to show that the full range of possibilities involving intermediate angles cannot.
. Bell proves by example that these special cases can be explained in terms of hidden variables, then proceeds to show that the full range of possibilities involving intermediate angles cannot.
 :
: where
where  is a
is a  and
and  provide the responses of the two detectors given the orientation vectors and the hidden variable:
provide the responses of the two detectors given the orientation vectors and the hidden variable: Crucially, the outcome of detector
Crucially, the outcome of detector  does not depend upon
does not depend upon  does not depend upon
does not depend upon  . Bell proves that the difference in correlation between these two choices of detector setting must satisfy the inequality
. Bell proves that the difference in correlation between these two choices of detector setting must satisfy the inequality However, it is easy to find situations where quantum mechanics violates the Bell inequality. For example, let the vectors
However, it is easy to find situations where quantum mechanics violates the Bell inequality. For example, let the vectors  while
while
 but
but
 Therefore, there is no local hidden-variable model that can reproduce the predictions of quantum mechanics for all choices of
Therefore, there is no local hidden-variable model that can reproduce the predictions of quantum mechanics for all choices of  Experimental results contradict the classical curves and match the curve predicted by quantum mechanics as long as experimental shortcomings are accounted for.
Experimental results contradict the classical curves and match the curve predicted by quantum mechanics as long as experimental shortcomings are accounted for.
 where as above,
where as above,  on her particle, and so do Bob and Charlie. The result of each measurement is either
on her particle, and so do Bob and Charlie. The result of each measurement is either  , Victor predicts that whenever the three measurements include one
, Victor predicts that whenever the three measurements include one  with eigenvalue
with eigenvalue  and
and  . Therefore, knowing Alice's result for a
. Therefore, knowing Alice's result for a  with each entry being either
with each entry being either  . This value can be deduced from
. This value can be deduced from because the square of either
because the square of either  . Each factor in parentheses equals
. Each factor in parentheses equals  and the product of Alice, Bob, and Charlie's results will be
and the product of Alice, Bob, and Charlie's results will be  will instead yield
will instead yield  from Victor, promised to always have an even number of ones, that is,
from Victor, promised to always have an even number of ones, that is,  , and send him back bits
, and send him back bits  . They win the game if
. They win the game if  , when they need to have an even number of ones. That is, they win the game iff
, when they need to have an even number of ones. That is, they win the game iff  . With local hidden variables the highest probability of victory they can have is 3/4, whereas using the quantum strategy above they win it with certainty. This is an example of
. With local hidden variables the highest probability of victory they can have is 3/4, whereas using the quantum strategy above they win it with certainty. This is an example of  In 2004,
In 2004,  . Physical quantities of interest — position, momentum, energy, spin — are represented by "observables", which are
. Physical quantities of interest — position, momentum, energy, spin — are represented by "observables", which are  is non-degenerate and the probability is given by
is non-degenerate and the probability is given by  , where
, where  is its associated eigenvector. More generally, the eigenvalue is degenerate and the probability is given by
is its associated eigenvector. More generally, the eigenvalue is degenerate and the probability is given by  , where
, where  is the projector onto its associated eigenspace. For the purposes of this discussion, we can take the eigenvalues to be non-degenerate.
is the projector onto its associated eigenspace. For the purposes of this discussion, we can take the eigenvalues to be non-degenerate.
 ,
,  and
and  . In a deterministic hidden-variable theory, there exists an underlying physical property that fixes the result found in the measurement. Conditional on the value of the underlying physical property, any given outcome (for example, a result of
. In a deterministic hidden-variable theory, there exists an underlying physical property that fixes the result found in the measurement. Conditional on the value of the underlying physical property, any given outcome (for example, a result of  for some density operator
for some density operator  . This mapping is continuous on the
. This mapping is continuous on the