| Revision as of 14:22, 15 October 2015 editJayBeeEll (talk | contribs)Extended confirmed users, New page reviewers28,164 edits →Derivative of the power function: clearer← Previous edit | Latest revision as of 01:13, 31 December 2024 edit undoDavid Eppstein (talk | contribs)Autopatrolled, Administrators226,304 edits Undid revision 1266289531 by Hu741f4 (talk) huh? This is not even an assertion. It is an accurate summary sentence for the rest of its paragraph.Tag: Undo | ||
| (729 intermediate revisions by more than 100 users not shown) | |||
| Line 1: | Line 1: | ||
| {{short description|Algebraic expansion of powers of a binomial}} | |||
| ] appear as the entries of ] where each entry is the sum of the two above it.]] | |||
| {{CS1 config|mode=cs1}} | |||
| In ], the '''binomial theorem''' (or '''binomial expansion''') describes the algebraic expansion of ] of a ]. According to the theorem, it is possible to expand the power {{math|(''x'' + ''y'')<sup>''n''</sup>}} into a ] involving terms of the form {{math|''a x''<sup>''b''</sup> ''y''<sup>''c''</sup>}}<!-- U+200A (hair space) -->, where the exponents {{math|''b''}} and {{math|''c''}} are ]s with {{math|''b'' + ''c'' {{=}} ''n''}}, and the ] {{math|''a''}} of each term is a specific ] depending on {{math|''n''}} and {{math|''b''}}. For example, | |||
| {{Image frame|width=215 | |||
| |content= | |||
| <math> | |||
| \begin{array}{c} | |||
| 1 \\ | |||
| 1 \quad 1 \\ | |||
| 1 \quad 2 \quad 1 \\ | |||
| 1 \quad 3 \quad 3 \quad 1 \\ | |||
| 1 \quad 4 \quad 6 \quad 4 \quad 1 \\ | |||
| 1 \quad 5 \quad 10 \quad 10 \quad 5 \quad 1 \\ | |||
| 1 \quad 6 \quad 15 \quad 20 \quad 15 \quad 6 \quad 1 \\ | |||
| 1 \quad 7 \quad 21 \quad 35 \quad 35 \quad 21 \quad 7 \quad 1 | |||
| \end{array} | |||
| </math> | |||
| |caption=The ] <math>\tbinom{n}{k}</math> appears as the {{mvar|k}}th entry in the {{mvar|n}}th row of ] (where the top is the 0th row <math>\tbinom{0}{0}</math>). Each entry is the sum of the two above it.}} | |||
| In ], the '''binomial theorem''' (or '''binomial expansion''') describes the ] of ] of a ]. According to the theorem, the power {{tmath|\textstyle (x+y)^n}} expands into a ] with terms of the form {{tmath|\textstyle ax^ky^m }}, where the exponents {{tmath|k}} and {{tmath|m}} are ]s satisfying {{tmath|1= k + m = n}} and the ] {{tmath|a}} of each term is a specific ] depending on {{tmath|n}} and {{tmath|k}}. For example, for {{tmath|1= n = 4}}, | |||
| <math display=block>(x+y)^4 = x^4 + 4 x^3y + 6 x^2 y^2 + 4 x y^3 + y^4. </math> | |||
| The coefficient {{tmath|a}} in each term {{tmath|\textstyle ax^ky^m }} is known as the ] {{tmath|\tbinom nk}} or {{tmath|\tbinom{n}{m} }} (the two have the same value). These coefficients for varying {{tmath|n}} and {{tmath|k}} can be arranged to form ]. These numbers also occur in ], where {{tmath|\tbinom nk}} gives the number of different ] (i.e. subsets) of {{tmath|k}} ] that can be chosen from an {{tmath|n}}-element ]. Therefore {{tmath|\tbinom nk}} is usually pronounced as "{{tmath|n}} choose {{tmath|k}}". | |||
| :<math>(x+y)^4 \;=\; x^4 \,+\, 4 x^3y \,+\, 6 x^2 y^2 \,+\, 4 x y^3 \,+\, y^4.</math> | |||
| == Statement == | |||
| The coefficient {{math|''a''}} in the term of {{math|''a x''<sup>''b''</sup> ''y''<sup>''c''</sup>}} is known as the ] <math>\tbinom nb</math> or <math>\tbinom nc</math> (the two have the same value). These coefficients for varying {{math|''n''}} and {{math|''b''}} can be arranged to form ]. These numbers also arise in ], where <math>\tbinom nb</math> gives the number of different ] of {{math|''b''}} ] that can be chosen from an {{math|''n''}}-element ]. | |||
| According to the theorem, the expansion of any nonnegative integer power {{mvar|n}} of the binomial {{math|''x'' + ''y''}} is a sum of the form | |||
| <math display="block">(x+y)^n = {n \choose 0}x^n y^0 + {n \choose 1}x^{n-1} y^1 + {n \choose 2}x^{n-2} y^2 + \cdots + {n \choose n}x^0 y^n,</math> | |||
| where each <math> \tbinom nk </math> is a positive integer known as a ], defined as | |||
| <math display=block>\binom nk = \frac{n!}{k!\,(n-k)!} = \frac{n(n-1)(n-2)\cdots(n-k + 1)}{k(k-1)(k-2)\cdots2\cdot1}.</math> | |||
| ==History== | |||
| Special cases of the binomial theorem were known from ancient times. The 4th century B.C. ] ] mentioned the special case of the binomial theorem for exponent 2.<ref name=wolfram>{{cite web|url=http://mathworld.wolfram.com/BinomialTheorem.html|title=Binomial Theorem|website=Wolfram MathWorld|last=Weisstein|first=Eric W.}}</ref><ref name="Coolidge">{{cite journal|url=http://www.jstor.org/pss/2305028|title=The Story of the Binomial Theorem|first=J. L.|last=Coolidge|journal=The American Mathematical Monthly|volume=56|issue=3|date=1949|pp=147–157}}</ref> There is evidence that the binomial theorem for cubes was known by the 6th century in India.<ref name=wolfram/><ref name="Coolidge"/> | |||
| This formula is also referred to as the '''binomial formula''' or the '''binomial identity'''. Using ], it can be written more concisely as | |||
| Binomial coefficients, as combinatorial quantities expressing the number of ways of selecting ''k'' objects out of ''n'' without replacement, were of interest to the ancient Hindus. The earliest known reference to this combinatorial problem is the ''Chandaḥśāstra'' by the Hindu lyricist ] (c. 200 B.C.), which contains a method for its solution.<ref name=Chinese>{{cite book|title=A history of Chinese mathematics|author1=Jean-Claude Martzloff|author2=S.S. Wilson|author3=J. Gernet|author4=J. Dhombres|publisher=Springer|year=1987}}</ref>{{rp|230}} The commentator ] from the 10th century A.D. explains this method using what is now known as ].<ref name=Chinese/> By the 6th century A.D., the Hindu mathematicians probably knew how to express this as a quotient <math>\frac{n!}{(n-k)!k!}</math>,<ref name="Biggs">{{cite journal|last=Biggs|first=N. L.|title=The roots of combinatorics|journal=Historia Math.|volume=6|date=1979|issue=2|pp=109-136|doi=10.1016/0315-0860(79)90074-0}}</ref> and a clear statement of this rule can be found in the 12th century text ''Lilavati'' by ].<ref name="Biggs"/> | |||
| <math display="block">(x+y)^n = \sum_{k=0}^n {n \choose k}x^{n-k}y^k = \sum_{k=0}^n {n \choose k}x^{k}y^{n-k}.</math> | |||
| The final expression follows from the previous one by the symmetry of {{mvar|x}} and {{mvar|y}} in the first expression, and by comparison it follows that the sequence of binomial coefficients in the formula is symmetrical, <math display=inline>\binom nk = \binom n{n-k}.</math> | |||
| The binomial theorem as such can be found in the work of 11th-century ] ], who described the triangular pattern of the binomial coefficients.<ref name=Karaji>{{MacTutor|id=Al-Karaji|title=Abu Bekr ibn Muhammad ibn al-Husayn Al-Karaji}}</ref> He also provided a ] of both the binomial theorem and Pascal's triangle, using a primitive form of ].<ref name=Karaji/> The Persian poet and mathematician ] was probably familiar with the formula to higher orders, although many of his mathematical works are lost.<ref name="Coolidge"/> The binomial expansions of small degrees were known in the 13th century mathematical works of ]<ref>{{Cite web | |||
| | last = Landau | |||
| | first = James A. | |||
| | title = <nowiki>Historia Matematica Mailing List Archive: Re: Pascal's Triangle</nowiki> | |||
| | work = Archives of Historia Matematica | |||
| | format = mailing list email | |||
| | accessdate = 2007-04-13 | |||
| | date = 1999-05-08 | |||
| | url = http://archives.math.utk.edu/hypermail/historia/may99/0073.html | |||
| }}</ref> and also ].<ref name="Coolidge"/> Yang Hui attributes the method to a much earlier 11th century text of ], although those writings are now also lost.<ref name=Chinese/>{{rp|142}} | |||
| A simple variant of the binomial formula is obtained by ] {{math|1}} for {{mvar|y}}, so that it involves only a single ]. In this form, the formula reads | |||
| In 1544, ] introduced the term "binomial coefficient" and showed how to use them to express <math>(1+a)^n</math> in terms of <math>(1+a)^{n-1}</math>, via "Pascal's triangle".<ref name=Kline>{{cite book|title=History of mathematical thought|first=Morris|last=Kline|page=273|publisher=Oxford University Press|year=1972}}</ref> ] studied the eponymous triangle comprehensively in the ] ''Traité du triangle arithmétique'' (1653). However, the pattern of numbers was already known to the European mathematicians of the late Renaissance, including Stifel, ], and ].<ref name=Kline/> | |||
| <math display=block>\begin{align} | |||
| (x+1)^n | |||
| &= {n \choose 0}x^0 + {n \choose 1}x^1 + {n \choose 2}x^2 + \cdots + {n \choose n}x^n \\ | |||
| &= \sum_{k=0}^n {n \choose k}x^k. \vphantom{\Bigg)} | |||
| \end{align}</math><!-- \vphantom{\Bigg)} works around a mediawiki scrollbar bug --> | |||
| == Examples == | |||
| ] is generally credited with the generalised binomial theorem, valid for any rational exponent.<ref>{{cite book|title=Elements of the History of Mathematics Paperback|date= 18 November 1998|first= N.|last=Bourbaki|others= J. Meldrum (Translator)|isbn=978-3540647676}}</ref><ref name=Kline/> | |||
| The first few cases of the binomial theorem are: | |||
| <math display="block">\begin{align} | |||
| According to the theorem, it is possible | |||
| (x+y)^0 & = 1, \\ | |||
| to expand any power of ''x'' + ''y'' into a sum of the form | |||
| (x+y)^1 & = x + y, \\ | |||
| :<math>(x+y)^n = {n \choose 0}x^n y^0 + {n \choose 1}x^{n-1}y^1 + {n \choose 2}x^{n-2}y^2 + \cdots + {n \choose n-1}x^1 y^{n-1} + {n \choose n}x^0 y^n, | |||
| (x+y)^2 & = x^2 + 2xy + y^2, \\ | |||
| </math> | |||
| where each <math> \tbinom nk </math> is a specific positive integer known as a ]. (When an exponent is zero, the corresponding power expression is taken to be 1 and this multiplicative factor is often omitted from the term. Hence one often sees the right side written as <math>\binom{n}{0} x^n + \ldots</math>.) This formula is also referred to as the '''binomial formula''' or the '''binomial identity'''. Using ], it can be written as | |||
| :<math>(x+y)^n = \sum_{k=0}^n {n \choose k}x^{n-k}y^k = \sum_{k=0}^n {n \choose k}x^{k}y^{n-k}. | |||
| </math> | |||
| The final expression follows from the previous one by the symmetry of ''x'' and ''y'' in the first expression, and by comparison it follows that the sequence of binomial coefficients in the formula is symmetrical. | |||
| A simple variant of the binomial formula is obtained by ] 1 for ''y'', so that it involves only a single ]. In this form, the formula reads | |||
| :<math>(1+x)^n = {n \choose 0}x^0 + {n \choose 1}x^1 + {n \choose 2}x^2 + \cdots + {n \choose {n-1}}x^{n-1} + {n \choose n}x^n,</math> | |||
| or equivalently | |||
| :<math>(1+x)^n = \sum_{k=0}^n {n \choose k}x^k.</math> | |||
| ==Examples== | |||
| ] | |||
| The most basic example of the binomial theorem is the formula for the ] of {{nowrap|''x'' + ''y''}}: | |||
| :<math>(x + y)^2 = x^2 + 2xy + y^2.\!</math> | |||
| The binomial coefficients 1, 2, 1 appearing in this expansion correspond to the second row of Pascal's triangle (Note that the top is row 0). The coefficients of higher powers of {{nowrap|''x'' + ''y''}} correspond to later rows of the triangle: | |||
| :<math> | |||
| \begin{align} | |||
| \\ | |||
| (x+y)^3 & = x^3 + 3x^2y + 3xy^2 + y^3, \\ | (x+y)^3 & = x^3 + 3x^2y + 3xy^2 + y^3, \\ | ||
| (x+y)^4 & = x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4, |
(x+y)^4 & = x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4, | ||
| \end{align}</math> | |||
| (x+y)^5 & = x^5 + 5x^4y + 10x^3y^2 + 10x^2y^3 + 5xy^4 + y^5, \\ | |||
| In general, for the expansion of {{math|(''x'' + ''y'')<sup>''n''</sup>}} on the right side in the {{mvar|n}}th row (numbered so that the top row is the 0th row): | |||
| (x+y)^6 & = x^6 + 6x^5y + 15x^4y^2 + 20x^3y^3 + 15x^2y^4 + 6xy^5 + y^6, \\ | |||
| * the exponents of {{mvar|x}} in the terms are {{math|''n'', ''n'' − 1, ..., 2, 1, 0}} (the last term implicitly contains {{math|1=''x''<sup>0</sup> = 1}}); | |||
| (x+y)^7 & = x^7 + 7x^6y + 21x^5y^2 + 35x^4y^3 + 35x^3y^4 + 21x^2y^5 + 7xy^6 + y^7. | |||
| * the exponents of {{mvar|y}} in the terms are {{math|0, 1, 2, ..., ''n'' − 1, ''n''}} (the first term implicitly contains {{math|1=''y''<sup>0</sup> = 1}}); | |||
| \end{align} | |||
| * the coefficients form the {{mvar|n}}th row of Pascal's triangle; | |||
| </math> | |||
| * before combining like terms, there are {{math|2<sup>''n''</sup>}} terms {{math|''x''<sup>''i''</sup>''y''<sup>''j''</sup>}} in the expansion (not shown); | |||
| Notice that | |||
| * after combining like terms, there are {{math|''n'' + 1}} terms, and their coefficients sum to {{math|2<sup>''n''</sup>}}. | |||
| #the powers of ''x'' go down until it reaches 0 (<math>x^0=1</math>), starting value is ''n'' (the ''n'' in <math>(x+y)^n</math>.) | |||
| An example illustrating the last two points: <math display="block">\begin{align} | |||
| #the powers of ''y'' go up from 0 (<math>y^0=1</math>) until it reaches ''n'' (also the ''n'' in <math>(x+y)^n</math>.) | |||
| (x+y)^3 & = xxx + xxy + xyx + xyy + yxx + yxy + yyx + yyy & (2^3 \text{ terms}) \\ | |||
| #the nth row of the Pascal's Triangle will be the coefficients of the expanded binomial. | |||
| & = x^3 + 3x^2y + 3xy^2 + y^3 & (3 + 1 \text{ terms}) | |||
| #for each line, the number of products (i.e. the sum of the coefficients) is equal to <math>2^n</math>. | |||
| \end{align}</math> with <math>1 + 3 + 3 + 1 = 2^3</math>. | |||
| #for each line, the number of product groups is equal to <math>n+1</math>. | |||
| The binomial theorem can be applied to the powers of any binomial. For example, | |||
| A simple example with a specific positive value of {{math|''y''}}: | |||
| :<math>\begin{align} | |||
| <math display="block">\begin{align} | |||
| (x+2)^3 &= x^3 + 3x^2(2) + 3x(2)^2 + 2^3 \\ | (x+2)^3 &= x^3 + 3x^2(2) + 3x(2)^2 + 2^3 \\ | ||
| &= x^3 + 6x^2 + 12x + 8.\end{align}</math> | &= x^3 + 6x^2 + 12x + 8. | ||
| \end{align}</math> | |||
| A simple example with a specific negative value of {{math|''y''}}: | |||
| For a binomial involving subtraction, the theorem can be applied as long as the ] of the second term is used. This has the effect of changing the sign of every other term in the expansion: | |||
| <math display="block">\begin{align} | |||
| :<math>(x-y)^3 = x^3 - 3x^2y + 3xy^2 - y^3.\!</math> | |||
| (x-2)^3 &= x^3 - 3x^2(2) + 3x(2)^2 - 2^3 \\ | |||
| &= x^3 - 6x^2 + 12x - 8. | |||
| \end{align}</math> | |||
| === Geometric explanation === | |||
| Another useful example is that of the expansion of the following square roots: | |||
| ] | |||
| :<math>\sqrt{1+x} = \textstyle 1 + \frac{1}{2}x - \frac{1}{8}x^2 + \frac{1}{16}x^3 - \frac{5}{128}x^4 + \frac{7}{256}x^5 - \cdots</math> | |||
| For positive values of {{mvar|a}} and {{mvar|b}}, the binomial theorem with {{math|1=''n'' = 2}} is the geometrically evident fact that a square of side {{math|''a'' + ''b''}} can be cut into a square of side {{mvar|a}}, a square of side {{mvar|b}}, and two rectangles with sides {{mvar|a}} and {{mvar|b}}. With {{math|1=''n'' = 3}}, the theorem states that a cube of side {{math|''a'' + ''b''}} can be cut into a cube of side {{mvar|a}}, a cube of side {{mvar|b}}, three {{math|''a'' × ''a'' × ''b''}} rectangular boxes, and three {{math|''a'' × ''b'' × ''b''}} rectangular boxes. | |||
| In ], this picture also gives a geometric proof of the ] <math>(x^n)'=nx^{n-1}:</math><ref name="barth2004">{{cite journal | last = Barth | first = Nils R.| title = Computing Cavalieri's Quadrature Formula by a Symmetry of the ''n''-Cube | doi = 10.2307/4145193 | jstor = 4145193 | journal = The American Mathematical Monthly | volume = 111| issue = 9| pages = 811–813 | date=2004}}</ref> if one sets <math>a=x</math> and <math>b=\Delta x,</math> interpreting {{mvar|b}} as an ] change in {{mvar|a}}, then this picture shows the infinitesimal change in the volume of an {{mvar|n}}-dimensional ], <math>(x+\Delta x)^n,</math> where the coefficient of the linear term (in <math>\Delta x</math>) is <math>nx^{n-1},</math> the area of the {{mvar|n}} faces, each of dimension {{math|''n'' − 1}}: | |||
| :<math>\frac{1}{\sqrt{1+x}} = \textstyle 1 -\frac{1}{2}x + \frac{3}{8}x^2 - \frac{5}{16}x^3 + \frac{35}{128}x^4 - \frac{63}{256}x^5 + \cdots</math> | |||
| <math display="block">(x+\Delta x)^n = x^n + nx^{n-1}\Delta x + \binom{n}{2}x^{n-2}(\Delta x)^2 + \cdots.</math> | |||
| Substituting this into the ] via a ] and taking limits means that the higher order terms, <math>(\Delta x)^2</math> and higher, become negligible, and yields the formula <math>(x^n)'=nx^{n-1},</math> interpreted as | |||
| Sometimes it may be useful to expand negative exponents when <math>|x| < 1</math>: | |||
| :"the infinitesimal rate of change in volume of an {{mvar|n}}-cube as side length varies is the area of {{mvar|n}} of its {{math|(''n'' − 1)}}-dimensional faces". | |||
| :<math>(1+x)^{-1} = \frac{1}{1+x} = 1 - x + x^2 - x^3 + x^4 - x^5 + \cdots</math> | |||
| ===Geometric explanation=== | |||
| ] | |||
| For positive values of ''a'' and ''b'', the binomial theorem with ''n'' = 2 is the geometrically evident fact that a square of side {{nowrap|''a'' + ''b''}} can be cut into a square of side ''a'', a square of side ''b'', and two rectangles with sides ''a'' and ''b''. With ''n'' = 3, the theorem states that a cube of side {{nowrap|''a'' + ''b''}} can be cut into a cube of side ''a'', a cube of side ''b'', three ''a''×''a''×''b'' rectangular boxes, and three ''a''×''b''×''b'' rectangular boxes. | |||
| In ], this picture also gives a geometric proof of the ] <math>(x^n)'=nx^{n-1}:</math><ref name="barth2004">{{Cite journal | last = Barth | first = Nils R.| title = Computing Cavalieri's Quadrature Formula by a Symmetry of the ''n''-Cube | doi = 10.2307/4145193 | jstor = 4145193 | journal = The American Mathematical Monthly| publisher = Mathematical Association of America| issn = 0002-9890| volume = 111| issue = 9| pages = 811–813 | date=2004 | pmid = | pmc =| postscript = , , }}</ref> if one sets <math>a=x</math> and <math>b=\Delta x,</math> interpreting ''b'' as an infinitesimal change in ''a,'' then this picture shows the infinitesimal change in the volume of an ''n''-dimensional ], <math>(x+\Delta x)^n,</math> where the coefficient of the linear term (in <math>\Delta x</math>) is <math>nx^{n-1},</math> the area of the ''n'' faces, each of dimension <math>(n-1):</math> | |||
| :<math>(x+\Delta x)^n = x^n + nx^{n-1}\Delta x + \tbinom{n}{2}x^{n-2}(\Delta x)^2 + \cdots.</math> | |||
| Substituting this into the ] via a ] and taking limits means that the higher order terms – <math>(\Delta x)^2</math> and higher – become negligible, and yields the formula <math>(x^n)'=nx^{n-1},</math> interpreted as | |||
| :"the infinitesimal change in volume of an ''n''-cube as side length varies is the area of ''n'' of its <math>(n-1)</math>-dimensional faces". | |||
| If one integrates this picture, which corresponds to applying the ], one obtains ], the integral <math>\textstyle{\int x^{n-1}\,dx = \tfrac{1}{n} x^n}</math> – see ] for details.<ref name="barth2004" /> | If one integrates this picture, which corresponds to applying the ], one obtains ], the integral <math>\textstyle{\int x^{n-1}\,dx = \tfrac{1}{n} x^n}</math> – see ] for details.<ref name="barth2004" /> | ||
| {{clear}} | {{clear}} | ||
| == |
== Binomial coefficients == | ||
| {{ |
{{Main|Binomial coefficient}} | ||
| The coefficients that appear in the binomial expansion are called '''binomial coefficients'''. These are usually written <math> |
The coefficients that appear in the binomial expansion are called '''binomial coefficients'''. These are usually written <math>\tbinom{n}{k},</math> and pronounced "{{mvar|n}} choose {{mvar|k}}". | ||
| === |
=== Formulas === | ||
| The coefficient of ''x''<sup>''n'' |
The coefficient of {{math|''x''<sup>''n''−''k''</sup>''y''<sup>''k''</sup>}} is given by the formula | ||
| <math display="block">\binom{n}{k} = \frac{n!}{k! \; (n-k)!},</math> | |||
| which is defined in terms of the ] function {{math|''n''!}}. Equivalently, this formula can be written | |||
| <math display="block">\binom{n}{k} = \frac{n (n-1) \cdots (n-k+1)}{k (k-1) \cdots 1} = \prod_{\ell=1}^k \frac{n-\ell+1}{\ell} = \prod_{\ell=0}^{k-1} \frac{n-\ell}{k - \ell}</math> | |||
| with {{mvar|k}} factors in both the numerator and denominator of the ]. Although this formula involves a fraction, the binomial coefficient <math>\tbinom{n}{k}</math> is actually an ]. | |||
| === Combinatorial interpretation === | |||
| :<math>{n \choose k} = \frac{n!}{k!\,(n-k)!}</math>, | |||
| The binomial coefficient <math> \tbinom nk </math> can be interpreted as the number of ways to choose {{mvar|k}} elements from an {{mvar|n}}-element set (a ]). This is related to binomials for the following reason: if we write {{math|1=(''x'' + ''y'')<sup>''n''</sup>}} as a ] | |||
| <math display="block">(x+y)(x+y)(x+y)\cdots(x+y),</math> | |||
| then, according to the ], there will be one term in the expansion for each choice of either {{mvar|x}} or {{mvar|y}} from each of the binomials of the product. For example, there will only be one term {{math|''x''<sup>''n''</sup>}}, corresponding to choosing {{mvar|x}} from each binomial. However, there will be several terms of the form {{math|''x''<sup>''n''−2</sup>''y''<sup>2</sup>}}, one for each way of choosing exactly two binomials to contribute a {{mvar|y}}. Therefore, after ], the coefficient of {{math|''x''<sup>''n''−2</sup>''y''<sup>2</sup>}} will be equal to the number of ways to choose exactly {{math|2}} elements from an {{mvar|n}}-element set. | |||
| == Proofs == | |||
| which is defined in terms of the ] function ''n''!. Equivalently, this formula can be written | |||
| === Combinatorial proof === | |||
| :<math>{n \choose k} = \frac{n (n-1) \cdots (n-k+1)}{k (k-1) \cdots 1} = \prod_{\ell=1}^k \frac{n-\ell+1}{\ell} = \prod_{\ell=0}^{k-1} \frac{n-\ell}{k - \ell}</math> | |||
| Expanding {{math|1=(''x'' + ''y'')<sup>''n''</sup>}} yields the sum of the {{math|2<sup>''n''</sup>}} products of the form {{math|1=''e''<sub>1</sub>''e''<sub>2</sub> ... ''e''<sub>''n''</sub>}} where each {{math|''e''<sub>''i''</sub>}} is {{mvar|''x''}} or {{mvar|y}}. Rearranging factors shows that each product equals {{math|''x''<sup>''n''−''k''</sup>''y''<sup>''k''</sup>}} for some {{mvar|k}} between {{math|0}} and {{mvar|n}}. For a given {{mvar|k}}, the following are proved equal in succession: | |||
| * the number of terms equal to {{math|1=''x''<sup>''n''−''k''</sup>''y''<sup>''k''</sup>}} in the expansion | |||
| with ''k'' factors in both the numerator and denominator of the ]. Note that, although this formula involves a fraction, the binomial coefficient <math> \tbinom nk </math> is actually an ]. | |||
| * the number of {{mvar|n}}-character {{math|''x'',''y''}} strings having {{mvar|y}} in exactly {{mvar|k}} positions | |||
| * the number of {{mvar|k}}-element subsets of {{math|1={{mset|1, 2, ..., ''n''}}}} | |||
| ===Combinatorial interpretation=== | |||
| * <math>\tbinom{n}{k},</math> either by definition, or by a short combinatorial argument if one is defining <math>\tbinom{n}{k}</math> as <math>\tfrac{n!}{k! (n-k)!}.</math> | |||
| The binomial coefficient <math> \tbinom nk </math> can be interpreted as the number of ways to choose ''k'' elements from an ''n''-element set. This is related to binomials for the following reason: if we write (''x'' + ''y'')<sup>''n''</sup> as a ] | |||
| :<math>(x+y)(x+y)(x+y)\cdots(x+y),</math> | |||
| then, according to the ], there will be one term in the expansion for each choice of either ''x'' or ''y'' from each of the binomials of the product. For example, there will only be one term ''x''<sup>''n''</sup>, corresponding to choosing ''x'' from each binomial. However, there will be several terms of the form ''x''<sup>''n''−2</sup>''y''<sup>2</sup>, one for each way of choosing exactly two binomials to contribute a ''y''. Therefore, after ], the coefficient of ''x''<sup>''n''−2</sup>''y''<sup>2</sup> will be equal to the number of ways to choose exactly 2 elements from an ''n''-element set. | |||
| ==Proofs== | |||
| ===Combinatorial proof=== | |||
| ====Example==== | |||
| The coefficient of ''xy''<sup>2</sup> in | |||
| :<math>\begin{align} | |||
| (x+y)^3 &= (x+y)(x+y)(x+y) \\ | |||
| &= xxx + xxy + xyx + \underline{xyy} + yxx + \underline{yxy} + \underline{yyx} + yyy \\ | |||
| &= x^3 + 3x^2y + \underline{3xy^2} + y^3. | |||
| \end{align} \, </math> | |||
| equals <math>\tbinom{3}{2}=3</math> because there are three ''x'',''y'' strings of length 3 with exactly two ''y'''s, namely, | |||
| :<math>xyy, \; yxy, \; yyx,</math> | |||
| corresponding to the three 2-element subsets of { 1, 2, 3 }, namely, | |||
| :<math>\{2,3\},\;\{1,3\},\;\{1,2\}, </math> | |||
| where each subset specifies the positions of the ''y'' in a corresponding string. | |||
| ====General case==== | |||
| Expanding (''x'' + ''y'')<sup>''n''</sup> yields the sum of the 2<sup> ''n''</sup> products of the form ''e''<sub>1</sub>''e''<sub>2</sub> ... ''e''<sub> ''n''</sub> where each ''e''<sub> ''i''</sub> is ''x'' or ''y''. Rearranging factors shows that each product equals ''x''<sup>''n''−''k''</sup>''y''<sup>''k''</sup> for some ''k'' between 0 and ''n''. For a given ''k'', the following are proved equal in succession: | |||
| *the number of copies of ''x''<sup>''n'' − ''k''</sup>''y''<sup>''k''</sup> in the expansion | |||
| *the number of ''n''-character ''x'',''y'' strings having ''y'' in exactly ''k'' positions | |||
| *the number of ''k''-element subsets of { 1, 2, ..., ''n''} | |||
| *<math>{n \choose k}</math> (this is either by definition, or by a short combinatorial argument if one is defining <math>{n \choose k}</math> as <math>\frac{n!}{k!\,(n-k)!}</math>). | |||
| This proves the binomial theorem. | This proves the binomial theorem. | ||
| === |
==== Example ==== | ||
| The coefficient of {{math|''xy''<sup>2</sup>}} in | |||
| ] yields another proof of the binomial theorem. When ''n'' = 0, both sides equal 1, since ''x''<sup>0</sup> = 1 and <math>\tbinom{0}{0}=1</math>. | |||
| <math display="block">\begin{align} | |||
| Now suppose that the equality holds for a given ''n''; we will prove it for ''n'' + 1. | |||
| (x+y)^3 &= (x+y)(x+y)(x+y) \\ | |||
| For ''j'', ''k'' ≥ 0, let <sub> ''j,k''</sub> denote the coefficient of ''x''<sup>''j''</sup>''y''<sup>''k''</sup> in the polynomial ''ƒ''(''x'', ''y''). | |||
| &= xxx + xxy + xyx + \underline{xyy} + yxx + \underline{yxy} + \underline{yyx} + yyy \\ | |||
| By the inductive hypothesis, (''x'' + ''y'')<sup>''n''</sup> is a polynomial in ''x'' and ''y'' such that <sub> ''j,k''</sub> is <math>\tbinom{n}{k}</math> if ''j'' + ''k'' = ''n'', and 0 otherwise. | |||
| &= x^3 + 3x^2y + \underline{3xy^2} + y^3 | |||
| The identity | |||
| \end{align}</math> | |||
| equals <math>\tbinom{3}{2}=3</math> because there are three {{math|''x'',''y''}} strings of length 3 with exactly two {{mvar|y}}'s, namely, | |||
| <math display="block">xyy, \; yxy, \; yyx,</math> | |||
| corresponding to the three 2-element subsets of {{math|{{mset|1, 2, 3}}}}, namely, | |||
| <math display="block">\{2,3\},\;\{1,3\},\;\{1,2\}, </math> | |||
| where each subset specifies the positions of the {{mvar|y}} in a corresponding string. | |||
| === Inductive proof === | |||
| :<math> (x+y)^{n+1} = x(x+y)^n + y(x+y)^n, \, </math> | |||
| ] yields another proof of the binomial theorem. When {{math|1=''n'' = 0}}, both sides equal {{math|1}}, since {{math|1=''x''<sup>0</sup> = 1}} and <math>\tbinom{0}{0}=1.</math> Now suppose that the equality holds for a given {{mvar|n}}; we will prove it for {{math|1=''n'' + 1}}. For {{math|1=''j'', ''k'' ≥ 0}}, let {{math|1=<sub>''j'',''k''</sub>}} denote the coefficient of {{math|1=''x''<sup>''j''</sup>''y''<sup>''k''</sup>}} in the polynomial {{math|1=''f''(''x'', ''y'')}}. By the inductive hypothesis, {{math|1=(''x'' + ''y'')<sup>''n''</sup>}} is a polynomial in {{mvar|x}} and {{mvar|y}} such that {{math|1=<sub>''j'',''k''</sub>}} is <math>\tbinom{n}{k}</math> if {{math|1=''j'' + ''k'' = ''n''}}, and {{mvar|0}} otherwise. The identity | |||
| <math display="block"> (x+y)^{n+1} = x(x+y)^n + y(x+y)^n</math> | |||
| shows that {{math|1=(''x'' + ''y'')<sup>''n''+1</sup>}} is also a polynomial in {{mvar|x}} and {{mvar|y}}, and | |||
| <math display="block"> _{j,k} = _{j-1,k} + _{j,k-1},</math> | |||
| since if {{math|1=''j'' + ''k'' = ''n'' + 1}}, then {{math|1=(''j'' − 1) + ''k'' = ''n''}} and {{math|1=''j'' + (''k'' − 1) = ''n''}}. Now, the right hand side is | |||
| <math display="block"> \binom{n}{k} + \binom{n}{k-1} = \binom{n+1}{k},</math> | |||
| by ].<ref> – inductive proofs {{webarchive |url=https://web.archive.org/web/20150224130932/http://proofs.wiki/Binomial_theorem |date=February 24, 2015 }}</ref> On the other hand, if {{math|1=''j'' + ''k'' ≠ ''n'' + 1}}, then {{math|1=(''j'' – 1) + ''k'' ≠ ''n''}} and {{math|1=''j'' + (''k'' – 1) ≠ ''n''}}, so we get {{math|1=0 + 0 = 0}}. Thus | |||
| <math display="block">(x+y)^{n+1} = \sum_{k=0}^{n+1} \binom{n+1}{k} x^{n+1-k} y^k,</math> | |||
| which is the inductive hypothesis with {{math|1=''n'' + 1}} substituted for {{mvar|n}} and so completes the inductive step. | |||
| == Generalizations == | |||
| shows that (''x'' + ''y'')<sup>''n''+1</sup> also is a polynomial in ''x'' and ''y'', and | |||
| === Newton's generalized binomial theorem === | |||
| :<math> _{j,k} = _{j-1,k} + _{j,k-1},</math> | |||
| {{Main|Binomial series}} | |||
| Around 1665, ] generalized the binomial theorem to allow real exponents other than nonnegative integers. (The same generalization also applies to ] exponents.) In this generalization, the finite sum is replaced by an ]. In order to do this, one needs to give meaning to binomial coefficients with an arbitrary upper index, which cannot be done using the usual formula with factorials. However, for an arbitrary number {{mvar|r}}, one can define | |||
| <math display="block">{r \choose k}=\frac{r(r-1) \cdots (r-k+1)}{k!} =\frac{(r)_k}{k!},</math><!--This is not the same as \frac{r!}{k!(r−k)!}. Please do not change it.--> | |||
| where <math>(\cdot)_k</math> is the ], here standing for a ]. This agrees with the usual definitions when {{mvar|r}} is a nonnegative integer. Then, if {{mvar|x}} and {{mvar|y}} are real numbers with {{math|{{abs|''x''}} > {{abs|''y''}}}},<ref name=convergence group=Note>This is to guarantee convergence. Depending on {{mvar|r}}, the series may also converge sometimes when {{math|1={{abs|''x''}} = {{abs|''y''}}}}.</ref> and {{mvar|r}} is any complex number, one has | |||
| <math display="block">\begin{align} | |||
| (x+y)^r & =\sum_{k=0}^\infty {r \choose k} x^{r-k} y^k \\ | |||
| &= x^r + r x^{r-1} y + \frac{r(r-1)}{2!} x^{r-2} y^2 + \frac{r(r-1)(r-2)}{3!} x^{r-3} y^3 + \cdots. | |||
| \end{align}</math> | |||
| When {{mvar|r}} is a nonnegative integer, the binomial coefficients for {{math|1=''k'' > ''r''}} are zero, so this equation reduces to the usual binomial theorem, and there are at most {{math|1=''r'' + 1}} nonzero terms. For other values of {{mvar|r}}, the series typically has infinitely many nonzero terms. | |||
| since if ''j'' + ''k'' = ''n'' + 1, then (''j'' − 1) + ''k'' = ''n'' and ''j'' + (''k'' − 1) = ''n''. Now, the right hand side is | |||
| For example, {{math|1=''r'' = 1/2}} gives the following series for the square root: | |||
| :<math> \binom{n}{k} + \binom{n}{k-1} = \binom{n+1}{k},</math> | |||
| <math display="block">\sqrt{1+x} = 1 + \frac{1}{2}x - \frac{1}{8}x^2 + \frac{1}{16}x^3 - \frac{5}{128}x^4 + \frac{7}{256}x^5 - \cdots.</math> | |||
| Taking {{math|1=''r'' = −1}}, the generalized binomial series gives the ], valid for {{math|{{abs|''x''}} < 1}}: | |||
| by ].<ref>{{dead link|date=September 2015}} - inductive proofs</ref> On the other hand, if ''j'' +''k'' ≠ ''n'' + 1, then (''j'' – 1) + ''k'' ≠ ''n'' and ''j'' +(''k'' – 1) ≠ ''n'', so we get 0 + 0 = 0. Thus | |||
| <math display="block">(1+x)^{-1} = \frac{1}{1+x} = 1 - x + x^2 - x^3 + x^4 - x^5 + \cdots.</math> | |||
| More generally, with {{math|1=''r'' = −''s''}}, we have for {{math|{{abs|''x''}} < 1}}:<ref name=wolfram2>{{cite web| url=https://mathworld.wolfram.com/NegativeBinomialSeries.html|title=Negative Binomial Series|website=Wolfram MathWorld|last=Weisstein|first=Eric W.}}</ref> | |||
| :<math>(x+y)^{n+1} = \sum_{k=0}^{n+1} \tbinom{n+1}{k} x^{n+1-k} y^k,</math> | |||
| <math display="block">\frac{1}{(1+x)^s} = \sum_{k=0}^\infty {-s \choose k} x^k = \sum_{k=0}^\infty {s+k-1 \choose k} (-1)^k x^k.</math> | |||
| So, for instance, when {{math|1=''s'' = 1/2}}, | |||
| which is the inductive hypothesis with ''n'' + 1 substituted for ''n'' and so completes the inductive step. | |||
| <math display="block">\frac{1}{\sqrt{1+x}} = 1 - \frac{1}{2}x + \frac{3}{8}x^2 - \frac{5}{16}x^3 + \frac{35}{128}x^4 - \frac{63}{256}x^5 + \cdots.</math> | |||
| Replacing {{mvar|x}} with {{mvar|-x}} yields: | |||
| ==Generalisations== | |||
| <math display="block">\frac{1}{(1-x)^s} = \sum_{k=0}^\infty {s+k-1 \choose k} (-1)^k (-x)^k = \sum_{k=0}^\infty {s+k-1 \choose k} x^k.</math> | |||
| So, for instance, when {{math|1=''s'' = 1/2}}, we have for {{math|{{abs|''x''}} < 1}}: | |||
| ===Newton's generalised binomial theorem=== | |||
| <math display="block">\frac{1}{\sqrt{1-x}} = 1 + \frac{1}{2}x + \frac{3}{8}x^2 + \frac{5}{16}x^3 + \frac{35}{128}x^4 + \frac{63}{256}x^5 + \cdots.</math> | |||
| {{main|Binomial series}} | |||
| Around 1665, ] generalised the formula to allow real exponents other than nonnegative integers. In addition, the formula can be generalised to complex exponents. In this generalisation, the finite sum is replaced by an ]. In order to do this, one needs to give meaning to binomial coefficients with an arbitrary upper index, which cannot be done using the above formula with factorials; however factoring out (''n'' − ''k'')! from numerator and denominator in that formula, and replacing ''n'' by ''r'' which now stands for an arbitrary number, one can define | |||
| === Further generalizations === | |||
| :<math>{r \choose k}=\frac{r\,(r-1) \cdots (r-k+1)}{k!} =\frac{(r)_k}{k!},</math> | |||
| The generalized binomial theorem can be extended to the case where {{mvar|x}} and {{mvar|y}} are complex numbers. For this version, one should again assume {{math|{{abs|''x''}} > {{abs|''y''}}}}<ref name=convergence group=Note /> and define the powers of {{math|1=''x'' + ''y''}} and {{mvar|x}} using a ] ] defined on an open disk of radius {{math|{{abs|''x''}}}} centered at {{mvar|x}}. The generalized binomial theorem is valid also for elements {{mvar|x}} and {{mvar|y}} of a ] as long as {{math|1=''xy'' = ''yx''}}, and {{mvar|x}} is invertible, and {{math|{{norm|''y''/''x''}} < 1}}. | |||
| <!-- | |||
| This is not the same as \frac{r!}{k!\,(r−k)!}. Factorials are typically only defined on natural number arguments, but even if you are using factorials generalised (e.g. by the \Gamma function) to non-integer values, they are still undefined on the negative integers. To get the usual binomial theorem as a special case of this so-called generalisation, we had better define the binomial coefficient when ''r'' is an integer, but in that case ''r''−''k'' will be a negative integer for sufficiently large ''k'', so one cannot use any formula involving the factorial <math>(r−k)!</math>. | |||
| A version of the binomial theorem is valid for the following ]-like family of polynomials: for a given real constant {{mvar|c}}, define <math> x^{(0)} = 1 </math> and | |||
| This negative comment about "not the same as…" seems to be needed. People keep coming along and completing this formula with this expression involving factorials, missing the point of this section. | |||
| <math display="block"> x^{(n)} = \prod_{k=1}^{n}</math> | |||
| ~~~~perhaps someone could put a better explanation in! Here is an attempt!. | |||
| for <math> n > 0.</math> Then<ref name="Sokolowsky">{{cite journal| url=https://cms.math.ca/publications/crux/issue/?volume=5&issue=2| title=Problem 352|first1=Dan|last1=Sokolowsky|first2=Basil C.|last2=Rennie|journal=Crux Mathematicorum|volume=5|issue=2|date=1979 | pages=55–56}}</ref> | |||
| The problem with substituting \frac{r!}{k!\,(r−k)!} is that the ! ends up being used for negative numbers which doesn't work with the definition of !. Consequently, the notation here is used because if you look at it for a negative value of n, the value is still defined with this notation. That being said, many text books are careless about it. | |||
| <math display="block"> (a + b)^{(n)} = \sum_{k=0}^{n}\binom{n}{k}a^{(n-k)}b^{(k)}.</math> | |||
| --> | |||
| The case {{math|1=''c'' = 0}} recovers the usual binomial theorem. | |||
| where <math>(\cdot)_k</math> is the ] here standing for a ]. Then, if ''x'' and ''y'' are real numbers with |''x''| > |''y''|,<ref name=convergence group=Notes>This is to guarantee convergence. Depending on ''r'', the series may also converge sometimes when |''x''| = |''y''|.</ref> and ''r'' is any ], one has | |||
| More generally, a sequence <math>\{p_n\}_{n=0}^\infty</math> of polynomials is said to be '''of binomial type''' if | |||
| :<math> | |||
| * <math> \deg p_n = n </math> for all <math>n</math>, | |||
| \begin{align} | |||
| * <math> p_0(0) = 1 </math>, and | |||
| (x+y)^r & =\sum_{k=0}^\infty {r \choose k} x^{r-k} y^k \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad(2) \\ | |||
| * <math> p_n(x+y) = \sum_{k=0}^n \binom{n}{k} p_k(x) p_{n-k}(y) </math> for all <math>x</math>, <math>y</math>, and <math>n</math>. | |||
| & = x^r + r x^{r-1} y + \frac{r(r-1)}{2!} x^{r-2} y^2 + \frac{r(r-1)(r-2)}{3!} x^{r-3} y^3 + \cdots. | |||
| An operator <math>Q</math> on the space of polynomials is said to be the ''basis operator'' of the sequence <math>\{p_n\}_{n=0}^\infty</math> if <math>Qp_0 = 0</math> and <math> Q p_n = n p_{n-1} </math> for all <math> n \geqslant 1 </math>. A sequence <math>\{p_n\}_{n=0}^\infty</math> is binomial if and only if its basis operator is a ].<ref>{{cite book |last=Aigner |first=Martin |author-link=Martin Aigner |title=Combinatorial Theory |url=https://archive.org/details/combinatorialthe0000aign |url-access=limited |date=1979 |publisher=Springer |isbn=0-387-90376-3 |page=105 }}</ref> Writing <math> E^a </math> for the shift by <math> a </math> operator, the Delta operators corresponding to the above "Pochhammer" families of polynomials are the backward difference <math> I - E^{-c} </math> for <math> c>0 </math>, the ordinary derivative for <math> c=0 </math>, and the forward difference <math> E^{-c} - I </math> for <math> c<0 </math>. | |||
| \end{align} | |||
| </math> | |||
| When ''r'' is a nonnegative integer, the binomial coefficients for ''k'' > ''r'' are zero, so (2) specializes to (1), and there are at most ''r'' + 1 nonzero terms. For other values of ''r'', the series (2) has infinitely many nonzero terms, at least if ''x'' and ''y'' are nonzero. | |||
| === Multinomial theorem === | |||
| This is important when one is working with infinite series and would like to represent them in terms of ]s. | |||
| {{Main|Multinomial theorem}} | |||
| The binomial theorem can be generalized to include powers of sums with more than two terms. The general version is | |||
| <math display="block">(x_1 + x_2 + \cdots + x_m)^n = \sum_{k_1+k_2+\cdots +k_m = n} \binom{n}{k_1, k_2, \ldots, k_m} x_1^{k_1} x_2^{k_2} \cdots x_m^{k_m}, </math> | |||
| Taking ''r'' = −''s'' leads to a useful formula: | |||
| where the summation is taken over all sequences of nonnegative integer indices {{math|''k''<sub>1</sub>}} through {{math|''k''<sub>''m''</sub>}} such that the sum of all {{math|''k''<sub>''i''</sub>}} is {{mvar|n}}. (For each term in the expansion, the exponents must add up to {{mvar|n}}). The coefficients <math> \tbinom{n}{k_1,\cdots,k_m} </math> are known as multinomial coefficients, and can be computed by the formula | |||
| :<math>\frac{1}{(1-x)^s} = \sum_{k=0}^\infty {s+k-1 \choose k} x^k \equiv \sum_{k=0}^\infty {s+k-1 \choose s-1} x^k.</math> | |||
| <math display="block"> \binom{n}{k_1, k_2, \ldots, k_m} = \frac{n!}{k_1! \cdot k_2! \cdots k_m!}.</math> | |||
| Combinatorially, the multinomial coefficient <math>\tbinom{n}{k_1,\cdots,k_m}</math> counts the number of different ways to ] an {{mvar|n}}-element set into ] ]s of sizes {{math|1=''k''<sub>1</sub>, ..., ''k''<sub>''m''</sub>}}. | |||
| Further specializing to ''s'' = 1 yields the ]. | |||
| === {{anchor|multi-binomial}} Multi-binomial theorem === | |||
| ====Generalisations==== | |||
| When working in more dimensions, it is often useful to deal with products of binomial expressions. By the binomial theorem this is equal to | |||
| Formula (2) can be generalised to the case where ''x'' and ''y'' are ]. For this version, one should assume |''x''| > |''y''|<ref name=convergence group=Notes/> and define the powers of ''x'' + ''y'' and ''x'' using a ] ] defined on an open disk of radius |''x''| centered at ''x''. | |||
| <math display="block"> (x_1+y_1)^{n_1}\dotsm(x_d+y_d)^{n_d} = \sum_{k_1=0}^{n_1}\dotsm\sum_{k_d=0}^{n_d} \binom{n_1}{k_1} x_1^{k_1}y_1^{n_1-k_1} \dotsc \binom{n_d}{k_d} x_d^{k_d}y_d^{n_d-k_d}. </math> | |||
| This may be written more concisely, by ], as | |||
| Formula (2) is valid also for elements ''x'' and ''y'' of a ] as long as ''xy'' = ''yx'', ''x'' is invertible, and ||''y/x''|| < 1. | |||
| <math display="block"> (x+y)^\alpha = \sum_{\nu \le \alpha} \binom{\alpha}{\nu} x^\nu y^{\alpha - \nu}.</math> | |||
| === |
=== General Leibniz rule === | ||
| {{Main|General Leibniz rule}} | |||
| {{main|Multinomial theorem}} | |||
| The binomial theorem can be generalised to include powers of sums with more than two terms. The general version is | |||
| The general Leibniz rule gives the {{mvar|n}}th derivative of a product of two functions in a form similar to that of the binomial theorem:<ref>{{cite book |last=Olver |first=Peter J. |author-link=Peter J. Olver |year=2000 |title=Applications of Lie Groups to Differential Equations |publisher=Springer |pages=318–319 |isbn=9780387950006 |url=https://books.google.com/books?id=sI2bAxgLMXYC&pg=PA318 }}</ref> | |||
| :<math>(x_1 + x_2 + \cdots + x_m)^n | |||
| <math display="block">(fg)^{(n)}(x) = \sum_{k=0}^n \binom{n}{k} f^{(n-k)}(x) g^{(k)}(x).</math> | |||
| = \sum_{k_1+k_2+\cdots +k_m = n} {n \choose k_1, k_2, \ldots, k_m} | |||
| x_1^{k_1} x_2^{k_2} \cdots x_m^{k_m}. </math> | |||
| Here, the superscript {{math|(''n'')}} indicates the {{mvar|n}}th derivative of a function, <math>f^{(n)}(x) = \tfrac{d^n}{dx^n}f(x)</math>. If one sets {{math|1=''f''(''x'') = ''e''{{sup|''ax''}}}} and {{math|1=''g''(''x'') = ''e''{{sup|''bx''}}}}, cancelling the common factor of {{math|''e''{{sup|(''a'' + ''b'')''x''}}}} from each term gives the ordinary binomial theorem.<ref>{{cite book |last1=Spivey |first1=Michael Z. |title=The Art of Proving Binomial Identities |date=2019 |publisher=CRC Press |isbn=978-1351215800 |page=71}}</ref> | |||
| where the summation is taken over all sequences of nonnegative integer indices ''k''<sub>1</sub> through ''k''<sub>''m''</sub> such that the sum of all ''k''<sub>''i''</sub> is ''n''. (For each term in the expansion, the exponents must add up to ''n''). The coefficients <math> \tbinom n{k_1,\cdots,k_m} </math> are known as multinomial coefficients, and can be computed by the formula | |||
| ==History== | |||
| :<math> {n \choose k_1, k_2, \ldots, k_m} | |||
| Special cases of the binomial theorem were known since at least the 4th century BC when ] ] mentioned the special case of the binomial theorem for exponent <math>n=2</math>.<ref name="Coolidge">{{cite journal|title=The Story of the Binomial Theorem|first=J. L.|last=Coolidge|journal=The American Mathematical Monthly| volume=56| issue=3|date=1949|pages=147–157|doi=10.2307/2305028|jstor = 2305028}}</ref> Greek mathematician ] cubed various binomials, including <math>x-1</math>.<ref name="Coolidge" /> Indian mathematician ]'s method for finding cube roots, from around 510 AD, suggests that he knew the binomial formula for exponent <math>n=3</math>.<ref name="Coolidge" /> | |||
| = \frac{n!}{k_1!\, k_2! \cdots k_m!}.</math> | |||
| Binomial coefficients, as combinatorial quantities expressing the number of ways of selecting {{mvar|k}} objects out of {{mvar|n}} without replacement (]), were of interest to ancient Indian mathematicians. The ] '']'' (c. 300 BC) describes the number of combinations of philosophical categories, senses, or other things, with correct results up through {{tmath|1= n = 4}} (probably obtained by listing all possibilities and counting them)<ref name=biggs>{{cite journal |last=Biggs |first=Norman L. |author-link=Norman L. Biggs |title=The roots of combinatorics |journal=Historia Mathematica |volume=6 |date=1979 |issue=2 |pages=109–136 |doi=10.1016/0315-0860(79)90074-0 |doi-access=free}}</ref> and a suggestion that higher combinations could likewise be found.<ref>{{cite journal |last=Datta |first=Bibhutibhushan |author-link=Bibhutibhushan Datta |url=https://archive.org/details/in.ernet.dli.2015.165748/page/n139/ |title=The Jaina School of Mathematics |journal=Bulletin of the Calcutta Mathematical Society |volume=27 |year=1929 |at=5. 115–145 (esp. 133–134) }} Reprinted as "The Mathematical Achievements of the Jainas" in {{cite book|editor-last=Chattopadhyaya |editor-first=Debiprasad |title=Studies in the History of Science in India |volume=2 |place=New Delhi |publisher=Editorial Enterprises |year=1982 |pages=684–716}}</ref> The '']'' by the Indian lyricist ] (3rd or 2nd century BC) somewhat crypically describes a method of arranging two types of syllables to form ]s of various lengths and counting them; as interpreted and elaborated by Piṅgala's 10th-century commentator ] his "method of pyramidal expansion" (''meru-prastāra'') for counting metres is equivalent to ].<ref>{{cite journal |last=Bag |first=Amulya Kumar |title=Binomial theorem in ancient India |journal=Indian Journal of History of Science |volume=1 |number=1 |year=1966 |pages=68–74 |url=http://repository.ias.ac.in/70374/1/10-pub.pdf }} {{pb}} {{cite journal |last=Shah |first=Jayant |year=2013 |journal=Gaṇita Bhāratī |volume=35 |number=1–4 |pages=43–96 |title=A History of Piṅgala's Combinatorics |id={{ResearchGatePub|353496244}} }} () {{pb}} Survey sources: {{pb}} {{cite book |last=Edwards |first=A. W. F. |author-link=A. W. F. Edwards |year=1987 |chapter=The combinatorial numbers in India |title=Pascal's Arithmetical Triangle |place=London |publisher=Charles Griffin |isbn=0-19-520546-4 |chapter-url=https://archive.org/details/pascalsarithmeti0000edwa/page/27 |pages=27–33 |chapter-url-access=limited }} {{pb}} {{cite book |last=Divakaran |first=P. P. |year=2018 |title=The Mathematics of India: Concepts, Methods, Connections |chapter=Combinatorics |at=§5.5 {{pgs|135–140}} |publisher=Springer; Hindustan Book Agency |doi=10.1007/978-981-13-1774-3_5 |isbn=978-981-13-1773-6 }} {{pb}} {{cite book |last=Roy |first=Ranjan |author-link=Ranjan Roy |year=2021 |title=Series and Products in the Development of Mathematics |edition=2 |volume=1 |publisher=Cambridge University Press |chapter=The Binomial Theorem |at=Ch. 4, {{pgs|77–104}} |isbn=978-1-108-70945-3 |doi=10.1017/9781108709453.005 }}</ref> ] (6th century AD) describes another method for computing combination counts by adding numbers in columns.<ref name=gupta>{{cite journal |last=Gupta |first=Radha Charan |author-link=Radha Charan Gupta |title=Varāhamihira's Calculation of {{tmath|{}^nC_r}} and the Discovery of Pascal's Triangle |journal=Gaṇita Bhāratī |volume=14 |number=1–4 |year=1992 |pages=45–49 }} Reprinted in {{cite book |editor-last=Ramasubramanian |editor-first=K. |year=2019 |title=Gaṇitānanda |publisher=Springer |doi=10.1007/978-981-13-1229-8_29 |pages=285–289 }}</ref> By the 9th century at latest Indian mathematicians learned to express this as a product of fractions {{tmath| \tfrac{n}1 \times \tfrac{n - 1}2 \times \cdots \times \tfrac{n - k + 1}{n-k} }}, and clear statements of this rule can be found in ]'s ''Pāṭīgaṇita'' (8th–9th century), ]'s '']'' (c. 850), and ]'s ''Līlāvatī'' (12th century).{{r|gupta}}{{r|biggs}}<ref>{{cite book |year=1959|title=The Patiganita of Sridharacarya |editor-last=Shukla |editor-first=Kripa Shankar |editor-link= Kripa Shankar Shukla |publisher=Lucknow University |chapter-url=https://archive.org/details/Patiganita/page/n294/mode/1up |chapter=Combinations of Savours |at=Vyavahāras 1.9, {{pgs|97}} (text), {{pgs|58–59}} (translation) }}</ref> | |||
| Combinatorially, the multinomial coefficient <math>\tbinom n{k_1,\cdots,k_m}</math> counts the number of different ways to ] an ''n''-element set into ] ]s of sizes ''k''<sub>1</sub>, ..., ''k''<sub>''m''</sub>. | |||
| The Persian mathematician ] (953–1029) wrote a now-lost book containing the binomial theorem and a table of binomial coefficients, often credited as their first appearance.<ref name=rashed>{{cite journal |last=Rashed |first=Roshdi |author-link=Roshdi Rashed |year=1972 |title=L'induction mathématique: al-Karajī, al-Samawʾal |journal=Archive for History of Exact Sciences |volume=9 |issue=1 |pages=1–21 |jstor=41133347 |doi=10.1007/BF00348537 |language=fr }} Translated into English by A. F. W. Armstrong in {{Cite book |last=Rashed |first=Roshdi |year=1994 |title=The Development of Arabic Mathematics: Between Arithmetic and Algebra |chapter=Mathematical Induction: al-Karajī and al-Samawʾal |chapter-url=https://archive.org/details/RoshdiRashedauth.TheDevelopmentOfArabicMathematicsBetweenArithmeticAndAlgebraSpringerNetherlands1994/page/n71/ |at=§1.4, {{pgs|62–81}} |doi=10.1007/978-94-017-3274-1_2 |publisher=Kluwer |isbn=0-7923-2565-6 |quote="The first formulation of the binomial and the table of binomial coefficients, to our knowledge, is to be found in a text by al-Karajī, cited by al-Samawʾal in ''al-Bāhir''." }}</ref><ref>{{Cite encyclopedia |title=Al-Karajī |encyclopedia=Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures |last=Sesiano |first=Jacques |editor-last=Selin |editor-first=Helaine |editor-link=Helaine Selin |year=1997 |publisher=Springer |doi=10.1007/978-94-017-1416-7_11 |isbn=978-94-017-1418-1 |pages=475–476 |quote=Another contained the first known explanation of the arithmetical (Pascal's) triangle; the passage in question survived through al-Samawʾal's ''Bāhir'' (twelfth century) which heavily drew from the ''Badīʿ''. }}</ref><ref> | |||
| === {{anchor|multi-binomial}} The multi-binomial theorem === | |||
| {{cite journal |last=Berggren |first=John Lennart |year=1985 |title=History of mathematics in the Islamic world: The present state of the art |journal=Review of Middle East Studies |volume=19 |number=1 |pages=9–33 |doi=10.1017/S0026318400014796 }} Republished in {{Cite book |title=From Alexandria, Through Baghdad |editor1-last=Sidoli |editor1-first=Nathan |editor2-last=Brummelen |editor2-first=Glen Van |editor2-link=Glen Van Brummelen |year=2014 |publisher=Springer |isbn=978-3-642-36735-9 |doi=10.1007/978-3-642-36736-6_4 |pages=51–71 |quote= since the table of binomial coefficients had been previously found in such late works as those of al-Kāshī (fifteenth century) and Naṣīr al-Dīn al-Ṭūsī (thirteenth century), some had suggested that the table was a Chinese import. However, the use of the binomial coefficients by Islamic mathematicians of the eleventh century, in a context which had deep roots in Islamic mathematics, suggests strongly that the table was a local discovery – most probably of al-Karajī.}}</ref> | |||
| It is often useful when working in more dimensions, to deal with products of binomial expressions. By the binomial theorem this is equal to | |||
| An explicit statement of the binomial theorem appears in ]'s ''al-Bāhir'' (12th century), there credited to al-Karajī.<ref>{{cite journal |last=Yadegari |first=Mohammad |year=1980 |title=The Binomial Theorem: A Widespread Concept in Medieval Islamic Mathematics |journal=Historia Mathematica |volume=7 |issue=4 |pages=401–406 |doi=10.1016/0315-0860(80)90004-X |doi-access=free }}</ref>{{r|rashed}} Al-Samawʾal algebraically expanded the square, cube, and fourth power of a binomial, each in terms of the previous power, and noted that similar proofs could be provided for higher powers, an early form of ]. He then provided al-Karajī's table of binomial coefficients (Pascal's triangle turned on its side) up to {{tmath|1= n = 12}} and a rule for generating them equivalent to the ] {{tmath|1=\textstyle \binom{n}{k} = \binom{n-1}{k-1} + \binom{n-1}{k} }}.{{r|rashed}}<ref name=Karaji>{{MacTutor|id=Al-Karaji|title=Abu Bekr ibn Muhammad ibn al-Husayn Al-Karaji}}</ref> The Persian poet and mathematician ] was probably familiar with the formula to higher orders, although many of his mathematical works are lost.<ref name="Coolidge" /> The binomial expansions of small degrees were known in the 13th century mathematical works of ]<ref>{{cite web | last = Landau | first = James A. | title = Historia Matematica Mailing List Archive: Re: Pascal's Triangle | work = Archives of Historia Matematica | format = mailing list email | access-date = 2007-04-13 | date = 1999-05-08 | url = http://archives.math.utk.edu/hypermail/historia/may99/0073.html | archive-date = 2021-02-24 | archive-url = https://web.archive.org/web/20210224081637/http://archives.math.utk.edu/hypermail/historia/may99/0073.html | url-status = dead }}</ref> and also ].<ref name="Coolidge" /> Yang Hui attributes the method to a much earlier 11th century text of ], although those writings are now also lost.<ref>{{cite book |title=A History of Chinese Mathematics |chapter=Jia Xian and Liu Yi |last=Martzloff |first=Jean-Claude |translator-last=Wilson |translator-first=Stephen S. |publisher=Springer |year=1997 |orig-year=French ed. 1987 |isbn=3-540-54749-5 |page=142 |chapter-url=https://archive.org/details/historyofchinese0000mart_g2q8/page/142/mode/2up?&q=%22depends+on+the+binomial+expansion%22 |chapter-url-access=limited }}</ref> | |||
| In Europe, descriptions of the construction of Pascal's triangle can be found as early as ]'s ''De arithmetica'' (13th century).<ref>{{cite journal |last=Hughes |first=Barnabas|year=1989 |title=The arithmetical triangle of Jordanus de Nemore |journal=Historia Mathematica |volume=16 |number=3 |pages=213–223 |doi=10.1016/0315-0860(89)90018-9 }}</ref> In 1544, ] introduced the term "binomial coefficient" and showed how to use them to express <math>(1+x)^n</math> in terms of <math>(1+x)^{n-1}</math>, via "Pascal's triangle".<ref name=Kline>{{cite book|title=History of mathematical thought|first=Morris| last=Kline| author-link=Morris Kline|page=273|publisher=Oxford University Press|year=1972}}</ref> Other 16th century mathematicians including ] and ] also knew of it.<ref name=Kline /> 17th-century mathematician ] studied the eponymous triangle comprehensively in his ''Traité du triangle arithmétique''.<ref>{{Cite book |last=Katz |first=Victor |author-link=Victor Katz |title=A History of Mathematics: An Introduction |edition=3rd |publisher=Addison-Wesley |year=2009 |orig-year=1993 |isbn=978-0-321-38700-4 |at=§ 14.3, {{pgs|487–497}} |chapter=Elementary Probability }}</ref> | |||
| :<math> (x_{1}+y_{1})^{n_{1}}\dotsm(x_{d}+y_{d})^{n_{d}} = \sum_{k_{1}=0}^{n_{1}}\dotsm\sum_{k_{d}=0}^{n_{d}} \binom{n_{1}}{k_{1}}\, x_{1}^{k_{1}}y_{1}^{n_{1}-k_{1}}\;\dotsc\;\binom{n_{d}}{k_{d}}\, x_{d}^{k_{d}}y_{d}^{n_{d}-k_{d}}. </math> | |||
| By the early 17th century, some specific cases of the generalized binomial theorem, such as for <math>n=\tfrac{1}{2}</math>, can be found in the work of ]' ''Arithmetica Logarithmica'' (1624).{{r|stillwell}} ] is generally credited with discovering the generalized binomial theorem, valid for any real exponent, in 1665, inspired by the work of ]'s ''Arithmetic Infinitorum'' and his method of interpolation.<ref name=Kline /><ref>{{cite book |title=Elements of the History of Mathematics |date=1994 |first=N. |last=Bourbaki |author-link=Nicolas Bourbaki |translator=J. Meldrum |translator-link=John D. P. Meldrum |publisher=Springer |isbn=3-540-19376-6 |url-access=registration |url=https://archive.org/details/elementsofhistor0000bour}}</ref><ref name="Coolidge" /><ref>{{Cite journal |last=Whiteside |first=D. T. |author-link=Tom Whiteside |date=1961 |title=Newton's Discovery of the General Binomial Theorem |url=https://www.cambridge.org/core/journals/mathematical-gazette/article/abs/newtons-discovery-of-the-general-binomial-theorem/19B5921B0248598CFB6441FCE085D113 |journal=The Mathematical Gazette |language=en |volume=45 |issue=353 |pages=175–180 |doi=10.2307/3612767 |jstor=3612767 }}</ref>{{r|stillwell}} A logarithmic version of the theorem for fractional exponents was discovered independently by ] who wrote down his formula in 1670.<ref name=stillwell>{{cite book |last=Stillwell |first=John |author-link=John Stillwell |title=Mathematics and its history |date=2010 |publisher=Springer |isbn=978-1-4419-6052-8 |page=186 |edition=3rd}}</ref> | |||
| This may be written more concisely, by ], as | |||
| == Applications == | |||
| :<math> (x+y)^\alpha = \sum_{\nu \le \alpha} \binom{\alpha}{\nu} \, x^\nu y^{\alpha - \nu}.</math> | |||
| === Multiple-angle identities === | |||
| ==Applications== | |||
| For the ] the binomial theorem can be combined with ] to yield ] for the ] and ]. According to De Moivre's formula, | |||
| <math display="block">\cos\left(nx\right)+i\sin\left(nx\right) = \left(\cos x+i\sin x\right)^n.</math> | |||
| Using the binomial theorem, the expression on the right can be expanded, and then the real and imaginary parts can be taken to yield formulas for {{math|cos(''nx'')}} and {{math|sin(''nx'')}}. For example, since | |||
| ===Multiple-angle identities=== | |||
| <math display="block">\left(\cos x + i\sin x\right)^2 = \cos^2 x + 2i \cos x \sin x - \sin^2 x | |||
| For the ] the binomial theorem can be combined with ] to yield ] for the ] and ]. According to De Moivre's formula, | |||
| = (\cos^2 x-\sin^2 x) + i(2\cos x\sin x),</math> | |||
| But De Moivre's formula identifies the left side with <math>(\cos x+i\sin x)^2 = \cos(2x)+i\sin(2x)</math>, so | |||
| Using the binomial theorem, the expression on the right can be expanded, and then the real and imaginary parts can be taken to yield formulas for cos(''nx'') and sin(''nx''). For example, since | |||
| <math display="block">\cos(2x) = \cos^2 x - \sin^2 x \quad\text{and}\quad\sin(2x) = 2 \cos x \sin x,</math> | |||
| De Moivre's formula tells us that | |||
| :<math>\cos(2x) = \cos^2 x - \sin^2 x \quad\text{and}\quad\sin(2x) = 2 \cos x \sin x,</math> | |||
| which are the usual double-angle identities. Similarly, since | which are the usual double-angle identities. Similarly, since | ||
| <math display="block">\left(\cos x + i\sin x\right)^3 = \cos^3 x + 3i \cos^2 x \sin x - 3 \cos x \sin^2 x - i \sin^3 x,</math> | |||
| De Moivre's formula yields | De Moivre's formula yields | ||
| <math display="block">\cos(3x) = \cos^3 x - 3 \cos x \sin^2 x \quad\text{and}\quad \sin(3x) = 3\cos^2 x \sin x - \sin^3 x.</math> | |||
| In general, | In general, | ||
| <math display="block">\cos(nx) = \sum_{k\text{ even}} (-1)^{k/2} {n \choose k}\cos^{n-k} x \sin^k x</math> | |||
| and | and | ||
| <math display="block">\sin(nx) = \sum_{k\text{ odd}} (-1)^{(k-1)/2} {n \choose k}\cos^{n-k} x \sin^k x.</math>There are also similar formulas using ]. | |||
| ===Series for e=== | === Series for ''e'' === | ||
| The ] is often defined by the formula | The ] is often defined by the formula | ||
| <math display="block">e = \lim_{n\to\infty} \left(1 + \frac{1}{n}\right)^n.</math> | |||
| Applying the binomial theorem to this expression yields the usual ] for {{mvar|e}}. In particular: | |||
| :<math>e = \lim_{n\to\infty} \left(1 + \frac{1}{n}\right)^n.</math> | |||
| <math display="block">\left(1 + \frac{1}{n}\right)^n = 1 + {n \choose 1}\frac{1}{n} + {n \choose 2}\frac{1}{n^2} + {n \choose 3}\frac{1}{n^3} + \cdots + {n \choose n}\frac{1}{n^n}.</math> | |||
| The {{mvar|k}}th term of this sum is | |||
| Applying the binomial theorem to this expression yields the usual ] for ''e''. In particular: | |||
| <math display="block">{n \choose k}\frac{1}{n^k} = \frac{1}{k!}\cdot\frac{n(n-1)(n-2)\cdots (n-k+1)}{n^k}</math> | |||
| As {{math|''n'' → ∞}}, the rational expression on the right approaches {{math|1}}, and therefore | |||
| :<math>\left(1 + \frac{1}{n}\right)^n = 1 + {n \choose 1}\frac{1}{n} + {n \choose 2}\frac{1}{n^2} + {n \choose 3}\frac{1}{n^3} + \cdots + {n \choose n}\frac{1}{n^n}.</math> | |||
| <math display="block">\lim_{n\to\infty} {n \choose k}\frac{1}{n^k} = \frac{1}{k!}.</math> | |||
| This indicates that {{mvar|e}} can be written as a series: | |||
| The ''k''th term of this sum is | |||
| <math display="block">e=\sum_{k=0}^\infty\frac{1}{k!}=\frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \cdots.</math> | |||
| Indeed, since each term of the binomial expansion is an ] of {{mvar|n}}, it follows from the ] for series that the sum of this infinite series is equal to {{mvar|e}}. | |||
| :<math>{n \choose k}\frac{1}{n^k} \;=\; \frac{1}{k!}\cdot\frac{n(n-1)(n-2)\cdots (n-k+1)}{n^k}</math> | |||
| === Probability === | |||
| As ''n'' → ∞, the rational expression on the right approaches one, and therefore | |||
| The binomial theorem is closely related to the probability mass function of the ]. The probability of a (countable) collection of independent Bernoulli trials <math>\{X_t\}_{t\in S}</math> with probability of success <math>p\in </math> all not happening is | |||
| :<math> P\biggl(\bigcap_{t\in S} X_t^C\biggr) = (1-p)^{|S|} = \sum_{n=0}^{|S|} {|S| \choose n} (-p)^n.</math> | |||
| An upper bound for this quantity is <math> e^{-p|S|}.</math><ref>{{Cite book |title=Elements of Information Theory |chapter=Data Compression |last1=Cover |first1=Thomas M. |author1-link=Thomas M. Cover |last2=Thomas |first2=Joy A. |author2-link=Joy A. Thomas |date=1991 |publisher=Wiley |isbn=9780471062592 |at=Ch. 5, {{pgs|78–124}} |doi=10.1002/0471200611.ch5}}<!-- a specific page number would be helpful. previously this citation noted p. 320 but that's not in this chapter. --> </ref> | |||
| == In abstract algebra == | |||
| :<math>\lim_{n\to\infty} {n \choose k}\frac{1}{n^k} = \frac{1}{k!}.</math> | |||
| The binomial theorem is valid more generally for two elements {{math|''x''}} and {{math|''y''}} in a ], or even a ], provided that {{math|1=''xy'' = ''yx''}}. For example, it holds for two {{math|''n'' × ''n''}} matrices, provided that those matrices commute; this is useful in computing powers of a matrix.<ref>{{cite book |last=Artin |first=Michael |author-link=Michael Artin |title=Algebra |edition=2nd |year=2011 |publisher=Pearson |at=equation (4.7.11)}}</ref> | |||
| This indicates that ''e'' can be written as a series: | |||
| The binomial theorem can be stated by saying that the ] {{math|1={{mset|1, ''x'', ''x''<sup>2</sup>, ''x''<sup>3</sup>, ...}}}} is of ]. | |||
| :<math>e = \frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \cdots.</math> | |||
| Indeed, since each term of the binomial expansion is an ] of ''n'', it follows from the ] for series that the sum of this infinite series is equal to ''e''. | |||
| ===Derivative of the power function=== | |||
| In finding the derivative of the power function ''f''(''x'') = ''x''<sup>''n''</sup> for integer ''n'' using the definition of derivative, one must expand the binomial (''x'' + ''h'')<sup>''n''</sup>. | |||
| ===Nth derivative of a product=== | |||
| To indicate the formula for the derivative of order ''n'' of the product of two functions, the formula of the binomial theorem is used symbolically.<ref>{{cite book |last=Seely |first=Robert T. |title=Calculus of One and Several Variables |location=Glenview |publisher=Scott, Foresman |year=1973 |isbn=0-673-07779-9 }}</ref> | |||
| ==The binomial theorem in abstract algebra== | |||
| Formula (1) is valid more generally for any elements ''x'' and ''y'' of a ] satisfying ''xy'' = ''yx''. The ] is true even more generally: ] suffices in place of ]. | |||
| The binomial theorem can be stated by saying that the ] { 1, ''x'', ''x''<sup>2</sup>, ''x''<sup>3</sup>, ... } is of ]. | |||
| ==In popular culture== | |||
| *The binomial theorem is mentioned in the ] in the comic opera ]. | |||
| *] is described by Sherlock Holmes as having written ]. | |||
| == See also == | == See also == | ||
| {{portal|Mathematics}} | {{portal|Mathematics}} | ||
| {{colbegin}} | |||
| * ] | * ] | ||
| * ] | * ] | ||
| * ] | * ] | ||
| * ] | * ] | ||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | * ] | ||
| * ] | |||
| {{colend}} | |||
| * ] | |||
| * ] | |||
| ==Notes== | == Notes == | ||
| {{reflist|group= |
{{reflist|group=Note}} | ||
| ==References== | == References == | ||
| {{reflist}} | {{reflist|30em}} | ||
| ==Further reading== | == Further reading == | ||
| * {{cite book |last1=Graham |first1=Ronald |author1-link=Ronald Graham |last2=Knuth |first2=Donald |author2-link=Donald Knuth |first3=Oren |last3=Patashnik |author3-link=Oren Patashnik |title=] |publisher=Addison Wesley |year=1994 |edition=2nd |at=Ch. 5, {{pgs|153–256}} |chapter=Binomial Coefficients |isbn=978-0-201-55802-9 }} | |||
| {{refbegin}} | |||
| *{{cite journal|last=Bag|first=Amulya Kumar|year=1966|title=Binomial theorem in ancient India|journal=Indian J. History Sci|volume=1|issue=1|pages=68–74}} | |||
| *{{cite book|last1=Graham|first1=Ronald|first2=Donald |last2=Knuth|first3= Oren|last3= Patashnik|title=Concrete Mathematics|publisher=Addison Wesley|year=1994|edition=2nd|pages=153–256|chapter=(5) Binomial Coefficients|isbn=0-201-55802-5|oclc=17649857}} | |||
| {{refend}} | |||
| == External links == | == External links == | ||
| {{ |
{{Wikibooks|Combinatorics|Binomial Theorem|The Binomial Theorem}} | ||
| *{{SpringerEOM|id=Newton_binomial|first=E.D.|last= Solomentsev|title=Newton binomial}} | * {{SpringerEOM|id=Newton_binomial|first=E.D.|last= Solomentsev|title=Newton binomial}} | ||
| * by ], and by Bruce Colletti and Jeff Bryant, ], 2007. | * by ], and by Bruce Colletti and Jeff Bryant, ], 2007. | ||
| *{{PlanetMath attribution | |||
| |urlname=InductiveProofOfBinomialTheorem |title=inductive proof of binomial theorem | |||
| }} | |||
| {{Calculus topics}} | |||
| {{Authority control}} | |||
| {{PlanetMath attribution|id=338|title=inductive proof of binomial theorem}} | |||
| {{Authority control}} | |||
| {{DEFAULTSORT:Binomial Theorem}} | |||
| ] | ] | ||
| ] | ] | ||
| ] | ] | ||
Latest revision as of 01:13, 31 December 2024
Algebraic expansion of powers of a binomialThe binomial coefficient appears as the kth entry in the nth row of Pascal's triangle (where the top is the 0th row ). Each entry is the sum of the two above it.
In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, the power expands into a polynomial with terms of the form , where the exponents and are nonnegative integers satisfying and the coefficient of each term is a specific positive integer depending on and . For example, for ,
The coefficient in each term is known as the binomial coefficient or (the two have the same value). These coefficients for varying and can be arranged to form Pascal's triangle. These numbers also occur in combinatorics, where gives the number of different combinations (i.e. subsets) of elements that can be chosen from an -element set. Therefore is usually pronounced as " choose ".
Statement
According to the theorem, the expansion of any nonnegative integer power n of the binomial x + y is a sum of the form where each is a positive integer known as a binomial coefficient, defined as
This formula is also referred to as the binomial formula or the binomial identity. Using summation notation, it can be written more concisely as
The final expression follows from the previous one by the symmetry of x and y in the first expression, and by comparison it follows that the sequence of binomial coefficients in the formula is symmetrical,
A simple variant of the binomial formula is obtained by substituting 1 for y, so that it involves only a single variable. In this form, the formula reads
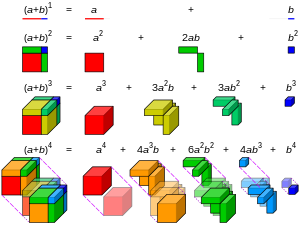
Examples
The first few cases of the binomial theorem are: In general, for the expansion of (x + y) on the right side in the nth row (numbered so that the top row is the 0th row):
- the exponents of x in the terms are n, n − 1, ..., 2, 1, 0 (the last term implicitly contains x = 1);
- the exponents of y in the terms are 0, 1, 2, ..., n − 1, n (the first term implicitly contains y = 1);
- the coefficients form the nth row of Pascal's triangle;
- before combining like terms, there are 2 terms xy in the expansion (not shown);
- after combining like terms, there are n + 1 terms, and their coefficients sum to 2.
An example illustrating the last two points: with .
A simple example with a specific positive value of y:
A simple example with a specific negative value of y:
Geometric explanation
For positive values of a and b, the binomial theorem with n = 2 is the geometrically evident fact that a square of side a + b can be cut into a square of side a, a square of side b, and two rectangles with sides a and b. With n = 3, the theorem states that a cube of side a + b can be cut into a cube of side a, a cube of side b, three a × a × b rectangular boxes, and three a × b × b rectangular boxes.
In calculus, this picture also gives a geometric proof of the derivative if one sets and interpreting b as an infinitesimal change in a, then this picture shows the infinitesimal change in the volume of an n-dimensional hypercube, where the coefficient of the linear term (in ) is the area of the n faces, each of dimension n − 1: Substituting this into the definition of the derivative via a difference quotient and taking limits means that the higher order terms, and higher, become negligible, and yields the formula interpreted as
- "the infinitesimal rate of change in volume of an n-cube as side length varies is the area of n of its (n − 1)-dimensional faces".
If one integrates this picture, which corresponds to applying the fundamental theorem of calculus, one obtains Cavalieri's quadrature formula, the integral – see proof of Cavalieri's quadrature formula for details.
Binomial coefficients
Main article: Binomial coefficientThe coefficients that appear in the binomial expansion are called binomial coefficients. These are usually written and pronounced "n choose k".
Formulas
The coefficient of xy is given by the formula which is defined in terms of the factorial function n!. Equivalently, this formula can be written with k factors in both the numerator and denominator of the fraction. Although this formula involves a fraction, the binomial coefficient is actually an integer.
Combinatorial interpretation
The binomial coefficient can be interpreted as the number of ways to choose k elements from an n-element set (a combination). This is related to binomials for the following reason: if we write (x + y) as a product then, according to the distributive law, there will be one term in the expansion for each choice of either x or y from each of the binomials of the product. For example, there will only be one term x, corresponding to choosing x from each binomial. However, there will be several terms of the form xy, one for each way of choosing exactly two binomials to contribute a y. Therefore, after combining like terms, the coefficient of xy will be equal to the number of ways to choose exactly 2 elements from an n-element set.
Proofs
Combinatorial proof
Expanding (x + y) yields the sum of the 2 products of the form e1e2 ... en where each ei is x or y. Rearranging factors shows that each product equals xy for some k between 0 and n. For a given k, the following are proved equal in succession:
- the number of terms equal to xy in the expansion
- the number of n-character x,y strings having y in exactly k positions
- the number of k-element subsets of {1, 2, ..., n}
- either by definition, or by a short combinatorial argument if one is defining as
This proves the binomial theorem.
Example
The coefficient of xy in equals because there are three x,y strings of length 3 with exactly two y's, namely, corresponding to the three 2-element subsets of {1, 2, 3}, namely, where each subset specifies the positions of the y in a corresponding string.
Inductive proof
Induction yields another proof of the binomial theorem. When n = 0, both sides equal 1, since x = 1 and Now suppose that the equality holds for a given n; we will prove it for n + 1. For j, k ≥ 0, let j,k denote the coefficient of xy in the polynomial f(x, y). By the inductive hypothesis, (x + y) is a polynomial in x and y such that j,k is if j + k = n, and 0 otherwise. The identity shows that (x + y) is also a polynomial in x and y, and since if j + k = n + 1, then (j − 1) + k = n and j + (k − 1) = n. Now, the right hand side is by Pascal's identity. On the other hand, if j + k ≠ n + 1, then (j – 1) + k ≠ n and j + (k – 1) ≠ n, so we get 0 + 0 = 0. Thus which is the inductive hypothesis with n + 1 substituted for n and so completes the inductive step.
Generalizations
Newton's generalized binomial theorem
Main article: Binomial seriesAround 1665, Isaac Newton generalized the binomial theorem to allow real exponents other than nonnegative integers. (The same generalization also applies to complex exponents.) In this generalization, the finite sum is replaced by an infinite series. In order to do this, one needs to give meaning to binomial coefficients with an arbitrary upper index, which cannot be done using the usual formula with factorials. However, for an arbitrary number r, one can define where is the Pochhammer symbol, here standing for a falling factorial. This agrees with the usual definitions when r is a nonnegative integer. Then, if x and y are real numbers with |x| > |y|, and r is any complex number, one has
When r is a nonnegative integer, the binomial coefficients for k > r are zero, so this equation reduces to the usual binomial theorem, and there are at most r + 1 nonzero terms. For other values of r, the series typically has infinitely many nonzero terms.
For example, r = 1/2 gives the following series for the square root:
Taking r = −1, the generalized binomial series gives the geometric series formula, valid for |x| < 1:
More generally, with r = −s, we have for |x| < 1:
So, for instance, when s = 1/2,
Replacing x with -x yields:
So, for instance, when s = 1/2, we have for |x| < 1:
Further generalizations
The generalized binomial theorem can be extended to the case where x and y are complex numbers. For this version, one should again assume |x| > |y| and define the powers of x + y and x using a holomorphic branch of log defined on an open disk of radius |x| centered at x. The generalized binomial theorem is valid also for elements x and y of a Banach algebra as long as xy = yx, and x is invertible, and ‖y/x‖ < 1.
A version of the binomial theorem is valid for the following Pochhammer symbol-like family of polynomials: for a given real constant c, define and for Then The case c = 0 recovers the usual binomial theorem.
More generally, a sequence of polynomials is said to be of binomial type if
- for all ,
- , and
- for all , , and .
An operator on the space of polynomials is said to be the basis operator of the sequence if and for all . A sequence is binomial if and only if its basis operator is a Delta operator. Writing for the shift by operator, the Delta operators corresponding to the above "Pochhammer" families of polynomials are the backward difference for , the ordinary derivative for , and the forward difference for .
Multinomial theorem
Main article: Multinomial theoremThe binomial theorem can be generalized to include powers of sums with more than two terms. The general version is
where the summation is taken over all sequences of nonnegative integer indices k1 through km such that the sum of all ki is n. (For each term in the expansion, the exponents must add up to n). The coefficients are known as multinomial coefficients, and can be computed by the formula
Combinatorially, the multinomial coefficient counts the number of different ways to partition an n-element set into disjoint subsets of sizes k1, ..., km.
Multi-binomial theorem
When working in more dimensions, it is often useful to deal with products of binomial expressions. By the binomial theorem this is equal to
This may be written more concisely, by multi-index notation, as
General Leibniz rule
Main article: General Leibniz ruleThe general Leibniz rule gives the nth derivative of a product of two functions in a form similar to that of the binomial theorem:
Here, the superscript (n) indicates the nth derivative of a function, . If one sets f(x) = e and g(x) = e, cancelling the common factor of e from each term gives the ordinary binomial theorem.
History
Special cases of the binomial theorem were known since at least the 4th century BC when Greek mathematician Euclid mentioned the special case of the binomial theorem for exponent . Greek mathematician Diophantus cubed various binomials, including . Indian mathematician Aryabhata's method for finding cube roots, from around 510 AD, suggests that he knew the binomial formula for exponent .
Binomial coefficients, as combinatorial quantities expressing the number of ways of selecting k objects out of n without replacement (combinations), were of interest to ancient Indian mathematicians. The Jain Bhagavati Sutra (c. 300 BC) describes the number of combinations of philosophical categories, senses, or other things, with correct results up through (probably obtained by listing all possibilities and counting them) and a suggestion that higher combinations could likewise be found. The Chandaḥśāstra by the Indian lyricist Piṅgala (3rd or 2nd century BC) somewhat crypically describes a method of arranging two types of syllables to form metres of various lengths and counting them; as interpreted and elaborated by Piṅgala's 10th-century commentator Halāyudha his "method of pyramidal expansion" (meru-prastāra) for counting metres is equivalent to Pascal's triangle. Varāhamihira (6th century AD) describes another method for computing combination counts by adding numbers in columns. By the 9th century at latest Indian mathematicians learned to express this as a product of fractions , and clear statements of this rule can be found in Śrīdhara's Pāṭīgaṇita (8th–9th century), Mahāvīra's Gaṇita-sāra-saṅgraha (c. 850), and Bhāskara II's Līlāvatī (12th century).
The Persian mathematician al-Karajī (953–1029) wrote a now-lost book containing the binomial theorem and a table of binomial coefficients, often credited as their first appearance. An explicit statement of the binomial theorem appears in al-Samawʾal's al-Bāhir (12th century), there credited to al-Karajī. Al-Samawʾal algebraically expanded the square, cube, and fourth power of a binomial, each in terms of the previous power, and noted that similar proofs could be provided for higher powers, an early form of mathematical induction. He then provided al-Karajī's table of binomial coefficients (Pascal's triangle turned on its side) up to and a rule for generating them equivalent to the recurrence relation . The Persian poet and mathematician Omar Khayyam was probably familiar with the formula to higher orders, although many of his mathematical works are lost. The binomial expansions of small degrees were known in the 13th century mathematical works of Yang Hui and also Chu Shih-Chieh. Yang Hui attributes the method to a much earlier 11th century text of Jia Xian, although those writings are now also lost.
In Europe, descriptions of the construction of Pascal's triangle can be found as early as Jordanus de Nemore's De arithmetica (13th century). In 1544, Michael Stifel introduced the term "binomial coefficient" and showed how to use them to express in terms of , via "Pascal's triangle". Other 16th century mathematicians including Niccolò Fontana Tartaglia and Simon Stevin also knew of it. 17th-century mathematician Blaise Pascal studied the eponymous triangle comprehensively in his Traité du triangle arithmétique.
By the early 17th century, some specific cases of the generalized binomial theorem, such as for , can be found in the work of Henry Briggs' Arithmetica Logarithmica (1624). Isaac Newton is generally credited with discovering the generalized binomial theorem, valid for any real exponent, in 1665, inspired by the work of John Wallis's Arithmetic Infinitorum and his method of interpolation. A logarithmic version of the theorem for fractional exponents was discovered independently by James Gregory who wrote down his formula in 1670.
Applications
Multiple-angle identities
For the complex numbers the binomial theorem can be combined with de Moivre's formula to yield multiple-angle formulas for the sine and cosine. According to De Moivre's formula,
Using the binomial theorem, the expression on the right can be expanded, and then the real and imaginary parts can be taken to yield formulas for cos(nx) and sin(nx). For example, since But De Moivre's formula identifies the left side with , so which are the usual double-angle identities. Similarly, since De Moivre's formula yields In general, and There are also similar formulas using Chebyshev polynomials.
Series for e
The number e is often defined by the formula
Applying the binomial theorem to this expression yields the usual infinite series for e. In particular:
The kth term of this sum is
As n → ∞, the rational expression on the right approaches 1, and therefore
This indicates that e can be written as a series:
Indeed, since each term of the binomial expansion is an increasing function of n, it follows from the monotone convergence theorem for series that the sum of this infinite series is equal to e.
Probability
The binomial theorem is closely related to the probability mass function of the negative binomial distribution. The probability of a (countable) collection of independent Bernoulli trials with probability of success all not happening is
An upper bound for this quantity is
In abstract algebra
The binomial theorem is valid more generally for two elements x and y in a ring, or even a semiring, provided that xy = yx. For example, it holds for two n × n matrices, provided that those matrices commute; this is useful in computing powers of a matrix.
The binomial theorem can be stated by saying that the polynomial sequence {1, x, x, x, ...} is of binomial type.
See also
- Binomial approximation
- Binomial distribution
- Binomial inverse theorem
- Binomial coefficient
- Stirling's approximation
- Tannery's theorem
- Polynomials calculating sums of powers of arithmetic progressions
- q-binomial theorem
Notes
- ^ This is to guarantee convergence. Depending on r, the series may also converge sometimes when |x| = |y|.
References
- ^ Barth, Nils R. (2004). "Computing Cavalieri's Quadrature Formula by a Symmetry of the n-Cube". The American Mathematical Monthly. 111 (9): 811–813. doi:10.2307/4145193. JSTOR 4145193.
- Binomial theorem – inductive proofs Archived February 24, 2015, at the Wayback Machine
- Weisstein, Eric W. "Negative Binomial Series". Wolfram MathWorld.
- Sokolowsky, Dan; Rennie, Basil C. (1979). "Problem 352". Crux Mathematicorum. 5 (2): 55–56.
- Aigner, Martin (1979). Combinatorial Theory. Springer. p. 105. ISBN 0-387-90376-3.
- Olver, Peter J. (2000). Applications of Lie Groups to Differential Equations. Springer. pp. 318–319. ISBN 9780387950006.
- Spivey, Michael Z. (2019). The Art of Proving Binomial Identities. CRC Press. p. 71. ISBN 978-1351215800.
- ^ Coolidge, J. L. (1949). "The Story of the Binomial Theorem". The American Mathematical Monthly. 56 (3): 147–157. doi:10.2307/2305028. JSTOR 2305028.
- ^ Biggs, Norman L. (1979). "The roots of combinatorics". Historia Mathematica. 6 (2): 109–136. doi:10.1016/0315-0860(79)90074-0.
- Datta, Bibhutibhushan (1929). "The Jaina School of Mathematics". Bulletin of the Calcutta Mathematical Society. 27. 5. 115–145 (esp. 133–134). Reprinted as "The Mathematical Achievements of the Jainas" in Chattopadhyaya, Debiprasad, ed. (1982). Studies in the History of Science in India. Vol. 2. New Delhi: Editorial Enterprises. pp. 684–716.
- Bag, Amulya Kumar (1966). "Binomial theorem in ancient India" (PDF). Indian Journal of History of Science. 1 (1): 68–74. Shah, Jayant (2013). "A History of Piṅgala's Combinatorics". Gaṇita Bhāratī. 35 (1–4): 43–96. ResearchGate:353496244. (Preprint) Survey sources: Edwards, A. W. F. (1987). "The combinatorial numbers in India". Pascal's Arithmetical Triangle. London: Charles Griffin. pp. 27–33. ISBN 0-19-520546-4. Divakaran, P. P. (2018). "Combinatorics". The Mathematics of India: Concepts, Methods, Connections. Springer; Hindustan Book Agency. §5.5 pp. 135–140. doi:10.1007/978-981-13-1774-3_5. ISBN 978-981-13-1773-6. Roy, Ranjan (2021). "The Binomial Theorem". Series and Products in the Development of Mathematics. Vol. 1 (2 ed.). Cambridge University Press. Ch. 4, pp. 77–104. doi:10.1017/9781108709453.005. ISBN 978-1-108-70945-3.
- ^ Gupta, Radha Charan (1992). "Varāhamihira's Calculation of and the Discovery of Pascal's Triangle". Gaṇita Bhāratī. 14 (1–4): 45–49. Reprinted in Ramasubramanian, K., ed. (2019). Gaṇitānanda. Springer. pp. 285–289. doi:10.1007/978-981-13-1229-8_29.
- Shukla, Kripa Shankar, ed. (1959). "Combinations of Savours". The Patiganita of Sridharacarya. Lucknow University. Vyavahāras 1.9, p. 97 (text), pp. 58–59 (translation).
- ^ Rashed, Roshdi (1972). "L'induction mathématique: al-Karajī, al-Samawʾal". Archive for History of Exact Sciences (in French). 9 (1): 1–21. doi:10.1007/BF00348537. JSTOR 41133347. Translated into English by A. F. W. Armstrong in Rashed, Roshdi (1994). "Mathematical Induction: al-Karajī and al-Samawʾal". The Development of Arabic Mathematics: Between Arithmetic and Algebra. Kluwer. §1.4, pp. 62–81. doi:10.1007/978-94-017-3274-1_2. ISBN 0-7923-2565-6.
The first formulation of the binomial and the table of binomial coefficients, to our knowledge, is to be found in a text by al-Karajī, cited by al-Samawʾal in al-Bāhir.
- Sesiano, Jacques (1997). "Al-Karajī". In Selin, Helaine (ed.). Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures. Springer. pp. 475–476. doi:10.1007/978-94-017-1416-7_11. ISBN 978-94-017-1418-1.
Another contained the first known explanation of the arithmetical (Pascal's) triangle; the passage in question survived through al-Samawʾal's Bāhir (twelfth century) which heavily drew from the Badīʿ.
-
Berggren, John Lennart (1985). "History of mathematics in the Islamic world: The present state of the art". Review of Middle East Studies. 19 (1): 9–33. doi:10.1017/S0026318400014796. Republished in Sidoli, Nathan; Brummelen, Glen Van, eds. (2014). From Alexandria, Through Baghdad. Springer. pp. 51–71. doi:10.1007/978-3-642-36736-6_4. ISBN 978-3-642-36735-9.
since the table of binomial coefficients had been previously found in such late works as those of al-Kāshī (fifteenth century) and Naṣīr al-Dīn al-Ṭūsī (thirteenth century), some had suggested that the table was a Chinese import. However, the use of the binomial coefficients by Islamic mathematicians of the eleventh century, in a context which had deep roots in Islamic mathematics, suggests strongly that the table was a local discovery – most probably of al-Karajī.
- Yadegari, Mohammad (1980). "The Binomial Theorem: A Widespread Concept in Medieval Islamic Mathematics". Historia Mathematica. 7 (4): 401–406. doi:10.1016/0315-0860(80)90004-X.
- O'Connor, John J.; Robertson, Edmund F. "Abu Bekr ibn Muhammad ibn al-Husayn Al-Karaji". MacTutor History of Mathematics Archive. University of St Andrews.
- Landau, James A. (1999-05-08). "Historia Matematica Mailing List Archive: Re: [HM] Pascal's Triangle". Archives of Historia Matematica. Archived from the original (mailing list email) on 2021-02-24. Retrieved 2007-04-13.
- Martzloff, Jean-Claude (1997) . "Jia Xian and Liu Yi". A History of Chinese Mathematics. Translated by Wilson, Stephen S. Springer. p. 142. ISBN 3-540-54749-5.
- Hughes, Barnabas (1989). "The arithmetical triangle of Jordanus de Nemore". Historia Mathematica. 16 (3): 213–223. doi:10.1016/0315-0860(89)90018-9.
- ^ Kline, Morris (1972). History of mathematical thought. Oxford University Press. p. 273.
- Katz, Victor (2009) . "Elementary Probability". A History of Mathematics: An Introduction (3rd ed.). Addison-Wesley. § 14.3, pp. 487–497. ISBN 978-0-321-38700-4.
- ^ Stillwell, John (2010). Mathematics and its history (3rd ed.). Springer. p. 186. ISBN 978-1-4419-6052-8.
- Bourbaki, N. (1994). Elements of the History of Mathematics. Translated by J. Meldrum. Springer. ISBN 3-540-19376-6.
- Whiteside, D. T. (1961). "Newton's Discovery of the General Binomial Theorem". The Mathematical Gazette. 45 (353): 175–180. doi:10.2307/3612767. JSTOR 3612767.
- Cover, Thomas M.; Thomas, Joy A. (1991). "Data Compression". Elements of Information Theory. Wiley. Ch. 5, pp. 78–124. doi:10.1002/0471200611.ch5. ISBN 9780471062592.
- Artin, Michael (2011). Algebra (2nd ed.). Pearson. equation (4.7.11).
Further reading
- Graham, Ronald; Knuth, Donald; Patashnik, Oren (1994). "Binomial Coefficients". Concrete Mathematics (2nd ed.). Addison Wesley. Ch. 5, pp. 153–256. ISBN 978-0-201-55802-9.
External links
- Solomentsev, E.D. (2001) . "Newton binomial". Encyclopedia of Mathematics. EMS Press.
- Binomial Theorem by Stephen Wolfram, and "Binomial Theorem (Step-by-Step)" by Bruce Colletti and Jeff Bryant, Wolfram Demonstrations Project, 2007.
- This article incorporates material from inductive proof of binomial theorem on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
| Calculus | |||||
|---|---|---|---|---|---|
| Precalculus | |||||
| Limits | |||||
| Differential calculus |
| ||||
| Integral calculus | |||||
| Vector calculus |
| ||||
| Multivariable calculus | |||||
| Sequences and series |
| ||||
| Special functions and numbers | |||||
| History of calculus | |||||
| Lists |
| ||||
| Miscellaneous topics |
| ||||
 The
The  appears as the kth entry in the nth row of
appears as the kth entry in the nth row of  ). Each entry is the sum of the two above it.
). Each entry is the sum of the two above it.
 expands into a
expands into a  , where the exponents
, where the exponents  and
and  are
are  and the
and the  of each term is a specific
of each term is a specific  and
and  ,
,

 (the two have the same value). These coefficients for varying
(the two have the same value). These coefficients for varying  where each
where each 



 In general, for the expansion of (x + y) on the right side in the nth row (numbered so that the top row is the 0th row):
In general, for the expansion of (x + y) on the right side in the nth row (numbered so that the top row is the 0th row):
 with
with  .
.


 if one sets
if one sets  and
and  interpreting b as an
interpreting b as an  where the coefficient of the linear term (in
where the coefficient of the linear term (in  ) is
) is  the area of the n faces, each of dimension n − 1:
the area of the n faces, each of dimension n − 1:
 Substituting this into the
Substituting this into the  and higher, become negligible, and yields the formula
and higher, become negligible, and yields the formula  interpreted as
interpreted as
 – see
– see  and pronounced "n choose k".
and pronounced "n choose k".
 which is defined in terms of the
which is defined in terms of the  with k factors in both the numerator and denominator of the
with k factors in both the numerator and denominator of the  then, according to the
then, according to the 
 equals
equals  because there are three x,y strings of length 3 with exactly two y's, namely,
because there are three x,y strings of length 3 with exactly two y's, namely,
 corresponding to the three 2-element subsets of {1, 2, 3}, namely,
corresponding to the three 2-element subsets of {1, 2, 3}, namely,
 where each subset specifies the positions of the y in a corresponding string.
where each subset specifies the positions of the y in a corresponding string.
 Now suppose that the equality holds for a given n; we will prove it for n + 1. For j, k ≥ 0, let j,k denote the coefficient of xy in the polynomial f(x, y). By the inductive hypothesis, (x + y) is a polynomial in x and y such that j,k is
Now suppose that the equality holds for a given n; we will prove it for n + 1. For j, k ≥ 0, let j,k denote the coefficient of xy in the polynomial f(x, y). By the inductive hypothesis, (x + y) is a polynomial in x and y such that j,k is  shows that (x + y) is also a polynomial in x and y, and
shows that (x + y) is also a polynomial in x and y, and
 since if j + k = n + 1, then (j − 1) + k = n and j + (k − 1) = n. Now, the right hand side is
since if j + k = n + 1, then (j − 1) + k = n and j + (k − 1) = n. Now, the right hand side is
 by
by  which is the inductive hypothesis with n + 1 substituted for n and so completes the inductive step.
which is the inductive hypothesis with n + 1 substituted for n and so completes the inductive step.
 where
where  is the
is the 






 and
and
 for
for  Then
Then
 The case c = 0 recovers the usual binomial theorem.
The case c = 0 recovers the usual binomial theorem.
 of polynomials is said to be of binomial type if
of polynomials is said to be of binomial type if
 for all
for all  , and
, and for all
for all  ,
,  , and
, and  on the space of polynomials is said to be the basis operator of the sequence
on the space of polynomials is said to be the basis operator of the sequence  and
and  for all
for all  . A sequence
. A sequence  for the shift by
for the shift by  for
for  , the ordinary derivative for
, the ordinary derivative for  , and the forward difference
, and the forward difference  for
for  .
.

 are known as multinomial coefficients, and can be computed by the formula
are known as multinomial coefficients, and can be computed by the formula




 . If one sets f(x) = e and g(x) = e, cancelling the common factor of e from each term gives the ordinary binomial theorem.
. If one sets f(x) = e and g(x) = e, cancelling the common factor of e from each term gives the ordinary binomial theorem.
 . Greek mathematician
. Greek mathematician  . Indian mathematician
. Indian mathematician  .
.
 , and clear statements of this rule can be found in
, and clear statements of this rule can be found in  and a rule for generating them equivalent to the
and a rule for generating them equivalent to the  . The Persian poet and mathematician
. The Persian poet and mathematician  in terms of
in terms of  , via "Pascal's triangle". Other 16th century mathematicians including
, via "Pascal's triangle". Other 16th century mathematicians including  , can be found in the work of
, can be found in the work of 
 But De Moivre's formula identifies the left side with
But De Moivre's formula identifies the left side with  , so
, so
 which are the usual double-angle identities. Similarly, since
which are the usual double-angle identities. Similarly, since
 De Moivre's formula yields
De Moivre's formula yields
 In general,
In general,
 and
and
 There are also similar formulas using
There are also similar formulas using 




 with probability of success
with probability of success  all not happening is
all not happening is


 and the Discovery of Pascal's Triangle". Gaṇita Bhāratī. 14 (1–4): 45–49. Reprinted in Ramasubramanian, K., ed. (2019). Gaṇitānanda. Springer. pp. 285–289.
and the Discovery of Pascal's Triangle". Gaṇita Bhāratī. 14 (1–4): 45–49. Reprinted in Ramasubramanian, K., ed. (2019). Gaṇitānanda. Springer. pp. 285–289.