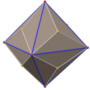
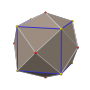
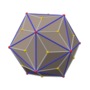
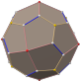
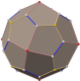
| Disdyakis dodecahedron | |
|---|---|
 (rotating and 3D model) | |
| Type | Catalan solid |
| Conway notation | mC |
| Coxeter diagram | |
| Face polygon |  scalene triangle |
| Faces | 48 |
| Edges | 72 |
| Vertices | 26 = 6 + 8 + 12 |
| Face configuration | V4.6.8 |
| Symmetry group | Oh, B3, , *432 |
| Dihedral angle | 155° 4' 56" |
| Dual polyhedron |  truncated cuboctahedron |
| Properties | convex, face-transitive |
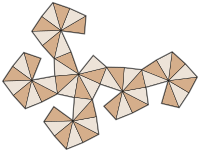 net | |
In geometry, a disdyakis dodecahedron, (also hexoctahedron, hexakis octahedron, octakis cube, octakis hexahedron, kisrhombic dodecahedron) or d48, is a Catalan solid with 48 faces and the dual to the Archimedean truncated cuboctahedron. As such it is face-transitive but with irregular face polygons. It resembles an augmented rhombic dodecahedron. Replacing each face of the rhombic dodecahedron with a flat pyramid creates a polyhedron that looks almost like the disdyakis dodecahedron, and is topologically equivalent to it.
More formally, the disdyakis dodecahedron is the Kleetope of the rhombic dodecahedron, and the barycentric subdivision of the cube or of the regular octahedron. The net of the rhombic dodecahedral pyramid also shares the same topology.
Symmetry
It has Oh octahedral symmetry. Its collective edges represent the reflection planes of the symmetry. It can also be seen in the corner and mid-edge triangulation of the regular cube and octahedron, and rhombic dodecahedron.
 Disdyakis dodecahedron |
 Deltoidal icositetrahedron |
 Rhombic dodecahedron |
 Hexahedron |
 Octahedron |
| Spherical polyhedron | |||
|---|---|---|---|

|

|

|

|
| (see rotating model) | Orthographic projections from 2-, 3- and 4-fold axes | ||
The edges of a spherical disdyakis dodecahedron belong to 9 great circles. Three of them form a spherical octahedron (gray in the images below). The remaining six form three square hosohedra (red, green and blue in the images below). They all correspond to mirror planes - the former in dihedral , and the latter in tetrahedral symmetry.
| Stereographic projections | |||
|---|---|---|---|

|
2-fold | 3-fold | 4-fold |

|

|

| |
Cartesian coordinates
Let .
Then the Cartesian coordinates for the vertices of a disdyakis dodecahedron centered at the origin are:
● permutations of (±a, 0, 0) (vertices of an octahedron)
● permutations of (±b, ±b, 0) (vertices of a cuboctahedron)
● (±c, ±c, ±c) (vertices of a cube)
| Convex hulls |
|---|
| Combining an octahedron, cube, and cuboctahedron to form the disdyakis dodecahedron. The convex hulls for these vertices scaled by result in Cartesian coordinates of unit circumradius, which are visualized in the figure below: |

|
Dimensions
If its smallest edges have length a, its surface area and volume are
The faces are scalene triangles. Their angles are , and .
Orthogonal projections
The truncated cuboctahedron and its dual, the disdyakis dodecahedron can be drawn in a number of symmetric orthogonal projective orientations. Between a polyhedron and its dual, vertices and faces are swapped in positions, and edges are perpendicular.
| Projective symmetry |
|||||||
|---|---|---|---|---|---|---|---|
| Image | 
|

|
|

|

|

|

|
| Dual image |

|
|

|

|

|
|

|
Related polyhedra and tilings

|

|
| Polyhedra similar to the disdyakis dodecahedron are duals to the Bowtie octahedron and cube, containing extra pairs triangular faces . | |
The disdyakis dodecahedron is one of a family of duals to the uniform polyhedra related to the cube and regular octahedron.
| Uniform octahedral polyhedra | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: , (*432) | (432) |
= (*332) |
(3*2) | |||||||
| {4,3} | t{4,3} | r{4,3} r{3} |
t{3,4} t{3} |
{3,4} {3} |
rr{4,3} s2{3,4} |
tr{4,3} | sr{4,3} | h{4,3} {3,3} |
h2{4,3} t{3,3} |
s{3,4} s{3} |
= |
= |
= |
||||||||
| Duals to uniform polyhedra | ||||||||||
| V4 | V3.8 | V(3.4) | V4.6 | V3 | V3.4 | V4.6.8 | V3.4 | V3 | V3.6 | V3 |
It is a polyhedra in a sequence defined by the face configuration V4.6.2n. This group is special for having all even number of edges per vertex and form bisecting planes through the polyhedra and infinite lines in the plane, and continuing into the hyperbolic plane for any n ≥ 7.
With an even number of faces at every vertex, these polyhedra and tilings can be shown by alternating two colors so all adjacent faces have different colors.
Each face on these domains also corresponds to the fundamental domain of a symmetry group with order 2,3,n mirrors at each triangle face vertex.
| *n32 symmetry mutation of omnitruncated tilings: 4.6.2n | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sym. *n32 |
Spherical | Euclid. | Compact hyperb. | Paraco. | Noncompact hyperbolic | |||||||
| *232 |
*332 |
*432 |
*532 |
*632 |
*732 |
*832 |
*∞32 |
|
|
|
| |
| Figures | 
|

|

|

|

|

|

|

|

|

|

| |
| Config. | 4.6.4 | 4.6.6 | 4.6.8 | 4.6.10 | 4.6.12 | 4.6.14 | 4.6.16 | 4.6.∞ | 4.6.24i | 4.6.18i | 4.6.12i | 4.6.6i |
| Duals | 
|

|

|

|

|

|

|

|

|

|

|

|
| Config. | V4.6.4 | V4.6.6 | V4.6.8 | V4.6.10 | V4.6.12 | V4.6.14 | V4.6.16 | V4.6.∞ | V4.6.24i | V4.6.18i | V4.6.12i | V4.6.6i |
| *n42 symmetry mutation of omnitruncated tilings: 4.8.2n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Symmetry *n42 |
Spherical | Euclidean | Compact hyperbolic | Paracomp. | ||||
| *242 |
*342 |
*442 |
*542 |
*642 |
*742 |
*842 ... |
*∞42 | |
| Omnitruncated figure |
 4.8.4 |
 4.8.6 |
 4.8.8 |
 4.8.10 |
 4.8.12 |
 4.8.14 |
 4.8.16 |
 4.8.∞ |
| Omnitruncated duals |
 V4.8.4 |
 V4.8.6 |
 V4.8.8 |
 V4.8.10 |
 V4.8.12 |
 V4.8.14 |
 V4.8.16 |
 V4.8.∞ |
See also
- First stellation of rhombic dodecahedron
- Disdyakis triacontahedron
- Kisrhombille tiling
- Great rhombihexacron—A uniform dual polyhedron with the same surface topology
References
- "Keyword: "forms" | ClipArt ETC".
- Conway, Symmetries of things, p.284
- Langer, Joel C.; Singer, David A. (2010), "Reflections on the lemniscate of Bernoulli: the forty-eight faces of a mathematical gem", Milan Journal of Mathematics, 78 (2): 643–682, doi:10.1007/s00032-010-0124-5, MR 2781856
- Koca, Mehmet; Ozdes Koca, Nazife; Koc, Ramazon (2010). "Catalan Solids Derived From 3D-Root Systems and Quaternions". Journal of Mathematical Physics. 51 (4). arXiv:0908.3272. doi:10.1063/1.3356985.
- Symmetrohedra: Polyhedra from Symmetric Placement of Regular Polygons Craig S. Kaplan
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
- The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 285, kisRhombic dodecahedron)
External links
- Weisstein, Eric W., "Disdyakis dodecahedron" ("Catalan solid") at MathWorld.
- Disdyakis Dodecahedron (Hexakis Octahedron) Interactive Polyhedron Model
| Convex polyhedra | |||||
|---|---|---|---|---|---|
| Platonic solids (regular) | |||||
| Archimedean solids (semiregular or uniform) | |||||
| Catalan solids (duals of Archimedean) |
| ||||
| Dihedral regular | |||||
| Dihedral uniform |
| ||||
| Dihedral others | |||||
| Degenerate polyhedra are in italics. | |||||

 .
. result in Cartesian coordinates of unit
result in Cartesian coordinates of unit 
 ,
,  and
and  .
.