| This article is an orphan, as no other articles link to it. Please introduce links to this page from related articles; try the Find link tool for suggestions. (November 2015) |
Multidimensional Digital Signal Processing (MDSP) refers to the extension of Digital signal processing (DSP) techniques to signals that vary in more than one dimension. While conventional DSP typically deals with one-dimensional data, such as time-varying audio signals, MDSP involves processing signals in two or more dimensions. Many of the principles from one-dimensional DSP, such as Fourier transforms and filter design, have analogous counterparts in multidimensional signal processing.
Modern general-purpose computing on graphics processing units (GPGPUs) have an excellent throughput on vector operations and numeric manipulations through a high degree of parallel computations. Processing digital signals, particularly multidimensional signals, often involves a series of vector operations on massive numbers of independent data samples, GPGPUs are now widely employed to accelerate multidimensional DSP, such as image processing, video codecs, radar signal analysis, sonar signal processing, and ultrasound scanning. Conceptually, GPGPUs dramatically reduce the computation complexity when compared with central processing units (CPUs), digital signal processors (DSPs), or other FPGA accelerators.
Motivation
Processing multidimensional signals is a common problem in scientific research and/or engineering computations. Typically, a DSP problem's computation complexity grows exponentially with the number of dimensions. Notwithstanding, with a high degree of time and storage complexity, it is extremely difficult to process multidimensional signals in real-time. Although many fast algorithms (e.g. FFT) have been proposed for 1-D DSP problems, they are still not efficient enough to be adapted in high dimensional DSP problems. Therefore, it is still hard to obtain the desired computation results with digital signal processors. Hence, better algorithms and hardware architecture are needed to accelerate multidimensional DSP computations.
Existing approaches
Practically, to accelerate multidimensional DSP, some common approaches have been proposed and developed in the past decades.
Lower sampling rate
A makeshift to achieve a real-time requirement in multidimensional DSP applications is to use a lower sampling rate, which can efficiently reduce the number of samples to be processed at one time and thereby decrease the total processing time. However, this can lead to the aliasing problem due to the sampling theorem and poor-quality outputs. In some applications, such as military radars and medical images, we are eager to have highly precise and accurate results. In such cases, using a lower sampling rate to reduce the amount of computation in the multidimensional DSP domain is not always allowable.
Digital signal processors
Digital signal processors are designed specifically to process vector operations. They have been widely used in DSP computations for decades. However, most digital signal processors are only capable of manipulating a few operations in parallel. This kind of design is sufficient to accelerate audio processing (1-D signals) and image processing (2-D signals). However, with a large number of data samples of multidimensional signals, this is still not powerful enough to retrieve computation results in real-time.
Supercomputer assistance
In order to accelerate multidimensional DSP computations, using dedicated supercomputers or cluster computers is required in some circumstances, e.g., weather forecasting and military radars. Nevertheless, using supercomputers designated to simply perform DSP operations takes considerable money cost and energy consumption. Also, it is not practical and suitable for all multidimensional DSP applications.
GPU acceleration
GPUs are originally devised to accelerate image processing and video stream rendering. Moreover, since modern GPUs have good ability to perform numeric computations in parallel with a relatively low cost and better energy efficiency, GPUs are becoming a popular alternative to replace supercomputers performing multidimensional DSP.
GPGPU computations
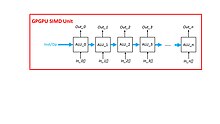
Modern GPU designs are mainly based on the SIMD (Single Instruction Multiple Data) computation paradigm. This type of GPU devices is so-called general-purpose GPUs (GPGPUs).
GPGPUs are able to perform an operation on multiple independent data concurrently with their vector or SIMD functional units. A modern GPGPU can spawn thousands of concurrent threads and process all threads in a batch manner. With this nature, GPGPUs can be employed as DSP accelerators easily while many DSP problems can be solved by divide-and-conquer algorithms. A large scale and complex DSP problem can be divided into a bunch of small numeric problems and be processed altogether at one time so that the overall time complexity can be reduced significantly. For example, multiplying two M × M matrices can be processed by M × M concurrent threads on a GPGPU device without any output data dependency. Therefore, theoretically, by means of GPGPU acceleration, we can gain up to M × M speedup compared with a traditional CPU or digital signal processor.
GPU programming languages
Currently, there are several existing programming languages or interfaces which support GPGPU programming.
CUDA
CUDA is the standard interface to program NVIDIA GPUs. NVIDIA also provides many CUDA libraries to support DSP acceleration on NVIDIA GPU devices.
OpenCL
OpenCL is an industrial standard which was originally proposed by Apple Inc. and is maintained and developed by the Khronos Group now. OpenCL provides C++ like APIs for programming different devices universally, including GPGPUs.
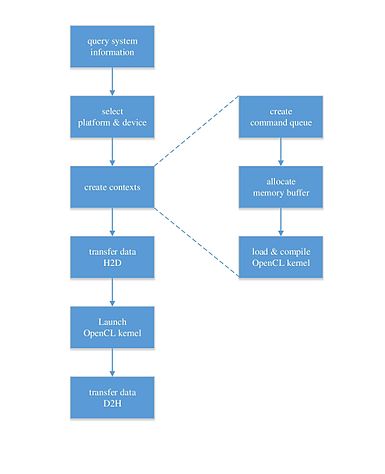
The following figure illustrates the execution flow of launching an OpenCL program on a GPU device. The CPU first detects OpenCL devices (GPU in this case) and then invokes a just-in-time compiler to translate the OpenCL source code into target binary. CPU then sends data to GPU to perform computations. When the GPU is processing data, CPU is free to process its own tasks.
C++ AMP
C++ AMP is a programming model proposed by Microsoft. C++ AMP is a C++ based library designed for programming SIMD processors
OpenACC
OpenACC is a programming standard for parallel computing developed by Cray, CAPS, NVIDIA and PGI. OpenAcc targets programming for CPU and GPU heterogeneous systems with C, C++, and Fortran extensions.
Examples of GPU programming for multidimensional DSP
m × m matrix multiplication
Suppose A and B are two m × m matrices and we would like to compute C = A × B.
To compute each element in C takes m multiplications and (m – 1) additions. Therefore, with a CPU implementation, the time complexity to achieve this computation is Θ(n) in the following C example. However, we have known that elements in C are independent of each other. Hence, the computation can be fully parallelized by SIMD processors, such as GPGPU devices. With a GPGPU implementation, the time complexity significantly reduces to Θ(n) by unrolling the for-loop as shown in the following OpenCL example.
// MxM matrix multiplication in C
void matrixMul(
float *A, // input matrix A
float *B, // input matrix B
float *C, // output matrix C
int size) // size of the matrices
{
// N x N x N iterations
for (int row = 0; row < size; row++) {
for (int col = 0; col < size; col++) {
int id = row * size + col;
float sum = 0.0;
for (int m = 0; m < size; m++) {
sum += (A * B);
}
C = sum;
}
}
}
// MxM matrix multiplication in OpenCL
__kernel void matrixMul(
__global float *A, // input matrix A
__global float *B, // input matrix B
__global float *C, // output matrix C
__global int size) // size of the matrices
{
size_t id = get_global_id(0); // each thread works on an element
size_t row = id / size;
size_t col = id % size;
float sum = 0.0;
// N iterations
for (int m = 0; m < size; m++) {
sum += (A * B);
}
C = sum;
}
Multidimensional convolution
Convolution is a frequently used operation in DSP. To compute the 2-D convolution of two m × m signals, it requires m multiplications and m × (m – 1) additions for an output element. That is, the overall time complexity is Θ(n) for the entire output signal. As the following OpenCL example shows, with GPGPU acceleration, the total computation time effectively decreases to Θ(n) since all output elements are data independent.
2-D convolution equation:
// 2-D convolution implementation in OpenCL
__kernel void convolution(
__global float *x, // input signal x
__global float *h, // filter h
__global float *y, // output signal y
__global int size) // size of ROS of the input signal and filter
{
size_t id = get_global_id(0); // each thread works on an element
size_t row = size + size - 1; // number of rows of the output signal
size_t col = size + size - 1; // number of columns of the output signal
size_t n1 = id / row;
size_t n2 = id % col;
float sum = 0.0;
// N x N iterations
for (int k1 = 0; k1 < size; k1++) {
for (int k2 = 0; k2 < size; k2++) {
sum += (x * h);
}
}
C = sum;
}
Note that, although the example demonstrated above is a 2-D convolution, a similar approach can be adopted for a higher dimension system. Overall, for a s-D convolution, a GPGPU implementation has time complexity Θ(n), whereas a CPU implementation has time complexity Θ(n).
M-D convolution equation:
Multidimensional discrete time fourier transform (M-D DTFT)
In addition to convolution, the discrete-time Fourier transform (DTFT) is another technique which is often used in system analysis.
Practically, to implement an M-D DTFT, we can perform M times 1-D DFTF and matrix transpose with respect to each dimension. With a 1-D DTFT operation, GPGPU can conceptually reduce the complexity from Θ(n) to Θ(n) as illustrated by the following example of OpenCL implementation. That is, an M-D DTFT the complexity of GPGPU can be computed on a GPU with a complexity of Θ(n). While some GPGPUs are also equipped with hardware FFT accelerators internally, this implementation might be also optimized by invoking the FFT APIs or libraries provided by GPU manufacture.
// DTFT in OpenCL
__kernel void convolution(
__global float *x_re,
__global float *x_im,
__global float *X_re,
__global float *X_im,
__global int size)
{
size_t id = get_global_id(0); // each thread works on an element
X_re = 0.0;
X_im = 0.0;
for (int i = 0; i < size; i++) {
X_re += (x_re * cos(2 * 3.1415 * id / size) - x_im * sin(2 * 3.1415 * id / size));
X_im += (x_re * sin(2 * 3.1415 * id / size) + x_im * cos(2 * 3.1415 * id / size));
}
}
Real applications
Digital filter design
Designing a multidimensional digital filter is a big challenge, especially IIR filters. Typically it relies on computers to solve difference equations and obtain a set of approximated solutions. While GPGPU computation is becoming popular, several adaptive algorithms have been proposed to design multidimensional FIR and/or IIR filters by means of GPGPUs.
Radar signal reconstruction and analysis
Radar systems usually need to reconstruct numerous 3-D or 4-D data samples in real-time. Traditionally, particularly in military, this needs supercomputers' support. Nowadays, GPGPUs are also employed to replace supercomputers to process radar signals. For example, to process synthetic aperture radar (SAR) signals, it usually involves multidimensional FFT computations. GPGPUs can be used to rapidly perform FFT and/or iFFT in this kind of applications.
Self-driving cars
Many self-driving cars apply 3-D image recognition techniques to auto control the vehicles. Clearly, to accommodate the fast changing exterior environment, the recognition and decision processes must be done in real-time. GPGPUs are excellent devices to achieve the goal.
Medical image processing
In order to have accurate diagnosis, 2-D or 3-D medical signals, such as ultrasound, X-ray, MRI, and CT, often require very high sampling rate and image resolutions to reconstruct images. By applying GPGPUs' superior computation power, it was shown that we can acquire better-quality medical images
References
- Chu, Slo-Li; Hsiao, Chih-Chieh (2010-09-01). "OpenCL: Make Ubiquitous Supercomputing Possible". 2010 IEEE 12th International Conference on High Performance Computing and Communications (HPCC). pp. 556–561. doi:10.1109/HPCC.2010.56. ISBN 978-1-4244-8335-8. S2CID 14586211.
- Lindholm, E.; Nickolls, J.; Oberman, S.; Montrym, J. (2008-03-01). "NVIDIA Tesla: A Unified Graphics and Computing Architecture". IEEE Micro. 28 (2): 39–55. doi:10.1109/MM.2008.31. ISSN 0272-1732. S2CID 2793450.
- Kim, Hyesoon; Vuduc, Richard; Baghsorkhi, Sara; Choi, Jee; Hwu, Wen-Mei W. (2012). Hill, Mark D. (ed.). Performance Analysis and Tuning for General Purpose Graphics Processing Units (GPGPU). Morgan & Claypool Publishers. doi:10.2200/S00451ED1V01Y201209CAC020. ISBN 978-1-60845-954-4.
- "Parallel Programming and Computing Platform | CUDA | NVIDIA | NVIDIA". www.nvidia.com. Archived from the original on 2014-01-06. Retrieved 2015-11-05.
- "OpenCL – The open standard for parallel programming of heterogeneous systems". www.khronos.org. 21 July 2013. Retrieved 2015-11-05.
- "C++ AMP (C++ Accelerated Massive Parallelism)". msdn.microsoft.com. Retrieved 2015-11-05.
- "OpenACC Home | www.openacc.org". www.openacc.org. Retrieved 2015-11-05.
- "OpenCL™ Optimization Case Study Fast Fourier Transform – Part II – AMD". AMD. Retrieved 2015-11-05.
- Nehab, Diego; Maximo, André; Lima, Rodolfo S.; Hoppe, Hugues (2011-01-01). "GPU-efficient recursive filtering and summed-area tables". Proceedings of the 2011 SIGGRAPH Asia Conference. SA '11. New York, NY, USA: ACM. pp. 176:1–176:12. doi:10.1145/2024156.2024210. ISBN 978-1-4503-0807-6. S2CID 3014398.
- Pharr, Matt; Fernando, Randima (2005). GPU Gems 2: Programming Techniques For High-Performance Graphics And General-Purpose Computation. Pearson Addison Wesley. ISBN 978-0-321-33559-3.
- Hwu, Wen-mei W. (2011). GPU Computing Gems Emerald Edition. San Francisco, CA, USA: Morgan Kaufmann Publishers Inc. ISBN 978-0-12-385963-1.
- Clemente, C.; Di Bisceglie, M.; Di Santo, M.; Ranaldo, N.; Spinelli, M. (2009-10-01). "Processing of synthetic Aperture Radar data with GPGPU". 2009 IEEE Workshop on Signal Processing Systems. pp. 309–314. doi:10.1109/SIPS.2009.5336272. ISBN 978-1-4244-4335-2. S2CID 18932083.
- Liu, Bin; Wang, Kaizhi; Liu, Xingzhao; Yu, Wenxian (2009-10-01). "An Efficient SAR Processor Based on GPU via CUDA". 2009 2nd International Congress on Image and Signal Processing. pp. 1–5. doi:10.1109/CISP.2009.5304418. ISBN 978-1-4244-4129-7. S2CID 18801932.
- Monsurro, P.; Trifiletti, A.; Lannutti, F. (2014-06-01). "Implementing radar algorithms on CUDA hardware". 2014 Proceedings of the 21st International Conference Mixed Design of Integrated Circuits and Systems (MIXDES). pp. 455–458. doi:10.1109/MIXDES.2014.6872240. ISBN 978-83-63578-05-3. S2CID 16482715.
- Fang, Jianbin; Varbanescu, A.L.; Shen, Jie; Sips, H.; Saygili, G.; van der Maaten, L. (2012-12-01). "Accelerating Cost Aggregation for Real-Time Stereo Matching". 2012 IEEE 18th International Conference on Parallel and Distributed Systems. pp. 472–481. doi:10.1109/ICPADS.2012.71. ISBN 978-1-4673-4565-1. S2CID 14737126.
- "Medical Imaging|NVIDIA". www.nvidia.com. Retrieved 2015-11-07.
- Heng, Yang; Gu, Lixu (2005-01-01). "GPU-based Volume Rendering for Medical Image Visualization". 2005 IEEE Engineering in Medicine and Biology 27th Annual Conference. Vol. 5. pp. 5145–5148. doi:10.1109/IEMBS.2005.1615635. ISBN 978-0-7803-8741-6. PMID 17281405. S2CID 17401263.
| Digital signal processing | |
|---|---|
| Theory | |
| Sub-fields | |
| Techniques | |
| Sampling | |
| Programming languages | |
|---|---|
| Parallel computing | |
|---|---|
| General | |
| Levels | |
| Multithreading | |
| Theory | |
| Elements | |
| Coordination | |
| Programming | |
| Hardware | |
| APIs | |
| Problems | |




