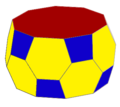
| Uniform pentagonal antiprism | |
|---|---|

| |
| Type | Prismatic uniform polyhedron |
| Elements | F = 12, E = 20 V = 10 (χ = 2) |
| Faces by sides | 10{3}+2{5} |
| Schläfli symbol | s{2,10} sr{2,5} |
| Wythoff symbol | | 2 2 5 |
| Coxeter diagram | |
| Symmetry group | D5d, , (2*5), order 20 |
| Rotation group | D5, , (522), order 10 |
| References | U77(c) |
| Dual | Pentagonal trapezohedron |
| Properties | convex |
 Vertex figure 3.3.3.5 | |

In geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of ten triangles for a total of twelve faces. Hence, it is a non-regular dodecahedron.
Geometry
If the faces of the pentagonal antiprism are all regular, it is a semiregular polyhedron. It can also be considered as a parabidiminished icosahedron, a shape formed by removing two pentagonal pyramids from a regular icosahedron leaving two nonadjacent pentagonal faces; a related shape, the metabidiminished icosahedron (one of the Johnson solids), is likewise form from the icosahedron by removing two pyramids, but its pentagonal faces are adjacent to each other. The two pentagonal faces of either shape can be augmented with pyramids to form the icosahedron.
Relation to polytopes
The pentagonal antiprism occurs as a constituent element in some higher-dimensional polytopes. Two rings of ten pentagonal antiprisms each bound the hypersurface of the four-dimensional grand antiprism. If these antiprisms are augmented with pentagonal prism pyramids and linked with rings of five tetrahedra each, the 600-cell is obtained.
See also
The pentagonal antiprism can be truncated and alternated to form a snub antiprism:
| Antiprism A5 |
Truncated tA5 |
Alternated htA5 |
|---|---|---|

|
|

|
| s{2,10} | ts{2,10} | ss{2,10} |
| v:10; e:20; f:12 | v:40; e:60; f:22 | v:20; e:50; f:32 |
| Antiprism name | Digonal antiprism | (Trigonal) Triangular antiprism |
(Tetragonal) Square antiprism |
Pentagonal antiprism | Hexagonal antiprism | Heptagonal antiprism | ... | Apeirogonal antiprism |
|---|---|---|---|---|---|---|---|---|
| Polyhedron image | ... | |||||||
| Spherical tiling image | Plane tiling image | |||||||
| Vertex config. | 2.3.3.3 | 3.3.3.3 | 4.3.3.3 | 5.3.3.3 | 6.3.3.3 | 7.3.3.3 | ... | ∞.3.3.3 |
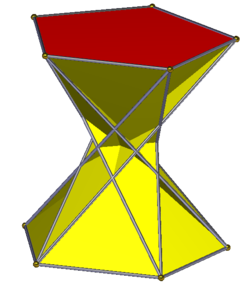
Crossed antiprism
A crossed pentagonal antiprism is topologically identical to the pentagonal antiprism, although it can't be made uniform. The sides are isosceles triangles. It has d5d symmetry, order 10. Its vertex configuration is 3.3/2.3.5, with one triangle retrograde and its vertex arrangement is the same as a pentagonal prism.
External links
- Weisstein, Eric W. "Antiprism". MathWorld.
- Pentagonal Antiprism: Interactive Polyhedron Model
- Virtual Reality Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra
- polyhedronisme A5
| Convex polyhedra | |||||
|---|---|---|---|---|---|
| Platonic solids (regular) | |||||
| Archimedean solids (semiregular or uniform) | |||||
| Catalan solids (duals of Archimedean) |
| ||||
| Dihedral regular | |||||
| Dihedral uniform |
| ||||
| Dihedral others | |||||
| Degenerate polyhedra are in italics. | |||||
This polyhedron-related article is a stub. You can help Misplaced Pages by expanding it. |