The Bauhinia blakeana flower on the Hong Kong region flag has C5 symmetry; the star on each petal has D5 symmetry. |
 The Yin and Yang symbol has C2 symmetry of geometry with inverted colors |
In geometry, a point group is a mathematical group of symmetry operations (isometries in a Euclidean space) that have a fixed point in common. The coordinate origin of the Euclidean space is conventionally taken to be a fixed point, and every point group in dimension d is then a subgroup of the orthogonal group O(d). Point groups are used to describe the symmetries of geometric figures and physical objects such as molecules.
Each point group can be represented as sets of orthogonal matrices M that transform point x into point y according to y = Mx. Each element of a point group is either a rotation (determinant of M = 1), or it is a reflection or improper rotation (determinant of M = −1).
The geometric symmetries of crystals are described by space groups, which allow translations and contain point groups as subgroups. Discrete point groups in more than one dimension come in infinite families, but from the crystallographic restriction theorem and one of Bieberbach's theorems, each number of dimensions has only a finite number of point groups that are symmetric over some lattice or grid with that number of dimensions. These are the crystallographic point groups.
Chiral and achiral point groups, reflection groups
Point groups can be classified into chiral (or purely rotational) groups and achiral groups. The chiral groups are subgroups of the special orthogonal group SO(d): they contain only orientation-preserving orthogonal transformations, i.e., those of determinant +1. The achiral groups contain also transformations of determinant −1. In an achiral group, the orientation-preserving transformations form a (chiral) subgroup of index 2.
Finite Coxeter groups or reflection groups are those point groups that are generated purely by a set of reflectional mirrors passing through the same point. A rank n Coxeter group has n mirrors and is represented by a Coxeter–Dynkin diagram. Coxeter notation offers a bracketed notation equivalent to the Coxeter diagram, with markup symbols for rotational and other subsymmetry point groups. Reflection groups are necessarily achiral (except for the trivial group containing only the identity element).
List of point groups
One dimension
There are only two one-dimensional point groups, the identity group and the reflection group.
| Group | Coxeter | Coxeter diagram | Order | Description |
|---|---|---|---|---|
| C1 | 1 | identity | ||
| D1 | 2 | reflection group |
Two dimensions
Point groups in two dimensions, sometimes called rosette groups.
They come in two infinite families:
- Cyclic groups Cn of n-fold rotation groups
- Dihedral groups Dn of n-fold rotation and reflection groups
Applying the crystallographic restriction theorem restricts n to values 1, 2, 3, 4, and 6 for both families, yielding 10 groups.
| Group | Intl | Orbifold | Coxeter | Order | Description |
|---|---|---|---|---|---|
| Cn | n | n• | n | cyclic: n-fold rotations; abstract group Zn, the group of integers under addition modulo n | |
| Dn | nm | *n• | 2n | dihedral: cyclic with reflections; abstract group Dihn, the dihedral group |
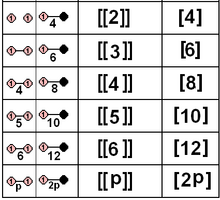
The subset of pure reflectional point groups, defined by 1 or 2 mirrors, can also be given by their Coxeter group and related polygons. These include 5 crystallographic groups. The symmetry of the reflectional groups can be doubled by an isomorphism, mapping both mirrors onto each other by a bisecting mirror, doubling the symmetry order.
| Reflective | Rotational | Related polygons | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Group | Coxeter group | Coxeter diagram | Order | Subgroup | Coxeter | Order | |||
| D1 | A1 | 2 | C1 | 1 | digon | ||||
| D2 | A1 | 4 | C2 | 2 | rectangle | ||||
| D3 | A2 | 6 | C3 | 3 | equilateral triangle | ||||
| D4 | BC2 | 8 | C4 | 4 | square | ||||
| D5 | H2 | 10 | C5 | 5 | regular pentagon | ||||
| D6 | G2 | 12 | C6 | 6 | regular hexagon | ||||
| Dn | I2(n) | 2n | Cn | n | regular polygon | ||||
| D2×2 | A1×2 | ] = | 8 | ||||||
| D3×2 | A2×2 | ] = | 12 | ||||||
| D4×2 | BC2×2 | ] = | 16 | ||||||
| D5×2 | H2×2 | ] = | 20 | ||||||
| D6×2 | G2×2 | ] = | 24 | ||||||
| Dn×2 | I2(n)×2 | ] = | 4n | ||||||
Three dimensions
Main article: Point groups in three dimensionsPoint groups in three dimensions, sometimes called molecular point groups after their wide use in studying symmetries of molecules.
They come in 7 infinite families of axial groups (also called prismatic), and 7 additional polyhedral groups (also called Platonic). In Schönflies notation,
- Axial groups: Cn, S2n, Cnh, Cnv, Dn, Dnd, Dnh
- Polyhedral groups: T, Td, Th, O, Oh, I, Ih
Applying the crystallographic restriction theorem to these groups yields the 32 crystallographic point groups.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (*) When the Intl entries are duplicated, the first is for even n, the second for odd n. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Reflection groups

The reflection point groups, defined by 1 to 3 mirror planes, can also be given by their Coxeter group and related polyhedra. The group can be doubled, written as ], mapping the first and last mirrors onto each other, doubling the symmetry to 48, and isomorphic to the group.
| Schönflies | Coxeter group | Coxeter diagram | Order | Related regular and prismatic polyhedra | |||
|---|---|---|---|---|---|---|---|
| Td | A3 | 24 | tetrahedron | ||||
| Td×Dih1 = Oh | A3×2 = BC3 | ] = | = |
48 | stellated octahedron | ||
| Oh | BC3 | 48 | cube, octahedron | ||||
| Ih | H3 | 120 | icosahedron, dodecahedron | ||||
| D3h | A2×A1 | 12 | triangular prism | ||||
| D3h×Dih1 = D6h | A2×A1×2 | ,2] | = |
24 | hexagonal prism | ||
| D4h | BC2×A1 | 16 | square prism | ||||
| D4h×Dih1 = D8h | BC2×A1×2 | ,2] = | = |
32 | octagonal prism | ||
| D5h | H2×A1 | 20 | pentagonal prism | ||||
| D6h | G2×A1 | 24 | hexagonal prism | ||||
| Dnh | I2(n)×A1 | 4n | n-gonal prism | ||||
| Dnh×Dih1 = D2nh | I2(n)×A1×2 | ,2] | = |
8n | |||
| D2h | A1 | 8 | cuboid | ||||
| D2h×Dih1 | A1×2 | ,2] = | = |
16 | |||
| D2h×Dih3 = Oh | A1×6 | ] = | = |
48 | |||
| C3v | A2 | 6 | hosohedron | ||||
| C4v | BC2 | 8 | |||||
| C5v | H2 | 10 | |||||
| C6v | G2 | 12 | |||||
| Cnv | I2(n) | 2n | |||||
| Cnv×Dih1 = C2nv | I2(n)×2 | ] = | = |
4n | |||
| C2v | A1 | 4 | |||||
| C2v×Dih1 | A1×2 | ] | = |
8 | |||
| Cs | A1 | 2 | |||||
Four dimensions
Main article: Point groups in four dimensionsThe four-dimensional point groups (chiral as well as achiral) are listed in Conway and Smith, Section 4, Tables 4.1–4.3.

The following list gives the four-dimensional reflection groups (excluding those that leave a subspace fixed and that are therefore lower-dimensional reflection groups). Each group is specified as a Coxeter group, and like the polyhedral groups of 3D, it can be named by its related convex regular 4-polytope. Related pure rotational groups exist for each with half the order, and can be represented by the bracket Coxeter notation with a '+' exponent, for example has three 3-fold gyration points and symmetry order 60. Front-back symmetric groups like and can be doubled, shown as double brackets in Coxeter's notation, for example ] with its order doubled to 240.
| Coxeter group/notation | Coxeter diagram | Order | Related polytopes | ||
|---|---|---|---|---|---|
| A4 | 120 | 5-cell | |||
| A4×2 | ] | 240 | 5-cell dual compound | ||
| BC4 | 384 | 16-cell / tesseract | |||
| D4 | 192 | demitesseractic | |||
| D4×2 = BC4 | <> = | = |
384 | ||
| D4×6 = F4 | ] = | = |
1152 | ||
| F4 | 1152 | 24-cell | |||
| F4×2 | ] | 2304 | 24-cell dual compound | ||
| H4 | 14400 | 120-cell / 600-cell | |||
| A3×A1 | 48 | tetrahedral prism | |||
| A3×A1×2 | ,2] = | = |
96 | octahedral prism | |
| BC3×A1 | 96 | ||||
| H3×A1 | 240 | icosahedral prism | |||
| A2×A2 | 36 | duoprism | |||
| A2×BC2 | 48 | ||||
| A2×H2 | 60 | ||||
| A2×G2 | 72 | ||||
| BC2×BC2 | 64 | ||||
| BC2×2 | ] | 128 | |||
| BC2×H2 | 80 | ||||
| BC2×G2 | 96 | ||||
| H2×H2 | 100 | ||||
| H2×G2 | 120 | ||||
| G2×G2 | 144 | ||||
| I2(p)×I2(q) | 4pq | ||||
| I2(2p)×I2(q) | ,2,q] = | = |
8pq | ||
| I2(2p)×I2(2q) | ],2,] = | = |
16pq | ||
| I2(p)×2 | ] | 8p | |||
| I2(2p)×2 | ],2,]] = ] | = |
32p | ||
| A2×A1×A1 | 24 | ||||
| BC2×A1×A1 | 32 | ||||
| H2×A1×A1 | 40 | ||||
| G2×A1×A1 | 48 | ||||
| I2(p)×A1×A1 | 8p | ||||
| I2(2p)×A1×A1×2 | ,2,2] = | = |
16p | ||
| I2(p)×A1×2 | ] = | = |
16p | ||
| I2(2p)×A1×4 | ],2,] = | = |
32p | ||
| A1×A1×A1×A1 | 16 | 4-orthotope | |||
| A1×A1×A1×2 | ,2,2] = | = |
32 | ||
| A1×A1×4 | ],2,] = | = |
64 | ||
| A1×A1×6 | ,2] = | = |
96 | ||
| A1×24 | ] = | = |
384 | ||
Five dimensions

The following table gives the five-dimensional reflection groups (excluding those that are lower-dimensional reflection groups), by listing them as Coxeter groups. Related chiral groups exist for each with half the order, and can be represented by the bracket Coxeter notation with a '+' exponent, for example has four 3-fold gyration points and symmetry order 360.
| Coxeter group/notation | Coxeter diagrams |
Order | Related regular and prismatic polytopes | ||
|---|---|---|---|---|---|
| A5 | 720 | 5-simplex | |||
| A5×2 | ] | 1440 | 5-simplex dual compound | ||
| BC5 | 3840 | 5-cube, 5-orthoplex | |||
| D5 | 1920 | 5-demicube | |||
| D5×2 | <> | 3840 | |||
| A4×A1 | 240 | 5-cell prism | |||
| A4×A1×2 | ,2] | 480 | |||
| BC4×A1 | 768 | tesseract prism | |||
| F4×A1 | 2304 | 24-cell prism | |||
| F4×A1×2 | ,2] | 4608 | |||
| H4×A1 | 28800 | 600-cell or 120-cell prism | |||
| D4×A1 | 384 | demitesseract prism | |||
| A3×A2 | 144 | duoprism | |||
| A3×A2×2 | ,2,3] | 288 | |||
| A3×BC2 | 192 | ||||
| A3×H2 | 240 | ||||
| A3×G2 | 288 | ||||
| A3×I2(p) | 48p | ||||
| BC3×A2 | 288 | ||||
| BC3×BC2 | 384 | ||||
| BC3×H2 | 480 | ||||
| BC3×G2 | 576 | ||||
| BC3×I2(p) | 96p | ||||
| H3×A2 | 720 | ||||
| H3×BC2 | 960 | ||||
| H3×H2 | 1200 | ||||
| H3×G2 | 1440 | ||||
| H3×I2(p) | 240p | ||||
| A3×A1 | 96 | ||||
| BC3×A1 | 192 | ||||
| H3×A1 | 480 | ||||
| A2×A1 | 72 | duoprism prism | |||
| A2×BC2×A1 | 96 | ||||
| A2×H2×A1 | 120 | ||||
| A2×G2×A1 | 144 | ||||
| BC2×A1 | 128 | ||||
| BC2×H2×A1 | 160 | ||||
| BC2×G2×A1 | 192 | ||||
| H2×A1 | 200 | ||||
| H2×G2×A1 | 240 | ||||
| G2×A1 | 288 | ||||
| I2(p)×I2(q)×A1 | 8pq | ||||
| A2×A1 | 48 | ||||
| BC2×A1 | 64 | ||||
| H2×A1 | 80 | ||||
| G2×A1 | 96 | ||||
| I2(p)×A1 | 16p | ||||
| A1 | 32 | 5-orthotope | |||
| A1×(2!) | ,2,2,2] | 64 | |||
| A1×(2!×2!) | ],2,,2] | 128 | |||
| A1×(3!) | ,2,2] | 192 | |||
| A1×(3!×2!) | ,2,] | 384 | |||
| A1×(4!) | ,2]] | 768 | |||
| A1×(5!) | ] | 3840 | |||
Six dimensions

The following table gives the six-dimensional reflection groups (excluding those that are lower-dimensional reflection groups), by listing them as Coxeter groups. Related pure rotational groups exist for each with half the order, and can be represented by the bracket Coxeter notation with a '+' exponent, for example has five 3-fold gyration points and symmetry order 2520.
| Coxeter group | Coxeter diagram |
Order | Related regular and prismatic polytopes | |
|---|---|---|---|---|
| A6 | 5040 (7!) | 6-simplex | ||
| A6×2 | ] | 10080 (2×7!) | 6-simplex dual compound | |
| BC6 | 46080 (2×6!) | 6-cube, 6-orthoplex | ||
| D6 | 23040 (2×6!) | 6-demicube | ||
| E6 | 51840 (72×6!) | 122, 221 | ||
| A5×A1 | 1440 (2×6!) | 5-simplex prism | ||
| BC5×A1 | 7680 (2×5!) | 5-cube prism | ||
| D5×A1 | 3840 (2×5!) | 5-demicube prism | ||
| A4×I2(p) | 240p | duoprism | ||
| BC4×I2(p) | 768p | |||
| F4×I2(p) | 2304p | |||
| H4×I2(p) | 28800p | |||
| D4×I2(p) | 384p | |||
| A4×A1 | 480 | |||
| BC4×A1 | 1536 | |||
| F4×A1 | 4608 | |||
| H4×A1 | 57600 | |||
| D4×A1 | 768 | |||
| A3 | 576 | |||
| A3×BC3 | 1152 | |||
| A3×H3 | 2880 | |||
| BC3 | 2304 | |||
| BC3×H3 | 5760 | |||
| H3 | 14400 | |||
| A3×I2(p)×A1 | 96p | duoprism prism | ||
| BC3×I2(p)×A1 | 192p | |||
| H3×I2(p)×A1 | 480p | |||
| A3×A1 | 192 | |||
| BC3×A1 | 384 | |||
| H3×A1 | 960 | |||
| I2(p)×I2(q)×I2(r) | 8pqr | triaprism | ||
| I2(p)×I2(q)×A1 | 16pq | |||
| I2(p)×A1 | 32p | |||
| A1 | 64 | 6-orthotope | ||
Seven dimensions
The following table gives the seven-dimensional reflection groups (excluding those that are lower-dimensional reflection groups), by listing them as Coxeter groups. Related chiral groups exist for each with half the order, defined by an even number of reflections, and can be represented by the bracket Coxeter notation with a '+' exponent, for example has six 3-fold gyration points and symmetry order 20160.
| Coxeter group | Coxeter diagram | Order | Related polytopes | |
|---|---|---|---|---|
| A7 | 40320 (8!) | 7-simplex | ||
| A7×2 | ] | 80640 (2×8!) | 7-simplex dual compound | |
| BC7 | 645120 (2×7!) | 7-cube, 7-orthoplex | ||
| D7 | 322560 (2×7!) | 7-demicube | ||
| E7 | 2903040 (8×9!) | 321, 231, 132 | ||
| A6×A1 | 10080 (2×7!) | |||
| BC6×A1 | 92160 (2×6!) | |||
| D6×A1 | 46080 (2×6!) | |||
| E6×A1 | 103680 (144×6!) | |||
| A5×I2(p) | 1440p | |||
| BC5×I2(p) | 7680p | |||
| D5×I2(p) | 3840p | |||
| A5×A1 | 2880 | |||
| BC5×A1 | 15360 | |||
| D5×A1 | 7680 | |||
| A4×A3 | 2880 | |||
| A4×BC3 | 5760 | |||
| A4×H3 | 14400 | |||
| BC4×A3 | 9216 | |||
| BC4×BC3 | 18432 | |||
| BC4×H3 | 46080 | |||
| H4×A3 | 345600 | |||
| H4×BC3 | 691200 | |||
| H4×H3 | 1728000 | |||
| F4×A3 | 27648 | |||
| F4×BC3 | 55296 | |||
| F4×H3 | 138240 | |||
| D4×A3 | 4608 | |||
| D4×BC3 | 9216 | |||
| D4×H3 | 23040 | |||
| A4×I2(p)×A1 | 480p | |||
| BC4×I2(p)×A1 | 1536p | |||
| D4×I2(p)×A1 | 768p | |||
| F4×I2(p)×A1 | 4608p | |||
| H4×I2(p)×A1 | 57600p | |||
| A4×A1 | 960 | |||
| BC4×A1 | 3072 | |||
| F4×A1 | 9216 | |||
| H4×A1 | 115200 | |||
| D4×A1 | 1536 | |||
| A3×A1 | 1152 | |||
| A3×BC3×A1 | 2304 | |||
| A3×H3×A1 | 5760 | |||
| BC3×A1 | 4608 | |||
| BC3×H3×A1 | 11520 | |||
| H3×A1 | 28800 | |||
| A3×I2(p)×I2(q) | 96pq | |||
| BC3×I2(p)×I2(q) | 192pq | |||
| H3×I2(p)×I2(q) | 480pq | |||
| A3×I2(p)×A1 | 192p | |||
| BC3×I2(p)×A1 | 384p | |||
| H3×I2(p)×A1 | 960p | |||
| A3×A1 | 384 | |||
| BC3×A1 | 768 | |||
| H3×A1 | 1920 | |||
| I2(p)×I2(q)×I2(r)×A1 | 16pqr | |||
| I2(p)×I2(q)×A1 | 32pq | |||
| I2(p)×A1 | 64p | |||
| A1 | 128 | |||
Eight dimensions
The following table gives the eight-dimensional reflection groups (excluding those that are lower-dimensional reflection groups), by listing them as Coxeter groups. Related chiral groups exist for each with half the order, defined by an even number of reflections, and can be represented by the bracket Coxeter notation with a '+' exponent, for example has seven 3-fold gyration points and symmetry order 181440.
| Coxeter group | Coxeter diagram | Order | Related polytopes | |
|---|---|---|---|---|
| A8 | 362880 (9!) | 8-simplex | ||
| A8×2 | ] | 725760 (2×9!) | 8-simplex dual compound | |
| BC8 | 10321920 (28!) | 8-cube, 8-orthoplex | ||
| D8 | 5160960 (28!) | 8-demicube | ||
| E8 | 696729600 (192×10!) | 421, 241, 142 | ||
| A7×A1 | 80640 | 7-simplex prism | ||
| BC7×A1 | 645120 | 7-cube prism | ||
| D7×A1 | 322560 | 7-demicube prism | ||
| E7×A1 | 5806080 | 321 prism, 231 prism, 142 prism | ||
| A6×I2(p) | 10080p | duoprism | ||
| BC6×I2(p) | 92160p | |||
| D6×I2(p) | 46080p | |||
| E6×I2(p) | 103680p | |||
| A6×A1 | 20160 | |||
| BC6×A1 | 184320 | |||
| D6×A1 | 92160 | |||
| E6×A1 | 207360 | |||
| A5×A3 | 17280 | |||
| BC5×A3 | 92160 | |||
| D5×A3 | 46080 | |||
| A5×BC3 | 34560 | |||
| BC5×BC3 | 184320 | |||
| D5×BC3 | 92160 | |||
| A5×H3 | ||||
| BC5×H3 | ||||
| D5×H3 | ||||
| A5×I2(p)×A1 | ||||
| BC5×I2(p)×A1 | ||||
| D5×I2(p)×A1 | ||||
| A5×A1 | ||||
| BC5×A1 | ||||
| D5×A1 | ||||
| A4×A4 | ||||
| BC4×A4 | ||||
| D4×A4 | ||||
| F4×A4 | ||||
| H4×A4 | ||||
| BC4×BC4 | ||||
| D4×BC4 | ||||
| F4×BC4 | ||||
| H4×BC4 | ||||
| D4×D4 | ||||
| F4×D4 | ||||
| H4×D4 | ||||
| F4×F4 | ||||
| H4×F4 | ||||
| H4×H4 | ||||
| A4×A3×A1 | duoprism prisms | |||
| A4×BC3×A1 | ||||
| A4×H3×A1 | ||||
| BC4×A3×A1 | ||||
| BC4×BC3×A1 | ||||
| BC4×H3×A1 | ||||
| H4×A3×A1 | ||||
| H4×BC3×A1 | ||||
| H4×H3×A1 | ||||
| F4×A3×A1 | ||||
| F4×BC3×A1 | ||||
| F4×H3×A1 | ||||
| D4×A3×A1 | ||||
| D4×BC3×A1 | ||||
| D4×H3×A1 | ||||
| A4×I2(p)×I2(q) | triaprism | |||
| BC4×I2(p)×I2(q) | ||||
| F4×I2(p)×I2(q) | ||||
| H4×I2(p)×I2(q) | ||||
| D4×I2(p)×I2(q) | ||||
| A4×I2(p)×A1 | ||||
| BC4×I2(p)×A1 | ||||
| F4×I2(p)×A1 | ||||
| H4×I2(p)×A1 | ||||
| D4×I2(p)×A1 | ||||
| A4×A1 | ||||
| BC4×A1 | ||||
| F4×A1 | ||||
| H4×A1 | ||||
| D4×A1 | ||||
| A3×A3×I2(p) | ||||
| BC3×A3×I2(p) | ||||
| H3×A3×I2(p) | ||||
| BC3×BC3×I2(p) | ||||
| H3×BC3×I2(p) | ||||
| H3×H3×I2(p) | ||||
| A3×A3×A1 | ||||
| BC3×A3×A1 | ||||
| H3×A3×A1 | ||||
| BC3×BC3×A1 | ||||
| H3×BC3×A1 | ||||
| H3×H3×A1 | ||||
| A3×I2(p)×I2(q)×A1 | ||||
| BC3×I2(p)×I2(q)×A1 | ||||
| H3×I2(p)×I2(q)×A1 | ||||
| A3×I2(p)×A1 | ||||
| BC3×I2(p)×A1 | ||||
| H3×I2(p)×A1 | ||||
| A3×A1 | ||||
| BC3×A1 | ||||
| H3×A1 | ||||
| I2(p)×I2(q)×I2(r)×I2(s) | 16pqrs | |||
| I2(p)×I2(q)×I2(r)×A1 | 32pqr | |||
| I2(p)×I2(q)×A1 | 64pq | |||
| I2(p)×A1 | 128p | |||
| A1 | 256 | |||
See also
- Point groups in two dimensions
- Point groups in three dimensions
- Point groups in four dimensions
- Crystallography
- Crystallographic point group
- Molecular symmetry
- Space group
- X-ray diffraction
- Bravais lattice
- Infrared spectroscopy of metal carbonyls
References
- ^ Conway, John H.; Smith, Derek A. (2003). On quaternions and octonions: their geometry, arithmetic, and symmetry. A K Peters. ISBN 978-1-56881-134-5.
- The Crystallographic Space groups in Geometric algebra, D. Hestenes and J. Holt, Journal of Mathematical Physics. 48, 023514 (2007) (22 pages)
Further reading
- H. S. M. Coxeter (1995), F. Arthur Sherk; Peter McMullen; Anthony C. Thompson; Asia Ivic Weiss (eds.), Kaleidoscopes: Selected Writings of H. S. M. Coxeter, Wiley-Interscience Publication, ISBN 978-0-471-01003-6
- (Paper 23) H. S. M. Coxeter, Regular and Semi-Regular Polytopes II,
- H. S. M. Coxeter; W. O. J. Moser (1980), Generators and Relations for Discrete Groups (4th ed.), New York: Springer-Verlag
- N. W. Johnson (2018), "Chapter 11: Finite symmetry groups", Geometries and Transformations
External links
- Web-based point group tutorial (needs Java and Flash)
- Subgroup enumeration (needs Java)
- The Geometry Center: 2.1 Formulas for Symmetries in Cartesian Coordinates (two dimensions)
- The Geometry Center: 10.1 Formulas for Symmetries in Cartesian Coordinates (three dimensions)