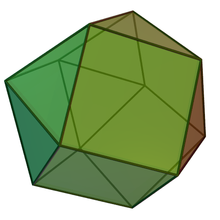
| Triangular orthobicupola | |
|---|---|
 | |
| Type | Johnson J26 – J27 – J28 |
| Faces | 2+6 triangles 6 squares |
| Edges | 24 |
| Vertices | 12 |
| Vertex configuration | 6(3.4) 6(3.4.3.4) |
| Symmetry group | D3h |
| Dual polyhedron | Trapezo-rhombic dodecahedron |
| Properties | convex |
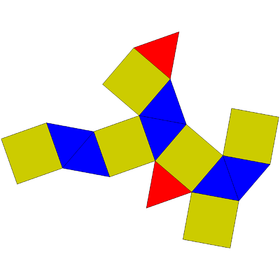
| Net | |
 | |
In geometry, the triangular orthobicupola is one of the Johnson solids (J27). As the name suggests, it can be constructed by attaching two triangular cupolas (J3) along their bases. It has an equal number of squares and triangles at each vertex; however, it is not vertex-transitive. It is also called an anticuboctahedron, twisted cuboctahedron or disheptahedron. It is also a canonical polyhedron.
A Johnson solid is one of 92 strictly convex polyhedra that is composed of regular polygon faces but are not uniform polyhedra (that is, they are not Platonic solids, Archimedean solids, prisms, or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.
The triangular orthobicupola is the first in an infinite set of orthobicupolae.
Construction
The triangular orthobicupola can be constructed by attaching two triangular cupolas onto their bases. Similar to the cuboctahedron, which would be known as the triangular gyrobicupola, the difference is that the two triangular cupolas that make up the triangular orthobicupola are joined so that pairs of matching sides abut (hence, "ortho"); the cuboctahedron is joined so that triangles abut squares and vice versa. Given a triangular orthobicupola, a 60-degree rotation of one cupola before the joining yields a cuboctahedron. Hence, another name for the triangular orthobicupola is the anticuboctahedron. Because the triangular orthobicupola has the property of convexity and its faces are regular polygons—eight equilateral triangles and six squares—it is categorized as a Johnson solid. It is enumerated as the twenty-seventh Johnson solid
Properties
The surface area and the volume of a triangular orthobicupola are the same as those with cuboctahedron. Its surface area can be obtained by summing all of its polygonal faces, and its volume is by slicing it off into two triangular cupolas and adding their volume. With edge length , they are:
The dual polyhedron of a triangular orthobicupola is the trapezo-rhombic dodecahedron. It has 6 rhombic and 6 trapezoidal faces, and is similar to the rhombic dodecahedron.
References
- Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603.
- Ogievetsky, O.; Shlosman, S. (2021). "Platonic compounds and cylinders". In Novikov, S.; Krichever, I.; Ogievetsky, O.; Shlosman, S. (eds.). Integrability, Quantization, and Geometry: II. Quantum Theories and Algebraic Geometry. American Mathematical Society. p. 477. ISBN 978-1-4704-5592-7.
- ^ Becker, David A. (2012). "A Peculiarly Cerebroid Convex Zygo-Dodecahedron is an Axiomatically Balanced "House of Blues": The Circle of Fifths to the Circle of Willis to Cadherin Cadenzas". Symmetry. 4 (4): 644–666. Bibcode:2012Symm....4..644B. doi:10.3390/sym4040644.
- ^ Berman, M. (1971). "Regular-faced convex polyhedra". Journal of the Franklin Institute. 291 (5): 329–352. doi:10.1016/0016-0032(71)90071-8. MR 0290245.
- Francis, D. (2013). "Johnson solids & their acronyms". Word Ways. 46 (3): 177.

 and the
and the  of a triangular orthobicupola are the same as those with cuboctahedron. Its surface area can be obtained by summing all of its polygonal faces, and its volume is by slicing it off into two triangular cupolas and adding their volume. With edge length
of a triangular orthobicupola are the same as those with cuboctahedron. Its surface area can be obtained by summing all of its polygonal faces, and its volume is by slicing it off into two triangular cupolas and adding their volume. With edge length  , they are:
, they are:
