| Revision as of 02:33, 1 February 2006 editSalix alba (talk | contribs)Edit filter managers, Administrators26,099 edits Major reworking of other diagrams← Previous edit | Latest revision as of 21:24, 23 December 2024 edit undoMeno25 (talk | contribs)Autopatrolled, Administrators215,965 edits →See also | ||
| Line 1: | Line 1: | ||
| {{Short description|Diagram that shows all possible logical relations between a collection of sets}} | |||
| '''Venn diagrams''' are illustrations used in the branch of mathematics known as ]. They are used to show the ] or ] relationship between different groups of things (sets). | |||
| {{Use dmy dates|date=May 2020|cs1-dates=y}} | |||
| {{Use list-defined references|date=January 2022}} | |||
| ]s shared by the ] (upper left), ] (upper right), and ] (bottom) alphabets]] | |||
| {{Probability fundamentals}} | |||
| A '''Venn diagram''' is a widely used ] style that shows the logical relation between ], popularized by ] (1834–1923) in the 1880s. The diagrams are used to teach elementary ], and to illustrate simple set relationships in ], ], ], ] and ]. A Venn diagram uses simple closed curves drawn on a plane to represent sets. Very often, these curves are circles or ellipses. | |||
| A Venn diagram shows all the logical relations between the sets. ]s are similar, but do not need to show all the relations. | |||
| Similar ideas had been proposed before Venn such as by ] in 1712 (''Nucleus Logicoe Wiesianoe'') and ] ('']'') in 1768. The idea was popularised by Venn in ''Symbolic Logic'', Chapter V "Diagrammatic Representation", published in 1881. | |||
| == Examples == | |||
| == Details == | |||
| ] | |||
| {{anchor|Primary|Simple|Cylindrical|Metric|2|3}}A Venn diagram, also called a ''set diagram'' or ''logic diagram'', shows ''all'' possible logical relations between a finite collection of different sets. These diagrams depict ]s as points in the plane, and sets as regions inside closed curves. A Venn diagram consists of multiple overlapping closed curves, usually circles, each representing a set. The points inside a curve labelled ''S'' represent elements of the set ''S'', while points outside the boundary represent elements not in the set ''S''. This lends itself to intuitive visualizations; for example, the set of all elements that are members of both sets ''S'' and ''T'', denoted ''S'' ∩ ''T'' and read "the intersection of ''S'' and ''T''", is represented visually by the area of overlap of the regions ''S'' and ''T''.<ref name="Peil_2020"/> | |||
| In Venn diagrams, the curves are overlapped in every possible way, showing all possible relations between the sets. They are thus a special case of ]s, which do not necessarily show all relations. Venn diagrams were conceived around 1880 by John Venn. They are used to teach elementary set theory, as well as illustrate simple set relationships in probability, logic, statistics, linguistics, and computer science. | |||
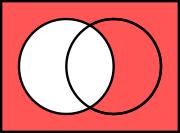
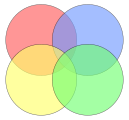
| The orange circle (set ''A'') might represent, for example, all living creatures which are two-legged. The blue circle, (set ''B'') might represent all living creatures which can fly. The area where the blue and orange circles overlap (which is called the ''intersection'') contains all living creatures which both can fly '''and''' which have two legs - for example, parrots. (Imagine each separate type of creature as a ] somewhere in the diagram). | |||
| A Venn diagram in which the area of each shape is proportional to the number of elements it contains is called an '''area-proportional''' (or '''scaled''') '''Venn diagram'''. | |||
| Humans and penguins would be in the orange circle, in the part which does not overlap with the blue circle. Mosquitos have six legs, and fly, so the point for mosquitos would be in the part of the blue circle which does not overlap with the orange one. Things which do not have two legs and cannot fly (for example, whales and rattlesnakes) would all be represented by points outside both circles. Technically, the Venn diagram above can be interpreted as "the relationships of set ''A'' and set ''B'' which may have some (but not all) elements in common". | |||
| ==Example== | |||
| The combined area of sets ''A'' and ''B'' is called the ''union'' of sets ''A'' and ''B''. The union in this case contains all things which either have two legs, or which fly, or both. That the circles overlap implies that the union of the two sets is not empty - that, in fact, there '''are''' creatures that are in '''both''' the orange and blue circles. | |||
| ] | |||
| This example involves two sets of creatures, represented here as colored circles. The orange circle represents all types of creatures that have two legs. The blue circle represents creatures that can fly. Each separate type of creature can be imagined as a point somewhere in the diagram. Living creatures that have two legs ''and'' can fly—for example, parrots—are then in both sets, so they correspond to points in the region where the blue and orange circles overlap. This overlapping region would only contain those elements (in this example, creatures) that are members of both the orange set (two-legged creatures) and the blue set (flying creatures). | |||
| Humans and penguins are bipedal, and so are in the orange circle, but since they cannot fly, they appear in the left part of the orange circle, where it does not overlap with the blue circle. Mosquitoes can fly, but have six, not two, legs, so the point for mosquitoes is in the part of the blue circle that does not overlap with the orange one. Creatures that are neither two-legged nor able to fly (for example, whales and spiders) would all be represented by points outside both circles. | |||
| Sometimes a rectangle, (called the ''Universe'') is drawn around the Venn diagram to show the space of all possible things. As mentioned above, a whale would be represented by a point that is not in the union, but is in the Universe (of living creatures, or of all things, depending on how one chose to define the Universe for a particular diagram). | |||
| The combined region of the two sets is called their '']'', denoted by {{nowrap|A ∪ B}}, where A is the orange circle and B the blue. The union in this case contains all living creatures that either are two-legged or can fly (or both). The region included in both A and B, where the two sets overlap, is called the '']'' of A and B, denoted by {{nowrap|A ∩ B}}. | |||
| ==Similar diagrams== | |||
| == {{anchor|Symmetric|n}}History == | |||
| === Euler diagrams === | |||
| ] window with Venn diagram in ]]] | |||
| ] | |||
| Venn diagrams were introduced in 1880 by ] in a paper entitled "On the Diagrammatic and Mechanical Representation of Propositions and Reasonings"<ref name="Venn_2014"/> in the ''Philosophical Magazine and Journal of Science'',<ref name="PM"/> about the different ways to represent ]s by diagrams.<ref name="Venn1880_1"/><ref name="Venn1880_2"/><ref name="Sandifer2003"/> The use of these types of diagrams in ], according to ] and Mark Weston, predates Venn but are "rightly associated" with him as he "comprehensively surveyed and formalized their usage, and was the first to generalize them".<ref name="Ruskey2005"/> | |||
| ]s are similar to Venn Diagrams, but do not need all the possible relations. In the diagram on the right, one set is entirely inside another one. Let's say that set ''A'' is all the different types of cheeses that can be found in the world, and set ''B'' is all the foodstuffs that can be found in the world. From the diagram, you can see that all cheeses are foodstuffs, but not all foodstuffs are cheeses. Further, set ''C'' (let's say, things made of metal) has no elements (members of the set) in common with set ''B'', and from this we can logically assert that no cheeses are metal things (and vice versa). The diagram can be interpreted as: | |||
| :set ''A'' is a proper subset of set ''B'', but set ''C'' has no elements in common with set ''B''. | |||
| Or, as a ] | |||
| * All ''A''s are ''B''s | |||
| * No ''C''s are ''B''s | |||
| * Therefore No ''C''s are ''A''s. | |||
| * Therefore No ''A''s are ''C''s. | |||
| Diagrams of overlapping circles representing unions and intersections were introduced by Catalan philosopher ] (c. 1232–1315/1316) in the 13th century, who used them to illustrate combinations of basic principles.<ref name="Baron_1969" /> ] (1646–1716) produced similar diagrams in the 17th century (though much of this work was unpublished), as did Johann Christian Lange in a work from 1712 describing ]'s contributions to logic.<ref name="Leibniz_1690" /><ref name="Baron_1969" /> ]s, which are similar to Venn diagrams but don't necessarily contain all possible unions and intersections, were first made prominent by mathematician ] in the 18th century.<ref group="note" name="NB_1"/><ref name="Venn1881"/><ref name="Gailand_1967"/> | |||
| === Johnston diagram === | |||
| Venn did not use the term "Venn diagram" and referred to the concept as "Eulerian Circles".<ref name="Sandifer2003"/> He became acquainted with Euler diagrams in 1862 and wrote that Venn diagrams did not occur to him "till much later", while attempting to adapt Euler diagrams to ].<ref name="Maths Today">{{cite magazine|title=The Venn Behind the Diagram|last=Verburgt|first=Lukas M.|volume=59|issue=2|date=April 2023|pages=53–55|magazine=Mathematics Today|publisher=]}}</ref> In the opening sentence of his 1880 article Venn wrote that Euler diagrams were the only diagrammatic representation of logic to gain "any general acceptance".<ref name="Venn1880_1"/><ref name="Venn1880_2"/> | |||
| ]s are used to illustrate statements in ] such as ''A and not B'' and are a visual way of illustrating ]s. They can be identical in appearance to Venn diagrams, but do not represent sets of object. | |||
| Venn viewed his diagrams as a pedagogical tool, analogous to verification of physical concepts through experiment. As an example of their applications, he noted that a three-set diagram could show the ]: 'All ''A'' is some ''B''. No ''B'' is any ''C''. Hence, no ''A'' is any ''C''.'<ref name="Maths Today"/> | |||
| ===Peirce diagrams=== | |||
| '''Peirce diagrams''', devised by ], are extensions to Venn diagrams which include information on existential statements, disjunctive information, probabilities, and relations. . | |||
| ] (Lewis Carroll) includes "Venn's Method of Diagrams" as well as "Euler's Method of Diagrams" in an "Appendix, Addressed to Teachers" of his book ''Symbolic Logic'' (4th edition published in 1896). The term "Venn diagram" was later used by ] in 1918, in his book ''A Survey of Symbolic Logic''.<ref name="Ruskey2005"/><ref name="Lewis1918"/> | |||
| ==Extensions to higher numbers of sets== | |||
| Venn was keen to find ‘symmetrical figures…elegant in themselves’ and he | |||
| devised a four set diagram using ]. | |||
| In the 20th century, Venn diagrams were further developed. ] showed, in 1963, that the existence of an ''n''-Venn diagram with ''n''-fold ] implied that ''n'' was a ].<ref name="Henderson_1963"/> He also showed that such symmetric Venn diagrams exist when ''n'' is five or seven. In 2002, Peter Hamburger found symmetric Venn diagrams for ''n'' = 11 and in 2003, Griggs, Killian, and Savage showed that symmetric Venn diagrams exist for all other primes. These combined results show that rotationally symmetric Venn diagrams exist, if and only if ''n'' is a prime number.<ref name="Ruskey_2006"/> | |||
| ===Edward-Venn diagrams=== | |||
| {| align="right" | |||
| | ] | |||
| | ] | |||
| |- | |||
| | ] | |||
| | ] | |||
| |} | |||
| Venn diagrams typically have three sets. ] generalised the concept to higher numbers of sets. This was achieved by projecting the Venn diagram onto a ]. Three sets can be easily represented by taking three hemispheres at right angles (''x''≥0, ''y''≥0 and ''z''≥0). A fourth sets can be represented by taking curves similar to the seam on a tennis ball which winds up and down around the equator. The resulting sets can then be projected back to the plane to give ''cogwheel'' diagrams with increasing numbers of teeth. | |||
| These diagrams were devised while designing a ] window in memoriam to Venn. | |||
| Venn diagrams and Euler diagrams were incorporated as part of instruction in set theory, as part of the ] movement in the 1960s. Since then, they have also been adopted in the curriculum of other fields such as reading.<ref name="Strategies"/> | |||
| ===Other diagrams=== | |||
| ==Popular culture== | |||
| Edward-Venn diagrams are topologically equivalent to diagrams devised by ] which were based around intersecting ]s with increasing numbers of sides. They are also 2-dimensional representations of ]s. | |||
| Venn diagrams have been commonly used in ]s.<ref>{{cite news |last1=Leo |first1=Alex |title=Jesus, Karaoke, And Serial Killers: The Funniest Venn Diagrams The Web Has To Offer |url=https://www.huffpost.com/entry/funniest-venn-diagrams-th_n_347552 |access-date=2 October 2024 |work=Huffpost |date=March 18, 2010}}</ref> At least one politician has been mocked for misusing Venn diagrams.<ref>{{cite news |last1=Moran |first1=Lee |title=Scott Walker Gets Mercilessly Mocked By Twitter Users Over Venn Diagram Fail |url=https://www.huffpost.com/entry/scott-walker-venn-diagram-meme_n_5c14e6d5e4b05d7e5d8258cc |access-date=2 October 2024 |work=HuffPost |date=December 15, 2018}}</ref> | |||
| ==Overview== | |||
| Smith devised similar ''n''-set diagrams using ] curves with equations ''y''=sin(2<sup>''i''</sup>''x'')/2<sup>''i''</sup>, 0≤i≤''n''-2. | |||
| {{See also|Set (mathematics)#Basic operations}} | |||
| {{Gallery|File:Venn0001.svg|] of two sets <math>~A \cap B</math> | |||
| |File:Venn0111.svg|] of two sets <math>~A \cup B</math> | |||
| |File:Venn0110.svg|] of two sets <math>A~\triangle~B</math> | |||
| |File:Venn0010.svg|] of ''A'' (left) in ''B'' (right) <math>A^c \cap B~=~B \setminus A</math> | |||
| |File:Venn1010.svg|] of A in U <math>A^c~=~U \setminus A</math> | |||
| }} | |||
| A Venn diagram is constructed with a collection of simple closed curves drawn in a plane. According to Lewis,<ref name="Lewis1918"/> the "principle of these diagrams is that classes be represented by regions in such relation to one another that all the possible logical relations of these classes can be indicated in the same diagram. That is, the diagram initially leaves room for any possible relation of the classes, and the actual or given relation, can then be specified by indicating that some particular region is null or is not-null".<ref name="Lewis1918"/>{{rp|157}} | |||
| Venn diagrams normally comprise overlapping ]s. The interior of the circle symbolically represents the elements of the set, while the exterior represents elements that are not members of the set. For instance, in a two-set Venn diagram, one circle may represent the group of all ]en objects, while the other circle may represent the set of all tables. The overlapping region, or ''intersection'', would then represent the set of all wooden tables. Shapes other than circles can be employed as shown below by Venn's own higher set diagrams. Venn diagrams do not generally contain information on the relative or absolute sizes (]) of sets. That is, they are ] diagrams generally not drawn to scale. | |||
| Samuel Dodgson (a.k.a. ]) devised a five set diagram. | |||
| Venn diagrams are similar to Euler diagrams. However, a Venn diagram for ''n'' component sets must contain all 2<sup>''n''</sup> hypothetically possible zones, that correspond to some combination of inclusion or exclusion in each of the component sets.<ref name="Weisstein_2020"/> Euler diagrams contain only the actually possible zones in a given context. In Venn diagrams, a shaded zone may represent an empty zone, whereas in an Euler diagram, the corresponding zone is missing from the diagram. For example, if one set represents ''dairy products'' and another ''cheeses'', the Venn diagram contains a zone for cheeses that are not dairy products. Assuming that in the context ''cheese'' means some type of dairy product, the Euler diagram has the cheese zone entirely contained within the dairy-product zone—there is no zone for (non-existent) non-dairy cheese. This means that as the number of contours increases, Euler diagrams are typically less visually complex than the equivalent Venn diagram, particularly if the number of non-empty intersections is small.<ref name="Kent_2004"/> | |||
| The difference between Euler and Venn diagrams can be seen in the following example. Take the three sets: | |||
| ==Origins== | |||
| * <math>A = \{1,\, 2,\, 5\}</math> | |||
| * <math>B = \{1,\, 6\}</math> | |||
| * <math>C = \{4,\, 7\}</math> | |||
| The Euler and the Venn diagram of those sets are: | |||
| ] was a ] ] ] and ] who introduced the Venn diagram in ]. | |||
| <gallery widths="300"> | |||
| A stained glass window in ], ], commemorates his invention. | |||
| File:3-set Euler diagram.svg|Euler diagram | |||
| File:3-set Venn diagram.svg|Venn diagram | |||
| </gallery> | |||
| =={{anchor|Elegant|4|5|6|7|8|9|10|11}}Extensions to higher numbers of sets== | |||
| ==References== | |||
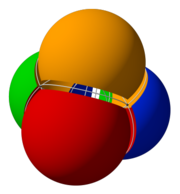
| Venn diagrams typically represent two or three sets, but there are forms that allow for higher numbers. Shown below, four intersecting spheres form the highest order Venn diagram that has the symmetry of a ] and can be visually represented. The 16 intersections correspond to the vertices of a ] (or the cells of a ], respectively). | |||
| * ] ''Another Fine Math You've Got Me Into'' 1992 ch4 | |||
| * A.W.F. Edwards. ''Cogwheels of the Mind: the story of Venn diagrams'', Johns Hopkins University Press, Baltimore and London, 2004. | |||
| {|class="wikitable" style="text-align:center; width: 100%;" | |||
| * | |||
| | style="vertical-align:top;"| ] | |||
| | style="vertical-align:top;"| ]<br> | |||
| ]]]] | |||
| | style="vertical-align:top;"| ]<br> | |||
| ]]]]]] | |||
| | style="vertical-align:top;"| ]<br> | |||
| ]]]] | |||
| | style="vertical-align:top;"| ] | |||
| |} | |||
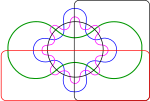
| For higher numbers of sets, some loss of symmetry in the diagrams is unavoidable. Venn was keen to find "symmetrical figures ... elegant in themselves,"<ref name="Venn1881"/> that represented higher numbers of sets, and he devised an ''elegant'' four-set diagram using ]s (see below). He also gave a construction for Venn diagrams for ''any'' number of sets, where each successive curve that delimits a set interleaves with previous curves, starting with the three-circle diagram. | |||
| <gallery widths="200px"><!---perrow=3--> | |||
| Image:Venn4.svg|Venn's construction for four sets (use ] to compute, the digit 1 means in the set, and the digit 0 means not in the set) | |||
| Image:Venn5.svg|Venn's construction for five sets | |||
| Image:Venn6.svg|Venn's construction for six sets | |||
| Image:Venn's four ellipse construction.svg|Venn's four-set diagram using ellipses | |||
| Image:CirclesN4xb.svg|'''Non-example:''' This ] is {{em|not}} a Venn diagram for four sets as it has only 14 regions as opposed to 2<sup>4</sup> = 16 regions (including the white region); there is no region where only the yellow and blue, or only the red and green circles meet. | |||
| File:Symmetrical 5-set Venn diagram.svg|Five-set Venn diagram using congruent ellipses in a five-fold ] arrangement devised by ]. Labels have been simplified for greater readability; for example, '''A''' denotes {{nowrap|'''A''' ∩ '''B'''<sup>c</sup> ∩ '''C'''<sup>c</sup> ∩ '''D'''<sup>c</sup> ∩ '''E'''<sup>c</sup>}}, while '''BCE''' denotes {{nowrap|'''A'''<sup>c</sup> ∩ '''B''' ∩ '''C''' ∩ '''D'''<sup>c</sup> ∩ '''E'''}}. | |||
| File:6-set_Venn_diagram.svg|Six-set Venn diagram made of only triangles | |||
| </gallery> | |||
| ==={{anchor|Edwards-Venn|Adelaide|Hamilton|Massey|Victoria|Palmerston North|Manawatu}}Edwards–Venn diagrams=== | |||
| <gallery widths="150px"> | |||
| Image:Venn-three.svg| Three sets | |||
| Image:Edwards-Venn-four.svg| Four sets | |||
| Image:Edwards-Venn-five.svg| Five sets | |||
| Image:Edwards-Venn-six.svg| Six sets | |||
| </gallery> | |||
| ] constructed a series of Venn diagrams for higher numbers of sets by segmenting the surface of a sphere, which became known as Edwards–Venn diagrams.<ref name="Edwards_2004"/> For example, three sets can be easily represented by taking three hemispheres of the sphere at right angles (''x'' = 0, ''y'' = 0 and ''z'' = 0). A fourth set can be added to the representation, by taking a curve similar to the seam on a tennis ball, which winds up and down around the equator, and so on. The resulting sets can then be projected back to a plane, to give ''cogwheel'' diagrams with increasing numbers of teeth—as shown here. These diagrams were devised while designing a ] window in memory of Venn.<ref name="Edwards_2004"/> | |||
| ===Other diagrams=== | |||
| Edwards–Venn diagrams are ] to diagrams devised by ], which were based around intersecting ]s with increasing numbers of sides. They are also two-dimensional representations of ]s. | |||
| ] devised similar ''n''-set diagrams using ] curves<ref name="Edwards_2004"/> with the series of equations | |||
| <math display="block">y_i = \frac{\sin\left(2^i x\right)}{2^i} \text{ where } 0 \leq i \leq n-1 \text{ and } i \in \mathbb{N}. </math> | |||
| ] (also known as Lewis Carroll) devised a five-set diagram known as ]. Joaquin and Boyles, on the other hand, proposed supplemental rules for the standard Venn diagram, in order to account for certain problem cases. For instance, regarding the issue of representing singular statements, they suggest to consider the Venn diagram circle as a representation of a set of things, and use ] and set theory to treat categorical statements as statements about sets. Additionally, they propose to treat singular statements as statements about ]. So, for example, to represent the statement "a is F" in this retooled Venn diagram, a small letter "a" may be placed inside the circle that represents the set F.<ref name="Joaquin_2017"/> | |||
| =={{anchor|Johnston}}Related concepts== | |||
| ] | |||
| Venn diagrams correspond to ]s for the propositions <math>x\in A</math>, <math>x\in B</math>, etc., in the sense that each region of Venn diagram corresponds to one row of the truth table.<ref name="Grimaldi_2004"/><ref name="Johnson_2001"/> This type is also known as Johnston diagram. Another way of representing sets is with John F. Randolph's ]s. | |||
| ==See also== | ==See also== | ||
| * ] (by ]) | |||
| * ] | |||
| * ] | * ] | ||
| * ] | * ] | ||
| * ] (and as further derivation ] and ]) | |||
| * ] | |||
| * ] – A stereographic projection of a regular octahedron makes a three-set Venn diagram, as three orthogonal great circles, each dividing space into two halves. | |||
| * ] | |||
| * ] | |||
| * ]s and ]s are similar to Venn diagrams. | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| ==Notes== | |||
| == External links == | |||
| {{Reflist|group="note"|refs= | |||
| {{commons|Category:Venn diagram}} | |||
| <ref group="note" name="NB_1">In Euler's ''Lettres à une princesse d'Allemagne sur divers sujets de physique et de philosophie'' (Saint Petersburg, Russia: l'Academie Impériale des Sciences, 1768), volume 2, In Venn's article, however, he suggests that the diagrammatic idea predates Euler, and is attributable to ] or Johann Christian Lange (in Lange's book ''Nucleus Logicae Weisianae'' (1712)).</ref> | |||
| * | |||
| }} | |||
| * - interactive Johnston diagram | |||
| * at ] | |||
| * | |||
| * at ] | |||
| * at ] | |||
| ==References== | |||
| === Tools for making Venn Diagrams === | |||
| {{Reflist|refs= | |||
| * ] | |||
| <ref name="Lewis1918">{{cite book |author-link=Clarence Irving Lewis |author-first=Clarence Irving |author-last=Lewis |date=1918 |url=https://archive.org/details/asurveyofsymboli00lewiuoft |title=A Survey of Symbolic Logic |location=Berkeley |publisher=]}}</ref> | |||
| * | |||
| <ref name="Sandifer2003">{{cite web |author-first=Ed |author-last=Sandifer |date=2003 |title=How Euler Did It |url=http://www.maa.org/editorial/euler/How%20Euler%20Did%20It%2003%20Venn%20Diagrams.pdf |publisher=] (MAA) |work=MAA Online |access-date=2009-10-26}}</ref> | |||
| * | |||
| <ref name="Ruskey2005">{{cite journal |author-last1=Ruskey |author-first1=Frank |author-link1=Frank Ruskey |author-last2=Weston |author-first2=Mark |title=A Survey of Venn Diagrams |journal=] |date=2005-06-18 |url=http://www.combinatorics.org/files/Surveys/ds5/VennEJC.html}}</ref> | |||
| * | |||
| <ref name="Gailand_1967">{{cite book |title=The Logic Diagram |author-first=Gailand |author-last=Mac Queen |date=October 1967 |type=Thesis |publisher=] |url=https://macsphere.mcmaster.ca/bitstream/11375/10794/1/fulltext.pdf |access-date=2017-04-14 |url-status=dead |archive-url=https://web.archive.org/web/20170414163921/https://macsphere.mcmaster.ca/bitstream/11375/10794/1/fulltext.pdf |archive-date=2017-04-14}} (NB. Has a detailed history of the evolution of logic diagrams including but not limited to the Venn diagram.)</ref> | |||
| <ref name="Venn1880_1">{{cite journal |author-last=Venn |author-first=John |author-link=John Venn |title=I. On the Diagrammatic and Mechanical Representation of Propositions and Reasonings |journal=] |volume=10 |issue=59 |date=July 1880 |series=5 |doi=10.1080/14786448008626877 |pages=1–18 |url=https://www.cis.upenn.edu/~bhusnur4/cit592_fall2014/venn%20diagrams.pdf |url-status=live |archive-url=https://web.archive.org/web/20170516204620/https://www.cis.upenn.edu/~bhusnur4/cit592_fall2014/venn%20diagrams.pdf |archive-date=2017-05-16}} </ref> | |||
| <ref name="Venn1880_2">{{cite journal |author-last=Venn |author-first=John |author-link=John Venn |date=1880 |url=https://archive.org/stream/proceedingsofcam4188083camb#page/47/mode/1up |title=On the employment of geometrical diagrams for the sensible representations of logical propositions |journal=] |volume=4 |pages=47–59}}</ref> | |||
| <ref name="Baron_1969">{{cite journal |author-last=Baron |author-first=Margaret E.|author-link=Margaret Baron |title=A Note on The Historical Development of Logic Diagrams |journal=] |volume=53 |issue=384 |pages=113–125 |date=May 1969 |jstor=3614533 |doi=10.2307/3614533|s2cid=125364002 }}</ref> | |||
| <ref name="Henderson_1963">{{cite journal |author-last=Henderson |author-first=David Wilson |author-link=David Wilson Henderson |title=Venn diagrams for more than four classes |journal=] |volume=70 |issue=4 |pages=424–426 |date=April 1963 |jstor=2311865 |doi=10.2307/2311865}}</ref> | |||
| <ref name="Ruskey_2006">{{cite journal |author-last1=Ruskey |author-first1=Frank |author-link1=Frank Ruskey |author-first2=Carla D. |author-last2=Savage |author-link2=Carla Savage |author-first3=Stan |author-last3=Wagon |author-link3=Stan Wagon |date=December 2006 |title=The Search for Simple Symmetric Venn Diagrams |journal=] |volume=53 |issue=11 |pages=1304–1311 |url=http://www.ams.org/notices/200611/fea-wagon.pdf}}</ref> | |||
| <ref name="Venn1881">{{cite book |author-first=John |author-last=Venn |author-link=John Venn |title=Symbolic logic |date=1881 |publisher=] |page= |url=https://archive.org/details/symboliclogic00venngoog |access-date=2013-04-09}}</ref> | |||
| <ref name="Edwards_2004">{{cite book |title=Cogwheels of the Mind: The Story of Venn Diagrams |author-first=Anthony William Fairbank |author-last=Edwards |author-link=Anthony William Fairbank Edwards<!-- |contribution=Foreword |contributor-first=Ian |contributor-last=Stewart --> |publisher=] |date=2004 |isbn=978-0-8018-7434-5 |location=Baltimore, Maryland, USA |page=65 |url=https://books.google.com/books?id=7_0Thy4V3JIC&pg=PA65}}.</ref> | |||
| <ref name="Grimaldi_2004">{{cite book |author-last=Grimaldi |author-first=Ralph P. |author-link=Ralph Grimaldi |title=Discrete and combinatorial mathematics |publisher=] |location=Boston |date=2004 |page=143 |isbn=978-0-201-72634-3}}</ref> | |||
| <ref name="Johnson_2001">{{cite book |author-last=Johnson |author-first=David L. |title=Elements of logic via numbers and sets |publisher=] |location=Berlin, Germany |date=2001 |series=Springer Undergraduate Mathematics Series |page= |isbn=978-3-540-76123-5 |chapter=3.3 Laws |chapter-url=https://books.google.com/books?id=8KtRMofBKc0C&pg=PA62 |url=https://archive.org/details/elementsoflogicv0000john/page/62 }}</ref> | |||
| <ref name="Kent_2004">{{cite web |title=Euler Diagrams 2004: Brighton, UK: September 22–23 |url=http://www.cs.kent.ac.uk/events/conf/2004/euler/eulerdiagrams.html |date=2004 |publisher=Reasoning with Diagrams project, University of Kent |access-date=2008-08-13}}</ref> | |||
| <ref name="Strategies">{{cite web |url=http://www.readingquest.org/strat/venn.html |title=Strategies for Reading Comprehension Venn Diagrams |access-date=2009-06-20 |archive-url=https://web.archive.org/web/20090429093334/http://readingquest.org/strat/venn.html |archive-date=2009-04-29 |url-status=dead}}</ref> | |||
| <ref name="Leibniz_1690">{{cite book |author-first=Gottfried Wilhelm |author-last=Leibniz |author-link=Gottfried Wilhelm Leibniz |chapter=De Formae Logicae per linearum ductus |orig-date=ca. 1690 |date=1903 |editor-first=Louis |editor-last=Couturat |editor-link=Louis Couturat |title=Opuscules et fragmentes inedits de Leibniz |language=la |pages=292–321}}</ref> | |||
| <ref name="Joaquin_2017">{{cite journal |author-last1=Joaquin |author-first1=Jeremiah Joven |author-last2=Boyles |author-first2=Robert James M. |date=June 2017 |title=Teaching Syllogistic Logic via a Retooled Venn Diagrammatical Technique |journal=] |volume=40 |issue=2 |doi=10.5840/teachphil201771767 |pages=161–180 |url=https://www.pdcnet.org/teachphil/content/teachphil_2017_0040_0002_0161_0180 |access-date=2020-05-12 |url-status=live |archive-url=https://web.archive.org/web/20181121120401/https://www.pdcnet.org/teachphil/content/teachphil_2017_0040_0002_0161_0180 |archive-date=2018-11-21}}</ref> | |||
| <ref name="Peil_2020">{{cite web |title=Intersection of Sets |url=http://web.mnstate.edu/peil/MDEV102/U1/S3/Intersection4.htm |access-date=2020-09-05 |website=web.mnstate.edu |archive-date=2020-08-04 |archive-url=https://web.archive.org/web/20200804163657/http://web.mnstate.edu/peil/MDEV102/U1/S3/Intersection4.htm |url-status=dead }}</ref> | |||
| <ref name="Venn_2014">{{cite web |author-last=Venn |author-first=John |title=On the Diagrammatic and Mechanical Representation of Propositions and Reasonings |url=https://www.cis.upenn.edu/~bhusnur4/cit592_fall2014/venn%20diagrams.pdf |website=Penn Engineering}}</ref> | |||
| <ref name="PM">{{cite news |title=The Philosophical Magazine: A Journal of Theoretical Experimental and Applied Physics |language=en |work=] |url=https://www.tandfonline.com/toc/tphm18/current |access-date=2021-08-06}}</ref> | |||
| <ref name="Weisstein_2020">{{cite web |author-last=Weisstein |author-first=Eric W. |title=Venn Diagram |url=https://mathworld.wolfram.com/VennDiagram.html |access-date=2020-09-05 |website=mathworld.wolfram.com |language=en}}</ref> | |||
| }} | |||
| ==Further reading== | |||
| === Tools for making Euler Diagrams === | |||
| {{refbegin}} | |||
| * | |||
| * {{cite web |author-first1=Ebadollah S. |author-last1=Mahmoodian |author-link1=Ebadollah S. Mahmoodian |author-first2=M. |author-last2=Rezaie |author-first3=F. |author-last3=Vatan |title=Generalization of Venn Diagram |work=Eighteenth Annual Iranian Mathematics Conference |location=Tehran and Isfahan, Iran |date=March 1987 |url=http://sharif.ir/~emahmood/papers/Generalized-Venn-Diagram1987.pdf |access-date=2017-05-01 |url-status=dead |archive-url=https://web.archive.org/web/20170501202223/http://sharif.ir/~emahmood/papers/Generalized-Venn-Diagram1987.pdf |archive-date=1 May 2017 }} | |||
| * {{cite journal |title=Venn diagrams for many sets |author-first=Anthony William Fairbank |author-last=Edwards |author-link=Anthony William Fairbank Edwards |journal=] |volume=121 |number=1646 |date=1989-01-07 |pages=51–56}} | |||
| * {{cite book |title=Coding for Digital Recording |chapter=4.10. Hamming distance |author-first=John |author-last=Watkinson |publisher=] |location=Stoneham, MA, USA |date=1990 |isbn=978-0-240-51293-8 |pages=94–99, foldout in backsleeve}} (NB. The book comes with a 3-page foldout of a seven-bit cylindrical Venn diagram.) | |||
| * {{cite book |author-first=Ian |author-last=Stewart |author-link=Ian Stewart (mathematician) |chapter=Chapter 4. Cogwheels of the Mind |chapter-url=https://books.google.com/books?id=u5GPE97-ZhsC&pg=PA51 |title=Another Fine Math You've Got Me Into |publisher=] (]) |edition=reprint of 1st |location=Mineola, New York, USA |date=June 2003 |orig-date=1992 |isbn=978-0-486-43181-9 |pages=51–64}} | |||
| * {{cite book |author-last=Glassner |author-first=Andrew |author-link=Andrew Glassner |title=Morphs, Mallards, and Montages: Computer-Aided Imagination |date=2004 |publisher=] |location=Wellesley, MA, USA |isbn=978-1568812311 |pages=161–184 |chapter=Venn and Now}} | |||
| * {{anchor|Newroz}}{{cite web |author-first1=Khalegh |author-last1=Mamakani |author-first2=Frank |author-last2=Ruskey |author-link2=Frank Ruskey |date=2012-07-27 |title=A New Rose: The First Simple Symmetric 11-Venn Diagram |arxiv=1207.6452 |url=http://webhome.cs.uvic.ca/~ruskey/Publications/Venn11/Venn11.html |access-date=2017-05-01 |url-status=live |archive-url=https://web.archive.org/web/20170501204303/http://webhome.cs.uvic.ca/~ruskey/Publications/Venn11/Venn11.html |archive-date=2017-05-01 |bibcode=2012arXiv1207.6452M |volume=1207 |pages=6452}} | |||
| {{refend}} | |||
| ==External links== | |||
| ] | |||
| {{Commons category|Venn diagrams}} | |||
| ] | |||
| * {{springer|title=Venn diagram|id=p/v096550}} | |||
| * at ] | |||
| * | |||
| * | |||
| * | |||
| * | |||
| * | |||
| {{Mathematical logic}} | |||
| ] | |||
| {{Set theory}} | |||
| ] | |||
| {{Authority control}} | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| {{Diagrams in logic}} | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
Latest revision as of 21:24, 23 December 2024
Diagram that shows all possible logical relations between a collection of sets

| Part of a series on statistics |
| Probability theory |
|---|
 |
A Venn diagram is a widely used diagram style that shows the logical relation between sets, popularized by John Venn (1834–1923) in the 1880s. The diagrams are used to teach elementary set theory, and to illustrate simple set relationships in probability, logic, statistics, linguistics and computer science. A Venn diagram uses simple closed curves drawn on a plane to represent sets. Very often, these curves are circles or ellipses.
Similar ideas had been proposed before Venn such as by Christian Weise in 1712 (Nucleus Logicoe Wiesianoe) and Leonhard Euler (Letters to a German Princess) in 1768. The idea was popularised by Venn in Symbolic Logic, Chapter V "Diagrammatic Representation", published in 1881.
Details
A Venn diagram, also called a set diagram or logic diagram, shows all possible logical relations between a finite collection of different sets. These diagrams depict elements as points in the plane, and sets as regions inside closed curves. A Venn diagram consists of multiple overlapping closed curves, usually circles, each representing a set. The points inside a curve labelled S represent elements of the set S, while points outside the boundary represent elements not in the set S. This lends itself to intuitive visualizations; for example, the set of all elements that are members of both sets S and T, denoted S ∩ T and read "the intersection of S and T", is represented visually by the area of overlap of the regions S and T.
In Venn diagrams, the curves are overlapped in every possible way, showing all possible relations between the sets. They are thus a special case of Euler diagrams, which do not necessarily show all relations. Venn diagrams were conceived around 1880 by John Venn. They are used to teach elementary set theory, as well as illustrate simple set relationships in probability, logic, statistics, linguistics, and computer science.
A Venn diagram in which the area of each shape is proportional to the number of elements it contains is called an area-proportional (or scaled) Venn diagram.
Example

This example involves two sets of creatures, represented here as colored circles. The orange circle represents all types of creatures that have two legs. The blue circle represents creatures that can fly. Each separate type of creature can be imagined as a point somewhere in the diagram. Living creatures that have two legs and can fly—for example, parrots—are then in both sets, so they correspond to points in the region where the blue and orange circles overlap. This overlapping region would only contain those elements (in this example, creatures) that are members of both the orange set (two-legged creatures) and the blue set (flying creatures).
Humans and penguins are bipedal, and so are in the orange circle, but since they cannot fly, they appear in the left part of the orange circle, where it does not overlap with the blue circle. Mosquitoes can fly, but have six, not two, legs, so the point for mosquitoes is in the part of the blue circle that does not overlap with the orange one. Creatures that are neither two-legged nor able to fly (for example, whales and spiders) would all be represented by points outside both circles.
The combined region of the two sets is called their union, denoted by A ∪ B, where A is the orange circle and B the blue. The union in this case contains all living creatures that either are two-legged or can fly (or both). The region included in both A and B, where the two sets overlap, is called the intersection of A and B, denoted by A ∩ B.
History

Venn diagrams were introduced in 1880 by John Venn in a paper entitled "On the Diagrammatic and Mechanical Representation of Propositions and Reasonings" in the Philosophical Magazine and Journal of Science, about the different ways to represent propositions by diagrams. The use of these types of diagrams in formal logic, according to Frank Ruskey and Mark Weston, predates Venn but are "rightly associated" with him as he "comprehensively surveyed and formalized their usage, and was the first to generalize them".
Diagrams of overlapping circles representing unions and intersections were introduced by Catalan philosopher Ramon Llull (c. 1232–1315/1316) in the 13th century, who used them to illustrate combinations of basic principles. Gottfried Wilhelm Leibniz (1646–1716) produced similar diagrams in the 17th century (though much of this work was unpublished), as did Johann Christian Lange in a work from 1712 describing Christian Weise's contributions to logic. Euler diagrams, which are similar to Venn diagrams but don't necessarily contain all possible unions and intersections, were first made prominent by mathematician Leonhard Euler in the 18th century.
Venn did not use the term "Venn diagram" and referred to the concept as "Eulerian Circles". He became acquainted with Euler diagrams in 1862 and wrote that Venn diagrams did not occur to him "till much later", while attempting to adapt Euler diagrams to Boolean logic. In the opening sentence of his 1880 article Venn wrote that Euler diagrams were the only diagrammatic representation of logic to gain "any general acceptance".
Venn viewed his diagrams as a pedagogical tool, analogous to verification of physical concepts through experiment. As an example of their applications, he noted that a three-set diagram could show the syllogism: 'All A is some B. No B is any C. Hence, no A is any C.'
Charles L. Dodgson (Lewis Carroll) includes "Venn's Method of Diagrams" as well as "Euler's Method of Diagrams" in an "Appendix, Addressed to Teachers" of his book Symbolic Logic (4th edition published in 1896). The term "Venn diagram" was later used by Clarence Irving Lewis in 1918, in his book A Survey of Symbolic Logic.
In the 20th century, Venn diagrams were further developed. David Wilson Henderson showed, in 1963, that the existence of an n-Venn diagram with n-fold rotational symmetry implied that n was a prime number. He also showed that such symmetric Venn diagrams exist when n is five or seven. In 2002, Peter Hamburger found symmetric Venn diagrams for n = 11 and in 2003, Griggs, Killian, and Savage showed that symmetric Venn diagrams exist for all other primes. These combined results show that rotationally symmetric Venn diagrams exist, if and only if n is a prime number.
Venn diagrams and Euler diagrams were incorporated as part of instruction in set theory, as part of the new math movement in the 1960s. Since then, they have also been adopted in the curriculum of other fields such as reading.
Popular culture
Venn diagrams have been commonly used in memes. At least one politician has been mocked for misusing Venn diagrams.
Overview
See also: Set (mathematics) § Basic operations-
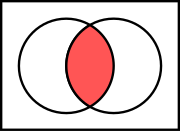 Intersection of two sets
Intersection of two sets
-
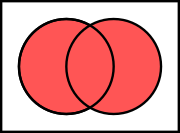 Union of two sets
Union of two sets
-
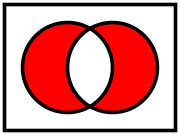 Symmetric difference of two sets
Symmetric difference of two sets
-
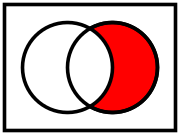 Relative complement of A (left) in B (right)
Relative complement of A (left) in B (right)
-
 Absolute complement of A in U
Absolute complement of A in U
A Venn diagram is constructed with a collection of simple closed curves drawn in a plane. According to Lewis, the "principle of these diagrams is that classes be represented by regions in such relation to one another that all the possible logical relations of these classes can be indicated in the same diagram. That is, the diagram initially leaves room for any possible relation of the classes, and the actual or given relation, can then be specified by indicating that some particular region is null or is not-null".
Venn diagrams normally comprise overlapping circles. The interior of the circle symbolically represents the elements of the set, while the exterior represents elements that are not members of the set. For instance, in a two-set Venn diagram, one circle may represent the group of all wooden objects, while the other circle may represent the set of all tables. The overlapping region, or intersection, would then represent the set of all wooden tables. Shapes other than circles can be employed as shown below by Venn's own higher set diagrams. Venn diagrams do not generally contain information on the relative or absolute sizes (cardinality) of sets. That is, they are schematic diagrams generally not drawn to scale.
Venn diagrams are similar to Euler diagrams. However, a Venn diagram for n component sets must contain all 2 hypothetically possible zones, that correspond to some combination of inclusion or exclusion in each of the component sets. Euler diagrams contain only the actually possible zones in a given context. In Venn diagrams, a shaded zone may represent an empty zone, whereas in an Euler diagram, the corresponding zone is missing from the diagram. For example, if one set represents dairy products and another cheeses, the Venn diagram contains a zone for cheeses that are not dairy products. Assuming that in the context cheese means some type of dairy product, the Euler diagram has the cheese zone entirely contained within the dairy-product zone—there is no zone for (non-existent) non-dairy cheese. This means that as the number of contours increases, Euler diagrams are typically less visually complex than the equivalent Venn diagram, particularly if the number of non-empty intersections is small.
The difference between Euler and Venn diagrams can be seen in the following example. Take the three sets:
The Euler and the Venn diagram of those sets are:
Extensions to higher numbers of sets
Venn diagrams typically represent two or three sets, but there are forms that allow for higher numbers. Shown below, four intersecting spheres form the highest order Venn diagram that has the symmetry of a simplex and can be visually represented. The 16 intersections correspond to the vertices of a tesseract (or the cells of a 16-cell, respectively).

|
 |
 |
 |

|
For higher numbers of sets, some loss of symmetry in the diagrams is unavoidable. Venn was keen to find "symmetrical figures ... elegant in themselves," that represented higher numbers of sets, and he devised an elegant four-set diagram using ellipses (see below). He also gave a construction for Venn diagrams for any number of sets, where each successive curve that delimits a set interleaves with previous curves, starting with the three-circle diagram.
-
 Venn's construction for four sets (use Gray code to compute, the digit 1 means in the set, and the digit 0 means not in the set)
Venn's construction for four sets (use Gray code to compute, the digit 1 means in the set, and the digit 0 means not in the set)
-
 Venn's construction for five sets
Venn's construction for five sets
-
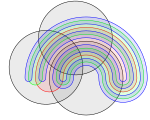 Venn's construction for six sets
Venn's construction for six sets
-
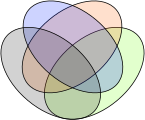 Venn's four-set diagram using ellipses
Venn's four-set diagram using ellipses
-
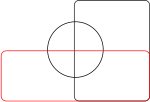
 Non-example: This Euler diagram is not a Venn diagram for four sets as it has only 14 regions as opposed to 2 = 16 regions (including the white region); there is no region where only the yellow and blue, or only the red and green circles meet.
Non-example: This Euler diagram is not a Venn diagram for four sets as it has only 14 regions as opposed to 2 = 16 regions (including the white region); there is no region where only the yellow and blue, or only the red and green circles meet.
-
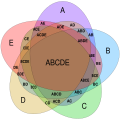 Five-set Venn diagram using congruent ellipses in a five-fold rotationally symmetrical arrangement devised by Branko Grünbaum. Labels have been simplified for greater readability; for example, A denotes A ∩ B ∩ C ∩ D ∩ E, while BCE denotes A ∩ B ∩ C ∩ D ∩ E.
Five-set Venn diagram using congruent ellipses in a five-fold rotationally symmetrical arrangement devised by Branko Grünbaum. Labels have been simplified for greater readability; for example, A denotes A ∩ B ∩ C ∩ D ∩ E, while BCE denotes A ∩ B ∩ C ∩ D ∩ E.
-
 Six-set Venn diagram made of only triangles (interactive version)
Six-set Venn diagram made of only triangles (interactive version)
Edwards–Venn diagrams
Anthony William Fairbank Edwards constructed a series of Venn diagrams for higher numbers of sets by segmenting the surface of a sphere, which became known as Edwards–Venn diagrams. For example, three sets can be easily represented by taking three hemispheres of the sphere at right angles (x = 0, y = 0 and z = 0). A fourth set can be added to the representation, by taking a curve similar to the seam on a tennis ball, which winds up and down around the equator, and so on. The resulting sets can then be projected back to a plane, to give cogwheel diagrams with increasing numbers of teeth—as shown here. These diagrams were devised while designing a stained-glass window in memory of Venn.
Other diagrams
Edwards–Venn diagrams are topologically equivalent to diagrams devised by Branko Grünbaum, which were based around intersecting polygons with increasing numbers of sides. They are also two-dimensional representations of hypercubes.
Henry John Stephen Smith devised similar n-set diagrams using sine curves with the series of equations
Charles Lutwidge Dodgson (also known as Lewis Carroll) devised a five-set diagram known as Carroll's square. Joaquin and Boyles, on the other hand, proposed supplemental rules for the standard Venn diagram, in order to account for certain problem cases. For instance, regarding the issue of representing singular statements, they suggest to consider the Venn diagram circle as a representation of a set of things, and use first-order logic and set theory to treat categorical statements as statements about sets. Additionally, they propose to treat singular statements as statements about set membership. So, for example, to represent the statement "a is F" in this retooled Venn diagram, a small letter "a" may be placed inside the circle that represents the set F.
Related concepts

Venn diagrams correspond to truth tables for the propositions , , etc., in the sense that each region of Venn diagram corresponds to one row of the truth table. This type is also known as Johnston diagram. Another way of representing sets is with John F. Randolph's R-diagrams.
See also
- Existential graph (by Charles Sanders Peirce)
- Logical connective
- Information diagram
- Marquand diagram (and as further derivation Veitch chart and Karnaugh map)
- Spherical octahedron – A stereographic projection of a regular octahedron makes a three-set Venn diagram, as three orthogonal great circles, each dividing space into two halves.
- Stanhope Demonstrator
- Three circles model
- Triquetra
- Vesica piscis
- UpSet plot
Notes
- In Euler's Lettres à une princesse d'Allemagne sur divers sujets de physique et de philosophie (Saint Petersburg, Russia: l'Academie Impériale des Sciences, 1768), volume 2, pages 95-126. In Venn's article, however, he suggests that the diagrammatic idea predates Euler, and is attributable to Christian Weise or Johann Christian Lange (in Lange's book Nucleus Logicae Weisianae (1712)).
References
- "Intersection of Sets". web.mnstate.edu. Archived from the original on 2020-08-04. Retrieved 2020-09-05.
- Venn, John. "On the Diagrammatic and Mechanical Representation of Propositions and Reasonings" (PDF). Penn Engineering.
- "The Philosophical Magazine: A Journal of Theoretical Experimental and Applied Physics". Taylor & Francis. Retrieved 2021-08-06.
- ^ Venn, John (July 1880). "I. On the Diagrammatic and Mechanical Representation of Propositions and Reasonings" (PDF). The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 5. 10 (59): 1–18. doi:10.1080/14786448008626877. Archived (PDF) from the original on 2017-05-16.
- ^ Venn, John (1880). "On the employment of geometrical diagrams for the sensible representations of logical propositions". Proceedings of the Cambridge Philosophical Society. 4: 47–59.
- ^ Sandifer, Ed (2003). "How Euler Did It" (PDF). MAA Online. The Mathematical Association of America (MAA). Retrieved 2009-10-26.
- ^ Ruskey, Frank; Weston, Mark (2005-06-18). "A Survey of Venn Diagrams". The Electronic Journal of Combinatorics.
- ^ Baron, Margaret E. (May 1969). "A Note on The Historical Development of Logic Diagrams". The Mathematical Gazette. 53 (384): 113–125. doi:10.2307/3614533. JSTOR 3614533. S2CID 125364002.
- Leibniz, Gottfried Wilhelm (1903) . "De Formae Logicae per linearum ductus". In Couturat, Louis (ed.). Opuscules et fragmentes inedits de Leibniz (in Latin). pp. 292–321.
- ^ Venn, John (1881). Symbolic logic. Macmillan. p. 108. Retrieved 2013-04-09.
- Mac Queen, Gailand (October 1967). The Logic Diagram (PDF) (Thesis). McMaster University. Archived from the original (PDF) on 2017-04-14. Retrieved 2017-04-14. (NB. Has a detailed history of the evolution of logic diagrams including but not limited to the Venn diagram.)
- ^ Verburgt, Lukas M. (April 2023). "The Venn Behind the Diagram". Mathematics Today. Vol. 59, no. 2. Institute of Mathematics and its Applications. pp. 53–55.
- ^ Lewis, Clarence Irving (1918). A Survey of Symbolic Logic. Berkeley: University of California Press.
- Henderson, David Wilson (April 1963). "Venn diagrams for more than four classes". American Mathematical Monthly. 70 (4): 424–426. doi:10.2307/2311865. JSTOR 2311865.
- Ruskey, Frank; Savage, Carla D.; Wagon, Stan (December 2006). "The Search for Simple Symmetric Venn Diagrams" (PDF). Notices of the AMS. 53 (11): 1304–1311.
- "Strategies for Reading Comprehension Venn Diagrams". Archived from the original on 2009-04-29. Retrieved 2009-06-20.
- Leo, Alex (2010-03-18). "Jesus, Karaoke, And Serial Killers: The Funniest Venn Diagrams The Web Has To Offer". Huffpost. Retrieved 2024-10-02.
- Moran, Lee (2018-12-15). "Scott Walker Gets Mercilessly Mocked By Twitter Users Over Venn Diagram Fail". HuffPost. Retrieved 2024-10-02.
- Weisstein, Eric W. "Venn Diagram". mathworld.wolfram.com. Retrieved 2020-09-05.
- "Euler Diagrams 2004: Brighton, UK: September 22–23". Reasoning with Diagrams project, University of Kent. 2004. Retrieved 2008-08-13.
- ^ Edwards, Anthony William Fairbank (2004). Cogwheels of the Mind: The Story of Venn Diagrams. Baltimore, Maryland, USA: Johns Hopkins University Press. p. 65. ISBN 978-0-8018-7434-5..
- Joaquin, Jeremiah Joven; Boyles, Robert James M. (June 2017). "Teaching Syllogistic Logic via a Retooled Venn Diagrammatical Technique". Teaching Philosophy. 40 (2): 161–180. doi:10.5840/teachphil201771767. Archived from the original on 2018-11-21. Retrieved 2020-05-12.
- Grimaldi, Ralph P. (2004). Discrete and combinatorial mathematics. Boston: Addison-Wesley. p. 143. ISBN 978-0-201-72634-3.
- Johnson, David L. (2001). "3.3 Laws". Elements of logic via numbers and sets. Springer Undergraduate Mathematics Series. Berlin, Germany: Springer-Verlag. p. 62. ISBN 978-3-540-76123-5.
Further reading
- Mahmoodian, Ebadollah S.; Rezaie, M.; Vatan, F. (March 1987). "Generalization of Venn Diagram" (PDF). Eighteenth Annual Iranian Mathematics Conference. Tehran and Isfahan, Iran. Archived from the original (PDF) on 2017-05-01. Retrieved 2017-05-01.
- Edwards, Anthony William Fairbank (1989-01-07). "Venn diagrams for many sets". New Scientist. 121 (1646): 51–56.
- Watkinson, John (1990). "4.10. Hamming distance". Coding for Digital Recording. Stoneham, MA, USA: Focal Press. pp. 94–99, foldout in backsleeve. ISBN 978-0-240-51293-8. (NB. The book comes with a 3-page foldout of a seven-bit cylindrical Venn diagram.)
- Stewart, Ian (June 2003) . "Chapter 4. Cogwheels of the Mind". Another Fine Math You've Got Me Into (reprint of 1st ed.). Mineola, New York, USA: Dover Publications, Inc. (W. H. Freeman). pp. 51–64. ISBN 978-0-486-43181-9.
- Glassner, Andrew (2004). "Venn and Now". Morphs, Mallards, and Montages: Computer-Aided Imagination. Wellesley, MA, USA: A. K. Peters. pp. 161–184. ISBN 978-1568812311.
- Mamakani, Khalegh; Ruskey, Frank (2012-07-27). "A New Rose: The First Simple Symmetric 11-Venn Diagram". p. 6452. arXiv:1207.6452. Bibcode:2012arXiv1207.6452M. Archived from the original on 2017-05-01. Retrieved 2017-05-01.
External links
- "Venn diagram", Encyclopedia of Mathematics, EMS Press, 2001
- Lewis Carroll's Logic Game – Venn vs. Euler at Cut-the-knot
- Six sets Venn diagrams made from triangles
- Interactive seven sets Venn diagram
- VBVenn, a free open source program for calculating and graphing quantitative two-circle Venn diagrams
- InteractiVenn, a web-based tool for visualizing Venn diagrams
- DeepVenn, a tool for creating area-proportional Venn Diagrams
| Mathematical logic | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| General | |||||||||
| Theorems (list) and paradoxes | |||||||||
| Logics |
| ||||||||
| Set theory |
| ||||||||
| Formal systems (list), language and syntax |
| ||||||||
| Proof theory | |||||||||
| Model theory | |||||||||
| Computability theory | |||||||||
| Related | |||||||||
| Set theory | ||
|---|---|---|
| Overview |  | |
| Axioms | ||
| Operations |
| |
| ||
| Set types | ||
| Theories | ||
| ||
| Set theorists | ||
| Diagrams in logic | ||
|---|---|---|












 ,
,  , etc., in the sense that each region of Venn diagram corresponds to one row of the truth table. This type is also known as Johnston diagram. Another way of representing sets is with John F. Randolph's
, etc., in the sense that each region of Venn diagram corresponds to one row of the truth table. This type is also known as Johnston diagram. Another way of representing sets is with John F. Randolph's