| Revision as of 11:03, 23 November 2018 edit196.8.123.44 (talk)No edit summary← Previous edit | Latest revision as of 15:41, 17 December 2024 edit undoTheNerdzilla (talk | contribs)Extended confirmed users1,528 edits Reverted 1 edit by 64.107.190.90 (talk): Unexplained removalTags: Twinkle Undo | ||
| (451 intermediate revisions by more than 100 users not shown) | |||
| Line 1: | Line 1: | ||
| {{pp-pc|small=yes}} | |||
| {{distinguish|text=the unrelated adage ]}} | |||
| {{Use American English|date=July 2021}} | |||
| {{Short description|Observation that in many real-life datasets, the leading digit is likely to be small}} | |||
| {{For|the unrelated adage|Benford's law of controversy}} | |||
| ] | ] | ||
| ] | ] | ||
| {{Use dmy dates|date= |
{{Use dmy dates|date=September 2020}} | ||
| '''Benford's law''', also |
'''Benford's law''', also known as the '''Newcomb–Benford law''', the '''law of anomalous numbers''', or the '''first-digit law''', is an observation that in many real-life sets of numerical ], the ] is likely to be small.<ref name=BergerHill2011>Arno Berger and Theodore P. Hill, , 2011.</ref> In sets that obey the law, the number 1 appears as the leading significant digit about 30% of the time, while 9 appears as the leading significant digit less than 5% of the time. Uniformly distributed digits would each occur about 11.1% of the time.<ref>{{cite web |url=http://mathworld.wolfram.com/BenfordsLaw.html |author = Weisstein, Eric W. |title=Benford's Law |website = MathWorld, A Wolfram web resource |access-date = 7 June 2015}}</ref> Benford's law also makes predictions about the distribution of second digits, third digits, digit combinations, and so on. | ||
| The graph to the right shows Benford's law for ], one of infinitely many cases of a generalized law regarding numbers expressed in arbitrary (integer) bases, which rules out the possibility that the phenomenon might be an artifact of the base-10 number system. Further generalizations published in 1995<ref>{{cite journal |url=https://projecteuclid.org/euclid.ss/1177009869 |author=Hill, Theodore |title=A Statistical Derivation of the Significant-Digit Law |journal=Statistical Science |year=1995 |volume=10 |issue=4 |doi=10.1214/ss/1177009869|doi-access=free }}</ref> included analogous statements for both the ''n''th leading digit and the joint distribution of the leading ''n'' digits, the latter of which leads to a corollary wherein the significant digits are shown to be a ] quantity. | |||
| The graph to the right shows Benford's law for ]. There is a generalization of the law to numbers expressed in other bases (for example, ]), and also a generalization from leading 1 digit to leading ''n'' digits. | |||
| It has been shown that this result applies to a wide variety of data sets, including electricity bills, street addresses, stock prices, house prices, population numbers, death rates, lengths of rivers, ] and ]s<ref>Paul H. Kvam, Brani Vidakovic, ''Nonparametric Statistics with Applications to Science and Engineering'', p. |
It has been shown that this result applies to a wide variety of data sets, including electricity bills, street addresses, stock prices, house prices, population numbers, death rates, lengths of rivers, and ] and ]s.<ref>Paul H. Kvam, Brani Vidakovic, ''Nonparametric Statistics with Applications to Science and Engineering'', p. 158.</ref> Like other general principles about natural data—for example, the fact that many data sets are well approximated by a ]—there are illustrative examples and explanations that cover many of the cases where Benford's law applies, though there are many other cases where Benford's law applies that resist simple explanations.<ref name=BergerHill2020>{{cite journal |last1=Berger |first1=Arno |last2=Hill |first2=Theodore P. |title=The mathematics of Benford's law: a primer |journal=Stat. Methods Appl. |date=June 30, 2020 |volume=30 |issue=3 |pages=779–795 |doi=10.1007/s10260-020-00532-8 |arxiv=1909.07527 |s2cid=202583554 |url=https://doi.org/10.1007/s10260-020-00532-8 }}</ref><ref>{{Cite journal |last1=Cai |first1=Zhaodong |last2=Faust |first2=Matthew |last3=Hildebrand |first3=A. J. |last4=Li |first4=Junxian |last5=Zhang |first5=Yuan |date=2020-03-15 |title=The Surprising Accuracy of Benford's Law in Mathematics |url=https://doi.org/10.1080/00029890.2020.1690387 |journal=The American Mathematical Monthly |volume=127 |issue=3 |pages=217–237 |doi=10.1080/00029890.2020.1690387 |arxiv=1907.08894 |s2cid=198147766 |issn=0002-9890}}</ref> Benford's law tends to be most accurate when values are distributed across multiple ], especially if the process generating the numbers is described by a ] (which is common in nature). | ||
| The law is named after physicist ], who stated it in 1938 in an article titled "The Law of Anomalous Numbers",<ref name=Benford>{{Cite journal | author = Frank Benford | author-link = Frank Benford | title = The law of anomalous numbers | journal = ] | volume = 78 | issue = 4 |date=March 1938 | pages = 551–572 | jstor=984802 | bibcode = 1938PAPhS..78..551B }}</ref> although it had been previously stated by ] in 1881.<ref name=Newcomb /><ref name=Formann2010 /> | |||
| The law is similar in concept, though not identical in distribution, to ]. | |||
| ==Definition== | ==Definition== | ||
| ] bar. Picking a random ''x'' position ] on this number line, roughly 30% of the time the first digit of the number will be 1.]] | ] bar. Picking a random ''x'' position ] on this number line, roughly 30% of the time the first digit of the number will be 1.]] | ||
| A set of numbers is said to satisfy Benford's law if the leading digit {{mvar|d}} ({{math|{{var|d}} ∈ {{mset|1, ..., 9}}}}) occurs with ] | A set of numbers is said to satisfy Benford's law if the leading digit {{mvar|d}} ({{math|{{var|d}} ∈ {{mset|1, ..., 9}}}}) occurs with ]<ref name="Miller2015" /> | ||
| : <math>P(d)=\log_{10}(d+1)-\log_{10}(d)=\log_{10} |
: <math>P(d) = \log_{10}(d + 1) - \log_{10}(d) = \log_{10}\left(\frac{d + 1}{d}\right) = \log_{10}\left(1 + \frac{1}{d}\right).</math> | ||
| The leading digits in such a set thus have the following distribution: | The leading digits in such a set thus have the following distribution: | ||
| {| class="wikitable" | {| class="wikitable" | ||
| |- | |||
| ! {{nobold|{{mvar|d}}}} !! {{tmath|P(d)}} !! Relative size of {{tmath|P(d)}} | ! {{nobold|{{mvar|d}}}} !! {{tmath|P(d)}} !! Relative size of {{tmath|P(d)}} | ||
| |- | |- | ||
| | 1 || |
| 1 ||{{right}} {{bartable|30.1|%|10}} | ||
| |- | |- | ||
| | 2 || |
| 2 ||{{right}} {{bartable|17.6|%|10}} | ||
| |- | |- | ||
| | 3 || |
| 3 ||{{right}} {{bartable|12.5|%|10}} | ||
| |- | |- | ||
| | 4 || |
| 4 ||{{right}} {{bartable| 9.7|%|10}} | ||
| |- | |- | ||
| | 5 || |
| 5 ||{{right}} {{bartable| 7.9|%|10}} | ||
| |- | |- | ||
| | 6 || |
| 6 ||{{right}} {{bartable| 6.7|%|10}} | ||
| |- | |- | ||
| | 7 || |
| 7 ||{{right}} {{bartable| 5.8|%|10}} | ||
| |- | |- | ||
| | 8 || |
| 8 ||{{right}} {{bartable| 5.1|%|10}} | ||
| |- | |- | ||
| | 9 || |
| 9 ||{{right}} {{bartable| 4.6|%|10}} | ||
| |} | |} | ||
| The quantity {{tmath|P(d)}} is proportional to the space between {{mvar|d}} and {{math|{{var|d}} + 1}} on a ]. Therefore, this is the distribution expected if |
The quantity {{tmath|P(d)}} is proportional to the space between {{mvar|d}} and {{math|{{var|d}} + 1}} on a ]. Therefore, this is the distribution expected if the ''logarithms'' of the numbers (but not the numbers themselves) are ]. | ||
| For example, a number {{mvar|x}}, constrained to lie between 1 and 10, starts with the digit 1 if {{math|1 ≤ {{var|x}} < 2}}, and starts with the digit 9 if {{math|9 ≤ {{var|x}} < 10}}. Therefore, |
For example, a number {{mvar|x}}, constrained to lie between 1 and 10, starts with the digit 1 if {{math|1 ≤ {{var|x}} < 2}}, and starts with the digit 9 if {{math|9 ≤ {{var|x}} < 10}}. Therefore, {{mvar|x}} starts with the digit 1 if {{math|log 1 ≤ log {{var|x}} < log 2}}, or starts with 9 if {{math|log 9 ≤ log ''x'' < log 10}}. The interval {{math|}} is much wider than the interval {{math|}} (0.30 and 0.05 respectively); therefore if log {{mvar|x}} is uniformly and randomly distributed, it is much more likely to fall into the wider interval than the narrower interval, i.e. more likely to start with 1 than with 9; the probabilities are proportional to the interval widths, giving the equation above (as well as the generalization to other bases besides decimal). | ||
| Benford's law is sometimes stated in a stronger form, asserting that the ] of the logarithm of data is typically close to uniformly distributed between 0 and 1; from this, the main claim about the distribution of first digits can be derived. | Benford's law is sometimes stated in a stronger form, asserting that the ] of the logarithm of data is typically close to uniformly distributed between 0 and 1; from this, the main claim about the distribution of first digits can be derived.<ref name=BergerHill2020/> | ||
| === |
===In other bases=== | ||
| , hover over a graph to show the value for each point.]] | , hover over a graph to show the value for each point.)]] | ||
| An extension of Benford's law predicts the distribution of first digits in other ] besides ]; in fact, any base {{math|''b'' ≥ 2}}. The general form is: | An extension of Benford's law predicts the distribution of first digits in other ] besides ]; in fact, any base {{math|''b'' ≥ 2}}. The general form is<ref>{{Cite web |last=Pimbley |first=J. M. |date=2014 |title=Benford's Law as a Logarithmic Transformation |url=http://www.maxwell-consulting.com/Benford_Logarithmic_Transformation.pdf |archive-url=https://ghostarchive.org/archive/20221009/http://www.maxwell-consulting.com/Benford_Logarithmic_Transformation.pdf |archive-date=2022-10-09 |url-status=live |access-date=2020-11-15 |website=Maxwell Consulting, LLC}}</ref> | ||
| : <math>P(d)=\ |
: <math>P(d) = \log_b(d + 1) - \log_b(d) = \log_b\left(1 + \frac{1}{d}\right).</math> | ||
| For {{math|1=''b'' |
For {{math|1=''b'' = 2, 1}} (the ] and ]) number systems, Benford's law is true but trivial: All binary and unary numbers (except for 0 or the empty set) start with the digit 1. (On the other hand, the ] is not trivial, even for binary numbers.<ref>{{Cite book |last=Khosravani |first=A. |title=Transformation Invariance of Benford Variables and their Numerical Modeling |publisher=Recent Researches in Automatic Control and Electronics |year=2012 |isbn=978-1-61804-080-0 |pages=57–61}}</ref>) | ||
| == |
==Examples== | ||
| ] of the world as of July 2010. Black dots indicate the distribution predicted by Benford's law.|thumb|right]] | ] of the world as of July 2010. Black dots indicate the distribution predicted by Benford's law.|thumb|right]] | ||
| Examining a list of the heights of the ] shows that 1 is by far the most common leading digit, ''irrespective of the unit of measurement'' ( |
Examining a list of the heights of the ] shows that 1 is by far the most common leading digit, ''irrespective of the unit of measurement'' (see "scale invariance" below): | ||
| {| class="wikitable" | {| class="wikitable" style="text-align:right" | ||
| !rowspan="2"| Leading<br/> digit | |||
| !colspan=2| m | |||
| !colspan=2| ft | |||
| !rowspan="2"| Per<br/> Benford's law | |||
| |- | |- | ||
| ! Count | |||
| ! rowspan="2" style="width:17%;"| Leading digit | |||
| ! Share | |||
| ! colspan=2 | meters | |||
| ! Count | |||
| ! colspan=2 | feet | |||
| ! Share | |||
| ! rowspan="2" style="width:17%;"| In Benford's law | |||
| |- | |||
| ! style="width:16%;"| Count | |||
| ! style="width:17%;"| % | |||
| ! style="width:16%;"| Count | |||
| ! style="width:17%;"| % | |||
| |- | |- | ||
| | 1 | | 1 | ||
| | |
| 23 | ||
| | |
| 39.7 % | ||
| | |
| 15 | ||
| | |
| 25.9 % | ||
| | 30. |
| 30.1 % | ||
| |- | |- | ||
| | 2 | | 2 | ||
| | |
| 12 | ||
| | |
| 20.7 % | ||
| | 8 | | 8 | ||
| | 13. |
| 13.8 % | ||
| | 17. |
| 17.6 % | ||
| |- | |- | ||
| | 3 | | 3 | ||
| | |
| 6 | ||
| | |
| 10.3 % | ||
| | |
| 5 | ||
| | |
| 8.6 % | ||
| | 12. |
| 12.5 % | ||
| |- | |- | ||
| | 4 | | 4 | ||
| | |
| 5 | ||
| | |
| 8.6 % | ||
| | |
| 7 | ||
| | |
| 12.1 % | ||
| | 9. |
| 9.7 % | ||
| |- | |- | ||
| | 5 | | 5 | ||
| | 2 | |||
| | 3.4 % | |||
| | 9 | |||
| | 15.5 % | |||
| | 7.9 % | |||
| |- | |||
| | 6 | |||
| | 5 | |||
| | 8.6 % | |||
| | 4 | | 4 | ||
| | 6. |
| 6.9 % | ||
| | |
| 6.7 % | ||
| | 16.7% | |||
| | 7.9% | |||
| |- | |- | ||
| | 7 | |||
| | 1 | |||
| | 1.7 % | |||
| | 3 | |||
| | 5.2 % | |||
| | 5.8 % | |||
| |- | |||
| | 8 | |||
| | 4 | |||
| | 6.9 % | |||
| | 6 | | 6 | ||
| | 10.3 % | |||
| | 5.1 % | |||
| |- | |||
| | 9 | |||
| | 0 | |||
| | 0 % | |||
| | 1 | | 1 | ||
| | 1. |
| 1.7 % | ||
| | 4.6 % | |||
| |} | |||
| Another example is the leading digit of {{math|2<sup>''n''</sup>}}. The sequence of the first 96 leading digits (1, 2, 4, 8, 1, 3, 6, 1, 2, 5, 1, 2, 4, 8, 1, 3, 6, 1, ... {{OEIS|A008952}}) exhibits closer adherence to Benford’s law than is expected for random sequences of the same length, because it is derived from a geometric sequence.<ref name=":0" /> | |||
| {| class="wikitable" style="text-align:right" | |||
| !rowspan="2"| Leading<br/> digit | |||
| !colspan=2| Occurrence | |||
| !rowspan="2"| Per<br/> Benford's law | |||
| |- | |||
| ! Count | |||
| ! Share | |||
| |- | |||
| | 1 | |||
| | 29 | |||
| | 30.2 % | |||
| | 30.1 % | |||
| |- | |||
| | 2 | |||
| | 17 | |||
| | 17.7 % | |||
| | 17.6 % | |||
| |- | |||
| | 3 | |||
| | 12 | |||
| | 12.5 % | |||
| | 12.5 % | |||
| |- | |||
| | 4 | |||
| | 10 | |||
| | 10.4 % | |||
| | 9.7 % | |||
| |- | |||
| | 5 | | 5 | ||
| | |
| 7 | ||
| | |
| 7.3 % | ||
| | 7.9 % | |||
| |- | |||
| | 6 | |||
| | 6 | |||
| | 6.3 % | |||
| | 6.7 % | |||
| |- | |- | ||
| | 7 | | 7 | ||
| | |
| 5 | ||
| | |
| 5.2 % | ||
| | |
| 5.8 % | ||
| | 3.3% | |||
| | 5.8% | |||
| |- | |- | ||
| | 8 | | 8 | ||
| | 5 | | 5 | ||
| | |
| 5.2 % | ||
| | |
| 5.1 % | ||
| | 1.7% | |||
| | 5.1% | |||
| |- | |- | ||
| | 9 | | 9 | ||
| | |
| 5 | ||
| | |
| 5.2 % | ||
| | |
| 4.6 % | ||
| | 3.3% | |||
| | 4.6% | |||
| |} | |} | ||
| Another example is the leading digit of {{math|2<sup>''n''</sup>}}: | |||
| :1, 2, 4, 8, 1, 3, 6, 1, 2, 5, 1, 2, 4, 8, 1, 3, 6, 1... {{OEIS|A008952}} | |||
| ==History== | ==History== | ||
| The discovery of Benford's law goes back to 1881, when the American astronomer ] noticed that in ] |
The discovery of Benford's law goes back to 1881, when the Canadian-American astronomer ] noticed that in ]s the earlier pages (that started with 1) were much more worn than the other pages.<ref name=Newcomb>{{Cite journal | author = Simon Newcomb | s2cid = 124556624 | author-link = Simon Newcomb | title = Note on the frequency of use of the different digits in natural numbers | journal = ] | volume = 4 | issue = 1/4 | year = 1881 | pages = 39–40 | doi = 10.2307/2369148 | jstor = 2369148 | bibcode = 1881AmJM....4...39N }}</ref> Newcomb's published result is the first known instance of this observation and includes a distribution on the second digit as well. Newcomb proposed a law that the probability of a single number ''N'' being the first digit of a number was equal to log(''N'' + 1) − log(''N''). | ||
| The phenomenon was again noted in 1938 by the physicist ],<ref name=Benford/> who tested it on data from 20 different domains and was credited for it. His data set included the surface areas of 335 rivers, the sizes of 3259 US populations, 104 ]s, 1800 ]s, 5000 entries from a mathematical handbook, 308 numbers contained in an issue of '']'', the street addresses of the first 342 persons listed in ''American Men of Science'' and 418 death rates. The total number of observations used in the paper was 20,229. This discovery was later named after Benford (making it an example of ]). | The phenomenon was again noted in 1938 by the physicist ],<ref name=Benford/> who tested it on data from 20 different domains and was credited for it. His data set included the surface areas of 335 rivers, the sizes of 3259 US populations, 104 ]s, 1800 ]s, 5000 entries from a mathematical handbook, 308 numbers contained in an issue of '']'', the street addresses of the first 342 persons listed in ''American Men of Science'' and 418 death rates. The total number of observations used in the paper was 20,229. This discovery was later named after Benford (making it an example of ]). | ||
| In 1995, ] proved the result about mixed distributions mentioned ].<ref name=Hill1995/> | In 1995, ] proved the result about mixed distributions mentioned ].<ref name=Hill1995/><ref name="Hill1995b">{{cite journal |last1=Hill |first1=Theodore P. |title=Base-invariance implies Benford's law |journal=Proceedings of the American Mathematical Society |volume=123 |issue=3 |year=1995 |pages=887–895 |issn=0002-9939 |doi=10.1090/S0002-9939-1995-1233974-8 |doi-access=free}}</ref> | ||
| ==Explanations== | ==Explanations== | ||
| Benford's law tends to apply most accurately to data that span several ]. As a rule of thumb, the more orders of magnitude that the data evenly covers, the more accurately Benford's law applies. For instance, one can expect that Benford's law would apply to a list of numbers representing the populations of United Kingdom settlements. But if a "settlement" is defined as a village with population between 300 and 999, then Benford's law will not apply.<ref name="dspguide">{{cite book |chapter-url=http://www.dspguide.com/ch34.htm |title=The Scientist and Engineer's Guide to Digital Signal Processing |section=Chapter 34: Explaining Benford's Law. The Power of Signal Processing |author=Steven W. Smith |access-date=15 December 2012}}</ref><ref name="fewster">{{Cite journal|first=R. M. |last=Fewster |author-link=Rachel Fewster|s2cid=39595550 |title=A simple explanation of Benford's Law |journal=The American Statistician |year=2009 |volume=63 |issue=1 |pages=26–32 |doi=10.1198/tast.2009.0005 |url=https://www.stat.auckland.ac.nz/~fewster/RFewster_Benford.pdf |archive-url=https://ghostarchive.org/archive/20221009/https://www.stat.auckland.ac.nz/~fewster/RFewster_Benford.pdf |archive-date=2022-10-09 |url-status=live |citeseerx=10.1.1.572.6719}}</ref> | |||
| Consider the probability distributions shown below, referenced to a ]. In each case, the total area in red is the relative probability that the first digit is 1, and the total area in blue is the relative probability that the first digit is 8. For the first distribution, the size of the areas of red and blue are approximately proportional to the widths of each red and blue bar. Therefore, the numbers drawn from this distribution will approximately follow Benford's law. On the other hand, for the second distribution, the ratio of the areas of red and blue is very different from the ratio of the widths of each red and blue bar. Rather, the relative areas of red and blue are determined more by the heights of the bars than the widths. Accordingly, the first digits in this distribution do not satisfy Benford's law at all.<ref name=fewster /> | |||
| ===Overview=== | |||
| Benford's law tends to apply most accurately to data that are distributed uniformly across several orders of magnitude. As a rule of thumb, the more orders of magnitude that the data evenly covers, the more accurately Benford's law applies. For instance, one can expect that Benford's law would apply to a list of numbers representing the populations of UK settlements, or representing the values of small insurance claims. But if a "village" is defined as a settlement with population between 300 and 999, or a "small insurance claim" is defined as a claim between $50 and $99, then Benford's law will not apply.<ref name="dspguide">{{cite web|url=http://www.dspguide.com/ch34.htm |title=The Scientist and Engineer's Guide to Digital Signal Processing, chapter 34, Explaining Benford's Law |author=Steven W. Smith |accessdate=15 December 2012}} (especially ).</ref><ref name="fewster">{{Cite journal|first=R. M. |last=Fewster |title=A simple explanation of Benford's Law |journal=The American Statistician |year=2009 |volume=63 |issue=1 |pages=26–32 |doi=10.1198/tast.2009.0005 |postscript=<!--None--> |url=https://www.stat.auckland.ac.nz/~fewster/RFewster_Benford.pdf }}</ref> | |||
| Consider the probability distributions shown below, referenced to a ].<ref name="logscale">This section discusses and plots probability distributions of the logarithms of a variable. This is not the same as taking a regular probability distribution of a variable, and simply plotting it on a log scale. Instead, one multiplies the distribution by a certain function. The log scale distorts the horizontal distances, so the height has to be changed also, in order for the area under each section of the curve to remain true to the original distribution. See, for example, . Specifically: <math>P(\log x) d(\log x) = (1/x) P(\log x) dx</math>.</ref> | |||
| In each case, the total area in red is the relative probability that the first digit is 1, and the total area in blue is the relative probability that the first digit is 8. | |||
| {| | {| | ||
| ] | |] | ||
| | | | | ||
| ] | ] | ||
| |} | |} | ||
| Thus, real-world distributions that span several ] rather uniformly (e.g., stock-market prices and populations of villages, towns, and cities) are likely to satisfy Benford's law very accurately. On the other hand, a distribution mostly or entirely within one order of magnitude (e.g., ]s or heights of human adults) is unlikely to satisfy Benford's law very accurately, if at all.<ref name=dspguide /><ref name=fewster /> However, the difference between applicable and inapplicable regimes is not a sharp cut-off: as the distribution gets narrower, the deviations from Benford's law increase gradually. | |||
| For the left distribution, the size of the ''areas'' of red and blue are approximately proportional to the ''widths'' of each red and blue bar. Therefore, the numbers drawn from this distribution will approximately follow Benford's law. On the other hand, for the right distribution, the ratio of the areas of red and blue is very different from the ratio of the widths of each red and blue bar. Rather, the relative areas of red and blue are determined more by the ''height'' of the bars than the widths. Accordingly, the first digits in this distribution do not satisfy Benford's law at all.<ref name=fewster /> | |||
| (This discussion is not a full explanation of Benford's law, because it has not explained why data sets are so often encountered that, when plotted as a probability distribution of the logarithm of the variable, are relatively uniform over several orders of magnitude.<ref name=BergerHillExplain>Arno Berger and Theodore P. Hill, , 2011. The authors describe this argument but say it "still leaves open the question of why it is reasonable to assume that the logarithm of the spread, as opposed to the spread itself—or, say, the log log spread—should be large" and that "assuming large spread on a logarithmic scale is ''equivalent'' to assuming an approximate conformance with " (italics added), something which they say lacks a "simple explanation".</ref>) | |||
| Thus, real-world distributions that span several ] rather uniformly (e.g. populations of villages / towns / cities, stock-market prices), are likely to satisfy Benford's law to a very high accuracy. On the other hand, a distribution that is mostly or entirely within one order of magnitude (e.g. heights of human adults, or IQ scores) is unlikely to satisfy Benford's law very accurately, or at all.<ref name=dspguide /><ref name=fewster /> However, it is not a sharp line: As the distribution gets narrower, the discrepancies from Benford's law ''typically'' increase gradually. | |||
| ===Krieger–Kafri entropy explanation=== | |||
| In terms of conventional ] (referenced to a linear scale rather than log scale, i.e. P(x)dx rather than P(log x) d(log x)), the equivalent criterion is that Benford's law will be very accurately satisfied when P(x) is approximately proportional to 1/x over several orders-of-magnitude variation in x.<ref name="logscale" /> | |||
| In 1970 ] proved what is now called the Krieger generator theorem.<ref name="Krieger1970">{{cite journal |last1=Krieger |first1=Wolfgang |title=On entropy and generators of measure-preserving transformations |journal=Transactions of the American Mathematical Society |volume=149 |issue=2 |year=1970 |pages=453 |issn=0002-9947 |doi=10.1090/S0002-9947-1970-0259068-3 |doi-access=free}}</ref><ref name="Downarowicz2011">{{cite book |author=Downarowicz, Tomasz |title=Entropy in Dynamical Systems |url=https://books.google.com/books?id=avUGMc787v8C&pg=PA106 |date=12 May 2011 |publisher=Cambridge University Press |isbn=978-1-139-50087-6 |page=106}}</ref> The Krieger generator theorem might be viewed as a justification for the assumption in the Kafri ball-and-box model that, in a given base <math>B</math> with a fixed number of digits 0, 1, ..., ''n'', ..., <math>B - 1</math>, digit ''n'' is equivalent to a Kafri box containing ''n'' non-interacting balls. Other scientists and statisticians have suggested entropy-related explanations{{which|date=October 2023}} for Benford's law.<ref>{{cite book |author=Smorodinsky, Meir |year=1971 |chapter=Chapter IX. Entropy and generators. Krieger's theorem |title=Ergodic Theory, Entropy |series=Lecture Notes in Mathematics |volume=214 |pages=54–57 |publisher=Springer |location=Berlin, Heidelberg |doi=10.1007/BFb0066096|isbn=978-3-540-05556-3 }}</ref><ref name="Jolion2001">{{cite journal |last1=Jolion |first1=Jean-Michel |title=Images and Benford's Law |journal=Journal of Mathematical Imaging and Vision |volume=14 |issue=1 |year=2001 |pages=73–81 |issn=0924-9907 |doi=10.1023/A:1008363415314 |bibcode=2001JMIV...14...73J |s2cid=34151059}}</ref><ref name="Miller2015">{{cite book |editor=Miller, Steven J. |editor-link=Steven J. Miller |title=Benford's Law: Theory and Applications |url=https://books.google.com/books?id=J_NnBgAAQBAJ&pg=309 |page=309 |date=9 June 2015 |publisher=Princeton University Press |isbn=978-1-4008-6659-5}}</ref><ref name="Lemons2019">{{cite journal |last1=Lemons |first1=Don S. |title=Thermodynamics of Benford's first digit law |journal=American Journal of Physics |volume=87 |issue=10 |year=2019 |pages=787–790 |issn=0002-9505 |doi=10.1119/1.5116005 |arxiv=1604.05715 |bibcode=2019AmJPh..87..787L |s2cid=119207367}}</ref> | |||
| This discussion is not a ''full'' explanation of Benford's law, because we have not explained ''why'' we so often come across data-sets that, when plotted as a probability distribution of the logarithm of the variable, are relatively uniform over several orders of magnitude.<ref name=BergerHillExplain>Arno Berger and Theodore P Hill, . The authors describe this argument, but say it "still leaves open the question of why it is reasonable to assume that the logarithm of the spread, as opposed to the spread itself—or, say, the log log spread—should be large." Moreover, they say: "assuming large spread on a logarithmic scale is ''equivalent'' to assuming an approximate conformance with " (italics added), something which they say lacks a "simple explanation".</ref> | |||
| ===Multiplicative fluctuations=== | ===Multiplicative fluctuations=== | ||
| Many real-world examples of Benford's law arise from multiplicative fluctuations.<ref name=Pietronero>{{cite journal|title=Explaining the uneven distribution of numbers in nature: the laws of Benford and Zipf |author=L. Pietronero |author2=E. Tosatti |author3=V. Tosatti|author4=A. Vespignani |journal=Physica A |year=2001 |volume=293 |pages=297–304 |doi=10.1016/S0378-4371(00)00633-6|bibcode = 2001PhyA..293..297P |
Many real-world examples of Benford's law arise from multiplicative fluctuations.<ref name=Pietronero>{{cite journal |title=Explaining the uneven distribution of numbers in nature: the laws of Benford and Zipf |author=L. Pietronero |author2=E. Tosatti |author3=V. Tosatti |author4=A. Vespignani |journal=Physica A |year=2001 |volume=293 |issue=1–2 |pages=297–304 |doi=10.1016/S0378-4371(00)00633-6 |bibcode = 2001PhyA..293..297P |arxiv=cond-mat/9808305}}</ref> For example, if a stock price starts at $100, and then each day it gets multiplied by a randomly chosen factor between 0.99 and 1.01, then over an extended period the probability distribution of its price satisfies Benford's law with higher and higher accuracy. | ||
| The reason is that the ''logarithm'' of the stock price is undergoing a ], so over time its probability distribution will get more and more broad and smooth (see ]).<ref name=Pietronero/> (More technically, the ] says that multiplying more and more random variables will create a ] with larger and larger variance, so eventually it covers many orders of magnitude almost uniformly.) To be sure of approximate agreement with Benford's |
The reason is that the ''logarithm'' of the stock price is undergoing a ], so over time its probability distribution will get more and more broad and smooth (see ]).<ref name=Pietronero/> (More technically, the ] says that multiplying more and more random variables will create a ] with larger and larger variance, so eventually it covers many orders of magnitude almost uniformly.) To be sure of approximate agreement with Benford's law, the distribution has to be approximately invariant when scaled up by any factor up to 10; a ]ly distributed data set with wide dispersion would have this approximate property. | ||
| Unlike multiplicative fluctuations, ''additive'' fluctuations do not lead to Benford's law: They lead instead to ]s (again by the ]), which do not satisfy |
Unlike multiplicative fluctuations, ''additive'' fluctuations do not lead to Benford's law: They lead instead to ]s (again by the ]), which do not satisfy Benford's law. By contrast, that hypothetical stock price described above can be written as the ''product'' of many random variables (i.e. the price change factor for each day), so is ''likely'' to follow Benford's law quite well. | ||
| ===Multiple probability distributions=== | ===Multiple probability distributions=== | ||
| ] provided an alternative explanation by directing attention to the interrelation between the ] of the significant digits and the distribution of the ]. He showed in a simulation study that long |
] provided an alternative explanation by directing attention to the interrelation between the ] of the significant digits and the distribution of the ]. He showed in a simulation study that long-right-tailed distributions of a ] are compatible with the Newcomb–Benford law, and that for distributions of the ratio of two random variables the fit generally improves.<ref>{{cite journal |last1=Formann |first1=A. K. |year=2010 |title=The Newcomb–Benford law in its relation to some common distributions |journal=PLOS ONE |volume=5 |issue=5 |page=e10541 |doi=10.1371/journal.pone.0010541 |pmid=20479878 |pmc=2866333 |bibcode=2010PLoSO...510541F |doi-access=free}}</ref> For numbers drawn from certain distributions (]s, human heights) the Benford's law fails to hold because these variates obey a normal distribution, which is known not to satisfy Benford's law,<ref name=Formann2010>{{Cite journal | ||
| | last1 = Formann | first1 = A. K. | | last1 = Formann | first1 = A. K. | ||
| | title = The |
| title = The Newcomb–Benford Law in Its Relation to Some Common Distributions | ||
| | doi = 10.1371/journal.pone.0010541 | | doi = 10.1371/journal.pone.0010541 | ||
| | journal = |
| journal = PLOS ONE | ||
| | volume = 5 | | volume = 5 | ||
| | issue = 5 | | issue = 5 | ||
| Line 186: | Line 236: | ||
| | editor1-last = Morris | | editor1-last = Morris | ||
| | editor1-first = Richard James | | editor1-first = Richard James | ||
| | bibcode = 2010PLoSO...510541F | |||
| |bibcode = 2010PLoSO...510541F }}</ref> since normal distributions can't span several orders of magnitude and the ] of their logarithms will not be (even approximately) uniformly distributed. | |||
| | doi-access = free | |||
| However, if one "mixes" numbers from those distributions, for example by taking numbers from newspaper articles, Benford's law reappears. This can also be proven mathematically: if one repeatedly "randomly" chooses a ] (from an uncorrelated set) and then randomly chooses a number according to that distribution, the resulting list of numbers will obey Benford's Law.<ref name=Hill1995>{{Cite journal | |||
| }}</ref> since normal distributions can't span several orders of magnitude and the ] of their logarithms will not be (even approximately) uniformly distributed. However, if one "mixes" numbers from those distributions, for example, by taking numbers from newspaper articles, Benford's law reappears. This can also be proven mathematically: if one repeatedly "randomly" chooses a ] (from an uncorrelated set) and then randomly chooses a number according to that distribution, the resulting list of numbers will obey Benford's law.<ref name=Hill1995>{{Cite journal | |||
| | author = Theodore P. Hill | | author = Theodore P. Hill | ||
| | author-link = Theodore P. Hill | | author-link = Theodore P. Hill | ||
| Line 193: | Line 244: | ||
| | journal = Statistical Science | | journal = Statistical Science | ||
| | volume = 10 | | volume = 10 | ||
| | issue = 4 | |||
| | pages = 354–363 | | pages = 354–363 | ||
| | year = 1995 | | year = 1995 | ||
| Line 198: | Line 250: | ||
| | doi = 10.1214/ss/1177009869 | | doi = 10.1214/ss/1177009869 | ||
| | mr = 1421567 | | mr = 1421567 | ||
| | doi-access = free | |||
| |format=PDF}}</ref><ref name=Hill1998>{{Cite journal | |||
| }}</ref><ref name=Hill1998>{{Cite journal | |||
| | author = Theodore P. Hill | | author = Theodore P. Hill | ||
| | author-link = Theodore P. Hill | | author-link = Theodore P. Hill | ||
| Line 204: | Line 257: | ||
| | journal = ] | | journal = ] | ||
| | volume = 86 | | volume = 86 | ||
| |date=July–August 1998 | | date = July–August 1998 | ||
| | page = 358 | | page = 358 | ||
| | url = http://people.math.gatech.edu/~hill/publications/PAPER%20PDFS/TheFirstDigitPhenomenonAmericanScientist1996.pdf | | url = http://people.math.gatech.edu/~hill/publications/PAPER%20PDFS/TheFirstDigitPhenomenonAmericanScientist1996.pdf | ||
| |format=PDF | |||
| | bibcode = 1998AmSci..86..358H | | bibcode = 1998AmSci..86..358H | ||
| | doi = 10.1511/1998.4.358 | | doi = 10.1511/1998.4.358 | ||
| | issue = 4| s2cid = 13553246 | |||
| | issue = 4}}</ref> A similar probabilistic explanation for the appearance of Benford's Law in everyday-life numbers has been advanced by showing that it arises naturally when one considers mixtures of uniform distributions.<ref>Élise Janvresse and Thierry de la Rue (2004), "From Uniform Distributions to Benford's Law", ''Journal of Applied Probability'', 41 1203–1210 {{doi|10.1239/jap/1101840566}} {{MR|2122815}} </ref> | |||
| }}</ref> A similar probabilistic explanation for the appearance of Benford's law in everyday-life numbers has been advanced by showing that it arises naturally when one considers mixtures of uniform distributions.<ref>{{cite journal | last1 = Janvresse | first1 = Élise | last2 = Thierry | year = 2004 | title = From Uniform Distributions to Benford's Law | url = http://lmrs.univ-rouen.fr/Persopage/Delarue/Publis/PDF/uniform_distribution_to_Benford_law.pdf | journal = Journal of Applied Probability | volume = 41 | issue = 4 | pages = 1203–1210 | doi = 10.1239/jap/1101840566 | mr = 2122815 | access-date = 13 August 2015 | archive-url = https://web.archive.org/web/20160304125725/http://lmrs.univ-rouen.fr/Persopage/Delarue/Publis/PDF/uniform_distribution_to_Benford_law.pdf | archive-date = 4 March 2016 | url-status = dead }}</ref> | |||
| === |
===Invariance=== | ||
| In a list of lengths, the distribution of first digits of numbers in the list may be generally similar regardless of whether all the lengths are expressed in metres, yards, feet, inches, etc. The same applies to monetary units. | |||
| This is not |
This is not always the case. For example, the height of adult humans almost always starts with a 1 or 2 when measured in metres and almost always starts with 4, 5, 6, or 7 when measured in feet. But in a list of lengths spread evenly over many orders of magnitude—for example, a list of 1000 lengths mentioned in scientific papers that includes the measurements of molecules, bacteria, plants, and galaxies—it is reasonable to expect the distribution of first digits to be the same no matter whether the lengths are written in metres or in feet. | ||
| When the distribution of the first digits of a data set is ] (independent of the units that the data are expressed in), it is always given by Benford's law.<ref name=Pinkham>{{cite journal | last1 = Pinkham | first1 = Roger S. | year = 1961 | title = On the Distribution of First Significant Digits | url = http://projecteuclid.org/DPubS?service=UI&version=1.0&verb=Display&handle=euclid.aoms/1177704862 | journal = Ann. Math. Statist. | volume = 32 | issue = 4 | pages = 1223–1230 | doi = 10.1214/aoms/1177704862 | doi-access = free }}</ref><ref name="wolfram">{{Cite web |url=https://mathworld.wolfram.com/BenfordsLaw.html |title=Benford's Law |first=Eric W. |last=Weisstein |website=mathworld.wolfram.com}}</ref> | |||
| But consider a list of lengths that is spread evenly over many orders of magnitude. For example, a list of 1000 lengths mentioned in scientific papers will include the measurements of molecules, bacteria, plants, and galaxies. If one writes all those lengths in meters, or writes them all in feet, it is reasonable to expect that the distribution of first digits should be the same on the two lists. | |||
| For example, the first (non-zero) digit on the aforementioned list of lengths should have the same distribution whether the unit of measurement is feet or yards. But there are three feet in a yard, so the probability that the first digit of a length in yards is 1 must be the same as the probability that the first digit of a length in feet is 3, 4, or 5; similarly, the probability that the first digit of a length in yards is 2 must be the same as the probability that the first digit of a length in feet is 6, 7, or 8. Applying this to all possible measurement scales gives the logarithmic distribution of Benford's law. | |||
| In these situations, where the distribution of first digits of a data set is ] (or independent of the units that the data are expressed in), the distribution of first digits is always given by Benford's Law.<ref name=Pinkham>Roger S. Pinkham, , Ann. Math. Statist. Volume 32, Number 4 (1961), 1223-1230.</ref><ref name=wolfram></ref> | |||
| Benford's law for first digits is ] invariant for number systems. There are conditions and proofs of sum invariance, inverse invariance, and addition and subtraction invariance.<ref>{{Cite web |last=Jamain |first=Adrien |date=September 2001 |title=Benford's Law |url=https://wwwf.imperial.ac.uk/~nadams/classificationgroup/Benfords-Law.pdf |archive-url=https://ghostarchive.org/archive/20221009/https://wwwf.imperial.ac.uk/~nadams/classificationgroup/Benfords-Law.pdf |archive-date=2022-10-09 |url-status=live |access-date=2020-11-15 |website=Imperial College of London}}</ref><ref>{{Cite journal |last=Berger |first=Arno |date=June 2011 |title=A basic theory of Benford's Law |url=https://projecteuclid.org/download/pdfview_1/euclid.ps/1311860830 |journal=Probability Surveys |volume=8 (2011) |pages=1–126}}</ref> | |||
| For example, the first (non-zero) digit on this list of lengths should have the same distribution whether the unit of measurement is feet or yards. But there are three feet in a yard, so the probability that the first digit of a length in yards is 1 must be the same as the probability that the first digit of a length in feet is 3, 4, or 5; similarly the probability that the first digit of a length in yards is 2 must be the same as the probability that the first digit of a length in feet is 6, 7, or 8. Applying this to all possible measurement scales gives the logarithmic distribution of Benford's law. | |||
| ==Applications== | ==Applications== | ||
| ===Accounting fraud detection=== | ===Accounting fraud detection=== | ||
| In 1972, ] suggested that the law could be used to detect possible ] in lists of socio-economic data submitted in support of public planning decisions. Based on the plausible assumption that people who |
In 1972, ] suggested that the law could be used to detect possible ] in lists of socio-economic data submitted in support of public planning decisions. Based on the plausible assumption that people who fabricate figures tend to distribute their digits fairly uniformly, a simple comparison of first-digit frequency distribution from the data with the expected distribution according to Benford's law ought to show up any anomalous results.<ref>{{Cite journal|first=Hal |last=Varian |author-link=Hal Varian |title=Benford's Law (Letters to the Editor) |journal=]|year=1972 |issue=3 |volume=26 |page=65 |doi=10.1080/00031305.1972.10478934}}</ref> | ||
| === |
===Use in criminal trials=== | ||
| In the United States, evidence based on Benford's law has been admitted in criminal cases at the federal, state, and local levels.<ref>{{cite episode| url = |
In the United States, evidence based on Benford's law has been admitted in criminal cases at the federal, state, and local levels.<ref>{{cite episode| url = https://www.wnycstudios.org/story/91699-from-benford-to-erdos| title =From Benford to Erdös | series = Radio Lab | series-link = Radio Lab | airdate = 2009-09-30 | number = 2009-10-09}}</ref> | ||
| ===Election data=== | ===Election data=== | ||
| ], a political scientist and statistician at the University of Michigan, was the first to apply the second-digit Benford's law-test (2BL-test) in ].<ref>Walter R. Mebane, Jr., "" (July 18, 2006).</ref> Such analysis is considered a simple, though not foolproof, method of identifying irregularities in election results.<ref>"", '']'' (February 22, 2007).</ref> Scientific consensus to support the applicability of Benford's law to elections has not been reached in the literature. A 2011 study by the political scientists Joseph Deckert, Mikhail Myagkov, and ] argued that Benford's law is problematic and misleading as a statistical indicator of election fraud.<ref>{{cite journal |last1=Deckert |first1=Joseph |last2=Myagkov |first2=Mikhail |last3=Ordeshook |first3=Peter C. |title=Benford's Law and the Detection of Election Fraud |journal=Political Analysis |date=2011 |volume=19 |issue=3 |pages=245–268 |doi=10.1093/pan/mpr014 |url=https://www.cambridge.org/core/journals/political-analysis/article/benfords-law-and-the-detection-of-election-fraud/3B1D64E822371C461AF3C61CE91AAF6D |language=en |issn=1047-1987|doi-access=free }}</ref> Their method was criticized by Mebane in a response, though he agreed that there are many caveats to the application of Benford's law to election data.<ref>{{cite journal |last1=Mebane |first1=Walter R. |title=Comment on "Benford's Law and the Detection of Election Fraud" |journal=Political Analysis |date=2011 |volume=19 |issue=3 |pages=269–272 |doi=10.1093/pan/mpr024 |url=https://www.cambridge.org/core/journals/political-analysis/article/comment-on-benfords-law-and-the-detection-of-election-fraud/BC29680D8B5469A54C7C9D865029FE7C |language=en |doi-access=free }}</ref> | |||
| Benford's Law has been invoked as evidence of fraud in the ],<ref>Stephen Battersby ''New Scientist'' 24 June 2009</ref> and also used to analyze other election results. However, other experts consider Benford's Law essentially useless as a statistical indicator of election fraud in general.<ref>Joseph Deckert, Mikhail Myagkov and Peter C. Ordeshook, (2010) '' {{webarchive |url=https://web.archive.org/web/20140517120934/http://vote.caltech.edu/sites/default/files/benford_pdf_4b97cc5b5b.pdf |date=17 May 2014 }}'', Caltech/MIT Voting Technology Project Working Paper No. 9</ref><ref>Charles R. Tolle, Joanne L. Budzien, and Randall A. LaViolette (2000) '']'', Chaos 10, 2, pp.331–336 (2000); {{doi|10.1063/1.166498}}</ref> | |||
| Benford's law ] in the ].<ref>Stephen Battersby ''New Scientist'' 24 June 2009</ref> An analysis by Mebane found that the second digits in vote counts for President ], the winner of the election, tended to differ significantly from the expectations of Benford's law, and that the ballot boxes with very few ] had a greater influence on the results, suggesting widespread ].<ref>Walter R. Mebane, Jr., "" (University of Michigan, June 29, 2009), pp. 22–23.</ref> Another study used ] simulations to find that the candidate ] received almost twice as many vote counts beginning with the digit 7 as would be expected according to Benford's law,<ref>{{cite journal |doi=10.1080/02664763.2013.838664 |arxiv=0906.2789|title=A first-digit anomaly in the 2009 Iranian presidential election|year=2014|last1=Roukema|first1=Boudewijn F.|journal=Journal of Applied Statistics|volume=41|pages=164–199|bibcode=2014JApS...41..164R|s2cid=88519550}}</ref> while an analysis from ] concluded that the probability that a fair election would produce both too few non-adjacent digits and the suspicious deviations in last-digit frequencies as found in the 2009 Iranian presidential election is less than 0.5 percent.<ref>Bernd Beber and Alexandra Scacco, "", '']'' (June 20, 2009).</ref> Benford's law has also been applied for forensic auditing and fraud detection on data from the ],<ref>Mark J. Nigrini, ''Benford's Law: Applications for Forensic Accounting, Auditing, and Fraud Detection'' (Hoboken, NJ: Wiley, 2012), pp. 132–35.</ref> the ] and ]s,<ref name="election-forensics">Walter R. Mebane, Jr., "Election Forensics: The Second-Digit Benford's Law Test and Recent American Presidential Elections" in ''Election Fraud: Detecting and Deterring Electoral Manipulation'', edited by R. Michael Alvarez et al. (Washington, D.C.: Brookings Institution Press, 2008), pp. 162–81. </ref> and the ];<ref>{{cite journal|first1=Susumu |last1=Shikano |first2=Verena |last2=Mack |title=When Does the Second-Digit Benford's Law-Test Signal an Election Fraud? Facts or Misleading Test Results |journal=Jahrbücher für Nationalökonomie und Statistik |date=2011 |pages=719–732 |volume=231 |issue=5–6 |doi=10.1515/jbnst-2011-5-610 |s2cid=153896048 }}</ref> the Benford's Law Test was found to be "worth taking seriously as a statistical test for fraud," although "is not sensitive to distortions we know significantly affected many votes."<ref name="election-forensics"/>{{Explain|date=November 2020|reason=What were the results? Was fraud detected?}} | |||
| Benford's law has also been misapplied to claim election fraud. When applying the law to ]'s election returns for ], ], and other localities in the ], the distribution of the first digit did not follow Benford's law. The misapplication was a result of looking at data that was tightly bound in range, which violates the assumption inherent in Benford's law that the range of the data be large. The first digit test was applied to precinct-level data, but because precincts rarely receive more than a few thousand votes or fewer than several dozen, Benford's law cannot be expected to apply. According to Mebane, "It is widely understood that the first digits of precinct vote counts are not useful for trying to diagnose election frauds."<ref>{{cite news|url=https://www.reuters.com/article/uk-factcheck-benford/fact-check-deviation-from-benfords-law-does-not-prove-election-fraud-idUSKBN27Q3AI|title=Fact check: Deviation from Benford's Law does not prove election fraud|date=November 10, 2020|work=]}}</ref><ref>{{cite web|url=https://physicsworld.com/a/benfords-law-and-the-2020-us-presidential-election-nothing-out-of-the-ordinary/|title=Benford's law and the 2020 US presidential election: nothing out of the ordinary|first= James|last= Dacey|date=November 19, 2020|publisher=]}}</ref> | |||
| ===Macroeconomic data=== | ===Macroeconomic data=== | ||
| Similarly, the macroeconomic data the Greek government reported to the European Union before entering the ] was shown to be probably fraudulent using Benford's law, albeit years after the country joined.<ref> |
Similarly, the macroeconomic data the Greek government reported to the European Union before entering the ] was shown to be probably fraudulent using Benford's law, albeit years after the country joined.<ref>William Goodman, , '']'', Royal Statistical Society (June 2016), p. 38.</ref><ref name="Goldacre">{{cite news | title= The special trick that helps identify dodgy stats |url= https://www.theguardian.com/commentisfree/2011/sep/16/bad-science-dodgy-stats| last= Goldacre| first= Ben| author-link= Ben Goldacre | date= 16 September 2011| work= ] | access-date= 1 February 2019}}</ref> | ||
| === Price digit analysis === | === Price digit analysis === | ||
| Benford's law |
Researchers have used Benford's law to detect ] patterns, in a Europe-wide study in consumer product prices before and after euro was introduced in 2002.<ref>{{Cite journal|last1=Sehity|first1=Tarek el|last2=Hoelzl|first2=Erik|last3=Kirchler|first3=Erich|date=2005-12-01|title=Price developments after a nominal shock: Benford's Law and psychological pricing after the euro introduction|journal=International Journal of Research in Marketing|volume=22|issue=4|pages=471–480|doi=10.1016/j.ijresmar.2005.09.002|s2cid=154273305 }}</ref> The idea was that, without psychological pricing, the first two or three digits of price of items should follow Benford's law. Consequently, if the distribution of digits deviates from Benford's law (such as having a lot of 9's), it means merchants may have used psychological pricing. | ||
| When ], for a brief period of time, the price of goods in euro was simply converted from the price of goods in local currencies before the replacement. As it is essentially impossible to use psychological pricing simultaneously on both price-in-euro and price-in-local-currency, during the transition period, psychological pricing would be disrupted even if it used to be present. It can only be re-established once consumers have gotten used to prices in a single currency again, this time in euro. | |||
| As the researchers expected, the distribution of first price digit followed Benford's law, but the distribution of the second and third digits deviated significantly from Benford's law before the introduction, then deviated less during the introduction, then deviated more again after the introduction. | |||
| ===Genome data=== | ===Genome data=== | ||
| The number of ]s and their relationship to genome size differs between ]s and ]s with the former showing a log-linear relationship and the latter a linear relationship. Benford's law has been used to test this observation with an excellent fit to the data in both cases.<ref name=Friar2012>{{cite journal | last1 = Friar | first1 = JL | last2 = Goldman | first2 = T | last3 = Pérez-Mercader | first3 = J | year = 2012 | title = Genome sizes and the benford distribution | journal = PLOS ONE | volume = 7 | issue = 5| page = e36624 | doi = 10.1371/journal.pone.0036624 |arxiv = 1205.6512 |bibcode = 2012PLoSO...736624F | pmid=22629319 | pmc=3356352}}</ref> | The number of ]s and their relationship to genome size differs between ]s and ]s with the former showing a log-linear relationship and the latter a linear relationship. Benford's law has been used to test this observation with an excellent fit to the data in both cases.<ref name=Friar2012>{{cite journal | last1 = Friar | first1 = JL | last2 = Goldman | first2 = T | last3 = Pérez-Mercader | first3 = J | year = 2012 | title = Genome sizes and the benford distribution | journal = PLOS ONE | volume = 7 | issue = 5| page = e36624 | doi = 10.1371/journal.pone.0036624 |arxiv = 1205.6512 |bibcode = 2012PLoSO...736624F | pmid=22629319 | pmc=3356352| doi-access = free }}</ref> | ||
| ===Scientific fraud detection=== | ===Scientific fraud detection=== | ||
| A test of regression coefficients in published papers showed agreement with Benford's law.<ref name=Diekmann2007>Diekmann A |
A test of regression coefficients in published papers showed agreement with Benford's law.<ref name=Diekmann2007>{{cite journal | last1 = Diekmann | first1 = A | s2cid = 117402608 | year = 2007 | title = Not the First Digit! Using Benford's Law to detect fraudulent scientific data | journal = J Appl Stat | volume = 34 | issue = 3| pages = 321–329 | doi = 10.1080/02664760601004940 | bibcode = 2007JApSt..34..321D | hdl = 20.500.11850/310246 | hdl-access = free }}</ref> As a comparison group subjects were asked to fabricate statistical estimates. The fabricated results conformed to Benford's law on first digits, but failed to obey Benford's law on second digits. | ||
| === Academic publishing networks === | |||
| Testing the number of published scientific papers of all registered researchers in Slovenia's national database was shown to strongly conform to Benford's law.<ref>{{Cite journal |last1=Tošić |first1=Aleksandar |last2=Vičič |first2=Jernej |date=2021-08-01 |title=Use of Benford's law on academic publishing networks |url=https://www.sciencedirect.com/science/article/pii/S1751157721000341 |journal=Journal of Informetrics |volume=15 |issue=3 |pages=101163 |doi=10.1016/j.joi.2021.101163 |issn=1751-1577}}</ref> Moreover, the authors were grouped by scientific field, and tests indicate natural sciences exhibit greater conformity than social sciences. | |||
| ==Statistical tests== | ==Statistical tests== | ||
| Although the ] |
Although the ] has been used to test for compliance with Benford's law it has low statistical power when used with small samples. | ||
| The ] and the ] are more powerful when the sample size is small particularly when Stephens's corrective factor is used.<ref name=Stephens1970>{{cite journal |last=Stephens |first=M. A. |year=1970 |title=Use of the Kolmogorov–Smirnov, |
The ] and the ] are more powerful when the sample size is small, particularly when Stephens's corrective factor is used.<ref name=Stephens1970>{{cite journal |last=Stephens |first=M. A. |year=1970 |title=Use of the Kolmogorov–Smirnov, Cramér–von Mises and related statistics without extensive tables |journal=] |volume=32 |issue=1 |pages=115–122 |doi=10.1111/j.2517-6161.1970.tb00821.x }}</ref> These tests may be unduly conservative when applied to discrete distributions. Values for the Benford test have been generated by Morrow.<ref name=Morrow2014>{{cite book |last = Morrow |first = John |title = Benford's Law, families of distributions and a test basis |location = London, UK |access-date = 2022-03-11 |date = August 2014 |url = http://cep.lse.ac.uk/_new/publications/series.asp?prog=CEP}}</ref> The critical values of the test statistics are shown below: | ||
| {| class="wikitable" | :{| class="wikitable" style="text-align:center;" | ||
| ! {{diagonal split header|Test| {{mvar|⍺}} }} | |||
| |- | |||
| ! {{diagonal split header|Test|''α''}} | |||
| ! 0.10 | ! 0.10 | ||
| ! 0.05 | ! 0.05 | ||
| ! 0.01 | ! 0.01 | ||
| |- | |- | ||
| | Kuiper |
| Kuiper | ||
| | 1.191 | | 1.191 | ||
| | 1.321 | | 1.321 | ||
| Line 271: | Line 334: | ||
| These critical values provide the minimum test statistic values required to reject the hypothesis of compliance with Benford's law at the given ]s. | These critical values provide the minimum test statistic values required to reject the hypothesis of compliance with Benford's law at the given ]s. | ||
| Two alternative tests specific to this law have been published: |
Two alternative tests specific to this law have been published: First, the max ({{mvar|m}}) statistic<ref name=Leemis2000>{{cite journal |last1=Leemis |first1=L. M. |last2=Schmeiser |first2=B. W. |last3=Evans |first3=D. L. |year=2000 |title=Survival distributions satisfying Benford's Law |journal=The American Statistician |volume=54 |issue=4 |pages=236–241 |doi=10.1080/00031305.2000.10474554 |s2cid=122607770}}</ref> is given by | ||
| :<math>m = \sqrt{N}\cdot\operatorname*\max_{i=1}^{9} \Big\{|\Pr (X \text{ has FSD}=i)-\log_{10}(1+1/i)| \Big\}\,</math> | |||
| and secondly, the distance (''d'') statistic<ref name=Cho2007>{{cite journal |last1=Cho |first1=W. K. T. |last2=Gaines |first2=B. J. |year=2007 |title=Breaking the (Benford) law: Statistical fraud detection in campaign finance |journal=The American Statistician |volume=61 |pages=218–223 |doi=10.1198/000313007X223496 |issue=3}}</ref> is given by | |||
| :<math>d= \sqrt{N \cdot \sum_{i=1}^{9}\Big^{2}},</math> | |||
| where FSD is the First Significant Digit and {{mvar|N}} is the sample size. Morrow has determined the critical values for both these statistics, which are shown below:<ref name="Morrow2010" /> | |||
| : <math>m = \sqrt{N} \cdot \max_{k=1}^9 \left\{\left|\Pr\left(X \text{ has FSD} = k\right) - \log_{10}\left(1 + \frac{1}{k}\right)\right|\right\}.</math> | |||
| {| class="wikitable" | |||
| |- | |||
| The leading factor <math>\sqrt{N}</math> does not appear in the original formula by Leemis;<ref name=Leemis2000/> it was added by Morrow in a later paper.<ref name=Morrow2014/> | |||
| ! {{diagonal split header|Statistic|''⍺''}} | |||
| Secondly, the distance ({{mvar|d}}) statistic<ref name=Cho2007>{{cite journal |last1=Cho |first1=W. K. T. |last2=Gaines |first2=B. J. |year=2007 |title=Breaking the (Benford) law: Statistical fraud detection in campaign finance |journal=The American Statistician |volume=61 |issue=3 |pages=218–223 |doi=10.1198/000313007X223496 |s2cid=7938920 }}</ref> is given by | |||
| : <math>d = \sqrt{N \cdot \sum_{l=1}^9 \left^2},</math> | |||
| where FSD is the first significant digit and {{mvar|N}} is the sample size. Morrow has determined the critical values for both these statistics, which are shown below:<ref name=Morrow2014/> | |||
| :{| class="wikitable" style="text-align:center;" | |||
| ! {{diagonal split header|Statistic|{{mvar|⍺}}}} | |||
| ! 0.10 | ! 0.10 | ||
| ! 0.05 | ! 0.05 | ||
| ! 0.01 | ! 0.01 | ||
| |- | |- | ||
| | Leemis' |
| Leemis's {{mvar|m}} | ||
| | 0.851 | | 0.851 | ||
| | 0.967 | | 0.967 | ||
| | 1.212 | | 1.212 | ||
| |- | |- | ||
| | Cho & Gaines's {{mvar|d}} | |||
| | Cho–Gaines' ''d'' | |||
| | 1.212 | | 1.212 | ||
| | 1.330 | | 1.330 | ||
| Line 295: | Line 363: | ||
| |} | |} | ||
| Morrow has also shown that for any random variable {{mvar|X}} (with a continuous ]) divided by its standard deviation ({{mvar|σ}}), some value {{mvar|A}} can be found so that the probability of the distribution of the first significant digit of the random variable <math>|X/\sigma|^A</math> will differ from Benford's law by less than {{nobr|{{mvar|ε}} > 0.}}<ref name=Morrow2014/> The value of {{mvar|A}} depends on the value of {{mvar|ε}} and the distribution of the random variable. | |||
| Nigrini<ref name=Nigrini1996>{{cite journal |last=Nigrini |first=M. |year=1996 |title=A taxpayer compliance application of Benford's Law |journal=J Amer Tax Assoc |volume=18 |pages=72–91}}</ref> has suggested the use of a ] | |||
| A method of accounting fraud detection based on bootstrapping and regression has been proposed.<ref name=Suh2011>{{cite journal |last1=Suh |first1=I. S. |last2=Headrick |first2=T. C. |last3=Minaburo |first3=S. |year=2011 |title=An effective and efficient analytic technique: A bootstrap regression procedure and Benford's Law |journal=J. Forensic & Investigative Accounting |volume=3 |issue=3}}</ref> | |||
| : <math> z = \frac { \, | p_o - p_e | - \frac{1}{2n} \, } { s_i } </math> | |||
| with | |||
| : <math> s_i = \left^{1/2}, </math> | |||
| If the goal is to conclude agreement with the Benford's law rather than disagreement, then the ]s mentioned above are inappropriate. In this case the specific ] should be applied. An empirical distribution is called equivalent to the Benford's law if a distance (for example total variation distance or the usual Euclidean distance) between the probability mass functions is sufficiently small. This method of testing with application to Benford's law is described in Ostrovski.<ref>{{cite journal |last=Ostrovski |first=Vladimir |date=May 2017 |title=Testing equivalence of multinomial distributions |journal=Statistics & Probability Letters |volume=124 |pages=77–82 |doi=10.1016/j.spl.2017.01.004 |s2cid=126293429 |url=https://www.researchgate.net/publication/312481284 }}</ref> | |||
| where |''x''| is the absolute value of ''x'', ''n'' is the sample size, {{sfrac|1|2''n''}} is a continuity correction factor, ''p''<sub>e</sub> is the proportion expected from Benford's law and ''p''<sub>o</sub> is the observed proportion in the sample. | |||
| ==Range of applicability== | |||
| Morrow has also shown that for any random variable ''X'' (with a continuous pdf) divided by its standard deviation (''σ''), a value ''A'' can be found such that the probability of the distribution of the first significant digit of the random variable ({{sfrac|''X''|''σ''}})<sup>''A''</sup> will differ from Benford's Law by less than ''ε'' > 0.<ref name="Morrow2010" /> The value of ''A'' depends on the value of ''ε'' and the distribution of the random variable. | |||
| ===Distributions known to obey Benford's law=== | |||
| Some well-known infinite ]s {{not a typo|provably}} satisfy Benford's law exactly (in the ] as more and more terms of the sequence are included). Among these are the ]s,<ref>{{cite journal | last1 = Washington | first1 = L. C. | year = 1981 | title = Benford's Law for Fibonacci and Lucas Numbers | journal = ] | volume = 19 | issue = 2| pages = 175–177| doi = 10.1080/00150517.1981.12430109 }}</ref><ref>{{cite journal | last1 = Duncan | first1 = R. L. | year = 1967 | title = An Application of Uniform Distribution to the Fibonacci Numbers | journal = ] | volume = 5 | issue = 2 | pages = 137–140| doi = 10.1080/00150517.1967.12431312 }}</ref> the ]s,<ref>{{cite journal | last1 = Sarkar | first1 = P. B. | year = 1973 | title = An Observation on the Significant Digits of Binomial Coefficients and Factorials | journal = Sankhya B | volume = 35 | pages = 363–364}}</ref> the powers of 2,<ref name=powers>In general, the sequence ''k''<sup>1</sup>, ''k''<sup>2</sup>, ''k''<sup>3</sup>, etc., satisfies Benford's law exactly, under the condition that log<sub>10</sub> ''k'' is an ]. This is a straightforward consequence of the ].</ref><ref name=":0">That the first 100 powers of 2 approximately satisfy Benford's law is mentioned by Ralph Raimi. {{cite journal | last1 = Raimi | first1 = Ralph A. | year = 1976 | title = The First Digit Problem | journal = ] | volume = 83 | issue = 7| pages = 521–538 | doi=10.2307/2319349| jstor = 2319349}}</ref> and the powers of almost any other number.<ref name=powers /> | |||
| Likewise, some continuous processes satisfy Benford's law exactly (in the asymptotic limit as the process continues through time). One is an ] or ] process: If a quantity is exponentially increasing or decreasing in time, then the percentage of time that it has each first digit satisfies Benford's law asymptotically (i.e. increasing accuracy as the process continues through time). | |||
| A method of accounting fraud detection based on bootstrapping and regression has been proposed.<ref name=Suh2011>{{cite journal |last1=Suh |first1=I. S. |last2=Headrick |first2=T. C. |last3=Minaburo |first3=S. |year=2011 |title=An effective and efficient analytic technique: A bootstrap regression procedure and Benford's Law |journal=J Forensic & Investigative Accounting |volume=3 |issue=3}}</ref> | |||
| ===Distributions known to disobey Benford's law=== | |||
| If the goal is to conclude agreement with the Benford's law rather than disagreement, then the ]s mentioned above are inappropriate. In this case the specific ] should be applied. An empirical distribution is called equivalent to the Benford's law if a distance (for example total variation distance or the usual Euclidean distance) between the probability mass functions is sufficiently small. This method of testing with application to Benford's law is described in Ostrovski (2017).<ref>{{cite journal|last1=Ostrovski|first1=Vladimir|date=May 2017|title=Testing equivalence of multinomial distributions|ssrn=2907258|journal=Statistics & Probability Letters|volume=124|pages=77–82|doi=10.1016/j.spl.2017.01.004|via=}}</ref> | |||
| The ]s and ]s of successive natural numbers do not obey this law.<ref name=Raimi1976>{{cite journal |last=Raimi |first=Ralph A. |date=Aug–Sep 1976 |title=The first digit problem |journal=] |volume=83 |issue=7 |pages=521–538 |doi=10.2307/2319349|jstor=2319349}}</ref> Prime numbers in a finite range follow a Generalized Benford’s law, that approaches uniformity as the size of the range approaches infinity.<ref>{{Cite web|last1=Zyga|first1=Lisa|last2=Phys.org|title=New Pattern Found in Prime Numbers|url=https://phys.org/news/2009-05-pattern-prime.html|access-date=2022-01-23|website=phys.org|language=en}}</ref> Lists of local telephone numbers violate Benford's law.<ref>{{Cite journal| issn = 0003-1305| volume = 61| issue = 3| pages = 218–223| last1 = Cho| first1 = Wendy K. Tam| last2 = Gaines| first2 = Brian J.| title = Breaking the (Benford) Law: Statistical Fraud Detection in Campaign Finance| journal = The American Statistician| accessdate = 2022-03-08| date = 2007| doi = 10.1198/000313007X223496| url = https://www.jstor.org/stable/27643897| jstor = 27643897| s2cid = 7938920}}</ref> Benford's law is violated by the populations of all places with a population of at least 2500 individuals from five US states according to the 1960 and 1970 censuses, where only 19 % began with digit 1 but 20 % began with digit 2, because truncation at 2500 introduces statistical bias.<ref name=Raimi1976/> The terminal digits in pathology reports violate Benford's law due to rounding.<ref name=Beer2009>{{cite journal |last1=Beer |first1=Trevor W. |s2cid=206987736 |year=2009 |title=Terminal digit preference: beware of Benford's law |journal=] |volume=62 |issue=2 |page=192 |doi=10.1136/jcp.2008.061721|pmid=19181640}}</ref> | |||
| Distributions that do not span several orders of magnitude will not follow Benford's law. Examples include height, weight, and IQ scores.<ref name=Formann2010/><ref>Singleton, Tommie W. (May 1, 2011). "", ''ISACA Journal'', ]. Retrieved Nov. 9, 2020.</ref> | |||
| ==Generalization to digits beyond the first== | |||
| , hover over a point to show its values.]] | |||
| It is possible to extend the law to digits beyond the first.<ref name=Hill1995sigdig>], "The Significant-Digit Phenomenon", The American Mathematical Monthly, Vol. 102, No. 4, (Apr., 1995), pp. 322–327. . .</ref> In particular, the probability of encountering a number starting with the string of digits ''n'' is given by: | |||
| ===Criteria for distributions expected and not expected to obey Benford's law=== | |||
| :<math> \log_{ 10 } \left( n + 1 \right )- \log_{ 10 } \left( n \right ) = \log_{ 10 } \left( 1 + \frac{ 1 }{ n } \right)</math> | |||
| A number of criteria, applicable particularly to accounting data, have been suggested where Benford's law can be expected to apply.<ref name=Durtschi2004>{{cite journal | last1 = Durtschi | first1 = C | last2 = Hillison | first2 = W | last3 = Pacini | first3 = C | year = 2004 | title = The effective use of Benford's law to assist in detecting fraud in accounting data | journal = J Forensic Accounting | volume = 5 | pages = 17–34}}</ref> | |||
| ;Distributions that can be expected to obey Benford's law | |||
| For example, the probability that a number starts with the digits 3, 1, 4 is {{math|log<sub>10</sub>(1 + 1/314) ≈ 0.00138}}, as in the figure on the right. | |||
| * When the mean is greater than the median and the skew is positive | |||
| * Numbers that result from mathematical combination of numbers: e.g. quantity × price | |||
| * Transaction level data: e.g. disbursements, sales | |||
| ;Distributions that would not be expected to obey Benford's law | |||
| This result can be used to find the probability that a particular digit occurs at a given position within a number. For instance, the probability that a "2" is encountered as the second digit is<ref name=Hill1995sigdig /> | |||
| * Where numbers are assigned sequentially: e.g. check numbers, invoice numbers | |||
| * Where numbers are influenced by human thought: e.g. prices set by psychological thresholds ($9.99) | |||
| * Accounts with a large number of firm-specific numbers: e.g. accounts set up to record $100 refunds | |||
| * Accounts with a built-in minimum or maximum | |||
| * Distributions that do not span an order of magnitude of numbers. | |||
| ===Benford’s law compliance theorem=== | |||
| :<math> \log_{ 10 } \left( 1 + \frac{ 1 }{ 12 } \right ) + \log_{ 10 } \left( 1 + \frac{ 1 }{ 22 } \right )+ \cdots + \log_{ 10 } \left( 1 + \frac{ 1 }{ 92 } \right) \approx 0.109 </math> | |||
| Mathematically, Benford’s law applies if the distribution being tested fits the "Benford’s law compliance theorem".<ref name="dspguide"/> The derivation says that Benford's law is followed if the ] of the logarithm of the probability density function is zero for all integer values. Most notably, this is satisfied if the Fourier transform is zero (or negligible) for ''n'' ≥ 1. This is satisfied if the distribution is wide (since wide distribution implies a narrow Fourier transform). Smith summarizes thus (p. 716): | |||
| <blockquote> | |||
| Benford's law is followed by distributions that are wide compared with unit distance along the logarithmic scale. Likewise, the law is not followed by distributions that are narrow compared with unit distance … If the distribution is wide compared with unit distance on the log axis, it means that the spread in the set of numbers being examined is much greater than ten. | |||
| </blockquote> | |||
| In short, Benford’s law requires that the numbers in the distribution being measured have a spread across at least an order of magnitude. | |||
| And the probability that ''d'' (''d'' = 0, 1, ..., 9) is encountered as the ''n''-th (''n'' > 1) digit is | |||
| ==Tests with common distributions== | |||
| :<math> \sum_{ k = 10^{ n - 2 } }^{ 10^{ n - 1 } - 1 } \log_{ 10 } \left( 1 + \frac{ 1 }{ 10k + d } \right )</math> | |||
| Benford's law was empirically tested against the numbers (up to the 10th digit) generated by a number of important distributions, including the ], the ], the ], and others.<ref name=Formann2010 /> | |||
| The uniform distribution, as might be expected, does not obey Benford's law. In contrast, the ] of ] is well-described by Benford's law. | |||
| The distribution of the ''n''-th digit, as ''n'' increases, rapidly approaches a uniform distribution with 10% for each of the ten digits, as shown below.<ref name=Hill1995sigdig /> Four digits is often enough to assume a uniform distribution of 10% as '0' appears 10.0176% of the time in the fourth digit while '9' appears 9.9824% of the time. | |||
| {| class="wikitable" | |||
| !Digit | |||
| !0 | |||
| !1 | |||
| !2 | |||
| !3 | |||
| !4 | |||
| !5 | |||
| !6 | |||
| !7 | |||
| !8 | |||
| !9 | |||
| |- | |||
| !1st | |||
| | {{N/A}} | |||
| |30.1% | |||
| |17.6% | |||
| |12.5% | |||
| |9.7% | |||
| |7.9% | |||
| |6.7% | |||
| |5.8% | |||
| |5.1% | |||
| |4.6% | |||
| |- | |||
| !2nd | |||
| |12% | |||
| |11.4% | |||
| |10.9% | |||
| |10.4% | |||
| |10% | |||
| |9.7% | |||
| |9.3% | |||
| |9% | |||
| |8.8% | |||
| |8.5% | |||
| |- | |||
| !3rd | |||
| |10.2% | |||
| |10.1% | |||
| |10.1% | |||
| |10.1% | |||
| |10% | |||
| |10% | |||
| |9.9% | |||
| |9.9% | |||
| |9.9% | |||
| |9.8% | |||
| |} | |||
| Neither the normal distribution nor the ratio distribution of two normal distributions (the ]) obey Benford's law. Although the ] does not obey Benford's law, the ratio distribution of two half-normal distributions does. Neither the right-truncated normal distribution nor the ratio distribution of two right-truncated normal distributions are well described by Benford's law. This is not surprising as this distribution is weighted towards larger numbers. | |||
| ==Tests with common distributions== | |||
| Benford's law was empirically tested against the numbers (up to the 10th digit) generated by a number of important distributions, including the ], the ], the ], the ], the ], the ] and the ].<ref name=Formann2010 /> In addition to these the ] of two uniform distributions, the ratio distribution of two exponential distributions, the ratio distribution of two half-normal distributions, the ratio distribution of two right-truncated normal distributions, the ratio distribution of two chi-square distributions (the ]) and the ] distribution were tested. | |||
| Benford's law also describes the exponential distribution and the ratio distribution of two exponential distributions well. The fit of chi-squared distribution depends on the ] (df) with good agreement with df = 1 and decreasing agreement as the df increases. The ''F''-distribution is fitted well for low degrees of freedom. With increasing dfs the fit decreases but much more slowly than the chi-squared distribution. The fit of the log-normal distribution depends on the ] and the ] of the distribution. The variance has a much greater effect on the fit than does the mean. Larger values of both parameters result in better agreement with the law. The ratio of two log normal distributions is a log normal so this distribution was not examined. | |||
| Other distributions that have been examined include the |
Other distributions that have been examined include the Muth distribution, ], ], ], ] and the ] all of which show reasonable agreement with the law.<ref name=Leemis2000 /><ref name="Dümbgen2008">{{cite journal|last1=Dümbgen|first1=L|last2=Leuenberger|first2=C|s2cid =2596996|year=2008|title=Explicit bounds for the approximation error in Benford's Law|journal =Electronic Communications in Probability|volume=13|pages=99–112|doi=10.1214/ECP.v13-1358 |arxiv=0705.4488}}</ref> The ] – a density increases with increasing value of the random variable – does not show agreement with this law.<ref name="Dümbgen2008"/> | ||
| ==Generalization to digits beyond the first== | |||
| ==Distributions known to obey Benford's law== | |||
| }}, hover over a point to show its values.)]] | |||
| Some well-known infinite ]s {{not a typo|provably}} satisfy Benford's Law exactly (in the ] as more and more terms of the sequence are included). Among these are the ]s,<ref>{{cite journal | last1 = Washington | first1 = L. C. | year = 1981 | title = Benford's Law for Fibonacci and Lucas Numbers | url = | journal = ] | volume = 19 | issue = 2| pages = 175–177 }}</ref><ref>{{cite journal | last1 = Duncan | first1 = R. L. | year = 1967 | title = An Application of Uniform Distribution to the Fibonacci Numbers | url = | journal = ] | volume = 5 | issue = | pages = 137–140 }}</ref> the ]s,<ref>{{cite journal | last1 = Sarkar | first1 = P. B. | year = 1973 | title = An Observation on the Significant Digits of Binomial Coefficients and Factorials | url = | journal = ] B | volume = 35 | issue = | pages = 363–364 }}</ref> the powers of 2,<ref name=powers>In general, the sequence ''k''<sup>1</sup>, ''k''<sup>2</sup>, ''k''<sup>3</sup>, etc., satisfies Benford's Law exactly, under the condition that log<sub>10</sub> ''k'' is an ]. This is a straightforward consequence of the ].</ref><ref>That the first 100 powers of 2 approximately satisfy Benford's Law is mentioned by Ralph Raimi. {{cite journal | last1 = Raimi | first1 = Ralph A. | year = 1976 | title = The First Digit Problem | url = | journal = ] | volume = 83 | issue = 7| pages = 521–538 | doi=10.2307/2319349}}</ref> and the powers of ''almost'' any other number.<ref name=powers /> | |||
| It is possible to extend the law to digits beyond the first.<ref name=Hill1995sigdig>{{cite journal | last1 = Hill | first1 = Theodore P. | author-link = Theodore P. Hill | year = 1995 | title = The Significant-Digit Phenomenon | url = http://digitalcommons.calpoly.edu/cgi/viewcontent.cgi?article=1041&context=rgp_rsr | journal = The American Mathematical Monthly | volume = 102 | issue = 4| pages = 322–327 | jstor = 2974952 | doi = 10.1080/00029890.1995.11990578}}</ref> In particular, for any given number of digits, the probability of encountering a number starting with the string of digits ''n'' of that length{{snd}} discarding leading zeros{{snd}} is given by | |||
| : <math>\log_{10}(n + 1) - \log_{10}(n) = \log_{10}\left(1 + \frac{1}{n}\right).</math> | |||
| Likewise, some continuous processes satisfy Benford's Law exactly (in the asymptotic limit as the process continues through time). One is an ] or ] process: If a quantity is exponentially increasing or decreasing in time, then the percentage of time that it has each first digit satisfies Benford's Law asymptotically (i.e. increasing accuracy as the process continues through time). | |||
| Thus, the probability that a number starts with the digits 3, 1, 4 (some examples are 3.14, 3.142, {{pi}}, 314280.7, and 0.00314005) is {{math|log<sub>10</sub>(1 + 1/314) ≈ 0.00138}}, as in the box with the log-log graph on the right. | |||
| ==Distributions known to disobey Benford's law== | |||
| Square roots and reciprocals do not obey this law.<ref name=Raimi1976>{{cite journal |last=Raimi |first=Ralph A. |date=Aug–Sep 1976 |title=The first digit problem |url= |journal=] |volume=83 |issue=7 |pages=521–538 |doi=10.2307/2319349}}</ref> Also, Benford's law does not apply to ] such as ]. Telephone directories violate Benford's law because the numbers have a mostly fixed length and do not have the initial digit 1.<ref>The ] uses 1 as a long distance prefix, and much of the rest of the world reserves it to begin special 3-digit numbers like ].</ref> Benford's law is violated by the populations of all places with population at least 2500 from five US states according to the 1960 and 1970 censuses, where only 19% began with digit 1 but 20% began with digit 2, for the simple reason that the truncation at 2500 introduces statistical bias.<ref name=Raimi1976/> The terminal digits in pathology reports violate Benford's law due to rounding, and the fact that terminal digits are never expected to follow Benford's law in the first place.<ref name=Beer2009>{{cite journal |last=Beer |first1=Trevor W. |year=2009 |title=Terminal digit preference: beware of Benford's Law |url= |journal=] |volume=62 |issue=2 |page=192 |doi=10.1136/jcp.2008.061721}}</ref> | |||
| This result can be used to find the probability that a particular digit occurs at a given position within a number. For instance, the probability that a "2" is encountered as the second digit is<ref name=Hill1995sigdig /> | |||
| ==Criteria for distributions expected and not expected to obey Benford's Law== | |||
| A number of criteria—applicable particularly to accounting data—have been suggested where Benford's Law can be expected to apply and not to apply.<ref name=Durtschi2004>{{cite journal | last1 = Durtschi | first1 = C | last2 = Hillison | first2 = W | last3 = Pacini | first3 = C | year = 2004 | title = The effective use of Benford's Law to assist in detecting fraud in accounting data | url = | journal = J Forensic Accounting | volume = 5 | issue = | pages = 17–34 }}</ref> | |||
| : <math>\log_{10}\left(1 + \frac{1}{12}\right) + \log_{10}\left(1 + \frac{1}{22}\right) + \cdots + \log_{10}\left(1 + \frac{1}{92}\right) \approx 0.109.</math> | |||
| ;Distributions that can be expected to obey Benford's Law: | |||
| * When the mean is greater than the median and the skew is positive | |||
| * Numbers that result from mathematical combination of numbers: e.g. quantity × price | |||
| * Transaction level data: e.g. disbursements, sales | |||
| * Numbers produced when doing any multiplicative calculations with an Oughtred slide rule, since the answers naturally fall into the right logarithmic distribution. | |||
| And the probability that ''d'' (''d'' = 0, 1, ..., 9) is encountered as the ''n''-th (''n'' > 1) digit is | |||
| ;Distributions that would not be expected to obey Benford's Law: | |||
| * Where numbers are assigned sequentially: e.g. check numbers, invoice numbers | |||
| : <math>\sum_{k=10^{n-2}}^{10^{n-1}-1} \log_{10}\left(1 + \frac{1}{10k + d}\right).</math> | |||
| * Where numbers are influenced by human thought: e.g. prices set by psychological thresholds ($1.99) | |||
| * Accounts with a large number of firm-specific numbers: e.g. accounts set up to record $100 refunds | |||
| The distribution of the ''n''-th digit, as ''n'' increases, rapidly approaches a uniform distribution with 10% for each of the ten digits, as shown below.<ref name=Hill1995sigdig /> Four digits is often enough to assume a uniform distribution of 10% as "0" appears 10.0176% of the time in the fourth digit, while "9" appears 9.9824% of the time. | |||
| * Accounts with a built-in minimum or maximum | |||
| {| class="wikitable" style="text-align:right" | |||
| * Where no transaction is recorded | |||
| ! Digit | |||
| ! 0 | |||
| ! 1 | |||
| ! 2 | |||
| ! 3 | |||
| ! 4 | |||
| ! 5 | |||
| ! 6 | |||
| ! 7 | |||
| ! 8 | |||
| ! 9 | |||
| |- | |||
| ! 1st | |||
| | {{N/A}} | |||
| | 30.1% | |||
| | 17.6% | |||
| | 12.5% | |||
| | 9.7% | |||
| | 7.9% | |||
| | 6.7% | |||
| | 5.8% | |||
| | 5.1% | |||
| | 4.6% | |||
| |- | |||
| ! 2nd | |||
| | 12.0% | |||
| | 11.4% | |||
| | 10.9% | |||
| | 10.4% | |||
| | 10.0% | |||
| | 9.7% | |||
| | 9.3% | |||
| | 9.0% | |||
| | 8.8% | |||
| | 8.5% | |||
| |- | |||
| ! 3rd | |||
| | 10.2% | |||
| | 10.1% | |||
| | 10.1% | |||
| | 10.1% | |||
| | 10.0% | |||
| | 10.0% | |||
| | 9.9% | |||
| | 9.9% | |||
| | 9.9% | |||
| | 9.8% | |||
| |} | |||
| ==Moments== | ==Moments== | ||
| ] and ] of random variables for the digits 1 to 9 following this law have been calculated:<ref name=Scott2001>Scott, P.D.; Fasli, M. (2001) {{Webarchive|url=https://web.archive.org/web/20141213023657/http://dces.essex.ac.uk/technical-reports/2001/CSM-349.pdf |date=13 December 2014 }}. ''CSM Technical Report'' 349, Department of Computer Science, Univ. Essex</ref> | |||
| * ] 3.440 | * ] 3.440 | ||
| * ] 6.057 | * ] 6.057 | ||
| Line 414: | Line 488: | ||
| * ] −0.548 | * ] −0.548 | ||
| For the |
For the two-digit distribution according to Benford's law these values are also known:<ref name=Suh2010>{{cite journal | last1 = Suh | first1 = I. S. | last2 = Headrick | first2 = T. C. | year = 2010 | title = A comparative analysis of the bootstrap versus traditional statistical procedures applied to digital analysis based on Benford's law | url = http://www.bus.lsu.edu/accounting/faculty/lcrumbley/jfia/Articles/Abstracts/abs_2010v2n2a7.pdf | journal = Journal of Forensic and Investigative Accounting | volume = 2 | issue = 2 | pages = 144–175 | access-date = 30 June 2012 | archive-date = 7 October 2018 | archive-url = https://web.archive.org/web/20181007005451/http://www.bus.lsu.edu/accounting/faculty/lcrumbley/jfia/Articles/Abstracts/abs_2010v2n2a7.pdf | url-status = dead }}</ref> | ||
| * ] 38.590 | * ] 38.590 | ||
| * ] 621.832 | * ] 621.832 | ||
| Line 420: | Line 494: | ||
| * ] −0.547 | * ] −0.547 | ||
| A table of the exact probabilities for the joint occurrence of the first two digits according to Benford's law is available,<ref name=Suh2010/> as is the population correlation between the first and second digits:<ref name=Suh2010/> {{nowrap|1=''ρ'' = 0.0561 |
A table of the exact probabilities for the joint occurrence of the first two digits according to Benford's law is available,<ref name=Suh2010/> as is the population correlation between the first and second digits:<ref name=Suh2010/> {{nowrap|1=''ρ'' = 0.0561}}. | ||
| ==In popular culture== | |||
| Benford's law has appeared as a plot device in some twenty-first century popular entertainment. | |||
| * Television crime drama '']'' used Benford's law in the 2006 episode "The Running Man" to help solve a series of burglaries.<ref name="wolfram"/> | |||
| *The 2016 film ] relied on Benford's law to expose theft of funds from a robotics company. | |||
| * The 2017 ] series ] used Benford's law to analyze a cartel member's financial statements and uncover fraud. | |||
| * The 2021 ] novel ''Infinite 2'' applied Benford's law to test whether the characters are in a simulation or reality. | |||
| * In the novel ] by ] Paul Brown (Forensic Accountant at Hendley Associates) explains Benford's law to Jack Ryan Jr when discussing methods to unveil fraud in accounting books. | |||
| ==See also== | ==See also== | ||
| * ] | |||
| * ] | * ] | ||
| ==References== | ==References== | ||
| {{Reflist |
{{Reflist}} | ||
| ==Further reading== | ==Further reading== | ||
| {{Refbegin}} | {{Refbegin}} | ||
| * {{Cite journal | * {{Cite journal | ||
| |author1=Arno Berger |
|author1=Arno Berger |author2=Theodore P. Hill | ||
| | title =What |
| title =What is...Benford's law? | ||
| | journal = Notices of the AMS | | journal = Notices of the AMS | ||
| | volume = 64 | | volume = 64 | ||
| Line 439: | Line 520: | ||
| | year = 2017 | | year = 2017 | ||
| | pages = 132–134 | | pages = 132–134 | ||
| | url = |
| url = https://www.ams.org/publications/journals/notices/201702/rnoti-p132.pdf | ||
| | doi=10.1090/noti1477 | | doi=10.1090/noti1477 | ||
| | doi-access = free | |||
| }} | |||
| }} | |||
| * {{Cite book | * {{Cite book | ||
| |author1=Arno Berger |
|author1=Arno Berger |author2=Theodore P. Hill | ||
| |name-list-style=amp | title = An Introduction to Benford's Law | |||
| | publisher = Princeton University Press | | publisher = Princeton University Press | ||
| | year = 2015 | | year = 2015 | ||
| Line 450: | Line 532: | ||
| }} | }} | ||
| * Alex Ely Kossovsky. '''', 2014, World Scientific Publishing. {{ISBN|978-981-4583-68-8}}. | * Alex Ely Kossovsky. '''', 2014, World Scientific Publishing. {{ISBN|978-981-4583-68-8}}. | ||
| * {{cite web|url=http://mathworld.wolfram.com/BenfordsLaw.html |title=Benford's Law – |
* {{cite web|url=http://mathworld.wolfram.com/BenfordsLaw.html |title=Benford's Law – Wolfram MathWorld |publisher=Mathworld.wolfram.com |date=14 June 2012 |access-date=2012-06-26}} | ||
| * {{Cite book | |||
| | author = Mark J. Nigrini | |||
| | title = Benford's Law: Applications for Forensic Accounting, Auditing, and Fraud Detection | |||
| | publisher = John Wiley & Sons | |||
| | year = 2012 | |||
| | page = 330 | |||
| | isbn = 978-1-118-15285-0 | |||
| }} | |||
| * {{Cite journal | * {{Cite journal | ||
| | author = Alessandro Gambini | | author = Alessandro Gambini | ||
| Line 473: | Line 547: | ||
| | display-authors = 1 | | display-authors = 1 | ||
| | issue = 4 | | issue = 4 | ||
| | url = http://amsacta.unibo.it/3517/1/postprint_ExMath.pdf | |||
| }} | |||
| | doi-access = free | |||
| }} | |||
| * {{Cite journal | * {{Cite journal | ||
| | author = Sehity | | author = Sehity | ||
| | title = Price developments after a nominal shock: Benford's |
| title = Price developments after a nominal shock: Benford's law and psychological pricing after the euro introduction | ||
| | journal = International Journal of Research in Marketing | | journal = International Journal of Research in Marketing | ||
| | volume = 22 | | volume = 22 | ||
| Line 486: | Line 562: | ||
| | last3 = Kirchler | | last3 = Kirchler | ||
| | first3 = Erich | | first3 = Erich | ||
| | author3-link=Erich Kirchler | |||
| | issue = 4 | | issue = 4 | ||
| | s2cid = 154273305 | |||
| }} | |||
| }} | |||
| * {{Cite journal | |||
| * {{Cite book | |||
| | year = 2011 | | year = 2011 | ||
| | title = |
| title = Scatter and regularity implies Benford's law...and more | ||
| | isbn=978-9814327756 | |||
| | journal = Zenil: Randomness through computation: some answers, more questions | |||
| | ISBN=9814327751 | |||
| | issue = | |||
| | pages = 58–69 | | pages = 58–69 | ||
| | doi = 10.1142/9789814327756_0004 | | doi = 10.1142/9789814327756_0004 | ||
| |author1 = Nicolas Gauvrit|author2 = Jean-Paul Delahaye| |
|author1 = Nicolas Gauvrit|author-link1 = Nicolas Gauvrit|author2 = Jean-Paul Delahaye| s2cid = 88518074 | ||
| | author-link2 = Jean-Paul Delahaye | |||
| | bibcode = 2009arXiv0910.1359G | |||
| | |
| bibcode = 2009arXiv0910.1359G | ||
| | arxiv = 0910.1359 | |||
| }} | |||
| }} | |||
| * {{Cite journal | * {{Cite journal | ||
| | author = Bernhard Rauch | | author = Bernhard Rauch | ||
| Line 506: | Line 582: | ||
| | author3 = Gernot Brähler | | author3 = Gernot Brähler | ||
| | author4 = Stefan Engel | | author4 = Stefan Engel | ||
| | s2cid = 155072460 | |||
| |date=August 2011 | |date=August 2011 | ||
| | title = Fact and Fiction in EU-Governmental Economic Data | | title = Fact and Fiction in EU-Governmental Economic Data | ||
| Line 515: | Line 592: | ||
| }} | }} | ||
| * {{Cite journal | * {{Cite journal | ||
| |author1=Wendy Cho |
|author1=Wendy Cho |author2=Brian Gaines | ||
| |s2cid=7938920 | |||
| |lastauthoramp=yes |date=August 2007 | |||
| |name-list-style=amp |date=August 2007 | |||
| | title = Breaking the (Benford) Law: statistical fraud detection in campaign finance | | title = Breaking the (Benford) Law: statistical fraud detection in campaign finance | ||
| | journal = ] | | journal = ] | ||
| Line 524: | Line 602: | ||
| | doi = 10.1198/000313007X223496 | | doi = 10.1198/000313007X223496 | ||
| }} | }} | ||
| * {{cite journal | title = The Law of Harmony in Statistics: An Investigation of the Metrical Interdependence of Social Phenomena. by L. V. Furlan | |
* {{cite journal | title = The Law of Harmony in Statistics: An Investigation of the Metrical Interdependence of Social Phenomena. by L. V. Furlan | last1 = Geiringer | first1 = Hilda | journal = Journal of the American Statistical Association | year = 1948 | volume = 43 | pages = 325–328 | jstor = 2280379 | doi = 10.2307/2280379 | last2 = Furlan | first2 = L. V. | issue = 242 | author-link1 = Hilda Geiringer}} | ||
| {{Refend}} | {{Refend}} | ||
| ==External links== | ==External links== | ||
| {{ |
{{Commons category}} | ||
| * , an online bibliographic database on Benford's law. | |||
| * An open source project showing Benford's law in action against publicly available datasets. | |||
| ===General audience=== | |||
| * {{Cite journal |last=Benford |first=Frank |date=1938 |title=The Law of Anomalous Numbers |url=https://www.jstor.org/stable/984802 |journal=Proceedings of the American Philosophical Society |volume=78 |issue=4 |pages=551–572 |jstor=984802 |bibcode=1938PAPhS..78..551B |issn=0003-049X}} - Benford's original publication | |||
| * , an online bibliographic database on Benford's Law. | |||
| * Website includes 15 data sets, 10 Excel templates, photos, documents, and other miscellaneous items related to Benford's Law | |||
| * , 1998 article from '']''. | |||
| * , ] radio segment by ] | |||
| * , Radio segment from the ] program | |||
| * by Jon Walthoe, Robert Hunt and Mike Pearson, ''Plus Magazine'', September 1999 | |||
| * | |||
| * , showing first-digit distributions of various sequences evolve over time, interactive. | |||
| * A script for generating random numbers compliant with Benford's Law. | |||
| * An open source project showing Benford's Law in action against publicly available datasets. | |||
| * Implementation with Microsoft Analysis Services. | |||
| * {{cite web|last=Mould|first=Steve|title=Number 1 and Benford's Law|url=http://www.numberphile.com/videos/benfords_law.html|work=Numberphile|publisher=]}} | |||
| * An example of Benford's Law appearing in house price data. | |||
| * , lecture on Benford's Law. | |||
| * Interactive graphic: | |||
| ===More mathematical=== | |||
| * {{MathWorld | urlname=BenfordsLaw | title=Benford's Law}} | |||
| * by ] | |||
| * , at ]. | |||
| * | |||
| * {{arxiv|1612.04200}} - Few more Comments on Benford's Law | |||
| {{ProbDistributions|discrete-finite}} | {{ProbDistributions|discrete-finite}} | ||
| {{Authority control}} | |||
| {{DEFAULTSORT:Benford's Law}} | |||
| ] | ] | ||
| ] | ] | ||
Latest revision as of 15:41, 17 December 2024
Observation that in many real-life datasets, the leading digit is likely to be small For the unrelated adage, see Benford's law of controversy.

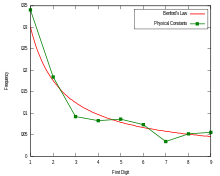
Benford's law, also known as the Newcomb–Benford law, the law of anomalous numbers, or the first-digit law, is an observation that in many real-life sets of numerical data, the leading digit is likely to be small. In sets that obey the law, the number 1 appears as the leading significant digit about 30% of the time, while 9 appears as the leading significant digit less than 5% of the time. Uniformly distributed digits would each occur about 11.1% of the time. Benford's law also makes predictions about the distribution of second digits, third digits, digit combinations, and so on.
The graph to the right shows Benford's law for base 10, one of infinitely many cases of a generalized law regarding numbers expressed in arbitrary (integer) bases, which rules out the possibility that the phenomenon might be an artifact of the base-10 number system. Further generalizations published in 1995 included analogous statements for both the nth leading digit and the joint distribution of the leading n digits, the latter of which leads to a corollary wherein the significant digits are shown to be a statistically dependent quantity.
It has been shown that this result applies to a wide variety of data sets, including electricity bills, street addresses, stock prices, house prices, population numbers, death rates, lengths of rivers, and physical and mathematical constants. Like other general principles about natural data—for example, the fact that many data sets are well approximated by a normal distribution—there are illustrative examples and explanations that cover many of the cases where Benford's law applies, though there are many other cases where Benford's law applies that resist simple explanations. Benford's law tends to be most accurate when values are distributed across multiple orders of magnitude, especially if the process generating the numbers is described by a power law (which is common in nature).
The law is named after physicist Frank Benford, who stated it in 1938 in an article titled "The Law of Anomalous Numbers", although it had been previously stated by Simon Newcomb in 1881.
The law is similar in concept, though not identical in distribution, to Zipf's law.
Definition

A set of numbers is said to satisfy Benford's law if the leading digit d (d ∈ {1, ..., 9}) occurs with probability
The leading digits in such a set thus have the following distribution:
| d | | Relative size of |
|---|---|---|
| 1 | 30.1% | 30.1 |
| 2 | 17.6% | 17.6 |
| 3 | 12.5% | 12.5 |
| 4 | 9.7% | 9.7 |
| 5 | 7.9% | 7.9 |
| 6 | 6.7% | 6.7 |
| 7 | 5.8% | 5.8 |
| 8 | 5.1% | 5.1 |
| 9 | 4.6% | 4.6 |
The quantity is proportional to the space between d and d + 1 on a logarithmic scale. Therefore, this is the distribution expected if the logarithms of the numbers (but not the numbers themselves) are uniformly and randomly distributed.
For example, a number x, constrained to lie between 1 and 10, starts with the digit 1 if 1 ≤ x < 2, and starts with the digit 9 if 9 ≤ x < 10. Therefore, x starts with the digit 1 if log 1 ≤ log x < log 2, or starts with 9 if log 9 ≤ log x < log 10. The interval is much wider than the interval (0.30 and 0.05 respectively); therefore if log x is uniformly and randomly distributed, it is much more likely to fall into the wider interval than the narrower interval, i.e. more likely to start with 1 than with 9; the probabilities are proportional to the interval widths, giving the equation above (as well as the generalization to other bases besides decimal).
Benford's law is sometimes stated in a stronger form, asserting that the fractional part of the logarithm of data is typically close to uniformly distributed between 0 and 1; from this, the main claim about the distribution of first digits can be derived.
In other bases

An extension of Benford's law predicts the distribution of first digits in other bases besides decimal; in fact, any base b ≥ 2. The general form is
For b = 2, 1 (the binary and unary) number systems, Benford's law is true but trivial: All binary and unary numbers (except for 0 or the empty set) start with the digit 1. (On the other hand, the generalization of Benford's law to second and later digits is not trivial, even for binary numbers.)
Examples

Examining a list of the heights of the 58 tallest structures in the world by category shows that 1 is by far the most common leading digit, irrespective of the unit of measurement (see "scale invariance" below):
| Leading digit |
m | ft | Per Benford's law | ||
|---|---|---|---|---|---|
| Count | Share | Count | Share | ||
| 1 | 23 | 39.7 % | 15 | 25.9 % | 30.1 % |
| 2 | 12 | 20.7 % | 8 | 13.8 % | 17.6 % |
| 3 | 6 | 10.3 % | 5 | 8.6 % | 12.5 % |
| 4 | 5 | 8.6 % | 7 | 12.1 % | 9.7 % |
| 5 | 2 | 3.4 % | 9 | 15.5 % | 7.9 % |
| 6 | 5 | 8.6 % | 4 | 6.9 % | 6.7 % |
| 7 | 1 | 1.7 % | 3 | 5.2 % | 5.8 % |
| 8 | 4 | 6.9 % | 6 | 10.3 % | 5.1 % |
| 9 | 0 | 0 % | 1 | 1.7 % | 4.6 % |
Another example is the leading digit of 2. The sequence of the first 96 leading digits (1, 2, 4, 8, 1, 3, 6, 1, 2, 5, 1, 2, 4, 8, 1, 3, 6, 1, ... (sequence A008952 in the OEIS)) exhibits closer adherence to Benford’s law than is expected for random sequences of the same length, because it is derived from a geometric sequence.
| Leading digit |
Occurrence | Per Benford's law | |
|---|---|---|---|
| Count | Share | ||
| 1 | 29 | 30.2 % | 30.1 % |
| 2 | 17 | 17.7 % | 17.6 % |
| 3 | 12 | 12.5 % | 12.5 % |
| 4 | 10 | 10.4 % | 9.7 % |
| 5 | 7 | 7.3 % | 7.9 % |
| 6 | 6 | 6.3 % | 6.7 % |
| 7 | 5 | 5.2 % | 5.8 % |
| 8 | 5 | 5.2 % | 5.1 % |
| 9 | 5 | 5.2 % | 4.6 % |
History
The discovery of Benford's law goes back to 1881, when the Canadian-American astronomer Simon Newcomb noticed that in logarithm tables the earlier pages (that started with 1) were much more worn than the other pages. Newcomb's published result is the first known instance of this observation and includes a distribution on the second digit as well. Newcomb proposed a law that the probability of a single number N being the first digit of a number was equal to log(N + 1) − log(N).
The phenomenon was again noted in 1938 by the physicist Frank Benford, who tested it on data from 20 different domains and was credited for it. His data set included the surface areas of 335 rivers, the sizes of 3259 US populations, 104 physical constants, 1800 molecular weights, 5000 entries from a mathematical handbook, 308 numbers contained in an issue of Reader's Digest, the street addresses of the first 342 persons listed in American Men of Science and 418 death rates. The total number of observations used in the paper was 20,229. This discovery was later named after Benford (making it an example of Stigler's law).
In 1995, Ted Hill proved the result about mixed distributions mentioned below.
Explanations
Benford's law tends to apply most accurately to data that span several orders of magnitude. As a rule of thumb, the more orders of magnitude that the data evenly covers, the more accurately Benford's law applies. For instance, one can expect that Benford's law would apply to a list of numbers representing the populations of United Kingdom settlements. But if a "settlement" is defined as a village with population between 300 and 999, then Benford's law will not apply.
Consider the probability distributions shown below, referenced to a log scale. In each case, the total area in red is the relative probability that the first digit is 1, and the total area in blue is the relative probability that the first digit is 8. For the first distribution, the size of the areas of red and blue are approximately proportional to the widths of each red and blue bar. Therefore, the numbers drawn from this distribution will approximately follow Benford's law. On the other hand, for the second distribution, the ratio of the areas of red and blue is very different from the ratio of the widths of each red and blue bar. Rather, the relative areas of red and blue are determined more by the heights of the bars than the widths. Accordingly, the first digits in this distribution do not satisfy Benford's law at all.
Thus, real-world distributions that span several orders of magnitude rather uniformly (e.g., stock-market prices and populations of villages, towns, and cities) are likely to satisfy Benford's law very accurately. On the other hand, a distribution mostly or entirely within one order of magnitude (e.g., IQ scores or heights of human adults) is unlikely to satisfy Benford's law very accurately, if at all. However, the difference between applicable and inapplicable regimes is not a sharp cut-off: as the distribution gets narrower, the deviations from Benford's law increase gradually.
(This discussion is not a full explanation of Benford's law, because it has not explained why data sets are so often encountered that, when plotted as a probability distribution of the logarithm of the variable, are relatively uniform over several orders of magnitude.)
Krieger–Kafri entropy explanation
In 1970 Wolfgang Krieger proved what is now called the Krieger generator theorem. The Krieger generator theorem might be viewed as a justification for the assumption in the Kafri ball-and-box model that, in a given base with a fixed number of digits 0, 1, ..., n, ..., , digit n is equivalent to a Kafri box containing n non-interacting balls. Other scientists and statisticians have suggested entropy-related explanations for Benford's law.
Multiplicative fluctuations
Many real-world examples of Benford's law arise from multiplicative fluctuations. For example, if a stock price starts at $100, and then each day it gets multiplied by a randomly chosen factor between 0.99 and 1.01, then over an extended period the probability distribution of its price satisfies Benford's law with higher and higher accuracy.
The reason is that the logarithm of the stock price is undergoing a random walk, so over time its probability distribution will get more and more broad and smooth (see above). (More technically, the central limit theorem says that multiplying more and more random variables will create a log-normal distribution with larger and larger variance, so eventually it covers many orders of magnitude almost uniformly.) To be sure of approximate agreement with Benford's law, the distribution has to be approximately invariant when scaled up by any factor up to 10; a log-normally distributed data set with wide dispersion would have this approximate property.
Unlike multiplicative fluctuations, additive fluctuations do not lead to Benford's law: They lead instead to normal probability distributions (again by the central limit theorem), which do not satisfy Benford's law. By contrast, that hypothetical stock price described above can be written as the product of many random variables (i.e. the price change factor for each day), so is likely to follow Benford's law quite well.
Multiple probability distributions
Anton Formann provided an alternative explanation by directing attention to the interrelation between the distribution of the significant digits and the distribution of the observed variable. He showed in a simulation study that long-right-tailed distributions of a random variable are compatible with the Newcomb–Benford law, and that for distributions of the ratio of two random variables the fit generally improves. For numbers drawn from certain distributions (IQ scores, human heights) the Benford's law fails to hold because these variates obey a normal distribution, which is known not to satisfy Benford's law, since normal distributions can't span several orders of magnitude and the Significand of their logarithms will not be (even approximately) uniformly distributed. However, if one "mixes" numbers from those distributions, for example, by taking numbers from newspaper articles, Benford's law reappears. This can also be proven mathematically: if one repeatedly "randomly" chooses a probability distribution (from an uncorrelated set) and then randomly chooses a number according to that distribution, the resulting list of numbers will obey Benford's law. A similar probabilistic explanation for the appearance of Benford's law in everyday-life numbers has been advanced by showing that it arises naturally when one considers mixtures of uniform distributions.
Invariance
In a list of lengths, the distribution of first digits of numbers in the list may be generally similar regardless of whether all the lengths are expressed in metres, yards, feet, inches, etc. The same applies to monetary units.
This is not always the case. For example, the height of adult humans almost always starts with a 1 or 2 when measured in metres and almost always starts with 4, 5, 6, or 7 when measured in feet. But in a list of lengths spread evenly over many orders of magnitude—for example, a list of 1000 lengths mentioned in scientific papers that includes the measurements of molecules, bacteria, plants, and galaxies—it is reasonable to expect the distribution of first digits to be the same no matter whether the lengths are written in metres or in feet.
When the distribution of the first digits of a data set is scale-invariant (independent of the units that the data are expressed in), it is always given by Benford's law.
For example, the first (non-zero) digit on the aforementioned list of lengths should have the same distribution whether the unit of measurement is feet or yards. But there are three feet in a yard, so the probability that the first digit of a length in yards is 1 must be the same as the probability that the first digit of a length in feet is 3, 4, or 5; similarly, the probability that the first digit of a length in yards is 2 must be the same as the probability that the first digit of a length in feet is 6, 7, or 8. Applying this to all possible measurement scales gives the logarithmic distribution of Benford's law.
Benford's law for first digits is base invariant for number systems. There are conditions and proofs of sum invariance, inverse invariance, and addition and subtraction invariance.
Applications
Accounting fraud detection
In 1972, Hal Varian suggested that the law could be used to detect possible fraud in lists of socio-economic data submitted in support of public planning decisions. Based on the plausible assumption that people who fabricate figures tend to distribute their digits fairly uniformly, a simple comparison of first-digit frequency distribution from the data with the expected distribution according to Benford's law ought to show up any anomalous results.
Use in criminal trials
In the United States, evidence based on Benford's law has been admitted in criminal cases at the federal, state, and local levels.
Election data
Walter Mebane, a political scientist and statistician at the University of Michigan, was the first to apply the second-digit Benford's law-test (2BL-test) in election forensics. Such analysis is considered a simple, though not foolproof, method of identifying irregularities in election results. Scientific consensus to support the applicability of Benford's law to elections has not been reached in the literature. A 2011 study by the political scientists Joseph Deckert, Mikhail Myagkov, and Peter C. Ordeshook argued that Benford's law is problematic and misleading as a statistical indicator of election fraud. Their method was criticized by Mebane in a response, though he agreed that there are many caveats to the application of Benford's law to election data.
Benford's law has been used as evidence of fraud in the 2009 Iranian elections. An analysis by Mebane found that the second digits in vote counts for President Mahmoud Ahmadinejad, the winner of the election, tended to differ significantly from the expectations of Benford's law, and that the ballot boxes with very few invalid ballots had a greater influence on the results, suggesting widespread ballot stuffing. Another study used bootstrap simulations to find that the candidate Mehdi Karroubi received almost twice as many vote counts beginning with the digit 7 as would be expected according to Benford's law, while an analysis from Columbia University concluded that the probability that a fair election would produce both too few non-adjacent digits and the suspicious deviations in last-digit frequencies as found in the 2009 Iranian presidential election is less than 0.5 percent. Benford's law has also been applied for forensic auditing and fraud detection on data from the 2003 California gubernatorial election, the 2000 and 2004 United States presidential elections, and the 2009 German federal election; the Benford's Law Test was found to be "worth taking seriously as a statistical test for fraud," although "is not sensitive to distortions we know significantly affected many votes."
Benford's law has also been misapplied to claim election fraud. When applying the law to Joe Biden's election returns for Chicago, Milwaukee, and other localities in the 2020 United States presidential election, the distribution of the first digit did not follow Benford's law. The misapplication was a result of looking at data that was tightly bound in range, which violates the assumption inherent in Benford's law that the range of the data be large. The first digit test was applied to precinct-level data, but because precincts rarely receive more than a few thousand votes or fewer than several dozen, Benford's law cannot be expected to apply. According to Mebane, "It is widely understood that the first digits of precinct vote counts are not useful for trying to diagnose election frauds."
Macroeconomic data
Similarly, the macroeconomic data the Greek government reported to the European Union before entering the eurozone was shown to be probably fraudulent using Benford's law, albeit years after the country joined.
Price digit analysis
Researchers have used Benford's law to detect psychological pricing patterns, in a Europe-wide study in consumer product prices before and after euro was introduced in 2002. The idea was that, without psychological pricing, the first two or three digits of price of items should follow Benford's law. Consequently, if the distribution of digits deviates from Benford's law (such as having a lot of 9's), it means merchants may have used psychological pricing.
When the euro replaced local currencies in 2002, for a brief period of time, the price of goods in euro was simply converted from the price of goods in local currencies before the replacement. As it is essentially impossible to use psychological pricing simultaneously on both price-in-euro and price-in-local-currency, during the transition period, psychological pricing would be disrupted even if it used to be present. It can only be re-established once consumers have gotten used to prices in a single currency again, this time in euro.
As the researchers expected, the distribution of first price digit followed Benford's law, but the distribution of the second and third digits deviated significantly from Benford's law before the introduction, then deviated less during the introduction, then deviated more again after the introduction.
Genome data
The number of open reading frames and their relationship to genome size differs between eukaryotes and prokaryotes with the former showing a log-linear relationship and the latter a linear relationship. Benford's law has been used to test this observation with an excellent fit to the data in both cases.
Scientific fraud detection
A test of regression coefficients in published papers showed agreement with Benford's law. As a comparison group subjects were asked to fabricate statistical estimates. The fabricated results conformed to Benford's law on first digits, but failed to obey Benford's law on second digits.
Academic publishing networks
Testing the number of published scientific papers of all registered researchers in Slovenia's national database was shown to strongly conform to Benford's law. Moreover, the authors were grouped by scientific field, and tests indicate natural sciences exhibit greater conformity than social sciences.
Statistical tests
Although the chi-squared test has been used to test for compliance with Benford's law it has low statistical power when used with small samples.
The Kolmogorov–Smirnov test and the Kuiper test are more powerful when the sample size is small, particularly when Stephens's corrective factor is used. These tests may be unduly conservative when applied to discrete distributions. Values for the Benford test have been generated by Morrow. The critical values of the test statistics are shown below:
⍺ Test 0.10 0.05 0.01 Kuiper 1.191 1.321 1.579 Kolmogorov–Smirnov 1.012 1.148 1.420
These critical values provide the minimum test statistic values required to reject the hypothesis of compliance with Benford's law at the given significance levels.
Two alternative tests specific to this law have been published: First, the max (m) statistic is given by
The leading factor does not appear in the original formula by Leemis; it was added by Morrow in a later paper.
Secondly, the distance (d) statistic is given by
where FSD is the first significant digit and N is the sample size. Morrow has determined the critical values for both these statistics, which are shown below:
⍺Statistic 0.10 0.05 0.01 Leemis's m 0.851 0.967 1.212 Cho & Gaines's d 1.212 1.330 1.569
Morrow has also shown that for any random variable X (with a continuous PDF) divided by its standard deviation (σ), some value A can be found so that the probability of the distribution of the first significant digit of the random variable will differ from Benford's law by less than ε > 0. The value of A depends on the value of ε and the distribution of the random variable.
A method of accounting fraud detection based on bootstrapping and regression has been proposed.
If the goal is to conclude agreement with the Benford's law rather than disagreement, then the goodness-of-fit tests mentioned above are inappropriate. In this case the specific tests for equivalence should be applied. An empirical distribution is called equivalent to the Benford's law if a distance (for example total variation distance or the usual Euclidean distance) between the probability mass functions is sufficiently small. This method of testing with application to Benford's law is described in Ostrovski.
Range of applicability
Distributions known to obey Benford's law
Some well-known infinite integer sequences provably satisfy Benford's law exactly (in the asymptotic limit as more and more terms of the sequence are included). Among these are the Fibonacci numbers, the factorials, the powers of 2, and the powers of almost any other number.
Likewise, some continuous processes satisfy Benford's law exactly (in the asymptotic limit as the process continues through time). One is an exponential growth or decay process: If a quantity is exponentially increasing or decreasing in time, then the percentage of time that it has each first digit satisfies Benford's law asymptotically (i.e. increasing accuracy as the process continues through time).
Distributions known to disobey Benford's law
The square roots and reciprocals of successive natural numbers do not obey this law. Prime numbers in a finite range follow a Generalized Benford’s law, that approaches uniformity as the size of the range approaches infinity. Lists of local telephone numbers violate Benford's law. Benford's law is violated by the populations of all places with a population of at least 2500 individuals from five US states according to the 1960 and 1970 censuses, where only 19 % began with digit 1 but 20 % began with digit 2, because truncation at 2500 introduces statistical bias. The terminal digits in pathology reports violate Benford's law due to rounding.
Distributions that do not span several orders of magnitude will not follow Benford's law. Examples include height, weight, and IQ scores.
Criteria for distributions expected and not expected to obey Benford's law
A number of criteria, applicable particularly to accounting data, have been suggested where Benford's law can be expected to apply.
- Distributions that can be expected to obey Benford's law
- When the mean is greater than the median and the skew is positive
- Numbers that result from mathematical combination of numbers: e.g. quantity × price
- Transaction level data: e.g. disbursements, sales
- Distributions that would not be expected to obey Benford's law
- Where numbers are assigned sequentially: e.g. check numbers, invoice numbers
- Where numbers are influenced by human thought: e.g. prices set by psychological thresholds ($9.99)
- Accounts with a large number of firm-specific numbers: e.g. accounts set up to record $100 refunds
- Accounts with a built-in minimum or maximum
- Distributions that do not span an order of magnitude of numbers.
Benford’s law compliance theorem
Mathematically, Benford’s law applies if the distribution being tested fits the "Benford’s law compliance theorem". The derivation says that Benford's law is followed if the Fourier transform of the logarithm of the probability density function is zero for all integer values. Most notably, this is satisfied if the Fourier transform is zero (or negligible) for n ≥ 1. This is satisfied if the distribution is wide (since wide distribution implies a narrow Fourier transform). Smith summarizes thus (p. 716):
Benford's law is followed by distributions that are wide compared with unit distance along the logarithmic scale. Likewise, the law is not followed by distributions that are narrow compared with unit distance … If the distribution is wide compared with unit distance on the log axis, it means that the spread in the set of numbers being examined is much greater than ten.
In short, Benford’s law requires that the numbers in the distribution being measured have a spread across at least an order of magnitude.
Tests with common distributions
Benford's law was empirically tested against the numbers (up to the 10th digit) generated by a number of important distributions, including the uniform distribution, the exponential distribution, the normal distribution, and others.
The uniform distribution, as might be expected, does not obey Benford's law. In contrast, the ratio distribution of two uniform distributions is well-described by Benford's law.
Neither the normal distribution nor the ratio distribution of two normal distributions (the Cauchy distribution) obey Benford's law. Although the half-normal distribution does not obey Benford's law, the ratio distribution of two half-normal distributions does. Neither the right-truncated normal distribution nor the ratio distribution of two right-truncated normal distributions are well described by Benford's law. This is not surprising as this distribution is weighted towards larger numbers.
Benford's law also describes the exponential distribution and the ratio distribution of two exponential distributions well. The fit of chi-squared distribution depends on the degrees of freedom (df) with good agreement with df = 1 and decreasing agreement as the df increases. The F-distribution is fitted well for low degrees of freedom. With increasing dfs the fit decreases but much more slowly than the chi-squared distribution. The fit of the log-normal distribution depends on the mean and the variance of the distribution. The variance has a much greater effect on the fit than does the mean. Larger values of both parameters result in better agreement with the law. The ratio of two log normal distributions is a log normal so this distribution was not examined.
Other distributions that have been examined include the Muth distribution, Gompertz distribution, Weibull distribution, gamma distribution, log-logistic distribution and the exponential power distribution all of which show reasonable agreement with the law. The Gumbel distribution – a density increases with increasing value of the random variable – does not show agreement with this law.
Generalization to digits beyond the first

It is possible to extend the law to digits beyond the first. In particular, for any given number of digits, the probability of encountering a number starting with the string of digits n of that length – discarding leading zeros – is given by
Thus, the probability that a number starts with the digits 3, 1, 4 (some examples are 3.14, 3.142, π, 314280.7, and 0.00314005) is log10(1 + 1/314) ≈ 0.00138, as in the box with the log-log graph on the right.
This result can be used to find the probability that a particular digit occurs at a given position within a number. For instance, the probability that a "2" is encountered as the second digit is
And the probability that d (d = 0, 1, ..., 9) is encountered as the n-th (n > 1) digit is
The distribution of the n-th digit, as n increases, rapidly approaches a uniform distribution with 10% for each of the ten digits, as shown below. Four digits is often enough to assume a uniform distribution of 10% as "0" appears 10.0176% of the time in the fourth digit, while "9" appears 9.9824% of the time.
| Digit | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1st | — | 30.1% | 17.6% | 12.5% | 9.7% | 7.9% | 6.7% | 5.8% | 5.1% | 4.6% |
| 2nd | 12.0% | 11.4% | 10.9% | 10.4% | 10.0% | 9.7% | 9.3% | 9.0% | 8.8% | 8.5% |
| 3rd | 10.2% | 10.1% | 10.1% | 10.1% | 10.0% | 10.0% | 9.9% | 9.9% | 9.9% | 9.8% |
Moments
Average and moments of random variables for the digits 1 to 9 following this law have been calculated:
For the two-digit distribution according to Benford's law these values are also known:
A table of the exact probabilities for the joint occurrence of the first two digits according to Benford's law is available, as is the population correlation between the first and second digits: ρ = 0.0561.
In popular culture
Benford's law has appeared as a plot device in some twenty-first century popular entertainment.
- Television crime drama NUMB3RS used Benford's law in the 2006 episode "The Running Man" to help solve a series of burglaries.
- The 2016 film The Accountant relied on Benford's law to expose theft of funds from a robotics company.
- The 2017 Netflix series Ozark used Benford's law to analyze a cartel member's financial statements and uncover fraud.
- The 2021 Jeremy Robinson novel Infinite 2 applied Benford's law to test whether the characters are in a simulation or reality.
- In the novel Tom Clancy Point of Contact by Mike Maiden Paul Brown (Forensic Accountant at Hendley Associates) explains Benford's law to Jack Ryan Jr when discussing methods to unveil fraud in accounting books.
See also
References
- Arno Berger and Theodore P. Hill, Benford's Law Strikes Back: No Simple Explanation in Sight for Mathematical Gem, 2011.
- Weisstein, Eric W. "Benford's Law". MathWorld, A Wolfram web resource. Retrieved 7 June 2015.
- Hill, Theodore (1995). "A Statistical Derivation of the Significant-Digit Law". Statistical Science. 10 (4). doi:10.1214/ss/1177009869.
- Paul H. Kvam, Brani Vidakovic, Nonparametric Statistics with Applications to Science and Engineering, p. 158.
- ^ Berger, Arno; Hill, Theodore P. (30 June 2020). "The mathematics of Benford's law: a primer". Stat. Methods Appl. 30 (3): 779–795. arXiv:1909.07527. doi:10.1007/s10260-020-00532-8. S2CID 202583554.
- Cai, Zhaodong; Faust, Matthew; Hildebrand, A. J.; Li, Junxian; Zhang, Yuan (15 March 2020). "The Surprising Accuracy of Benford's Law in Mathematics". The American Mathematical Monthly. 127 (3): 217–237. arXiv:1907.08894. doi:10.1080/00029890.2020.1690387. ISSN 0002-9890. S2CID 198147766.
- ^ Frank Benford (March 1938). "The law of anomalous numbers". Proc. Am. Philos. Soc. 78 (4): 551–572. Bibcode:1938PAPhS..78..551B. JSTOR 984802.
- ^ Simon Newcomb (1881). "Note on the frequency of use of the different digits in natural numbers". American Journal of Mathematics. 4 (1/4): 39–40. Bibcode:1881AmJM....4...39N. doi:10.2307/2369148. JSTOR 2369148. S2CID 124556624.
- ^ Formann, A. K. (2010). Morris, Richard James (ed.). "The Newcomb–Benford Law in Its Relation to Some Common Distributions". PLOS ONE. 5 (5): e10541. Bibcode:2010PLoSO...510541F. doi:10.1371/journal.pone.0010541. PMC 2866333. PMID 20479878.
- ^ Miller, Steven J., ed. (9 June 2015). Benford's Law: Theory and Applications. Princeton University Press. p. 309. ISBN 978-1-4008-6659-5.
- They should strictly be bars but are shown as lines for clarity.
- Pimbley, J. M. (2014). "Benford's Law as a Logarithmic Transformation" (PDF). Maxwell Consulting, LLC. Archived (PDF) from the original on 9 October 2022. Retrieved 15 November 2020.
- Khosravani, A. (2012). Transformation Invariance of Benford Variables and their Numerical Modeling. Recent Researches in Automatic Control and Electronics. pp. 57–61. ISBN 978-1-61804-080-0.
- ^ That the first 100 powers of 2 approximately satisfy Benford's law is mentioned by Ralph Raimi. Raimi, Ralph A. (1976). "The First Digit Problem". American Mathematical Monthly. 83 (7): 521–538. doi:10.2307/2319349. JSTOR 2319349.
- ^ Theodore P. Hill (1995). "A Statistical Derivation of the Significant-Digit Law". Statistical Science. 10 (4): 354–363. doi:10.1214/ss/1177009869. MR 1421567.
- Hill, Theodore P. (1995). "Base-invariance implies Benford's law". Proceedings of the American Mathematical Society. 123 (3): 887–895. doi:10.1090/S0002-9939-1995-1233974-8. ISSN 0002-9939.
- ^ Steven W. Smith. "Chapter 34: Explaining Benford's Law. The Power of Signal Processing". The Scientist and Engineer's Guide to Digital Signal Processing. Retrieved 15 December 2012.
- ^ Fewster, R. M. (2009). "A simple explanation of Benford's Law" (PDF). The American Statistician. 63 (1): 26–32. CiteSeerX 10.1.1.572.6719. doi:10.1198/tast.2009.0005. S2CID 39595550. Archived (PDF) from the original on 9 October 2022.
- Arno Berger and Theodore P. Hill, Benford's Law Strikes Back: No Simple Explanation in Sight for Mathematical Gem, 2011. The authors describe this argument but say it "still leaves open the question of why it is reasonable to assume that the logarithm of the spread, as opposed to the spread itself—or, say, the log log spread—should be large" and that "assuming large spread on a logarithmic scale is equivalent to assuming an approximate conformance with " (italics added), something which they say lacks a "simple explanation".
- Krieger, Wolfgang (1970). "On entropy and generators of measure-preserving transformations". Transactions of the American Mathematical Society. 149 (2): 453. doi:10.1090/S0002-9947-1970-0259068-3. ISSN 0002-9947.
- Downarowicz, Tomasz (12 May 2011). Entropy in Dynamical Systems. Cambridge University Press. p. 106. ISBN 978-1-139-50087-6.
- Smorodinsky, Meir (1971). "Chapter IX. Entropy and generators. Krieger's theorem". Ergodic Theory, Entropy. Lecture Notes in Mathematics. Vol. 214. Berlin, Heidelberg: Springer. pp. 54–57. doi:10.1007/BFb0066096. ISBN 978-3-540-05556-3.
- Jolion, Jean-Michel (2001). "Images and Benford's Law". Journal of Mathematical Imaging and Vision. 14 (1): 73–81. Bibcode:2001JMIV...14...73J. doi:10.1023/A:1008363415314. ISSN 0924-9907. S2CID 34151059.
- Lemons, Don S. (2019). "Thermodynamics of Benford's first digit law". American Journal of Physics. 87 (10): 787–790. arXiv:1604.05715. Bibcode:2019AmJPh..87..787L. doi:10.1119/1.5116005. ISSN 0002-9505. S2CID 119207367.
- ^ L. Pietronero; E. Tosatti; V. Tosatti; A. Vespignani (2001). "Explaining the uneven distribution of numbers in nature: the laws of Benford and Zipf". Physica A. 293 (1–2): 297–304. arXiv:cond-mat/9808305. Bibcode:2001PhyA..293..297P. doi:10.1016/S0378-4371(00)00633-6.
- Formann, A. K. (2010). "The Newcomb–Benford law in its relation to some common distributions". PLOS ONE. 5 (5): e10541. Bibcode:2010PLoSO...510541F. doi:10.1371/journal.pone.0010541. PMC 2866333. PMID 20479878.
- Theodore P. Hill (July–August 1998). "The first digit phenomenon" (PDF). American Scientist. 86 (4): 358. Bibcode:1998AmSci..86..358H. doi:10.1511/1998.4.358. S2CID 13553246.
- Janvresse, Élise; Thierry (2004). "From Uniform Distributions to Benford's Law" (PDF). Journal of Applied Probability. 41 (4): 1203–1210. doi:10.1239/jap/1101840566. MR 2122815. Archived from the original (PDF) on 4 March 2016. Retrieved 13 August 2015.
- Pinkham, Roger S. (1961). "On the Distribution of First Significant Digits". Ann. Math. Statist. 32 (4): 1223–1230. doi:10.1214/aoms/1177704862.
- ^ Weisstein, Eric W. "Benford's Law". mathworld.wolfram.com.
- Jamain, Adrien (September 2001). "Benford's Law" (PDF). Imperial College of London. Archived (PDF) from the original on 9 October 2022. Retrieved 15 November 2020.
- Berger, Arno (June 2011). "A basic theory of Benford's Law". Probability Surveys. 8 (2011): 1–126.
- Varian, Hal (1972). "Benford's Law (Letters to the Editor)". The American Statistician. 26 (3): 65. doi:10.1080/00031305.1972.10478934.
- "From Benford to Erdös". Radio Lab. Episode 2009-10-09. 30 September 2009.
- Walter R. Mebane, Jr., "Election Forensics: Vote Counts and Benford’s Law" (July 18, 2006).
- "Election forensics", The Economist (February 22, 2007).
- Deckert, Joseph; Myagkov, Mikhail; Ordeshook, Peter C. (2011). "Benford's Law and the Detection of Election Fraud". Political Analysis. 19 (3): 245–268. doi:10.1093/pan/mpr014. ISSN 1047-1987.
- Mebane, Walter R. (2011). "Comment on "Benford's Law and the Detection of Election Fraud"". Political Analysis. 19 (3): 269–272. doi:10.1093/pan/mpr024.
- Stephen Battersby Statistics hint at fraud in Iranian election New Scientist 24 June 2009
- Walter R. Mebane, Jr., "Note on the presidential election in Iran, June 2009" (University of Michigan, June 29, 2009), pp. 22–23.
- Roukema, Boudewijn F. (2014). "A first-digit anomaly in the 2009 Iranian presidential election". Journal of Applied Statistics. 41: 164–199. arXiv:0906.2789. Bibcode:2014JApS...41..164R. doi:10.1080/02664763.2013.838664. S2CID 88519550.
- Bernd Beber and Alexandra Scacco, "The Devil Is in the Digits: Evidence That Iran's Election Was Rigged", The Washington Post (June 20, 2009).
- Mark J. Nigrini, Benford's Law: Applications for Forensic Accounting, Auditing, and Fraud Detection (Hoboken, NJ: Wiley, 2012), pp. 132–35.
- ^ Walter R. Mebane, Jr., "Election Forensics: The Second-Digit Benford's Law Test and Recent American Presidential Elections" in Election Fraud: Detecting and Deterring Electoral Manipulation, edited by R. Michael Alvarez et al. (Washington, D.C.: Brookings Institution Press, 2008), pp. 162–81. PDF
- Shikano, Susumu; Mack, Verena (2011). "When Does the Second-Digit Benford's Law-Test Signal an Election Fraud? Facts or Misleading Test Results". Jahrbücher für Nationalökonomie und Statistik. 231 (5–6): 719–732. doi:10.1515/jbnst-2011-5-610. S2CID 153896048.
- "Fact check: Deviation from Benford's Law does not prove election fraud". Reuters. 10 November 2020.
- Dacey, James (19 November 2020). "Benford's law and the 2020 US presidential election: nothing out of the ordinary". Physics World.
- William Goodman, The promises and pitfalls of Benford's law, Significance, Royal Statistical Society (June 2016), p. 38.
- Goldacre, Ben (16 September 2011). "The special trick that helps identify dodgy stats". The Guardian. Retrieved 1 February 2019.
- Sehity, Tarek el; Hoelzl, Erik; Kirchler, Erich (1 December 2005). "Price developments after a nominal shock: Benford's Law and psychological pricing after the euro introduction". International Journal of Research in Marketing. 22 (4): 471–480. doi:10.1016/j.ijresmar.2005.09.002. S2CID 154273305.
- Friar, JL; Goldman, T; Pérez-Mercader, J (2012). "Genome sizes and the benford distribution". PLOS ONE. 7 (5): e36624. arXiv:1205.6512. Bibcode:2012PLoSO...736624F. doi:10.1371/journal.pone.0036624. PMC 3356352. PMID 22629319.
- Diekmann, A (2007). "Not the First Digit! Using Benford's Law to detect fraudulent scientific data". J Appl Stat. 34 (3): 321–329. Bibcode:2007JApSt..34..321D. doi:10.1080/02664760601004940. hdl:20.500.11850/310246. S2CID 117402608.
- Tošić, Aleksandar; Vičič, Jernej (1 August 2021). "Use of Benford's law on academic publishing networks". Journal of Informetrics. 15 (3): 101163. doi:10.1016/j.joi.2021.101163. ISSN 1751-1577.
- Stephens, M. A. (1970). "Use of the Kolmogorov–Smirnov, Cramér–von Mises and related statistics without extensive tables". Journal of the Royal Statistical Society, Series B. 32 (1): 115–122. doi:10.1111/j.2517-6161.1970.tb00821.x.
- ^ Morrow, John (August 2014). Benford's Law, families of distributions and a test basis. London, UK. Retrieved 11 March 2022.
{{cite book}}: CS1 maint: location missing publisher (link) - ^ Leemis, L. M.; Schmeiser, B. W.; Evans, D. L. (2000). "Survival distributions satisfying Benford's Law". The American Statistician. 54 (4): 236–241. doi:10.1080/00031305.2000.10474554. S2CID 122607770.
- Cho, W. K. T.; Gaines, B. J. (2007). "Breaking the (Benford) law: Statistical fraud detection in campaign finance". The American Statistician. 61 (3): 218–223. doi:10.1198/000313007X223496. S2CID 7938920.
- Suh, I. S.; Headrick, T. C.; Minaburo, S. (2011). "An effective and efficient analytic technique: A bootstrap regression procedure and Benford's Law". J. Forensic & Investigative Accounting. 3 (3).
- Ostrovski, Vladimir (May 2017). "Testing equivalence of multinomial distributions". Statistics & Probability Letters. 124: 77–82. doi:10.1016/j.spl.2017.01.004. S2CID 126293429.
- Washington, L. C. (1981). "Benford's Law for Fibonacci and Lucas Numbers". The Fibonacci Quarterly. 19 (2): 175–177. doi:10.1080/00150517.1981.12430109.
- Duncan, R. L. (1967). "An Application of Uniform Distribution to the Fibonacci Numbers". The Fibonacci Quarterly. 5 (2): 137–140. doi:10.1080/00150517.1967.12431312.
- Sarkar, P. B. (1973). "An Observation on the Significant Digits of Binomial Coefficients and Factorials". Sankhya B. 35: 363–364.
- ^ In general, the sequence k, k, k, etc., satisfies Benford's law exactly, under the condition that log10 k is an irrational number. This is a straightforward consequence of the equidistribution theorem.
- ^ Raimi, Ralph A. (August–September 1976). "The first digit problem". American Mathematical Monthly. 83 (7): 521–538. doi:10.2307/2319349. JSTOR 2319349.
- Zyga, Lisa; Phys.org. "New Pattern Found in Prime Numbers". phys.org. Retrieved 23 January 2022.
- Cho, Wendy K. Tam; Gaines, Brian J. (2007). "Breaking the (Benford) Law: Statistical Fraud Detection in Campaign Finance". The American Statistician. 61 (3): 218–223. doi:10.1198/000313007X223496. ISSN 0003-1305. JSTOR 27643897. S2CID 7938920. Retrieved 8 March 2022.
- Beer, Trevor W. (2009). "Terminal digit preference: beware of Benford's law". J. Clin. Pathol. 62 (2): 192. doi:10.1136/jcp.2008.061721. PMID 19181640. S2CID 206987736.
- Singleton, Tommie W. (May 1, 2011). "Understanding and Applying Benford’s Law", ISACA Journal, Information Systems Audit and Control Association. Retrieved Nov. 9, 2020.
- Durtschi, C; Hillison, W; Pacini, C (2004). "The effective use of Benford's law to assist in detecting fraud in accounting data". J Forensic Accounting. 5: 17–34.
- ^ Dümbgen, L; Leuenberger, C (2008). "Explicit bounds for the approximation error in Benford's Law". Electronic Communications in Probability. 13: 99–112. arXiv:0705.4488. doi:10.1214/ECP.v13-1358. S2CID 2596996.
- ^ Hill, Theodore P. (1995). "The Significant-Digit Phenomenon". The American Mathematical Monthly. 102 (4): 322–327. doi:10.1080/00029890.1995.11990578. JSTOR 2974952.
- Scott, P.D.; Fasli, M. (2001) "Benford's Law: An empirical investigation and a novel explanation" Archived 13 December 2014 at the Wayback Machine. CSM Technical Report 349, Department of Computer Science, Univ. Essex
- ^ Suh, I. S.; Headrick, T. C. (2010). "A comparative analysis of the bootstrap versus traditional statistical procedures applied to digital analysis based on Benford's law" (PDF). Journal of Forensic and Investigative Accounting. 2 (2): 144–175. Archived from the original (PDF) on 7 October 2018. Retrieved 30 June 2012.
Further reading
- Arno Berger; Theodore P. Hill (2017). "What is...Benford's law?" (PDF). Notices of the AMS. 64 (2): 132–134. doi:10.1090/noti1477.
- Arno Berger & Theodore P. Hill (2015). An Introduction to Benford's Law. Princeton University Press. ISBN 978-0-691-16306-2.
- Alex Ely Kossovsky. Benford's Law: Theory, the General Law of Relative Quantities, and Forensic Fraud Detection Applications, 2014, World Scientific Publishing. ISBN 978-981-4583-68-8.
- "Benford's Law – Wolfram MathWorld". Mathworld.wolfram.com. 14 June 2012. Retrieved 26 June 2012.
- Alessandro Gambini; et al. (2012). "Probability of digits by dividing random numbers: A ψ and ζ functions approach" (PDF). Expositiones Mathematicae. 30 (4): 223–238. doi:10.1016/j.exmath.2012.03.001.
- Sehity; Hoelzl, Erik; Kirchler, Erich (2005). "Price developments after a nominal shock: Benford's law and psychological pricing after the euro introduction". International Journal of Research in Marketing. 22 (4): 471–480. doi:10.1016/j.ijresmar.2005.09.002. S2CID 154273305.
- Nicolas Gauvrit; Jean-Paul Delahaye (2011). Scatter and regularity implies Benford's law...and more. pp. 58–69. arXiv:0910.1359. Bibcode:2009arXiv0910.1359G. doi:10.1142/9789814327756_0004. ISBN 978-9814327756. S2CID 88518074.
- Bernhard Rauch; Max Göttsche; Gernot Brähler; Stefan Engel (August 2011). "Fact and Fiction in EU-Governmental Economic Data". German Economic Review. 12 (3): 243–255. doi:10.1111/j.1468-0475.2011.00542.x. S2CID 155072460.
- Wendy Cho & Brian Gaines (August 2007). "Breaking the (Benford) Law: statistical fraud detection in campaign finance". The American Statistician. 61 (3): 218–223. doi:10.1198/000313007X223496. S2CID 7938920.
- Geiringer, Hilda; Furlan, L. V. (1948). "The Law of Harmony in Statistics: An Investigation of the Metrical Interdependence of Social Phenomena. by L. V. Furlan". Journal of the American Statistical Association. 43 (242): 325–328. doi:10.2307/2280379. JSTOR 2280379.
External links
- Benford Online Bibliography, an online bibliographic database on Benford's law.
- Testing Benford's Law An open source project showing Benford's law in action against publicly available datasets.
- Benford, Frank (1938). "The Law of Anomalous Numbers". Proceedings of the American Philosophical Society. 78 (4): 551–572. Bibcode:1938PAPhS..78..551B. ISSN 0003-049X. JSTOR 984802. - Benford's original publication





 with a fixed number of digits 0, 1, ..., n, ...,
with a fixed number of digits 0, 1, ..., n, ...,  , digit n is equivalent to a Kafri box containing n non-interacting balls. Other scientists and statisticians have suggested entropy-related explanations for Benford's law.
, digit n is equivalent to a Kafri box containing n non-interacting balls. Other scientists and statisticians have suggested entropy-related explanations for Benford's law.

 does not appear in the original formula by Leemis; it was added by Morrow in a later paper.
does not appear in the original formula by Leemis; it was added by Morrow in a later paper.

 will differ from Benford's law by less than ε > 0. The value of A depends on the value of ε and the distribution of the random variable.
will differ from Benford's law by less than ε > 0. The value of A depends on the value of ε and the distribution of the random variable.


