Misplaced Pages

Revision as of 10:19, 12 February 2020

Gompertz–Makeham

Parameters	${\displaystyle \alpha \in \mathbb {R} ^{+}}$ ${\displaystyle \beta \in \mathbb {R} ^{+}}$ ${\displaystyle \lambda \in \mathbb {R} ^{+}}$
Support	${\displaystyle x\in \mathbb {R} ^{+}}$
PDF	${\displaystyle \left(\alpha e^{\beta x}+\lambda \right)\cdot \exp \left}$
CDF	${\displaystyle 1-\exp \left}$

The Gompertz–Makeham law states that the human death rate is the sum of an age-dependent component (the Gompertz function, named after Benjamin Gompertz), which increases exponentially with age and an age-independent component (the Makeham term, named after William Makeham). In a protected environment where external causes of death are rare (laboratory conditions, low mortality countries, etc.), the age-independent mortality component is often negligible. In this case the formula simplifies to a Gompertz law of mortality. In 1825, Benjamin Gompertz proposed an exponential increase in death rates with age.

The Gompertz–Makeham law of mortality describes the age dynamics of human mortality rather accurately in the age window from about 30 to 80 years of age. At more advanced ages, some studies have found that death rates increase more slowly – a phenomenon known as the late-life mortality deceleration – but more recent studies disagree.

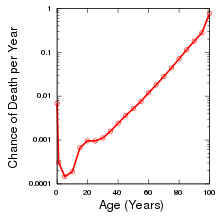
The decline in the human mortality rate before the 1950s was mostly due to a decrease in the age-independent (Makeham) mortality component, while the age-dependent (Gompertz) mortality component was surprisingly stable. Since the 1950s, a new mortality trend has started in the form of an unexpected decline in mortality rates at advanced ages and "rectangularization" of the survival curve.

The hazard function for the Gompertz-Makeham distribution is most often characterised as ${\displaystyle h(x)=\alpha e^{\beta x}+\lambda }$. The empirical magnitude of the beta-parameter is about .085, implying a doubling of mortality every .69/.085 = 8 years (Denmark, 2006).

The quantile function can be expressed in a closed-form expression using the Lambert W function:

${\displaystyle Q(u)={\frac {\alpha }{\beta \lambda }}-{\frac {1}{\lambda }}\ln(1-u)-{\frac {1}{\beta }}W_{0}\left}$

The Gompertz law is the same as a Fisher–Tippett distribution for the negative of age, restricted to negative values for the random variable (positive values for age).

See also

• Biodemography
• Biodemography of human longevity
• Gerontology
• Demography
• Life table
• Maximum life span
• Reliability theory of aging and longevity

References

1. Gompertz, B. (1825). "On the Nature of the Function Expressive of the Law of Human Mortality, and on a New Mode of Determining the Value of Life Contingencies". Philosophical Transactions of the Royal Society. 115: 513–585. doi:10.1098/rstl.1825.0026. JSTOR 107756.
2. ^ Gavrilov, Leonid A.; Gavrilova, Natalia S. (1991), The Biology of Life Span: A Quantitative Approach., New York: Harwood Academic Publisher, ISBN 3-7186-4983-7
3. Makeham, W. M. (1860). "On the Law of Mortality and the Construction of Annuity Tables". J. Inst. Actuaries and Assur. Mag. 8 (6): 301–310. JSTOR 41134925.
4. Gavrilov, Leonid A.; Gavrilova, Natalia S. (2011). "Mortality Measurement at Advanced Ages: A Study of the Social Security Administration Death Master File" (PDF). North American Actuarial Journal. 15 (3): 432–447. doi:10.1080/10920277.2011.10597629.
5. Gavrilov, L. A.; Gavrilova, N. S.; Nosov, V. N. (1983). "Human life span stopped increasing: Why?". Gerontology. 29 (3): 176–180. doi:10.1159/000213111.
6. Gavrilov, L. A.; Nosov, V. N. (1985). "A new trend in human mortality decline: derectangularization of the survival curve ". Age. 8 (3): 93. doi:10.1007/BF02432075.
7. Gavrilova, N. S.; Gavrilov, L. A. (2011). "Stárnutí a dlouhovekost: Zákony a prognózy úmrtnosti pro stárnoucí populace" [Ageing and Longevity: Mortality Laws and Mortality Forecasts for Ageing Populations]. Demografie (in Czech). 53 (2): 109–128.
8. Jodrá, P. (2009). "A closed-form expression for the quantile function of the Gompertz–Makeham distribution". Mathematics and Computers in Simulation. 79 (10): 3069–3075. doi:10.1016/j.matcom.2009.02.002.

• Actuarial science
• Medical aspects of death
• Population
• Senescence
• Statistical laws
• Applied probability