(Redirected from Hotelling's two-sample t-squared statistic)
Type of probability distribution
"Multivariate testing" redirects here. For other uses, see Multivariate testing (disambiguation).
Hotelling's T distribution
Probability density function |
Cumulative distribution function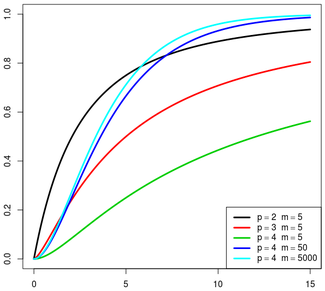 |
| Parameters |
p - dimension of the random variables
m - related to the sample size |
|---|
| Support |
 if if 
 otherwise. otherwise. |
|---|
In statistics, particularly in hypothesis testing, the Hotelling's T-squared distribution (T), proposed by Harold Hotelling, is a multivariate probability distribution that is tightly related to the F-distribution and is most notable for arising as the distribution of a set of sample statistics that are natural generalizations of the statistics underlying the Student's t-distribution.
The Hotelling's t-squared statistic (t) is a generalization of Student's t-statistic that is used in multivariate hypothesis testing.
Motivation
The distribution arises in multivariate statistics in undertaking tests of the differences between the (multivariate) means of different populations, where tests for univariate problems would make use of a t-test.
The distribution is named for Harold Hotelling, who developed it as a generalization of Student's t-distribution.
Definition
If the vector  is Gaussian multivariate-distributed with zero mean and unit covariance matrix
is Gaussian multivariate-distributed with zero mean and unit covariance matrix  and
and  is a
is a  random matrix with a Wishart distribution
random matrix with a Wishart distribution  with unit scale matrix and m degrees of freedom, and d and M are independent of each other, then the quadratic form
with unit scale matrix and m degrees of freedom, and d and M are independent of each other, then the quadratic form  has a Hotelling distribution (with parameters
has a Hotelling distribution (with parameters  and
and  ):
):

It can be shown that if a random variable X has Hotelling's T-squared distribution,  , then:
, then:

where  is the F-distribution with parameters p and m − p + 1.
is the F-distribution with parameters p and m − p + 1.
Hotelling t-squared statistic
Let  be the sample covariance:
be the sample covariance:

where we denote transpose by an apostrophe. It can be shown that  is a positive (semi) definite matrix and
is a positive (semi) definite matrix and  follows a p-variate Wishart distribution with n − 1 degrees of freedom.
The sample covariance matrix of the mean reads
follows a p-variate Wishart distribution with n − 1 degrees of freedom.
The sample covariance matrix of the mean reads  .
.
The Hotelling's t-squared statistic is then defined as:

which is proportional to the Mahalanobis distance between the sample mean and  . Because of this, one should expect the statistic to assume low values if
. Because of this, one should expect the statistic to assume low values if  , and high values if they are different.
, and high values if they are different.
From the distribution,

where  is the F-distribution with parameters p and n − p.
is the F-distribution with parameters p and n − p.
In order to calculate a p-value (unrelated to p variable here), note that the distribution of  equivalently implies that
equivalently implies that

Then, use the quantity on the left hand side to evaluate the p-value corresponding to the sample, which comes from the F-distribution. A confidence region may also be determined using similar logic.
Motivation
Further information: Multivariate normal distribution § Interval
Let  denote a p-variate normal distribution with location
denote a p-variate normal distribution with location  and known covariance
and known covariance  . Let
. Let

be n independent identically distributed (iid) random variables, which may be represented as  column vectors of real numbers. Define
column vectors of real numbers. Define

to be the sample mean with covariance  . It can be shown that
. It can be shown that

where  is the chi-squared distribution with p degrees of freedom.
is the chi-squared distribution with p degrees of freedom.
| Proof
|
|
Proof
Every positive-semidefinite symmetric matrix  has a positive-semidefinite symmetric square root has a positive-semidefinite symmetric square root  , and if it is nonsingular, then its inverse has a positive-definite square root , and if it is nonsingular, then its inverse has a positive-definite square root  . .
Since  , we have , we have
 Consequently
Consequently  and this is simply the sum of squares of
and this is simply the sum of squares of  independent standard normal random variables. Thus its distribution is independent standard normal random variables. Thus its distribution is 
Alternatively, one can argue using density functions and characteristic functions, as follows.
Proof
To show this use the fact that  and derive the characteristic function of the random variable
and derive the characteristic function of the random variable  . As usual, let . As usual, let  denote the determinant of the argument, as in denote the determinant of the argument, as in  . .
By definition of characteristic function, we have:

There are two exponentials inside the integral, so by multiplying the exponentials we add the exponents together, obtaining:

Now take the term  off the integral, and multiply everything by an identity off the integral, and multiply everything by an identity  , bringing one of them inside the integral: , bringing one of them inside the integral:

But the term inside the integral is precisely the probability density function of a multivariate normal distribution with covariance matrix  and mean and mean  , so when integrating over all , so when integrating over all  , it must yield , it must yield  per the probability axioms. We thus end up with: per the probability axioms. We thus end up with:

where  is an identity matrix of dimension is an identity matrix of dimension  . Finally, calculating the determinant, we obtain: . Finally, calculating the determinant, we obtain:

which is the characteristic function for a chi-square distribution with  degrees of freedom. degrees of freedom. 
|
Two-sample statistic
If  and
and  , with the samples independently drawn from two independent multivariate normal distributions with the same mean and covariance, and we define
, with the samples independently drawn from two independent multivariate normal distributions with the same mean and covariance, and we define

as the sample means, and


as the respective sample covariance matrices. Then

is the unbiased pooled covariance matrix estimate (an extension of pooled variance).
Finally, the Hotelling's two-sample t-squared statistic is

Related concepts
It can be related to the F-distribution by

The non-null distribution of this statistic is the noncentral F-distribution (the ratio of a non-central Chi-squared random variable and an independent central Chi-squared random variable)

with

where  is the difference vector between the population means.
is the difference vector between the population means.
In the two-variable case, the formula simplifies nicely allowing appreciation of how the correlation,  ,
between the variables affects
,
between the variables affects  . If we define
. If we define

and

then

Thus, if the differences in the two rows of the vector  are of the same sign, in general,
are of the same sign, in general,  becomes smaller as
becomes smaller as  becomes more positive. If the differences are of opposite sign
becomes more positive. If the differences are of opposite sign  becomes larger as
becomes larger as  becomes more positive.
becomes more positive.
A univariate special case can be found in Welch's t-test.
More robust and powerful tests than Hotelling's two-sample test have been proposed in the literature, see for example the interpoint distance based tests which can be applied also when the number of variables is comparable with, or even larger than, the number of subjects.
See also
References
- ^ Hotelling, H. (1931). "The generalization of Student's ratio". Annals of Mathematical Statistics. 2 (3): 360–378. doi:10.1214/aoms/1177732979.
- Johnson, R.A.; Wichern, D.W. (2002). Applied multivariate statistical analysis. Vol. 5. Prentice hall.
- Eric W. Weisstein, MathWorld
- ^ Mardia, K. V.; Kent, J. T.; Bibby, J. M. (1979). Multivariate Analysis. Academic Press. ISBN 978-0-12-471250-8.
- Fogelmark, Karl; Lomholt, Michael; Irbäck, Anders; Ambjörnsson, Tobias (3 May 2018). "Fitting a function to time-dependent ensemble averaged data". Scientific Reports. 8 (1): 6984. doi:10.1038/s41598-018-24983-y. PMC 5934400. Retrieved 19 August 2024.
- "6.5.4.3. Hotelling's T squared".
- End of chapter 4.2 of Johnson, R.A. & Wichern, D.W. (2002)
- Billingsley, P. (1995). "26. Characteristic Functions". Probability and measure (3rd ed.). Wiley. ISBN 978-0-471-00710-4.
- Marozzi, M. (2016). "Multivariate tests based on interpoint distances with application to magnetic resonance imaging". Statistical Methods in Medical Research. 25 (6): 2593–2610. doi:10.1177/0962280214529104. PMID 24740998.
- Marozzi, M. (2015). "Multivariate multidistance tests for high-dimensional low sample size case-control studies". Statistics in Medicine. 34 (9): 1511–1526. doi:10.1002/sim.6418. PMID 25630579.
External links
Category:


 if
if 
 otherwise.
otherwise. is
is  and
and  is a
is a  random matrix with a
random matrix with a  with unit
with unit  has a Hotelling distribution (with parameters
has a Hotelling distribution (with parameters  and
and  ):
):

 , then:
, then:

 is the
is the  be the
be the 
 follows a p-variate
follows a p-variate  .
.

 . Because of this, one should expect the statistic to assume low values if
. Because of this, one should expect the statistic to assume low values if  , and high values if they are different.
, and high values if they are different.

 is the
is the  equivalently implies that
equivalently implies that

 denote a
denote a  . Let
. Let

 column vectors of real numbers. Define
column vectors of real numbers. Define

 . It can be shown that
. It can be shown that

 is the
is the  has a positive-semidefinite symmetric square root
has a positive-semidefinite symmetric square root  , and if it is nonsingular, then its inverse has a positive-definite square root
, and if it is nonsingular, then its inverse has a positive-definite square root  .
.
 , we have
, we have
 Consequently
Consequently  and this is simply the sum of squares of
and this is simply the sum of squares of  independent standard normal random variables. Thus its distribution is
independent standard normal random variables. Thus its distribution is 
 and derive the
and derive the  . As usual, let
. As usual, let  denote the
denote the  .
.


 off the integral, and multiply everything by an identity
off the integral, and multiply everything by an identity  , bringing one of them inside the integral:
, bringing one of them inside the integral:

 and mean
and mean  , so when integrating over all
, so when integrating over all  , it must yield
, it must yield  per the
per the 
 is an identity matrix of dimension
is an identity matrix of dimension 

 and
and  , with the samples
, with the samples 







 is the difference vector between the population means.
is the difference vector between the population means.
 ,
between the variables affects
,
between the variables affects 


 are of the same sign, in general,
are of the same sign, in general,