Maximal entropy random walk (MERW) is a popular type of biased random walk on a graph, in which transition probabilities are chosen accordingly to the principle of maximum entropy, which says that the probability distribution which best represents the current state of knowledge is the one with largest entropy. While standard random walk chooses for every vertex uniform probability distribution among its outgoing edges, locally maximizing entropy rate, MERW maximizes it globally (average entropy production) by assuming uniform probability distribution among all paths in a given graph.
MERW is used in various fields of science. A direct application is choosing probabilities to maximize transmission rate through a constrained channel, analogously to Fibonacci coding. Its properties also made it useful for example in analysis of complex networks, like link prediction, community detection, robust transport over networks and centrality measures. Also in image analysis, for example for detecting visual saliency regions, object localization, tampering detection or tractography problem.
Additionally, it recreates some properties of quantum mechanics, suggesting a way to repair the discrepancy between diffusion models and quantum predictions, like Anderson localization.
Basic model

Right: example of their evolution on the same inhomogeneous 2D lattice with cyclic boundary conditions – probability density after 10, 100 and 1000 steps while starting from the same vertex. The small boxes represent defects: all vertices but the marked ones have additional self-loop (edge to itself). For regular lattices (no defects), GRW and MERW are identical. While defects do not strongly affect the local behavior, they lead to a completely different global stationary probability here. While GRW (and based on it standard diffusion) leads to nearly uniform stationary density, MERW has strong localization property, imprisoning the walkers in entropic wells in analogy to electrons in defected lattice of semi-conductor.
Consider a graph with vertices, defined by an adjacency matrix : if there is an edge from vertex to , 0 otherwise. For simplicity assume it is an undirected graph, which corresponds to a symmetric ; however, MERW can also be generalized for directed and weighted graphs (for example Boltzmann distribution among paths instead of uniform).
We would like to choose a random walk as a Markov process on this graph: for every vertex and its outgoing edge to , choose probability of the walker randomly using this edge after visiting . Formally, find a stochastic matrix (containing the transition probabilities of a Markov chain) such that
- for all and
- for all .
Assuming this graph is connected and not periodic, ergodic theory says that evolution of this stochastic process leads to some stationary probability distribution such that .
Using Shannon entropy for every vertex and averaging over probability of visiting this vertex (to be able to use its entropy), we get the following formula for average entropy production (entropy rate) of the stochastic process:
This definition turns out to be equivalent to the asymptotic average entropy (per length) of the probability distribution in the space of paths for this stochastic process.
In the standard random walk, referred to here as generic random walk (GRW), we naturally choose that each outgoing edge is equally probable:
- .
For a symmetric it leads to a stationary probability distribution with
- .
It locally maximizes entropy production (uncertainty) for every vertex, but usually leads to a suboptimal averaged global entropy rate .
MERW chooses the stochastic matrix which maximizes , or equivalently assumes uniform probability distribution among all paths in a given graph. Its formula is obtained by first calculating the dominant eigenvalue and corresponding eigenvector of the adjacency matrix, i.e. the largest with corresponding such that . Then stochastic matrix and stationary probability distribution are given by
for which every possible path of length from the -th to -th vertex has probability
- .
Its entropy rate is and the stationary probability distribution is
- .
In contrast to GRW, the MERW transition probabilities generally depend on the structure of the entire graph (are nonlocal). Hence, they should not be imagined as directly applied by the walker – if random-looking decisions are made based on the local situation, like a person would make, the GRW approach is more appropriate. MERW is based on the principle of maximum entropy, making it the safest assumption when we don't have any additional knowledge about the system. For example, it would be appropriate for modelling our knowledge about an object performing some complex dynamics – not necessarily random, like a particle.
Sketch of derivation
Assume for simplicity that the considered graph is indirected, connected and aperiodic, allowing to conclude from the Perron–Frobenius theorem that the dominant eigenvector is unique. Hence can be asymptotically () approximated by (or in bra–ket notation).
MERW requires uniform distribution along paths. The number of paths with length and vertex in the center is
- ,
hence for all ,
- .
Analogously calculating probability distribution for two succeeding vertices, one obtains that the probability of being at the -th vertex and next at the -th vertex is
- .
Dividing by the probability of being at the -th vertex, i.e. , gives for the conditional probability of the -th vertex being next after the -th vertex
- .
Weighted MERW: Boltzmann path ensemble
We have assumed that for MERW corresponding to uniform ensemble among paths. However, the above derivation works for real nonnegative . Parametrizing and asking for probability of length path , we get:
As in Boltzmann distribution of paths for energy defined as sum of over given path. For example, it allows to calculate probability distribution of patterns in Ising model.
Examples
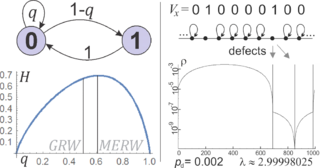
Let us first look at a simple nontrivial situation: Fibonacci coding, where we want to transmit a message as a sequence of 0s and 1s, but not using two successive 1s: after a 1 there has to be a 0. To maximize the amount of information transmitted in such sequence, we should assume uniform probability distribution in the space of all possible sequences fulfilling this constraint. To practically use such long sequences, after 1 we have to use 0, but there remains a freedom of choosing the probability of 0 after 0. Let us denote this probability by , then entropy coding would allow encoding a message using this chosen probability distribution. The stationary probability distribution of symbols for a given turns out to be . Hence, entropy production is , which is maximized for , known as the golden ratio. In contrast, standard random walk would choose suboptimal . While choosing larger reduces the amount of information produced after 0, it also reduces frequency of 1, after which we cannot write any information.
A more complex example is the defected one-dimensional cyclic lattice: let say 1000 nodes connected in a ring, for which all nodes but the defects have a self-loop (edge to itself). In standard random walk (GRW) the stationary probability distribution would have defect probability being 2/3 of probability of the non-defect vertices – there is nearly no localization, also analogously for standard diffusion, which is infinitesimal limit of GRW. For MERW we have to first find the dominant eigenvector of the adjacency matrix – maximizing in:
for all positions , where for defects, 0 otherwise. Substituting and multiplying the equation by −1 we get:
where is minimized now, becoming the analog of energy. The formula inside the bracket is discrete Laplace operator, making this equation a discrete analogue of stationary Schrodinger equation. As in quantum mechanics, MERW predicts that the probability distribution should lead exactly to the one of quantum ground state: with its strongly localized density (in contrast to standard diffusion). Taking the infinitesimal limit, we can get standard continuous stationary (time-independent) Schrodinger equation ( for ) here.
See also
References
- Sinatra, Roberta; Gómez-Gardeñes, Jesús; Lambiotte, Renaud; Nicosia, Vincenzo; Latora, Vito (2011). "Maximal-entropy random walks in complex networks with limited information" (PDF). Physical Review E. 83 (3): 030103. arXiv:1007.4936. Bibcode:2011PhRvE..83c0103S. doi:10.1103/PhysRevE.83.030103. ISSN 1539-3755. PMID 21517435. S2CID 6984660.
- Li, Rong-Hua; Yu, Jeffrey Xu; Liu, Jianquan (2011). Link prediction: the power of maximal entropy random walk (PDF). Association for Computing Machinery Conference on Information and Knowledge Management. p. 1147. doi:10.1145/2063576.2063741. S2CID 15309519. Archived from the original (PDF) on 12 February 2017.
- Ochab, J.K.; Burda, Z. (2013). "Maximal entropy random walk in community detection". The European Physical Journal Special Topics. 216 (1): 73–81. arXiv:1208.3688. Bibcode:2013EPJST.216...73O. doi:10.1140/epjst/e2013-01730-6. ISSN 1951-6355. S2CID 56409069.
- Chen, Y.; Georgiou, T.T.; Pavon, M.; Tannenbaum, A. (2016). "Robust transport over networks". IEEE Transactions on Automatic Control. 62 (9): 4675–4682. arXiv:1603.08129. Bibcode:2016arXiv160308129C. doi:10.1109/TAC.2016.2626796. PMC 5600536. PMID 28924302.
- Delvenne, Jean-Charles; Libert, Anne-Sophie (2011). "Centrality measures and thermodynamic formalism for complex networks". Physical Review E. 83 (4): 046117. arXiv:0710.3972. Bibcode:2011PhRvE..83d6117D. doi:10.1103/PhysRevE.83.046117. ISSN 1539-3755. PMID 21599250. S2CID 25816198.
- Jin-Gang Yu; Ji Zhao; Jinwen Tian; Yihua Tan (2014). "Maximal Entropy Random Walk for Region-Based Visual Saliency". IEEE Transactions on Cybernetics. 44 (9). Institute of Electrical and Electronics Engineers (IEEE): 1661–1672. doi:10.1109/tcyb.2013.2292054. ISSN 2168-2267. PMID 25137693. S2CID 20962642.
- L. Wang, J. Zhao, X. Hu, J. Lu, Weakly supervised object localization via maximal entropy random walk, ICIP, 2014.
- Korus, Pawel; Huang, Jiwu (2016). "Improved Tampering Localization in Digital Image Forensics Based on Maximal Entropy Random Walk". IEEE Signal Processing Letters. 23 (1). Institute of Electrical and Electronics Engineers (IEEE): 169–173. Bibcode:2016ISPL...23..169K. doi:10.1109/lsp.2015.2507598. ISSN 1070-9908. S2CID 16305991.
- Galinsky, Vitaly L.; Frank, Lawrence R. (2015). "Simultaneous Multi-Scale Diffusion Estimation and Tractography Guided by Entropy Spectrum Pathways". IEEE Transactions on Medical Imaging. 34 (5). Institute of Electrical and Electronics Engineers (IEEE): 1177–1193. doi:10.1109/tmi.2014.2380812. ISSN 0278-0062. PMC 4417445. PMID 25532167.
- Burda, Z.; Duda, J.; Luck, J. M.; Waclaw, B. (23 April 2009). "Localization of the Maximal Entropy Random Walk". Physical Review Letters. 102 (16): 160602. arXiv:0810.4113. Bibcode:2009PhRvL.102p0602B. doi:10.1103/physrevlett.102.160602. ISSN 0031-9007. PMID 19518691. S2CID 32134048.
- J. Duda, Extended Maximal Entropy Random Walk, PhD Thesis, 2012.
External links
- Gábor Simonyi, Y. Lin, Z. Zhang, "Mean first-passage time for maximal-entropy random walks in complex networks". Scientific Reports, 2014.
- Electron Conductance Models Using Maximal Entropy Random Walks Wolfram Demonstration Project
 vertices, defined by an
vertices, defined by an  :
:  if there is an edge from vertex
if there is an edge from vertex  to
to  , 0 otherwise. For simplicity assume it is an
, 0 otherwise. For simplicity assume it is an  ; however, MERW can also be generalized for directed and
; however, MERW can also be generalized for directed and  of the walker randomly using this edge after visiting
of the walker randomly using this edge after visiting  (containing the transition probabilities of a Markov chain) such that
(containing the transition probabilities of a Markov chain) such that
 for all
for all  and
and for all
for all  such that
such that  .
.

 .
. .
. .
.
 and corresponding
and corresponding  of the adjacency matrix, i.e. the largest
of the adjacency matrix, i.e. the largest  with corresponding
with corresponding  such that
such that  . Then stochastic matrix and stationary probability distribution are given by
. Then stochastic matrix and stationary probability distribution are given by

 from the
from the  .
. and the stationary probability distribution
and the stationary probability distribution  .
. can be asymptotically (
can be asymptotically ( ) approximated by
) approximated by  (or
(or  in
in  of paths with length
of paths with length  and vertex
and vertex  ,
, .
. .
. , gives for the
, gives for the  for MERW corresponding to uniform ensemble among paths. However, the above derivation works for real nonnegative
for MERW corresponding to uniform ensemble among paths. However, the above derivation works for real nonnegative  and asking for probability of length
and asking for probability of length  , we get:
, we get:

 over given path. For example, it allows to calculate probability distribution of patterns in
over given path. For example, it allows to calculate probability distribution of patterns in  , then
, then  . Hence, entropy production is
. Hence, entropy production is  , which is maximized for
, which is maximized for  , known as the
, known as the  . While choosing larger
. While choosing larger 
 , where
, where  for defects, 0 otherwise. Substituting
for defects, 0 otherwise. Substituting  and multiplying the equation by −1 we get:
and multiplying the equation by −1 we get:

 is minimized now, becoming the analog of energy. The formula inside the bracket is
is minimized now, becoming the analog of energy. The formula inside the bracket is  with its strongly localized density (in contrast to standard diffusion). Taking the
with its strongly localized density (in contrast to standard diffusion). Taking the  for
for  ) here.
) here.