Probability mass function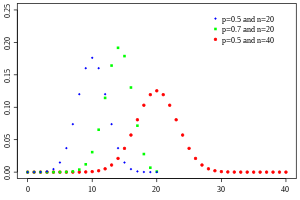 | |||
Cumulative distribution function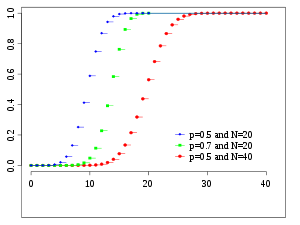 | |||
| Notation | |||
|---|---|---|---|
| Parameters |
– number of trials – success probability for each trial | ||
| Support | – number of successes | ||
| PMF | |||
| CDF | (the regularized incomplete beta function) | ||
| Mean | |||
| Median | or | ||
| Mode | or | ||
| Variance | |||
| Skewness | |||
| Excess kurtosis | |||
| Entropy |
in shannons. For nats, use the natural log in the log. | ||
| MGF | |||
| CF | |||
| PGF | |||
| Fisher information |
(for fixed ) | ||
| Part of a series on statistics |
| Probability theory |
|---|
 |

with n and k as in Pascal's triangle
The probability that a ball in a Galton box with 8 layers (n = 8) ends up in the central bin (k = 4) is 70/256.
In probability theory and statistics, the binomial distribution with parameters n and p is the discrete probability distribution of the number of successes in a sequence of n independent experiments, each asking a yes–no question, and each with its own Boolean-valued outcome: success (with probability p) or failure (with probability q = 1 − p). A single success/failure experiment is also called a Bernoulli trial or Bernoulli experiment, and a sequence of outcomes is called a Bernoulli process; for a single trial, i.e., n = 1, the binomial distribution is a Bernoulli distribution. The binomial distribution is the basis for the binomial test of statistical significance.
The binomial distribution is frequently used to model the number of successes in a sample of size n drawn with replacement from a population of size N. If the sampling is carried out without replacement, the draws are not independent and so the resulting distribution is a hypergeometric distribution, not a binomial one. However, for N much larger than n, the binomial distribution remains a good approximation, and is widely used.
Definitions
Probability mass function
If the random variable X follows the binomial distribution with parameters n ∈ and p ∈ [0, 1], we write X ~ B(n, p). The probability of getting exactly k successes in n independent Bernoulli trials (with the same rate p) is given by the probability mass function:
for k = 0, 1, 2, ..., n, where
is the binomial coefficient. The formula can be understood as follows: p q is the probability of obtaining the sequence of n independent Bernoulli trials in which k trials are "successes" and the remaining n − k trials result in "failure". Since the trials are independent with probabilities remaining constant between them, any sequence of n trials with k successes (and n − k failures) has the same probability of being achieved (regardless of positions of successes within the sequence). There are such sequences, since the binomial coefficient counts the number of ways to choose the positions of the k successes among the n trials. The binomial distribution is concerned with the probability of obtaining any of these sequences, meaning the probability of obtaining one of them (p q) must be added times, hence .
In creating reference tables for binomial distribution probability, usually, the table is filled in up to n/2 values. This is because for k > n/2, the probability can be calculated by its complement as
Looking at the expression f(k, n, p) as a function of k, there is a k value that maximizes it. This k value can be found by calculating
and comparing it to 1. There is always an integer M that satisfies
f(k, n, p) is monotone increasing for k < M and monotone decreasing for k > M, with the exception of the case where (n + 1)p is an integer. In this case, there are two values for which f is maximal: (n + 1) p and (n + 1) p − 1. M is the most probable outcome (that is, the most likely, although this can still be unlikely overall) of the Bernoulli trials and is called the mode.
Equivalently, M − p < np ≤ M + 1 − p. Taking the floor function, we obtain M = floor(np).
Example
Suppose a biased coin comes up heads with probability 0.3 when tossed. The probability of seeing exactly 4 heads in 6 tosses is
Cumulative distribution function
The cumulative distribution function can be expressed as:
where is the "floor" under k, i.e. the greatest integer less than or equal to k.
It can also be represented in terms of the regularized incomplete beta function, as follows:
which is equivalent to the cumulative distribution functions of the beta distribution and of the F-distribution:
Some closed-form bounds for the cumulative distribution function are given below.
Properties
Expected value and variance
If X ~ B(n, p), that is, X is a binomially distributed random variable, n being the total number of experiments and p the probability of each experiment yielding a successful result, then the expected value of X is:
This follows from the linearity of the expected value along with the fact that X is the sum of n identical Bernoulli random variables, each with expected value p. In other words, if are identical (and independent) Bernoulli random variables with parameter p, then X = X1 + ... + Xn and
The variance is:
This similarly follows from the fact that the variance of a sum of independent random variables is the sum of the variances.
Higher moments
The first 6 central moments, defined as , are given by
The non-central moments satisfy
and in general
where are the Stirling numbers of the second kind, and is the th falling power of . A simple bound follows by bounding the Binomial moments via the higher Poisson moments:
This shows that if , then is at most a constant factor away from
Mode
Usually the mode of a binomial B(n, p) distribution is equal to , where is the floor function. However, when (n + 1)p is an integer and p is neither 0 nor 1, then the distribution has two modes: (n + 1)p and (n + 1)p − 1. When p is equal to 0 or 1, the mode will be 0 and n correspondingly. These cases can be summarized as follows:
Proof: Let
For only has a nonzero value with . For we find and for . This proves that the mode is 0 for and for .
Let . We find
- .
From this follows
So when is an integer, then and is a mode. In the case that , then only is a mode.
Median
In general, there is no single formula to find the median for a binomial distribution, and it may even be non-unique. However, several special results have been established:
- If np is an integer, then the mean, median, and mode coincide and equal np.
- Any median m must lie within the interval .
- A median m cannot lie too far away from the mean: .
- The median is unique and equal to m = round(np) when |m − np| ≤ min{p, 1 − p} (except for the case when p = 1/2 and n is odd).
- When p is a rational number (with the exception of p = 1/2\ and n odd) the median is unique.
- When and n is odd, any number m in the interval is a median of the binomial distribution. If and n is even, then is the unique median.
Tail bounds
For k ≤ np, upper bounds can be derived for the lower tail of the cumulative distribution function , the probability that there are at most k successes. Since , these bounds can also be seen as bounds for the upper tail of the cumulative distribution function for k ≥ np.
Hoeffding's inequality yields the simple bound
which is however not very tight. In particular, for p = 1, we have that F(k; n, p) = 0 (for fixed k, n with k < n), but Hoeffding's bound evaluates to a positive constant.
A sharper bound can be obtained from the Chernoff bound:
where D(a ∥ p) is the relative entropy (or Kullback-Leibler divergence) between an a-coin and a p-coin (i.e. between the Bernoulli(a) and Bernoulli(p) distribution):
Asymptotically, this bound is reasonably tight; see for details.
One can also obtain lower bounds on the tail F(k; n, p), known as anti-concentration bounds. By approximating the binomial coefficient with Stirling's formula it can be shown that
which implies the simpler but looser bound
For p = 1/2 and k ≥ 3n/8 for even n, it is possible to make the denominator constant:
Statistical inference
Estimation of parameters
See also: Beta distribution § Bayesian inferenceWhen n is known, the parameter p can be estimated using the proportion of successes:
This estimator is found using maximum likelihood estimator and also the method of moments. This estimator is unbiased and uniformly with minimum variance, proven using Lehmann–Scheffé theorem, since it is based on a minimal sufficient and complete statistic (i.e.: x). It is also consistent both in probability and in MSE. This statistic is asymptotically normal thanks to the central limit theorem, because it is the same as taking the mean over Bernoulli samples. It has a variance of , a property which is used in various ways, such as in Wald's confidence intervals.
A closed form Bayes estimator for p also exists when using the Beta distribution as a conjugate prior distribution. When using a general as a prior, the posterior mean estimator is:
The Bayes estimator is asymptotically efficient and as the sample size approaches infinity (n → ∞), it approaches the MLE solution. The Bayes estimator is biased (how much depends on the priors), admissible and consistent in probability. Using the Bayesian estimator with the Beta distribution can be used with Thompson sampling.
For the special case of using the standard uniform distribution as a non-informative prior, , the posterior mean estimator becomes:
(A posterior mode should just lead to the standard estimator.) This method is called the rule of succession, which was introduced in the 18th century by Pierre-Simon Laplace.
When relying on Jeffreys prior, the prior is , which leads to the estimator:
When estimating p with very rare events and a small n (e.g.: if x = 0), then using the standard estimator leads to which sometimes is unrealistic and undesirable. In such cases there are various alternative estimators. One way is to use the Bayes estimator , leading to:
Another method is to use the upper bound of the confidence interval obtained using the rule of three:
Confidence intervals for the parameter p
Main article: Binomial proportion confidence interval See also: Z-test § Comparing the Proportions of Two BinomialsEven for quite large values of n, the actual distribution of the mean is significantly nonnormal. Because of this problem several methods to estimate confidence intervals have been proposed.
In the equations for confidence intervals below, the variables have the following meaning:
- n1 is the number of successes out of n, the total number of trials
- is the proportion of successes
- is the quantile of a standard normal distribution (i.e., probit) corresponding to the target error rate . For example, for a 95% confidence level the error = 0.05, so = 0.975 and = 1.96.
Wald method
Main article: Binomial proportion confidence interval § Wald intervalA continuity correction of 0.5/n may be added.
Agresti–Coull method
Main article: Binomial proportion confidence interval § Agresti–Coull interval
Here the estimate of p is modified to
This method works well for n > 10 and n1 ≠ 0, n. See here for . For n1 = 0, n use the Wilson (score) method below.
Arcsine method
Main article: Binomial proportion confidence interval § Arcsine transformation
Wilson (score) method
Main article: Binomial proportion confidence interval § Wilson score intervalThe notation in the formula below differs from the previous formulas in two respects:
- Firstly, zx has a slightly different interpretation in the formula below: it has its ordinary meaning of 'the xth quantile of the standard normal distribution', rather than being a shorthand for 'the (1 − x)th quantile'.
- Secondly, this formula does not use a plus-minus to define the two bounds. Instead, one may use to get the lower bound, or use to get the upper bound. For example: for a 95% confidence level the error = 0.05, so one gets the lower bound by using , and one gets the upper bound by using .
Comparison
The so-called "exact" (Clopper–Pearson) method is the most conservative. (Exact does not mean perfectly accurate; rather, it indicates that the estimates will not be less conservative than the true value.)
The Wald method, although commonly recommended in textbooks, is the most biased.
Related distributions
Sums of binomials
If X ~ B(n, p) and Y ~ B(m, p) are independent binomial variables with the same probability p, then X + Y is again a binomial variable; its distribution is Z = X + Y ~ B(n + m, p):
A Binomial distributed random variable X ~ B(n, p) can be considered as the sum of n Bernoulli distributed random variables. So the sum of two Binomial distributed random variables X ~ B(n, p) and Y ~ B(m, p) is equivalent to the sum of n + m Bernoulli distributed random variables, which means Z = X + Y ~ B(n + m, p). This can also be proven directly using the addition rule.
However, if X and Y do not have the same probability p, then the variance of the sum will be smaller than the variance of a binomial variable distributed as B(n + m, p).
Poisson binomial distribution
The binomial distribution is a special case of the Poisson binomial distribution, which is the distribution of a sum of n independent non-identical Bernoulli trials B(pi).
Ratio of two binomial distributions
This result was first derived by Katz and coauthors in 1978.
Let X ~ B(n, p1) and Y ~ B(m, p2) be independent. Let T = (X/n) / (Y/m).
Then log(T) is approximately normally distributed with mean log(p1/p2) and variance ((1/p1) − 1)/n + ((1/p2) − 1)/m.
Conditional binomials
If X ~ B(n, p) and Y | X ~ B(X, q) (the conditional distribution of Y, given X), then Y is a simple binomial random variable with distribution Y ~ B(n, pq).
For example, imagine throwing n balls to a basket UX and taking the balls that hit and throwing them to another basket UY. If p is the probability to hit UX then X ~ B(n, p) is the number of balls that hit UX. If q is the probability to hit UY then the number of balls that hit UY is Y ~ B(X, q) and therefore Y ~ B(n, pq).
Since and , by the law of total probability,
Since the equation above can be expressed as
Factoring and pulling all the terms that don't depend on out of the sum now yields
After substituting in the expression above, we get
Notice that the sum (in the parentheses) above equals by the binomial theorem. Substituting this in finally yields
and thus as desired.
Bernoulli distribution
The Bernoulli distribution is a special case of the binomial distribution, where n = 1. Symbolically, X ~ B(1, p) has the same meaning as X ~ Bernoulli(p). Conversely, any binomial distribution, B(n, p), is the distribution of the sum of n independent Bernoulli trials, Bernoulli(p), each with the same probability p.
Normal approximation
See also: Binomial proportion confidence interval § Normal approximation interval
If n is large enough, then the skew of the distribution is not too great. In this case a reasonable approximation to B(n, p) is given by the normal distribution
and this basic approximation can be improved in a simple way by using a suitable continuity correction. The basic approximation generally improves as n increases (at least 20) and is better when p is not near to 0 or 1. Various rules of thumb may be used to decide whether n is large enough, and p is far enough from the extremes of zero or one:
- One rule is that for n > 5 the normal approximation is adequate if the absolute value of the skewness is strictly less than 0.3; that is, if
This can be made precise using the Berry–Esseen theorem.
- A stronger rule states that the normal approximation is appropriate only if everything within 3 standard deviations of its mean is within the range of possible values; that is, only if
- This 3-standard-deviation rule is equivalent to the following conditions, which also imply the first rule above.
The rule is totally equivalent to request that
Moving terms around yields:
Since , we can apply the square power and divide by the respective factors and , to obtain the desired conditions:
Notice that these conditions automatically imply that . On the other hand, apply again the square root and divide by 3,
Subtracting the second set of inequalities from the first one yields:
and so, the desired first rule is satisfied,
- Another commonly used rule is that both values np and n(1 − p) must be greater than or equal to 5. However, the specific number varies from source to source, and depends on how good an approximation one wants. In particular, if one uses 9 instead of 5, the rule implies the results stated in the previous paragraphs.
Assume that both values and are greater than 9. Since , we easily have that
We only have to divide now by the respective factors and , to deduce the alternative form of the 3-standard-deviation rule:
The following is an example of applying a continuity correction. Suppose one wishes to calculate Pr(X ≤ 8) for a binomial random variable X. If Y has a distribution given by the normal approximation, then Pr(X ≤ 8) is approximated by Pr(Y ≤ 8.5). The addition of 0.5 is the continuity correction; the uncorrected normal approximation gives considerably less accurate results.
This approximation, known as de Moivre–Laplace theorem, is a huge time-saver when undertaking calculations by hand (exact calculations with large n are very onerous); historically, it was the first use of the normal distribution, introduced in Abraham de Moivre's book The Doctrine of Chances in 1738. Nowadays, it can be seen as a consequence of the central limit theorem since B(n, p) is a sum of n independent, identically distributed Bernoulli variables with parameter p. This fact is the basis of a hypothesis test, a "proportion z-test", for the value of p using x/n, the sample proportion and estimator of p, in a common test statistic.
For example, suppose one randomly samples n people out of a large population and ask them whether they agree with a certain statement. The proportion of people who agree will of course depend on the sample. If groups of n people were sampled repeatedly and truly randomly, the proportions would follow an approximate normal distribution with mean equal to the true proportion p of agreement in the population and with standard deviation
Poisson approximation
The binomial distribution converges towards the Poisson distribution as the number of trials goes to infinity while the product np converges to a finite limit. Therefore, the Poisson distribution with parameter λ = np can be used as an approximation to B(n, p) of the binomial distribution if n is sufficiently large and p is sufficiently small. According to rules of thumb, this approximation is good if n ≥ 20 and p ≤ 0.05 such that np ≤ 1, or if n > 50 and p < 0.1 such that np < 5, or if n ≥ 100 and np ≤ 10.
Concerning the accuracy of Poisson approximation, see Novak, ch. 4, and references therein.
Limiting distributions
- Poisson limit theorem: As n approaches ∞ and p approaches 0 with the product np held fixed, the Binomial(n, p) distribution approaches the Poisson distribution with expected value λ = np.
- de Moivre–Laplace theorem: As n approaches ∞ while p remains fixed, the distribution of
- approaches the normal distribution with expected value 0 and variance 1. This result is sometimes loosely stated by saying that the distribution of X is asymptotically normal with expected value 0 and variance 1. This result is a specific case of the central limit theorem.
Beta distribution
The binomial distribution and beta distribution are different views of the same model of repeated Bernoulli trials. The binomial distribution is the PMF of k successes given n independent events each with a probability p of success. Mathematically, when α = k + 1 and β = n − k + 1, the beta distribution and the binomial distribution are related by a factor of n + 1:
Beta distributions also provide a family of prior probability distributions for binomial distributions in Bayesian inference:
Given a uniform prior, the posterior distribution for the probability of success p given n independent events with k observed successes is a beta distribution.
Computational methods
Random number generation
Further information: Pseudo-random number samplingMethods for random number generation where the marginal distribution is a binomial distribution are well-established. One way to generate random variates samples from a binomial distribution is to use an inversion algorithm. To do so, one must calculate the probability that Pr(X = k) for all values k from 0 through n. (These probabilities should sum to a value close to one, in order to encompass the entire sample space.) Then by using a pseudorandom number generator to generate samples uniformly between 0 and 1, one can transform the calculated samples into discrete numbers by using the probabilities calculated in the first step.
History
This distribution was derived by Jacob Bernoulli. He considered the case where p = r/(r + s) where p is the probability of success and r and s are positive integers. Blaise Pascal had earlier considered the case where p = 1/2, tabulating the corresponding binomial coefficients in what is now recognized as Pascal's triangle.
See also
- Logistic regression
- Multinomial distribution
- Negative binomial distribution
- Beta-binomial distribution
- Binomial measure, an example of a multifractal measure.
- Statistical mechanics
- Piling-up lemma, the resulting probability when XOR-ing independent Boolean variables
References
- Westland, J. Christopher (2020). Audit Analytics: Data Science for the Accounting Profession. Chicago, IL, USA: Springer. p. 53. ISBN 978-3-030-49091-1.
- Feller, W. (1968). An Introduction to Probability Theory and Its Applications (Third ed.). New York: Wiley. p. 151 (theorem in section VI.3).
- Wadsworth, G. P. (1960). Introduction to Probability and Random Variables. New York: McGraw-Hill. p. 52.
- Jowett, G. H. (1963). "The Relationship Between the Binomial and F Distributions". Journal of the Royal Statistical Society, Series D. 13 (1): 55–57. doi:10.2307/2986663. JSTOR 2986663.
- See Proof Wiki
- Knoblauch, Andreas (2008), "Closed-Form Expressions for the Moments of the Binomial Probability Distribution", SIAM Journal on Applied Mathematics, 69 (1): 197–204, doi:10.1137/070700024, JSTOR 40233780
- Nguyen, Duy (2021), "A probabilistic approach to the moments of binomial random variables and application", The American Statistician, 75 (1): 101–103, doi:10.1080/00031305.2019.1679257, S2CID 209923008
- D. Ahle, Thomas (2022), "Sharp and Simple Bounds for the raw Moments of the Binomial and Poisson Distributions", Statistics & Probability Letters, 182: 109306, arXiv:2103.17027, doi:10.1016/j.spl.2021.109306
- See also Nicolas, André (January 7, 2019). "Finding mode in Binomial distribution". Stack Exchange.
- Neumann, P. (1966). "Über den Median der Binomial- and Poissonverteilung". Wissenschaftliche Zeitschrift der Technischen Universität Dresden (in German). 19: 29–33.
- Lord, Nick. (July 2010). "Binomial averages when the mean is an integer", The Mathematical Gazette 94, 331-332.
- ^ Kaas, R.; Buhrman, J.M. (1980). "Mean, Median and Mode in Binomial Distributions". Statistica Neerlandica. 34 (1): 13–18. doi:10.1111/j.1467-9574.1980.tb00681.x.
- Hamza, K. (1995). "The smallest uniform upper bound on the distance between the mean and the median of the binomial and Poisson distributions". Statistics & Probability Letters. 23: 21–25. doi:10.1016/0167-7152(94)00090-U.
- Nowakowski, Sz. (2021). "Uniqueness of a Median of a Binomial Distribution with Rational Probability". Advances in Mathematics: Scientific Journal. 10 (4): 1951–1958. arXiv:2004.03280. doi:10.37418/amsj.10.4.9. ISSN 1857-8365. S2CID 215238991.
- ^ Arratia, R.; Gordon, L. (1989). "Tutorial on large deviations for the binomial distribution". Bulletin of Mathematical Biology. 51 (1): 125–131. doi:10.1007/BF02458840. PMID 2706397. S2CID 189884382.
- Robert B. Ash (1990). Information Theory. Dover Publications. p. 115. ISBN 9780486665214.
- Matoušek, J.; Vondrak, J. "The Probabilistic Method" (PDF). lecture notes. Archived (PDF) from the original on 2022-10-09.
- Wilcox, Rand R. (1979). "Estimating the Parameters of the Beta-Binomial Distribution". Educational and Psychological Measurement. 39 (3): 527–535. doi:10.1177/001316447903900302. ISSN 0013-1644. S2CID 121331083.
- Marko Lalovic (https://stats.stackexchange.com/users/105848/marko-lalovic), Jeffreys prior for binomial likelihood, URL (version: 2019-03-04): https://stats.stackexchange.com/q/275608
- Razzaghi, Mehdi (2002). "On the estimation of binomial success probability with zero occurrence in sample". Journal of Modern Applied Statistical Methods. 1 (2): 326–332. doi:10.22237/jmasm/1036110000.
- ^ Brown, Lawrence D.; Cai, T. Tony; DasGupta, Anirban (2001), "Interval Estimation for a Binomial Proportion", Statistical Science, 16 (2): 101–133, CiteSeerX 10.1.1.323.7752, doi:10.1214/ss/1009213286, retrieved 2015-01-05
- Agresti, Alan; Coull, Brent A. (May 1998), "Approximate is better than 'exact' for interval estimation of binomial proportions" (PDF), The American Statistician, 52 (2): 119–126, doi:10.2307/2685469, JSTOR 2685469, retrieved 2015-01-05
- Gulotta, Joseph. "Agresti-Coull Interval Method". pellucid.atlassian.net. Retrieved 18 May 2021.
- "Confidence intervals". itl.nist.gov. Retrieved 18 May 2021.
- Pires, M. A. (2002). "Confidence intervals for a binomial proportion: comparison of methods and software evaluation" (PDF). In Klinke, S.; Ahrend, P.; Richter, L. (eds.). Proceedings of the Conference CompStat 2002. Short Communications and Posters. Archived (PDF) from the original on 2022-10-09.
- Wilson, Edwin B. (June 1927), "Probable inference, the law of succession, and statistical inference" (PDF), Journal of the American Statistical Association, 22 (158): 209–212, doi:10.2307/2276774, JSTOR 2276774, archived from the original (PDF) on 2015-01-13, retrieved 2015-01-05
- "Confidence intervals". Engineering Statistics Handbook. NIST/Sematech. 2012. Retrieved 2017-07-23.
- Dekking, F.M.; Kraaikamp, C.; Lopohaa, H.P.; Meester, L.E. (2005). A Modern Introduction of Probability and Statistics (1 ed.). Springer-Verlag London. ISBN 978-1-84628-168-6.
- Wang, Y. H. (1993). "On the number of successes in independent trials" (PDF). Statistica Sinica. 3 (2): 295–312. Archived from the original (PDF) on 2016-03-03.
- Katz, D.; et al. (1978). "Obtaining confidence intervals for the risk ratio in cohort studies". Biometrics. 34 (3): 469–474. doi:10.2307/2530610. JSTOR 2530610.
- Taboga, Marco. "Lectures on Probability Theory and Mathematical Statistics". statlect.com. Retrieved 18 December 2017.
- ^ Box, Hunter and Hunter (1978). Statistics for experimenters. Wiley. p. 130. ISBN 9780471093152.
- Chen, Zac (2011). H2 Mathematics Handbook (1 ed.). Singapore: Educational Publishing House. p. 350. ISBN 9789814288484.
- "6.4: Normal Approximation to the Binomial Distribution - Statistics LibreTexts". 2023-05-29. Archived from the original on 2023-05-29. Retrieved 2023-10-07.
{{cite web}}: CS1 maint: bot: original URL status unknown (link) - NIST/SEMATECH, "7.2.4. Does the proportion of defectives meet requirements?" e-Handbook of Statistical Methods.
- "12.4 – Approximating the Binomial Distribution | STAT 414". Pennstate: Statistics Online Courses. 2023-03-28. Archived from the original on 2023-03-28. Retrieved 2023-10-08.
{{cite news}}: CS1 maint: bot: original URL status unknown (link) - Chen, Zac (2011). H2 mathematics handbook (1 ed.). Singapore: Educational publishing house. p. 348. ISBN 9789814288484.
- ^ NIST/SEMATECH, "6.3.3.1. Counts Control Charts", e-Handbook of Statistical Methods.
- "The Connection Between the Poisson and Binomial Distributions". 2023-03-13. Archived from the original on 2023-03-13. Retrieved 2023-10-08.
{{cite web}}: CS1 maint: bot: original URL status unknown (link) - Novak S.Y. (2011) Extreme value methods with applications to finance. London: CRC/ Chapman & Hall/Taylor & Francis. ISBN 9781-43983-5746.
- MacKay, David (2003). Information Theory, Inference and Learning Algorithms. Cambridge University Press; First Edition. ISBN 978-0521642989.
- "Beta distribution".
- Devroye, Luc (1986) Non-Uniform Random Variate Generation, New York: Springer-Verlag. (See especially Chapter X, Discrete Univariate Distributions)
- Kachitvichyanukul, V.; Schmeiser, B. W. (1988). "Binomial random variate generation". Communications of the ACM. 31 (2): 216–222. doi:10.1145/42372.42381. S2CID 18698828.
- Katz, Victor (2009). "14.3: Elementary Probability". A History of Mathematics: An Introduction. Addison-Wesley. p. 491. ISBN 978-0-321-38700-4.
- Mandelbrot, B. B., Fisher, A. J., & Calvet, L. E. (1997). A multifractal model of asset returns. 3.2 The Binomial Measure is the Simplest Example of a Multifractal
- Except the trivial case p = 0, which must be checked separately.
Further reading
- Hirsch, Werner Z. (1957). "Binomial Distribution—Success or Failure, How Likely Are They?". Introduction to Modern Statistics. New York: MacMillan. pp. 140–153.
- Neter, John; Wasserman, William; Whitmore, G. A. (1988). Applied Statistics (Third ed.). Boston: Allyn & Bacon. pp. 185–192. ISBN 0-205-10328-6.
External links
- Interactive graphic: Univariate Distribution Relationships
- Binomial distribution formula calculator
- Difference of two binomial variables: X-Y or |X-Y|
- Querying the binomial probability distribution in WolframAlpha
- Confidence (credible) intervals for binomial probability, p: online calculator available at causaScientia.org

 – number of trials
– number of trials – success probability for each trial
– success probability for each trial
 – number of successes
– number of successes
 (the
(the 
 or
or 
 or
or 








 )
)


 such sequences, since the binomial coefficient
such sequences, since the binomial coefficient  .
.





 is the "floor" under k, i.e. the
is the "floor" under k, i.e. the 



 are identical (and independent) Bernoulli random variables with parameter p, then X = X1 + ... + Xn and
are identical (and independent) Bernoulli random variables with parameter p, then X = X1 + ... + Xn and


![{\displaystyle \mu _{c}=\operatorname {E} \left)^{c}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c5ea3e05b674668550675c3c4593c725a1ec86b) , are given by
, are given by



 are the
are the  is the
is the  th
th 
 , then
, then  is at most a constant factor away from
is at most a constant factor away from 
 is the
is the 

 only
only  has a nonzero value with
has a nonzero value with  . For
. For  we find
we find  and
and  for
for  . This proves that the mode is 0 for
. This proves that the mode is 0 for  . We find
. We find
 .
.
 is an integer, then
is an integer, then  is a mode. In the case that
is a mode. In the case that  , then only
, then only  is a mode.
is a mode.
 .
. .
. and n is odd, any number m in the interval
and n is odd, any number m in the interval  is a median of the binomial distribution. If
is a median of the binomial distribution. If  is the unique median.
is the unique median. , the probability that there are at most k successes. Since
, the probability that there are at most k successes. Since  , these bounds can also be seen as bounds for the upper tail of the cumulative distribution function for k ≥ np.
, these bounds can also be seen as bounds for the upper tail of the cumulative distribution function for k ≥ np.







 , a property which is used in various ways, such as in
, a property which is used in various ways, such as in  as a prior, the
as a prior, the 
 , the posterior mean estimator becomes:
, the posterior mean estimator becomes:

 , which leads to the estimator:
, which leads to the estimator:

 which sometimes is unrealistic and undesirable. In such cases there are various alternative estimators. One way is to use the Bayes estimator
which sometimes is unrealistic and undesirable. In such cases there are various alternative estimators. One way is to use the Bayes estimator  , leading to:
, leading to:


 is the proportion of successes
is the proportion of successes is the
is the 
 . For example, for a 95%
. For example, for a 95% 


 . For n1 = 0, n use the Wilson (score) method below.
. For n1 = 0, n use the Wilson (score) method below.

 to get the lower bound, or use
to get the lower bound, or use  to get the upper bound. For example: for a 95% confidence level the error
to get the upper bound. For example: for a 95% confidence level the error  , and one gets the upper bound by using
, and one gets the upper bound by using  .
.

 and
and  , by the
, by the 
 the equation above can be expressed as
the equation above can be expressed as

 and pulling all the terms that don't depend on
and pulling all the terms that don't depend on 
 in the expression above, we get
in the expression above, we get

 by the
by the 
 as desired.
as desired.




 is totally equivalent to request that
is totally equivalent to request that


 and
and  , to obtain the desired conditions:
, to obtain the desired conditions:
 . On the other hand, apply again the square root and divide by 3,
. On the other hand, apply again the square root and divide by 3,



 are greater than 9. Since
are greater than 9. Since 
 and
and  , to deduce the alternative form of the 3-standard-deviation rule:
, to deduce the alternative form of the 3-standard-deviation rule:



