Misplaced Pages

This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (May 2023) (Learn how and when to remove this message)

You can help expand this article with text translated from the corresponding article in Chinese. (February 2017) Click for important translation instructions. View a machine-translated version of the Chinese article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Misplaced Pages. Do not translate text that appears unreliable or low-quality. If possible, verify the text with references provided in the foreign-language article. You must provide copyright attribution in the edit summary accompanying your translation by providing an interlanguage link to the source of your translation. A model attribution edit summary is Content in this edit is translated from the existing Chinese Misplaced Pages article at ]; see its history for attribution. You may also add the template {{Translated|zh|十一面體}} to the talk page. For more guidance, see Misplaced Pages:Translation.

A hendecahedron (or undecahedron) is a polyhedron with 11 faces. There are many topologically distinct forms of a hendecahedron, for example the decagonal pyramid, and enneagonal prism.

Three forms are Johnson solids: augmented hexagonal prism, biaugmented triangular prism, and elongated pentagonal pyramid.

Two classes, the bisymmetric and the sphenoid hendecahedra, are space-filling.

Name of hendecahedron

The name of hendecahedron is based on its meaning. Hen- represents one. Deca represents ten, and when combined with the polyhedron suffix -hedron, the name becomes Hendecahedron.

Common hendecahedron

In all the convex hendecahedra, there are a total of 440,564 convex ones with distinct differences in topology. There are significant differences in the structure of topology, which means two types of polyhedrons cannot be transformed by moving vertex positions, twisting, or scaling, such as a pentagonal pyramid and a nine diagonal column. They can't change with each other, so their topology structure is different. However, the pentagonal prism and enneagonal prism can interchange by stretching out or drawing back one of the nine sides of the scale, so the triangulum prism and the triangulum pyramid have no obvious difference in topology.

The common hendecahedrons are cones, cylinders, some Jason polyhedrons, and the semi-regular polyhedron. The semi-regular polyhedron here is not the Archimedean solid, but the enneagonal prism.

Other hendecahedrons include enneagonal prism, Spherical octagonal pyramid, two side taper triangular prism of the duality of six, side cone Angle and bisymmetric hendecahedron, which can close shop space.

Bisymmetric hendecahedron

The bisymmetric hendecahedron is a space-filling polyhedron which can be assembled into layers of interpenetrating "boat-shaped" tetramers, which in turn are then stacked to fill space; it is hence a three-dimensional analogue of the Cairo pentagon.

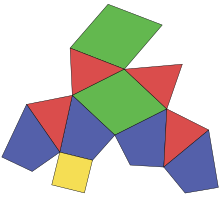
Sphenoid hendecahedron

The sphenoid hendecahedron is a space-filling polyhedron which can be assembled into layers of the Floret tiling, which in turn are stacked to fill space.

Hendecahedra in chemistry

In chemistry, after removing all 18 sides in borane hydrogen ions (), it is an octadecahedron. If making a perpendicular to the center of gravity to the surface of a boron atom, a new polyhedron is constructed, which is 18 surface structures of the dual polyhedron, also one of hendecahedrons.

Convex

There are 440,564 topologically distinct convex hendecahedra, excluding mirror images, having at least 8 vertices. (Two polyhedra are "topologically distinct" if they have intrinsically different arrangements of faces and vertices, such that it is impossible to distort one into the other simply by changing the lengths of edges or the angles between edges or faces.)

References

1. Inchbald (1996)
2. Counting polyhedra

• Thomas H. Sidebotham. The A to Z of Mathematics: A Basic Guide. John Wiley & Sons. 2003: 237. ISBN 9780471461630
• Steven Dutch: How Many Polyhedra are There? (http://www.uwgb.edu/dutchs/symmetry/POLYHOW M.HTM)
• Counting polyhedra (http://www.numericana.com/data/polycount.htm) numericana.com
• Inchbald, Guy. "Five Space-Filling Polyhedra." The Mathematical Gazette 80, no. 489 (November 1996): 466-475
• Space-Filling Bisymmetric Hendecahedron.
• Anderson, Ian. "Constructing Tournament Designs." The Mathematical Gazette 73, no. 466 (December 1989): 284-292
• Holleman, A. F.; Wiberg, E., Inorganic Chemistry, San Diego: Academic Press: 1165, 2001, ISBN 0-12-352651-5
• Inchbald, Guy (1996). "Five space-filling polyhedra". The Mathematical Gazette. 80 (489): 466–475. doi:10.2307/3618509. ISSN 0025-5572. JSTOR 3618509. Zbl 0885.52011.

External links

• Weisstein, Eric W. "Undecahedron". MathWorld.

This polyhedron-related article is a stub. You can help Misplaced Pages by expanding it.

• v
• t
• e

• Polyhedra
• Polyhedron stubs