
A heptahedron (pl.: heptahedra) is a polyhedron having seven sides, or faces.
A heptahedron can take a large number of different basic forms, or topologies. The most familiar are the hexagonal pyramid and the pentagonal prism. Also notable is the tetrahemihexahedron, which can be seen as a tessellation of the real projective plane. No heptahedra are regular.
Topologically distinct heptahedron
Convex
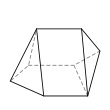
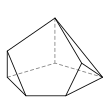
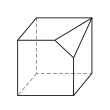
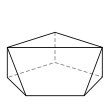
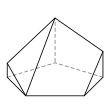
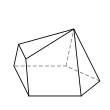
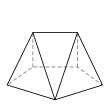
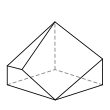
There are 34 topologically distinct convex heptahedra, excluding mirror images. (Two polyhedra are "topologically distinct" if they have intrinsically different arrangements of faces and vertices, such that it is impossible to distort one into the other simply by changing the lengths of edges or the angles between edges or faces.)
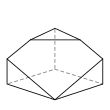
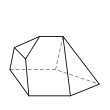
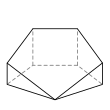
An example of each type is depicted below, along with the number of sides on each of the faces. The images are ordered by descending number of six-sided faces (if any), followed by descending number of five-sided faces (if any), and so on.
|

|

|
|
|
|

|

|
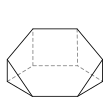
 Hexagonal pyramid
|

|
|
|
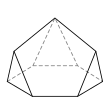
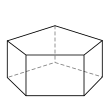 Pentagonal prism
|
|

|
|
|
|

|
|
|
|

|
|

|
|

|
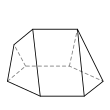
 Elongated triangular pyramid
|
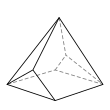
|

|
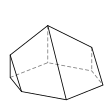
 Diminished cube
|
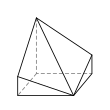
|

|
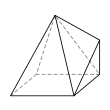
|
Concave
| This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (May 2015) (Learn how and when to remove this message) |
|
Six topologically distinct concave heptahedra (excluding mirror images) can be formed by combining two tetrahedra in various configurations. The third, fourth and fifth of these have a face with collinear adjacent edges, and the sixth has a face that is not simply connected. | |
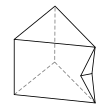  13 topologically distinct heptahedra (excluding mirror images) can be formed by cutting notches out of the edges of a triangular prism or square pyramid. Two examples are shown. |
  A variety of non-simply-connected heptahedra are possible. Two examples are shown. |
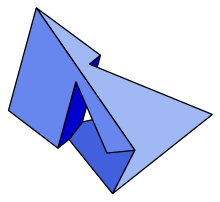
One particularly interesting example is the Szilassi polyhedron, a Toroidal polyhedron with 7 non-convex six sided faces.
References
- Frank Chester. "The Geometry of the Chestahedron". Retrieved 8 August 2022.
- "Counting polyhedra". numericana.com. 5 April 2015.
- Szilassi, Lajos (1986), "Regular toroids" (PDF), Structural Topology, 13: 69–80
External links
- Polyhedra with 4–7 Faces by Steven Dutch
- Weisstein, Eric W. "Heptahedron". MathWorld.
| Polyhedra | |
|---|---|
| Listed by number of faces and type | |
| 1–10 faces | |
| 11–20 faces | |
| >20 faces |
|
| elemental things |
|
| convex polyhedron |
|
| non-convex polyhedron |
|
| prismatoids | |





