Misplaced Pages

Omnitruncated simplicial honeycomb

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
(Redirected from Omnitruncated simplectic honeycomb)

In geometry an omnitruncated simplicial honeycomb or omnitruncated n-simplex honeycomb is an n-dimensional uniform tessellation, based on the symmetry of the A ~ n {\displaystyle {\tilde {A}}_{n}} affine Coxeter group. Each is composed of omnitruncated simplex facets. The vertex figure for each is an irregular n-simplex.

The facets of an omnitruncated simplicial honeycomb are called permutahedra and can be positioned in n+1 space with integral coordinates, permutations of the whole numbers (0,1,..,n).

n A ~ 1 + {\displaystyle {\tilde {A}}_{1+}} Image Tessellation Facets Vertex figure Facets per vertex figure Vertices per vertex figure
1 A ~ 1 {\displaystyle {\tilde {A}}_{1}} Apeirogon
 Line segment Line segment 1 2
2 A ~ 2 {\displaystyle {\tilde {A}}_{2}} Hexagonal tiling
hexagon 		Equilateral triangle
 3 hexagons 3
3 A ~ 3 {\displaystyle {\tilde {A}}_{3}} Bitruncated cubic honeycomb
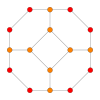Truncated octahedron 		irr. tetrahedron
 4 truncated octahedron 4
4 A ~ 4 {\displaystyle {\tilde {A}}_{4}} Omnitruncated 4-simplex honeycomb
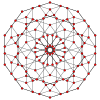Omnitruncated 4-simplex 		irr. 5-cell
 5 omnitruncated 4-simplex 5
5 A ~ 5 {\displaystyle {\tilde {A}}_{5}} Omnitruncated 5-simplex honeycomb
Omnitruncated 5-simplex 		irr. 5-simplex
 6 omnitruncated 5-simplex 6
6 A ~ 6 {\displaystyle {\tilde {A}}_{6}} Omnitruncated 6-simplex honeycomb
Omnitruncated 6-simplex 		irr. 6-simplex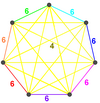
 7 omnitruncated 6-simplex 7
7 A ~ 7 {\displaystyle {\tilde {A}}_{7}} Omnitruncated 7-simplex honeycomb
Omnitruncated 7-simplex 		irr. 7-simplex
 8 omnitruncated 7-simplex 8
8 A ~ 8 {\displaystyle {\tilde {A}}_{8}} Omnitruncated 8-simplex honeycomb
Omnitruncated 8-simplex 		irr. 8-simplex
 9 omnitruncated 8-simplex 9

Projection by folding

The (2n-1)-simplex honeycombs can be projected into the n-dimensional omnitruncated hypercubic honeycomb by a geometric folding operation that maps two pairs of mirrors into each other, sharing the same vertex arrangement:

A ~ 3 {\displaystyle {\tilde {A}}_{3}} A ~ 5 {\displaystyle {\tilde {A}}_{5}} A ~ 7 {\displaystyle {\tilde {A}}_{7}} A ~ 9 {\displaystyle {\tilde {A}}_{9}} ...
C ~ 2 {\displaystyle {\tilde {C}}_{2}} C ~ 3 {\displaystyle {\tilde {C}}_{3}} C ~ 4 {\displaystyle {\tilde {C}}_{4}} C ~ 5 {\displaystyle {\tilde {C}}_{5}} ...

See also

References

  • George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
  • Branko Grünbaum, Uniform tilings of 3-space. Geombinatorics 4(1994), 49 - 56.
  • Norman Johnson Uniform Polytopes, Manuscript (1991)
  • Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8
  • Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
    • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, (1.9 Uniform space-fillings)
    • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III,
Fundamental convex regular and uniform honeycombs in dimensions 2–9
Space Family A ~ n − 1 {\displaystyle {\tilde {A}}_{n-1}} C ~ n − 1 {\displaystyle {\tilde {C}}_{n-1}} B ~ n − 1 {\displaystyle {\tilde {B}}_{n-1}} D ~ n − 1 {\displaystyle {\tilde {D}}_{n-1}} G ~ 2 {\displaystyle {\tilde {G}}_{2}} / F ~ 4 {\displaystyle {\tilde {F}}_{4}} / E ~ n − 1 {\displaystyle {\tilde {E}}_{n-1}}
E Uniform tiling 0 δ3 hδ3 qδ3 Hexagonal
E Uniform convex honeycomb 0 δ4 hδ4 qδ4
E Uniform 4-honeycomb 0 δ5 hδ5 qδ5 24-cell honeycomb
E Uniform 5-honeycomb 0 δ6 hδ6 qδ6
E Uniform 6-honeycomb 0 δ7 hδ7 qδ7 222
E Uniform 7-honeycomb 0 δ8 hδ8 qδ8 133 • 331
E Uniform 8-honeycomb 0 δ9 hδ9 qδ9 152 • 251 • 521
E Uniform 9-honeycomb 0 δ10 hδ10 qδ10
E Uniform 10-honeycomb 0 δ11 hδ11 qδ11
E Uniform (n-1)-honeycomb 0 δn hδn qδn 1k2 • 2k1 • k21
Categories: