A quantum computer is a computer that exploits quantum mechanical phenomena. On small scales, physical matter exhibits properties of both particles and waves, and quantum computing leverages this behavior using specialized hardware. Classical physics cannot explain the operation of these quantum devices, and a scalable quantum computer could perform some calculations exponentially faster than any modern "classical" computer. Theoretically a large-scale quantum computer could break some widely used encryption schemes and aid physicists in performing physical simulations; however, the current state of the art is largely experimental and impractical, with several obstacles to useful applications.
The basic unit of information in quantum computing, the qubit (or "quantum bit"), serves the same function as the bit in classical computing. However, unlike a classical bit, which can be in one of two states (a binary), a qubit can exist in a superposition of its two "basis" states, a state that is in an abstract sense "between" the two basis states. When measuring a qubit, the result is a probabilistic output of a classical bit. If a quantum computer manipulates the qubit in a particular way, wave interference effects can amplify the desired measurement results. The design of quantum algorithms involves creating procedures that allow a quantum computer to perform calculations efficiently and quickly.
Quantum computers are not yet practical for real work. Physically engineering high-quality qubits has proven challenging. If a physical qubit is not sufficiently isolated from its environment, it suffers from quantum decoherence, introducing noise into calculations. National governments have invested heavily in experimental research that aims to develop scalable qubits with longer coherence times and lower error rates. Example implementations include superconductors (which isolate an electrical current by eliminating electrical resistance) and ion traps (which confine a single atomic particle using electromagnetic fields).
In principle, a classical computer can solve the same computational problems as a quantum computer, given enough time. Quantum advantage comes in the form of time complexity rather than computability, and quantum complexity theory shows that some quantum algorithms are exponentially more efficient than the best-known classical algorithms. A large-scale quantum computer could in theory solve computational problems unsolvable by a classical computer in any reasonable amount of time. This concept of extra ability has been called "quantum supremacy". While such claims have drawn significant attention to the discipline, near-term practical use cases remain limited.
History
For a chronological guide, see Timeline of quantum computing and communication.For many years, the fields of quantum mechanics and computer science formed distinct academic communities. Modern quantum theory developed in the 1920s to explain perplexing physical phenomena observed at atomic scales, and digital computers emerged in the following decades to replace human computers for tedious calculations. Both disciplines had practical applications during World War II; computers played a major role in wartime cryptography, and quantum physics was essential for nuclear physics used in the Manhattan Project.
As physicists applied quantum mechanical models to computational problems and swapped digital bits for qubits, the fields of quantum mechanics and computer science began to converge. In 1980, Paul Benioff introduced the quantum Turing machine, which uses quantum theory to describe a simplified computer. When digital computers became faster, physicists faced an exponential increase in overhead when simulating quantum dynamics, prompting Yuri Manin and Richard Feynman to independently suggest that hardware based on quantum phenomena might be more efficient for computer simulation. In a 1984 paper, Charles Bennett and Gilles Brassard applied quantum theory to cryptography protocols and demonstrated that quantum key distribution could enhance information security.
Quantum algorithms then emerged for solving oracle problems, such as Deutsch's algorithm in 1985, the Bernstein–Vazirani algorithm in 1993, and Simon's algorithm in 1994. These algorithms did not solve practical problems, but demonstrated mathematically that one could gain more information by querying a black box with a quantum state in superposition, sometimes referred to as quantum parallelism.

Peter Shor built on these results with his 1994 algorithm for breaking the widely used RSA and Diffie–Hellman encryption protocols, which drew significant attention to the field of quantum computing. In 1996, Grover's algorithm established a quantum speedup for the widely applicable unstructured search problem. The same year, Seth Lloyd proved that quantum computers could simulate quantum systems without the exponential overhead present in classical simulations, validating Feynman's 1982 conjecture.
Over the years, experimentalists have constructed small-scale quantum computers using trapped ions and superconductors. In 1998, a two-qubit quantum computer demonstrated the feasibility of the technology, and subsequent experiments have increased the number of qubits and reduced error rates.
In 2019, Google AI and NASA announced that they had achieved quantum supremacy with a 54-qubit machine, performing a computation that is impossible for any classical computer. However, the validity of this claim is still being actively researched.
Quantum information processing
See also: Introduction to quantum mechanicsComputer engineers typically describe a modern computer's operation in terms of classical electrodynamics. Within these "classical" computers, some components (such as semiconductors and random number generators) may rely on quantum behavior, but these components are not isolated from their environment, so any quantum information quickly decoheres. While programmers may depend on probability theory when designing a randomized algorithm, quantum mechanical notions like superposition and interference are largely irrelevant for program analysis.
Quantum programs, in contrast, rely on precise control of coherent quantum systems. Physicists describe these systems mathematically using linear algebra. Complex numbers model probability amplitudes, vectors model quantum states, and matrices model the operations that can be performed on these states. Programming a quantum computer is then a matter of composing operations in such a way that the resulting program computes a useful result in theory and is implementable in practice.
As physicist Charlie Bennett describes the relationship between quantum and classical computers,
A classical computer is a quantum computer ... so we shouldn't be asking about "where do quantum speedups come from?" We should say, "well, all computers are quantum. ... Where do classical slowdowns come from?"
Quantum information
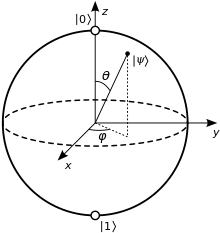
Just as the bit is the basic concept of classical information theory, the qubit is the fundamental unit of quantum information. The same term qubit is used to refer to an abstract mathematical model and to any physical system that is represented by that model. A classical bit, by definition, exists in either of two physical states, which can be denoted 0 and 1. A qubit is also described by a state, and two states often written and serve as the quantum counterparts of the classical states 0 and 1. However, the quantum states and belong to a vector space, meaning that they can be multiplied by constants and added together, and the result is again a valid quantum state. Such a combination is known as a superposition of and .
A two-dimensional vector mathematically represents a qubit state. Physicists typically use Dirac notation for quantum mechanical linear algebra, writing 'ket psi' for a vector labeled . Because a qubit is a two-state system, any qubit state takes the form , where and are the standard basis states, and and are the probability amplitudes, which are in general complex numbers. If either or is zero, the qubit is effectively a classical bit; when both are nonzero, the qubit is in superposition. Such a quantum state vector acts similarly to a (classical) probability vector, with one key difference: unlike probabilities, probability amplitudes are not necessarily positive numbers. Negative amplitudes allow for destructive wave interference.
When a qubit is measured in the standard basis, the result is a classical bit. The Born rule describes the norm-squared correspondence between amplitudes and probabilities—when measuring a qubit , the state collapses to with probability , or to with probability . Any valid qubit state has coefficients and such that . As an example, measuring the qubit would produce either or with equal probability.
Each additional qubit doubles the dimension of the state space. As an example, the vector 1/√2|00⟩ + 1/√2|01⟩ represents a two-qubit state, a tensor product of the qubit |0⟩ with the qubit 1/√2|0⟩ + 1/√2|1⟩. This vector inhabits a four-dimensional vector space spanned by the basis vectors |00⟩, |01⟩, |10⟩, and |11⟩. The Bell state 1/√2|00⟩ + 1/√2|11⟩ is impossible to decompose into the tensor product of two individual qubits—the two qubits are entangled because neither qubit has a state vector of its own. In general, the vector space for an n-qubit system is 2-dimensional, and this makes it challenging for a classical computer to simulate a quantum one: representing a 100-qubit system requires storing 2 classical values.
Unitary operators
See also: Unitarity (physics)The state of this one-qubit quantum memory can be manipulated by applying quantum logic gates, analogous to how classical memory can be manipulated with classical logic gates. One important gate for both classical and quantum computation is the NOT gate, which can be represented by a matrix Mathematically, the application of such a logic gate to a quantum state vector is modelled with matrix multiplication. Thus
- and .
The mathematics of single qubit gates can be extended to operate on multi-qubit quantum memories in two important ways. One way is simply to select a qubit and apply that gate to the target qubit while leaving the remainder of the memory unaffected. Another way is to apply the gate to its target only if another part of the memory is in a desired state. These two choices can be illustrated using another example. The possible states of a two-qubit quantum memory are The controlled NOT (CNOT) gate can then be represented using the following matrix: As a mathematical consequence of this definition, , , , and . In other words, the CNOT applies a NOT gate ( from before) to the second qubit if and only if the first qubit is in the state . If the first qubit is , nothing is done to either qubit.
In summary, quantum computation can be described as a network of quantum logic gates and measurements. However, any measurement can be deferred to the end of quantum computation, though this deferment may come at a computational cost, so most quantum circuits depict a network consisting only of quantum logic gates and no measurements.
Quantum parallelism
Quantum parallelism is the heuristic that quantum computers can be thought of as evaluating a function for multiple input values simultaneously. This can be achieved by preparing a quantum system in a superposition of input states and applying a unitary transformation that encodes the function to be evaluated. The resulting state encodes the function's output values for all input values in the superposition, allowing for the computation of multiple outputs simultaneously. This property is key to the speedup of many quantum algorithms. However, "parallelism" in this sense is insufficient to speed up a computation, because the measurement at the end of the computation gives only one value. To be useful, a quantum algorithm must also incorporate some other conceptual ingredient.
Quantum programming
Further information: Quantum programmingThere are a number of models of computation for quantum computing, distinguished by the basic elements in which the computation is decomposed.
Gate array
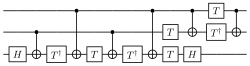
A quantum gate array decomposes computation into a sequence of few-qubit quantum gates. A quantum computation can be described as a network of quantum logic gates and measurements. However, any measurement can be deferred to the end of quantum computation, though this deferment may come at a computational cost, so most quantum circuits depict a network consisting only of quantum logic gates and no measurements.
Any quantum computation (which is, in the above formalism, any unitary matrix of size over qubits) can be represented as a network of quantum logic gates from a fairly small family of gates. A choice of gate family that enables this construction is known as a universal gate set, since a computer that can run such circuits is a universal quantum computer. One common such set includes all single-qubit gates as well as the CNOT gate from above. This means any quantum computation can be performed by executing a sequence of single-qubit gates together with CNOT gates. Though this gate set is infinite, it can be replaced with a finite gate set by appealing to the Solovay-Kitaev theorem. Implementation of Boolean functions using the few-qubit quantum gates is presented here.
Measurement-based quantum computing
A measurement-based quantum computer decomposes computation into a sequence of Bell state measurements and single-qubit quantum gates applied to a highly entangled initial state (a cluster state), using a technique called quantum gate teleportation.
Adiabatic quantum computing
An adiabatic quantum computer, based on quantum annealing, decomposes computation into a slow continuous transformation of an initial Hamiltonian into a final Hamiltonian, whose ground states contain the solution.
Neuromorphic quantum computing
Neuromorphic quantum computing (abbreviated as ‘n.quantum computing’) is an unconventional computing type of computing that uses neuromorphic computing to perform quantum operations. It was suggested that quantum algorithms, which are algorithms that run on a realistic model of quantum computation, can be computed equally efficiently with neuromorphic quantum computing. Both, traditional quantum computing and neuromorphic quantum computing are physics-based unconventional computing approaches to computations and do not follow the von Neumann architecture. They both construct a system (a circuit) that represents the physical problem at hand and then leverage their respective physics properties of the system to seek the “minimum”. Neuromorphic quantum computing and quantum computing share similar physical properties during computation.
Topological quantum computing
A topological quantum computer decomposes computation into the braiding of anyons in a 2D lattice.
Quantum Turing machine
A quantum Turing machine is the quantum analog of a Turing machine. All of these models of computation—quantum circuits, one-way quantum computation, adiabatic quantum computation, and topological quantum computation—have been shown to be equivalent to the quantum Turing machine; given a perfect implementation of one such quantum computer, it can simulate all the others with no more than polynomial overhead. This equivalence need not hold for practical quantum computers, since the overhead of simulation may be too large to be practical.
Noisy intermediate-scale quantum computing
The threshold theorem shows how increasing the number of qubits can mitigate errors, yet fully fault-tolerant quantum computing remains "a rather distant dream". According to some researchers, noisy intermediate-scale quantum (NISQ) machines may have specialized uses in the near future, but noise in quantum gates limits their reliability. Scientists at Harvard University successfully created "quantum circuits" that correct errors more efficiently than alternative methods, which may potentially remove a major obstacle to practical quantum computers. The Harvard research team was supported by MIT, QuEra Computing, Caltech, and Princeton University and funded by DARPA's Optimization with Noisy Intermediate-Scale Quantum devices (ONISQ) program.
Quantum cryptography and cybersecurity

Quantum computing has significant potential applications in the fields of cryptography and cybersecurity. Quantum cryptography, which relies on the principles of quantum mechanics, offers the possibility of secure communication channels that are resistant to eavesdropping. Quantum key distribution (QKD) protocols, such as BB84, enable the secure exchange of cryptographic keys between parties, ensuring the confidentiality and integrity of communication. Moreover, quantum random number generators (QRNGs) can produce high-quality random numbers, which are essential for secure encryption.
However, quantum computing also poses challenges to traditional cryptographic systems. Shor's algorithm, a quantum algorithm for integer factorization, could potentially break widely used public-key cryptography schemes like RSA, which rely on the difficulty of factoring large numbers. Post-quantum cryptography, which involves the development of cryptographic algorithms that are resistant to attacks by both classical and quantum computers, is an active area of research aimed at addressing this concern.
Ongoing research in quantum cryptography and post-quantum cryptography is crucial for ensuring the security of communication and data in the face of evolving quantum computing capabilities. Advances in these fields, such as the development of new QKD protocols, the improvement of QRNGs, and the standardization of post-quantum cryptographic algorithms, will play a key role in maintaining the integrity and confidentiality of information in the quantum era.
Communication
Further information: Quantum information scienceQuantum cryptography enables new ways to transmit data securely; for example, quantum key distribution uses entangled quantum states to establish secure cryptographic keys. When a sender and receiver exchange quantum states, they can guarantee that an adversary does not intercept the message, as any unauthorized eavesdropper would disturb the delicate quantum system and introduce a detectable change. With appropriate cryptographic protocols, the sender and receiver can thus establish shared private information resistant to eavesdropping.
Modern fiber-optic cables can transmit quantum information over relatively short distances. Ongoing experimental research aims to develop more reliable hardware (such as quantum repeaters), hoping to scale this technology to long-distance quantum networks with end-to-end entanglement. Theoretically, this could enable novel technological applications, such as distributed quantum computing and enhanced quantum sensing.
Algorithms
Progress in finding quantum algorithms typically focuses on this quantum circuit model, though exceptions like the quantum adiabatic algorithm exist. Quantum algorithms can be roughly categorized by the type of speedup achieved over corresponding classical algorithms.
Quantum algorithms that offer more than a polynomial speedup over the best-known classical algorithm include Shor's algorithm for factoring and the related quantum algorithms for computing discrete logarithms, solving Pell's equation, and more generally solving the hidden subgroup problem for abelian finite groups. These algorithms depend on the primitive of the quantum Fourier transform. No mathematical proof has been found that shows that an equally fast classical algorithm cannot be discovered, but evidence suggests that this is unlikely. Certain oracle problems like Simon's problem and the Bernstein–Vazirani problem do give provable speedups, though this is in the quantum query model, which is a restricted model where lower bounds are much easier to prove and doesn't necessarily translate to speedups for practical problems.
Other problems, including the simulation of quantum physical processes from chemistry and solid-state physics, the approximation of certain Jones polynomials, and the quantum algorithm for linear systems of equations have quantum algorithms appearing to give super-polynomial speedups and are BQP-complete. Because these problems are BQP-complete, an equally fast classical algorithm for them would imply that no quantum algorithm gives a super-polynomial speedup, which is believed to be unlikely.
Some quantum algorithms, like Grover's algorithm and amplitude amplification, give polynomial speedups over corresponding classical algorithms. Though these algorithms give comparably modest quadratic speedup, they are widely applicable and thus give speedups for a wide range of problems.
Simulation of quantum systems
Main article: Quantum simulationSince chemistry and nanotechnology rely on understanding quantum systems, and such systems are impossible to simulate in an efficient manner classically, quantum simulation may be an important application of quantum computing. Quantum simulation could also be used to simulate the behavior of atoms and particles at unusual conditions such as the reactions inside a collider. In June 2023, IBM computer scientists reported that a quantum computer produced better results for a physics problem than a conventional supercomputer.
About 2% of the annual global energy output is used for nitrogen fixation to produce ammonia for the Haber process in the agricultural fertilizer industry (even though naturally occurring organisms also produce ammonia). Quantum simulations might be used to understand this process and increase the energy efficiency of production. It is expected that an early use of quantum computing will be modeling that improves the efficiency of the Haber–Bosch process by the mid-2020s although some have predicted it will take longer.
Post-quantum cryptography
Main article: Post-quantum cryptographyA notable application of quantum computation is for attacks on cryptographic systems that are currently in use. Integer factorization, which underpins the security of public key cryptographic systems, is believed to be computationally infeasible with an ordinary computer for large integers if they are the product of few prime numbers (e.g., products of two 300-digit primes). By comparison, a quantum computer could solve this problem exponentially faster using Shor's algorithm to find its factors. This ability would allow a quantum computer to break many of the cryptographic systems in use today, in the sense that there would be a polynomial time (in the number of digits of the integer) algorithm for solving the problem. In particular, most of the popular public key ciphers are based on the difficulty of factoring integers or the discrete logarithm problem, both of which can be solved by Shor's algorithm. In particular, the RSA, Diffie–Hellman, and elliptic curve Diffie–Hellman algorithms could be broken. These are used to protect secure Web pages, encrypted email, and many other types of data. Breaking these would have significant ramifications for electronic privacy and security.
Identifying cryptographic systems that may be secure against quantum algorithms is an actively researched topic under the field of post-quantum cryptography. Some public-key algorithms are based on problems other than the integer factorization and discrete logarithm problems to which Shor's algorithm applies, like the McEliece cryptosystem based on a problem in coding theory. Lattice-based cryptosystems are also not known to be broken by quantum computers, and finding a polynomial time algorithm for solving the dihedral hidden subgroup problem, which would break many lattice based cryptosystems, is a well-studied open problem. It has been proven that applying Grover's algorithm to break a symmetric (secret key) algorithm by brute force requires time equal to roughly 2 invocations of the underlying cryptographic algorithm, compared with roughly 2 in the classical case, meaning that symmetric key lengths are effectively halved: AES-256 would have the same security against an attack using Grover's algorithm that AES-128 has against classical brute-force search (see Key size).
Search problems
Main article: Grover's algorithmThe most well-known example of a problem that allows for a polynomial quantum speedup is unstructured search, which involves finding a marked item out of a list of items in a database. This can be solved by Grover's algorithm using queries to the database, quadratically fewer than the queries required for classical algorithms. In this case, the advantage is not only provable but also optimal: it has been shown that Grover's algorithm gives the maximal possible probability of finding the desired element for any number of oracle lookups. Many examples of provable quantum speedups for query problems are based on Grover's algorithm, including Brassard, Høyer, and Tapp's algorithm for finding collisions in two-to-one functions, and Farhi, Goldstone, and Gutmann's algorithm for evaluating NAND trees.
Problems that can be efficiently addressed with Grover's algorithm have the following properties:
- There is no searchable structure in the collection of possible answers,
- The number of possible answers to check is the same as the number of inputs to the algorithm, and
- There exists a Boolean function that evaluates each input and determines whether it is the correct answer.
For problems with all these properties, the running time of Grover's algorithm on a quantum computer scales as the square root of the number of inputs (or elements in the database), as opposed to the linear scaling of classical algorithms. A general class of problems to which Grover's algorithm can be applied is a Boolean satisfiability problem, where the database through which the algorithm iterates is that of all possible answers. An example and possible application of this is a password cracker that attempts to guess a password. Breaking symmetric ciphers with this algorithm is of interest to government agencies.
Quantum annealing
Quantum annealing relies on the adiabatic theorem to undertake calculations. A system is placed in the ground state for a simple Hamiltonian, which slowly evolves to a more complicated Hamiltonian whose ground state represents the solution to the problem in question. The adiabatic theorem states that if the evolution is slow enough the system will stay in its ground state at all times through the process. Adiabatic optimization may be helpful for solving computational biology problems.
Machine learning
Main article: Quantum machine learningSince quantum computers can produce outputs that classical computers cannot produce efficiently, and since quantum computation is fundamentally linear algebraic, some express hope in developing quantum algorithms that can speed up machine learning tasks.
For example, the HHL Algorithm, named after its discoverers Harrow, Hassidim, and Lloyd, is believed to provide speedup over classical counterparts. Some research groups have recently explored the use of quantum annealing hardware for training Boltzmann machines and deep neural networks.
Deep generative chemistry models emerge as powerful tools to expedite drug discovery. However, the immense size and complexity of the structural space of all possible drug-like molecules pose significant obstacles, which could be overcome in the future by quantum computers. Quantum computers are naturally good for solving complex quantum many-body problems and thus may be instrumental in applications involving quantum chemistry. Therefore, one can expect that quantum-enhanced generative models including quantum GANs may eventually be developed into ultimate generative chemistry algorithms.
Engineering

As of 2023, classical computers outperform quantum computers for all real-world applications. While current quantum computers may speed up solutions to particular mathematical problems, they give no computational advantage for practical tasks. Scientists and engineers are exploring multiple technologies for quantum computing hardware and hope to develop scalable quantum architectures, but serious obstacles remain.
Challenges
There are a number of technical challenges in building a large-scale quantum computer. Physicist David DiVincenzo has listed these requirements for a practical quantum computer:
- Physically scalable to increase the number of qubits
- Qubits that can be initialized to arbitrary values
- Quantum gates that are faster than decoherence time
- Universal gate set
- Qubits that can be read easily.
Sourcing parts for quantum computers is also very difficult. Superconducting quantum computers, like those constructed by Google and IBM, need helium-3, a nuclear research byproduct, and special superconducting cables made only by the Japanese company Coax Co.
The control of multi-qubit systems requires the generation and coordination of a large number of electrical signals with tight and deterministic timing resolution. This has led to the development of quantum controllers that enable interfacing with the qubits. Scaling these systems to support a growing number of qubits is an additional challenge.
Decoherence
One of the greatest challenges involved with constructing quantum computers is controlling or removing quantum decoherence. This usually means isolating the system from its environment as interactions with the external world cause the system to decohere. However, other sources of decoherence also exist. Examples include the quantum gates, and the lattice vibrations and background thermonuclear spin of the physical system used to implement the qubits. Decoherence is irreversible, as it is effectively non-unitary, and is usually something that should be highly controlled, if not avoided. Decoherence times for candidate systems in particular, the transverse relaxation time T2 (for NMR and MRI technology, also called the dephasing time), typically range between nanoseconds and seconds at low temperature. Currently, some quantum computers require their qubits to be cooled to 20 millikelvin (usually using a dilution refrigerator) in order to prevent significant decoherence. A 2020 study argues that ionizing radiation such as cosmic rays can nevertheless cause certain systems to decohere within milliseconds.
As a result, time-consuming tasks may render some quantum algorithms inoperable, as attempting to maintain the state of qubits for a long enough duration will eventually corrupt the superpositions.
These issues are more difficult for optical approaches as the timescales are orders of magnitude shorter and an often-cited approach to overcoming them is optical pulse shaping. Error rates are typically proportional to the ratio of operating time to decoherence time; hence any operation must be completed much more quickly than the decoherence time.
As described by the threshold theorem, if the error rate is small enough, it is thought to be possible to use quantum error correction to suppress errors and decoherence. This allows the total calculation time to be longer than the decoherence time if the error correction scheme can correct errors faster than decoherence introduces them. An often-cited figure for the required error rate in each gate for fault-tolerant computation is 10, assuming the noise is depolarizing.
Meeting this scalability condition is possible for a wide range of systems. However, the use of error correction brings with it the cost of a greatly increased number of required qubits. The number required to factor integers using Shor's algorithm is still polynomial, and thought to be between L and L, where L is the number of binary digits in the number to be factored; error correction algorithms would inflate this figure by an additional factor of L. For a 1000-bit number, this implies a need for about 10 bits without error correction. With error correction, the figure would rise to about 10 bits. Computation time is about L or about 10 steps and at 1 MHz, about 10 seconds. However, the encoding and error-correction overheads increase the size of a real fault-tolerant quantum computer by several orders of magnitude. Careful estimates show that at least 3 million physical qubits would factor 2,048-bit integer in 5 months on a fully error-corrected trapped-ion quantum computer. In terms of the number of physical qubits, to date, this remains the lowest estimate for practically useful integer factorization problem sizing 1,024-bit or larger.
Another approach to the stability-decoherence problem is to create a topological quantum computer with anyons, quasi-particles used as threads, and relying on braid theory to form stable logic gates.
Quantum supremacy
Physicist John Preskill coined the term quantum supremacy to describe the engineering feat of demonstrating that a programmable quantum device can solve a problem beyond the capabilities of state-of-the-art classical computers. The problem need not be useful, so some view the quantum supremacy test only as a potential future benchmark.
In October 2019, Google AI Quantum, with the help of NASA, became the first to claim to have achieved quantum supremacy by performing calculations on the Sycamore quantum computer more than 3,000,000 times faster than they could be done on Summit, generally considered the world's fastest computer. This claim has been subsequently challenged: IBM has stated that Summit can perform samples much faster than claimed, and researchers have since developed better algorithms for the sampling problem used to claim quantum supremacy, giving substantial reductions to the gap between Sycamore and classical supercomputers and even beating it.
In December 2020, a group at USTC implemented a type of Boson sampling on 76 photons with a photonic quantum computer, Jiuzhang, to demonstrate quantum supremacy. The authors claim that a classical contemporary supercomputer would require a computational time of 600 million years to generate the number of samples their quantum processor can generate in 20 seconds.
Claims of quantum supremacy have generated hype around quantum computing, but they are based on contrived benchmark tasks that do not directly imply useful real-world applications.
In January 2024, a study published in Physical Review Letters provided direct verification of quantum supremacy experiments by computing exact amplitudes for experimentally generated bitstrings using a new-generation Sunway supercomputer, demonstrating a significant leap in simulation capability built on a multiple-amplitude tensor network contraction algorithm. This development underscores the evolving landscape of quantum computing, highlighting both the progress and the complexities involved in validating quantum supremacy claims.
Skepticism
Despite high hopes for quantum computing, significant progress in hardware, and optimism about future applications, a 2023 Nature spotlight article summarized current quantum computers as being "For now, absolutely nothing". The article elaborated that quantum computers are yet to be more useful or efficient than conventional computers in any case, though it also argued that in the long term such computers are likely to be useful. A 2023 Communications of the ACM article found that current quantum computing algorithms are "insufficient for practical quantum advantage without significant improvements across the software/hardware stack". It argues that the most promising candidates for achieving speedup with quantum computers are "small-data problems", for example in chemistry and materials science. However, the article also concludes that a large range of the potential applications it considered, such as machine learning, "will not achieve quantum advantage with current quantum algorithms in the foreseeable future", and it identified I/O constraints that make speedup unlikely for "big data problems, unstructured linear systems, and database search based on Grover's algorithm".
This state of affairs can be traced to several current and long-term considerations.
- Conventional computer hardware and algorithms are not only optimized for practical tasks, but are still improving rapidly, particularly GPU accelerators.
- Current quantum computing hardware generates only a limited amount of entanglement before getting overwhelmed by noise.
- Quantum algorithms provide speedup over conventional algorithms only for some tasks, and matching these tasks with practical applications proved challenging. Some promising tasks and applications require resources far beyond those available today. In particular, processing large amounts of non-quantum data is a challenge for quantum computers.
- Some promising algorithms have been "dequantized", i.e., their non-quantum analogues with similar complexity have been found.
- If quantum error correction is used to scale quantum computers to practical applications, its overhead may undermine speedup offered by many quantum algorithms.
- Complexity analysis of algorithms sometimes makes abstract assumptions that do not hold in applications. For example, input data may not already be available encoded in quantum states, and "oracle functions" used in Grover's algorithm often have internal structure that can be exploited for faster algorithms.
In particular, building computers with large numbers of qubits may be futile if those qubits are not connected well enough and cannot maintain sufficiently high degree of entanglement for a long time. When trying to outperform conventional computers, quantum computing researchers often look for new tasks that can be solved on quantum computers, but this leaves the possibility that efficient non-quantum techniques will be developed in response, as seen for Quantum supremacy demonstrations. Therefore, it is desirable to prove lower bounds on the complexity of best possible non-quantum algorithms (which may be unknown) and show that some quantum algorithms asymptomatically improve upon those bounds.
Some researchers have expressed skepticism that scalable quantum computers could ever be built, typically because of the issue of maintaining coherence at large scales, but also for other reasons.
Bill Unruh doubted the practicality of quantum computers in a paper published in 1994. Paul Davies argued that a 400-qubit computer would even come into conflict with the cosmological information bound implied by the holographic principle. Skeptics like Gil Kalai doubt that quantum supremacy will ever be achieved. Physicist Mikhail Dyakonov has expressed skepticism of quantum computing as follows:
- "So the number of continuous parameters describing the state of such a useful quantum computer at any given moment must be... about 10... Could we ever learn to control the more than 10 continuously variable parameters defining the quantum state of such a system? My answer is simple. No, never."
Physical realizations
Further information: List of proposed quantum registers
A practical quantum computer must use a physical system as a programmable quantum register. Researchers are exploring several technologies as candidates for reliable qubit implementations. Superconductors and trapped ions are some of the most developed proposals, but experimentalists are considering other hardware possibilities as well.
The first quantum logic gates were implemented with trapped ions and prototype general purpose machines with up to 20 qubits have been realized. However, the technology behind these devices combines complex vacuum equipment, lasers, microwave and radio frequency equipment making full scale processors difficult to integrate with standard computing equipment. Moreover, the trapped ion system itself has engineering challenges to overcome.
The largest commercial systems are based on superconductor devices and have scaled to 2000 qubits. However, the error rates for larger machines have been on the order of 5%. Technologically these devices are all cryogenic and scaling to large numbers of qubits requires wafer-scale integration, a serious engineering challenge by itself.
Research efforts to create stabler qubits for quantum computing include topological quantum computer approaches. For example, Microsoft is working on a computer based on the quantum properties of two-dimensional quasiparticles called anyons.
Potential applications
With focus on business management's point of view, the potential applications of quantum computing into four major categories are cybersecurity, data analytics and artificial intelligence, optimization and simulation, and data management and searching.
Investment in quantum computing research has increased in the public and private sectors. As one consulting firm summarized,
... investment dollars are pouring in, and quantum-computing start-ups are proliferating. ... While quantum computing promises to help businesses solve problems that are beyond the reach and speed of conventional high-performance computers, use cases are largely experimental and hypothetical at this early stage.
Theory
Computability
Further information: Computability theoryAny computational problem solvable by a classical computer is also solvable by a quantum computer. Intuitively, this is because it is believed that all physical phenomena, including the operation of classical computers, can be described using quantum mechanics, which underlies the operation of quantum computers.
Conversely, any problem solvable by a quantum computer is also solvable by a classical computer. It is possible to simulate both quantum and classical computers manually with just some paper and a pen, if given enough time. More formally, any quantum computer can be simulated by a Turing machine. In other words, quantum computers provide no additional power over classical computers in terms of computability. This means that quantum computers cannot solve undecidable problems like the halting problem, and the existence of quantum computers does not disprove the Church–Turing thesis.
Complexity
Main article: Quantum complexity theoryWhile quantum computers cannot solve any problems that classical computers cannot already solve, it is suspected that they can solve certain problems faster than classical computers. For instance, it is known that quantum computers can efficiently factor integers, while this is not believed to be the case for classical computers.
The class of problems that can be efficiently solved by a quantum computer with bounded error is called BQP, for "bounded error, quantum, polynomial time". More formally, BQP is the class of problems that can be solved by a polynomial-time quantum Turing machine with an error probability of at most 1/3. As a class of probabilistic problems, BQP is the quantum counterpart to BPP ("bounded error, probabilistic, polynomial time"), the class of problems that can be solved by polynomial-time probabilistic Turing machines with bounded error. It is known that and is widely suspected that , which intuitively would mean that quantum computers are more powerful than classical computers in terms of time complexity.
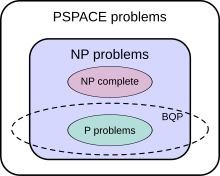
The exact relationship of BQP to P, NP, and PSPACE is not known. However, it is known that ; that is, all problems that can be efficiently solved by a deterministic classical computer can also be efficiently solved by a quantum computer, and all problems that can be efficiently solved by a quantum computer can also be solved by a deterministic classical computer with polynomial space resources. It is further suspected that BQP is a strict superset of P, meaning there are problems that are efficiently solvable by quantum computers that are not efficiently solvable by deterministic classical computers. For instance, integer factorization and the discrete logarithm problem are known to be in BQP and are suspected to be outside of P. On the relationship of BQP to NP, little is known beyond the fact that some NP problems that are believed not to be in P are also in BQP (integer factorization and the discrete logarithm problem are both in NP, for example). It is suspected that ; that is, it is believed that there are efficiently checkable problems that are not efficiently solvable by a quantum computer. As a direct consequence of this belief, it is also suspected that BQP is disjoint from the class of NP-complete problems (if an NP-complete problem were in BQP, then it would follow from NP-hardness that all problems in NP are in BQP).
See also
- D-Wave Systems – Canadian quantum computing company
- Electronic quantum holography – Information storage technology
- Glossary of quantum computing
- IARPA – American government agencyPages displaying short descriptions of redirect targets
- IonQ – US information technology company
- List of emerging technologies – New technologies actively in development
- List of quantum processors – List of quantum computer components
- Magic state distillation – Quantum computing algorithm
- Metacomputing – Computing for the purpose of computing
- Natural computing – terminology introduced to encompass three classes of methodsPages displaying wikidata descriptions as a fallback
- Optical computing – Computer that uses photons or light waves
- Quantum bus – device which can be used to store or transfer information between independent qubits in a quantum computerPages displaying wikidata descriptions as a fallback
- Quantum cognition – Application of quantum theory mathematics to cognitive phenomena
- Quantum sensor – Device measuring quantum mechanical effects
- Quantum volume – Metric for a quantum computer's capabilities
- Quantum weirdness – Unintuitive aspects of quantum mechanics
- Rigetti Computing – American quantum computing company
- Supercomputer – Type of extremely powerful computer
- Theoretical computer science – Subfield of computer science and mathematics
- Unconventional computing – Computing by new or unusual methods
- Valleytronics – Experimental area in semiconductors
Notes
- As used in this article, "exponentially faster" has a precise complexity theoretical meaning. Usually, it means that as a function of input size in bits, the best known classical algorithm for a problem requires an exponentially growing number of steps, while a quantum algorithm uses only a polynomial number of steps.
- The standard basis is also the computational basis.
References
- Aaronson 2013, p. 132.
- Zwiebach, Barton (2022). Mastering Quantum Mechanics: Essentials, Theory, and Applications. MIT Press. §1. ISBN 978-0-262-04613-8.
Quantum physics has replaced classical physics as the correct fundamental description of our physical universe. It is used routinely to describe most phenomena that occur at short distances. The era of quantum physics began in earnest in 1925 with the discoveries of Erwin Schrödinger and Werner Heisenberg. The seeds for these discoveries were planted by Max Planck, Albert Einstein, Niels Bohr, Louis de Broglie, and others.
- Weinberg, Steven (2015). "Historical Introduction". Lectures on Quantum Mechanics (2nd ed.). Cambridge University Press. pp. 1–30. ISBN 978-1-107-11166-0.
- Ceruzzi, Paul E. (2012). Computing: A Concise History. Cambridge, Massachusetts: MIT Press. pp. 3, 46. ISBN 978-0-262-31038-3. OCLC 796812982.
- Hodges, Andrew (2014). Alan Turing: The Enigma. Princeton, New Jersey: Princeton University Press. p. xviii. ISBN 9780691164724.
- Mårtensson-Pendrill, Ann-Marie (1 November 2006). "The Manhattan project—a part of physics history". Physics Education. 41 (6): 493–501. Bibcode:2006PhyEd..41..493M. doi:10.1088/0031-9120/41/6/001. ISSN 0031-9120. S2CID 120294023.
- ^ Benioff, Paul (1980). "The computer as a physical system: A microscopic quantum mechanical Hamiltonian model of computers as represented by Turing machines". Journal of Statistical Physics. 22 (5): 563–591. Bibcode:1980JSP....22..563B. doi:10.1007/bf01011339. S2CID 122949592.
- Buluta, Iulia; Nori, Franco (2 October 2009). "Quantum Simulators". Science. 326 (5949): 108–111. Bibcode:2009Sci...326..108B. doi:10.1126/science.1177838. ISSN 0036-8075. PMID 19797653. S2CID 17187000.
- Manin, Yu. I. (1980). Vychislimoe i nevychislimoe [Computable and Noncomputable] (in Russian). Soviet Radio. pp. 13–15. Archived from the original on 10 May 2013. Retrieved 4 March 2013.
- Feynman, Richard (June 1982). "Simulating Physics with Computers" (PDF). International Journal of Theoretical Physics. 21 (6/7): 467–488. Bibcode:1982IJTP...21..467F. doi:10.1007/BF02650179. S2CID 124545445. Archived from the original (PDF) on 8 January 2019. Retrieved 28 February 2019.
- Nielsen & Chuang 2010, p. 214.
- ^ Bennett, Charles H.; Brassard, Gilles (December 1984). Quantum cryptography: Public key distribution and coin tossing. IEEE International Conference on Computers, Systems & Signal Processing. Bangalore, India. pp. 175–179. arXiv:2003.06557. doi:10.1016/j.tcs.2014.05.025.
- Brassard, G. (2005). "Brief history of quantum cryptography: A personal perspective". IEEE Information Theory Workshop on Theory and Practice in Information-Theoretic Security, 2005. Awaji Island, Japan: IEEE. pp. 19–23. arXiv:quant-ph/0604072. doi:10.1109/ITWTPI.2005.1543949. ISBN 978-0-7803-9491-9. S2CID 16118245.
- Deutsch, D. (8 July 1985). "Quantum theory, the Church–Turing principle and the universal quantum computer". Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences. 400 (1818): 97–117. Bibcode:1985RSPSA.400...97D. doi:10.1098/rspa.1985.0070. ISSN 0080-4630. S2CID 1438116.
- Bernstein, Ethan; Vazirani, Umesh (1993). "Quantum complexity theory". Proceedings of the twenty-fifth annual ACM symposium on Theory of computing – STOC '93. San Diego, California, United States: ACM Press. pp. 11–20. doi:10.1145/167088.167097. ISBN 978-0-89791-591-5. S2CID 676378.
- Simon, D. R. (1994). "On the power of quantum computation". Proceedings 35th Annual Symposium on Foundations of Computer Science. Santa Fe, New Mexico, USA: IEEE Comput. Soc. Press. pp. 116–123. doi:10.1109/SFCS.1994.365701. ISBN 978-0-8186-6580-6. S2CID 7457814.
- Nielsen & Chuang 2010, p. 30-32.
- Shor 1994.
- Grover, Lov K. (1996). A fast quantum mechanical algorithm for database search. ACM symposium on Theory of computing. Philadelphia: ACM Press. pp. 212–219. arXiv:quant-ph/9605043. doi:10.1145/237814.237866. ISBN 978-0-89791-785-8.
- ^ Nielsen & Chuang 2010, p. 7.
- ^ Lloyd, Seth (23 August 1996). "Universal Quantum Simulators". Science. 273 (5278): 1073–1078. Bibcode:1996Sci...273.1073L. doi:10.1126/science.273.5278.1073. ISSN 0036-8075. PMID 8688088. S2CID 43496899.
- Cao, Yudong; Romero, Jonathan; Olson, Jonathan P.; Degroote, Matthias; Johnson, Peter D.; et al. (9 October 2019). "Quantum Chemistry in the Age of Quantum Computing". Chemical Reviews. 119 (19): 10856–10915. arXiv:1812.09976. doi:10.1021/acs.chemrev.8b00803. ISSN 0009-2665. PMID 31469277. S2CID 119417908.
- ^ Grumbling & Horowitz 2019, pp. 164–169.
- Chuang, Isaac L.; Gershenfeld, Neil; Kubinec, Markdoi (April 1998). "Experimental Implementation of Fast Quantum Searching". Physical Review Letters. 80 (15). American Physical Society: 3408–3411. Bibcode:1998PhRvL..80.3408C. doi:10.1103/PhysRevLett.80.3408.
- Holton, William Coffeen. "quantum computer". Encyclopedia Britannica. Encyclopædia Britannica. Retrieved 4 December 2021.
- Gibney, Elizabeth (23 October 2019). "Hello quantum world! Google publishes landmark quantum supremacy claim". Nature. 574 (7779): 461–462. Bibcode:2019Natur.574..461G. doi:10.1038/d41586-019-03213-z. PMID 31645740.
- ^ Lay summary: Martinis, John; Boixo, Sergio (23 October 2019). "Quantum Supremacy Using a Programmable Superconducting Processor". Nature. 574 (7779). Google AI: 505–510. arXiv:1910.11333. Bibcode:2019Natur.574..505A. doi:10.1038/s41586-019-1666-5. PMID 31645734. S2CID 204836822. Retrieved 27 April 2022.
• Journal article: Arute, Frank; Arya, Kunal; Babbush, Ryan; Bacon, Dave; Bardin, Joseph C.; et al. (23 October 2019). "Quantum supremacy using a programmable superconducting processor". Nature. 574 (7779): 505–510. arXiv:1910.11333. Bibcode:2019Natur.574..505A. doi:10.1038/s41586-019-1666-5. PMID 31645734. S2CID 204836822. - Aaronson, Scott (30 October 2019). "Opinion | Why Google's Quantum Supremacy Milestone Matters". The New York Times. ISSN 0362-4331. Retrieved 25 September 2021.
- Pednault, Edwin (22 October 2019). "On 'Quantum Supremacy'". IBM Research Blog. Retrieved 9 February 2021.
- Pan, Feng; Zhang, Pan (4 March 2021). "Simulating the Sycamore quantum supremacy circuits". arXiv:2103.03074 .
- Bennett, Charlie (31 July 2020). Information Is Quantum: How Physics Helped Explain the Nature of Information and What Can Be Done With It (Videotape). Event occurs at 1:08:22 – via YouTube.
- Nielsen & Chuang 2010, p. 13.
- ^ Mermin 2007, p. 17.
- ^ Mermin 2007, p. 18.
- Aaronson 2013, p. 110.
- Nielsen & Chuang 2010, p. 30–32.
- Mermin 2007, pp. 38–39.
- Kurgalin, Sergei; Borzunov, Sergei (2021). Concise guide to quantum computing: algorithms, exercises, and implementations. Texts in computer science. Cham: Springer. ISBN 978-3-030-65054-4.
- Das, A.; Chakrabarti, B. K. (2008). "Quantum Annealing and Analog Quantum Computation". Rev. Mod. Phys. 80 (3): 1061–1081. arXiv:0801.2193. Bibcode:2008RvMP...80.1061D. CiteSeerX 10.1.1.563.9990. doi:10.1103/RevModPhys.80.1061. S2CID 14255125.
- Nayak, Chetan; Simon, Steven; Stern, Ady; Das Sarma, Sankar (2008). "Nonabelian Anyons and Quantum Computation". Reviews of Modern Physics. 80 (3): 1083–1159. arXiv:0707.1889. Bibcode:2008RvMP...80.1083N. doi:10.1103/RevModPhys.80.1083. S2CID 119628297.
- Chi-Chih Yao, A. (1993). "Quantum circuit complexity". Proceedings of 1993 IEEE 34th Annual Foundations of Computer Science. pp. 352–361. doi:10.1109/SFCS.1993.366852. ISBN 0-8186-4370-6. S2CID 195866146.
- Raussendorf, Robert; Browne, Daniel E.; Briegel, Hans J. (25 August 2003). "Measurement-based quantum computation on cluster states". Physical Review A. 68 (2): 022312. arXiv:quant-ph/0301052. Bibcode:2003PhRvA..68b2312R. doi:10.1103/PhysRevA.68.022312. S2CID 6197709.
- Aharonov, Dorit; van Dam, Wim; Kempe, Julia; Landau, Zeph; Lloyd, Seth; Regev, Oded (1 January 2008). "Adiabatic Quantum Computation Is Equivalent to Standard Quantum Computation". SIAM Review. 50 (4): 755–787. arXiv:quant-ph/0405098. Bibcode:2008SIAMR..50..755A. doi:10.1137/080734479. ISSN 0036-1445. S2CID 1503123.
- Freedman, Michael H.; Larsen, Michael; Wang, Zhenghan (1 June 2002). "A Modular Functor Which is Universal for Quantum Computation". Communications in Mathematical Physics. 227 (3): 605–622. arXiv:quant-ph/0001108. Bibcode:2002CMaPh.227..605F. doi:10.1007/s002200200645. ISSN 0010-3616. S2CID 8990600.
- Nielsen & Chuang 2010, p. 481.
- ^ Preskill, John (6 August 2018). "Quantum Computing in the NISQ era and beyond". Quantum. 2: 79. arXiv:1801.00862. Bibcode:2018Quant...2...79P. doi:10.22331/q-2018-08-06-79. S2CID 44098998.
- Bluvstein, Dolev; Evered, Simon J.; Geim, Alexandra A.; Li, Sophie H.; Zhou, Hengyun; Manovitz, Tom; Ebadi, Sepehr; Cain, Madelyn; Kalinowski, Marcin; Hangleiter, Dominik; Ataides, J. Pablo Bonilla; Maskara, Nishad; Cong, Iris; Gao, Xun; Rodriguez, Pedro Sales (6 December 2023). "Logical quantum processor based on reconfigurable atom arrays". Nature. 626 (7997): 58–65. arXiv:2312.03982. doi:10.1038/s41586-023-06927-3. ISSN 1476-4687. PMC 10830422. PMID 38056497. S2CID 266052773.
- Freedberg Jr., Sydney J. (7 December 2023). "'Off to the races': DARPA, Harvard breakthrough brings quantum computing years closer". Breaking Defense. Retrieved 9 December 2023.
- "DARPA-Funded Research Leads to Quantum Computing Breakthrough". darpa.mil. 6 December 2023. Retrieved 5 January 2024.
- Choudhury, Rizwan (30 December 2023). "Top 7 innovation stories of 2023 – Interesting Engineering". interestingengineering.com. Retrieved 6 January 2024.
- Pirandola, S.; Andersen, U. L.; Banchi, L.; Berta, M.; Bunandar, D.; Colbeck, R.; Englund, D.; Gehring, T.; Lupo, C.; Ottaviani, C.; Pereira, J.; Razavi, M.; Shamsul Shaari, J.; Tomamichel, M.; Usenko, V. C.; Vallone, G.; Villoresi, P.; Wallden, P. (2020). "Advances in quantum cryptography". Advances in Optics and Photonics. 12 (4): 1012–1236. arXiv:1906.01645. Bibcode:2020AdOP...12.1012P. doi:10.1364/AOP.361502.
- Pirandola, S.; Andersen, U. L.; Banchi, L.; Berta, M.; Bunandar, D.; Colbeck, R.; Englund, D.; Gehring, T.; Lupo, C.; Ottaviani, C.; Pereira, J. L.; Razavi, M.; Shamsul Shaari, J.; Tomamichel, M.; Usenko, V. C. (14 December 2020). "Advances in quantum cryptography". Advances in Optics and Photonics. 12 (4): 1017. arXiv:1906.01645. Bibcode:2020AdOP...12.1012P. doi:10.1364/AOP.361502. ISSN 1943-8206. S2CID 174799187.
- Xu, Feihu; Ma, Xiongfeng; Zhang, Qiang; Lo, Hoi-Kwong; Pan, Jian-Wei (26 May 2020). "Secure quantum key distribution with realistic devices". Reviews of Modern Physics. 92 (2): 025002-3. arXiv:1903.09051. Bibcode:2020RvMP...92b5002X. doi:10.1103/RevModPhys.92.025002. S2CID 210942877.
- Xu, Guobin; Mao, Jianzhou; Sakk, Eric; Wang, Shuangbao Paul (22 March 2023). "An Overview of Quantum-Safe Approaches: Quantum Key Distribution and Post-Quantum Cryptography". 2023 57th Annual Conference on Information Sciences and Systems (CISS). IEEE. p. 3. doi:10.1109/CISS56502.2023.10089619. ISBN 978-1-6654-5181-9.
- Kozlowski, Wojciech; Wehner, Stephanie (25 September 2019). "Towards Large-Scale Quantum Networks". Proceedings of the Sixth Annual ACM International Conference on Nanoscale Computing and Communication. ACM. pp. 1–7. arXiv:1909.08396. doi:10.1145/3345312.3345497. ISBN 978-1-4503-6897-1.
- Guo, Xueshi; Breum, Casper R.; Borregaard, Johannes; Izumi, Shuro; Larsen, Mikkel V.; Gehring, Tobias; Christandl, Matthias; Neergaard-Nielsen, Jonas S.; Andersen, Ulrik L. (23 December 2019). "Distributed quantum sensing in a continuous-variable entangled network". Nature Physics. 16 (3): 281–284. arXiv:1905.09408. doi:10.1038/s41567-019-0743-x. ISSN 1745-2473. S2CID 256703226.
- ^ Jordan, Stephen (14 October 2022) . "Quantum Algorithm Zoo". Archived from the original on 29 April 2018.
- Aaronson, Scott; Arkhipov, Alex (6 June 2011). "The computational complexity of linear optics". Proceedings of the forty-third annual ACM symposium on Theory of computing. San Jose, California: Association for Computing Machinery. pp. 333–342. arXiv:1011.3245. doi:10.1145/1993636.1993682. ISBN 978-1-4503-0691-1.
- ^ Nielsen & Chuang 2010, p. 42.
- Norton, Quinn (15 February 2007). "The Father of Quantum Computing". Wired.
- Ambainis, Andris (Spring 2014). "What Can We Do with a Quantum Computer?". Institute for Advanced Study.
- Chang, Kenneth (14 June 2023). "Quantum Computing Advance Begins New Era, IBM Says – A quantum computer came up with better answers to a physics problem than a conventional supercomputer". The New York Times. Archived from the original on 14 June 2023. Retrieved 15 June 2023.
- Kim, Youngseok; et al. (14 June 2023). "Evidence for the utility of quantum computing before fault tolerance". Nature. 618 (7965): 500–505. Bibcode:2023Natur.618..500K. doi:10.1038/s41586-023-06096-3. PMC 10266970. PMID 37316724.
- Morello, Andrea (21 November 2018). Lunch & Learn: Quantum Computing. Sibos TV. Archived from the original on 15 February 2021. Retrieved 4 February 2021 – via YouTube.
{{cite AV media}}: CS1 maint: bot: original URL status unknown (link) - Ruane, Jonathan; McAfee, Andrew; Oliver, William D. (1 January 2022). "Quantum Computing for Business Leaders". Harvard Business Review. ISSN 0017-8012. Retrieved 12 April 2023.
- Budde, Florian; Volz, Daniel (12 July 2019). "Quantum computing and the chemical industry | McKinsey". www.mckinsey.com. McKinsey and Company. Retrieved 12 April 2023.
- Bourzac, Katherine (30 October 2017). "Chemistry is quantum computing's killer app". cen.acs.org. American Chemical Society. Retrieved 12 April 2023.
- Lenstra, Arjen K. (2000). "Integer Factoring" (PDF). Designs, Codes and Cryptography. 19 (2/3): 101–128. doi:10.1023/A:1008397921377. S2CID 9816153. Archived from the original (PDF) on 10 April 2015.
- Nielsen & Chuang 2010, p. 216.
- ^ Bernstein, Daniel J. (2009). "Introduction to post-quantum cryptography". Post-Quantum Cryptography. Berlin, Heidelberg: Springer. pp. 1–14. doi:10.1007/978-3-540-88702-7_1. ISBN 978-3-540-88701-0. S2CID 61401925.
- See also pqcrypto.org, a bibliography maintained by Daniel J. Bernstein and Tanja Lange on cryptography not known to be broken by quantum computing.
- McEliece, R. J. (January 1978). "A Public-Key Cryptosystem Based On Algebraic Coding Theory" (PDF). DSNPR. 44: 114–116. Bibcode:1978DSNPR..44..114M.
- Kobayashi, H.; Gall, F. L. (2006). "Dihedral Hidden Subgroup Problem: A Survey". Information and Media Technologies. 1 (1): 178–185. doi:10.2197/ipsjdc.1.470.
- Bennett, Charles H.; Bernstein, Ethan; Brassard, Gilles; Vazirani, Umesh (October 1997). "Strengths and Weaknesses of Quantum Computing". SIAM Journal on Computing. 26 (5): 1510–1523. arXiv:quant-ph/9701001. Bibcode:1997quant.ph..1001B. doi:10.1137/s0097539796300933. S2CID 13403194.
- Brassard, Gilles; Høyer, Peter; Tapp, Alain (2016). "Quantum Algorithm for the Collision Problem". In Kao, Ming-Yang (ed.). Encyclopedia of Algorithms. New York, New York: Springer. pp. 1662–1664. arXiv:quant-ph/9705002. doi:10.1007/978-1-4939-2864-4_304. ISBN 978-1-4939-2864-4. S2CID 3116149.
- Farhi, Edward; Goldstone, Jeffrey; Gutmann, Sam (23 December 2008). "A Quantum Algorithm for the Hamiltonian NAND Tree". Theory of Computing. 4 (1): 169–190. doi:10.4086/toc.2008.v004a008. ISSN 1557-2862. S2CID 8258191.
- Williams, Colin P. (2011). Explorations in Quantum Computing. Springer. pp. 242–244. ISBN 978-1-84628-887-6.
- Grover, Lov (29 May 1996). "A fast quantum mechanical algorithm for database search". arXiv:quant-ph/9605043.
- Ambainis, Ambainis (June 2004). "Quantum search algorithms". ACM SIGACT News. 35 (2): 22–35. arXiv:quant-ph/0504012. Bibcode:2005quant.ph..4012A. doi:10.1145/992287.992296. S2CID 11326499.
- Rich, Steven; Gellman, Barton (1 February 2014). "NSA seeks to build quantum computer that could crack most types of encryption". The Washington Post.
- Outeiral, Carlos; Strahm, Martin; Morris, Garrett; Benjamin, Simon; Deane, Charlotte; Shi, Jiye (2021). "The prospects of quantum computing in computational molecular biology". WIREs Computational Molecular Science. 11. arXiv:2005.12792. doi:10.1002/wcms.1481. S2CID 218889377.
- Biamonte, Jacob; Wittek, Peter; Pancotti, Nicola; Rebentrost, Patrick; Wiebe, Nathan; Lloyd, Seth (September 2017). "Quantum machine learning". Nature. 549 (7671): 195–202. arXiv:1611.09347. Bibcode:2017Natur.549..195B. doi:10.1038/nature23474. ISSN 0028-0836. PMID 28905917. S2CID 64536201.
- Harrow, Aram; Hassidim, Avinatan; Lloyd, Seth (2009). "Quantum algorithm for solving linear systems of equations". Physical Review Letters. 103 (15): 150502. arXiv:0811.3171. Bibcode:2009PhRvL.103o0502H. doi:10.1103/PhysRevLett.103.150502. PMID 19905613. S2CID 5187993.
- Benedetti, Marcello; Realpe-Gómez, John; Biswas, Rupak; Perdomo-Ortiz, Alejandro (9 August 2016). "Estimation of effective temperatures in quantum annealers for sampling applications: A case study with possible applications in deep learning". Physical Review A. 94 (2): 022308. arXiv:1510.07611. Bibcode:2016PhRvA..94b2308B. doi:10.1103/PhysRevA.94.022308.
- Ajagekar, Akshay; You, Fengqi (5 December 2020). "Quantum computing assisted deep learning for fault detection and diagnosis in industrial process systems". Computers & Chemical Engineering. 143: 107119. arXiv:2003.00264. doi:10.1016/j.compchemeng.2020.107119. ISSN 0098-1354. S2CID 211678230.
- Ajagekar, Akshay; You, Fengqi (1 December 2021). "Quantum computing based hybrid deep learning for fault diagnosis in electrical power systems". Applied Energy. 303: 117628. Bibcode:2021ApEn..30317628A. doi:10.1016/j.apenergy.2021.117628. ISSN 0306-2619.
- Gao, Xun; Anschuetz, Eric R.; Wang, Sheng-Tao; Cirac, J. Ignacio; Lukin, Mikhail D. (2022). "Enhancing Generative Models via Quantum Correlations". Physical Review X. 12 (2): 021037. arXiv:2101.08354. Bibcode:2022PhRvX..12b1037G. doi:10.1103/PhysRevX.12.021037. S2CID 231662294.
- Li, Junde; Topaloglu, Rasit; Ghosh, Swaroop (9 January 2021). "Quantum Generative Models for Small Molecule Drug Discovery". arXiv:2101.03438 .
- ^ Brooks, Michael (24 May 2023). "Quantum computers: what are they good for?". Nature. 617 (7962): S1 – S3. Bibcode:2023Natur.617S...1B. doi:10.1038/d41586-023-01692-9. PMID 37225885. S2CID 258847001.
- ^ Torsten Hoefler; Thomas Häner; Matthias Troyer (May 2023). "Disentangling Hype from Practicality: On Realistically Achieving Quantum Advantage". Communications of the ACM.
- Dyakonov, Mikhail (15 November 2018). "The Case Against Quantum Computing". IEEE Spectrum.
- DiVincenzo, David P. (13 April 2000). "The Physical Implementation of Quantum Computation". Fortschritte der Physik. 48 (9–11): 771–783. arXiv:quant-ph/0002077. Bibcode:2000ForPh..48..771D. doi:10.1002/1521-3978(200009)48:9/11<771::AID-PROP771>3.0.CO;2-E. S2CID 15439711.
- Giles, Martin (17 January 2019). "We'd have more quantum computers if it weren't so hard to find the damn cables". MIT Technology Review. Retrieved 17 May 2021.
- Pauka SJ, Das K, Kalra B, Moini A, Yang Y, Trainer M, Bousquet A, Cantaloube C, Dick N, Gardner GC, Manfra MJ, Reilly DJ (2021). "A cryogenic CMOS chip for generating control signals for multiple qubits". Nature Electronics. 4 (4): 64–70. arXiv:1912.01299. doi:10.1038/s41928-020-00528-y. S2CID 231715555.
- DiVincenzo, David P. (1995). "Quantum Computation". Science. 270 (5234): 255–261. Bibcode:1995Sci...270..255D. CiteSeerX 10.1.1.242.2165. doi:10.1126/science.270.5234.255. S2CID 220110562.
- Zu, H.; Dai, W.; de Waele, A.T.A.M. (2022). "Development of Dilution refrigerators – A review". Cryogenics. 121. doi:10.1016/j.cryogenics.2021.103390. ISSN 0011-2275. S2CID 244005391.
- Jones, Nicola (19 June 2013). "Computing: The quantum company". Nature. 498 (7454): 286–288. Bibcode:2013Natur.498..286J. doi:10.1038/498286a. PMID 23783610.
- Vepsäläinen, Antti P.; Karamlou, Amir H.; Orrell, John L.; Dogra, Akshunna S.; Loer, Ben; et al. (August 2020). "Impact of ionizing radiation on superconducting qubit coherence". Nature. 584 (7822): 551–556. arXiv:2001.09190. Bibcode:2020Natur.584..551V. doi:10.1038/s41586-020-2619-8. ISSN 1476-4687. PMID 32848227. S2CID 210920566.
- Amy, Matthew; Matteo, Olivia; Gheorghiu, Vlad; Mosca, Michele; Parent, Alex; Schanck, John (30 November 2016). "Estimating the cost of generic quantum pre-image attacks on SHA-2 and SHA-3". arXiv:1603.09383 .
- Dyakonov, M. I. (14 October 2006). S. Luryi; Xu, J.; Zaslavsky, A. (eds.). "Is Fault-Tolerant Quantum Computation Really Possible?". Future Trends in Microelectronics. Up the Nano Creek: 4–18. arXiv:quant-ph/0610117. Bibcode:2006quant.ph.10117D.
- Ahsan, Muhammad (2015). Architecture Framework for Trapped-ion Quantum Computer based on Performance Simulation Tool. OCLC 923881411.
- Ahsan, Muhammad; Meter, Rodney Van; Kim, Jungsang (28 December 2016). "Designing a Million-Qubit Quantum Computer Using a Resource Performance Simulator". ACM Journal on Emerging Technologies in Computing Systems. 12 (4): 39:1–39:25. arXiv:1512.00796. doi:10.1145/2830570. ISSN 1550-4832. S2CID 1258374.
- Gidney, Craig; Ekerå, Martin (15 April 2021). "How to factor 2048 bit RSA integers in 8 hours using 20 million noisy qubits". Quantum. 5: 433. arXiv:1905.09749. Bibcode:2021Quant...5..433G. doi:10.22331/q-2021-04-15-433. ISSN 2521-327X. S2CID 162183806.
- Freedman, Michael H.; Kitaev, Alexei; Larsen, Michael J.; Wang, Zhenghan (2003). "Topological quantum computation". Bulletin of the American Mathematical Society. 40 (1): 31–38. arXiv:quant-ph/0101025. doi:10.1090/S0273-0979-02-00964-3. MR 1943131.
- Monroe, Don (1 October 2008). "Anyons: The breakthrough quantum computing needs?". New Scientist.
- Preskill, John (26 March 2012). "Quantum computing and the entanglement frontier". arXiv:1203.5813 .
- Preskill, John (6 August 2018). "Quantum Computing in the NISQ era and beyond". Quantum. 2: 79. arXiv:1801.00862. Bibcode:2018Quant...2...79P. doi:10.22331/q-2018-08-06-79.
- Boixo, Sergio; Isakov, Sergei V.; Smelyanskiy, Vadim N.; Babbush, Ryan; Ding, Nan; et al. (2018). "Characterizing Quantum Supremacy in Near-Term Devices". Nature Physics. 14 (6): 595–600. arXiv:1608.00263. Bibcode:2018NatPh..14..595B. doi:10.1038/s41567-018-0124-x. S2CID 4167494.
- Savage, Neil (5 July 2017). "Quantum Computers Compete for "Supremacy"". Scientific American.
- Giles, Martin (20 September 2019). "Google researchers have reportedly achieved 'quantum supremacy'". MIT Technology Review. Retrieved 15 May 2020.
- Tavares, Frank (23 October 2019). "Google and NASA Achieve Quantum Supremacy". NASA. Retrieved 16 November 2021.
- Pednault, Edwin; Gunnels, John A.; Nannicini, Giacomo; Horesh, Lior; Wisnieff, Robert (22 October 2019). "Leveraging Secondary Storage to Simulate Deep 54-qubit Sycamore Circuits". arXiv:1910.09534 .
- Cho, Adrian (23 October 2019). "IBM casts doubt on Google's claims of quantum supremacy". Science. doi:10.1126/science.aaz6080. ISSN 0036-8075. S2CID 211982610.
- Liu, Yong (Alexander); Liu, Xin (Lucy); Li, Fang (Nancy); Fu, Haohuan; Yang, Yuling; et al. (14 November 2021). "Closing the "quantum supremacy" gap". Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis. SC '21. New York, New York: Association for Computing Machinery. pp. 1–12. arXiv:2110.14502. doi:10.1145/3458817.3487399. ISBN 978-1-4503-8442-1. S2CID 239036985.
- Bulmer, Jacob F. F.; Bell, Bryn A.; Chadwick, Rachel S.; Jones, Alex E.; Moise, Diana; et al. (28 January 2022). "The boundary for quantum advantage in Gaussian boson sampling". Science Advances. 8 (4): eabl9236. arXiv:2108.01622. Bibcode:2022SciA....8.9236B. doi:10.1126/sciadv.abl9236. ISSN 2375-2548. PMC 8791606. PMID 35080972.
- McCormick, Katie (10 February 2022). "Race Not Over Between Classical and Quantum Computers". Physics. 15: 19. Bibcode:2022PhyOJ..15...19M. doi:10.1103/Physics.15.19. S2CID 246910085.
- Pan, Feng; Chen, Keyang; Zhang, Pan (2022). "Solving the Sampling Problem of the Sycamore Quantum Circuits". Physical Review Letters. 129 (9): 090502. arXiv:2111.03011. Bibcode:2022PhRvL.129i0502P. doi:10.1103/PhysRevLett.129.090502. PMID 36083655. S2CID 251755796.
- Cho, Adrian (2 August 2022). "Ordinary computers can beat Google's quantum computer after all". Science. 377. doi:10.1126/science.ade2364.
- "Google's 'quantum supremacy' usurped by researchers using ordinary supercomputer". TechCrunch. 5 August 2022. Retrieved 7 August 2022.
- Ball, Philip (3 December 2020). "Physicists in China challenge Google's 'quantum advantage'". Nature. 588 (7838): 380. Bibcode:2020Natur.588..380B. doi:10.1038/d41586-020-03434-7. PMID 33273711. S2CID 227282052.
- Garisto, Daniel. "Light-based Quantum Computer Exceeds Fastest Classical Supercomputers". Scientific American. Retrieved 7 December 2020.
- Conover, Emily (3 December 2020). "The new light-based quantum computer Jiuzhang has achieved quantum supremacy". Science News. Retrieved 7 December 2020.
- Zhong, Han-Sen; Wang, Hui; Deng, Yu-Hao; Chen, Ming-Cheng; Peng, Li-Chao; et al. (3 December 2020). "Quantum computational advantage using photons". Science. 370 (6523): 1460–1463. arXiv:2012.01625. Bibcode:2020Sci...370.1460Z. doi:10.1126/science.abe8770. ISSN 0036-8075. PMID 33273064. S2CID 227254333.
- Roberson, Tara M. (21 May 2020). "{{subst:title case|Can hype be a force for good?}}". Public Understanding of Science. 29 (5): 544–552. doi:10.1177/0963662520923109. ISSN 0963-6625. PMID 32438851. S2CID 218831653.
- Cavaliere, Fabio; Mattsson, John; Smeets, Ben (September 2020). "The security implications of quantum cryptography and quantum computing". Network Security. 2020 (9): 9–15. doi:10.1016/S1353-4858(20)30105-7. ISSN 1353-4858. S2CID 222349414.
- Liu, Yong; Chen, Yaojian; Guo, Chu; Song, Jiawei; Shi, Xinmin; Gan, Lin; Wu, Wenzhao; Wu, Wei; Fu, Haohuan; Liu, Xin; Chen, Dexun; Zhao, Zhifeng; Yang, Guangwen; Gao, Jiangang (16 January 2024). "Verifying Quantum Advantage Experiments with Multiple Amplitude Tensor Network Contraction". Physical Review Letters. 132 (3): 030601. arXiv:2212.04749. Bibcode:2024PhRvL.132c0601L. doi:10.1103/PhysRevLett.132.030601. ISSN 0031-9007. PMID 38307065.
- Monroe, Don (December 2022). "Quantum Computers and the Universe". Communications of the ACM.
- Swayne, Matt (20 June 2023). "PsiQuantum Sees 700x Reduction in Computational Resource Requirements to Break Elliptic Curve Cryptography With a Fault Tolerant Quantum Computer". The Quanrum Insider.
- Unruh, Bill (1995). "Maintaining coherence in Quantum Computers". Physical Review A. 51 (2): 992–997. arXiv:hep-th/9406058. Bibcode:1995PhRvA..51..992U. doi:10.1103/PhysRevA.51.992. PMID 9911677. S2CID 13980886.
- Davies, Paul (6 March 2007). "The implications of a holographic universe for quantum information science and the nature of physical law". arXiv:quant-ph/0703041.
- Regan, K. W. (23 April 2016). "Quantum Supremacy and Complexity". Gödel's Lost Letter and P=NP.
- Kalai, Gil (May 2016). "The Quantum Computer Puzzle" (PDF). Notices of the AMS. 63 (5): 508–516.
- Rinott, Yosef; Shoham, Tomer; Kalai, Gil (13 July 2021). "Statistical Aspects of the Quantum Supremacy Demonstration". arXiv:2008.05177 .
- Dyakonov, Mikhail (15 November 2018). "The Case Against Quantum Computing". IEEE Spectrum. Retrieved 3 December 2019.
- Dyakonov, Mikhail (24 March 2020). Will We Ever Have a Quantum Computer?. Springer. ISBN 9783030420185. Retrieved 22 May 2020.
- Russell, John (10 January 2019). "IBM Quantum Update: Q System One Launch, New Collaborators, and QC Center Plans". HPCwire. Retrieved 9 January 2023.
- Tacchino, Francesco; Chiesa, Alessandro; Carretta, Stefano; Gerace, Dario (19 December 2019). "Quantum Computers as Universal Quantum Simulators: State-of-the-Art and Perspectives". Advanced Quantum Technologies. 3 (3): 1900052. arXiv:1907.03505. doi:10.1002/qute.201900052. ISSN 2511-9044. S2CID 195833616.
- Grumbling & Horowitz 2019, p. 127.
- Grumbling & Horowitz 2019, p. 114.
- Grumbling & Horowitz 2019, p. 119.
- Grumbling & Horowitz 2019, p. 126.
- Mackie, Kurt (8 February 2024). "Microsoft Quantum Computing Getting DARPA Funding". rcpmag.com. Retrieved 9 February 2024.
- Gent, Edd (5 July 2023). "Microsoft Wants to Build a Quantum Supercomputer Within a Decade". Singularity Hub. Retrieved 18 October 2024.
- Lucian Armasu (22 November 2016). "Microsoft Aims To Create World's First Topological Quantum Computer". Tom's Hardware. Retrieved 18 October 2024.
- Leong, Kelvin; Sung, Anna (November 2022). "What Business Managers Should Know About Quantum Computing?" (PDF). Journal of Interdisciplinary Sciences. Retrieved 13 August 2023.
- Gibney, Elizabeth (2 October 2019). "Quantum gold rush: the private funding pouring into quantum start-ups". Nature. 574 (7776): 22–24. Bibcode:2019Natur.574...22G. doi:10.1038/d41586-019-02935-4. PMID 31578480. S2CID 203626236.
- Rodrigo, Chris Mills (12 February 2020). "Trump budget proposal boosts funding for artificial intelligence, quantum computing". The Hill. Retrieved 11 July 2021.
- Biondi, Matteo; Heid, Anna; Henke, Nicolaus; Mohr, Niko; Pautasso, Lorenzo; et al. (14 December 2021). "Quantum computing use cases are getting real—what you need to know". McKinsey & Company. Retrieved 1 April 2022.
- Nielsen & Chuang 2010, p. 29.
- Nielsen & Chuang 2010, p. 126.
- Nielsen & Chuang 2010, p. 41.
- Nielsen & Chuang 2010, p. 201.
- Bernstein, Ethan; Vazirani, Umesh (1997). "Quantum Complexity Theory". SIAM Journal on Computing. 26 (5): 1411–1473. CiteSeerX 10.1.1.144.7852. doi:10.1137/S0097539796300921.
Sources
- Aaronson, Scott (2013). Quantum Computing Since Democritus. Cambridge University Press. doi:10.1017/CBO9780511979309. ISBN 978-0-521-19956-8. OCLC 829706638.
- Grumbling, Emily; Horowitz, Mark, eds. (2019). Quantum Computing: Progress and Prospects. Washington, DC: The National Academies Press. doi:10.17226/25196. ISBN 978-0-309-47970-7. OCLC 1091904777. S2CID 125635007.
- Mermin, N. David (2007). Quantum Computer Science: An Introduction. doi:10.1017/CBO9780511813870. ISBN 978-0-511-34258-5. OCLC 422727925.
- Nielsen, Michael; Chuang, Isaac (2010). Quantum Computation and Quantum Information (10th anniversary ed.). doi:10.1017/CBO9780511976667. ISBN 978-0-511-99277-3. OCLC 700706156. S2CID 59717455.
- Shor, Peter W. (1994). Algorithms for Quantum Computation: Discrete Logarithms and Factoring. Symposium on Foundations of Computer Science. Santa Fe, New Mexico: IEEE. pp. 124–134. doi:10.1109/SFCS.1994.365700. ISBN 978-0-8186-6580-6.
Further reading
Textbooks
- Akama, Seiki (2014). Elements of Quantum Computing: History, Theories and Engineering Applications. Springer. doi:10.1007/978-3-319-08284-4. ISBN 978-3-319-08284-4. OCLC 884786739.
- Benenti, Giuliano; Casati, Giulio; Rossini, Davide; Strini, Giuliano (2019). Principles of Quantum Computation and Information: A Comprehensive Textbook (2nd ed.). doi:10.1142/10909. ISBN 978-981-3237-23-0. OCLC 1084428655. S2CID 62280636.
- Bernhardt, Chris (2019). Quantum Computing for Everyone. MIT Press. ISBN 978-0-262-35091-4. OCLC 1082867954.
- Hidary, Jack D. (2021). Quantum Computing: An Applied Approach (2nd ed.). doi:10.1007/978-3-030-83274-2. ISBN 978-3-03-083274-2. OCLC 1272953643. S2CID 238223274.
- Hiroshi, Imai; Masahito, Hayashi, eds. (2006). Quantum Computation and Information: From Theory to Experiment. Topics in Applied Physics. Vol. 102. doi:10.1007/3-540-33133-6. ISBN 978-3-540-33133-9.
- Hughes, Ciaran; Isaacson, Joshua; Perry, Anastasia; Sun, Ranbel F.; Turner, Jessica (2021). Quantum Computing for the Quantum Curious. doi:10.1007/978-3-030-61601-4. ISBN 978-3-03-061601-4. OCLC 1244536372. S2CID 242566636.
- Jaeger, Gregg (2007). Quantum Information: An Overview. doi:10.1007/978-0-387-36944-0. ISBN 978-0-387-36944-0. OCLC 186509710.
- Johnston, Eric R.; Harrigan, Nic; Gimeno-Segovia, Mercedes (2019). Programming Quantum Computers: Essential Algorithms and Code Samples. O'Reilly Media, Incorporated. ISBN 978-1-4920-3968-6. OCLC 1111634190.
- Kaye, Phillip; Laflamme, Raymond; Mosca, Michele (2007). An Introduction to Quantum Computing. OUP Oxford. ISBN 978-0-19-857000-4. OCLC 85896383.
- Kitaev, Alexei Yu.; Shen, Alexander H.; Vyalyi, Mikhail N. (2002). Classical and Quantum Computation. American Mathematical Soc. ISBN 978-0-8218-3229-5. OCLC 907358694.
- Kurgalin, Sergei; Borzunov, Sergei (2021). Concise Guide to Quantum Computing: Algorithms, Exercises, and Implementations. Springer. doi:10.1007/978-3-030-65052-0. ISBN 978-3-030-65052-0.
- Stolze, Joachim; Suter, Dieter (2004). Quantum Computing: A Short Course from Theory to Experiment. doi:10.1002/9783527617760. ISBN 978-3-527-61776-0. OCLC 212140089.
- Susskind, Leonard; Friedman, Art (2014). Quantum Mechanics: The Theoretical Minimum. New York: Basic Books. ISBN 978-0-465-08061-8.
- Wichert, Andreas (2020). Principles of Quantum Artificial Intelligence: Quantum Problem Solving and Machine Learning (2nd ed.). doi:10.1142/11938. ISBN 978-981-12-2431-7. OCLC 1178715016. S2CID 225498497.
- Wong, Thomas (2022). Introduction to Classical and Quantum Computing (PDF). Rooted Grove. ISBN 979-8-9855931-0-5. OCLC 1308951401. Archived from the original (PDF) on 29 January 2022. Retrieved 6 February 2022.
- Zeng, Bei; Chen, Xie; Zhou, Duan-Lu; Wen, Xiao-Gang (2019). Quantum Information Meets Quantum Matter. arXiv:1508.02595. doi:10.1007/978-1-4939-9084-9. ISBN 978-1-4939-9084-9. OCLC 1091358969. S2CID 118528258.
Academic papers
- Abbot, Derek; Doering, Charles R.; Caves, Carlton M.; Lidar, Daniel M.; Brandt, Howard E.; et al. (2003). "Dreams versus Reality: Plenary Debate Session on Quantum Computing". Quantum Information Processing. 2 (6): 449–472. arXiv:quant-ph/0310130. Bibcode:2003QuIP....2..449A. doi:10.1023/B:QINP.0000042203.24782.9a. hdl:2027.42/45526. S2CID 34885835.
- Berthiaume, Andre (1 December 1998). "Quantum Computation". Solution Manual for Quantum Mechanics. pp. 233–234. doi:10.1142/9789814541893_0016. ISBN 978-981-4541-88-6. S2CID 128255429 – via Semantic Scholar.
- DiVincenzo, David P. (2000). "The Physical Implementation of Quantum Computation". Fortschritte der Physik. 48 (9–11): 771–783. arXiv:quant-ph/0002077. Bibcode:2000ForPh..48..771D. doi:10.1002/1521-3978(200009)48:9/11<771::AID-PROP771>3.0.CO;2-E. S2CID 15439711.
- DiVincenzo, David P. (1995). "Quantum Computation". Science. 270 (5234): 255–261. Bibcode:1995Sci...270..255D. CiteSeerX 10.1.1.242.2165. doi:10.1126/science.270.5234.255. S2CID 220110562. Table 1 lists switching and dephasing times for various systems.
- Jeutner, Valentin (2021). "The Quantum Imperative: Addressing the Legal Dimension of Quantum Computers". Morals & Machines. 1 (1): 52–59. doi:10.5771/2747-5174-2021-1-52. S2CID 236664155.
- Krantz, P.; Kjaergaard, M.; Yan, F.; Orlando, T. P.; Gustavsson, S.; Oliver, W. D. (17 June 2019). "A Quantum Engineer's Guide to Superconducting Qubits". Applied Physics Reviews. 6 (2): 021318. arXiv:1904.06560. Bibcode:2019ApPRv...6b1318K. doi:10.1063/1.5089550. ISSN 1931-9401. S2CID 119104251.
- Mitchell, Ian (1998). "Computing Power into the 21st Century: Moore's Law and Beyond".
- Simon, Daniel R. (1994). "On the Power of Quantum Computation". Institute of Electrical and Electronics Engineers Computer Society Press.
External links
 Media related to Quantum computer at Wikimedia Commons
Media related to Quantum computer at Wikimedia Commons Learning materials related to Quantum computing at Wikiversity
Learning materials related to Quantum computing at Wikiversity- Stanford Encyclopedia of Philosophy: "Quantum Computing" by Amit Hagar and Michael E. Cuffaro.
- "Quantum computation, theory of", Encyclopedia of Mathematics, EMS Press, 2001
- Quantum computing for the very curious by Andy Matuschak and Michael Nielsen
- Lectures
- Quantum computing for the determined – 22 video lectures by Michael Nielsen
- Video Lectures by David Deutsch
- Lectures at the Institut Henri Poincaré (slides and videos)
- Online lecture on An Introduction to Quantum Computing, Edward Gerjuoy (2008)
- Lomonaco, Sam. Four Lectures on Quantum Computing given at Oxford University in July 2006
| Quantum information science | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| General | |||||||||
| Theorems | |||||||||
| Quantum communication |
| ||||||||
| Quantum algorithms | |||||||||
| Quantum complexity theory | |||||||||
| Quantum processor benchmarks | |||||||||
| Quantum computing models | |||||||||
| Quantum error correction | |||||||||
| Physical implementations |
| ||||||||
| Quantum programming | |||||||||
| Emerging technologies | |||||
|---|---|---|---|---|---|
| Fields |
| ||||
| Quantum mechanics | |
|---|---|
| Background | |
| Fundamentals | |
| Formulations | |
| Equations | |
| Interpretations | |
| Experiments | |
| Science | |
| Technology |
|
| Extensions | |
| Related | |
 is a point on the surface of the sphere, partway between the poles,
is a point on the surface of the sphere, partway between the poles,  and
and  .
. 'ket
'ket  . Because a qubit is a two-state system, any qubit state takes the form
. Because a qubit is a two-state system, any qubit state takes the form  , where
, where  and
and  are the
are the  , or to
, or to  .
Any valid qubit state has coefficients
.
Any valid qubit state has coefficients  .
As an example, measuring the qubit
.
As an example, measuring the qubit  would produce either
would produce either  Mathematically, the application of such a logic gate to a quantum state vector is modelled with
Mathematically, the application of such a logic gate to a quantum state vector is modelled with  and
and  .
. The
The  As a mathematical consequence of this definition,
As a mathematical consequence of this definition,  ,
,  ,
,  , and
, and  . In other words, the CNOT applies a NOT gate (
. In other words, the CNOT applies a NOT gate ( from before) to the second qubit if and only if the first qubit is in the state
from before) to the second qubit if and only if the first qubit is in the state  . If the first qubit is
. If the first qubit is  , nothing is done to either qubit.
, nothing is done to either qubit.
 over
over  qubits) can be represented as a network of quantum logic gates from a fairly small family of gates. A choice of gate family that enables this construction is known as a
qubits) can be represented as a network of quantum logic gates from a fairly small family of gates. A choice of gate family that enables this construction is known as a  queries to the database, quadratically fewer than the
queries to the database, quadratically fewer than the  queries required for classical algorithms. In this case, the advantage is not only provable but also optimal: it has been shown that Grover's algorithm gives the maximal possible probability of finding the desired element for any number of oracle lookups. Many examples of provable quantum speedups for query problems are based on Grover's algorithm, including
queries required for classical algorithms. In this case, the advantage is not only provable but also optimal: it has been shown that Grover's algorithm gives the maximal possible probability of finding the desired element for any number of oracle lookups. Many examples of provable quantum speedups for query problems are based on Grover's algorithm, including  and is widely suspected that
and is widely suspected that  , which intuitively would mean that quantum computers are more powerful than classical computers in terms of
, which intuitively would mean that quantum computers are more powerful than classical computers in terms of  ; that is, all problems that can be efficiently solved by a deterministic classical computer can also be efficiently solved by a quantum computer, and all problems that can be efficiently solved by a quantum computer can also be solved by a deterministic classical computer with polynomial space resources. It is further suspected that BQP is a strict superset of P, meaning there are problems that are efficiently solvable by quantum computers that are not efficiently solvable by deterministic classical computers. For instance, integer factorization and the
; that is, all problems that can be efficiently solved by a deterministic classical computer can also be efficiently solved by a quantum computer, and all problems that can be efficiently solved by a quantum computer can also be solved by a deterministic classical computer with polynomial space resources. It is further suspected that BQP is a strict superset of P, meaning there are problems that are efficiently solvable by quantum computers that are not efficiently solvable by deterministic classical computers. For instance, integer factorization and the  ; that is, it is believed that there are efficiently checkable problems that are not efficiently solvable by a quantum computer. As a direct consequence of this belief, it is also suspected that BQP is disjoint from the class of
; that is, it is believed that there are efficiently checkable problems that are not efficiently solvable by a quantum computer. As a direct consequence of this belief, it is also suspected that BQP is disjoint from the class of