
Monte Carlo methods, or Monte Carlo experiments, are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results. The underlying concept is to use randomness to solve problems that might be deterministic in principle. The name comes from the Monte Carlo Casino in Monaco, where the primary developer of the method, mathematician Stanisław Ulam, was inspired by his uncle's gambling habits.
Monte Carlo methods are mainly used in three distinct problem classes: optimization, numerical integration, and generating draws from a probability distribution. They can also be used to model phenomena with significant uncertainty in inputs, such as calculating the risk of a nuclear power plant failure. Monte Carlo methods are often implemented using computer simulations, and they can provide approximate solutions to problems that are otherwise intractable or too complex to analyze mathematically.
Monte Carlo methods are widely used in various fields of science, engineering, and mathematics, such as physics, chemistry, biology, statistics, artificial intelligence, finance, and cryptography. They have also been applied to social sciences, such as sociology, psychology, and political science. Monte Carlo methods have been recognized as one of the most important and influential ideas of the 20th century, and they have enabled many scientific and technological breakthroughs.
Monte Carlo methods also have some limitations and challenges, such as the trade-off between accuracy and computational cost, the curse of dimensionality, the reliability of random number generators, and the verification and validation of the results.
Overview
Monte Carlo methods vary, but tend to follow a particular pattern:
- Define a domain of possible inputs
- Generate inputs randomly from a probability distribution over the domain
- Perform a deterministic computation of the outputs
- Aggregate the results

For example, consider a quadrant (circular sector) inscribed in a unit square. Given that the ratio of their areas is π/4, the value of π can be approximated using a Monte Carlo method:
- Draw a square, then inscribe a quadrant within it
- Uniformly scatter a given number of points over the square
- Count the number of points inside the quadrant, i.e. having a distance from the origin of less than 1
- The ratio of the inside-count and the total-sample-count is an estimate of the ratio of the two areas, π/4. Multiply the result by 4 to estimate π.
In this procedure the domain of inputs is the square that circumscribes the quadrant. One can generate random inputs by scattering grains over the square then perform a computation on each input (test whether it falls within the quadrant). Aggregating the results yields our final result, the approximation of π.
There are two important considerations:
- If the points are not uniformly distributed, then the approximation will be poor.
- The approximation is generally poor if only a few points are randomly placed in the whole square. On average, the approximation improves as more points are placed.
Uses of Monte Carlo methods require large amounts of random numbers, and their use benefitted greatly from pseudorandom number generators, which are far quicker to use than the tables of random numbers that had been previously used for statistical sampling.
Application
Monte Carlo methods are often used in physical and mathematical problems and are most useful when it is difficult or impossible to use other approaches. Monte Carlo methods are mainly used in three problem classes: optimization, numerical integration, and generating draws from a probability distribution.
In physics-related problems, Monte Carlo methods are useful for simulating systems with many coupled degrees of freedom, such as fluids, disordered materials, strongly coupled solids, and cellular structures (see cellular Potts model, interacting particle systems, McKean–Vlasov processes, kinetic models of gases).
Other examples include modeling phenomena with significant uncertainty in inputs such as the calculation of risk in business and, in mathematics, evaluation of multidimensional definite integrals with complicated boundary conditions. In application to systems engineering problems (space, oil exploration, aircraft design, etc.), Monte Carlo–based predictions of failure, cost overruns and schedule overruns are routinely better than human intuition or alternative "soft" methods.
In principle, Monte Carlo methods can be used to solve any problem having a probabilistic interpretation. By the law of large numbers, integrals described by the expected value of some random variable can be approximated by taking the empirical mean (a.k.a. the 'sample mean') of independent samples of the variable. When the probability distribution of the variable is parameterized, mathematicians often use a Markov chain Monte Carlo (MCMC) sampler. The central idea is to design a judicious Markov chain model with a prescribed stationary probability distribution. That is, in the limit, the samples being generated by the MCMC method will be samples from the desired (target) distribution. By the ergodic theorem, the stationary distribution is approximated by the empirical measures of the random states of the MCMC sampler.
In other problems, the objective is generating draws from a sequence of probability distributions satisfying a nonlinear evolution equation. These flows of probability distributions can always be interpreted as the distributions of the random states of a Markov process whose transition probabilities depend on the distributions of the current random states (see McKean–Vlasov processes, nonlinear filtering equation). In other instances, a flow of probability distributions with an increasing level of sampling complexity arise (path spaces models with an increasing time horizon, Boltzmann–Gibbs measures associated with decreasing temperature parameters, and many others). These models can also be seen as the evolution of the law of the random states of a nonlinear Markov chain. A natural way to simulate these sophisticated nonlinear Markov processes is to sample multiple copies of the process, replacing in the evolution equation the unknown distributions of the random states by the sampled empirical measures. In contrast with traditional Monte Carlo and MCMC methodologies, these mean-field particle techniques rely on sequential interacting samples. The terminology mean field reflects the fact that each of the samples (a.k.a. particles, individuals, walkers, agents, creatures, or phenotypes) interacts with the empirical measures of the process. When the size of the system tends to infinity, these random empirical measures converge to the deterministic distribution of the random states of the nonlinear Markov chain, so that the statistical interaction between particles vanishes.
Simple Monte Carlo
Suppose one wants to know the expected value μ of a population (and knows that μ exists), but does not have a formula available to compute it. The simple Monte Carlo method gives an estimate for μ by running n simulations and averaging the simulations’ results. It has no restrictions on the probability distribution of the inputs to the simulations, requiring only that the inputs are randomly generated and are independent of each other and that μ exists. A sufficiently large n will produce a value for m that is arbitrarily close to μ; more formally, it will be the case that, for any ε > 0, |μ – m| ≤ ε.
Typically, the algorithm to obtain m is
s = 0; for i = 1 to n do run the simulation for the i time, giving result ri; s = s + ri; repeat m = s / n;
An example
Suppose we want to know how many times we should expect to throw three eight-sided dice for the total of the dice throws to be at least T. We know the expected value exists. The dice throws are randomly distributed and independent of each other. So simple Monte Carlo is applicable:
s = 0; for i = 1 to n do throw the three dice until T is met or first exceeded; ri = the number of throws; s = s + ri; repeat m = s / n;
If n is large enough, m will be within ε of μ for any ε > 0.
Determining a sufficiently large n
General formula
Let ε = |μ – m| > 0. Choose the desired confidence level – the percent chance that, when the Monte Carlo algorithm completes, m is indeed within ε of μ. Let z be the z-score corresponding to that confidence level.
Let s be the estimated variance, sometimes called the “sample” variance; it is the variance of the results obtained from a relatively small number k of “sample” simulations. Choose a k; Driels and Shin observe that “even for sample sizes an order of magnitude lower than the number required, the calculation of that number is quite stable."
The following algorithm computes s in one pass while minimizing the possibility that accumulated numerical error produces erroneous results:
s1 = 0; run the simulation for the first time, producing result r1; m1 = r1; //mi is the mean of the first i simulations for i = 2 to k do run the simulation for the i time, producing result ri; δi = ri - mi-1; mi = mi-1 + (1/i)δi; si = si-1 + ((i - 1)/i)(δi); repeat s = sk/(k - 1);
Note that, when the algorithm completes, mk is the mean of the k results.
n is sufficiently large when
If n ≤ k, then mk = m; sufficient sample simulations were done to ensure that mk is within ε of μ. If n > k, then n simulations can be run “from scratch,” or, since k simulations have already been done, one can just run n – k more simulations and add their results into those from the sample simulations:
s = mk * k; for i = k + 1 to n do run the simulation for the i time, giving result ri; s = s + ri; m = s / n;
A formula when simulations' results are bounded
An alternate formula can be used in the special case where all simulation results are bounded above and below.
Choose a value for ε that is twice the maximum allowed difference between μ and m. Let 0 < δ < 100 be the desired confidence level, expressed as a percentage. Let every simulation result r1, r2, …ri, … rn be such that a ≤ ri ≤ b for finite a and b. To have confidence of at least δ that |μ – m| < ε/2, use a value for n such that
For example, if δ = 99%, then n ≥ 2(b – a )ln(2/0.01)/ε ≈ 10.6(b – a )/ε.
Computational costs
Despite its conceptual and algorithmic simplicity, the computational cost associated with a Monte Carlo simulation can be staggeringly high. In general the method requires many samples to get a good approximation, which may incur an arbitrarily large total runtime if the processing time of a single sample is high. Although this is a severe limitation in very complex problems, the embarrassingly parallel nature of the algorithm allows this large cost to be reduced (perhaps to a feasible level) through parallel computing strategies in local processors, clusters, cloud computing, GPU, FPGA, etc.
History
Before the Monte Carlo method was developed, simulations tested a previously understood deterministic problem, and statistical sampling was used to estimate uncertainties in the simulations. Monte Carlo simulations invert this approach, solving deterministic problems using probabilistic metaheuristics (see simulated annealing).
An early variant of the Monte Carlo method was devised to solve the Buffon's needle problem, in which π can be estimated by dropping needles on a floor made of parallel equidistant strips. In the 1930s, Enrico Fermi first experimented with the Monte Carlo method while studying neutron diffusion, but he did not publish this work.
In the late 1940s, Stanisław Ulam invented the modern version of the Markov Chain Monte Carlo method while he was working on nuclear weapons projects at the Los Alamos National Laboratory. In 1946, nuclear weapons physicists at Los Alamos were investigating neutron diffusion in the core of a nuclear weapon. Despite having most of the necessary data, such as the average distance a neutron would travel in a substance before it collided with an atomic nucleus and how much energy the neutron was likely to give off following a collision, the Los Alamos physicists were unable to solve the problem using conventional, deterministic mathematical methods. Ulam proposed using random experiments. He recounts his inspiration as follows:
The first thoughts and attempts I made to practice were suggested by a question which occurred to me in 1946 as I was convalescing from an illness and playing solitaires. The question was what are the chances that a Canfield solitaire laid out with 52 cards will come out successfully? After spending a lot of time trying to estimate them by pure combinatorial calculations, I wondered whether a more practical method than "abstract thinking" might not be to lay it out say one hundred times and simply observe and count the number of successful plays. This was already possible to envisage with the beginning of the new era of fast computers, and I immediately thought of problems of neutron diffusion and other questions of mathematical physics, and more generally how to change processes described by certain differential equations into an equivalent form interpretable as a succession of random operations. Later , I described the idea to John von Neumann, and we began to plan actual calculations.
Being secret, the work of von Neumann and Ulam required a code name. A colleague of von Neumann and Ulam, Nicholas Metropolis, suggested using the name Monte Carlo, which refers to the Monte Carlo Casino in Monaco where Ulam's uncle would borrow money from relatives to gamble. Monte Carlo methods were central to the simulations required for further postwar development of nuclear weapons, including the design of the H-bomb, though severely limited by the computational tools at the time. Von Neumann, Nicholas Metropolis and others programmed the ENIAC computer to perform the first fully automated Monte Carlo calculations, of a fission weapon core, in the spring of 1948. In the 1950s Monte Carlo methods were used at Los Alamos for the development of the hydrogen bomb, and became popularized in the fields of physics, physical chemistry, and operations research. The Rand Corporation and the U.S. Air Force were two of the major organizations responsible for funding and disseminating information on Monte Carlo methods during this time, and they began to find a wide application in many different fields.
The theory of more sophisticated mean-field type particle Monte Carlo methods had certainly started by the mid-1960s, with the work of Henry P. McKean Jr. on Markov interpretations of a class of nonlinear parabolic partial differential equations arising in fluid mechanics. An earlier pioneering article by Theodore E. Harris and Herman Kahn, published in 1951, used mean-field genetic-type Monte Carlo methods for estimating particle transmission energies. Mean-field genetic type Monte Carlo methodologies are also used as heuristic natural search algorithms (a.k.a. metaheuristic) in evolutionary computing. The origins of these mean-field computational techniques can be traced to 1950 and 1954 with the work of Alan Turing on genetic type mutation-selection learning machines and the articles by Nils Aall Barricelli at the Institute for Advanced Study in Princeton, New Jersey.
Quantum Monte Carlo, and more specifically diffusion Monte Carlo methods can also be interpreted as a mean-field particle Monte Carlo approximation of Feynman–Kac path integrals. The origins of Quantum Monte Carlo methods are often attributed to Enrico Fermi and Robert Richtmyer who developed in 1948 a mean-field particle interpretation of neutron-chain reactions, but the first heuristic-like and genetic type particle algorithm (a.k.a. Resampled or Reconfiguration Monte Carlo methods) for estimating ground state energies of quantum systems (in reduced matrix models) is due to Jack H. Hetherington in 1984. In molecular chemistry, the use of genetic heuristic-like particle methodologies (a.k.a. pruning and enrichment strategies) can be traced back to 1955 with the seminal work of Marshall N. Rosenbluth and Arianna W. Rosenbluth.
The use of Sequential Monte Carlo in advanced signal processing and Bayesian inference is more recent. It was in 1993, that Gordon et al., published in their seminal work the first application of a Monte Carlo resampling algorithm in Bayesian statistical inference. The authors named their algorithm 'the bootstrap filter', and demonstrated that compared to other filtering methods, their bootstrap algorithm does not require any assumption about that state-space or the noise of the system. Another pioneering article in this field was Genshiro Kitagawa's, on a related "Monte Carlo filter", and the ones by Pierre Del Moral and Himilcon Carvalho, Pierre Del Moral, André Monin and Gérard Salut on particle filters published in the mid-1990s. Particle filters were also developed in signal processing in 1989–1992 by P. Del Moral, J. C. Noyer, G. Rigal, and G. Salut in the LAAS-CNRS in a series of restricted and classified research reports with STCAN (Service Technique des Constructions et Armes Navales), the IT company DIGILOG, and the LAAS-CNRS (the Laboratory for Analysis and Architecture of Systems) on radar/sonar and GPS signal processing problems. These Sequential Monte Carlo methodologies can be interpreted as an acceptance-rejection sampler equipped with an interacting recycling mechanism.
From 1950 to 1996, all the publications on Sequential Monte Carlo methodologies, including the pruning and resample Monte Carlo methods introduced in computational physics and molecular chemistry, present natural and heuristic-like algorithms applied to different situations without a single proof of their consistency, nor a discussion on the bias of the estimates and on genealogical and ancestral tree based algorithms. The mathematical foundations and the first rigorous analysis of these particle algorithms were written by Pierre Del Moral in 1996.
Branching type particle methodologies with varying population sizes were also developed in the end of the 1990s by Dan Crisan, Jessica Gaines and Terry Lyons, and by Dan Crisan, Pierre Del Moral and Terry Lyons. Further developments in this field were described in 1999 to 2001 by P. Del Moral, A. Guionnet and L. Miclo.
Definitions
There is no consensus on how Monte Carlo should be defined. For example, Ripley defines most probabilistic modeling as stochastic simulation, with Monte Carlo being reserved for Monte Carlo integration and Monte Carlo statistical tests. Sawilowsky distinguishes between a simulation, a Monte Carlo method, and a Monte Carlo simulation: a simulation is a fictitious representation of reality, a Monte Carlo method is a technique that can be used to solve a mathematical or statistical problem, and a Monte Carlo simulation uses repeated sampling to obtain the statistical properties of some phenomenon (or behavior).
Here are some examples:
- Simulation: Drawing one pseudo-random uniform variable from the interval can be used to simulate the tossing of a coin: If the value is less than or equal to 0.50 designate the outcome as heads, but if the value is greater than 0.50 designate the outcome as tails. This is a simulation, but not a Monte Carlo simulation.
- Monte Carlo method: Pouring out a box of coins on a table, and then computing the ratio of coins that land heads versus tails is a Monte Carlo method of determining the behavior of repeated coin tosses, but it is not a simulation.
- Monte Carlo simulation: Drawing a large number of pseudo-random uniform variables from the interval at one time, or once at many different times, and assigning values less than or equal to 0.50 as heads and greater than 0.50 as tails, is a Monte Carlo simulation of the behavior of repeatedly tossing a coin.
Kalos and Whitlock point out that such distinctions are not always easy to maintain. For example, the emission of radiation from atoms is a natural stochastic process. It can be simulated directly, or its average behavior can be described by stochastic equations that can themselves be solved using Monte Carlo methods. "Indeed, the same computer code can be viewed simultaneously as a 'natural simulation' or as a solution of the equations by natural sampling."
Convergence of the Monte Carlo simulation can be checked with the Gelman-Rubin statistic.
Monte Carlo and random numbers
The main idea behind this method is that the results are computed based on repeated random sampling and statistical analysis. The Monte Carlo simulation is, in fact, random experimentations, in the case that, the results of these experiments are not well known. Monte Carlo simulations are typically characterized by many unknown parameters, many of which are difficult to obtain experimentally. Monte Carlo simulation methods do not always require truly random numbers to be useful (although, for some applications such as primality testing, unpredictability is vital). Many of the most useful techniques use deterministic, pseudorandom sequences, making it easy to test and re-run simulations. The only quality usually necessary to make good simulations is for the pseudo-random sequence to appear "random enough" in a certain sense.
What this means depends on the application, but typically they should pass a series of statistical tests. Testing that the numbers are uniformly distributed or follow another desired distribution when a large enough number of elements of the sequence are considered is one of the simplest and most common ones. Weak correlations between successive samples are also often desirable/necessary.
Sawilowsky lists the characteristics of a high-quality Monte Carlo simulation:
- the (pseudo-random) number generator has certain characteristics (e.g. a long "period" before the sequence repeats)
- the (pseudo-random) number generator produces values that pass tests for randomness
- there are enough samples to ensure accurate results
- the proper sampling technique is used
- the algorithm used is valid for what is being modeled
- it simulates the phenomenon in question.
Pseudo-random number sampling algorithms are used to transform uniformly distributed pseudo-random numbers into numbers that are distributed according to a given probability distribution.
Low-discrepancy sequences are often used instead of random sampling from a space as they ensure even coverage and normally have a faster order of convergence than Monte Carlo simulations using random or pseudorandom sequences. Methods based on their use are called quasi-Monte Carlo methods.
In an effort to assess the impact of random number quality on Monte Carlo simulation outcomes, astrophysical researchers tested cryptographically secure pseudorandom numbers generated via Intel's RDRAND instruction set, as compared to those derived from algorithms, like the Mersenne Twister, in Monte Carlo simulations of radio flares from brown dwarfs. No statistically significant difference was found between models generated with typical pseudorandom number generators and RDRAND for trials consisting of the generation of 10 random numbers.
Monte Carlo simulation versus "what if" scenarios
There are ways of using probabilities that are definitely not Monte Carlo simulations – for example, deterministic modeling using single-point estimates. Each uncertain variable within a model is assigned a "best guess" estimate. Scenarios (such as best, worst, or most likely case) for each input variable are chosen and the results recorded.
By contrast, Monte Carlo simulations sample from a probability distribution for each variable to produce hundreds or thousands of possible outcomes. The results are analyzed to get probabilities of different outcomes occurring. For example, a comparison of a spreadsheet cost construction model run using traditional "what if" scenarios, and then running the comparison again with Monte Carlo simulation and triangular probability distributions shows that the Monte Carlo analysis has a narrower range than the "what if" analysis. This is because the "what if" analysis gives equal weight to all scenarios (see quantifying uncertainty in corporate finance), while the Monte Carlo method hardly samples in the very low probability regions. The samples in such regions are called "rare events".
Applications
Monte Carlo methods are especially useful for simulating phenomena with significant uncertainty in inputs and systems with many coupled degrees of freedom. Areas of application include:
Physical sciences
| Computational physics |
|---|
 |
| Potentials |
| Fluid dynamics |
| Monte Carlo methods |
| Particle |
| Scientists |
Monte Carlo methods are very important in computational physics, physical chemistry, and related applied fields, and have diverse applications from complicated quantum chromodynamics calculations to designing heat shields and aerodynamic forms as well as in modeling radiation transport for radiation dosimetry calculations. In statistical physics, Monte Carlo molecular modeling is an alternative to computational molecular dynamics, and Monte Carlo methods are used to compute statistical field theories of simple particle and polymer systems. Quantum Monte Carlo methods solve the many-body problem for quantum systems. In radiation materials science, the binary collision approximation for simulating ion implantation is usually based on a Monte Carlo approach to select the next colliding atom. In experimental particle physics, Monte Carlo methods are used for designing detectors, understanding their behavior and comparing experimental data to theory. In astrophysics, they are used in such diverse manners as to model both galaxy evolution and microwave radiation transmission through a rough planetary surface. Monte Carlo methods are also used in the ensemble models that form the basis of modern weather forecasting.
Engineering
Monte Carlo methods are widely used in engineering for sensitivity analysis and quantitative probabilistic analysis in process design. The need arises from the interactive, co-linear and non-linear behavior of typical process simulations. For example,
- In microelectronics engineering, Monte Carlo methods are applied to analyze correlated and uncorrelated variations in analog and digital integrated circuits.
- In geostatistics and geometallurgy, Monte Carlo methods underpin the design of mineral processing flowsheets and contribute to quantitative risk analysis.
- In fluid dynamics, in particular rarefied gas dynamics, where the Boltzmann equation is solved for finite Knudsen number fluid flows using the direct simulation Monte Carlo method in combination with highly efficient computational algorithms.
- In autonomous robotics, Monte Carlo localization can determine the position of a robot. It is often applied to stochastic filters such as the Kalman filter or particle filter that forms the heart of the SLAM (simultaneous localization and mapping) algorithm.
- In telecommunications, when planning a wireless network, the design must be proven to work for a wide variety of scenarios that depend mainly on the number of users, their locations and the services they want to use. Monte Carlo methods are typically used to generate these users and their states. The network performance is then evaluated and, if results are not satisfactory, the network design goes through an optimization process.
- In reliability engineering, Monte Carlo simulation is used to compute system-level response given the component-level response.
- In signal processing and Bayesian inference, particle filters and sequential Monte Carlo techniques are a class of mean-field particle methods for sampling and computing the posterior distribution of a signal process given some noisy and partial observations using interacting empirical measures.
Climate change and radiative forcing
The Intergovernmental Panel on Climate Change relies on Monte Carlo methods in probability density function analysis of radiative forcing.
Computational biology
Monte Carlo methods are used in various fields of computational biology, for example for Bayesian inference in phylogeny, or for studying biological systems such as genomes, proteins, or membranes. The systems can be studied in the coarse-grained or ab initio frameworks depending on the desired accuracy. Computer simulations allow monitoring of the local environment of a particular molecule to see if some chemical reaction is happening for instance. In cases where it is not feasible to conduct a physical experiment, thought experiments can be conducted (for instance: breaking bonds, introducing impurities at specific sites, changing the local/global structure, or introducing external fields).
Computer graphics
Path tracing, occasionally referred to as Monte Carlo ray tracing, renders a 3D scene by randomly tracing samples of possible light paths. Repeated sampling of any given pixel will eventually cause the average of the samples to converge on the correct solution of the rendering equation, making it one of the most physically accurate 3D graphics rendering methods in existence.
Applied statistics
The standards for Monte Carlo experiments in statistics were set by Sawilowsky. In applied statistics, Monte Carlo methods may be used for at least four purposes:
- To compare competing statistics for small samples under realistic data conditions. Although type I error and power properties of statistics can be calculated for data drawn from classical theoretical distributions (e.g., normal curve, Cauchy distribution) for asymptotic conditions (i. e, infinite sample size and infinitesimally small treatment effect), real data often do not have such distributions.
- To provide implementations of hypothesis tests that are more efficient than exact tests such as permutation tests (which are often impossible to compute) while being more accurate than critical values for asymptotic distributions.
- To provide a random sample from the posterior distribution in Bayesian inference. This sample then approximates and summarizes all the essential features of the posterior.
- To provide efficient random estimates of the Hessian matrix of the negative log-likelihood function that may be averaged to form an estimate of the Fisher information matrix.
Monte Carlo methods are also a compromise between approximate randomization and permutation tests. An approximate randomization test is based on a specified subset of all permutations (which entails potentially enormous housekeeping of which permutations have been considered). The Monte Carlo approach is based on a specified number of randomly drawn permutations (exchanging a minor loss in precision if a permutation is drawn twice—or more frequently—for the efficiency of not having to track which permutations have already been selected).
Artificial intelligence for games
Main article: Monte Carlo tree searchMonte Carlo methods have been developed into a technique called Monte-Carlo tree search that is useful for searching for the best move in a game. Possible moves are organized in a search tree and many random simulations are used to estimate the long-term potential of each move. A black box simulator represents the opponent's moves.
The Monte Carlo tree search (MCTS) method has four steps:
- Starting at root node of the tree, select optimal child nodes until a leaf node is reached.
- Expand the leaf node and choose one of its children.
- Play a simulated game starting with that node.
- Use the results of that simulated game to update the node and its ancestors.
The net effect, over the course of many simulated games, is that the value of a node representing a move will go up or down, hopefully corresponding to whether or not that node represents a good move.
Monte Carlo Tree Search has been used successfully to play games such as Go, Tantrix, Battleship, Havannah, and Arimaa.
See also: Computer GoDesign and visuals
Monte Carlo methods are also efficient in solving coupled integral differential equations of radiation fields and energy transport, and thus these methods have been used in global illumination computations that produce photo-realistic images of virtual 3D models, with applications in video games, architecture, design, computer generated films, and cinematic special effects.
Search and rescue
The US Coast Guard utilizes Monte Carlo methods within its computer modeling software SAROPS in order to calculate the probable locations of vessels during search and rescue operations. Each simulation can generate as many as ten thousand data points that are randomly distributed based upon provided variables. Search patterns are then generated based upon extrapolations of these data in order to optimize the probability of containment (POC) and the probability of detection (POD), which together will equal an overall probability of success (POS). Ultimately this serves as a practical application of probability distribution in order to provide the swiftest and most expedient method of rescue, saving both lives and resources.
Finance and business
See also: Monte Carlo methods in finance, Quasi-Monte Carlo methods in finance, Monte Carlo methods for option pricing, Stochastic modelling (insurance), and Stochastic asset modelMonte Carlo simulation is commonly used to evaluate the risk and uncertainty that would affect the outcome of different decision options. Monte Carlo simulation allows the business risk analyst to incorporate the total effects of uncertainty in variables like sales volume, commodity and labor prices, interest and exchange rates, as well as the effect of distinct risk events like the cancellation of a contract or the change of a tax law.
Monte Carlo methods in finance are often used to evaluate investments in projects at a business unit or corporate level, or other financial valuations. They can be used to model project schedules, where simulations aggregate estimates for worst-case, best-case, and most likely durations for each task to determine outcomes for the overall project. Monte Carlo methods are also used in option pricing, default risk analysis. Additionally, they can be used to estimate the financial impact of medical interventions.
Law
A Monte Carlo approach was used for evaluating the potential value of a proposed program to help female petitioners in Wisconsin be successful in their applications for harassment and domestic abuse restraining orders. It was proposed to help women succeed in their petitions by providing them with greater advocacy thereby potentially reducing the risk of rape and physical assault. However, there were many variables in play that could not be estimated perfectly, including the effectiveness of restraining orders, the success rate of petitioners both with and without advocacy, and many others. The study ran trials that varied these variables to come up with an overall estimate of the success level of the proposed program as a whole.
Library science
Monte Carlo approach had also been used to simulate the number of book publications based on book genre in Malaysia. The Monte Carlo simulation utilized previous published National Book publication data and book's price according to book genre in the local market. The Monte Carlo results were used to determine what kind of book genre that Malaysians are fond of and was used to compare book publications between Malaysia and Japan.
Other
Nassim Nicholas Taleb writes about Monte Carlo generators in his 2001 book Fooled by Randomness as a real instance of the reverse Turing test: a human can be declared unintelligent if their writing cannot be told apart from a generated one.
Use in mathematics
In general, the Monte Carlo methods are used in mathematics to solve various problems by generating suitable random numbers (see also Random number generation) and observing that fraction of the numbers that obeys some property or properties. The method is useful for obtaining numerical solutions to problems too complicated to solve analytically. The most common application of the Monte Carlo method is Monte Carlo integration.
Integration
Main article: Monte Carlo integration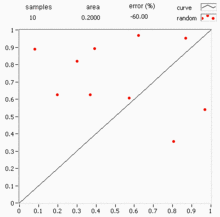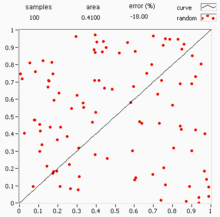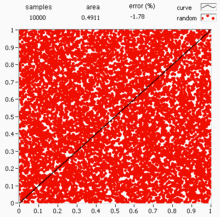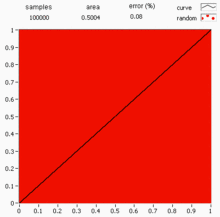

Deterministic numerical integration algorithms work well in a small number of dimensions, but encounter two problems when the functions have many variables. First, the number of function evaluations needed increases rapidly with the number of dimensions. For example, if 10 evaluations provide adequate accuracy in one dimension, then 10 points are needed for 100 dimensions—far too many to be computed. This is called the curse of dimensionality. Second, the boundary of a multidimensional region may be very complicated, so it may not be feasible to reduce the problem to an iterated integral. 100 dimensions is by no means unusual, since in many physical problems, a "dimension" is equivalent to a degree of freedom.
Monte Carlo methods provide a way out of this exponential increase in computation time. As long as the function in question is reasonably well-behaved, it can be estimated by randomly selecting points in 100-dimensional space, and taking some kind of average of the function values at these points. By the central limit theorem, this method displays convergence—i.e., quadrupling the number of sampled points halves the error, regardless of the number of dimensions.
A refinement of this method, known as importance sampling in statistics, involves sampling the points randomly, but more frequently where the integrand is large. To do this precisely one would have to already know the integral, but one can approximate the integral by an integral of a similar function or use adaptive routines such as stratified sampling, recursive stratified sampling, adaptive umbrella sampling or the VEGAS algorithm.
A similar approach, the quasi-Monte Carlo method, uses low-discrepancy sequences. These sequences "fill" the area better and sample the most important points more frequently, so quasi-Monte Carlo methods can often converge on the integral more quickly.
Another class of methods for sampling points in a volume is to simulate random walks over it (Markov chain Monte Carlo). Such methods include the Metropolis–Hastings algorithm, Gibbs sampling, Wang and Landau algorithm, and interacting type MCMC methodologies such as the sequential Monte Carlo samplers.
Simulation and optimization
Main article: Stochastic optimizationAnother powerful and very popular application for random numbers in numerical simulation is in numerical optimization. The problem is to minimize (or maximize) functions of some vector that often has many dimensions. Many problems can be phrased in this way: for example, a computer chess program could be seen as trying to find the set of, say, 10 moves that produces the best evaluation function at the end. In the traveling salesman problem the goal is to minimize distance traveled. There are also applications to engineering design, such as multidisciplinary design optimization. It has been applied with quasi-one-dimensional models to solve particle dynamics problems by efficiently exploring large configuration space. Reference is a comprehensive review of many issues related to simulation and optimization.
The traveling salesman problem is what is called a conventional optimization problem. That is, all the facts (distances between each destination point) needed to determine the optimal path to follow are known with certainty and the goal is to run through the possible travel choices to come up with the one with the lowest total distance. If instead of the goal being to minimize the total distance traveled to visit each desired destination but rather to minimize the total time needed to reach each destination, this goes beyond conventional optimization since travel time is inherently uncertain (traffic jams, time of day, etc.). As a result, to determine the optimal path a different simulation is required: optimization to first understand the range of potential times it could take to go from one point to another (represented by a probability distribution in this case rather than a specific distance) and then optimize the travel decisions to identify the best path to follow taking that uncertainty into account.
Inverse problems
Probabilistic formulation of inverse problems leads to the definition of a probability distribution in the model space. This probability distribution combines prior information with new information obtained by measuring some observable parameters (data). As, in the general case, the theory linking data with model parameters is nonlinear, the posterior probability in the model space may not be easy to describe (it may be multimodal, some moments may not be defined, etc.).
When analyzing an inverse problem, obtaining a maximum likelihood model is usually not sufficient, as normally information on the resolution power of the data is desired. In the general case many parameters are modeled, and an inspection of the marginal probability densities of interest may be impractical, or even useless. But it is possible to pseudorandomly generate a large collection of models according to the posterior probability distribution and to analyze and display the models in such a way that information on the relative likelihoods of model properties is conveyed to the spectator. This can be accomplished by means of an efficient Monte Carlo method, even in cases where no explicit formula for the a priori distribution is available.
The best-known importance sampling method, the Metropolis algorithm, can be generalized, and this gives a method that allows analysis of (possibly highly nonlinear) inverse problems with complex a priori information and data with an arbitrary noise distribution.
Philosophy
Popular exposition of the Monte Carlo Method was conducted by McCracken. The method's general philosophy was discussed by Elishakoff and Grüne-Yanoff and Weirich.
See also
- Auxiliary-field Monte Carlo
- Biology Monte Carlo method
- Direct simulation Monte Carlo
- Dynamic Monte Carlo method
- Ergodicity
- Genetic algorithms
- Kinetic Monte Carlo
- List of software for Monte Carlo molecular modeling
- Mean-field particle methods
- Monte Carlo method for photon transport
- Monte Carlo methods for electron transport
- Monte Carlo N-Particle Transport Code
- Morris method
- Multilevel Monte Carlo method
- Quasi-Monte Carlo method
- Sobol sequence
- Temporal difference learning
References
Citations
- Kalos & Whitlock 2008.
- Kroese, D. P.; Brereton, T.; Taimre, T.; Botev, Z. I. (2014). "Why the Monte Carlo method is so important today". WIREs Comput Stat. 6 (6): 386–392. doi:10.1002/wics.1314. S2CID 18521840.
- Hubbard, Douglas; Samuelson, Douglas A. (October 2009). "Modeling Without Measurements". OR/MS Today: 28–33.
- Metropolis, Nicholas; Rosenbluth, Arianna W.; Rosenbluth, Marshall N.; Teller, Augusta H.; Teller, Edward (June 1, 1953). "Equation of State Calculations by Fast Computing Machines". The Journal of Chemical Physics. 21 (6): 1087–1092. Bibcode:1953JChPh..21.1087M. doi:10.1063/1.1699114. ISSN 0021-9606. OSTI 4390578. S2CID 1046577.
- Hastings, W. K. (April 1, 1970). "Monte Carlo sampling methods using Markov chains and their applications". Biometrika. 57 (1): 97–109. Bibcode:1970Bimka..57...97H. doi:10.1093/biomet/57.1.97. ISSN 0006-3444. S2CID 21204149.
- Liu, Jun S.; Liang, Faming; Wong, Wing Hung (March 1, 2000). "The Multiple-Try Method and Local Optimization in Metropolis Sampling". Journal of the American Statistical Association. 95 (449): 121–134. doi:10.1080/01621459.2000.10473908. ISSN 0162-1459. S2CID 123468109.
- Spall, J. C. (2003). "Estimation via Markov Chain Monte Carlo". IEEE Control Systems Magazine. 23 (2): 34–45. doi:10.1109/MCS.2003.1188770.
- Hill, Stacy D.; Spall, James C. (2019). "Stationarity and Convergence of the Metropolis-Hastings Algorithm: Insights into Theoretical Aspects". IEEE Control Systems Magazine. 39: 56–67. doi:10.1109/MCS.2018.2876959. S2CID 58672766.
- ^ Kolokoltsov, Vassili (2010). Nonlinear Markov processes. Cambridge University Press. p. 375.
- ^ Del Moral, Pierre (2013). Mean field simulation for Monte Carlo integration. Chapman & Hall/CRC Press. p. 626.
Monographs on Statistics & Applied Probability
- Del Moral, P.; Doucet, A.; Jasra, A. (2006). "Sequential Monte Carlo samplers". Journal of the Royal Statistical Society, Series B. 68 (3): 411–436. arXiv:cond-mat/0212648. doi:10.1111/j.1467-9868.2006.00553.x. S2CID 12074789.
- ^ Owen, Art B. (2013). Monte Carlo Theory, Methods and Examples (PDF). Work in progress. pp. 15–36.
- ^ Driels, Morris R.; Shin, Young S. (April 2004). "Determining the number of Iterations for Monte Carlo Simulations of Weapon Effectiveness". Naval Postgraduate School Technical Report (March 2003 - March 2004): 10–11.
- Shonkwiler, R. W.; Mendivil, F. (2009). Explorations in Monte Carlo Methods. Springer.
- Atanassova, E.; Gurov, T.; Karaivanova, A.; Ivanovska, S.; Durchova, M.; Dimitrov, D. (2016). "On the parallelization approaches for Intel MIC architecture". AIP Conference Proceedings. 1773 (1): 070001. Bibcode:2016AIPC.1773g0001A. doi:10.1063/1.4964983.
- Cunha Jr, A.; Nasser, R.; Sampaio, R.; Lopes, H.; Breitman, K. (2014). "Uncertainty quantification through the Monte Carlo method in a cloud computing setting". Computer Physics Communications. 185 (5): 1355–1363. arXiv:2105.09512. Bibcode:2014CoPhC.185.1355C. doi:10.1016/j.cpc.2014.01.006. S2CID 32376269.
- Wei, J.; Kruis, F.E. (2013). "A GPU-based parallelized Monte-Carlo method for particle coagulation using an acceptance–rejection strategy". Chemical Engineering Science. 104: 451–459. Bibcode:2013ChEnS.104..451W. doi:10.1016/j.ces.2013.08.008.
- Lin, Y.; Wang, F.; Liu, B. (2018). "Random number generators for large-scale parallel Monte Carlo simulations on FPGA". Journal of Computational Physics. 360: 93–103. Bibcode:2018JCoPh.360...93L. doi:10.1016/j.jcp.2018.01.029.
- ^ Metropolis 1987.
- Eckhardt 1987.
- ^ Mazhdrakov, Benov & Valkanov 2018, p. 250.
- Haigh, Thomas; Priestley, Mark; Rope, Crispin (2014). "Los Alamos Bets on ENIAC: Nuclear Monte Carlo Simulations, 1947-1948". IEEE Annals of the History of Computing. 36 (3): 42–63. doi:10.1109/MAHC.2014.40. S2CID 17470931.
- McKean, Henry P. (1967). "Propagation of chaos for a class of non-linear parabolic equations". Lecture Series in Differential Equations, Catholic Univ. 7: 41–57.
- McKean, Henry P. (1966). "A class of Markov processes associated with nonlinear parabolic equations". Proc. Natl. Acad. Sci. USA. 56 (6): 1907–1911. Bibcode:1966PNAS...56.1907M. doi:10.1073/pnas.56.6.1907. PMC 220210. PMID 16591437.
- Herman, Kahn; Theodore, Harris E. (1951). "Estimation of particle transmission by random sampling" (PDF). Natl. Bur. Stand. Appl. Math. Ser. 12: 27–30.
- Turing, Alan M. (1950). "Computing machinery and intelligence". Mind. LIX (238): 433–460. doi:10.1093/mind/LIX.236.433.
- Barricelli, Nils Aall (1954). "Esempi numerici di processi di evoluzione". Methodos: 45–68.
- Barricelli, Nils Aall (1957). "Symbiogenetic evolution processes realized by artificial methods". Methodos: 143–182.
- ^ Del Moral, Pierre (2004). Feynman–Kac formulae. Genealogical and interacting particle approximations. Probability and Its Applications. Springer. p. 575. ISBN 9780387202686.
Series: Probability and Applications
- ^ Del Moral, P.; Miclo, L. (2000). "Branching and interacting particle systems approximations of Feynman–Kac formulae with applications to non-linear filtering". Séminaire de Probabilités XXXIV. Lecture Notes in Mathematics. Vol. 1729. Berlin: Springer. pp. 1–145. doi:10.1007/BFb0103798. ISBN 978-3-540-67314-9. MR 1768060.
- Del Moral, Pierre; Miclo, Laurent (2000). "A Moran particle system approximation of Feynman–Kac formulae". Stochastic Processes and Their Applications. 86 (2): 193–216. doi:10.1016/S0304-4149(99)00094-0.
- Del Moral, Pierre (2003). "Particle approximations of Lyapunov exponents connected to Schrödinger operators and Feynman–Kac semigroups". ESAIM Probability & Statistics. 7: 171–208. doi:10.1051/ps:2003001.
- Assaraf, Roland; Caffarel, Michel; Khelif, Anatole (2000). "Diffusion Monte Carlo Methods with a fixed number of walkers" (PDF). Phys. Rev. E. 61 (4): 4566–4575. Bibcode:2000PhRvE..61.4566A. doi:10.1103/physreve.61.4566. PMID 11088257. Archived from the original (PDF) on November 7, 2014.
- Caffarel, Michel; Ceperley, David; Kalos, Malvin (1993). "Comment on Feynman–Kac Path-Integral Calculation of the Ground-State Energies of Atoms". Phys. Rev. Lett. 71 (13): 2159. Bibcode:1993PhRvL..71.2159C. doi:10.1103/physrevlett.71.2159. PMID 10054598.
- ^ Hetherington, Jack H. (1984). "Observations on the statistical iteration of matrices". Phys. Rev. A. 30 (2713): 2713–2719. Bibcode:1984PhRvA..30.2713H. doi:10.1103/PhysRevA.30.2713.
- Fermi, Enrique; Richtmyer, Robert D. (1948). "Note on census-taking in Monte Carlo calculations" (PDF). LAM. 805 (A).
Declassified report Los Alamos Archive
- ^ Rosenbluth, Marshall N.; Rosenbluth, Arianna W. (1955). "Monte-Carlo calculations of the average extension of macromolecular chains". J. Chem. Phys. 23 (2): 356–359. Bibcode:1955JChPh..23..356R. doi:10.1063/1.1741967. S2CID 89611599.
- Gordon, N.J.; Salmond, D.J.; Smith, A.F.M. (April 1993). "Novel approach to nonlinear/non-Gaussian Bayesian state estimation". IEE Proceedings F - Radar and Signal Processing. 140 (2): 107–113. doi:10.1049/ip-f-2.1993.0015. ISSN 0956-375X. S2CID 12644877.
- Kitagawa, G. (1996). "Monte carlo filter and smoother for non-Gaussian nonlinear state space models". Journal of Computational and Graphical Statistics. 5 (1): 1–25. doi:10.2307/1390750. JSTOR 1390750.
- ^ Del Moral, Pierre (1996). "Non Linear Filtering: Interacting Particle Solution" (PDF). Markov Processes and Related Fields. 2 (4): 555–580. Archived from the original (PDF) on March 4, 2016. Retrieved June 11, 2015.
- Carvalho, Himilcon; Del Moral, Pierre; Monin, André; Salut, Gérard (July 1997). "Optimal Non-linear Filtering in GPS/INS Integration" (PDF). IEEE Transactions on Aerospace and Electronic Systems. 33 (3): 835–850. Bibcode:1997ITAES..33..835C. doi:10.1109/7.599254. S2CID 27966240. Archived from the original (PDF) on November 10, 2022. Retrieved June 11, 2015.
- P. Del Moral, G. Rigal, and G. Salut. "Estimation and nonlinear optimal control: An unified framework for particle solutions". LAAS-CNRS, Toulouse, Research Report no. 91137, DRET-DIGILOG- LAAS/CNRS contract, April (1991).
- P. Del Moral, G. Rigal, and G. Salut. "Nonlinear and non Gaussian particle filters applied to inertial platform repositioning." LAAS-CNRS, Toulouse, Research Report no. 92207, STCAN/DIGILOG-LAAS/CNRS Convention STCAN no. A.91.77.013, (94p.) September (1991).
- P. Del Moral, G. Rigal, and G. Salut. "Estimation and nonlinear optimal control: Particle resolution in filtering and estimation: Experimental results". Convention DRET no. 89.34.553.00.470.75.01, Research report no.2 (54p.), January (1992).
- P. Del Moral, G. Rigal, and G. Salut. "Estimation and nonlinear optimal control: Particle resolution in filtering and estimation: Theoretical results". Convention DRET no. 89.34.553.00.470.75.01, Research report no.3 (123p.), October (1992).
- P. Del Moral, J.-Ch. Noyer, G. Rigal, and G. Salut. "Particle filters in radar signal processing: detection, estimation and air targets recognition". LAAS-CNRS, Toulouse, Research report no. 92495, December (1992).
- P. Del Moral, G. Rigal, and G. Salut. "Estimation and nonlinear optimal control: Particle resolution in filtering and estimation". Studies on: Filtering, optimal control, and maximum likelihood estimation. Convention DRET no. 89.34.553.00.470.75.01. Research report no.4 (210p.), January (1993).
- Del Moral, Pierre (1998). "Measure Valued Processes and Interacting Particle Systems. Application to Non Linear Filtering Problems". Annals of Applied Probability. 8 (2) (Publications du Laboratoire de Statistique et Probabilités, 96-15 (1996) ed.): 438–495. CiteSeerX 10.1.1.55.5257. doi:10.1214/aoap/1028903535.
- Crisan, Dan; Gaines, Jessica; Lyons, Terry (1998). "Convergence of a branching particle method to the solution of the Zakai". SIAM Journal on Applied Mathematics. 58 (5): 1568–1590. doi:10.1137/s0036139996307371. S2CID 39982562.
- Crisan, Dan; Lyons, Terry (1997). "Nonlinear filtering and measure-valued processes". Probability Theory and Related Fields. 109 (2): 217–244. doi:10.1007/s004400050131. S2CID 119809371.
- Crisan, Dan; Lyons, Terry (1999). "A particle approximation of the solution of the Kushner–Stratonovitch equation". Probability Theory and Related Fields. 115 (4): 549–578. doi:10.1007/s004400050249. S2CID 117725141.
- Crisan, Dan; Del Moral, Pierre; Lyons, Terry (1999). "Discrete filtering using branching and interacting particle systems" (PDF). Markov Processes and Related Fields. 5 (3): 293–318.
- Del Moral, Pierre; Guionnet, Alice (1999). "On the stability of Measure Valued Processes with Applications to filtering". C. R. Acad. Sci. Paris. 39 (1): 429–434.
- Del Moral, Pierre; Guionnet, Alice (2001). "On the stability of interacting processes with applications to filtering and genetic algorithms". Annales de l'Institut Henri Poincaré. 37 (2): 155–194. Bibcode:2001AIHPB..37..155D. doi:10.1016/s0246-0203(00)01064-5.
- Ripley 1987
- ^ Sawilowsky 2003
- Kalos & Whitlock 2008
- Shojaeefard, M.H.; Khalkhali, A.; Yarmohammadisatri, Sadegh (2017). "An efficient sensitivity analysis method for modified geometry of Macpherson suspension based on Pearson Correlation Coefficient". Vehicle System Dynamics. 55 (6): 827–852. Bibcode:2017VSD....55..827S. doi:10.1080/00423114.2017.1283046. S2CID 114260173.
- Davenport 1992
- Route, Matthew (August 10, 2017). "Radio-flaring Ultracool Dwarf Population Synthesis". The Astrophysical Journal. 845 (1): 66. arXiv:1707.02212. Bibcode:2017ApJ...845...66R. doi:10.3847/1538-4357/aa7ede. S2CID 118895524.
- Vose 2008, p. 13.
- Vose 2008, p. 16.
- Jia, Xun; Ziegenhein, Peter; Jiang, Steve B (2014). "GPU-based high-performance computing for radiation therapy". Physics in Medicine and Biology. 59 (4): R151 – R182. Bibcode:2014PMB....59R.151J. doi:10.1088/0031-9155/59/4/R151. PMC 4003902. PMID 24486639.
- Hill, R.; Healy, B.; Holloway, L.; Kuncic, Z.; Thwaites, D.; Baldock, C. (March 2014). "Advances in kilovoltage x-ray beam dosimetry". Physics in Medicine and Biology. 59 (6): R183 – R231. Bibcode:2014PMB....59R.183H. doi:10.1088/0031-9155/59/6/R183. PMID 24584183. S2CID 18082594.
- Rogers, D.W.O. (2006). "Fifty years of Monte Carlo simulations for medical physics". Physics in Medicine and Biology. 51 (13): R287 – R301. Bibcode:2006PMB....51R.287R. doi:10.1088/0031-9155/51/13/R17. PMID 16790908. S2CID 12066026.
- Baeurle 2009
- Möller, W.; Eckstein, W. (March 1, 1984). "Tridyn — A TRIM simulation code including dynamic composition changes". Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms. 2 (1): 814–818. Bibcode:1984NIMPB...2..814M. doi:10.1016/0168-583X(84)90321-5.
- MacGillivray & Dodd 1982
- Golden 1979
- G. A. Bird, Molecular Gas Dynamics, Clarendon, Oxford (1976)
- Dietrich, S.; Boyd, I. (1996). "A Scalar optimized parallel implementation of the DSMC technique". Journal of Computational Physics. 126 (2): 328–42. Bibcode:1996JCoPh.126..328D. doi:10.1006/jcph.1996.0141.
- Chen, Shang-Ying; Hsu, Kuo-Chin; Fan, Chia-Ming (March 15, 2021). "Improvement of generalized finite difference method for stochastic subsurface flow modeling". Journal of Computational Physics. 429: 110002. Bibcode:2021JCoPh.42910002C. doi:10.1016/J.JCP.2020.110002. S2CID 228828681.
- Climate Change 2013 The Physical Science Basis (PDF). Cambridge University Press. 2013. p. 697. ISBN 978-1-107-66182-0. Retrieved July 6, 2023.
- Ojeda et al. 2009.
- Milik & Skolnick 1993.
- Cassey; Smith (2014). "Simulating confidence for the Ellison-Glaeser Index". Journal of Urban Economics. 81: 93. doi:10.1016/j.jue.2014.02.005.
- Sawilowsky & Fahoome 2003
- Spall, James C. (2005). "Monte Carlo Computation of the Fisher Information Matrix in Nonstandard Settings". Journal of Computational and Graphical Statistics. 14 (4): 889–909. CiteSeerX 10.1.1.142.738. doi:10.1198/106186005X78800. S2CID 16090098.
- Das, Sonjoy; Spall, James C.; Ghanem, Roger (2010). "Efficient Monte Carlo computation of Fisher information matrix using prior information". Computational Statistics & Data Analysis. 54 (2): 272–289. doi:10.1016/j.csda.2009.09.018.
- Chaslot, Guillaume; Bakkes, Sander; Szita, Istvan; Spronck, Pieter. "Monte-Carlo Tree Search: A New Framework for Game AI" (PDF). Sander.landofsand.com. Retrieved October 28, 2017.
- "Monte Carlo Tree Search - About". Archived from the original on November 29, 2015. Retrieved May 15, 2013.
- Chaslot, Guillaume M. J. -B; Winands, Mark H. M.; Van Den Herik, H. Jaap (2008). "Parallel Monte-Carlo Tree Search". Computers and Games. Lecture Notes in Computer Science. Vol. 5131. pp. 60–71. CiteSeerX 10.1.1.159.4373. doi:10.1007/978-3-540-87608-3_6. ISBN 978-3-540-87607-6.
- Bruns, Pete. Monte-Carlo Tree Search in the game of Tantrix: Cosc490 Final Report (PDF) (Report).
- Silver, David; Veness, Joel. "Monte-Carlo Planning in Large POMDPs" (PDF). 0.cs.ucl.ac.uk. Archived from the original (PDF) on July 18, 2016. Retrieved October 28, 2017.
- Lorentz, Richard J. (2011). "Improving Monte–Carlo Tree Search in Havannah". Computers and Games. Lecture Notes in Computer Science. Vol. 6515. pp. 105–115. Bibcode:2011LNCS.6515..105L. doi:10.1007/978-3-642-17928-0_10. ISBN 978-3-642-17927-3.
- Jakl, Tomas. "Arimaa challenge – comparison study of MCTS versus alpha-beta methods" (PDF). Arimaa.com. Retrieved October 28, 2017.
- Szirmay-Kalos 2008.
- "How the Coast Guard Uses Analytics to Search for Those Lost at Sea". Dice Insights. January 3, 2014.
- Stone, Lawrence D.; Kratzke, Thomas M.; Frost, John R. "Search Modeling and Optimization in USCG's Search and Rescue Optimal Planning System (SAROPS)" (PDF). Ifremer.fr. Retrieved October 28, 2017.
- "Project Risk Simulation (BETA)". risk.octigo.pl. Retrieved May 21, 2024.
- Carmona, René; Del Moral, Pierre; Hu, Peng; Oudjane, Nadia (2012). "An Introduction to Particle Methods with Financial Applications". In Carmona, René A.; Moral, Pierre Del; Hu, Peng; et al. (eds.). Numerical Methods in Finance. Springer Proceedings in Mathematics. Vol. 12. Springer Berlin Heidelberg. pp. 3–49. CiteSeerX 10.1.1.359.7957. doi:10.1007/978-3-642-25746-9_1. ISBN 978-3-642-25745-2.
- Kroese, D. P.; Taimre, T.; Botev, Z. I. (2011). Handbook of Monte Carlo Methods. John Wiley & Sons.
- Arenas, Daniel J.; Lett, Lanair A.; Klusaritz, Heather; Teitelman, Anne M. (2017). "A Monte Carlo simulation approach for estimating the health and economic impact of interventions provided at a student-run clinic". PLOS ONE. 12 (12): e0189718. Bibcode:2017PLoSO..1289718A. doi:10.1371/journal.pone.0189718. PMC 5746244. PMID 29284026.
- Elwart, Liz; Emerson, Nina; Enders, Christina; Fumia, Dani; Murphy, Kevin (December 2006). "Increasing Access to Restraining Orders for Low Income Victims of Domestic Violence: A Cost-Benefit Analysis of the Proposed Domestic Abuse Grant Program" (PDF). State Bar of Wisconsin. Archived from the original (PDF) on November 6, 2018. Retrieved December 12, 2016.
- Dahlan, Hadi Akbar (October 29, 2021). "Perbandingan Penerbitan dan Harga Buku Mengikut Genre di Malaysia dan Jepun Menggunakan Data Akses Terbuka dan Simulasi Monte Carlo" (PDF). Kajian Malaysia. 39 (2): 179–202. doi:10.21315/km2021.39.2.8. S2CID 240435973.
- ^ Press et al. 1996
- MEZEI, M (December 31, 1986). "Adaptive umbrella sampling: Self-consistent determination of the non-Boltzmann bias". Journal of Computational Physics. 68 (1): 237–248. Bibcode:1987JCoPh..68..237M. doi:10.1016/0021-9991(87)90054-4.
- Bartels, Christian; Karplus, Martin (December 31, 1997). "Probability Distributions for Complex Systems: Adaptive Umbrella Sampling of the Potential Energy". The Journal of Physical Chemistry B. 102 (5): 865–880. doi:10.1021/jp972280j.
- Del Moral, Pierre; Doucet, Arnaud; Jasra, Ajay (2006). "Sequential Monte Carlo samplers". Journal of the Royal Statistical Society, Series B. 68 (3): 411–436. arXiv:cond-mat/0212648. doi:10.1111/j.1467-9868.2006.00553.x. S2CID 12074789.
- Spall, J. C. (2003), Introduction to Stochastic Search and Optimization: Estimation, Simulation, and Control, Wiley, Hoboken, NJ. http://www.jhuapl.edu/ISSO
- Mosegaard & Tarantola 1995
- Tarantola 2005
- McCracken, D. D., (1955) The Monte Carlo Method, Scientific American, 192(5), pp. 90-97
- Elishakoff, I., (2003) Notes on Philosophy of the Monte Carlo Method, International Applied Mechanics, 39(7), pp.753-762
- Grüne-Yanoff, T., & Weirich, P. (2010). The philosophy and epistemology of simulation: A review, Simulation & Gaming, 41(1), pp. 20-50
Sources
- Anderson, Herbert L. (1986). "Metropolis, Monte Carlo and the MANIAC" (PDF). Los Alamos Science. 14: 96–108.
- Benov, Dobriyan M. (2016). "The Manhattan Project, the first electronic computer and the Monte Carlo method". Monte Carlo Methods and Applications. 22 (1): 73–79. doi:10.1515/mcma-2016-0102. S2CID 30198383.
- Baeurle, Stephan A. (2009). "Multiscale modeling of polymer materials using field-theoretic methodologies: A survey about recent developments". Journal of Mathematical Chemistry. 46 (2): 363–426. doi:10.1007/s10910-008-9467-3. S2CID 117867762.
- Berg, Bernd A. (2004). Markov Chain Monte Carlo Simulations and Their Statistical Analysis (With Web-Based Fortran Code). Hackensack, NJ: World Scientific. ISBN 978-981-238-935-0.
- Binder, Kurt (1995). The Monte Carlo Method in Condensed Matter Physics. New York: Springer. ISBN 978-0-387-54369-7.
- Caflisch, R. E. (1998). Monte Carlo and quasi-Monte Carlo methods. Acta Numerica. Vol. 7. Cambridge University Press. pp. 1–49.
- Davenport, J. H. (1992). "Primality testing revisited". Papers from the international symposium on Symbolic and algebraic computation - ISSAC '92. pp. 123–129. CiteSeerX 10.1.1.43.9296. doi:10.1145/143242.143290. ISBN 978-0-89791-489-5. S2CID 17322272.
- Doucet, Arnaud; Freitas, Nando de; Gordon, Neil (2001). Sequential Monte Carlo methods in practice. New York: Springer. ISBN 978-0-387-95146-1.
- Eckhardt, Roger (1987). "Stan Ulam, John von Neumann, and the Monte Carlo method" (PDF). Los Alamos Science (15): 131–137.
- Fishman, G. S. (1995). Monte Carlo: Concepts, Algorithms, and Applications. New York: Springer. ISBN 978-0-387-94527-9.
- C. Forastero and L. Zamora and D. Guirado and A. Lallena (2010). "A Monte Carlo tool to simulate breast cancer screening programmes". Phys. Med. Biol. 55 (17): 5213–5229. Bibcode:2010PMB....55.5213F. doi:10.1088/0031-9155/55/17/021. PMID 20714045. S2CID 30021759.
- Golden, Leslie M. (1979). "The Effect of Surface Roughness on the Transmission of Microwave Radiation Through a Planetary Surface". Icarus. 38 (3): 451–455. Bibcode:1979Icar...38..451G. doi:10.1016/0019-1035(79)90199-4.
- Gould, Harvey; Tobochnik, Jan (1988). An Introduction to Computer Simulation Methods, Part 2, Applications to Physical Systems. Reading: Addison-Wesley. ISBN 978-0-201-16504-3.
- Grinstead, Charles; Snell, J. Laurie (1997). Introduction to Probability. American Mathematical Society. pp. 10–11.
- Hammersley, J. M.; Handscomb, D. C. (1975). Monte Carlo Methods. London: Methuen. ISBN 978-0-416-52340-9.
- Hartmann, A.K. (2009). Practical Guide to Computer Simulations. World Scientific. ISBN 978-981-283-415-7. Archived from the original on February 11, 2009.
- Hubbard, Douglas (2007). How to Measure Anything: Finding the Value of Intangibles in Business. John Wiley & Sons. p. 46. ISBN 9780470110126.
- Hubbard, Douglas (2009). The Failure of Risk Management: Why It's Broken and How to Fix It. John Wiley & Sons.
- Kahneman, D.; Tversky, A. (1982). Judgement under Uncertainty: Heuristics and Biases. Cambridge University Press.
- Kalos, Malvin H.; Whitlock, Paula A. (2008). Monte Carlo Methods. Wiley-VCH. ISBN 978-3-527-40760-6.
- Kroese, D. P.; Taimre, T.; Botev, Z.I. (2011). Handbook of Monte Carlo Methods. New York: John Wiley & Sons. p. 772. ISBN 978-0-470-17793-8.
- MacGillivray, H. T.; Dodd, R. J. (1982). "Monte-Carlo simulations of galaxy systems". Astrophysics and Space Science. 86 (2): 419–435. doi:10.1007/BF00683346. S2CID 189849365.
- MacKeown, P. Kevin (1997). Stochastic Simulation in Physics. New York: Springer. ISBN 978-981-3083-26-4.
- Metropolis, N. (1987). "The beginning of the Monte Carlo method" (PDF). Los Alamos Science (1987 Special Issue dedicated to Stanislaw Ulam): 125–130.
- Metropolis, N.; Rosenbluth, Arianna W.; Rosenbluth, Marshall N.; Teller, Augusta H.; Teller, Edward (1953). "Equation of State Calculations by Fast Computing Machines". Journal of Chemical Physics. 21 (6): 1087. Bibcode:1953JChPh..21.1087M. doi:10.1063/1.1699114. OSTI 4390578. S2CID 1046577.
- Metropolis, N.; Ulam, S. (1949). "The Monte Carlo Method". Journal of the American Statistical Association. 44 (247): 335–341. doi:10.1080/01621459.1949.10483310. JSTOR 2280232. PMID 18139350.
- Milik, M.; Skolnick, J. (January 1993). "Insertion of peptide chains into lipid membranes: an off-lattice Monte Carlo dynamics model". Proteins. 15 (1): 10–25. doi:10.1002/prot.340150104. PMID 8451235. S2CID 7450512.
- Mosegaard, Klaus; Tarantola, Albert (1995). "Monte Carlo sampling of solutions to inverse problems" (PDF). J. Geophys. Res. 100 (B7): 12431–12447. Bibcode:1995JGR...10012431M. doi:10.1029/94JB03097. Archived from the original (PDF) on March 10, 2021. Retrieved November 1, 2017.
- Ojeda, P.; Garcia, M.; Londono, A.; Chen, N.Y. (February 2009). "Monte Carlo Simulations of Proteins in Cages: Influence of Confinement on the Stability of Intermediate States". Biophys. J. 96 (3): 1076–1082. Bibcode:2009BpJ....96.1076O. doi:10.1529/biophysj.107.125369. PMC 2716574. PMID 18849410.
- Int Panis, L.; De Nocker, L.; De Vlieger, I.; Torfs, R. (2001). "Trends and uncertainty in air pollution impacts and external costs of Belgian passenger car traffic". International Journal of Vehicle Design. 27 (1–4): 183–194. doi:10.1504/IJVD.2001.001963.
- Int Panis, L.; Rabl, A.; De Nocker, L.; Torfs, R. (2002). Sturm, P. (ed.). "Diesel or Petrol ? An environmental comparison hampered by uncertainty". Mitteilungen Institut für Verbrennungskraftmaschinen und Thermodynamik. Heft 81 Vol 1. Technische Universität Graz Austria: 48–54.
- Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (1996) . Numerical Recipes in Fortran 77: The Art of Scientific Computing. Fortran Numerical Recipes. Vol. 1 (2nd ed.). Cambridge University Press. ISBN 978-0-521-43064-7.
- Ripley, B. D. (1987). Stochastic Simulation. Wiley & Sons.
- Robert, C.; Casella, G. (2004). Monte Carlo Statistical Methods (2nd ed.). New York: Springer. ISBN 978-0-387-21239-5.
- Rubinstein, R. Y.; Kroese, D. P. (2007). Simulation and the Monte Carlo Method (2nd ed.). New York: John Wiley & Sons. ISBN 978-0-470-17793-8.
- Savvides, Savvakis C. (1994). "Risk Analysis in Investment Appraisal" (PDF). Project Appraisal Journal. 9 (1). doi:10.2139/ssrn.265905. S2CID 2809643.
- Sawilowsky, Shlomo S.; Fahoome, Gail C. (2003). Statistics via Monte Carlo Simulation with Fortran. Rochester Hills, MI: JMASM. ISBN 978-0-9740236-0-1.
- Sawilowsky, Shlomo S. (2003). "You think you've got trivials?". Journal of Modern Applied Statistical Methods. 2 (1): 218–225. doi:10.22237/jmasm/1051748460.
- Silver, David; Veness, Joel (2010). "Monte-Carlo Planning in Large POMDPs" (PDF). In Lafferty, J.; Williams, C. K. I.; Shawe-Taylor, J.; Zemel, R. S.; Culotta, A. (eds.). Advances in Neural Information Processing Systems 23. Neural Information Processing Systems 2010. Neural Information Processing Systems Foundation. Archived from the original (PDF) on May 25, 2012. Retrieved March 15, 2011.
- Szirmay-Kalos, László (2008). Monte Carlo Methods in Global Illumination - Photo-realistic Rendering with Randomization. VDM Verlag Dr. Mueller e.K. ISBN 978-3-8364-7919-6.
- Tarantola, Albert (2005). Inverse Problem Theory. Philadelphia: Society for Industrial and Applied Mathematics. ISBN 978-0-89871-572-9.
- Vose, David (2008). Risk Analysis, A Quantitative Guide (3rd ed.). John Wiley & Sons. ISBN 9780470512845.
- Mazhdrakov, Metodi; Benov, Dobriyan; Valkanov, Nikolai (2018). The Monte Carlo Method. Engineering Applications. ACMO Academic Press. ISBN 978-619-90684-3-4.
External links
 Media related to Monte Carlo method at Wikimedia Commons
Media related to Monte Carlo method at Wikimedia Commons


 .
.