In functional analysis and quantum information science, a positive operator-valued measure (POVM) is a measure whose values are positive semi-definite operators on a Hilbert space. POVMs are a generalization of projection-valued measures (PVM) and, correspondingly, quantum measurements described by POVMs are a generalization of quantum measurement described by PVMs (called projective measurements).
In rough analogy, a POVM is to a PVM what a mixed state is to a pure state. Mixed states are needed to specify the state of a subsystem of a larger system (see purification of quantum state); analogously, POVMs are necessary to describe the effect on a subsystem of a projective measurement performed on a larger system.
POVMs are the most general kind of measurement in quantum mechanics, and can also be used in quantum field theory. They are extensively used in the field of quantum information.
Definition
Let denote a Hilbert space and a measurable space with a Borel σ-algebra on . A POVM is a function defined on whose values are positive bounded self-adjoint operators on such that for every
is a non-negative countably additive measure on the σ-algebra and is the identity operator.
In quantum mechanics, the key property of a POVM is that it determines a probability measure on the outcome space, so that can be interpreted as the probability of the event when measuring a quantum state .
In the simplest case, in which is a finite set, is the power set of and is finite-dimensional, a POVM is equivalently a set of positive semi-definite Hermitian matrices that sum to the identity matrix,
A POVM differs from a projection-valued measure in that, for projection-valued measures, the values of are required to be orthogonal projections.
In the discrete case, the POVM element is associated with the measurement outcome , such that the probability of obtaining it when making a quantum measurement on the quantum state is given by
- ,
where is the trace operator. When the quantum state being measured is a pure state this formula reduces to
- .
The discrete case of a POVM generalizes the simplest case of a PVM, which is a set of orthogonal projectors that sum to the identity matrix:
The probability formulas for a PVM are the same as for the POVM. An important difference is that the elements of a POVM are not necessarily orthogonal. As a consequence, the number of elements of the POVM can be larger than the dimension of the Hilbert space they act in. On the other hand, the number of elements of the PVM is at most the dimension of the Hilbert space.
Naimark's dilation theorem
Main article: Naimark's dilation theorem- Note: An alternate spelling of this is "Neumark's Theorem"
Naimark's dilation theorem shows how POVMs can be obtained from PVMs acting on a larger space. This result is of critical importance in quantum mechanics, as it gives a way to physically realize POVM measurements.
In the simplest case, of a POVM with a finite number of elements acting on a finite-dimensional Hilbert space, Naimark's theorem says that if is a POVM acting on a Hilbert space of dimension , then there exists a PVM acting on a Hilbert space of dimension and an isometry such that for all ,
For the particular case of a rank-1 POVM, i.e., when for some (unnormalized) vectors , this isometry can be constructed as
and the PVM is given simply by . Note that here .
In the general case, the isometry and PVM can be constructed by defining , , and
Note that here , so this is a more wasteful construction.
In either case, the probability of obtaining outcome with this PVM, and the state suitably transformed by the isometry, is the same as the probability of obtaining it with the original POVM:
This construction can be turned into a recipe for a physical realisation of the POVM by extending the isometry into a unitary , that is, finding such that
for from 1 to . This can always be done.
The recipe for realizing the POVM described by on a quantum state is then to embed the quantum state in the Hilbert space , evolve it with the unitary , and make the projective measurement described by the PVM .
Post-measurement state
The post-measurement state is not determined by the POVM itself, but rather by the PVM that physically realizes it. Since there are infinitely many different PVMs that realize the same POVM, the operators alone do not determine what the post-measurement state will be. To see that, note that for any unitary the operators
will also have the property that , so that using the isometry
in the second construction above will also implement the same POVM. In the case where the state being measured is in a pure state , the resulting unitary takes it together with the ancilla to state
and the projective measurement on the ancilla will collapse to the state
on obtaining result . When the state being measured is described by a density matrix , the corresponding post-measurement state is given by
- .
We see therefore that the post-measurement state depends explicitly on the unitary . Note that while is always Hermitian, generally, does not have to be Hermitian.
Another difference from the projective measurements is that a POVM measurement is in general not repeatable. If on the first measurement result was obtained, the probability of obtaining a different result on a second measurement is
- ,
which can be nonzero if and are not orthogonal. In a projective measurement these operators are always orthogonal and therefore the measurement is always repeatable.
An example: unambiguous quantum state discrimination
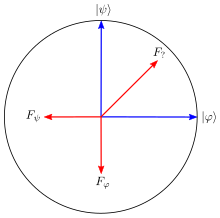
Suppose you have a quantum system with a 2-dimensional Hilbert space that you know is in either the state or the state , and you want to determine which one it is. If and are orthogonal, this task is easy: the set will form a PVM, and a projective measurement in this basis will determine the state with certainty. If, however, and are not orthogonal, this task is impossible, in the sense that there is no measurement, either PVM or POVM, that will distinguish them with certainty. The impossibility of perfectly discriminating between non-orthogonal states is the basis for quantum information protocols such as quantum cryptography, quantum coin flipping, and quantum money.
The task of unambiguous quantum state discrimination (UQSD) is the next best thing: to never make a mistake about whether the state is or , at the cost of sometimes having an inconclusive result. It is possible to do this with projective measurements. For example, if you measure the PVM , where is the quantum state orthogonal to , and obtain result , then you know with certainty that the state was . If the result was , then it is inconclusive. The analogous reasoning holds for the PVM , where is the state orthogonal to .
This is unsatisfactory, though, as you can't detect both and with a single measurement, and the probability of getting a conclusive result is smaller than with POVMs. The POVM that gives the highest probability of a conclusive outcome in this task is given by
where
Note that , so when outcome is obtained we are certain that the quantum state is , and when outcome is obtained we are certain that the quantum state is .
The probability of having a conclusive outcome is given by
when the quantum system is in state or with the same probability. This result is known as the Ivanović-Dieks-Peres limit, named after the authors who pioneered UQSD research.
Since the POVMs are rank-1, we can use the simple case of the construction above to obtain a projective measurement that physically realises this POVM. Labelling the three possible states of the enlarged Hilbert space as , , and , we see that the resulting unitary takes the state to
and similarly it takes the state to
A projective measurement then gives the desired results with the same probabilities as the POVM.
This POVM has been used to experimentally distinguish non-orthogonal polarisation states of a photon. The realisation of the POVM with a projective measurement was slightly different from the one described here.
See also
- SIC-POVM
- Quantum measurement
- Mathematical formulation of quantum mechanics
- Density matrix
- Quantum operation
- Projection-valued measure
- Vector measure
References
- Peres, Asher; Terno, Daniel R. (2004). "Quantum information and relativity theory". Reviews of Modern Physics. 76 (1): 93–123. arXiv:quant-ph/0212023. Bibcode:2004RvMP...76...93P. doi:10.1103/RevModPhys.76.93. S2CID 7481797.
- Davies, Edward Brian (1976). Quantum Theory of Open Systems. London: Acad. Press. p. 35. ISBN 978-0-12-206150-9.
- ^ M. Nielsen and I. Chuang, Quantum Computation and Quantum Information, Cambridge University Press, (2000)
- I. M. Gelfand and M. A. Neumark, On the embedding of normed rings into the ring of operators in Hilbert space, Rec. Math. N.S. 12(54) (1943), 197–213.
- ^ A. Peres. Quantum Theory: Concepts and Methods. Kluwer Academic Publishers, 1993.
- J. Preskill, Lecture Notes for Physics: Quantum Information and Computation, Chapter 3, http://theory.caltech.edu/~preskill/ph229/index.html
- J. Watrous. The Theory of Quantum Information. Cambridge University Press, 2018. Chapter 2.3, https://cs.uwaterloo.ca/~watrous/TQI/
- ^ J.A. Bergou; U. Herzog; M. Hillery (2004). "Discrimination of Quantum States". In M. Paris; J. Řeháček (eds.). Quantum State Estimation. Springer. pp. 417–465. doi:10.1007/978-3-540-44481-7_11. ISBN 978-3-540-44481-7.
- Chefles, Anthony (2000). "Quantum state discrimination". Contemporary Physics. 41 (6). Informa UK Limited: 401–424. arXiv:quant-ph/0010114v1. Bibcode:2000ConPh..41..401C. doi:10.1080/00107510010002599. ISSN 0010-7514. S2CID 119340381.
- Ivanovic, I.D. (1987). "How to differentiate between non-orthogonal states". Physics Letters A. 123 (6). Elsevier BV: 257–259. Bibcode:1987PhLA..123..257I. doi:10.1016/0375-9601(87)90222-2. ISSN 0375-9601.
- Dieks, D. (1988). "Overlap and distinguishability of quantum states". Physics Letters A. 126 (5–6). Elsevier BV: 303–306. Bibcode:1988PhLA..126..303D. doi:10.1016/0375-9601(88)90840-7. ISSN 0375-9601.
- Peres, Asher (1988). "How to differentiate between non-orthogonal states". Physics Letters A. 128 (1–2). Elsevier BV: 19. Bibcode:1988PhLA..128...19P. doi:10.1016/0375-9601(88)91034-1. ISSN 0375-9601.
- B. Huttner; A. Muller; J. D. Gautier; H. Zbinden; N. Gisin (1996). "Unambiguous quantum measurement of nonorthogonal states". Physical Review A. 54 (5). APS: 3783–3789. Bibcode:1996PhRvA..54.3783H. doi:10.1103/PhysRevA.54.3783. PMID 9913923.
- R. B. M. Clarke; A. Chefles; S. M. Barnett; E. Riis (2001). "Experimental demonstration of optimal unambiguous state discrimination". Physical Review A. 63 (4). APS: 040305(R). arXiv:quant-ph/0007063. Bibcode:2001PhRvA..63d0305C. doi:10.1103/PhysRevA.63.040305. S2CID 39481893.
- POVMs
- K. Kraus, States, Effects, and Operations, Lecture Notes in Physics 190, Springer (1983).
- A.S. Holevo, Probabilistic and statistical aspects of quantum theory, North-Holland Publ. Cy., Amsterdam (1982).
External links
| Spectral theory and -algebras | |
|---|---|
| Basic concepts | |
| Main results | |
| Special Elements/Operators | |
| Spectrum | |
| Decomposition | |
| Spectral Theorem | |
| Special algebras | |
| Finite-Dimensional | |
| Generalizations | |
| Miscellaneous | |
| Examples | |
| Applications |
|
| Functional analysis (topics – glossary) | |||||
|---|---|---|---|---|---|
| Spaces |
| ||||
| Theorems | |||||
| Operators | |||||
| Algebras | |||||
| Open problems | |||||
| Applications | |||||
| Advanced topics | |||||
| Analysis in topological vector spaces | |
|---|---|
| Basic concepts | |
| Derivatives | |
| Measurability | |
| Integrals | |
| Results | |
| Related | |
| Functional calculus | |
| Applications | |
 denote a
denote a  a
a  a
a  . A POVM is a function
. A POVM is a function  defined on
defined on 

 is the
is the  can be interpreted as the probability of the event
can be interpreted as the probability of the event  when measuring a
when measuring a  .
.
 that sum to the
that sum to the 
 is associated with the measurement outcome
is associated with the measurement outcome  , such that the probability of obtaining it when making a
, such that the probability of obtaining it when making a  is given by
is given by
 ,
, is the
is the  .
. that sum to the
that sum to the 
 of the POVM can be larger than the dimension of the Hilbert space they act in. On the other hand, the number of elements
of the POVM can be larger than the dimension of the Hilbert space they act in. On the other hand, the number of elements  of the PVM is at most the dimension of the Hilbert space.
of the PVM is at most the dimension of the Hilbert space.
 is a POVM acting on a Hilbert space
is a POVM acting on a Hilbert space  of dimension
of dimension  , then there exists a PVM
, then there exists a PVM  acting on a Hilbert space
acting on a Hilbert space  of dimension
of dimension  and an
and an  such that for all
such that for all 
 for some (unnormalized) vectors
for some (unnormalized) vectors  , this isometry can be constructed as
, this isometry can be constructed as

 . Note that here
. Note that here  .
.
 ,
,  , and
, and

 , so this is a more wasteful construction.
, so this is a more wasteful construction.

 into a unitary
into a unitary  , that is, finding
, that is, finding 
 the operators
the operators

 , so that using the isometry
, so that using the isometry

 , the resulting unitary
, the resulting unitary  takes it together with the ancilla to state
takes it together with the ancilla to state


 . When the state being measured is described by a density matrix
. When the state being measured is described by a density matrix  , the corresponding post-measurement state is given by
, the corresponding post-measurement state is given by
 .
. does not have to be Hermitian.
does not have to be Hermitian.
 on a second measurement is
on a second measurement is
 ,
, and
and  are not orthogonal. In a projective measurement these operators are always orthogonal and therefore the measurement is always repeatable.
are not orthogonal. In a projective measurement these operators are always orthogonal and therefore the measurement is always repeatable.
 and
and  . Note that on the Bloch sphere orthogonal states are antiparallel.
. Note that on the Bloch sphere orthogonal states are antiparallel. , and you want to determine which one it is. If
, and you want to determine which one it is. If  will form a PVM, and a projective measurement in this basis will determine the state with certainty. If, however,
will form a PVM, and a projective measurement in this basis will determine the state with certainty. If, however,  , where
, where  is the quantum state orthogonal to
is the quantum state orthogonal to  , then you know with certainty that the state was
, then you know with certainty that the state was  , then it is inconclusive. The analogous reasoning holds for the PVM
, then it is inconclusive. The analogous reasoning holds for the PVM  , where
, where  is the state orthogonal to
is the state orthogonal to 



 , so when outcome
, so when outcome  is obtained we are certain that the quantum state is
is obtained we are certain that the quantum state is  is obtained we are certain that the quantum state is
is obtained we are certain that the quantum state is 
 ,
,  , and
, and  , we see that the resulting unitary
, we see that the resulting unitary  takes the state
takes the state 
