| Order-6 octagonal tiling | |
|---|---|
 Poincaré disk model of the hyperbolic plane | |
| Type | Hyperbolic regular tiling |
| Vertex configuration | 8 |
| Schläfli symbol | {8,6} |
| Wythoff symbol | 6 | 8 2 |
| Coxeter diagram | |
| Symmetry group | , (*862) |
| Dual | Order-8 hexagonal tiling |
| Properties | Vertex-transitive, edge-transitive, face-transitive |
In geometry, the order-6 octagonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {8,6}.
Symmetry
This tiling represents a hyperbolic kaleidoscope of 8 mirrors meeting at a point and bounding regular octagon fundamental domains. This symmetry by orbifold notation is called *33333333 with 8 order-3 mirror intersections. In Coxeter notation can be represented as , removing two of three mirrors (passing through the octagon center) in the symmetry.
Uniform constructions
There are four uniform constructions of this tiling, three of them as constructed by mirror removal from the kaleidoscope. Removing the mirror between the order 2 and 6 points, , gives , (*883). Removing two mirrors as , leaves remaining mirrors (*444444).
| Uniform Coloring |

|

|

|
|
|---|---|---|---|---|
| Symmetry | (*862) |
= (*883) |
(*4232) |
(*444444) |
| Symbol | {8,6} | {8,6}1⁄2 | r(8,6,8) | |
| Coxeter diagram |
Related polyhedra and tiling
This tiling is topologically related as a part of sequence of regular tilings with octagonal faces, starting with the octagonal tiling, with Schläfli symbol {8,n}, and Coxeter diagram ![]()
![]()
![]()
![]()
![]() , progressing to infinity.
, progressing to infinity.
| Space | Spherical | Compact hyperbolic | Paracompact | |||||
|---|---|---|---|---|---|---|---|---|
| Tiling | 
|

|

|

|

|

|

| |
| Config. | 8.8 | 8 | 8 | 8 | 8 | 8 | 8 | ...8 |
| Regular tilings {n,6} | ||||||||
|---|---|---|---|---|---|---|---|---|
| Spherical | Euclidean | Hyperbolic tilings | ||||||
 {2,6} |
 {3,6} |
 {4,6} |
 {5,6} |
 {6,6} |
 {7,6} |
 {8,6} |
... |  {∞,6} |
| Uniform octagonal/hexagonal tilings | ||||||
|---|---|---|---|---|---|---|
| Symmetry: , (*862) | ||||||

|
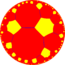
|

|

|

|

|

|
| {8,6} | t{8,6} |
r{8,6} | 2t{8,6}=t{6,8} | 2r{8,6}={6,8} | rr{8,6} | tr{8,6} |
| Uniform duals | ||||||

|

|

|

|

|

|

|
| V8 | V6.16.16 | V(6.8) | V8.12.12 | V6 | V4.6.4.8 | V4.12.16 |
| Alternations | ||||||
(*466) |
(8*3) |
(*4232) |
(6*4) |
(*883) |
(2*43) |
(862) |

|

|

| ||||
| h{8,6} | s{8,6} | hr{8,6} | s{6,8} | h{6,8} | hrr{8,6} | sr{8,6} |
| Alternation duals | ||||||

|
||||||
| V(4.6) | V3.3.8.3.8.3 | V(3.4.4.4) | V3.4.3.4.3.6 | V(3.8) | V3.4 | V3.3.6.3.8 |
See also
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
External links
- Weisstein, Eric W. "Hyperbolic tiling". MathWorld.
- Weisstein, Eric W. "Poincaré hyperbolic disk". MathWorld.
- Hyperbolic and Spherical Tiling Gallery
- KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
- Hyperbolic Planar Tessellations, Don Hatch
| Tessellation | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|   | ||||||||||||
| |||||||||||||
| |||||||||||||
| |||||||||||||