Truncated tetraheptagonal tiling

(Redirected from 742 symmetry) Hyperbolic tiling

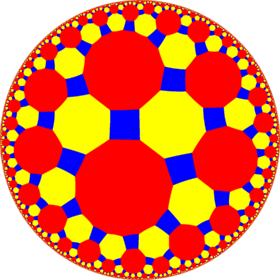Truncated tetraheptagonal tiling
Poincaré disk model of the hyperbolic plane
Type	Hyperbolic uniform tiling
Vertex configuration	4.8.14
Schläfli symbol	tr{7,4} or $t{\begin{Bmatrix}7\\4\end{Bmatrix}}$
Wythoff symbol	2 7 4 \|
Coxeter diagram
Symmetry group	, (*742)
Dual	Order-4-7 kisrhombille tiling
Properties	Vertex-transitive

In geometry, the truncated tetraheptagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of tr{4,7}.

Images

Poincaré disk projection, centered on 14-gon:

Symmetry

The dual to this tiling represents the fundamental domains of (*742) symmetry. There are three small index subgroups constructed from by mirror removal and alternation. In these images fundamental domains are alternately colored black and white, and mirrors exist on the boundaries between colors.

Small index subgroups of (*742)
Index	1	2		14
Diagram
Coxeter (orbifold)	= (*742)	= = (*772)	= (7*2)	= (*2222222)
Index	2	4		28
Diagram
Coxeter (orbifold)	= (742)	= = (772)		= (2222222)

Related polyhedra and tiling

Uniform heptagonal/square tilings v t e
Symmetry: , (*742)							, (742)	, (7*2)	, (*772)


{7,4}	t{7,4}	r{7,4}	2t{7,4}=t{4,7}	2r{7,4}={4,7}	rr{7,4}	tr{7,4}	sr{7,4}	s{7,4}	h{4,7}
Uniform duals


V7	V4.14.14	V4.7.4.7	V7.8.8	V4	V4.4.7.4	V4.8.14	V3.3.4.3.7	V3.3.7.3.7	V7

*n42 symmetry mutation of omnitruncated tilings: 4.8.2n v t e
Symmetry *n42	Spherical		Euclidean	Compact hyperbolic				Paracomp.
Symmetry *n42	*242	*342	*442	*542	*642	*742	*842 ...	*∞42
Omnitruncated figure	4.8.4	4.8.6	4.8.8	4.8.10	4.8.12	4.8.14	4.8.16	4.8.∞
Omnitruncated duals	V4.8.4	V4.8.6	V4.8.8	V4.8.10	V4.8.12	V4.8.14	V4.8.16	V4.8.∞

*nn2 symmetry mutations of omnitruncated tilings: 4.2n.2n v t e
Symmetry *nn2	Spherical		Euclidean	Compact hyperbolic				Paracomp.
Symmetry *nn2	*222	*332	*442	*552	*662	*772	*882 ...	*∞∞2
Figure
Config.	4.4.4	4.6.6	4.8.8	4.10.10	4.12.12	4.14.14	4.16.16	4.∞.∞
Dual
Config.	V4.4.4	V4.6.6	V4.8.8	V4.10.10	V4.12.12	V4.14.14	V4.16.16	V4.∞.∞

References

John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
"Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.

External links

Tessellation

Periodic
Pythagorean Rhombille Schwarz triangle Rectangle Domino Uniform tiling and honeycomb Coloring Convex Kisrhombille Wallpaper group Wythoff

Aperiodic
Ammann–Beenker Aperiodic set of prototiles List Einstein problem Socolar–Taylor Gilbert Penrose Pinwheel Quaquaversal Rep-tile and Self-tiling Sphinx Socolar Truchet

Other
Anisohedral and Isohedral Architectonic and catoptric Circle Limit III Computer graphics Honeycomb Isotoxal List Packing Pentagonal Problems Domino Wang Heesch's Squaring Dividing a square into similar rectangles Prototile Conway criterion Girih Regular Division of the Plane Regular grid Substitution Voronoi Voderberg

By vertex type

Spherical	2 3.n V3.n 4.n V4.n
Regular	2 3 4 6
Semi- regular	3.4.3.4 V3.4.3.4 3.4 3.∞ 3.6 V3.6 3.4.6.4 (3.6) 3.12 4.∞ 4.6.12 4.8
Hyper- bolic	3.4.3.5 3.4.3.6 3.4.3.7 3.4.3.8 3.4.3.∞ 3.5.3.5 3.5.3.6 3.6.3.6 3.6.3.8 3.7.3.7 3.8.3.8 3.4.3.4 3.∞.3.∞ 3.7 3.8 3.∞ 3.4 3 3 3 (3.4) (3.4) 3.4.6.4 3.4.7.4 3.4.8.4 3.4.∞.4 3.6.4.6 (3.7) (3.8) 3.14 3.16 3.∞ 4.5.4 4.6.4 4.7.4 4.8.4 4.∞.4 4 4 4 4 4 (4.5) (4.6) 4.6.12 4.6.14 V4.6.14 4.6.16 V4.6.16 4.6.∞ (4.7) (4.8) 4.8.10 V4.8.10 4.8.12 4.8.14 4.8.16 4.8.∞ 4.10 4.10.12 4.12 4.12.16 4.14 4.16 4.∞ 5 5 5 5 5.4.6.4 (5.6) 5.8 5.10 5.12 6 6 6 6 6.4.8.4 (6.8) 6.8 6.10 6.12 6.16 7 7 7 7.6 7.8 7.14 8 8 8 8 8.6 8.12 8.16 ∞ ∞ ∞ ∞ ∞.6 ∞.8

This hyperbolic geometry-related article is a stub. You can help Misplaced Pages by expanding it.

Categories:

Images

Symmetry

Related polyhedra and tiling

References

See also

External links